International Journal of Astronomy and Astrophysics
Vol.05 No.02(2015), Article ID:57070,9 pages
10.4236/ijaa.2015.52014
Time-Frequency Analysis of Asymmetric Triaxial Galaxy Model Including Effect of Spherical Dark Halo Component
Beena R. Gupta1, Vinay Kumar2*
1Department of Mathematics, Lakshmibai College, University of Delhi, New Delhi, India
2Department of Mathematics, Zakir Husain Delhi College, University of Delhi, New Delhi, India
Email: beenaguptalbc@gmail.com, *krvinayaidso@yahoo.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 31 March 2015; accepted 8 June 2015; published 11 June 2015
ABSTRACT
A method of time-frequency analysis (TFA) based on wavelets is applied to study the phase space structure of three-dimensional asymmetric triaxial galaxy enclosed by spherical dark halo component. The investigation is carried out in the presence and absence of dark halo component. Time-frequency analysis is based on the extraction of instantaneous frequency from the phase of the continuous wavelet transform. This method is comparatively fast and reliable. This method can differentiate periodic from quasi-periodic, chaotic sticky from chaotic non-sticky, ordered from chaotic and also, it can accurately determine the time interval of the resonance trapping and transitions too. Apart from that, the phenomenon of transient chaos can be explained with the help of time-frequency analysis. Comparison with the method of total angular momentum (denoted as Ltot) proposed recently is also presented.
Keywords:
Time-Frequency Analysis, Triaxial Galactic Potential, Instantaneous Frequency, Total Angular Momentum

1. Introduction
We know that the phase space of nonlinear dynamical systems consists of periodic, quasi-periodic and chaotic trajectories. Chaotic trajectories visit resonance islands, remain there for some time and then escape to the chaotic region during its evolution. To know the time interval of resonance trapping and resonance transition and to visualize the phenomenon of transient chaos are some important questions which compel us to study more about the application of different chaos indicators. Over the last few years, several chaos indicators have been introduced to study those aspects. Moreover, for dynamical system of two degrees of freedom, there are several chaos indicators such as the Poincare Surface of Section (PSS), Largest Lyapunov Characteristic Exponent (LLCE), Smaller Alignment Index (SALI). Fast Liapunov Indicators (FLI), the Generalized Alignment Index (GALI) and the Correlation Dimension (CD) (see [1] -[3] ). Visualization of the Poincare surfaces of section (PSS) is very useful for the study of the dynamical system of two degrees of freedom. But in case of three degrees of freedom, it becomes four-dimensional which is difficult to analyze. On the other hand, other indicators mentioned above require the solution of equations of motion and the first order variational equations whose computation is not easy in case of higher dimensional systems. Also, they do not tell about additional qualitative features like whether a trajectory is resonant or non-resonant. Recently in [4] , a new indicator 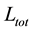 (i.e. Total angular momentum) is introduced to study the ordered and chaotic motion of the asymmetric triaxial galaxy, including the effect of spherical dark halo components.
(i.e. Total angular momentum) is introduced to study the ordered and chaotic motion of the asymmetric triaxial galaxy, including the effect of spherical dark halo components.  (TAM) is used to describe the nature of orbits in this potential and is proved to be a fast and reliable indicator in comparison to a Lyapunov characteristic exponent and P(f)-indicator. The method of total angular momentum can distinguish regular trajectory from chaotic. But there is no clarity about the other aspects such as stickiness, resonance trapping and transition and transient chaos, which must be investigated. In [4] , the effect of dark halo component in the chaotic region is shown with the help of the Poincare surface of section by reducing the three-dimensional galactic model to two dimensions. Time-frequency analysis based on the extraction of instantaneous frequency from wavelet transform is computed via two ways. The first method is the computation of instantaneous frequency of the phase of continuous wavelet transform (CWT) and the second method is based on the computation of instantaneous frequency from the amplitude of the continuous wavelet transform. The amplitude-based method is very well described in [5] . Characterization of the phase space of standard map and the Hamiltonian of the hydrogen atom (moving in crossed magnetic and elliptically polarized microwave fields) is presented using this method. On the other hand, phase-based approach is already explained in [6] - [9] . In [10] , we can see the application of the phase-based approach to the circular restricted three-body problem (Sun-Jupiter system) to explain the phenomenon of resonance transition and transport condition. The phenomenon of resonance trapping of chaotic trajectory, resonance transition and transient chaos (time dependent system causes an orbit move from regular to chaos and vice-versa (see [11] ) can be computed and visualized with the help of TFA. Identification between regular and chaotic, periodic and quasi-periodic, chaotic sticky and chaotic non-sticky is possible with the help of TFA. Also, the computational time for TFA is negligible as compared to other chaos indicators. The aim of this paper is two folded. The first is to establish the method of time-frequency analysis in comparison to total angular momentum. The second is to investigate and characterize the phase space structure of asymmetric triaxial galaxies in the presence and absence of spherical dark halo components.
(TAM) is used to describe the nature of orbits in this potential and is proved to be a fast and reliable indicator in comparison to a Lyapunov characteristic exponent and P(f)-indicator. The method of total angular momentum can distinguish regular trajectory from chaotic. But there is no clarity about the other aspects such as stickiness, resonance trapping and transition and transient chaos, which must be investigated. In [4] , the effect of dark halo component in the chaotic region is shown with the help of the Poincare surface of section by reducing the three-dimensional galactic model to two dimensions. Time-frequency analysis based on the extraction of instantaneous frequency from wavelet transform is computed via two ways. The first method is the computation of instantaneous frequency of the phase of continuous wavelet transform (CWT) and the second method is based on the computation of instantaneous frequency from the amplitude of the continuous wavelet transform. The amplitude-based method is very well described in [5] . Characterization of the phase space of standard map and the Hamiltonian of the hydrogen atom (moving in crossed magnetic and elliptically polarized microwave fields) is presented using this method. On the other hand, phase-based approach is already explained in [6] - [9] . In [10] , we can see the application of the phase-based approach to the circular restricted three-body problem (Sun-Jupiter system) to explain the phenomenon of resonance transition and transport condition. The phenomenon of resonance trapping of chaotic trajectory, resonance transition and transient chaos (time dependent system causes an orbit move from regular to chaos and vice-versa (see [11] ) can be computed and visualized with the help of TFA. Identification between regular and chaotic, periodic and quasi-periodic, chaotic sticky and chaotic non-sticky is possible with the help of TFA. Also, the computational time for TFA is negligible as compared to other chaos indicators. The aim of this paper is two folded. The first is to establish the method of time-frequency analysis in comparison to total angular momentum. The second is to investigate and characterize the phase space structure of asymmetric triaxial galaxies in the presence and absence of spherical dark halo components.
We have organized the paper as follows:
In Section 2, we have given a brief description of asymmetric triaxial galaxy enclosed by spherical dark halo component (3D). In Section 3, a brief description of TFA based on the phase of CWT and its implementation in Matlab are given. Results and discussion based on the application of TFA to the three-dimensional galactic model are shown in Section 4. The conclusion is given in Section 5.
2. Triaxial Galaxy Enclosed by Spherical Dark Halo Component in 3D
The potential for triaxial galaxy enclosed by spherical dark halo (see [4] ) component is given by
 (1)
(1)
where
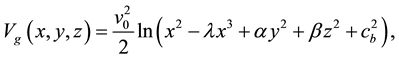 (2)
(2)
and
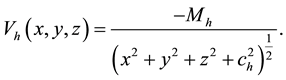 (3)
(3)
Equation (2) denotes a triaxial galaxy with a bulge and a small asymmetry introduced by the term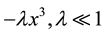 . The parameters
. The parameters  and
and 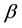 denote the flattening of the galaxy and
denote the flattening of the galaxy and 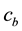 denotes the scale length of the bulge of the galaxy. The parameter
denotes the scale length of the bulge of the galaxy. The parameter  is used for consistency of galaxy units. Equation (3) presents a spherical dark halo component. Here
is used for consistency of galaxy units. Equation (3) presents a spherical dark halo component. Here 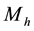 and
and 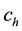 are the mass and the scale length of the dark halo com- ponent, respectively. Equations (1), (2) and (3) together represents the three-dimensional galactic model. Now we can write the equations of motion as follows,
are the mass and the scale length of the dark halo com- ponent, respectively. Equations (1), (2) and (3) together represents the three-dimensional galactic model. Now we can write the equations of motion as follows,
 (4)
(4)
The Hamiltonian of the potential given by Equation (1) can be expressed as
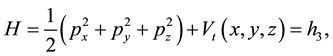 (5)
(5)
where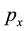 ,
,  and
and 



where 
Unit of length = 1 kpc;
Unit of mass = 2.325 ´ 107 Me;
Unit of time = 0.97748 ´ 108 yr;
Unit of velocity = 10 km×s-1;
Unit of energy (per unit mass) = 100 km2×s-2;
G = 1 (gravitational constant).
While integrating the equations of motion in (4) for the computation of all the orbits, we use the fixed value of 



3. Total Angular Momentum and Time-Frequency Analysis Based on Wavelets
3.1. Total Angular Momentum
Total angular momentum for a star of mass 

where



Note: 
3.2. Time-Frequency Analysis Based on Wavelets
Time-frequency analysis based on phase of continuous wavelet transform is described in this Section. At first we define continuous wavelet transform, instantaneous frequency and the mother wavelet. The continuous wavelet transform is defined in terms of

The function 






Here, 

Note: The parameter 


serves the purpose. Here due to the part 
ing to frequency. Due to this unique feature i.e. capability of adaptation of time window according to frequency range gives better localization in frequency and time.
3.3. Instantaneous Frequency and Ridge-Plot
Let us consider an analytic signal 


Now it’s unique polar representation is
where
and
where R and Im denote the real and imaginary part of the signal. Also a unique representation of 
Instantaneous frequency is defined as
The Ridge of the wavelet transform of



3.4. Implementation of Wavelet-Ridges in Matlab
The algorithm for computing ridges from the phase of continuous wavelet transform is already explained in [6] , [7] and [9] . Programs based on the algorithm for finding Ridge-plot can be made with the help of Wavelab routines written in Matlab (see [12] - [14] ). Computation of CWT is done by Wavelab routines written in Matlab. Stepwise procedure for finding Ridge-plot is given in Figure 1. The value of

4. Results and Discussion (Applicaion to Three Dimensional Triaxial Galaxy model)
In this Section, we analyze the data of Table 1 and Table 2 and discuss the plots obtained by integrating the
Figure 1. Procedure for finding instantaneous frequency (i.e. wavelet ridges) from the solution of equations of motion.
Table 1. Sample of five orbits for the triaxial galaxy model in presence of dark halo component and the corresponding results. The approximate C.P.U time for the execution of the programme for Ltot and Ridge-plot on the computer is given in second.
equation of motion (4) at the given initial conditions using Runge-Kutta (4/5) variable step-size Integrator. Phase-portrait and 
Table 2. Sample of orbits of the triaxial galaxy model in the absence of dark halo component and the corresponding results. The C.P.U time for the execution of the program for Ltot-plot and Ridge-plot on the computer are given in seconds.
At first, we discuss the results obtained using the Poincare surface of section in Figure 2. “Section condition” taken for the Poincare plot is 



We have selected a sample of five representative orbits for both cases. Time interval considered for the TFA is (1, 32768) except two figures (Figure 3 and Figure 4). For Figure 3 and Figure 4, the interval of time unit is taken as (1, 65536) to present the results in a better way. It adds an additional expense of eighteen seconds in the C.P.U time for the execution of the program. In Figure 5 and Figure 6, we consider the orbits at initial conditions (−9.55, 0, 0.1, 0, 5.8029, 0) and (−7.5, 0, −1, 0, 7.4008, 0) respectively. In Ridge-plots of both figures, we notice a completely flat Ridge throughout the motion. We know that frequency remains constant for the periodic orbit and hence both orbits are periodic.
Note: In [4] , at same initial condition (−9.55, 0, 0.1, 0, 5.8029, 0) the orbit is termed as quasiperiodic on the basis of 

Sample of orbits considered in Figure 7 and Figure 8 is at initial conditions (5.5, 0, 0.6, 0, 20.4251, 0) and (3, 0, 0.5, 0, 20.5996, 0) respectively. We observe a very little variation in Ridge curve (or instantaneous frequency) of both figures. In the plots of


Now we consider the orbits at initial conditions (−0.5, 0, 0.85, 0, 27.9848, 0) and (0.1, 0, 0.5, 0, 24.5701, 0) are shown in Figure 9 and Figure 10 respectively. If we look at both Ridge-plots, we can say that the trajectories are chaotic in nature. Also, highly asymmetric features and large deviation between maxima and between minima of 

Now, we consider the sample of trajectories at initial conditions (−0.9, 0, 0.85, 0, 27.6788, 0) and (1.7, 0, −1, 0, 22.2880, 0) presented in Figure 11 and Figure 12 respectively. If we look at 
Figure 2. Poincare surface of sections of triaxial galaxy model in presence (left side) and absence (right side) of dark halo component with parameteric values (Mh = 10000, Ch = 18, H = 68) and (Mh = 0, Ch = 8, H = 516) respectively.
Figure 3. Phase portrait (extreme left), Ltot-plot (middle) and Ridge-plot (extreme right) of a transient trajectory in presence of dark halo component at initialcondition (0.7, 0, 0.85, 0, 27.8624, 0).
Figure 4. Phase portrait (extreme left), Ltot-plot (middle) and Ridge-plot (extreme right) of a trajectory presenting transient chaos and resonance transition in absence of dark halo component at initial condition (0.01, 0, 0.1, 0,24.8801, 0).
Figure 5. Phase portrait (extreme left), Ltot-plot (middle) and Ridge-plot (extreme right) of a periodic trajectory in presence of dark halo component at initial condition (−9.55, 0, 0.1, 0, 5.8029, 0).
Figure 6. Phase portrait (extreme left), Ltot-plot (middle) and Ridge-plot (extreme right) of a periodic trajectory in absence of dark halo component at initial condition (−7.5, 0, −1, 0, 7.4008, 0).
Figure 7. Phase portrait (extreme left), Ltot-plot (middle) and Ridge-plot (extreme right) of a quasi-periodic trajectory in presence of dark halo component at initial condition (5.5, 0, 0.6, 0, 20.4251, 0).
Figure 8. Phase portrait (extreme left), Ltot-plot (middle) and Ridge-plot (extreme right) of a quasi-periodic trajectory in absence of dark halo component at initial condition (3, 0, 0.5, 0, 20.5996, 0).
Figure 9. Phase portrait (extreme left), Ltot-plot (middle) and Ridge-plot (extreme right) of a chaotic sticky trajectory in presence of dark halo component at initial condition (−0.5, 0, 0.85, 0, 27.9848, 0).
as chaotic non-sticky.
At last, we consider sample of two orbits at initial conditions (0.7, 0, 0.85, 0, 27.8624, 0) and (0.01, 0, 0.1, 0, 24.8801, 0) shown in Figure 3 and Figure 4 respectively. Again in the plots of
Figure 10. Phase portrait (extreme left), Ltot-plot (middle) and Ridge-plot (extreme right) of a chaotic sticky trajectory in absence of dark halo component at initial condition (0.1, 0, 0.5, 0, 24.5701, 0).
Figure 11. Phase portrait (extreme left), Ltot-plot (middle) and Ridge-plot (extreme right) of a chaotic non-sticky trajectory in presence of dark halo component at initial condition (−0.9, 0, 0.85, 0, 27.6788, 0).
Figure 12. Phase portrait (extreme left), Ltot-plot (middle) and Ridge-plot (extreme right) of a chaotic non-sticky trajectory in absence of dark halo component at initial condition (1.7, 0, −1, 0, 22.2880, 0).
phenomenon as in the previous case and hence we can say that these trajectories are chaotic. But in case of Ridge-plots scene is little different. We observe following things in the Ridge-plots:
1) Resonance trapping: In Figure 3 at time intervals (0, 13000), (19000, 25000) and (50000, 60000) approx we find a little variation in the frequency and besides that there is rapid change in frequency. Similarly, in Figure 4 at time intervals (0, 5000), (10000, 15000), (25000, 32000) and (41000, 60000) there is very little change in instantaneous frequency and besides that rapid change in frequency takes place. This is the case of resonance trapping which can be visualized and also accurately determined with the help of TFA.
2) Resonance transition: In Figure 4, we notice that at time unit 42,000 approx there is a jump from one type of resonance to another type of resonance and remains there for approx 18,000-time units. This phenomenon is known as resonance transition which is clearly observed in the Ridge-plot.
3) Transient Chaos: We know that in a time-dependent system a chaotic trajectory move from regular to chaos and vice versa (see [11] ). We call this phenomenon as transient chaos. We can visualize this phenomenon in the Ridge-plots.
5. Conclusions
As we have already discussed, the aim of the present work is to show the advantage of TFA in comparison to TFA and to explore some additional information of phase space structures of asymmetric triaxial galaxies in the presence and absence of the spherical dark halo component. Based on the discussion of Section 4, we can conclude that TFA has several advantages in comparison to TAM. We conclude following things:
1) TFA based on wavelets is comparatively fast and more reliable in comparison to TAM (C.P.U time taken for the computation of Ridge-plots for 32,768-time units is 15 seconds (maximum) whereas the time taken by TAM for 150-time units is 5 seconds (maximum)).
2) TFA can identify between periodic and quasi-periodic, chaotic sticky and non-sticky, and ordered and chaotic motion.
3) With the help of TFA, we can accurately determine and also visualize the event of trapping of a chaotic trajectory around resonance island (see Figure 3 and Figure 4).
4) The phenomenon of resonance transition and transient chaos can also be explained with the help of Ridge-plot (see Figure 3 and Figure 4).
5) Computational effort needed for programming of TFA based on wavelets is not easy in comparison to TAM. This is an important drawback of TFA based on wavelets. But once it is done, we can perform other computational works in comparatively negligible time.
6) We always search for an indicator which is applicable to higher-dimensional nonlinear dynamical systems. TFA is independent of the degree of freedom and requires the only solution of equations of motion which can be computed. Our present work is also an important example of the application to higher dimensional systems.
Thus, we can say that Time-frequency analysis based on wavelets can be given preference for the study of nonlinear dynamical systems for two or more degrees of freedom.
References
- Racoveanu, O. (2014) Comparison of Chaos Detection Methods in the Circular Restricted Three-Body Problem. Astronomische Nachrichten, 335, 877-885. http://dx.doi.org/10.1002/asna.201212110
- Smith, R.H. (1991) The Onset of Chaotic Motion in the Restricted Problem of Three Bodies. Ph.D. Thesis, University of Texas at Austin, Austin.
- Manos, T., Skokos, C.H. and Antonopoulos, C.H. (2008) Probing the Local Dynamics of Periodic Orbits by the Generalized Alignment Index (GALI) Method. International Journal of Bifurcation and Chaos, 22, 1-17. http://arxiv.org/pdf/1103.0700v3
- Caranicolas, N.D. and Zotos, E.E. (2011) Dark Halos Acting as Chaos Controllers in Asymmetric Triaxial Galaxy Models. Research in Astronomy and Astrophysics, 11, 811-823. http://dx.doi.org/10.1088/1674-4527/11/7/006
- Chandre, C., Wiggins, S. and Uzer, T. (2003) Time-Frequency Analysis of Chaotic Systems. Physica D, 181, 171-196.
- Deplart, N., Escudie, B., Guillemain, P., Kronland Martinet, R., Tchamichian, P. and Torresani, B. (1992) Asymptotic Wavelet and Gabor Analysis, Extraction of Instantaneous Frequency. IEEE Transactions on Information Theory, 38, 644-664.
- Vela-Arevalo, L.V. (2002) Time-Frequency Analysis Based on Wavelets for Hamiltonian Systems. Ph.D. Dissertation, California Institute of Technology, Pasadena. http://resolver.caltech.edu/CaltechETD:etd-03302004-115559
- Vela-Arevalo, L.V. and Wiggins, S. (2001) Time-Frequency Analysis of Classical Trajectories of Polyatomic Molecules. International Journal of Bifurcation and Chaos, 11, 1359-1380. http://dx.doi.org/10.1142/S0218127401002766
- Todorovska, M. (2001) Estimation of Instantaneous Frequency of Signals Using the Continuous Wavelet Transform. Department of Civil Engineering, University of Southern California, Report CE 01-07, 2001.
- Vela-Arevalo, L.V. (2004) Time-Frequency Analysis of the Restricted Three-Body Problem: Transport and Resonance Transitions. Classical and Quantum Gravity, 21, S351-S375.
- Kandrup, H.H., Vass, I.M. and Sideris, I.V. (2003) Transient Chaos and Resonant Phase Mixing in Violent Relaxation. Monthly Notice of the Royal Astronomical Society, 341, 927-936. http://dx.doi.org/10.1046/j.1365-8711.2003.06466.x
- http://www-stat.stanford.edu/~wavelab/
- The MathWorks, Inc. (2010) Matlab and Statistics Toolbox Release. The MathWorks, Inc., Natick.
- Mallat, S. (1999) A Wavelet Tour of Signal Processing. Academic Press, San Diego.
NOTES
*Corresponding author.






















