International Journal of Astronomy and Astrophysics
Vol.05 No.04(2015), Article ID:62225,11 pages
10.4236/ijaa.2015.54032
Distribution of Mass and Energy in Closed Model of the Universe
Fadel A. Bukhari
Department of Astronomy, Faculty of Science, King Abdulaziz University, Jeddah, Saudi Arabia

Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 2 February 2015; accepted 21 December 2015; published 25 December 2015
ABSTRACT
The universe’s horizon distance and volume are constructed in the closed cosmic model. The universe horizon distance distribution increases constantly for t < tme and decreases for t > tme. However, the universe’s horizon volume shows a sudden reduction in the range t = 0.5 Gyr − tme due to the change of the universe space from flat to curved then closed in the interval 15.1261 Gyr ≤ t ≤ tme. On the other hand, this distribution exhibits an abrupt rise in the range t = tme − t* due to the change of the universe space from closed then curved to flat in the interval 39.3822 ≤ t ≤ 40.7521 Gyr. The mass of radiation, matter and dark energy within the horizon volume of the universe are also investigated. These distributions reveal similar noticeable changes as the universe’s horizon volume distribution for the same reasons. The mass of radiation dominates up to t = 53221.5 yr, then the mass of matter becomes larger. Afterwards, both distributions of radiation and matter decrease while the distribution of dark energy rises until t = 10.1007 Gyr, where the mass of dark energy prevails up to t = tme. Hence, the distribution of dark energy reduces until t = 40.2892 Gyr, where the mass of matter becomes prominent again. At t = 53.6246 Gyr the masses of both matter and radiation become appreciably high such that the intercluster space will vanish and clusters of galaxies interfere with each other. Furthermore, not only the intergalactic medium will disappear, but also galaxies will collide and merge with each other to form extremely dense and close cosmological bodies. These very dense bodies will undergo further successive collisions and mergers under the action of central gravity, where the interstellar medium will vanish and the universe would develop to big crunch at tbc = 53.6251 Gyr. It is interesting to note that the horizon distance of the universe in the closed model at t = tme is in very good agreement with the maximum horizon distances in the five general cosmic models.
Keywords:
Dark Energy, Radiation, Closed Cosmic Model

1. Introduction
The distribution of density parameters of radiation, matter and dark energy in the closed cosmic model were investigated in a previous study [1] , where we discovered the main epochs of the universe history in this model. It is worthy now to study the distributions of equivalent mass of radiation, mass of matter and equivalent mass of dark energy within the horizon volume of the universe to get deeper sight of the universe evolution in the closed model.
The reason for considering the equivalent mass of radiation in this study is the significant value of the radiation density parameter in the early universe and before the big crunch as we have seen in [1] .
Therefore, it is vital to develop the distributions of the horizon distance and horizon volume of the universe in the closed model at various time ranges depending on the bases presented in [2] . Description of methodology is illustrated in Section 2, while algorithm would be shown in Section 3. Results and discussion are displayed in Section 4. Conclusion is given in Section 5.
2. Methodology
It is obvious from [2] that the horizon distance and horizon volume of the universe in closed cosmic model at the present time are respectively
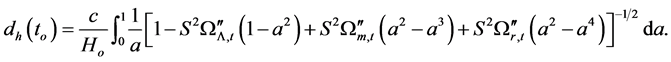 (1)
(1)
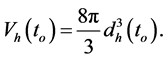 (2)
(2)
where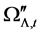 ,
, 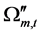 and
and  are given by
are given by
 (3)
(3)
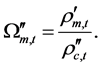 (4)
(4)
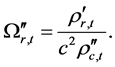 (5)
(5)
 (6)
(6)
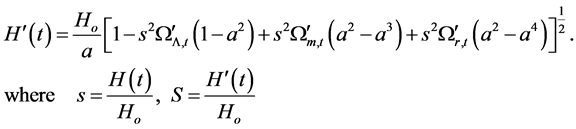 (7)
(7)
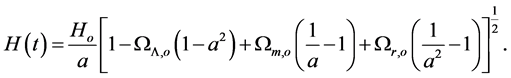 (8)
(8)
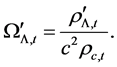 (9)
(9)
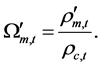 (10)
(10)
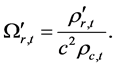 (11)
(11)
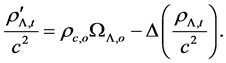 (12)
(12)



where t is the cosmic time in Gyr.

The horizon distance of the universe in the closed cosmic model at any given time is given by

Consequently, the change in the horizon distance of the universe in the time interval between two instants of scale factors 

The horizon volume of the universe in the closed model at any given time is expressed as

Equation (18) indicates that the horizon volume of the universe at t is a function of 

(1) Flat space (
We have seen in [2] that the horizon volume of the universe at time t in this case is given by

Therefore, it is obvious from Table 3 in [1] that Equation (19) is used in the time intervals



(2) Closed space (
We recall the equation of proper distance of extragalactic object

where

And the volume of space within 

where 


Hence Equation (22) gives

Assume

Substituting by (25) in (24) we get

Let

Substituting by (27) in (26) we have

Substituting by (23) in (28) yields

Suppose


Thus, the horizon volume of the universe in the closed cosmic model at time t in this case is expressed as

It is evident form Table 3 in [1] that Equation (23) is used in two time intervals extending through
(3) Open space (
Equations (21), (20) and (22) give


Assume

Substituting by (34) in (33) we have

Let

Substituting by (36) in (35) we get

Substituting by (32) in (37) yields

When

Therefore, the horizon volume of the universe in closed cosmic model at time t in this case is written as

It is clear form Table 3 in [1] that Equation (40) is used in the time intervals

The total density of the universe in the closed cosmic model at time t is

Substituting by (3)-(5) in (41) we get

where

From Equation (19), (30), (40) and (42) the total mass of the universe within the horizon volume in closed cosmic model at time t is

The masses of matter, radiation and dark energy within the horizon volume of the universe in closed cosmic model at time t are respectively



The time interval between two instants with scale factors 

However, during the universe contraction if 
3. Algorithm
In determination of the distributions of 
(1) Stage of the universe expansion.
a) Set 




b) Calculate
c) Start general DO loop
d)
e) Compute new value of cosmic time t numerically using (48), where
f) Obtain new value of the universe horizon distance 

g) Determine the corresponding values of 


h) Continue the general DO loop.
(2) Stage of the universe contraction
a) Set





b) Evaluate
c) Start general DO loop

d) Set
e) Obtain new value of cosmic time t numerically using (48), where
f) Compute new value of the universe horizon distance 

Sub steps (g) and (h) are similar to (g), (h) mentioned above in the stage of the universe expansion.
4. Results and Discussion
The distribution of the universe horizon distance in the closed cosmic model until 










The distribution of the universe horizon volume in the closed cosmic model up to 






The distribution of the universe horizon volume in the range 






Figure 1. (a) The distribution of the universe horizon distance in the closed cosmic model up to t = 0.5 Gyr; (b) The distribution of the universe horizon distance in the closed cosmic model in the range t = 0.5 Gyr - tme; (c) The distribution of the universe horizon distance in the closed cosmic model in the range t = tme - t*; (d) The distribution of the universe horizon distance in the closed cosmic model in the range t = t* - tn.


Figure 2. (a) The distribution of the universe horizon volume in the closed cosmic model up to t = 0.5 Gyr; (b) The distribution of the universe horizon volume in the closed cosmic model in the range t = 0.5 Gyr - tme; (c) The distribution of the universe horizon volume in the closed cosmic model in the range t = tme - t*; (d) The distribution of the universe horizon volume in the closed cosmic model in the range t = t* - tn.
the fact that the universe space changes from closed then curved to flat in the interval 


The distribution of mass and energy within the horizon volume of the universe in the closed cosmic model until 

























The distribution of mass and energy within the horizon volume of the universe in the closed model in the range 

















Figure 3. (a) The distribution of mass and energy in the closed cosmic model up to t = 0.5 Gyr; (b) The distribution of mass and energy in the closed cosmic model in the range t = 0.5 Gyr - tme; (c) The distribution of mass and energy in the closed cosmic model in the range t = tme - t*; (d) The distribution of the mass and energy in the closed cosmic model in the range t = t* - tn.
to flat in the range


The distribution of both matter and total mass coincide on each other and lie over the radiation distribution. The two distributions increase gradually up to

Estimations of 



Since the radius of the Coma cluster is 











It is also interesting to note from Table 1 that the horizon distance of the universe at maximum expansion is


Table 1. Estimations of the horizon distance, horizon volume, mass of radiation, mass of matter, mass of dark energy and the equivalent number of the Coma-like clusters to the mass of matter within the universe horizon volume in the closed cosmic model at special times.
where


The value of 

5. Conclusions
In this paper we have investigated the distributions of the universe horizon distance and the universe horizon volume in the closed cosmic model. It is found that the universe horizon distance distribution increases constantly for 





Distributions of mass of radiation, matter and dark energy within the horizon volume of the universe were also investigated in the closed cosmic model. These distributions reveal similar noticeable changes as the universe horizon volume distribution for the same reasons. The mass of radiation dominates up to





Cite this paper
Fadel A.Bukhari, (2015) Distribution of Mass and Energy in Closed Model of the Universe. International Journal of Astronomy and Astrophysics,05,291-301. doi: 10.4236/ijaa.2015.54032
References
- 1. Bukhari, F.A. (2013) A Closed Model of the Universe. International Journal of Astronomy and Astrophysics, 3, 189-198.
http://dx.doi.org/10.4236/ijaa.2013.32022 - 2. Bukhari, F.A. (2013) Cosmological Distances in Closed Model of the Universe. International Journal of Astronomy and Astrophysics, 3, 199-203.
http://dx.doi.org/10.4236/ijaa.2013.32023 - 3. Bukhari, F.A. (2013) Cosmological Distances in Five General Cosmic Models. International Journal of Astronomy and Astrophysics, 3, 183-188.
http://dx.doi.org/10.4236/ijaa.2013.32021 - 4. Bukhari, F.A. (2013) Five General Cosmic Models. Journal of King Abdulaziz University: Science, 25.
- 5. Ryden, B. (2003) Introduction to Cosmology. Addison & Wesley, Boston.
- 6. Schneider, P. (2010) Extragalactic Astronomy and Cosmology. Springer, New York.
- 7. Bukhari, F.A. (2015) Distribution of Mass and Energy in Five General Cosmic Models. International Journal of Astronomy and Astrophysics, 5, 20-27.
http://dx.doi.org/10.4236/ijaa.2015.51004







