International Journal of Astronomy and Astrophysics
Vol.04 No.04(2014), Article ID:52106,5 pages
10.4236/ijaa.2014.44056
The Jeans Equation Generalization for the Rotating Universe
Leonid M. Chechin, Aigerim T. Ibraimova
Astrophysical Institute Named After V.G. Fessenkov, Almaty, Kazakhstan
Email: chechin-lm@mail.ru, b_e_n_t_o_s@mail.ru
Academic Editor: Luigi Maxmilian Caligiuri, University of Calabria, Italy
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 23 September 2014; revised 20 October 2014; accepted 15 November 2014
ABSTRACT
The generalization of Jeans equation in expanding and rotating Universe is given. We found the generalized frequency of baryonic substrate oscillations in the rotating Universe. In doing this, two cases were considered: the generalized wave vector coincides with the Jeans wave vector and second case, when the generalized wave vector tends to zero.
Keywords:
Jeans Equations, Rotating Universe

1. Introduction
It is well known that discovery of cosmic vacuum radically changed main cosmological models [1] . By cosmic vacuum concept, it is possible to describe the basic properties of the Universe―expansion, accelerated expansion, epochs of evolution, etc.
Cosmic vacuum actively influences on the process of large-scale objects formation in the Universe, also (see, for example [2] ).
Moreover, cosmic vacuum (or dark energy) is the reason of Universe rotation. One of the first articles devoted to this problem searching was done by Ellis and Olive [3] . They pointed out that an inflationary episode in the very early Universe could solve the rotation problem and thus make the Mach principle redundant as an explanation. Earlier such possibility was proposed by Gamov [4] .
In our article [5] we found that Universe rotates by action of cosmic vacuum with angular velocity 
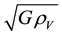 . Some other characteristics of the rotating Universe―coordinates of “axis of evil”, anisotropy of the deceleration parameter―were theoretically described in [6] .
. Some other characteristics of the rotating Universe―coordinates of “axis of evil”, anisotropy of the deceleration parameter―were theoretically described in [6] .
The Universe rotation, in its turn, can plays significant role for describing physical processes that are elapsing in it. Talk about the Universe rotation’s influence on the process of galaxy creation.
It’s well-known that classical approach to study the origin of galaxies is basing on Jeans equations [7] . Although this equation was derived for the classical cosmology, it hasn’t lost their relevance up to the present time. Lower we’ll enumerate some of modern articles devoted to such equation usage.
So, the Jeans equation generalization for the dark energy with nonstationary equation of state and its application to study the antigravitational instability of cosmic substrate in the Newtonian cosmology was done in article [8] .
Further, in [9] a system at equilibrium by time―independent distribution function 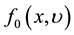 and two solutions of the modified Poisson and collisionless Boltzmann equations were described by Jeans equation. They were analyzed the Jeans instability mechanism, adopted for star formation, considering the Newtonian approximation of
and two solutions of the modified Poisson and collisionless Boltzmann equations were described by Jeans equation. They were analyzed the Jeans instability mechanism, adopted for star formation, considering the Newtonian approximation of 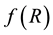 -gravity.
-gravity.
Moreover, the approach developed in this work admits direct generalizations for other modified Gauss-Bon- net theory, string-inspired gravity, etc. In these cases, the constrained Poisson equation may be even more complicated due to the presence of extra scalar(s) in non-local or string-inspired gravity.
Dark matter density profiles from the Jeans equation were considered in article [10] . They make a simple analytical study of radial profiles of dark matter structures, with special attention to the question of the central radial density profile. Recent numerical dark matter simulations show that the phase-space-like density profile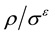 , is well fitted locally with a simple power law with
, is well fitted locally with a simple power law with 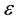 of the order 2 - 3. They shown that when the radial density profile is an exact power law
of the order 2 - 3. They shown that when the radial density profile is an exact power law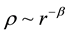 , the spherically symmetric and isotropic Jeans equations only admit the solutions where the density power slope is in the range
, the spherically symmetric and isotropic Jeans equations only admit the solutions where the density power slope is in the range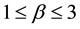 .
.
In [11] , it was considered dark matter angular momentum profile from the Jeans equation. Authors studied the form of the spherical Jeans equation when one includes angular momentum, and find that bulk motion leads to the introduction of extra term, which includes the average rotational velocity. They present a new connection between the radial profiles of the angular momentum and the velocity anisotropy, which is also in fair agreement with numerical findings. Finally they have shown how the spin parameter 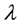 increases as a function of radius.
increases as a function of radius.
And last, stellar dynamics in the galactic centre―proper motions and anisotropy―was examined in [12] . Authors proposed a new analysis of the stellar dynamics in the Galactic centre, based on improved sky and line- of-sight velocities for more than one hundred stars in the central few arcseconds from the black hole candidate SgrA*. They explicitly include velocity anisotropy in estimating the central mass distribution. They also show how Leonard-Merritt and Bahcall-Tremainemass estimates give systematic offsets in the inferred mass of the central object when applied to finite concentric rings for power law clusters. Corrected Leonard-Merritt projected mass estimators and Jeans equation modeling confirm previous conclusions (from isotropic models) that a compact central concentration (central density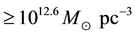 ) is present and dominates the potential between 0.01 and 1 pc. Depending on the modeling method used the derived central mass ranges between 2.6 and
) is present and dominates the potential between 0.01 and 1 pc. Depending on the modeling method used the derived central mass ranges between 2.6 and  for
for  kpc.
kpc.
2. The Jeans Equation Generalization for the Rotating Universe
As we said above the problem of stability the homogeneous distribution matter mathematically was formulated and solved in the framework of small perturbations theory at first by Jeans. He took into account two factors: gravity that tend to conserve a substance dividing into separate bunches, and pressure that have a tendency to smooth the appeared nonhomogeneities.
Recall the equations of hydrodynamics and gravitation in the Newtonian approximation for an ideal gas -
 (1)
(1)
where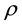 ―density,
―density,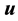 ―velocity,
―velocity, ―gravitational potential. Consider that unperturbed state is a stationary gas
―gravitational potential. Consider that unperturbed state is a stationary gas



To obtain a solution for the perturbations it is necessary use the method of decomposing an arbitrary pertur- bation on the system of orthogonal functions, and examining the time evolution of the perturbations’ components.
Following [7] , the perturbed solution is searched in the form of a plane wave with wave vector

where
Substituting these expressions into equations of hydrodynamics, we will consider only terms that are linear with respect to



In monograph [7] , that we’ll widely used later on, it is shown that the system (3), be generalized to the case of an expanding Universe reduces to the next differential equation of the second order

where 






The aim of our work is a further generalization of Equation (4) for the case of rotating Universe. For doing this, it is necessary take into account that rotation of the Universe changes Hubble “constant”.
In fact, this question was considered in our paper [13] . There it was shown that the rate of Universe expansion in direction perpendicular to the axis of rotation becomes larger than in the parallel direction. Therefore, the value of Hubble “constant” in perpendicular axis of rotation, is associated with the standard value 

In expression (6), 



This equation is the basis of our following searching. In doing this its second term plays the role of “friction” force. And this force, as it clear from physical consideration, increases “friction” at the centrifugal force presence. Beside, next searching of the generalized Jeans equation relates to the vacuum-dominated epoch that exactly allows consider the baryonic mass density as approximately invariable parameter.
Concerning third term of Equation (7) we mark that its standard physical interpretation is the Hook-like force.
3. Solutions of the Generalized Jeans Equations
For solving Equation (7) we set the standard designation

for oscillations’ frequency of baryonic substrate. So, equation (7) be accompanied with (8) is an ordinary diffe- rential equation of the second order with constant coefficients. Its general solution is as follows

where 

For searching these frequencies we’ll impose the general condition existence

that allows simplify expression (10) by decomposing it into the Taylor series. Thus, the generalized oscillation frequency of baryonic substrate in the rotating Universe takes on the form

From (12) clearly that the first frequency is

Hence, from (13) we find the standard critical value of Jeans vector module

The second frequency becomes more complicated and equals to

Now let discuss the generalized length of Jeans basing on (15). For doing this, in accordance with [7] , it is necessary equate to zero the oscillation frequency of baryonic substrate. So, taking into account (14), we get the generalized Jeans vector module from (15)

It is clear that the generalized wave vector module 

3.1. Case I:
First case relates to condition when generalized wave vector’s module coincides with the Jeans wave vector module, i.e.

Hence, with the value of Hubble constant [14] , we find the angular velocity of the Universe

From this expression we see that angular velocity depends both on the baryonic mass density as well as vacuum mass density.
3.2. Case II:
Now consider the case when generalized wave vector module tends to zero that corresponds to the absence of wave perturbations in baryonic matter density. In this case

Hence, we find the corresponding angular velocity of the Universe

This formula indicates that at matter dominated epoch 
4. Conclusions
As the result we can make the following conclusions.
1) In the framework of Big Bang model, the inflationary stage of the Universe evolution was described by condition 

2) In the case of cosmic vacuum neglecting

3) Rotation of the Universe, as it clears from general physical considerations, is an external factor that can produce the wave disturbances in protogalactic substrate. However, in some cases the rotation doesn’t leads to such wave existence (see expression (20)). Unfortunately, such types of astronomical observations based on the well-known deep sky surveys (HDF, CDF, GOODS, etc.) do not give the possibility of this effect detection.
Acknowledgements
The authors express their deep gratitude to JSC “National Centre of Space Research and Technology” for the support of this research in the budget program 055 subprogram 101 “Grant funding of scientific research”.
We also thank our reviewers whose remarks made our article physically more transparent.
References
- Byrd, G.G., Chernin, A.D. and Valtonen, M.J. (2007) Cosmology: Foundations and Frontiers. URSS, Moscow.
- Chernin, A.D. (2006) Cosmic Vacuum and Galaxy Formation. Astronomical and Astrophysical Transactions, 25, 205- 211. http://dx.doi.org/10.1080/10556790600938743
- Ellis, J. and Olive, K.A. (1983) Inflation Can Solve the Rotation Problem. Nature, 303, 679-681. http://dx.doi.org/10.1038/303679a0
- Gamov, G. (1946) Rotating Universe. Nature, 158, 549. http://dx.doi.org/10.1038/158549a0
- Chechin, L.M. (2010) The Cosmic Vacuum and the Rotation of Galaxies. Astronomy Reports, 54, 719-723. http://dx.doi.org/10.1134/S1063772910080044
- Chechin, L.M. (2013) On the Modern Status of the Universe Rotation Problem. Journal of Modern Physics, 4, 126- 132. http://dx.doi.org/10.4236/jmp.2013.48A012
- Zel’dovich, Ya.B. and Novikov, I.D. (1983) Structure and Evolution of the Universe, Relativistic Astrophysics. University of Chicago Press, Chicago.
- Chechin, L.M. (2006) Antigravitational Instability of Cosmic Substrate in the Newtonian Cosmology. Chinese Physics Letters, 23, 2344-2347. http://dx.doi.org/10.1088/0256-307X/23/8/104
- Capozziello, S., Laurientis, M., Martino, I., et al. (2000) Jeans Analysis of Self-Gravitating Systems in f(R) Gravity. arXiv:astro-ph/0001428v1
- Hansen, S.H. (2004) Dark Matter Density Profiles from the Jeans Equation. arXiv:astro-ph/0405371v2
- Kasper, B.S., Hansen, S.H., An, J.H., et al. (2009) Dark Matter Angular Momentum Profile from the Jeans Equation. ArXiv:0901.0928v3[astro-ph.Co]
- Genzel, R., Pichon, C., Eckart, A., et al. (2009) Stellar Dynamics in the Galactic Centre: Proper Motions and Anisotropy. ArXiv:astro-ph/0001428v1
- Chechin, L.M. and Ibraimova, A.T. (2013) Friedmann Equations in the Rotating Frame of Reference. The Bulletin of the National Academy of Sciences of the Republic of Kazakhstan, 15-19 (in Russian).
- Zel’dovich, Ya.B., Sazhin, M.V. and Dolgov, A.D. (1990) Early Universe Cosmology. Moscow State University, Mos- cow.
- Chandrasekhar, S. (1969) Ellipsoidal Figures of Equilibrium. Yale University Press, Dover.





