International Journal of Astronomy and Astrophysics
Vol.4 No.1(2014), Article ID:43416,15 pages DOI:10.4236/ijaa.2014.41006
Syzygy Effects Studies Performed Simultaneously with Foucault Pendulums and Torsinds during the Solar Eclipses of 13 November 2012 and 10 May 2013
1Astronomical Observatory, Stefan cel Mare University of Suceava, Suceava, Romania
2Main Astronomical Observatory of National Academy of Sciences, Kiev, Ukraine
3Tomsa Voda Technological Highschool, Solca, Romania
4Association AIRAMA, Paris, France
5Leibniz-Institut fur Analytische Wisenschaften-ISAS-e.V, Dortmund, Germany
Email: dimitrieolenici@hotmail.com, pugach@yandex.ru
Received 5 December 2013; revised 5 January 2014; accepted 13 January 2014
Keywords:Paraconical Pendulum; Antieclipse Effect; Torsind

1. Introduction
It is well known that in 1851 the physicist J.B.L. Foucault showed that the Earth’s rotation around its axis can be demonstrated by the rotation of the plane of oscillation of a very long pendulum, now called a “Foucault pendulum”.
1.1. The Allais effect
During the solar eclipses of 30th of June 1954 and 2nd of October 1959 Maurice Allais discovered that the plane of oscillation of a short pendulum suspended on a ball changed markedly. Now this pendulum is named paraconical pendulum and the perturbation is called the “Allais effect” [1] [2] .
1.2. The Jeverdan-Rusu-Antonescu Effect
During the solar eclipse on the 15th of February 1961, Gheorghe Jeverdan, Gheorghe Rusu and Virgil Antonescu discovered that the period of oscillation of a Foucault pendulum changed, a phenomenon now known as the Jeverdan-Rusu-Antonescu effect [3] .
1.3. The Anti-Eclipse Effect
In a series of experiments made by Dimitrie Olenici, it has been shown that the behavior of a pendulum is also changed when the experiment is made on the opposite side of Earth to that where the eclipse is visible and that similar effects also appear during lunar eclipses, conjunctions, oppositions and transits of planets ‑ in general during syzygies [4] .
1.4. The Eccentricity Effect
These observations have showed that around a syzygy, the ratio between the small semiaxis and the large semiaxis of the oscillation ellipse of the pendulum changes and also its chirality. These are other criteria that demonstrate changes of the behavior of a pendulum during syzygy [5] .
1.5. The Torsion Effect
In a series of experiments made by A. Pugach with the torsinds it has been demonstrated that these devices experience certain twisting effects during eclipses and other syzygies. We propose that these phenomena should be termed “torsion effect”.
Apparently the first person to apply a torsion balance in astronomical observations was the professor A.N. Kozyrev in Leningrad. He managed to determine the “true” position of celestial objects by using a torsion balance placed at the focus of the optical system of a telescope [6] .
Kozyrev also discovered that a torsion balance showed significant responses to solar eclipses [unpublished]. In the Main Astronomical Observatory of the National Academy of Sciences of Ukraine systematic observations of torsion balance and of the torsinds during solar eclipses have been conducted since 2008 [7] .
1.6. Generalization
The scientific community has taken an interest in torsion balance observations after discovering that the torsion balance (torsind) and the pendulum react to these astronomical events in similar ways [8] -[10] . The previous references contain descriptions of such simultaneous observations performed at different geographical locations.
Due to the fact that all these perturbations appear when three bodies of the solar system are in mutual syzygy, we propose that, collectively, they should be termed “syzygy effects”.
2. The Description of Our Foucault Pendulums
In these experiments we utilized two approximately identical Foucault pendulums. For these experiments two almost identically Foucault pendulums were used.
In order to eliminate the vortex of air produced by a bob shaped as a sphere and the twisting aerodynamic effects acting on a bob shaped as a vertical disc, a bob (B) having an aerodynamic form and configured as a horizontal lens was used.
The first pendulum had a length of 6.43 m and a bob made of lead weighting 8 kg and shaped as a horizontal lens with the diameter of 20 cm and a thickness of 4 cm at the center. This pendulum was installed in the Cacica salt mine, Suceava county, Romania (47˚38'N, 25˚54'E) at 75 m depth.
The second pendulum had a length of 6.15 m, and a bob made of brass weighting 13 kg and shaped as a horizontal lens with a diameter of 24 cm and a thickness of 6 cm at the center. This pendulum was installed in a special room in the Horodnic de Jos village in Suceava county, Romania (47˚46'N, 25˚48'E).
In order to prevent the suspension point from slowly sliding on the plate, fact that would eventually result in a deviation of the horizontal position, the planar plate supporting the ball (used by Maurice Allais for his paraconical pendulum) was replaced with a spherical cup, so that the ball tends always to remain in the center.
In both cases the suspension was constituted by an aluminum ring (R) of 6 cm diameter having at the top of its inner circumference a pivot (p) whose lower point was supported upon a ball (b). The ball oscillated in a spherical cup (c) of 10 cm radius of curvature. This cup was made from a strong steel casing of a swivel bearing. In order to reduce the friction in the cup, a drop of oil was added. The spherical cup was attached to a bracket that was firmly fixed to the ceiling of the experimental chamber. To the lower side of the ring, opposite to the pivot, there was fixed a small rod (r), from which was hung a long steel wire (w) of 1 mm diameter that supported the bob.
Through the bob passed a support screw (s) of 8 mm diameter and 70 cm length. The bob was mounted on this screw and held between two nuts.
The upper part of the screw was 46 cm long, and had on its upper end a cap nut to which was attached the other end of the steel wire (w) hanging from the suspension ring (R).
The part of the screw under the bob was 20 cm long, and had a sharp lower end which served as a pointer and oscillated over an alidade (A).
The alidade was shaped like the letter T. On one of the sides at the middle was mounted a small arm (a) on which was fixed a small piece of wood of 2 × 2 × 8 cm for guiding a similar piece to slide transversely like a shuttle (s).
An angular vernier (V) with the precision of 0.1˚ was provided at the end of the alidade. At the center of the alidade there was provided an inscribed cross with which it was possible to make measurements of the semi-axis of the oscillating ellipse of the pendulum.
In order to measure the period we used an electronic chronometer (Cr) with the accuracy of 0.001 sec.
For high accuracy in period determination we attached two cables to the switch on and of the chronometer. One of these was connected to the pendulum suspension cup and was thus electrically continuous down to the pointer and the other one was connected to an 8 cm of thin flexible metallic violin wire fixed on the shuttle. In order to start the chronometer the shuttle was placed so that the violin wire was at the equilibrium position of the pendulum. After the pendulum was released and its pointer touched the cord once switching on the chronometer the shuttle was retracted. After the pendulum performed 150 oscillations the shuttle was placed in the same previous position so that the pendulum pointer brushed once more the wire and so the chronometer was stopped. In this manner the pendulum itself started and stopped the chronometer. Figure 1 shows a sketch of our pendulums.
Also during the experiments we studied the change in the ratio e = b/a between the small semiaxis and the large semiaxis of the pendulum oscillation ellipse. For this purpose a cross of millimetric paper was placed on the alidade at the bottom dead center position of the pendulum.
3. Pendulum Experiments during the Solar Eclipse on the 13th of November 2012
The total solar eclipse on the 13th of November 13 2012 began at 19h37m58s UT reached its maximum at 22h12m58s UT and ended on the 14th of November at 0h45m34s UT. In Romania the eclipse was not visible. This eclipse was accompanied by other syzygies as follows:
a) November 12, 18h22m, conjunction Moon-Saturn, 4˚51' angular separation b) November 13, 22h12m, maximum of the eclipse c) November 14, 9h47m‑10h48m, occultation of Mercury by the Moon d) November 16, 9h44m, conjunction Moon-Mars, 3˚12' angular separation e) November 16, 23h18m, conjunction Moon-Pluto, 0˚12' angular separation

Figure 1. Sketch of pendulum structure.
f) November 17, 15h45m, inferior conjunction Mercury-Sun, 24' angular separation In order to cover all these alignments we made measurements starting in the evening of of November 12 until midday on November 18. After every start the measurements were made in series of six readings every 6 minutes. The days, serial numbers and starting hours were as follows:
In Horodnic the pendulum was started 26 times. The days, serial numbers and starting hours were: November 12 (1-19h31m, 2-20h33m, 3-21h30m, 4-22h25m); November 13 (5-19h17m, 6-20h05m, 7-20h55m, 8-21h46m, 9-22h40m, 10-23h38m, 11-0h31m); November 14 (12-19h43m, 13-20h40m, 14-21h42m, 15-16h00m, 16- 17h00m, 17-17h40m); November 17 (18-12h50m, 19-15h05m, 20-15h50m, 21-16h40m, 22-17h20m, 23- 18h15m); November 18 (24-7h15m, 25-9h10m, 26-12h45m).
In the Cacica salt mine the pendulum was started 17 times, as follows: November 12 (1-20h, 2-20h45m, 3-21h30m, 4-22h15m); November 13 (5-9h20m, 6-18h40m, 7-19h35m, 8-20h20m, 9-21h05m, 10-21h45m, 11-22h30m, 12-23h15m, 13-0h00m); November 14 (14-8h50m, 15-9h35m, 16-10h20m, 17-11h45m).
3.1. Results for the Azimuth
The graph in Figure 2 shows all the azimuth values obtained with the pendulum in Horodnic. The rows represent the azimuth values after 6 min (red), 12 min (yellow), 18 min (cyan), 24 min (purple), 30 min (brown) and 36 min (green) after starting. The vertical lines a, b, c, d, e and f show the times of the syzygies mentioned above.
Here we can see that the azimuth attained its maximum values in the interval delimited by the solar eclipse (line b), the occultation of Mercury by the Moon (c) and the conjunction Moon-Mars (d). These three alignments were close together in time and acted as a single prolonged eclipse.
Actually the occultation of Mercury by the Moon is also a type of eclipse. Another finding is that that before the eclipse the azimuth had small values preceded by the conjunction Moon-Saturn but during the conjunction Mercury Sun also the azimuth attained large values (line f).
In the graph of Figure 3 we can see all the azimuth values obtained with the pendulum in the Cacica salt mine after 6, 12, …36 minutes from the start.
Here the experiments were made during a shorter time interval which covered only first three syzygies (line a, line b and line c). But even so we can observe the same tendency with small values of the azimuth before the eclipse and with greater values during the eclipse (line b) and the occultation of Mercury by the Moon (line c). Therefore, because the pendulum behavior was affected during the solar eclipse (even though the eclipse was not visible at the place of observation) and also during the occultation of Mercury by the Moon, we can affirm that these experiments confirmed the Allais eclipse effect, the antieclipse effect and in general the syzygy effect.

Figure 2. Azimuth values, Horodnic, November 12-18.
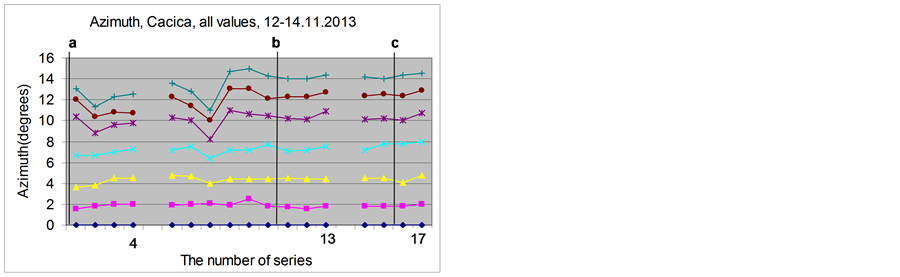
Figure 3. Azimuth values, Cacica, November 12-14.
Another interesting finding is that the curves after 6 minutes (red) and after 12 minutes (yellow) are much flatter than the curves after 30 minutes (brown) or 36 minutes (green). The differences between the azimuths after 6 minutes were hardly perceptible whereas after 36 minutes these differences are up to 12 degrees for the pendulum in Horodnic.
In our opinion this is due to the fact that after 36 minutes the pendulum energy is much smaller than after 6 minutes and thus the proportion between the external force responsible for the perturbation and the pendulum energy is quite different.
This suggests that to prove behavior anomalies of the pendulum requires measurements over long time intervals.
3.2. Results for the Eccentricity
Similar results were obtained in relation to the ratio e = b/a between the minor semi-axis b and the major semiaxis a of the oscillation ellipse of the pendulum, which also underwent significant changes during these syzygies. Figure 4 shows the values of the ratio e during the experiment in Horodnic.
The graphs of Figure 5 shows the parameter e during the experiment in the Cacica salt mine. Here the parameter e underwent very strange fluctuations.
An interesting finding was that while by the measurements in Horodnic the parameter e always increased slowly in an almost linear manner after every start, on the other hand, in the Cacica salt mine the ratio e always increased after the start for the first three measurements (over 18 minutes) and after that decreased slowly. In Figures 6(a) and 6(b) we can see this pattern of determinations during the night of the eclipse. We do not express any opinion as to the cause of this difference.
3.3. Results for the Chirality
By chirality we mean the sense in which the pendulum bob describes the ellipse of oscillation. Usually the sense in which the bob of a Foucault pendulum describes its ellipse is clockwise. In our experiments, which are performed with a Foucault pendulum that is not very long, sometimes this can become counterclockwise during syzygy.
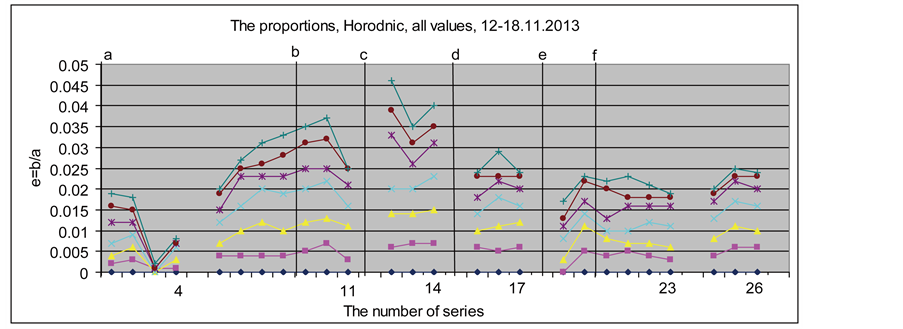
Figure 4. Ratio e = b/a, Horodnic, November 12-18.
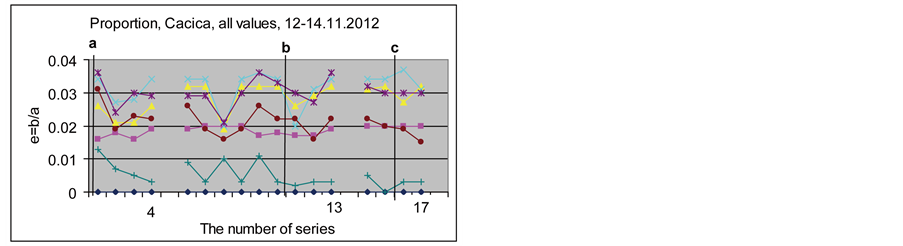
Figure 5. Ratio e = b/a, Cacica, November 12, 13, and 14.
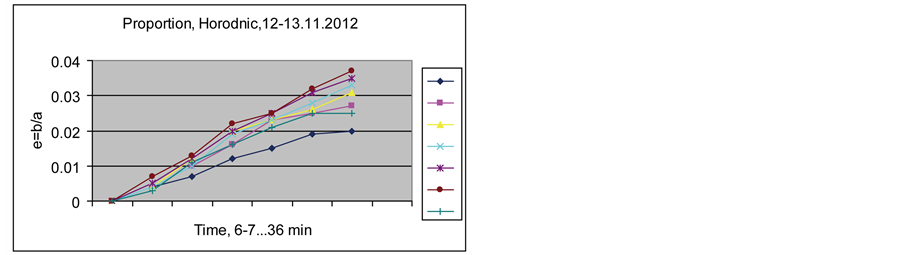 (a)
(a) (b)
(b)
Figure 6. (a) Ratio e in Horodnic during solar eclipse; (b) Ratio e in Cacica during solar eclipse.
In the table of Figure 7 we present the changes of chirality for the experiments with the pendulum in Horodnic performed during the solar eclipse of 2012 on the days of 12 and 13 November. A “+” sign is used for clockwise (as seen from above) and a “–” sign for anticlockwise. The starting hours of the pendulum is also shown.
The chirality was counterclockwise on the day of November 12 until the fourth release of the pendulum at 22 h 25 m (12 minutes after the eclipse maximum) and thereafter it became clockwise and remained so until the end of the experiment on November 18.
During the experiment in the Cacica salt mine the chirality was not recorded.
3.4. Results for the Period
The curve in Figure 8 shows the average values of the period for all the 26 series of determinations by the blue
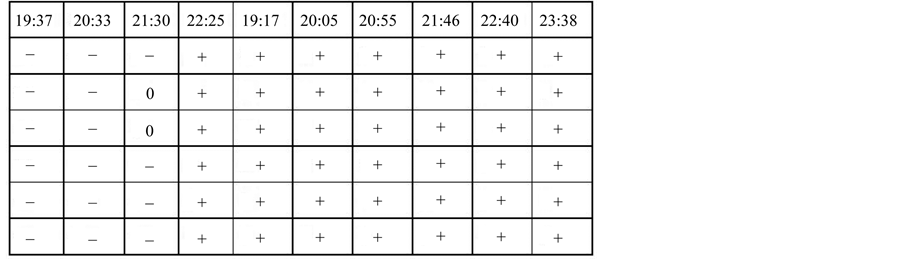
Figure 7. Chirality, Horodnic, 12.11.2012 (19h37m-24h) and 13.11.2012 (20h05m-0h13m).
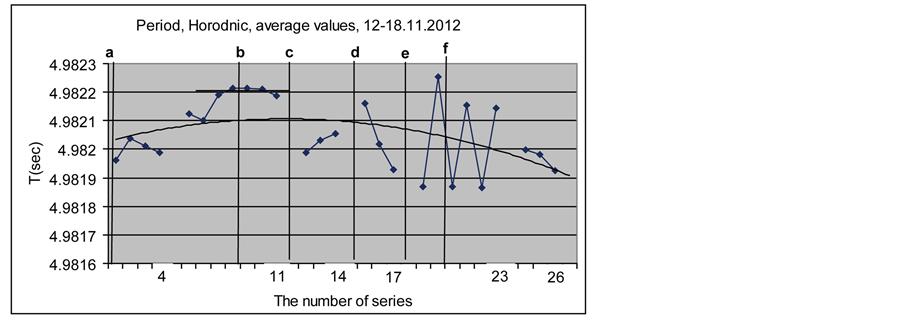
Figure 8. The average periods, Horodnic, 12-18.11.2012.
points. It is easy to see that the period had a tendency to increase reaching its maximum around the eclipse and the occultation of the Mercury by the Moon (the black curve is a polynomial representation).
Before the eclipse the period had rather small values (series number 5). Such period minima have also been seen during other eclipses. The fluctuations of the period during the eclipse were very small compared to the rest of the determinations.
The graph in Figure 9 shows the average period values for the experiment in the Cacica salt mine. We can see that during the solar eclipse and the occultation of Mercury by the Moon the period was also very stable similar to the experiment in Horodnic. Moreover, this graph seems to be like a mirror. Here in Cacica, before the eclipse, the period reached a great maximum (series number 3).
4. Pendulum Experiments during the Solar Eclipse of May 10, 2013
The solar eclipse of May 10 2013 began at 21h25m on May 9, reached its maximum at 0h26m on May 10 and ended at 3h25m on May 10. During this eclipse, the experiments in Horodnic and in the Cacica salt mine were performed with the same pendulums as described above. The days, the hours of start and the serial numbers of the determinations are given below. In this case, after each start, five determinations were made successively at intervals of seven minutes. The colors of the plots in the figures are: pink after 7 minutes, yellow after 14 minutes, cyan after 21 minutes, purple after 28 minutes and brown after 35 minutes respectively.
This eclipse was very interesting to study because it was not visible in Romania and also was accompanied by many planetary alignments as follows:
a) May 6, 20h57m, conjunction Moon-Uranus, angular separation 3˚3'
b) May 8, 0h35 m, conjunction Mercury-Mars, angular separation only 24'
c) May 9, 14h53m -16h, occultation of Mars by the Moond) May 9, 22h0h, conjunction Moon-Mercury, angular separation 27'
e) May 10, 0h26m, maximum of the solar eclipse
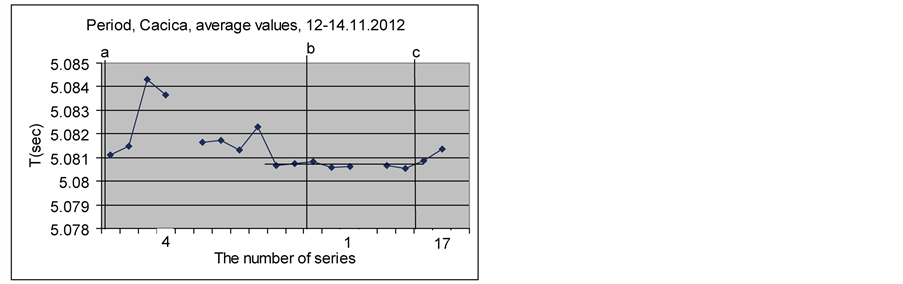
Figure 9. Average periods, Cacica, 12-14.11.2012.
f) May 11, 0h 49m, conjunction Moon–Venus, angular separation 2˚12'
g) May 11, 15h57m-May 12, 1h57m, occultation of Mercury by the Sun.
In Horodnic 42 series of determinations were performed as follows: May 5 (1-10h), May 6 (2-5h, 3-17h) May 7 (4-4h, 5-23h), May 8:(6-8h20m, 7-11h45m, 8-17h25m, 9-19h35m, 10-20h53m), May 9 (11-6h35m, 12-9h, 13-13h40m, 14-18h13m, 15-19h10m, 16-20h, 17-21h, 18-21h50m, 19-2h40m, 20-23h25m), May 10 (21-0h5m, 22-0h50m, 23-1h35m, 24-2h15m, 25-7h15m, 26-11h20m, 27-16h, 28-19h10m, 29-19h55m, 30-20h45m, 31-21h30m), May 11 (32-1h30m, 33-6h45m, 34–8h05m, 35-9h45m, 36-13h03, 37-15h20m, 38-17h40m, 39-20h, 40-20h55m, 41-22h), May 12 (42-4h).
Unfortunately only 12 series of determinations were made in the Cacica salt mine, but even so, the comparison with the corresponding determinations made simultaneously in Horodnic is of great consequence. The series of determinations made in the Cacica salt mine were as follows:
May 9 (1-12h30m, 2-22h18m, 3-23h), May 10 (4-0h39m, 5-1h20m, 6-2h, 7-21h31m, 8-22h10m, 9-23h, 10-23h45m), May11 (11-0h29m, 12-1h07m).
4.1. Results for the Azimuth
The azimuths obtained in the interval May 5 - 18, 2013 are plotted in the graphs of Figure 10.
The vertical lines show the syzygies around the eclipse.
In this experiment we can see a maximum before a deep minimum after the occultation of Mars by the Moon (c) followed by a deep minimum before the conjunction Moon-Mercury (line d) and the solar eclipse (line e). Also a great azimuth is seen around the conjunction Moon-Venus (line f). Once again the close combination of an eclipse and a conjunction produced great anomalies in the behavior of the pendulum.
In the Cacica salt mine the experiment covered (partially) four alignments: the occultation of Mars by the Moon (vertical line c), the conjunction Moon-Mercury (vertical line d), the solar eclipse (vertical line e) and the conjunction Moon-Venus (vertical line f).
From the graphs we can see that around the occultation of Mars by the Moon and the conjunction MoonMercury the azimuth had very small values and after that, during the solar eclipse and the conjunction MoonVenus, the azimuth had large values like those obtained by the experiment in Horodnic.
4.2. Results for the Eccentricity
The Figure 12 shows all the values of the ratio e = b/a obtained in Horodnic for all 42 series of determinations. The vertical lines show the syzygies covered by these experiments.
Here we can see that before the occultation of Mars by the Moon (vertical line c) the ratio e had great values and that also around the conjunction Moon–Mercury (vertical line d) and the solar eclipse (vertical line e) the proportion reached its greatest values.
Here we also observe the same tendency for the ratio to have large values around other syzygies.
The graphs in Figure 13 show all the values of the ratio in the Cacica salt mine experiments. The values of the ration begin on the evening of May 9, at the same time as the conjunction Moon-Mercury (vertical line d) and continue during the solar eclipse (vertical line e) and during the conjunction Moon-Venus (vertical line f).

Figure 10. Azimuth, Horodnic, 5-12.05.2013.
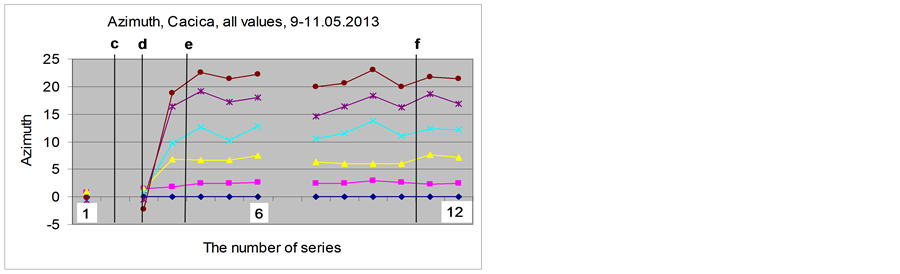
Figure 11. Azimuth, Cacica, May 9-11.05.2013.
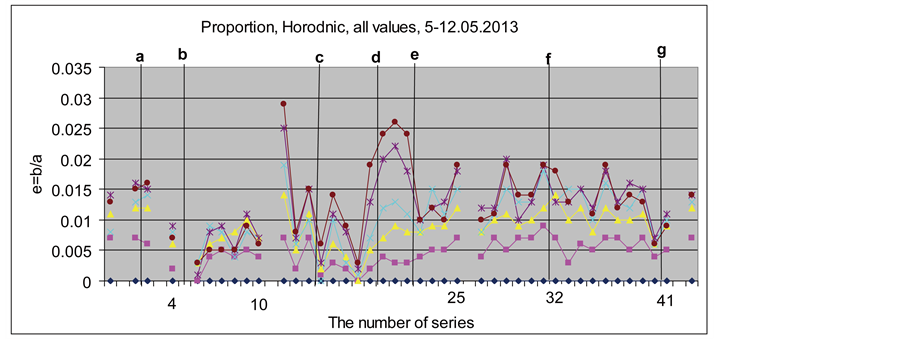
Figure 12. Ratio e = b/a, Horodnic, 5-12.05.2013.
Once again in the Cacica salt mine, as in the 2012 experiments, the proportion had great fluctuations in the second part of every series of determinations.
4.3. Results for the Period
Figure 14 shows the average period values for all 42 series of determinations in Horodnic. We can see that during the series 1 - 10 and during the series 23 - 42 the period fluctuated greatly. But during the series 11 - 21, which covered the Mars occultation by the Moon, the conjunction Moon-Mercury and the solar eclipse once again the period was very stable (the horizontal line). Unfortunately no period determin-ations were made in the Cacica salt mine.
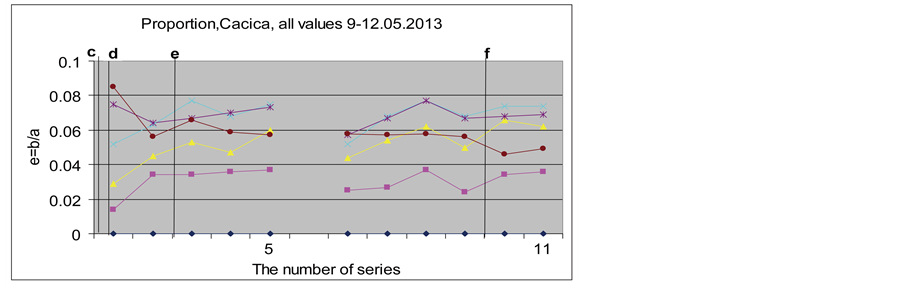
Figure 13. Ratio e = b/a, Cacica, 9-11.05.2013.
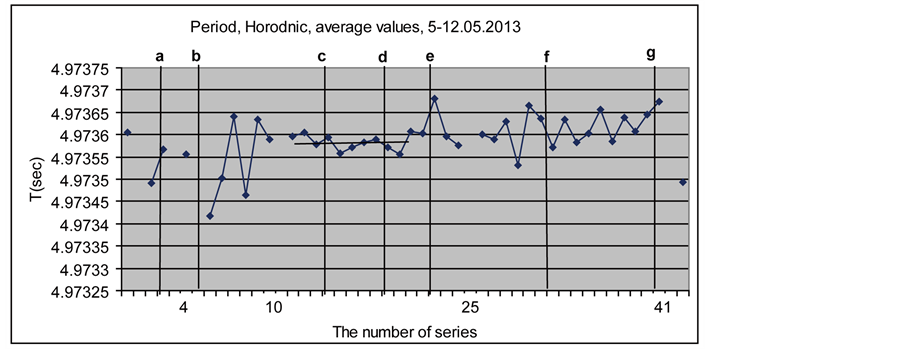
Figure 14. Period in Horodnic.
4.4. Results for the Chirality
In these experiments we represent the chirality by graphs. A “+1” value is used for clockwise rotation, and a “−1” value is used for anticlockwise rotation.
In the Horodnic experiments the chirality presents two changes in the days of 8 and 9 May (Figure 15).
The first change was on 8.05 at 17h25m. This was around 30 hours before the solar eclipse on 10.05, which reached its maximum at 0h26m. The second change began at 18h34m and finished at 21 h around 3 hours before eclipse.
Unfortunately only a small number of determinations were made in Cacica between May 9, 12 h 30 m until May 11, 1h42m.
But even so we see a change of chirality on May 9 which finished at 23h01m, around one hour before maximum of eclipse (Figure 16). The fact that in both experiments situated at around 30 km away, one on the surface of the Earth and another at 75 m deep, before the maximum of eclipse appeared, a change of chirality (practically in the same time) confirm the existence of the effect of chirality!
4.5. Results of the Observations
As a general conclusion from these pendulum experiments which were carried out in different places and in two successive years but for approximately the same astronomical configurations: even though some of the astronomical events were not optically visible and even though the determinations were not made non-stop 24 hours per day, the general trends of the curves exhibited a clear tendency to present great anomalies around eclipses and occultations. Also, careful analysis of the graphs shows moderate perturbations around all the syzygies. These results confirm the existence of the syzygy effects mentioned above. A much more detailed explanation will be presented in a future series of articles which will analyze syzygies of various types.
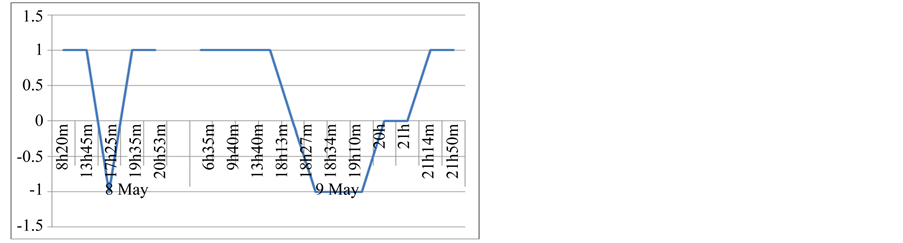
Figure 15. Chirality, Horodnic, 8.05-2013 (8h20m-20h35m) and 9.05.2013 (6h35m-21h50m).

Figure 16. Chirality, Cacica, 9-11.05.2013.
5. Description of the Torsind
The observations from 2012-2013 were carried out using a new type of instrument, the so-called torsind which is based on a disk suspended from a thread. Such a torsind is a specific type of torsion balance that uses a very light metal disc instead of the linear beam of a classical unit suspended from a monofilament made from natural silk instead of quartz or some other material. The design of such a device makes it insensitive to variations in gravitational potential and ensures that it is unaffected by gravitational influences (including tidal influences) from any direction. The torsind is capable of “feeling” a torque T as small as T = 6.47 × 10−12 Nm [11] .
The reading error of the torsind measurement does not exceed 0.5˚. Our devices are fully automated and do not require the presence of an observer but only need monitoring from time to time.
6. The Torsind Observations
The solar eclipse on the 13-14th of November 2012 was observed at the Main Astronomical Observatory NANU located in Kiev (Ukraine) with two torsinds WEB_1 and WEB_2. The devices occupied an isolated, shaded room with tightly closed doors and windows and entrance being not allowed to outsiders. Our observations were performed in very favorable conditions:
· absence of any mechanisms within 50 m, such as motors and generators or moving objects;
· absence of electrical and wireless devices (except for a single computer);
· no mechanical vibrations;
· complete silence and absence of strong light and heat radiation;
· closed room and no visitors.
Our measurements began 6.5 hours before the maximum phase of the eclipse and lasted continuously for 15 hours. One measurement was taken each minute. The results of the Kiev torsind measurements are shown in Figure 17 with red and blue lines. The dashed vertical lines indicate the beginning and the end of the eclipse on Earth. This eclipse was not visible in Romania or Ukraine.
Observations during the 9 - 10 May 2013 solar eclipse were carried out using three torsinds. One torsind

Figure 17. Summary of pendulum-torsind observations in 2012.
(WEB_1) remained in Kiev and the other two (W4 and W5) were installed in Romania. The device W4 was in an isolated enclosed room on a private estate in Comanesti, Suceava county (47˚50'N; 25˚59'E) a village located 10km east of Cacica, whereas the W5 device was taken into the Cacica salt mine and installed in a small isolated chamber at a depth of 40 m. In this room the conditions were almost ideal: constant temperature and humidity which have not changed over the centuries and absence of air flow, people, working mechanisms, noise, vibrations and other disturbances. The torsind WEB_1 operated in the same underground room June 2011 during our solar eclipse observation at that time [9] .
This time in 2013, torsind measurements began 9 hours before the maximum phase of the eclipse and continued for 24 hours. The resulting torsind observations are shown in Figure 18 by dark green (WEB_1), red (W4) and blue (W5) lines. The dotted lines show the eclipse phases: the beginning, maximum and end. This eclipse, like the eclipse in 2012, was not visible in Romania or Ukraine.
7. Statistical Confirmation of the Reliability of the Obtained Results
The pendulum measurements in Cacica (Figure 17) showed a significant deviation of the pendulum at the point A. How realistic is that deflection? A simple analysis shows that the deviation is not random, but rather is associated with the solar eclipse. Let us exclude point A (ordinate 11.0 deg) from the set of numerical measurements and for the remaining 12 points calculate the average value of this variable ao and its standard deviation SD.
ao = 14.28 deg; SD = ± 0.384 deg; 3SD = ± 1.152 deg Obviously, the deviation of point A from the mean value of ao (14.28 − 11.0 = 3.28 deg) significantly exceeds 3 SD. If we assume that the observed values are randomly distributed according to a Gaussian distribution, then the condition 3.28 deg > 3 SD means that the deviation of the point A is not due to accidental causes but is very real.
Moreover, similar reasoning shows that the deviation of the point B (whose ordinate is 12.8 deg) is also not accidental but has a real basis since
(14.28 − 12.8) deg > 1.152 deg Thus, statistical calculations confirm that just before the beginning of the eclipse on 13.11.2012 the pendulum deviated by more than 3 degrees from the mean value. This implies that the cause of this phenomenon was the solar eclipse.
The reality presence of the deviation of a Foucault pendulum during a solar eclipse on 09.05.2013 (Figure 19) does not require statistical confirmation. Over the years numerous observations have been made demonstrating the reality presence of the swing plane deviation. Thus, in this case, once again the Allais effect was confirmed.
The results from the measurements with the pendulum in Horodnic (May, 2013) require some statistical confirmation for the parameter e (the ratio e = b/a). Using the series of measurements shown in Figure 19 one can

Figure 18. Summary of pendulum-torsind observations in 2013.
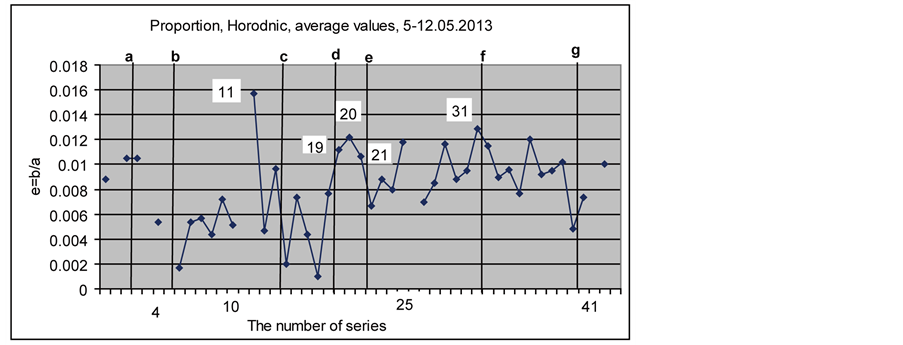
Figure 19. The average values of proportion in Horodnic, 5-12.05.2013.
calculate the mean values eo and SD as done above.
It turns out that the points marked on the graph (Figure 19) by symbols 11, 19, 20 and 21 deviate from the mean by an amount significantly greater than 3 SD. Thus, these points are also outside the statistical error and represent real deviations.
Accordingly these deviations are real and cannot be explained by measurement error. For us the most important fact is that the points 11, 19, 20 and 21 are near the occultation of Mars by the Moon (line c), the conjunction Moon-Mercury (line d), the solar eclipse (line e) and the conjunction Moon-Venus (line f) and thus it is reasonable to suppose that the change in the parameter “e” was caused by these syzygies.
8. Discussion
The main result of our study is that all instruments used clearly responded to these two solar eclipses. The type of reaction was that during solar eclipses the disk of the torsind rotated abnormally in one direction or the other while the azimuth of the plane of oscillation of the Foucault pendulum changed.
The variety of form of the curves for (WEB_1), (W4) and (W5) in Figure 18 most likely can be attributed to the variety of observation conditions. The most well-defined response was showed by the unit (W4) that was set up in the mine. The interference there was negligible. On the other hand the device (W5), which was in the most unfavorable conditions, did not show such a clear picture and responded to the eclipse with a wide minimum. The fact that in 2012 two semi-detached units WEB_1 and WEB_2 showed a similar reaction (Figure 17) is a good confirmation of this assumption.
These effects can hardly be explained by changes in the overall gravitational potential because gravitational potential increases or decreases slowly over time (its characteristic time for variation is around 1 week), whereas the effects registered by the pendulum occurred over a few hours.
Moreover, the changes observed with the torsind cannot be attributed to electromagnetic influences. The moist NaCl monoblock in the Cacica mine is an excellent screen and protects well devices from electromagnetic radiation over a wide range of wavelengths, from radio to hard X-rays.
Another very important result of our measurements is that the reaction of the pendulum occurs ahead of the torsind reaction. This is evident from the Figures 17 and 18. In the first case (2012) the time lead was approximately 3.8 hours and in 2013 it reached a value of 4.3 hours.
Such advance in time was first discovered in 2009 during our mutual observations of the solar eclipse that took place on January 26. Then the time lead “pendulum torsind” was about 1 hour and 40 minutes. This result is described in detail in our previous work [10] .
This fact is unusual in itself; however it is even more interesting because it helps us understand that the time shift does not depend on the geographical coordinates of the measuring instrument but presumably depends on the “spectral sensitivity” of the devices themselves and on the particular characteristics of the phenomenon studied.
The reliability and the validity of the pendulum observations in Cacica and Horodnic in 2013 are confirmed by the similarity of the results. The readings of both instruments steadily increased during the first half of the phenomenon from the beginning up to the maximum phase of the eclipse. In Figure 18 one can clearly see that the black and the dark green lines are almost parallel. This demonstrates that the planes of oscillation of both pendulums rotated clockwise. Thus apart from the statistical validation of measurements of the pendulum, we also have a direct graphical confirmation. (The scale of the graph for the Cacica pendulum measurements has been reduced by a factor of 2 in the figure for ease of presentation.)
It must also be noted that both of the eclipses were only optically visible on the opposite side of the Earth (in Australia and in the Pacific). However this did not prevent our devices “feeling” these events. Consequently, the body of the Earth appears not to be any obstacle for some carrier that transports torque and that causes the disk of the torsind and the plane of the oscillation of the pendulum to rotate. The unusual properties of this carrier have yet to be explored. We can only acknowledge its presence and emphasize that most clearly such a carrier manifests itself in times of syzygys.
9. Conclusions
New phenomena have been found that were unknown before organized torsind-pendulum observations.
This work raises the important question of the practical detection of latent vortex-like mechanical energy radiating from the Sun. This energy is not related to electromagnetism. It implies that a torsion component is present as a solar influence. The evidence found quite clearly points to this conclusion. During solar eclipses the disk of a torsind rotates and the plane of oscillation of a Foucault pendulum deviates. Classical astrophysical instruments such as spectrometers, photometers, polarimeters and so on are not appropriate for study of these phenomena. The observed effects cannot be explained in the framework of gravitation or electromagnetism and it is surmised that they may indicate a manifestation of a fifth fundamental interaction.
Not an exact coincidence moments of conjunctions c, d, e, f, with points 11, 19, 20, 21 and 31 (Figures 12, 14, 19) is caused by a simple fact that the reactions of pendulums and torsinds in the most cases are either ahead or late with respect to an observed phenomenon. It is clear from these observations as well as from the previously published results [8] -[11] . Such a mismatch indicates that not only the gravity can be the cause of the pendulum and torsind reactions.
Acknowledgements
The authors thank to Corneliu Zup and Radu Dartu, directors of the Salina Cacica and Mr. Doru Slevoaca, chief of the Cacica salt mine for permission and help in organization and to Thomas Goodey for logistic support.
We also are grateful to Mr Guy Berthault and the “Fondation Maurice Allais sous égide de la Fondation ParisTech” for helping with the building of the Foucault pendulum laboratory in Horodnic de Jos.
[1] References
[2] Allais, M.F.C. (1957) Mouvement du Pendule Paraconique et Eclipse Totale de Soleil du 30 Juin 1954. French Academy of Sciences, 245, 2001-2003.
[3] Allais, M. (1997) L’Anisotropie de l’Espace, Clement Juglar, Paris.
[4] Jeverdan, G.T., Rusu, G.I. and Antonescu, V. (1999) Experience a l'aide du pendule de Foucault pendant l`eclipse du soleil du 15 fevrier 1961. Science et Foi, 15, 36-44.
[5] Olenici, D. (2009) The Sarawak Antieclipse Pendulum Experiments. Anuarul Complexului Muzeal Bucovina, 2007- 2008-2009, Suceava.
[6] Olenici, D. (2011) Short History of our Research into the Allais and Jeverdan‑Rusu-Antonescu Effects. In: Munera, H.A., Ed., Should the Laws of Gravitation Be Reconsidered? Apeiron, Montreal, 223.
[7] Kozyrev, N.A. (1958) Causal or Asymmetrical Mechanics in the Linear Approximation. Pulkovo, 90 (in Russian).
[8] Pugach, A.F., et al. (2008) The First Experience of Solar Eclipse Observations with a Miniature Torsion Balance. Kinematics and Physics of Celestial Bodies, 24, 253‑258. http://dx.doi.org/10.3103/S088459130805005X
[9] Goodey, T.J., Pugach, A.F. and Olenici, D. (2010) Correlated Anomalous Effects Observed during the August 1st 2008 Solar Eclipse. Journal of Advanced Research in Physics, 1, 021007.
[10] Olenici, D. and Pugach, A.F. (2012) Precise Underground Observations of the Partial Solar Eclipse of 1 June 2011 Using a Foucault Pendulum and a Very Light Torsion Balance. International Journal of Astronomy and Astrophysics, 2, 204‑209. Http://stoner.phys.uaic.ro/jarp/index.php/jarp/article/view/40/22
[11] Pugach, A.F. and Olenici, D. (2012) Observations of Correlated Behavior of Two Light Torsion Balances and a Paraconical Pendulum in Separate Locations during the Solar Eclipse of January 26th, 2009. Advances in Astronomy, 2012, 263818. http://dx.doi.org/10.1155/2012/263818
[12] Pugach, A.F. (2013) The Torsind—A Device Based on a New Principle for Non‑Conventional Astronomical Observations. International Journal of Astronomy and Astrophysics, 3, 33-38. http://dx.doi.org/10.4236/ijaa.2013.32A006

