International Journal of Astronomy and Astrophysics
Vol.3 No.4(2013), Article ID:39348,4 pages DOI:10.4236/ijaa.2013.34046
A “Fine Structure Constant” for Inertia
1Department of Physics, Technion—Israel Institute of Technology, Haifa, Israel
2School of Education of the Kibbutz Movement, Oranim, Tivon, Israel
Email: phr89ah@techunix.technion.ac.il, harpaza@mh.org.il
Copyright © 2013 Amos Harpaz. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received July 24, 2013; revised August 21, 2013; accepted August 30, 2013
Keywords: Curved Fields; Stress Force; Inertia
ABSTRACT
We try to find a physical source for the inertial force, which contradicts the acceleration of an object. We find that when an object is accelerated, its gravitational field curves, and the stress force created in this curved field acts on the object against the accelerating force, thus supplying part of the inertial force that contradicts the acceleration. We also find that this force includes a term which is similar to the “fine structure constant” used in quantum mechanics. As well, we find that this term equals unity for a black hole object. Further work is needed in order to find whether the complete inertial force can be found in this way. The experimental results that may prove this approach are still very limited.
1. Introduction
When a material object is accelerated, it “performs” a force (an inertial force) that counters the external force that accelerates the object. This fact is most clearly shown in the way that the second law of Newton is formulated by D’Alambert (1743):
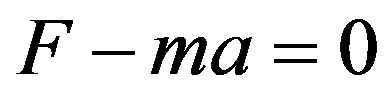 (1)
(1)
For many years, the questions were discussed about what the nature of this inertial force is, and whether it is created by an interaction.
Mach Principle (1883) states that the inertial properties of matter reflect the interaction of the accelerated mass with the entire material contents of the universe.
In a more popular language—the inertial force that acts against the accelerating (external) force is created by the interaction of the accelerated object with the distant galaxies. This principle actually treats acceleration as a relative phenomenon, where only the relative acceleration between the local object and the distant galaxies matters, without stating explicitly which one of them is “really” accelerated. This principle contradicts the Newtonian approach to acceleration, where acceleration was considered relative to an absolute space, thus giving acceleration an absolute measure. Using Mach principle, Einstein could formulate, first, the Principle of Equivalence (PE), which states the equivalence of the gravitational mass and the inertial mass, and later, the General Theory of Relativity (GTR), that formulates gravitation in the form of a geometric structure of space (see Wheeler for details [1]). D. W. Sciama [2] showed that if we assume that the interaction that causes acceleration falls with the distance like 1/r, then the contribution of distant galaxies prevails the contribution of nearby matter, and this can explain the isotropic nature of inertia. Up to date, the validity of Mach principle has not been established experimentally, and further more, it is not clear whether this principle should be considered as a “must” component of GTR. However, many scientists “like” this principle, and tend to include it in the general theory.
In order to understand better the nature of the forces involved when an object is accelerated, we should consider the forces created in curved fields (electric and gravitational fields).
2. The Reaction Force in a Curved Field
When we consider the process of acceleration of electric charges, we should recall that there is an extra force involved, which usually is not mentioned in standard works on this topic: This force is the stress force created in the curved electric field of the accelerated charge, which is curved due to the acceleration. We already know about an interaction connected with acceleration, which creates very important phenomena—the electromagnetic radiation. When a charge is accelerated, it radiates, and the power carried by the radiation is proportional to the acceleration (squared).
Similar to the electric field, the gravitational field of an accelerated mass curves too, and the phenomena connected with curved fields, are similar both for electric and gravitational fields.
In a curved field, there are force components which are perpendicular to the direction of the field, in addition to the regular parallel force components. Suppose that we have a force field Q, over a certain volume of space. The non-parallel force density, (f), of this field is given by: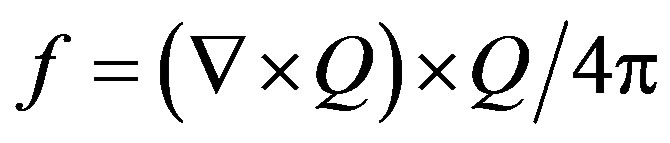 , which by using vector identities can be written as [3,4]:
, which by using vector identities can be written as [3,4]:
 (2)
(2)
Where n is the unit vector normal to the field lines, and Rc is the radius of curvature of the field lines, and we put for Q: Q = Q×s, where s is a unit vector along the field lines.
The first and third terms of Equation (2) cancel each other, and we are left with the second term, which is the stress force density, 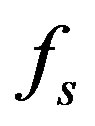 , given by:
, given by:
 (3)
(3)
which is the stress force that acts perpendicularly to the curved field lines.
When we relate this expression to a gravitational field of a mass m, then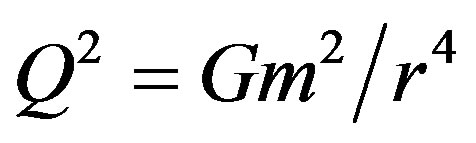 , and if the field is curved, then the stress force density is:
, and if the field is curved, then the stress force density is:
 (4)
(4)
In order to calculate the radius of curvature we have to calculate the expressions for the gravitational field of a mass particle m, moving with a constant acceleration in its own system of reference. Such a motion is called “a hyperbolic motion”, as it describes a hyperbola in Rindler coordinates (Rindler [5]). We shall use the method suggested by Gupta and Padmanabhan [6], where they calculate first the field equations of a particle (an electric charge) in its own system of reference, and then transform these equations to the system of free space, in which the particle is accelerated. In using this method for the calculation of electric field of an accelerated charge, they recovered the field equations as calculated by Schott [7], and by Fulton and Rohrlich [8]. We shall use this same method for the calculation of the gravitational field of an accelerated mass particle.
3. Gravity and Inertial force
The gravitational field of a mass particle in its own system of reference is spherically symmetric around the mass, usually displayed as straight lines of force emanating from the mass. When the particle is in motion, the field it emanates does not move with the particle motion. The field is emanated from the particle at each point along the particle path. After being emanated, the field “knows” nothing about further motions of the emitting particle. It expands in space at a constant velocity without any dependence on the particle further motion.
In the attached figure (Figure 1), the field emanated from the particle at the point z1, t1, reaches the point x, t2, while the particle moved from the point z1, t1 to point z2, t2. The particle may be stopped, or even be reversed during this time, but the field will continue its expansion, “knowing” nothing about the particle further behavior.
When the particle is accelerated, its field is not accelerated with the mass and it curves, because the field is an independent physical entity, and it continues to expand in space, at its own constant velocity (C in vacuum). This approach was actually suggested by Einstein [9], and also supported by Landau and Lifshitz [10].
Thus, when a field is emanated by a source in motion, the field does not participate in the source motion, and the relation between the particle and its emitted radiation, depends on the relation between the particle velocity (which may be of any kind of motion), and the radiation velocity, which depends on the surrounding space. More details about this topic, may be found in earlier papers, dealing with it [11,12].
By using the method of Gupta and Padmanabhan [6] mentioned above, the equations for the gravitational field of the accelerated mass in free space are calculated (although they dealt mainly with the calculations of electromagnetic fields, this method can be also used to calculate the gravitational field of particles at motion). The gravitational field is calculated first in the rest system of the particle, and then, these equations are transformed to the system in which the particle is accelerated in. These equations, given in cylindrical coordinates (z, ρ, Ɵ), are:
 (5)
(5)
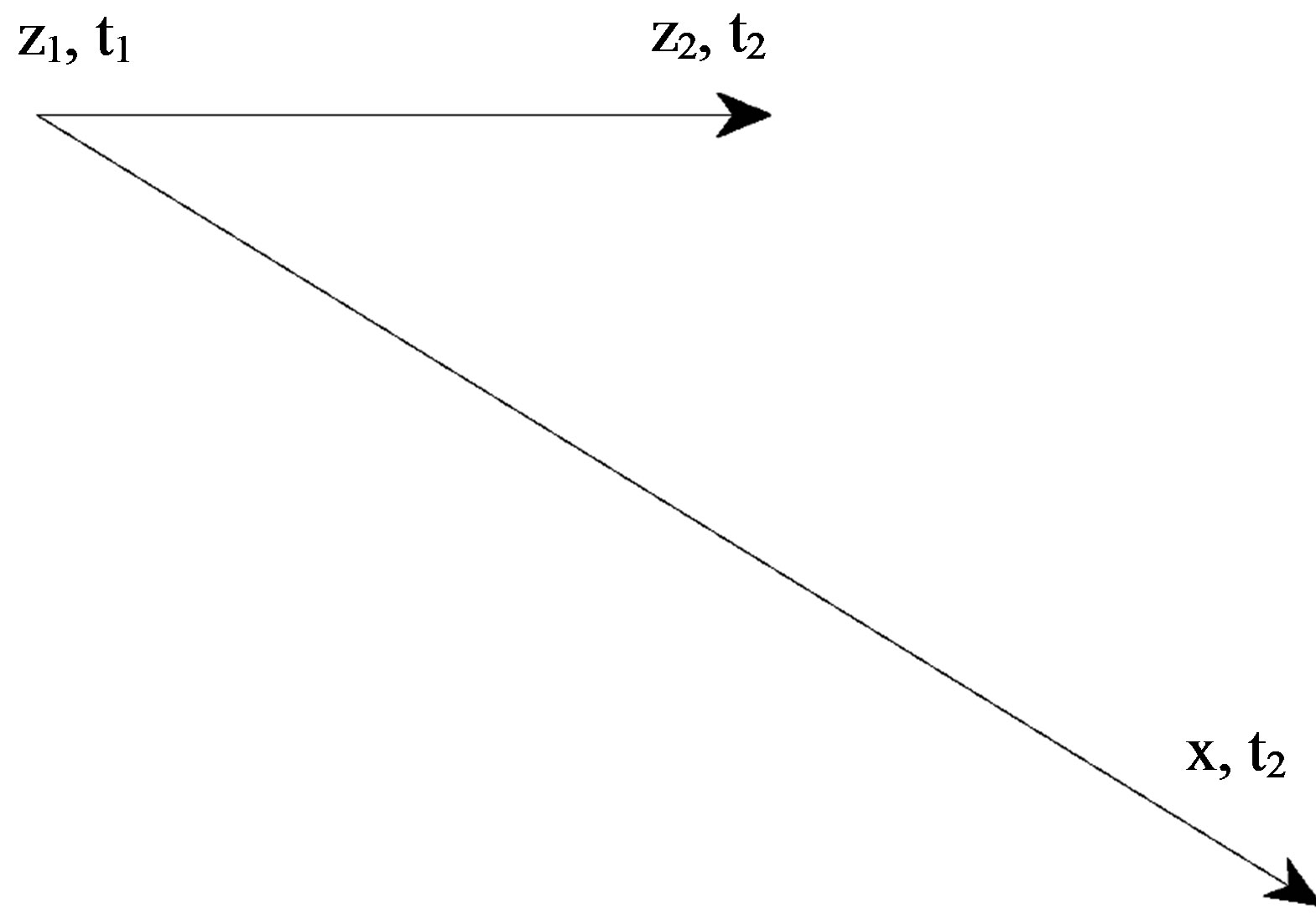
Figure 1. The field induced by a particle at motion.
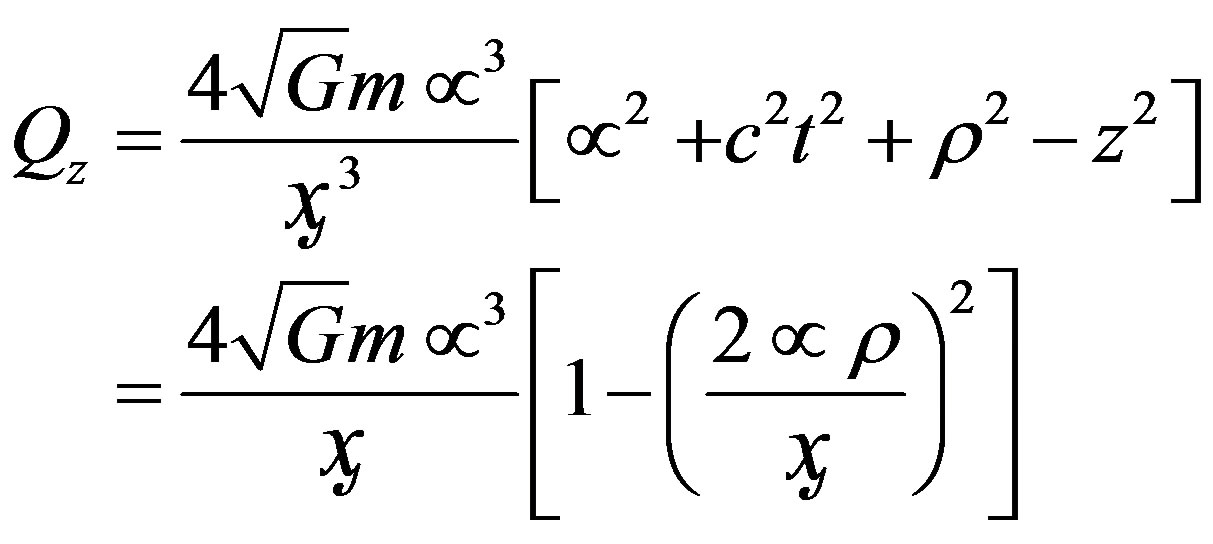 (6)
(6)
where 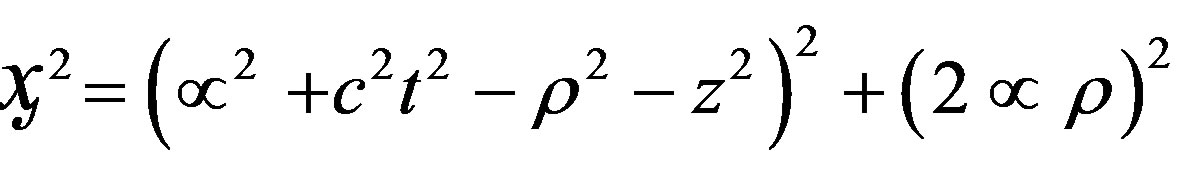 and
and
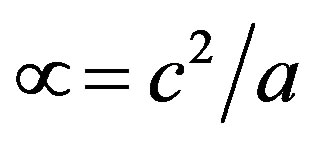 is the mass location at t = 0 (the turning point in Rindler coordinates. (Here a is the acceleration).
is the mass location at t = 0 (the turning point in Rindler coordinates. (Here a is the acceleration).
From these equations, the equations for the field lines can be calculated as shown by Singal [13], and from these equations we calculated the radius of curvature of the field lines (to be inserted in Equation (4)). It comes out also that 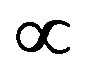 is the characteristic radius of curvature of the gravitational field lines (see Figure 2 and Equation (7)).
is the characteristic radius of curvature of the gravitational field lines (see Figure 2 and Equation (7)).
The radius of curvature of the field lines, (Rc), as calculated from Equations (5) and (6), is:
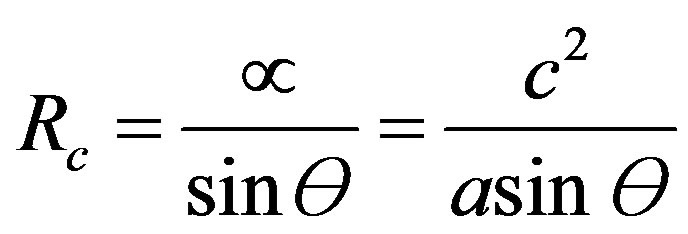 (7)
(7)
where Ɵ is the angle between the particle trajectory and the field line at the moment the field left the mass. The force density of the stress, fs in this case is:
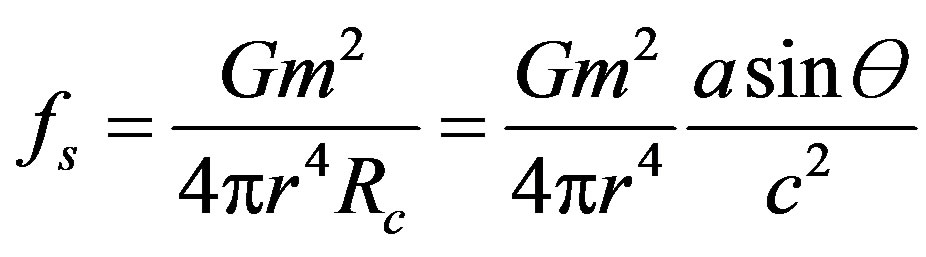 (8)
(8)
The components of fs which are perpendicular to the mass trajectory cancel, due to symmetry, and we are interested in the components of fs which are parallel to the mass trajectory, which are: fs parallel = fs sin Ø, where Ø is the angle between the field line and the mass trajectory. Close to the mass trajectory, Ø ≅ Ɵ, and we have for

Figure 2. The field lines of a particle accelerated linearly in free space.
fs parallel:
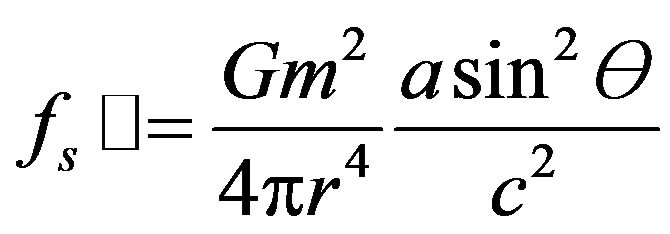 (8’)
(8’)
This curvature stress force (the parallel part of the stress force) acts on the accelerated mass, against the accelerating force. In order to find the parallel stress force, fsP, that acts on the accelerated mass against the accelerating force, we have to integrate on the stress force density, fsP, over the space around the mass.
We multiply fsP by the volume element: dØsinƟdƟr2dr. The integration over the angles yields ‒8π/3, and we get:
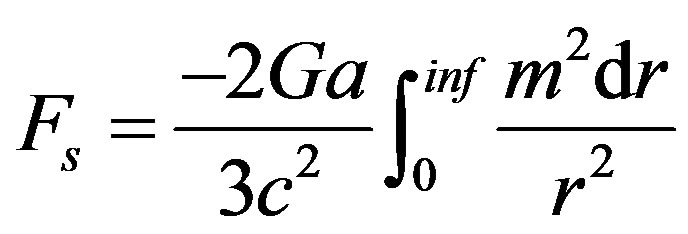 (9)
(9)
We perform the integration over r, for two parts of space: The space outside the mass [R > r, where R is the object’s radius (for simplicity, we deal with spherically symmetric objects only)], and the space inside the mass (r < R). In the outer integration, the limits on r are: R < r < inf, and in the inner part, the limits are 0 < r < R. In the inner part, the gravity at each r depends only on the mass included inward to this r.
The outer integral (Fs0) in Equation (9) (from R to infinity) yields:
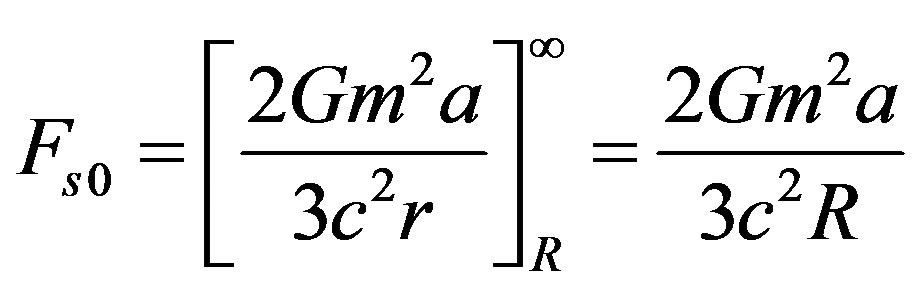 (10)
(10)
For the inner integral, Fsi (assuming a constant density) we put:
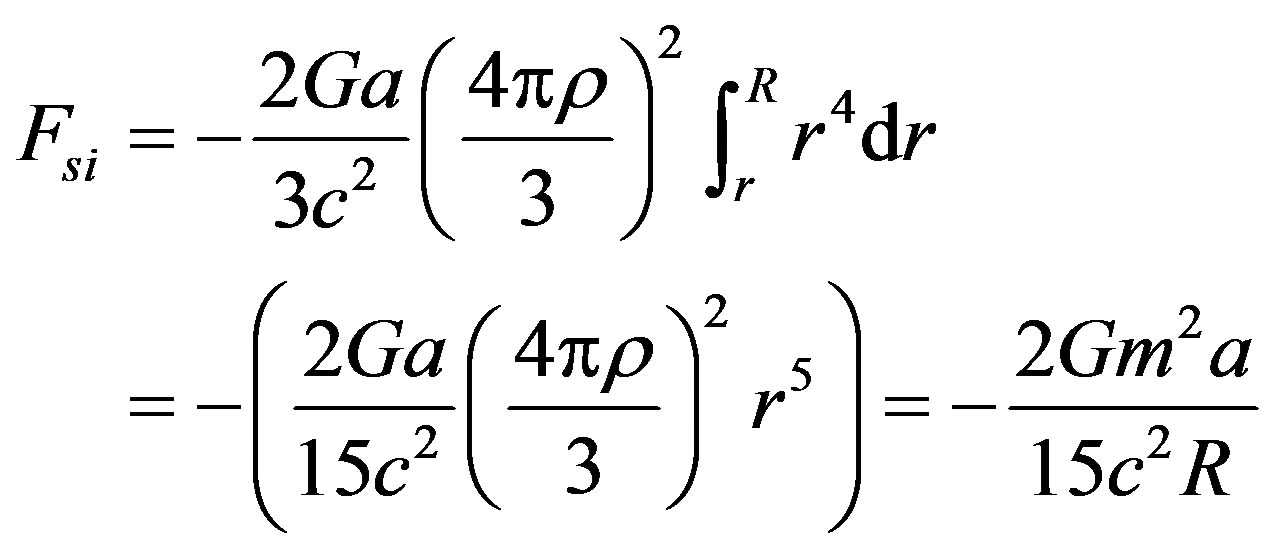 (0 ... R) (11)
(0 ... R) (11)
Adding Equations (10) and (11), we find:
 (12)
(12)
This can be written as:
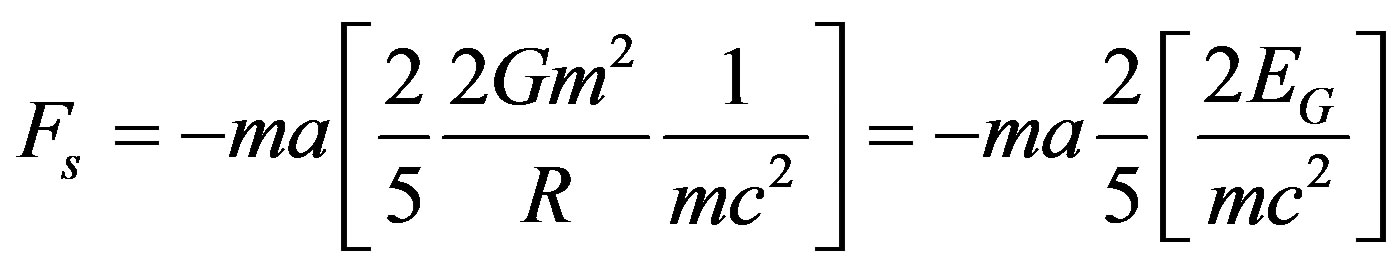 (13)
(13)
where EG is the gravitational energy of the object. The term in the square brackets in Equation (13), is actually of the form of the fine structure constant used in quantum mechanics [14]:
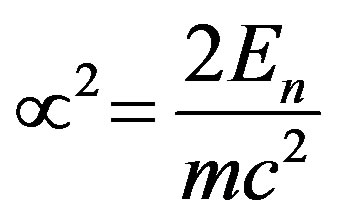
In a similar way, we may define a fine structure constant for inertia  by:
by:
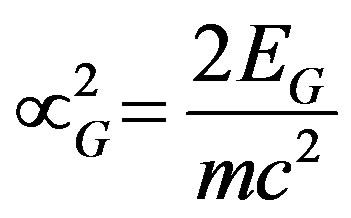
To get:
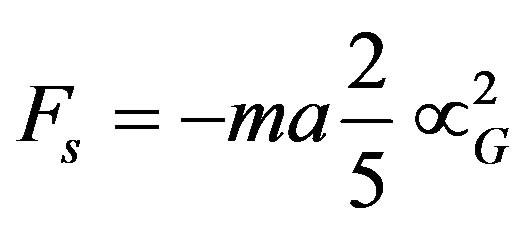 (13’)
(13’)
which shows that the stress force created in the curved gravitational field of the accelerated mass, is a part of the inertial force which acts against the acceleration.
4. The Fine Structure Constant for the Acceleration of a Black Hole
When the equations for the gravitational fine structure constant are implemented for a black hole, we do not calculate the reaction force created inside the object, since we have no hint about how do the mass inside the black hole is distributed. We calculate the reaction force in the space around the black hole, from its Schwarzschild radius, up to infinity. We multiply fsP by the Schwarzschild volume element:
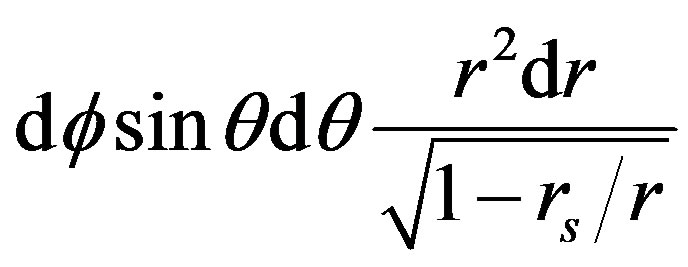 , where
, where 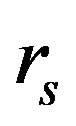 is the Schwarzschild radius of the mass. The integration over the angles again yields:
is the Schwarzschild radius of the mass. The integration over the angles again yields: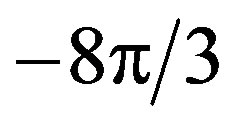 .
.
After the integration over the angles we have:
 (14)
(14)
The integral in Equation (14) yields:
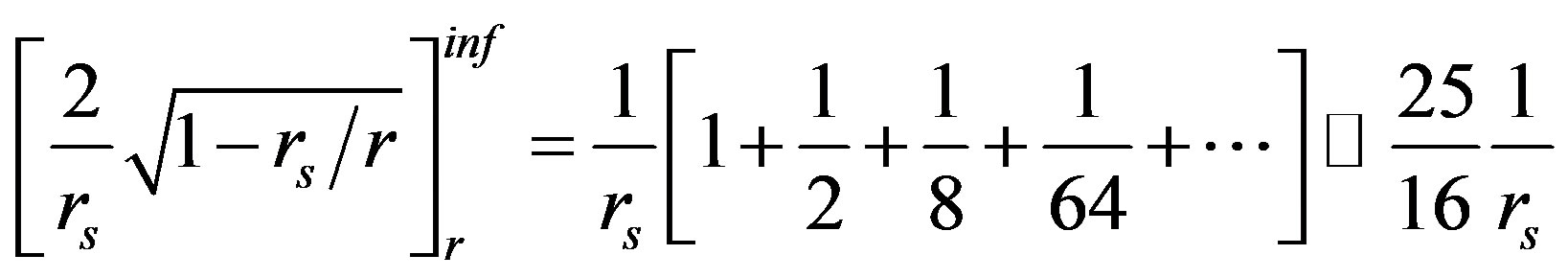 (15)
(15)
This result is obtained by expanding the square root like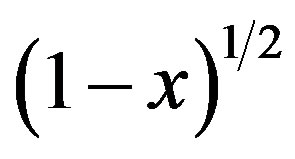 . Thus we have for the stress force, Fs:
. Thus we have for the stress force, Fs:
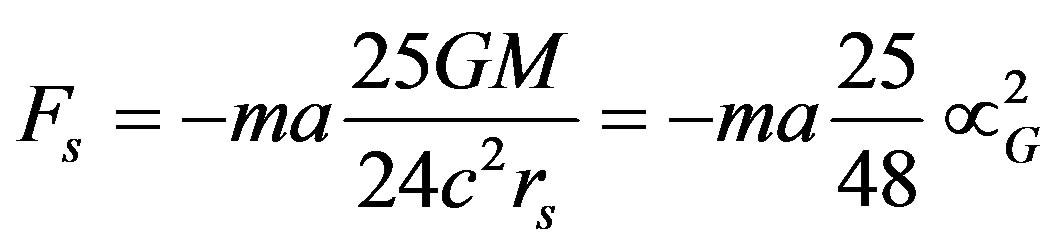 (16)
(16)
For a black hole, 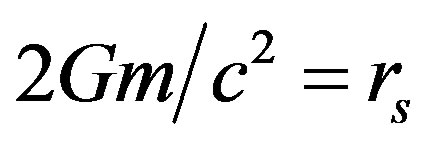 , so
, so , and we have:
, and we have:
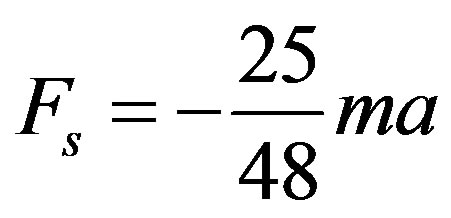 (16’)
(16’)
5. Conclusion
We find that when a mass is accelerated in free space, its gravitational field curves, due to the fact that the field is not accelerated with the mass—it is induced on space from the points along the mass trajectory. Due to this curvature, a stress force is created in the curved gravitational field, which acts on the accelerated mass as a reaction force. The external (accelerating) force has to overcome this reaction force, in order to maintain the acceleration. Calculation of this reaction force shows that, a kind of a “fine structure constant” appears in these calculations, which is equal to:  (where
(where 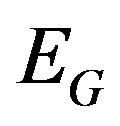 is the gravitational energy of the accelerated mass). This reaction force is a part of the inertial force, which contradicts the acceleration.
is the gravitational energy of the accelerated mass). This reaction force is a part of the inertial force, which contradicts the acceleration.
REFERENCES
- J. A. Wheeler, “Geometro Dynamic,” Academic Press, New York, 1962.
- D. W. Sciama, “The Unity of the Universe,” Faber and Faber, London, 1959.
- E. N. Parker, “Cosmical Magnetic Fields,” Clarendon Press, Oxford, 1979.
- E. R. Priest, “Solar Magneto-Hydrodynamics,” Reidel Pub. Company, Dordrecht, 1984.
- W. Rindler, “Special Relativity,” Oliver & Boyd, Edinburgh, 1966.
- A. Gupta and T. Padmanabhan, “Radiation from a Charged Particle and Radiation Reaction Reexamined,” Physical Review D, Vol. 57, No. 12, 1998, pp. 7241-7250. http://dx.doi.org/10.1103/PhysRevD.57.7241
- G. A. Schott, “Electromagnetic Radiation,” Cambridge University Press, Cambridge, 1912.
- R. Fulton and F. Rohrlich, “Classical Radiation from a Uniformly Accelerated Charge,” Annals of Physics, Vol. 9, No. 4, 1960, pp. 499-517. http://dx.doi.org/10.1016/0003-4916(60)90105-6
- A. Einstein and L. Infeld, “The Evolution of Physics,” Simon and Schuster, New York, 1938.
- L. D. Landau and E. M. Lifshitz, “Classical Theory of Fields,” 3rd Edition, Pergamon Press, Oxford, 1971, 45p.
- A. Harpaz and N. Soker, “Equation of Motion of an Electric Charge,” Foundations of Physics, Vol. 33, No. 8, 2003, pp. 1207-1221. http://dx.doi.org/10.1023/A:1025627024534
- A. Harpaz, “Electric Field in a Gravitational Field,” Foundations of Physics, Vol. 37, No. 4-5, 2007, pp. 763-772. http://dx.doi.org/10.1007/s10701-007-9118-8
- A. K. Singal, “The Equivalence Principle and an Electric Charge in a Gravitational Field II. A Uniformly Accelerated Charge Does Not Radiate,” General Relativity and Gravitation, Vol. 29, No. 11, 1997, pp. 1371-1390. http://dx.doi.org/10.1023/A:1018830012340
- H. L. Liboff, “Quantum Mechanics,” Addison Wessley, Reading, 1992.

