International Journal of Astronomy and Astrophysics
Vol.3 No.3(2013), Article ID:36511,14 pages DOI:10.4236/ijaa.2013.33029
Window Effect in the Power Spectrum Analysis of a Galaxy Redshift Survey
1Graduate School of Physical Sciences, Hiroshima University, Higashi-Hiroshima, Japan
2Tartu Observatory, Tõrevere, Estonia
Email: kazuhiro@hiroshima-u.ac.jp
Copyright © 2013 Takahiro Sato et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received July 7, 2013; revised August 9, 2013; accepted August 16, 2013
Keywords: Cosmology; Large-Scale Structure of Universe
ABSTRACT
We investigate the effect of the window function on the multipole power spectrum in two different ways. First, we consider the convolved power spectrum including the window effect, which is obtained by following the familiar (FKP) method developed by Feldman, Kaiser and Peacock. We show how the convolved multipole power spectrum is related to the original power spectrum, using the multipole moments of the window function. Second, we investigate the deconvolved power spectrum, which is obtained by using the Fourier deconvolution theorem. In the second approach, we measure the multipole power spectrum deconvolved from the window effect. We demonstrate how to deal with the window effect in these two approaches, applying them to the Sloan Digital Sky Survey (SDSS) luminous red galaxy (LRG) sample.
1. Introduction
One of the most fundamental problems in cosmology is the origin of an accelerated expansion of the Universe [1,2]. A hypothetical energy component, dark energy, may explain the accelerated expansion [3]. Modification of the gravity theory is an alternative way to explain it. In either case, this problem seems to be deeply rooted in the nature of fundamental physics, which has attracted many researchers. Dark energy surveys which aim at measuring redshifts of huge number of galaxies are in progress or planned [4,5]. These surveys provide us with a chance to test the hypothetical dark energy, as well as the gravity theory on the scales of cosmology. A key for distinguishing between the dark energy and modified gravity theory is a measurement of the evolution of cosmological perturbations.
Galaxy redshift surveys provide promising ways of measuring the dark energy properties. Here, a measurement of the baryon acoustic oscillations in the galaxy distribution plays a key role. Also, the spatial distribution of galaxies is distorted due to the peculiar motions, which is called the redshift-space distortion. The Kaiser effect is the redshift-space distortion in the linear regime of the density perturbations. It is caused by the bulk motion of galaxies [6]. The measurement of the Kaiser effect is thought to be useful for testing the general relativity and other modified gravity theories [7-9]. In these analyses, measuring the multiple power spectrum in the distribution of galaxies plays a key role (cf. [10,11]).
The multipole power spectrum is useful for measuring the redshift-space distortion [12-18]. The usefulness of the quadrupole power spectrum to constrain modified gravity models is demonstrated in Refs. [19,20], as well as the dark energy model [21]. An estimator of the quadrupole power spectrum is developed in Ref. [16]. However, the disadvantage of the method is not being compatible with the use of the fast Fourier transform (FFT). In the present paper, we consider different estimators of the quadrupole power spectrum which allows the use of the FFT. In this method, a full sample of a wide survey area is divided into smaller subsamples with equal areas. This approach was taken in Refs. [14,15]. In this case, the effect of the window function is crucial as we will show in the present paper. Thus, it must be properly taken into account when comparing the observational data with theoretical predictions.
The convolved power spectrum includes the effect of the window function [22-25]. In the first half of the present paper, we consider the convolved power spectrum. We develop a theoretical formula to incorporate the window effect into the multipole power spectra for the first time. We apply this formula to the Sloan Digital Sky Survey (SDSS) luminous red galaxy (LRG) sample from the data release (DR) 7, and investigate the behavior of the window function and its effect on the monopole and quadrupole spectra. We demonstrate how the window effect modifies the monopole spectrum and the quadrupole spectrum. In the second half, we consider the deconvolved power spectrum, which is developed in Ref. [26], and compare it with the results of the first approach.
This paper is organized as follows: In Section 2, we briefly review the power spectrum analysis and the window effect, where the convolved power spectrum is introduced. In Section 3, using the multipole moments of the window function, we derive the main formula to describe how the convolved multipole power spectrum is related to the original power spectrum. Then, a method to measure the multipole moments of the window function is presented. We also apply the method to the SDSS LRG DR 7. In Section 4, the method for measuring the deconvolved power spectrum is reviewed. Then, a comparison of the two approaches is given. Section 5 is devoted to summary and conclusions. In the appendix, we give a brief review of a theoretical model, which we adopted. Throughout this paper, we use units in which the velocity of light equals 1, and adopt the Hubble parameter  with
with .
.
2. Basic Formulas of the FKP Method
Let us first summarize the power spectrum analysis developed by Feldman, Kaiser and Peacock ([27], hereafter FKP). With this formulation we obtain the convolved power spectrum, including the window effect. We denote the number density field of galaxies by , where
, where  is the three-dimensional coordinate in the (fiducial) redshift space,
is the three-dimensional coordinate in the (fiducial) redshift space,  is the unit directional vector, and
is the unit directional vector, and 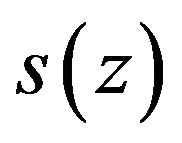 is the comoving distance of a fiducial cosmological model. According to Ref. [27], we introduce the fluctuation field
is the comoving distance of a fiducial cosmological model. According to Ref. [27], we introduce the fluctuation field
 (1)
(1)
where , with
, with  being the location of the
being the location of the  th object; similarly,
th object; similarly,  is the density of a synthetic catalog that has a mean number density
is the density of a synthetic catalog that has a mean number density  times that of the galaxy catalog. In the present paper, we adopt
times that of the galaxy catalog. In the present paper, we adopt . The synthetic catalog is a set of random points without any correlation, which can be constructed through a random process by mimicking the selection function of the galaxy catalog. For
. The synthetic catalog is a set of random points without any correlation, which can be constructed through a random process by mimicking the selection function of the galaxy catalog. For 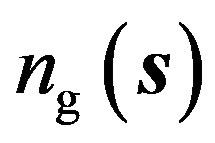 and
and , we assume
, we assume
 (2)
(2)
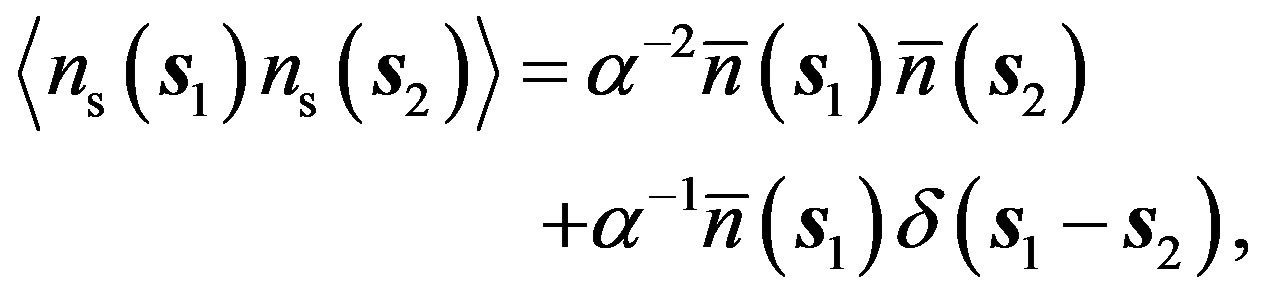 (3)
(3)
 (4)
(4)
where  denotes the mean number density of the galaxies, and
denotes the mean number density of the galaxies, and  is the two-point correlation function. These relations lead to
is the two-point correlation function. These relations lead to
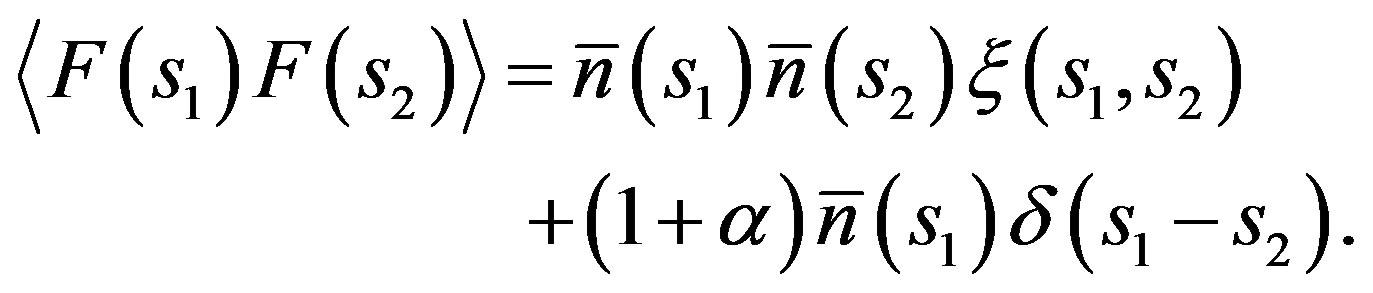 (5)
(5)
We introduce the Fourier coefficient of 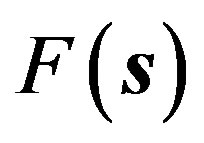 by
by
 (6)
(6)
where 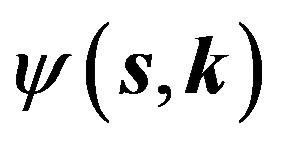 is the weight function (Throughout this paper, we assume
is the weight function (Throughout this paper, we assume ). The expectation value of
). The expectation value of
 is
is
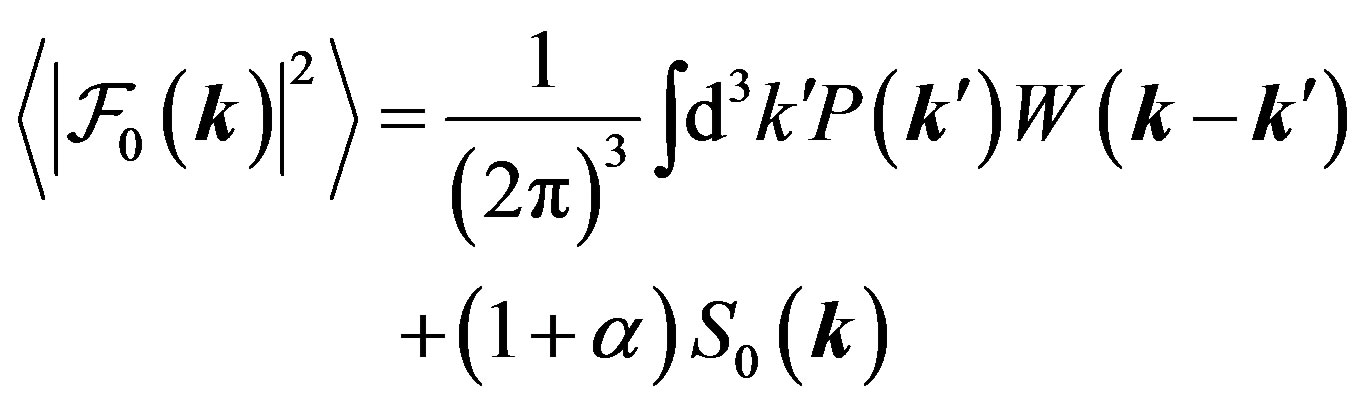 (7)
(7)
with
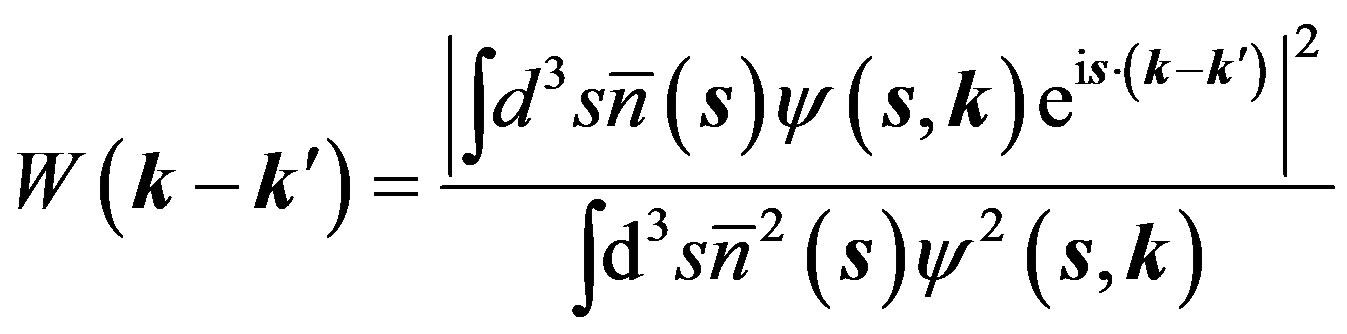 (8)
(8)
and
 (9)
(9)
where we used
 (10)
(10)
Here,  is the window function and
is the window function and 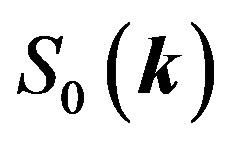 is the shotnoise. The estimator of the convolved power spectrum is taken
is the shotnoise. The estimator of the convolved power spectrum is taken
 (11)
(11)
whose expectation value is
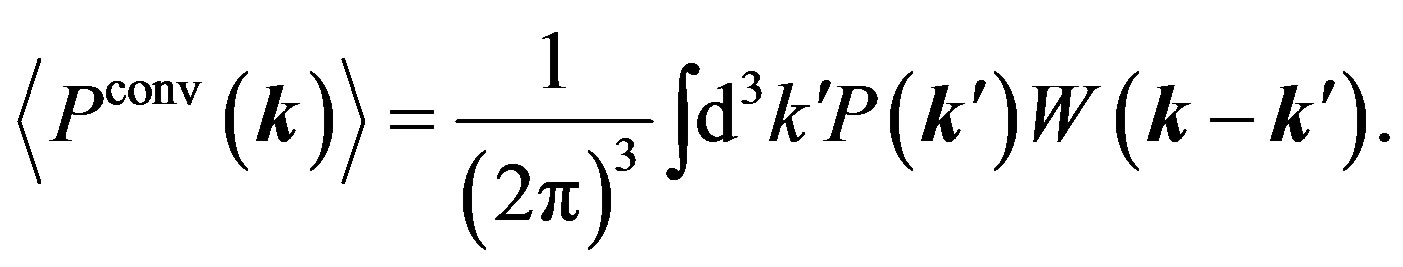 (12)
(12)
Hereafter, we omit , for simplicity.
, for simplicity.
3. Convolved Power Spectrum
In this section, using the multipole moments of the window function, we drive the main formulas for the convolved multipole power spectrum, Equations (33) and (34), which describe the relations between the convolved multipole power spectrum and the original multipole spectrum. We exemplify the behavior of the multipole moments of the window function and the convolved spectra, using the SDSS LRG sample from the DR 7.
3.1. Formulation
The estimator of the monopole power spectrum should be taken as
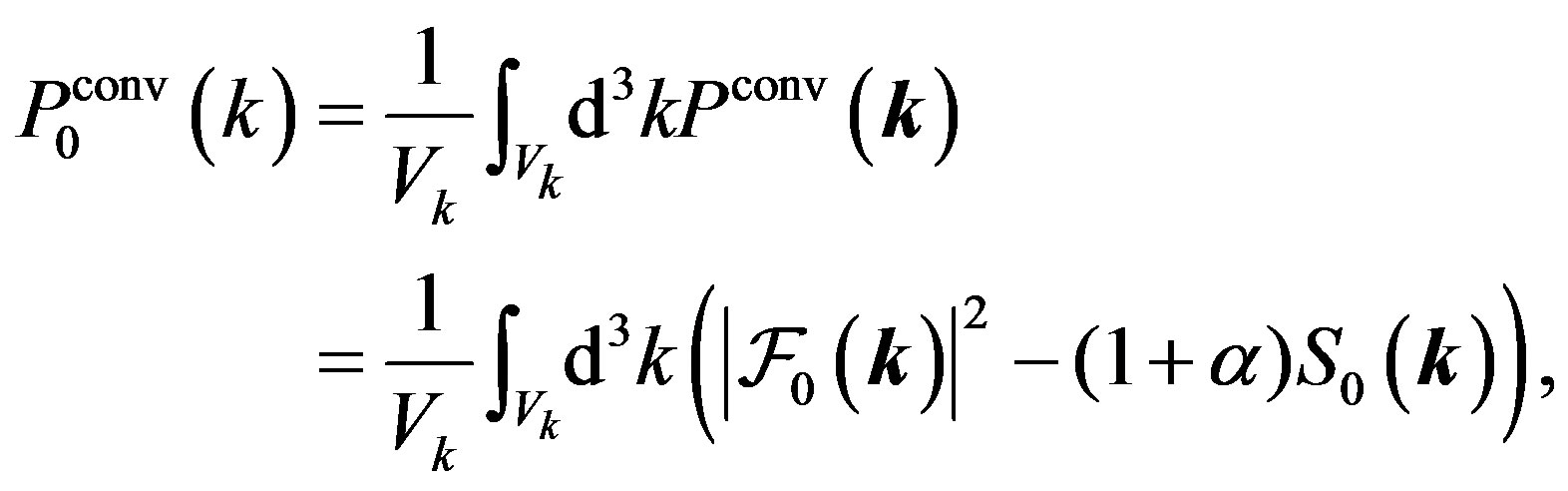 (13)
(13)
where  is the volume of the shell in the
is the volume of the shell in the 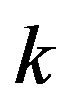 -space. Similarly, a higher multipole power spectrum can be obtained [16]. Using the quantity
-space. Similarly, a higher multipole power spectrum can be obtained [16]. Using the quantity
 (14)
(14)
where  is the Legendre polynomial, and
is the Legendre polynomial, and  is the unit wavenumber vector
is the unit wavenumber vector , the estimator for the higher multipole power spectrum should be taken as (cf. [16])
, the estimator for the higher multipole power spectrum should be taken as (cf. [16])
 (15)
(15)
with
 (16)
(16)
The expectation value of Equation (15) is
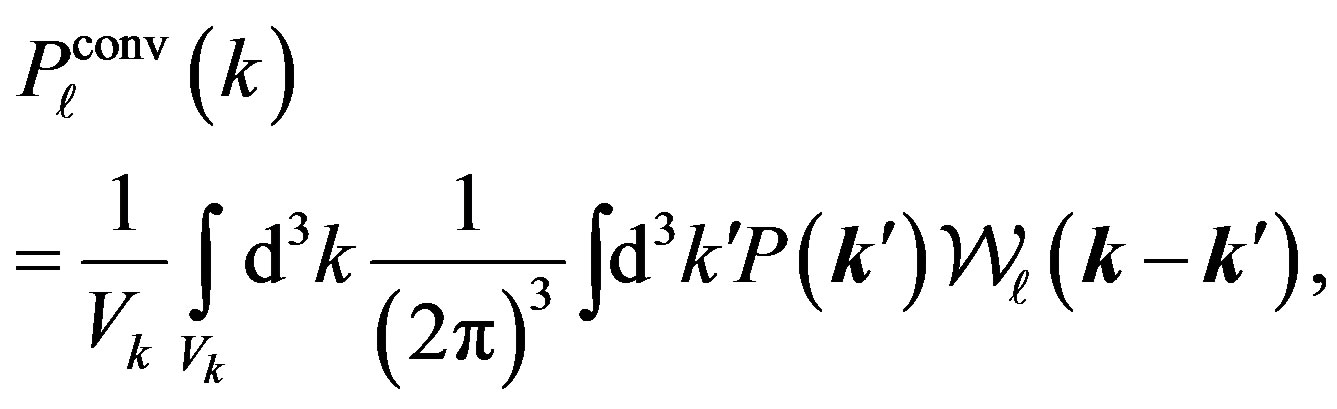 (17)
(17)
where we defined
 (18)
(18)
By adopting the distant observer approximation, we have
 (19)
(19)
and
 (20)
(20)
where  is the unit vector along the line of sight. We consider the shell in the Fourier space whose outer (inner) radius is
is the unit vector along the line of sight. We consider the shell in the Fourier space whose outer (inner) radius is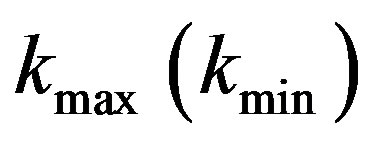 . The volume of the shell is
. The volume of the shell is 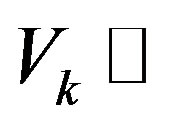
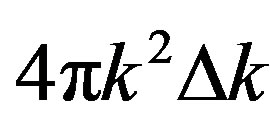 where
where  and
and , then
, then
 (21)
(21)
Let us consider the limit , then we have
, then we have
 (22)
(22)
Note that our definition of the multipole spectrum  is different from the conventional one by the factor
is different from the conventional one by the factor  [12,13].
[12,13].
Now we introduce the coordinate variables to describe  and
and . For
. For  and
and , we adopt
, we adopt
 (23)
(23)
respectively. As we consider the power spectrum and the window function averaged over the longitudinal variable around the axis of the direction , we may choose
, we may choose  so that
so that 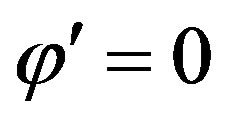 without loss of generality. Then, we choose the coordinate variable to describe
without loss of generality. Then, we choose the coordinate variable to describe 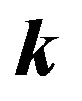 as
as
 (24)
(24)
where  and
and 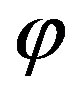 are the angle coordinates around
are the angle coordinates around  so as to be the polar axis. The matrix of the right hand side of Equation (24) denotes the rotation around the y-axis. See Figure 1 for the configuration. Note that
so as to be the polar axis. The matrix of the right hand side of Equation (24) denotes the rotation around the y-axis. See Figure 1 for the configuration. Note that
 (25)
(25)
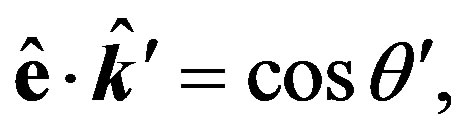 (26)
(26)
 (27)
(27)
Assuming the following formula within the distant observer approximation,
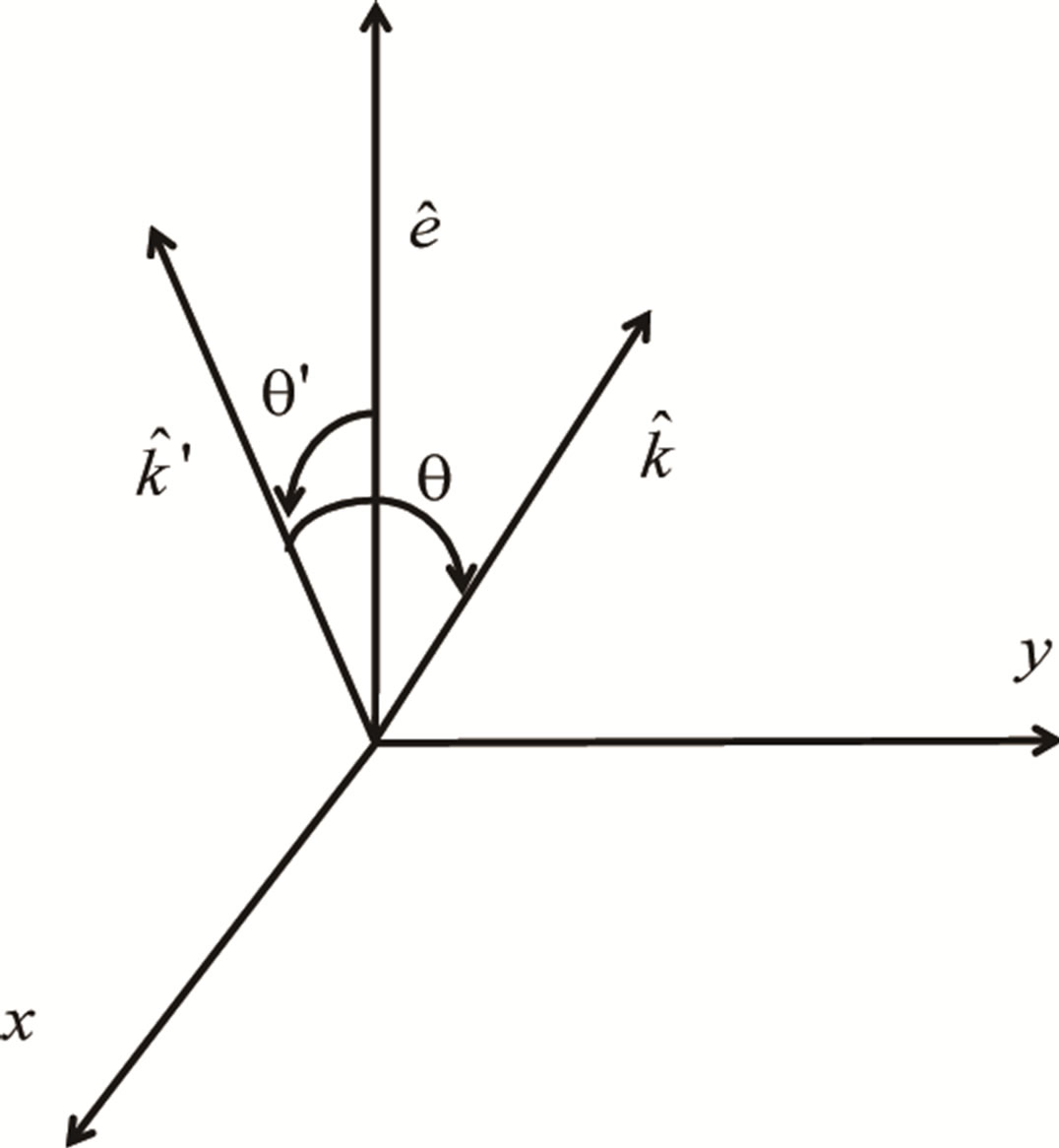
Figure 1. A sketch of the configuration of the vectors and coordinate variables.
 (28)
(28)
and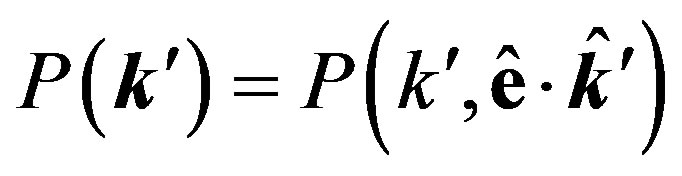 , Equation (20) yields
, Equation (20) yields
 (29)
(29)
Using (25), (26), and (23), we can write Equation (29) as
 (30)
(30)
 (31)
(31)
where . Using the relation
. Using the relation
 (32)
(32)
we obtain
 (33)
(33)
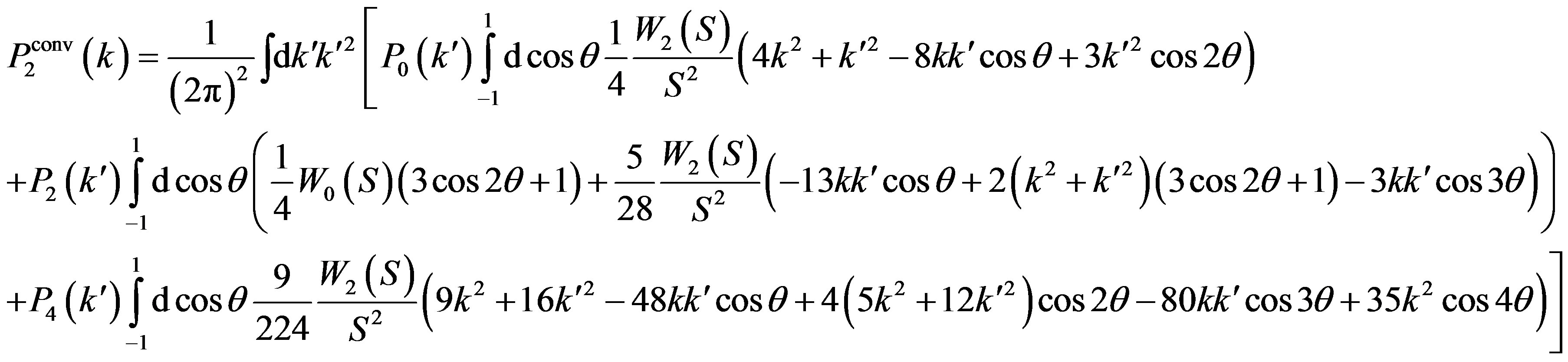 (34)
(34)
These formulas describe how the convolved spectra,  and
and , are modified due to the window effect, compared with the original spectrum. Using Equations (33) and (34), we define the quantity,
, are modified due to the window effect, compared with the original spectrum. Using Equations (33) and (34), we define the quantity,
 (35)
(35)
which is the correction factor connecting the original spectrum and the convolved power spectrum.
3.2. Measurement of the Multipole Moments of the Window Function
In this subsection, we explain a method to measure the multipole moment of the window function. The window function can be evaluated using the random catalog in a similar way of evaluating the power spectrum. Similar to the case of the power spectrum, we need to subtract the shotnoise contribution. Then, we adopt the following estimator for the window function , corresponding to the right hand side of Equation (8),
, corresponding to the right hand side of Equation (8),
 (36)
(36)
We consider the window function expanded in the form of Equation (28). Mimicking the method to obtain the multipole power spectrum, we introduce
 (37)
(37)
and use the following estimator for the multipole moment of the window function,
 (38)
(38)
In the present work, we use the SDSS public data from the DR7 [28]. Our LRG sample is restricted to the redshift range  -
- . In order to reduce the sidelobes of the survey window we remove some noncontiguous parts of the sample, which leads us to 7150 deg2 sky coverage with the total number
. In order to reduce the sidelobes of the survey window we remove some noncontiguous parts of the sample, which leads us to 7150 deg2 sky coverage with the total number  LRGs. The data reduction is the same as that described in Refs. [19,20,29,30]. In this subsection, we show general features of the window function of the LRG sample. In our approach, division of the full sample into subsamples is necessary because the line of sight direction is approximated by one direction
LRGs. The data reduction is the same as that described in Refs. [19,20,29,30]. In this subsection, we show general features of the window function of the LRG sample. In our approach, division of the full sample into subsamples is necessary because the line of sight direction is approximated by one direction , and the distant observer approximation is required. Each subsample is distributed in a narrow area. We consider the three cases of the division, which are demonstrated in Figure 2. The full sample is divided into 18, 32, and 72 subsamples, respectively. In those divisions of the full sample, each subsample has almost the same survey area, 398, 223, and 99 square degrees, respectively. Figure 2 shows the cases divided into 18 subsamples, 32 subsamples and 72 subsamples. Figure 3 shows
, and the distant observer approximation is required. Each subsample is distributed in a narrow area. We consider the three cases of the division, which are demonstrated in Figure 2. The full sample is divided into 18, 32, and 72 subsamples, respectively. In those divisions of the full sample, each subsample has almost the same survey area, 398, 223, and 99 square degrees, respectively. Figure 2 shows the cases divided into 18 subsamples, 32 subsamples and 72 subsamples. Figure 3 shows 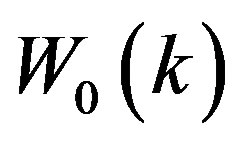 and
and  as a function of
as a function of , which are obtained by averaging the results over all subsamples. As demonstrated in Figure 3,
, which are obtained by averaging the results over all subsamples. As demonstrated in Figure 3,  and
and  can be fitted in the form,
can be fitted in the form,
 (39)
(39)
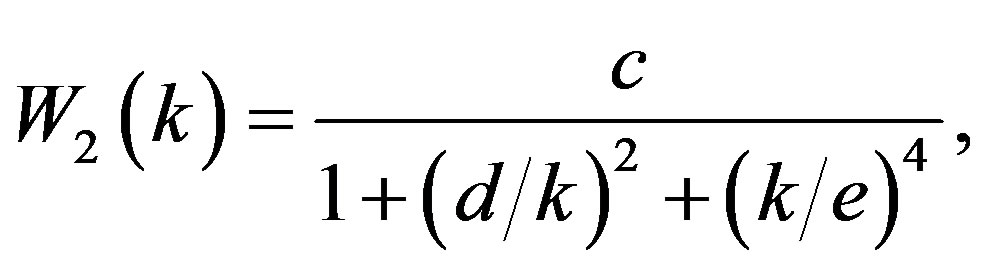 (40)
(40)
where the best fitting parameters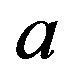 ,
,  ,
,  ,
,  and
and , which depend on the division of the full sample, are given in Table 1.
, which depend on the division of the full sample, are given in Table 1.
3.3. Measurement of the Convolved Power Spectrum
Let us demonstrate the convolved multiple power spectrum using the SDSS LRG sample from DR7. Figure 4

Figure 2. Angular distribution of the SDSS LRG sample. In the present paper, we consider the three cases of the division of the full sample into subsamples. This figure shows the three cases of the division, where the full sample is divided into 18 subsamples (upper panel), 32 subsamples (middle panel) and 72 subsamples (lower panel), with mean area of 397 square degrees, 223 square degrees and 99 square degrees per patch, respectively.

Figure 3.  and
and 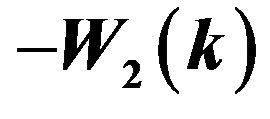 as a function of
as a function of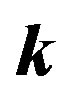 . The top left panel corresponds to the full sample without division into subsamples. In this case
. The top left panel corresponds to the full sample without division into subsamples. In this case 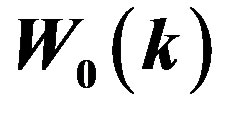 can be measured properly, but
can be measured properly, but  can not. The other three panels represent the cases where the full sample is divided into 18, 32, and 72 subsamples, with mean area 397, 223, and 99 square degrees per patch, respectively. The curves are the analytic functions, Equations (39) and (40) for
can not. The other three panels represent the cases where the full sample is divided into 18, 32, and 72 subsamples, with mean area 397, 223, and 99 square degrees per patch, respectively. The curves are the analytic functions, Equations (39) and (40) for 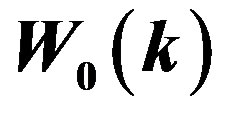 and
and , respectively.
, respectively.
Table 1. Values of the best fitting parameters for 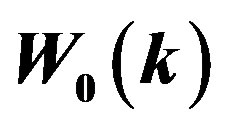 and
and 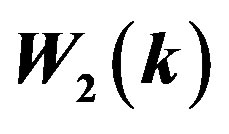 in Equations (39) and (40), respectively.
in Equations (39) and (40), respectively.



Figure 4. Convolved monopole power spectrum multiplied by the wavenumber  (left panel) and the quadrupole spectrum
(left panel) and the quadrupole spectrum  (right panel), respectively. In the left panel the curves from top to bottom correspond to the cases with no division of the full sample, to the division into 18, into 32, and into 72 subsamples, respectively. In the right panel, the results are for the cases with the division of the full sample into 18, into 32, and into 72 subsamples, respectively. The results with smaller subsamples have the smaller amplitude.
(right panel), respectively. In the left panel the curves from top to bottom correspond to the cases with no division of the full sample, to the division into 18, into 32, and into 72 subsamples, respectively. In the right panel, the results are for the cases with the division of the full sample into 18, into 32, and into 72 subsamples, respectively. The results with smaller subsamples have the smaller amplitude.
shows the monopole spectrum  (left panel) and the quadrupole spectrum
(left panel) and the quadrupole spectrum  (right panel), respectively. The results with different divisions of the full sample are plotted. Thus, due to varying strength of the window convolution, the spectrum depends on the particular division of the full sample. The amplitude of the convolved power spectrum in Figure 4 is smaller for divisions with smaller patch sizes. Thus, the window effect is more influential for divisions with smaller patches.
(right panel), respectively. The results with different divisions of the full sample are plotted. Thus, due to varying strength of the window convolution, the spectrum depends on the particular division of the full sample. The amplitude of the convolved power spectrum in Figure 4 is smaller for divisions with smaller patch sizes. Thus, the window effect is more influential for divisions with smaller patches.
Figure 5 plots 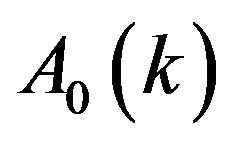 defined by Equation (35) for the monopole spectrum
defined by Equation (35) for the monopole spectrum . The curves are obtained by computing Equation (33) with
. The curves are obtained by computing Equation (33) with 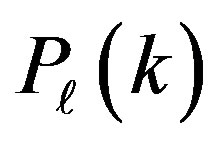 corresponding to a spatially flat cold dark matter model with cosmological constant and
corresponding to a spatially flat cold dark matter model with cosmological constant and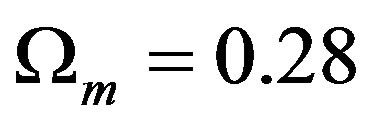 , and with the window function shown in Figure 3. For the power spectrum we used the nonlinear model, Equation (50), given in the appendix, where the transfer function without the baryon oscillations is used [31], for simplicity. The three curves in Figure 5 assume different divisions of the full sample, whose patch sizes are shown in the legend.
, and with the window function shown in Figure 3. For the power spectrum we used the nonlinear model, Equation (50), given in the appendix, where the transfer function without the baryon oscillations is used [31], for simplicity. The three curves in Figure 5 assume different divisions of the full sample, whose patch sizes are shown in the legend.
As shown in Figure 4, the amplitude of the convolved power spectrum depends on the division and the mean size of the subsamples. The amplitude becomes smaller when the mean patch area is reduced. Figure 6" target="_self"> Figure 6 shows the power spectrum , where
, where  is obtained by evaluating Equation (33), assuming the theoretical model from Figure 5. The amplitude of the power spectra becomes almost the same, which means that the amplitude is correctly restored, i.e., the window effect is properly treated by Equation (33).
is obtained by evaluating Equation (33), assuming the theoretical model from Figure 5. The amplitude of the power spectra becomes almost the same, which means that the amplitude is correctly restored, i.e., the window effect is properly treated by Equation (33).
Figure 7 shows 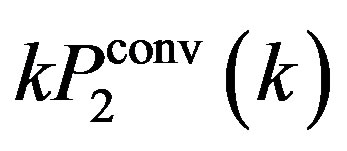 for different divisions of the full sample, with mean patch sizes
for different divisions of the full sample, with mean patch sizes  (a, left panel),
(a, left panel), 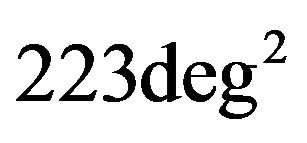 (b, center panel),
(b, center panel), 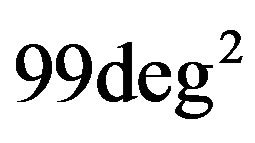 (c, right panel), respectively. The squares with error bars present
(c, right panel), respectively. The squares with error bars present  from the SDSS LRG sample, while the
from the SDSS LRG sample, while the

Figure 5.  as a function of
as a function of  for different divisions of the full sample. From the top to the bottom, the curves correspond to the cases with no division of the full sample, to the division into 18, 32, and 72 subsamples, respectively. Here, we assumed the
for different divisions of the full sample. From the top to the bottom, the curves correspond to the cases with no division of the full sample, to the division into 18, 32, and 72 subsamples, respectively. Here, we assumed the  cosmology with
cosmology with ,
,  ,
,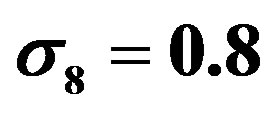 . The nonlinear power spectrum model, Equation (50), with
. The nonlinear power spectrum model, Equation (50), with  is adopted.
is adopted.
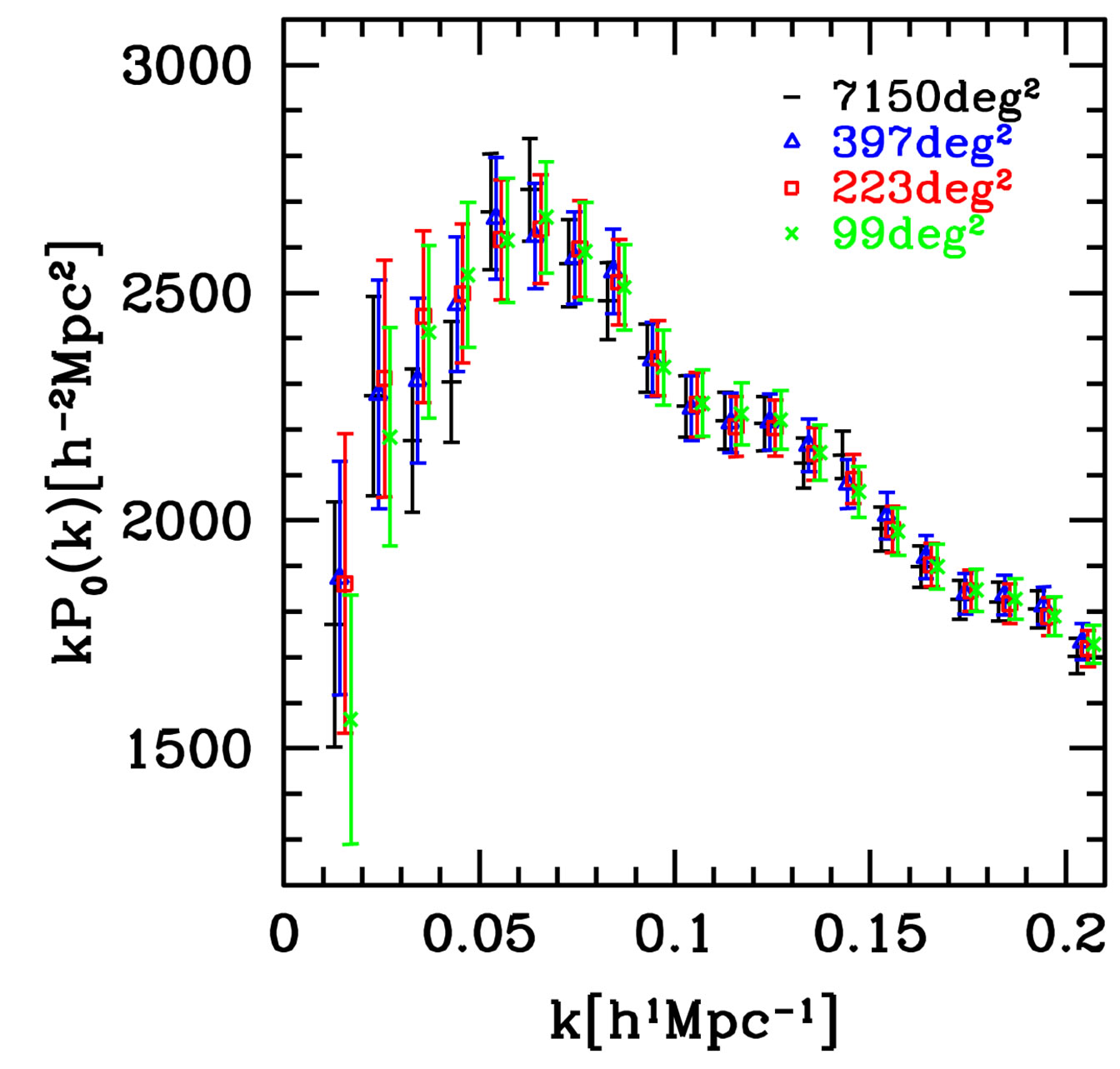
Figure 6. Convolved monopole spectrum divided by the factor , i.e.,
, i.e.,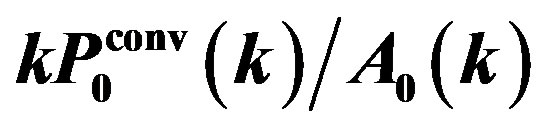 .
.
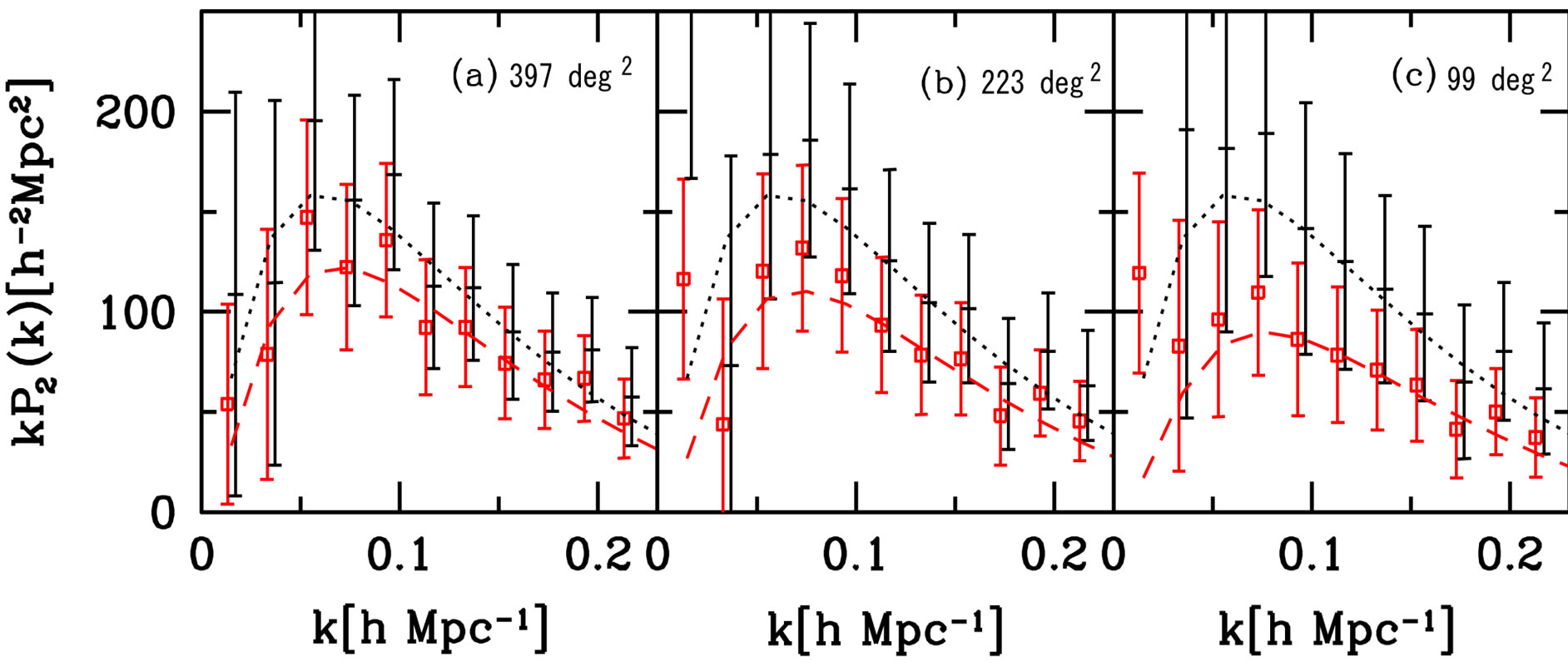
Figure 7. Quadrupole power spectra multiplied by the wavenumber 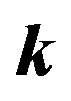 for different divisions of the full sample, with mean survey areas
for different divisions of the full sample, with mean survey areas  (a, left panel),
(a, left panel),  (b, center panel), and
(b, center panel), and  (c, right panel), respectively. The dotted curve is our theoretical model for
(c, right panel), respectively. The dotted curve is our theoretical model for , while the dashed curve is
, while the dashed curve is 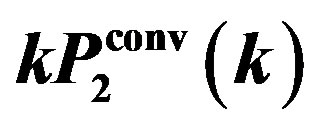 from Equation (34), where we used the same theoretical model as that in Figure 3. The squares with the error bars present the observed convolved spectrum,
from Equation (34), where we used the same theoretical model as that in Figure 3. The squares with the error bars present the observed convolved spectrum, . The dashes with the error bars show
. The dashes with the error bars show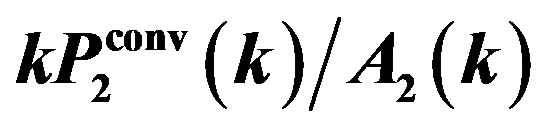 .
.
dashes with error bars show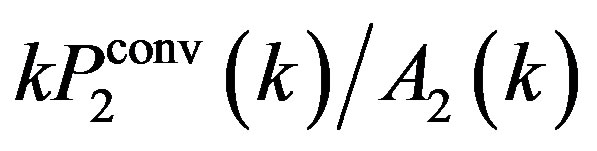 , where
, where
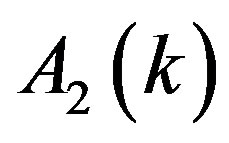 is obtained by computing Equation (34) in the same way as
is obtained by computing Equation (34) in the same way as . The dotted curves give the theoretical model for
. The dotted curves give the theoretical model for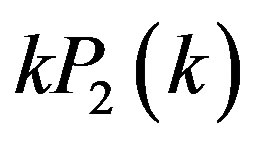 , where we used the same theoretical model as that in Figure 5. The dashed curves are the corresponding
, where we used the same theoretical model as that in Figure 5. The dashed curves are the corresponding , which are obtained by computing Equation (34). The ratio of the dashed curve to the dotted curve gives
, which are obtained by computing Equation (34). The ratio of the dashed curve to the dotted curve gives .
.
4. Deconvolved Power Spectrum
4.1. Formulation
In this section, we briefly review the method for deconvolving the window effect in the power spectrum measurement, which was developed in Ref. [26]. Taking the Fourier transform of Equation (12), we have
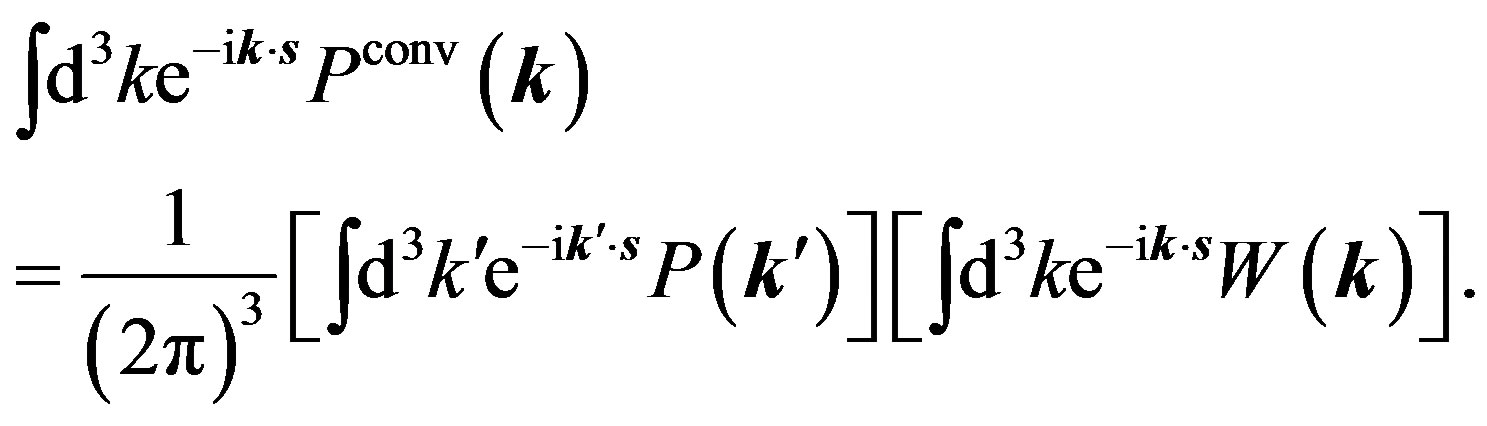 (41)
(41)
The inverse transformation of
 (42)
(42)
leads to
 (43)
(43)
In the case of a discrete density field of a galaxy catalog, we must also take the shotnoise into account. The estimators for the convolved power spectrum and the window function are Equations (11) and (36), respectively. We choose the estimator for the deconvolved power spectrum as
 (44)
(44)
where we defined
 (45)
(45)
 (46)
(46)
One can measure the deconvolved multipole power spectra from Equation (44) by
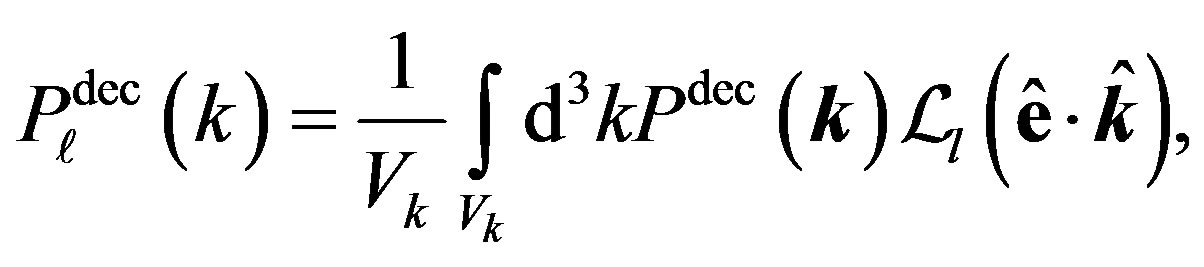 (47)
(47)
where 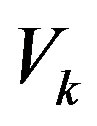 is a shell in the Fourier space. This deconvolved multipole power spectrum can be compared with theoretical predictions directly without taking the window effect into account.
is a shell in the Fourier space. This deconvolved multipole power spectrum can be compared with theoretical predictions directly without taking the window effect into account.
4.2. Comparison between the Convolved Spectrum and the Deconvolved Spectrum
Figure 8 compares the convolved and deconvolved power spectra of the LRG galaxy sample in the range of redshifts  (red crosses),
(red crosses), 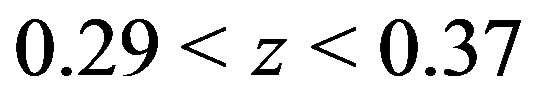 (blue bars) and
(blue bars) and  (green squares). The left panels are the monopole spectra, while the right ones are the quadrupole spectra, multiplied by the wavenumber. The upper panels are the deconvolved power spectra, while the lower ones the convolved spectra, where we used the division of the full sample into 18 subsamples with mean area 397 square degrees. The amplitude of the deconvolved spectrum is larger than that of the convolved spectrum. Figure 9 shows the multipole moments of the window function of the LRG galaxy sample
(green squares). The left panels are the monopole spectra, while the right ones are the quadrupole spectra, multiplied by the wavenumber. The upper panels are the deconvolved power spectra, while the lower ones the convolved spectra, where we used the division of the full sample into 18 subsamples with mean area 397 square degrees. The amplitude of the deconvolved spectrum is larger than that of the convolved spectrum. Figure 9 shows the multipole moments of the window function of the LRG galaxy sample 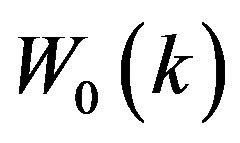 (black large crosses) and
(black large crosses) and  (red small crosses) for the redshift ranges
(red small crosses) for the redshift ranges 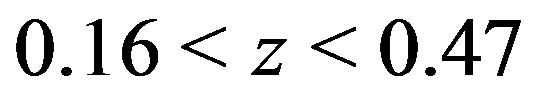 (upper left panel),
(upper left panel), 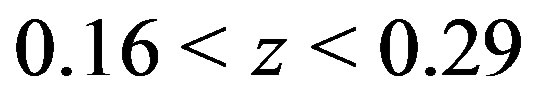 (upper right panel),
(upper right panel),  (lower left panel), and
(lower left panel), and 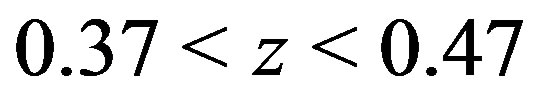 (lower right panel), respectively. Here each redshift bin is divided into 18 angular subsamples whose mean area is 397 square degrees. The amplitude of
(lower right panel), respectively. Here each redshift bin is divided into 18 angular subsamples whose mean area is 397 square degrees. The amplitude of  in the limit of small
in the limit of small 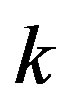 is larger when the survey volume is larger. The sign of
is larger when the survey volume is larger. The sign of  depends on the shape of the subsamples.
depends on the shape of the subsamples.
4.3. Covariance Matrix
In the following we determine the covariance matrices by utilizing mock catalogs corresponding to the SDSS LRG sample. Our mock catalogs are built by following the procedure described in Ref. [29]. The covariance matrices for the multipole spectra are defined by
 (48)
(48)
The correlation matrices, which describe the correlations between different wavenumbers, are defined by
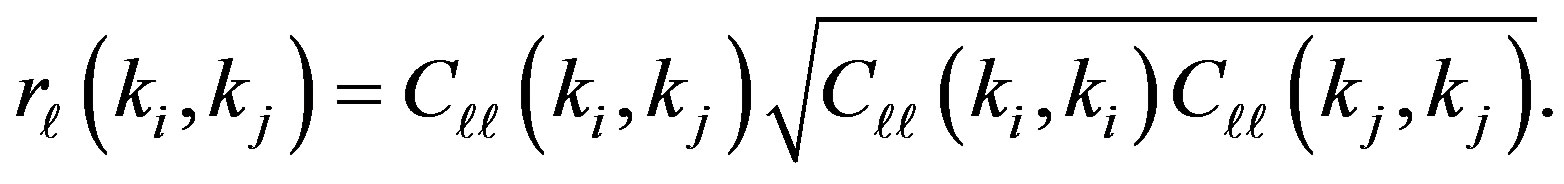 (49)
(49)
Figure 10 shows the correlation matrices of the monopole spectrum,  , on the
, on the  and
and  plane (
plane ( is in units of
is in units of ), which are computed from
), which are computed from  mock catalogs. The left panels are for the convolved spectra, while the right ones for the deconvolved power spectra. The top panels show the case without the division of the full sample, while the other panels (from bottom to top) represent the cases when the full sample is divided into subsamples, whose mean patch sizes are 99, 223 and 397 degrees, respectively. One can see that the off-diagonal components of the correlation matrices for the convolved spectrum are larger if the mean area of the subsample gets smaller. One can also find that the offdiagonal components for the deconvolved spectrum get reduced due to the deconvolution. The off-diagonal components of the correlation matrix for the deconvolved spectrum are not completely reduced to zero for the cases with the subsamples whose mean patch sizes are small.
mock catalogs. The left panels are for the convolved spectra, while the right ones for the deconvolved power spectra. The top panels show the case without the division of the full sample, while the other panels (from bottom to top) represent the cases when the full sample is divided into subsamples, whose mean patch sizes are 99, 223 and 397 degrees, respectively. One can see that the off-diagonal components of the correlation matrices for the convolved spectrum are larger if the mean area of the subsample gets smaller. One can also find that the offdiagonal components for the deconvolved spectrum get reduced due to the deconvolution. The off-diagonal components of the correlation matrix for the deconvolved spectrum are not completely reduced to zero for the cases with the subsamples whose mean patch sizes are small.
Figure 11 shows the correlation matrices for the quadrupole spectrum . Similar to Figure 10, the left panels are for the convolved spectra, while the right panels for the deconvolved power spectra. The division of the full sample into subsamples is needed for the quadrupole spectrum. This figure shows the cases when the full sample is divided into the subsamples, whose mean areas are 99, 223 and 397, respectively, from the bottom to the top panels. Similar to the case of the correlation matrix of the monopole spectrum, we see that the correlation between the different wavenumbers becomes significant for the case when the full sample is divided into smaller subsamples. The effect is more significant when the mean area of the subsample gets smaller. The correlation between the different wavenumbers is practically de-correlated while using the deconvolved power spectrum. Despite of the window deconvolution, the correlation between the different wavenumbers remains noticeable when the mean area of the subsample is small. These features are common to the correlation matrices of the monopole.
. Similar to Figure 10, the left panels are for the convolved spectra, while the right panels for the deconvolved power spectra. The division of the full sample into subsamples is needed for the quadrupole spectrum. This figure shows the cases when the full sample is divided into the subsamples, whose mean areas are 99, 223 and 397, respectively, from the bottom to the top panels. Similar to the case of the correlation matrix of the monopole spectrum, we see that the correlation between the different wavenumbers becomes significant for the case when the full sample is divided into smaller subsamples. The effect is more significant when the mean area of the subsample gets smaller. The correlation between the different wavenumbers is practically de-correlated while using the deconvolved power spectrum. Despite of the window deconvolution, the correlation between the different wavenumbers remains noticeable when the mean area of the subsample is small. These features are common to the correlation matrices of the monopole.
5. Summary and Conclusions
The window effect is very crucial when the power spectrum analysis is done by dividing the full sample into small subsamples. The division is necessary for obtaining the higher order multipole spectra within the distant observer approximation using the FFT. It is possible to compute the higher multipole spectra without the division of the full sample [16]. In that case the window effect is not so significant, however, the FFTs cannot be applied. The usage of the FFT is quite useful for performing the Fourier transform quickly. Thus, the technique for the treatment of the survey window in the power spectrum analysis will be quite important.
We investigated the effect of the window function on the multipole power spectrum via two different approaches. In the first approach, we gave the theoretical formula for the convolved multipole power spectra, Equations (33) and (34), which can be computed by measuring the multipole moments of the window function. The multipole moments of the window function were measured with the SDSS LRG sample, using the various divisions of the full sample into subsamples. The second approach is the measurement of the power spectrum deconvolved from the window effect. The advantage of the deconvolved power spectrum is the simplicity while comparing with theoretical models. The approximate de-correlation between the modes with different wavenumbers is also the advantage of the deconvolved power spectrum. We demonstrated the differences between these two approaches to dealing with the window effect for the multipole power spectrum.
6. Acknowledgements
This work was supported by Japan Society for Promotion of Science (JSPS) Grants-in-Aid for Scientific Research (Nos. 21540270, 21244033). This work was also supported by JSPS Core-to-Core Program “International Research Network for Dark Energy”. This work was done when T. Sato and G. Nakamura were Ph.D. students of Graduate School of Physical Sciences, Hiroshima University.
REFERENCES
- S. Perlmutter, et al., “Measurements of Ω and Λ from 42 High-Redshift Supernovae,” The Astrophysical Journal, Vol. 517, No. 2, 1999, p. 565. doi:10.1086/307221
- A. G. Riess, et al., “Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant,” The Astrophysical Journal, Vol. 116, No. 3, 1998, p. 1009. doi:10.1086/300499
- P. J. E. Peebles and B. Ratra, “The Cosmological Constant and Dark Energy,” Reviews of Modern Physics, Vol. 75, No. 2, 2003, pp. 559-606. doi:10.1103/RevModPhys.75.559
- A. Albrecht, et al., “Report of the Dark Energy Task Force,” 2006. arXiv:astro-ph/0609591
- J. A. Peacock, et al., “ESA-ESO Working Group on Fundamental Cosmology,” 2006. arXiv astro-ph/0610906
- N. Kaiser, “Clustering in Real Space and in Redshift Space,” Monthly Notices of the Royal Astronomical Society, Vol. 227, 1987, pp. 1-21.
- E. V. Linder, “Redshift Distortions as a Probe of Gravity,” Astroparticle Physics, Vol. 29, No. 5, 2008, pp. 336- 339. doi:10.1016/j.astropartphys.2008.03.002
- L. Guzzo, et al., “A Test of the Nature of Cosmic Acceleration Using Galaxy Redshift Distortions,” Nature, Vol. 451, 2008, pp. 541-544. doi:10.1038/nature06555
- R. Reyes, et al., “Confirmation of General Relativity on Large Scales from Weak Lensing and Galaxy Velocities,” Nature, Vol. 464, 2010. pp. 256-258. doi:10.1038/nature08857
- T. Okumura, et al., “Large-Scale Anisotropic Correlation Function of SDSS Luminous Red Galaxies,” The Astrophysical Journal, Vol. 676, No. 2, 2008, p. 889. doi:10.1086/528951
- A. Cabre and E. Gaztanaga, “Clustering of Luminous Red Galaxies—I. Large-Scale Redshift-Space Distortions,” Monthly Notices of the Royal Astronomical Society, Vol. 393, No. 4, 2009, pp. 1183-1208. doi:10.1111/j.1365-2966.2008.14281.x
- S. Cole, K. Fisher and D. H. Weinberg, “Fourier Analysis of Redshift Space Distortions and the Determination of Omega,” Monthly Notices of the Royal Astronomical Society, Vol. 267, 1994, pp. 785-799.
- A. J. S. Hamilton, “The Evolving Universe,” Kluwer Academic Publishers, Dordrecht, 1998. doi:10.1007/978-94-011-4960-0_17
- P. J. Outram, et al., “The 2dF QSO Redshift Survey—VI. Measuring Λ and β from Redshift-Space Distortions in the Power Spectrum,” Monthly Notices of the Royal Astronomical Society, Vol. 328, No. 1, 2001, pp. 174-184. doi:10.1046/j.1365-8711.2001.04852.x
- P. J. Outram, et al., “The 2dF QSO Redshift Survey—XIII. A Measurement of Λ from the Quasi-Stellar Object Power Spectrum, PS(k//, k⊥),” Monthly Notices of the Royal Astronomical Society, Vol. 348, No. 3, 2004, pp. 745-752. doi:10.1111/j.1365-2966.2004.07348.x
- K. Yamamoto, M. Nakamichi, A. Kamino, B. A. Bassett and H. Nishioka, “A Measurement of the Quadrupole Power Spectrum in the Clustering of the 2dF QSO Survey,” Publications of the Astronomical Society of Japan, Vol. 58, 2006, pp. 93-102. 415, No. 3, 2011, pp. 2876- 2891. http://pasj.asj.or.jp/v58/n1/580114/58012766.pdf
- C. Blake, et al., “The WiggleZ Dark Energy Survey: The Growth Rate of Cosmic Structure Since Redshift z = 0.9,” Monthly Notices of the Royal Astronomical Society, Vol. 415, No. 3, 2011, pp. 2876-2891.
- A. Taruya, S. Saito and T. Nishimichi, “Forecasting the Cosmological Constraints with Anisotropic Baryon Acoustic Oscillations from Multipole Expansion,” Physical Review D, Vol. 83, No. 10, 2011, Article ID: 103527. doi:10.1103/PhysRevD.83.103527
- K. Yamamoto, T. Sato and G. Hütsi, “Testing General Relativity with the Multipole Spectra of the SDSS Luminous Red Galaxies,” Progress of Theoretical Physics, Vol. 120, No. 3, 2008, pp. 609-614. doi:10.1143/PTP.120.609
- K. Yamamoto, G. Nakamura, G. Huetsi, T. Narikawa and T. Sato, “Constraint on the Cosmological f(R) Model from the Multipole Power Spectrum of the SDSS Luminous Red Galaxy Sample and Prospects for a Future Redshift Survey,” Physical Review D, Vol. 81, No. 10, 2010, Article ID: 103517. doi:10.1103/PhysRevD.81.103517
- K. Yamamoto, B. A. Bassett and H. Nishioka, “Dark Energy Reflections in the Redshift-Space Quadrupole,” Physical Review Letters, Vol. 94, No. 5, 2005, Article ID: 051301. doi:10.1103/PhysRevLett.94.051301
- W. Percival, et al., “Baryon Acoustic Oscillations in the Sloan Digital Sky Survey Data Release 7 Galaxy Sample,” Monthly Notices of the Royal Astronomical Society, Vol. 401, No. 4, 2010, pp. 2148-2168. doi:10.1111/j.1365-2966.2009.15812.x
- B. A. Reid, et al., “Thick Gas Discs in Faint Dwarf Galaxies,” Monthly Notices of the Royal Astronomical Society, Vol. 404, No. 1, 2010, pp. L60-L63. doi:10.1111/j.1745-3933.2010.00835.x
- W. Percival, et al., “The Shape of the Sloan Digital Sky Survey Data Release 5 Galaxy Power Spectrum,” The Astrophysical Journal, Vol. 657, No. 2, 2007, p. 645. doi:10.1086/510615
- S. Cole, et al., “The 2dF Galaxy Redshift Survey: PowerSpectrum Analysis of the Final Data Set and Cosmological Implications,” Monthly Notices of the Royal Astronomical Society, Vol. 362, No. 2, 2005, pp. 505-534. doi:10.1111/j.1365-2966.2005.09318.x
- T. Sato, G. Hütsi and K. Yamamoto, “Deconvolution of Window Effect in Galaxy Power Spectrum Analysis,” Progress of Theoretical Physics, Vol. 125, No. 1, 2011, pp. 187-197. doi:10.1143/PTP.125.187
- H. A. Feldman, N. Kaiser and J. A. Peacock, “PowerSpectrum Analysis of Three-Dimensional Redshift Surveys,” Astrophysical Journal, Vol. 426, No. 1, 1994, pp. 23-37. doi:10.1086/174036
- K. N. Abazajian, et al., “The Seventh Data Release of the Sloan Digital Sky Survey,” The Astrophysical Journal Supplement Series, Vol. 182, No. 2, 2009, p. 543. doi:10.1088/0067-0049/182/2/543
- G. Hütsi, “Acoustic Oscillations in the SDSS DR4 Luminous Red Galaxy Sample Power Spectrum,” Astronomy & Astrophysics, Vol. 449, No. 3, 2006, pp. 891-902. doi:10.1051/0004-6361:20053939
- G. Hütsi, “Power Spectrum of the SDSS Luminous Red Galaxies: Constraints on Cosmological Parameters,” Astronomy & Astrophysics, Vol. 459, No. 2, 2006, pp. 375- 389. doi:10.1051/0004-6361:20065377
- J. M. Bardeen, J. R. Bond, N. Kaiser and A. S. Szalay, “The Statistics of Peaks of Gaussian Random Fields,” The Astrophysical Journal, Vol. 304, 1986, pp. 15-61.
- J. A. Peacock and S. J. Dodds, “Reconstructing the Linear Power Spectrum of Cosmological Mass Fluctuations” Monthly Notices of the Royal Astronomical Society, Vol. 267, 1994, pp. 1020-1034.
Theoretical Model for the Power Spectrum
In this appendix, we explain the theoretical models adopted in the present paper. The simplest model for the galaxy power spectrum in the redshift-space is
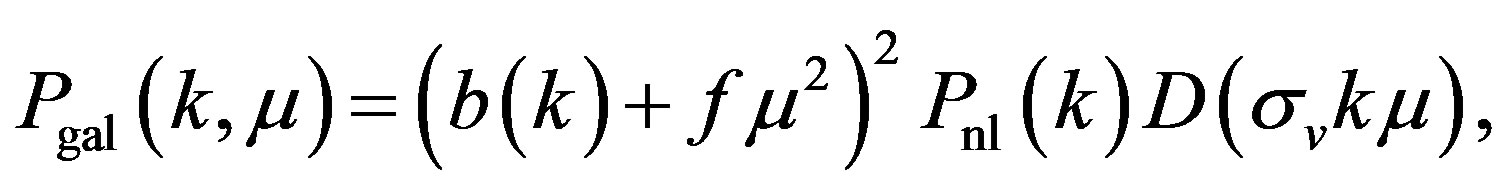 (50)
(50)
where 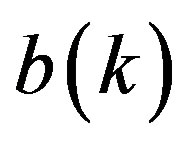 is the clustering bias,
is the clustering bias,  is the nonlinear matter power spectrum,
is the nonlinear matter power spectrum, 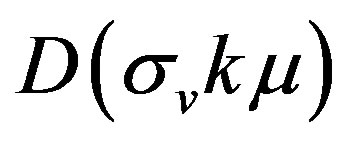 is the damping factor due to the finger of god effect, and
is the damping factor due to the finger of god effect, and  is the pair wise velocity dispersion. Assuming an exponential distribution function for the pairwise velocity, the damping function is
is the pair wise velocity dispersion. Assuming an exponential distribution function for the pairwise velocity, the damping function is

For the nonlinear matter power spectrum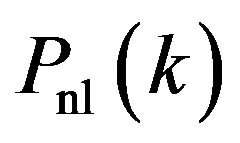 , we adopt the fitting formula by Peacock and Dodds (1994) [32].
, we adopt the fitting formula by Peacock and Dodds (1994) [32].

Figure 8. Comparison of the multipole power spectra of the SDSS LRG sample for redshift ranges  (red crosses),
(red crosses),  (blue bars) and
(blue bars) and  (green squares). The left panels show the monopole spectra, while the right ones the quadrupole power spectra, multiplied by the wavenumber. The upper panels are the deconvolved and the lower ones the convolved power spectra. In this analysis each redshift bin is divided into 18 angular subsamples whose mean area is 397 square degrees.
(green squares). The left panels show the monopole spectra, while the right ones the quadrupole power spectra, multiplied by the wavenumber. The upper panels are the deconvolved and the lower ones the convolved power spectra. In this analysis each redshift bin is divided into 18 angular subsamples whose mean area is 397 square degrees.
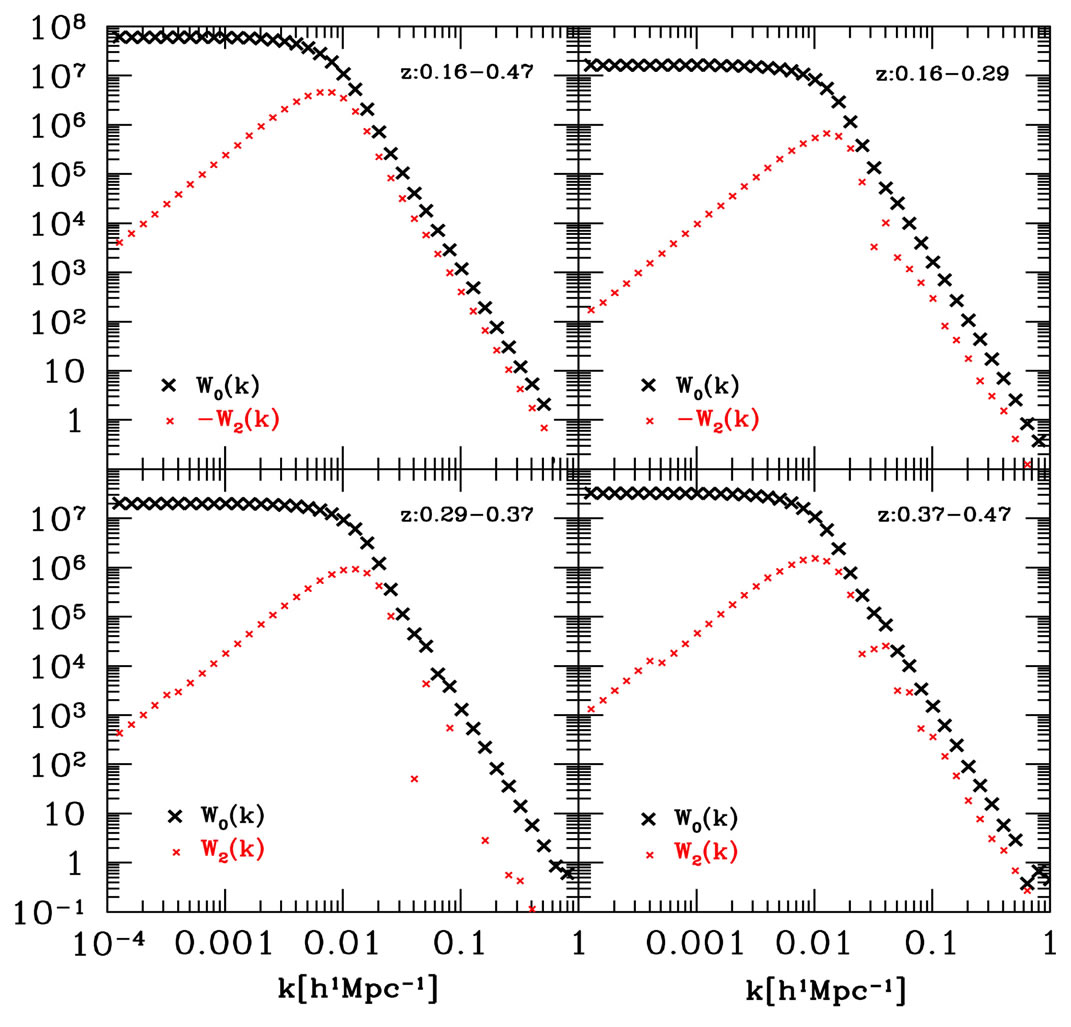
Figure 9. The window functions  (black crosses) and
(black crosses) and 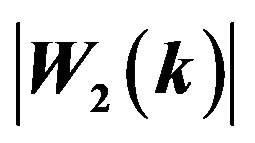 (red small crosses) assuming the full sample is divided into subsamples with redshift ranges,
(red small crosses) assuming the full sample is divided into subsamples with redshift ranges,  (upper right panel),
(upper right panel),  (lower left panel) and
(lower left panel) and  (lower right panel), which correspond to the analysis of Figure 1. The upper left panel is the case using the full redshift range
(lower right panel), which correspond to the analysis of Figure 1. The upper left panel is the case using the full redshift range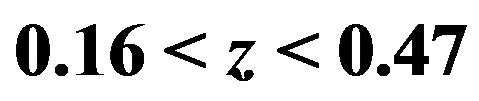 , which is the same as the upper right panel of Figure 3.
, which is the same as the upper right panel of Figure 3.



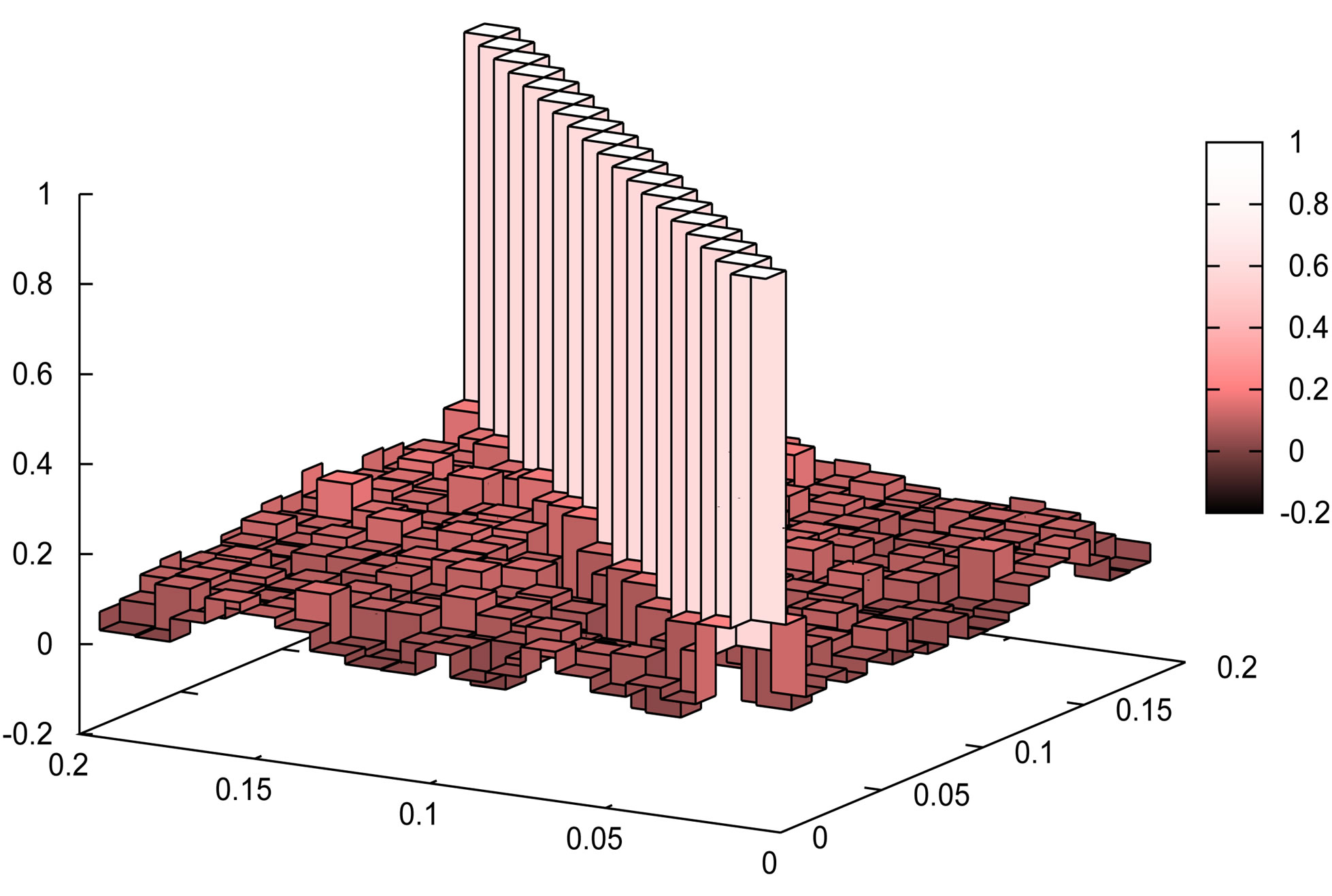
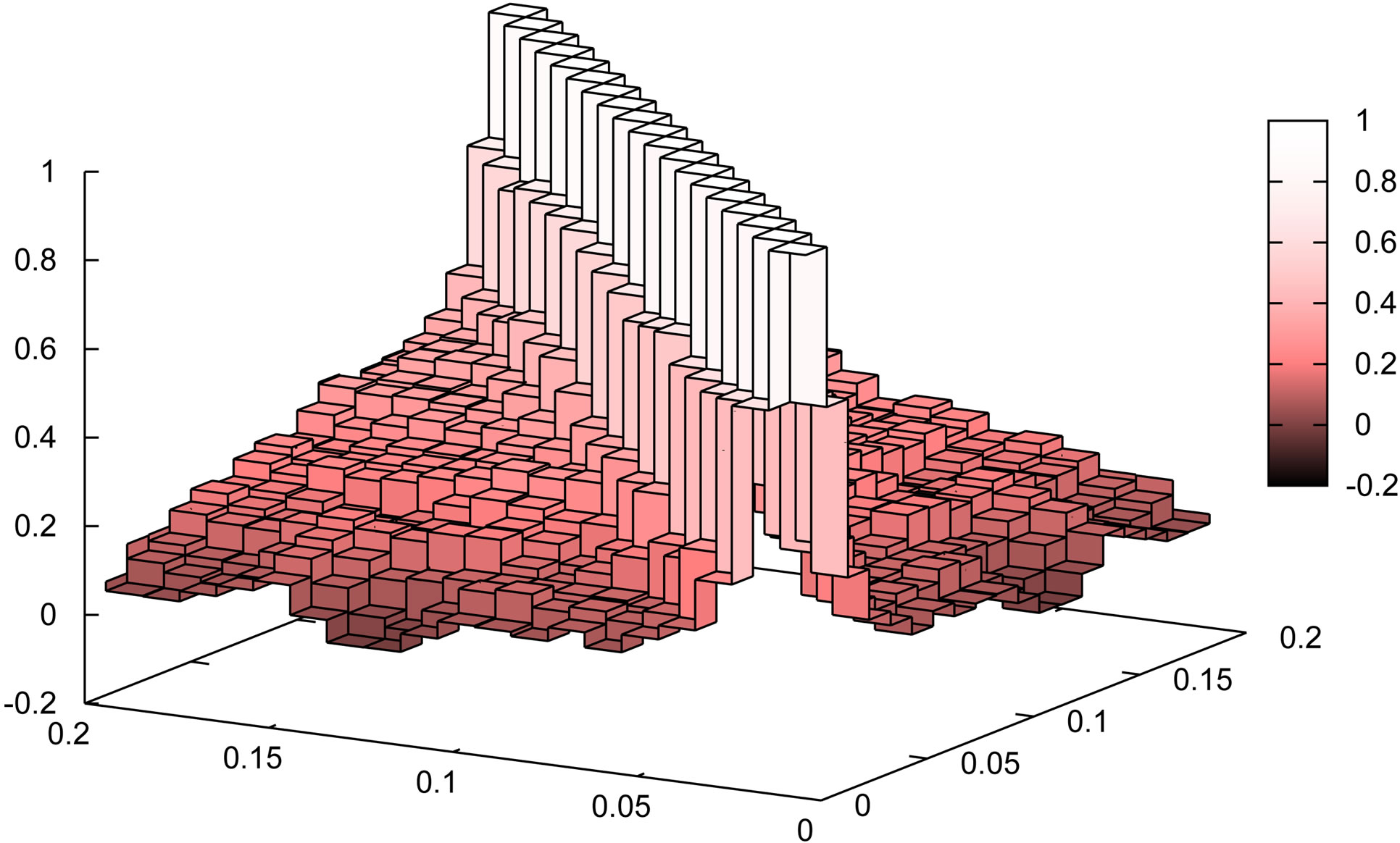
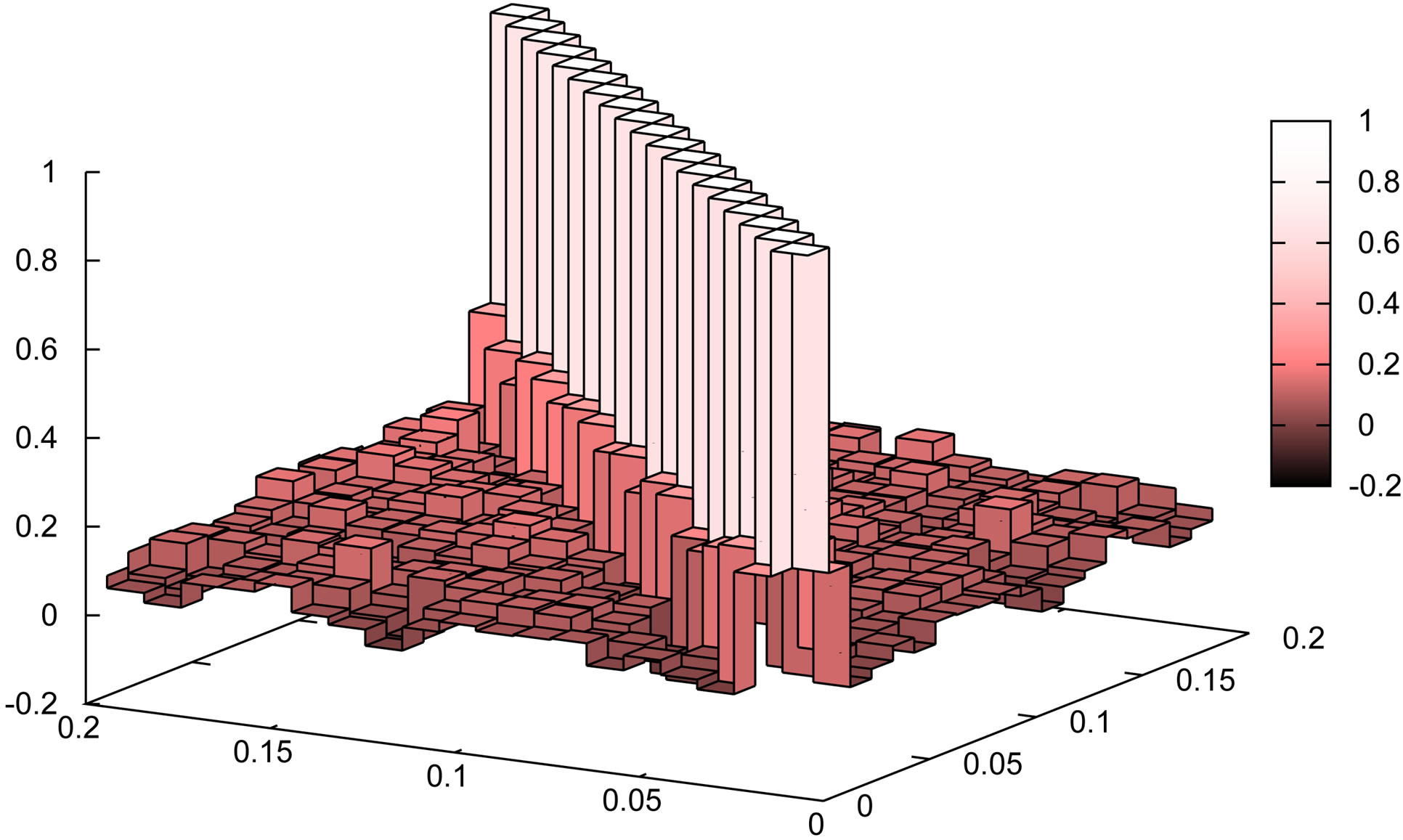

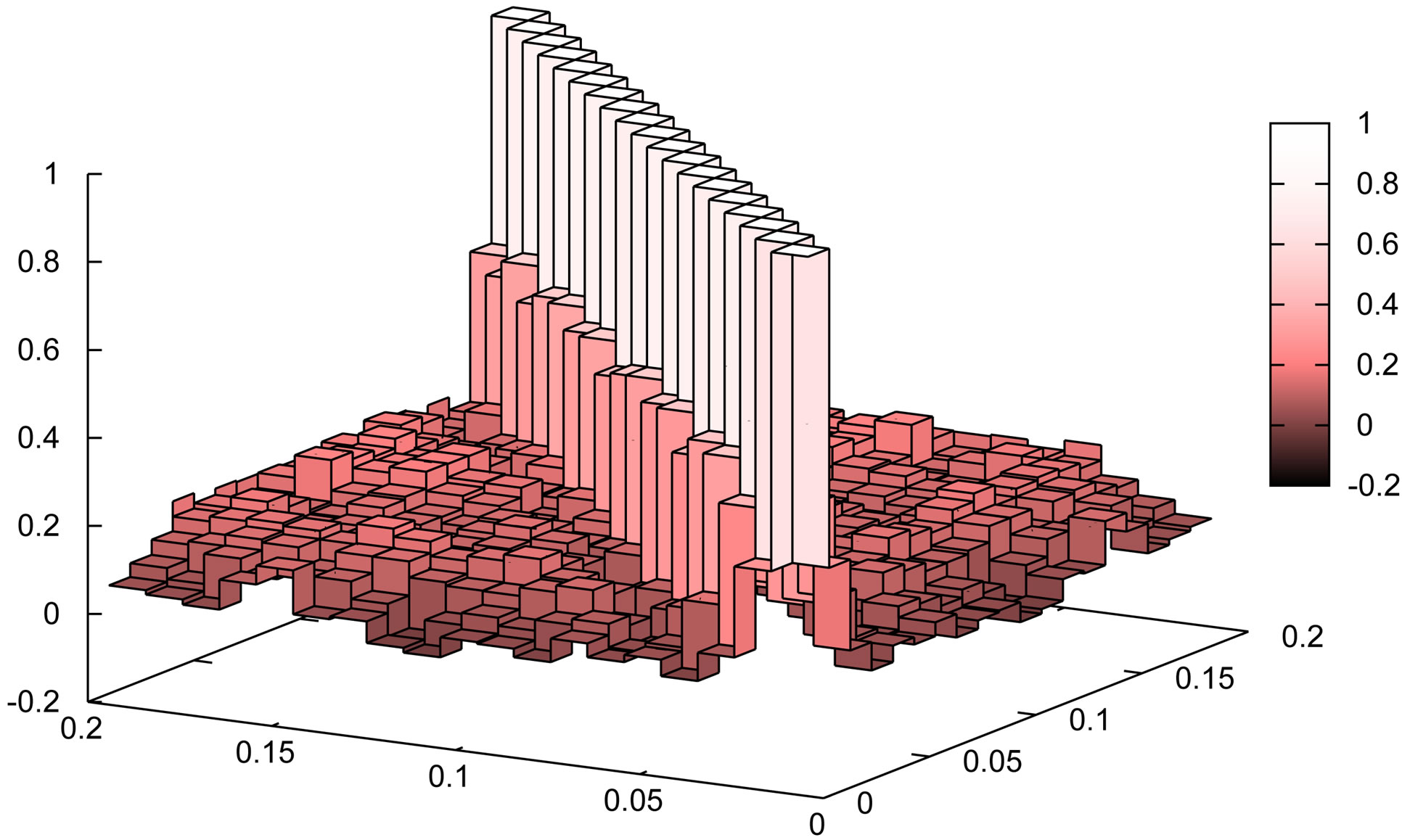
Figure 10. Correlation matrices of the monopole spectrum,  , for the convolved spectrum (left panels) and the deconvolved spectrum (right panels), respectively, on the
, for the convolved spectrum (left panels) and the deconvolved spectrum (right panels), respectively, on the  and
and 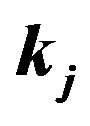 plane (
plane (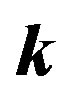 in units of
in units of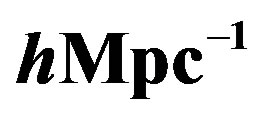 ). The top panels show the case with no division of the full sample, while the other lower panels (from bottom to top) show the cases when the full sample is divided into subsamples, whose mean area is 99, 223 and 397 square degrees, respectively.
). The top panels show the case with no division of the full sample, while the other lower panels (from bottom to top) show the cases when the full sample is divided into subsamples, whose mean area is 99, 223 and 397 square degrees, respectively.
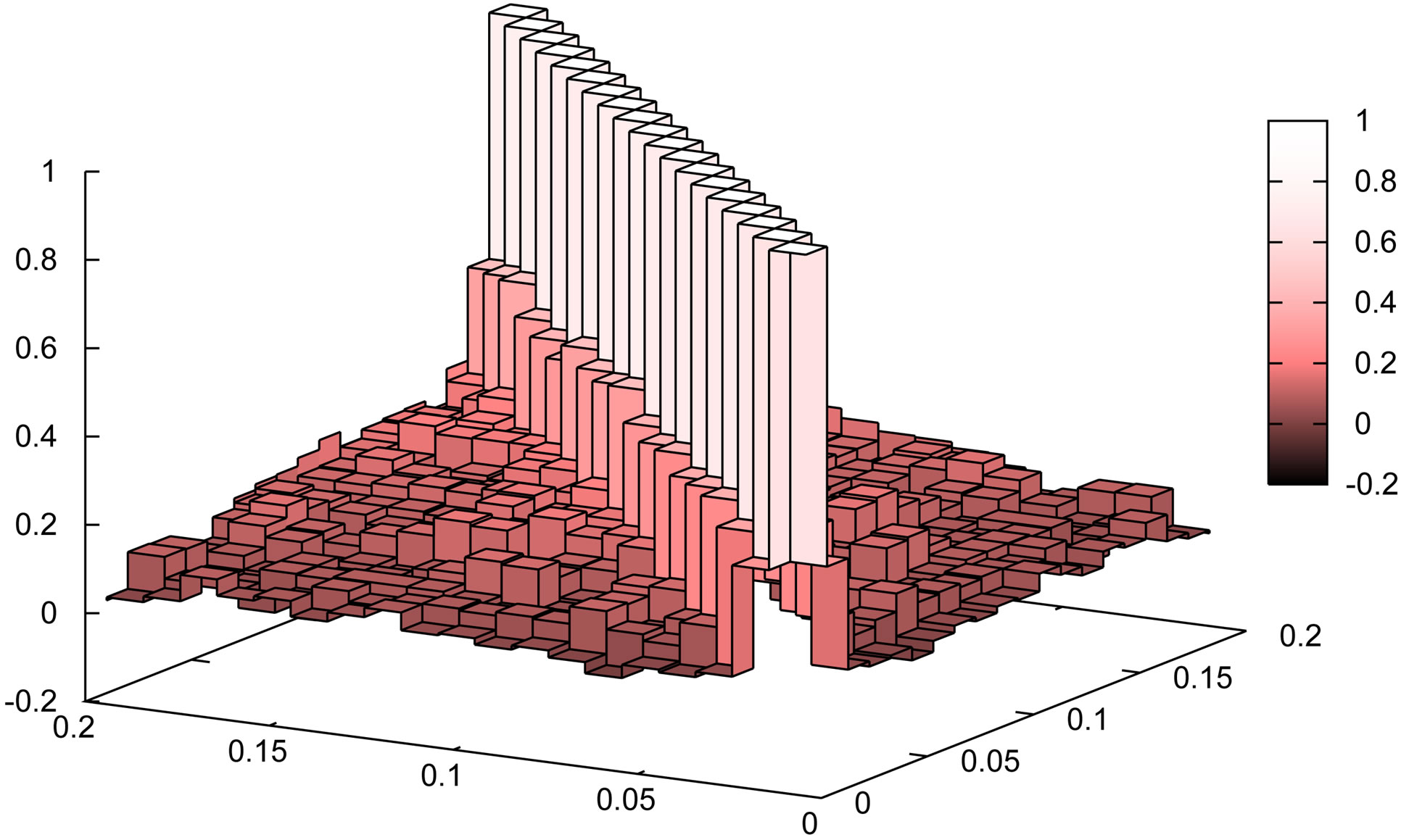
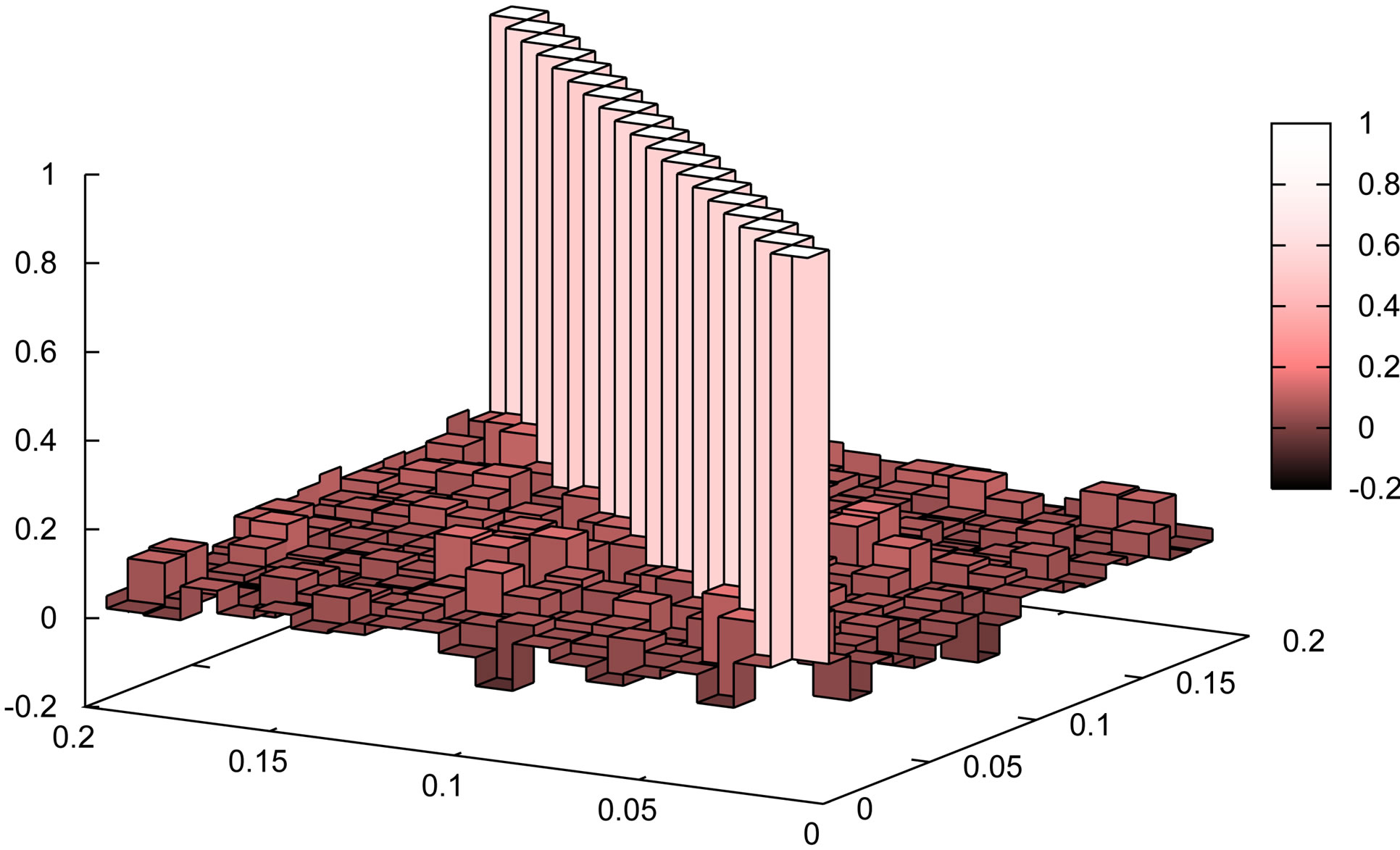



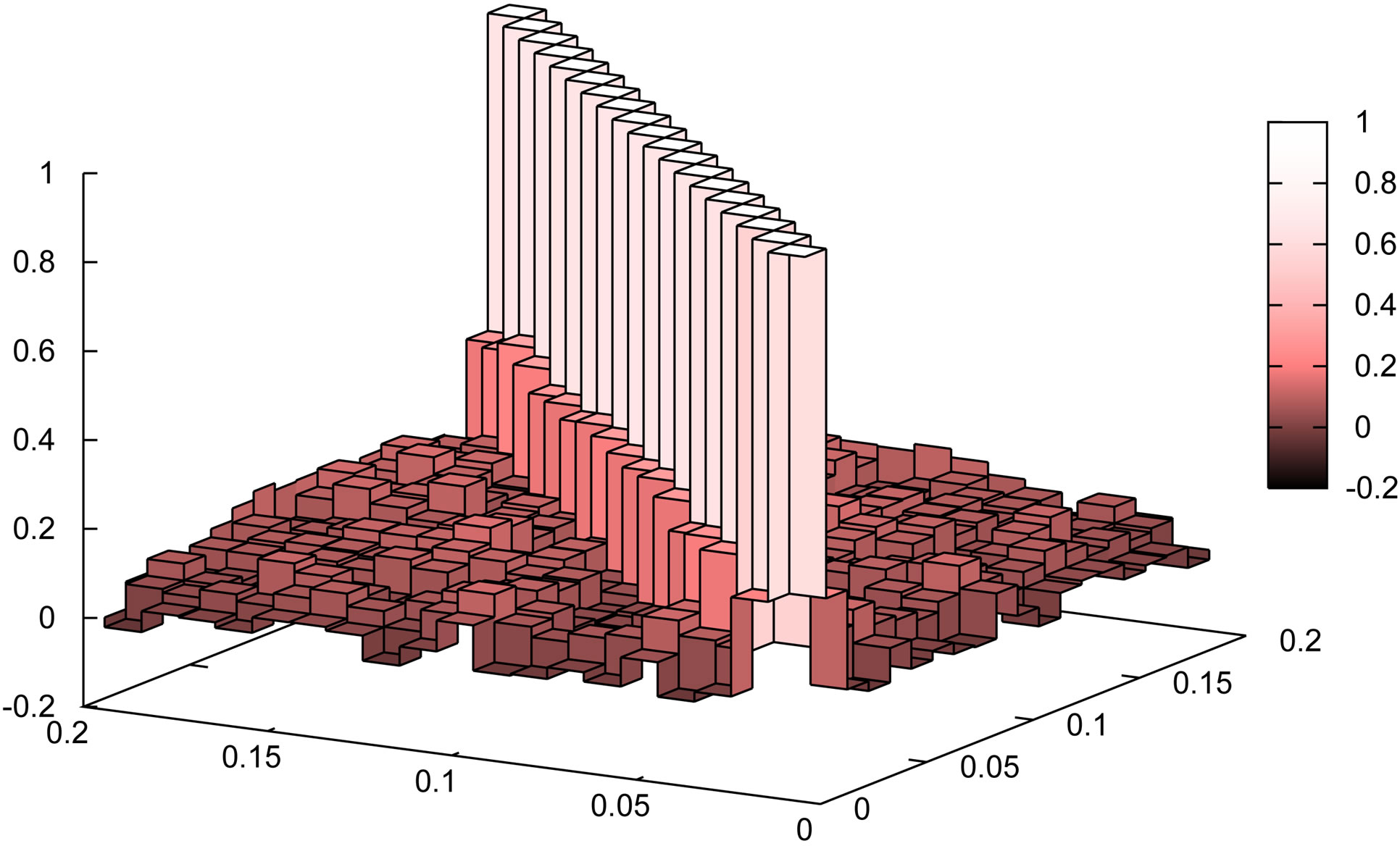
Figure 11. Correlation matrices of the quadrupole spectrum,  , for the convolved spectrum (left panels) and the deconvolved spectrum (right panels), respectively. From bottom to top, the panels show the cases when the full sample is divided into subsamples, whose mean area is 99, 223 and 397 square degrees, respectively.
, for the convolved spectrum (left panels) and the deconvolved spectrum (right panels), respectively. From bottom to top, the panels show the cases when the full sample is divided into subsamples, whose mean area is 99, 223 and 397 square degrees, respectively.

