International Journal of Astronomy and Astrophysics
Vol.3 No.2A(2013), Article ID:33318,6 pages DOI:10.4236/ijaa.2013.32A006
The Torsind—A Device Based on a New Principle for Non-Conventional Astronomical Observations
Main Astronomical Observatory of National Academy of Sciences, Kiev, Ukraine
Email: pugach@mao.kiev.ua, pugach@yandex.ru
Copyright © 2013 Alexander F. Pugach. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received April 10, 2013; revised May 12, 2013; accepted May 21, 2013
Keywords: Solar; Lunar Eclipses; Venus Transit; Torsion Balance; Torsind
ABSTRACT
The description of a new device which is an improved version of the classic torsion balance is given. The device, which is the so-called “torsind”, seemed to be very sensitive to solar/lunar eclipses, and a Venus transit. It even responded to a solar eclipse when installed underground. The results of the most well-documented cases are described.
1. Introduction
Nowadays scientific researchers often use devices in which the sensor is a mass freely suspended by a quartz, metal or synthetic fiber filament, or attached to a solid rod [1]. A torsion balance, a Foucault pendulum, a paraconical pendulum, a tilt-meter and other similar devices are examples of such units. Torsion balances are distinguished from other devices in this group by their very high sensitivity. Modern torsion balances clearly respond to applied torques of the order of 10−10 ~ 10−11 N∙m.
Starting in January, 2010, a new device “torsind” has been used at the Main Astronomical Observatory of the Ukrainian Academy of Science. It is used for monitoring of astronomical phenomena: solar and lunar eclipses, planetary transits and conjunctions. Torsind is a specific type of torsion balance that uses a very light metal disc instead of the linear beam of a classical unit, suspended from a monofilament made from natural silk, instead of quartz or a rigid suspension.
Our long-term studies have shown that such a device clearly responds to many astronomical phenomena [2]. Moreover, it even responds to certain events that are not visible at the point of measurement (observation).
2. Torsind Description
The mobile part of the torsion balances used in our experiments consists of a very light 120 mm diameter aluminum disk and a very thin suspension fiber (a specially treated natural silk thread about 20 μm in diameter). The design of such a balance makes it insensitive to variations in gravitational potential and ensures that it is unaffected by gravitational (tidal) influences from any direction. In addition, the symmetrical shape of the disc rules out the possibility of any affect on the disk due to air convection inside the housing. Such a convection is considered to be the main interference source in the classical torsion balance. The disk is marked with a dark dot referred hereafter as the “pointer”. The total weight of this suspended part is »100 mg or less.
The housing of the torsind is made from a quartz cylinder (Figure 1). Its height does not exceed 240 mm and wall thickness is about 2 mm. Top and bottom of the cylinder are covered with two round glass plates of a corresponding diameter. In order to exclude electrostatic

Figure 1. A general view of the torsind.
influences inner parts of the walls and bottom of the cylinder are completely surrounded by a reliably grounded aluminum foil. The edges of this quartz-glass housing are sealed from the inside with a silicon joint sealant material. The upper end of the silk suspension thread is attached by adhesive to the center of the upper glass plate. The sealing of the housings prevents interference due to air currents or humidity variations, and improves thermal stabilization.
A webcam connected to a computer was mounted above the upper face of the cylinder. The image from the camera was processed by custom-made software that determines the position of a marker and calculates its polar coordinates relative to the vertical axis of symmetry of the cylinder. One measurement was taken each minute. The reading error does not exceed 0.3˚.
The device used was fully automated one and did not require the presence of an observer. Since mid-2008 the torsind has been sited in an isolated, shaded room with tightly closed doors and windows, the entrance being disbarred to outsiders. Our observations were performed in very favorable conditions:
• absence of any mechanisms within 50 m, such as motors and generators or moving objects;
• absence of electrical and wireless devices (except for one computer);
• no mechanical vibrations;
• complete silence and absence of strong light and heat radiation.
• closed room, no visitors.
3. Particular Properties of the Torsind
1) The main feature of the device is the use of a silk thread because it has no reverse torque when twisted. The experiment was conducted as follows. A specially made adjuster allowed the suspension point of the thread to rotate around its vertical axis for any given angle or full rotations. The operator manually rotated the hang point of the thread for a certain number of degrees and registered how many degrees the disk will rotate in the opposite direction. Several twists were performed in both directions: both clockwise (plus) and counter-clockwise (minus).
It was noticed that the response was at least an order of magnitude weaker than the initial angle of twist (angle of roll-up). The experimental results are shown in the Figure 2. The twist response of the thread was only 8.5% of original angle of twist. As can be seen from the Figure 1, the linearity of this relationship is applicable over a large range of angles of twist.
This relationship was only true when the twisting rate was high (about 100 degrees per second). If the twist rate is small and does not exceed 1 degree per second then the reaction is zero. In other words reverse torque does not build in the thread.
This is well illustrated by actual observations. There are dozens of cases where the disk of the torsind slowly made several revolutions around its axis following which the marker of the device again pointed to the same azimuth, as before the start of rotation. This feature of the torsind is illustrated in Figure 3.
The observations made on 15.01.2012 are plotted in Figure 3. It shows the disc made three complete CCW revolutions at noon. Bear in mind that the dial of the torsind is graduated from 0˚ to 360˚ and transition through point 0 = 360 looks like a break and jump. Actually there is no gap. The marker position after these 3 revolutions remains almost unchanged. (The dotted red line in this graph is explained below).
This surprising property of a silk thread is due to its specific molecular structure. The basis of a thread is fibroin protein molecules, substances even stronger than Kevlar. Repetitive amino acid sequences of this protein form antiparallel pleated β-layers which are connected to
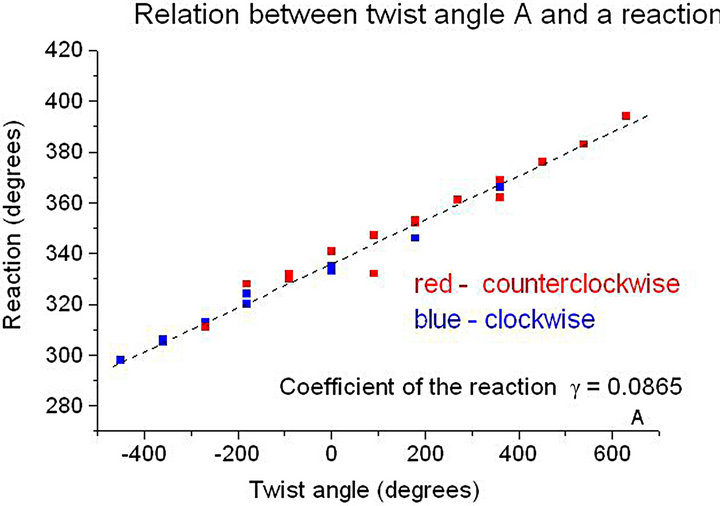
Figure 2. The relation between a twist angle A and a reaction.

Figure 3. After three complete revolutions at noon the disk remained its orientation that was before the rotation. Consequently, the reverse torque is zero.
each other by hydrogen bonds. These bonds are not very strong and allow for moderate mechanical offsetting of the layers. This explains the fact that under slow (necessarily slow!) rotation the layers can slide relative to each other. Moreover, it does not reduce the mechanical strength of the thread.
2) The torsind is not sensitive to changes in gravitational potential by definition. If it were not so, then the torsind should have been able to register a tidal wave from the Moon with a period of 12 hours. This phenomenon was not observed, however.
3) The torsind is not sensitive to changes of microload on a thread due to the daily change in the Sun’s height above and below the horizon. This property was shown as follows.
A special experiment was conducted to ensure that the daily variations in the solar gravity force (the difference “noon minus midnight”) do not affect the reading. For this purpose, an additional micro weight (448 μg) was repeatedly loaded and unloaded on the thread within two weeks. Statistical analysis of the resulting data (938 individual measurements) showed that this microloading has no effect on readings. The results of this experiment are shown in Figure 4. It can be seen that the average position of the marker for the entire period of measurement was 225.3˚ ± 0.20˚ (loaded), and 226.1˚ ± 0.18˚ (unloaded). That is, an additional load on the silk thread of the device does not cause rotation of the disk.
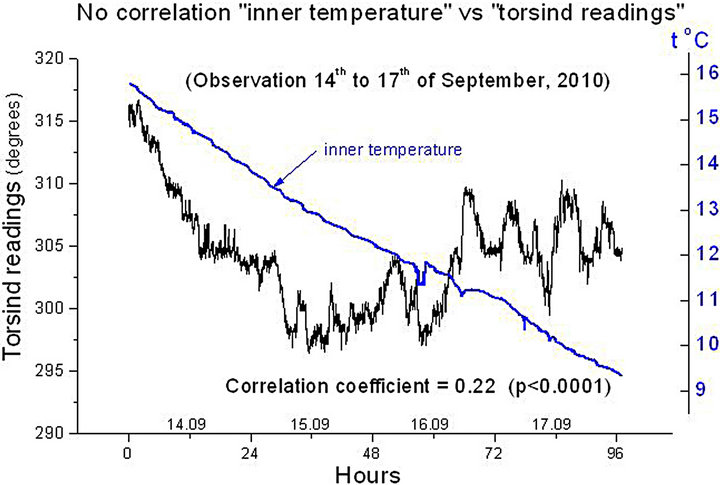
4) The effect of temperature variations on the readings was also investigated. A temperature sensor was installed inside the housing. Long-term measurements showed that the readings and the temperature inside the torsind were unrelated. Neither drastic temperature fluctuation (Figure 5(a)), nor microfluctuations temperature inside the device (Figure 5(b)) did not correlate with the torsind readings.
5) The dependence of the torsind readings on humidity
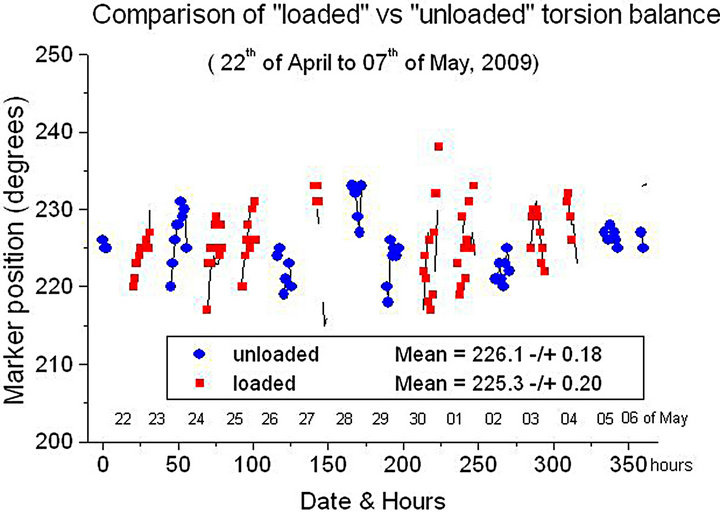
Figure 4. The difference between the readings of the loaded and unloaded torsind was not statistically significant.
 (a)
(a) (b)
(b)
Figure 5. (a) Torsind readings do not depend on macro changes in its own temperature; (b) Torsind readings do not depend on micro changes in its own temperature.
has not been investigated. Firstly, the torsind housing was tightly sealed. Secondly, the torsind does not respond to changes in barometric pressure. This fact is reflected in Figure 3. Here the red dotted line represents the barometer pressure. It is well known that atmospheric pressure is highly dependent on humidity. But in this case there is no significant correlation between the barometer readings and the torsind reaction.
6) Significant variations of the external electric field did not have an observable effect on the torsind readings. The growth of the electric field during a thunderstorm storm on 10.08.2011 and a close (50 meters) lightning discharge at 11 h 36 m UT did not affect the torsind readings.
7) Prolonged studies have shown that the following factors cannot be the cause of the significant pointer rotation and therefore should be excluded from further consideration:
• convective air flow inside the torsind housing;
• changes in outdoor weather parameters (temperature, humidity, barometer);
• tidal effects of the Moon and Sun;
• change in the degree of excitation of the ionosphere over the place of observation (see Figure 6, right lower panel);
• Coriolis acceleration;
• floor vibration;
• local mobile phone interference;
• a grounded aluminum screen excluded interference from static electricity and reduced magnetic pickups.
8) Currently, torsind metrology is impossible because of the lack of metrological standards. Moreover, we do not know what force acts on the disk of the device. However, we can calculate a torque value by observing angular acceleration of the disk. There are many such cases. One of the minimum acceleration values was calculated using observations on 01.15.2012 (device WEB_1) during a time interval of 07 h 16 m to 08 h 27 m UT. These data are presented in Figure 7 and the curve is approximately a parabola thus indicating that angular acceleration is approximately constant.
The average value of the acceleration Aang equals:
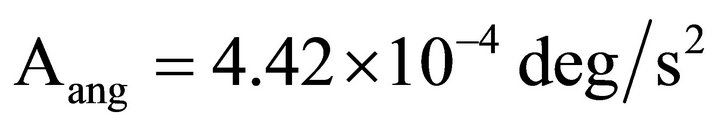
The torque T was calculated using a known radial distribution of mass in the torsind disk:

This value T can serve as a reliable indicator of the torsind sensitivity. The actual sensitivity may be even higher.
4. Why Torsind?
Silk monofilament as has been shown in paragraph 1 has no elastic properties. It cannot accumulate and save the reverse torque. Therefore the twisted torsind thread does not return a disc to its original position. Thus the torsind can not directly measure strength or magnitude of the applied torque. Therefore, the above-described device cannot be called as “a balance”. It is like a weather vane, which indicates direction of the wind only, but does not measure its speed.
The torsind determines a direction and angular velocity of the rotation only. Therefore, our instrument should be properly referred to as a “torsion indicator” or TORSIND.
5. Torsind in Action
Observations for the behavior of a torsind pointer during solar/lunar eclipses, and other astronomical phenomena have led to unexpected results [3-6]. The most interesting and well-documented cases are below.
5.1. Diurnal Background Variations
Several years ago the author found that the superlight torsion balances are constantly registering a periodic signal of unknown nature. Devices of different designs and different types of detectors were sensitive to this periodic background signal. The signal waveform can

Figure 6. The diurnal torsind reaction begins at sunrise and terminates at sunset.
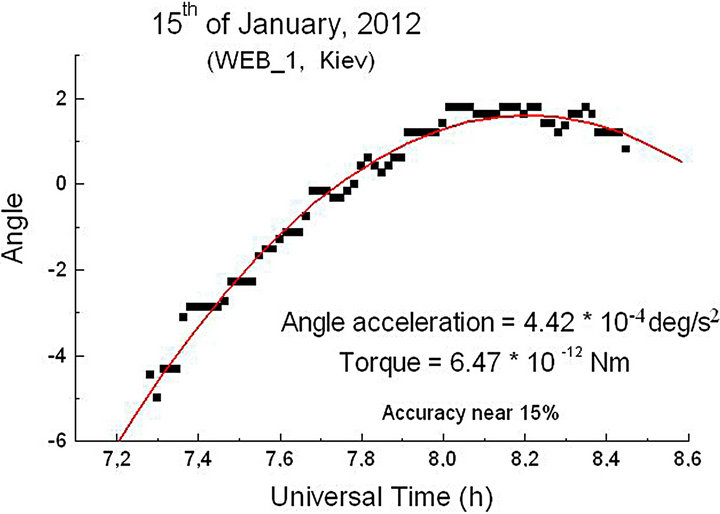
Figure 7. The disc angle acceleration on 15.01.2012.
vary greatly, but the period of the signal remained exactly 24 hours. Conventionally, this signal is called background daily variation (BDV). Subsequently the BDV was taken into account when analyzing the observations.
Four panels in the Figure 6 show these daily variations. The reaction of the instrument begins at sunrise, reaches a maximum near midday and gradually drops to the time of sunset. The sunrise and sunset points are indicated by the vertical red and blue arrows in the figure. At night the pointer fluctuations are minimal.
Amplitude of the BDV does not exceed 30 - 35 angle degrees. Usually it is lesser (see BDV in Figure 8). Therefore, the diurnal variations clearly recorded only when there are no other significant events.
5.2. Solar Eclipse on 26.01.2009
To account for the influence of BDV we began our observations 3 days prior to this astronomical event and ended 2 days after its completion [5]. Average curves showing the background variations are shown in Figure 9 by grey lines. The signal recorded on the day of the eclipse on January 26 is shown by a blue line. Obviously it differs from background variations.
5.3. Lunar Eclipse on 09.02.2009
The observations were performed in the same way [4]. Background measurements were carried out during 7, 8, 10, 11 and 12 February. They are shown in Figure 8 with thin grey lines. The result of observation on the day of the lunar eclipse is plotted as a thick blue line. Obviously, the amplitude of the signal on 9 February is much greater than that of background variations. This suggests that the lunar eclipse was the only cause of the large amplitude variation.
From this we may conclude that the increased torsind reactions during the solar/lunar eclipses were caused by these phenomena.
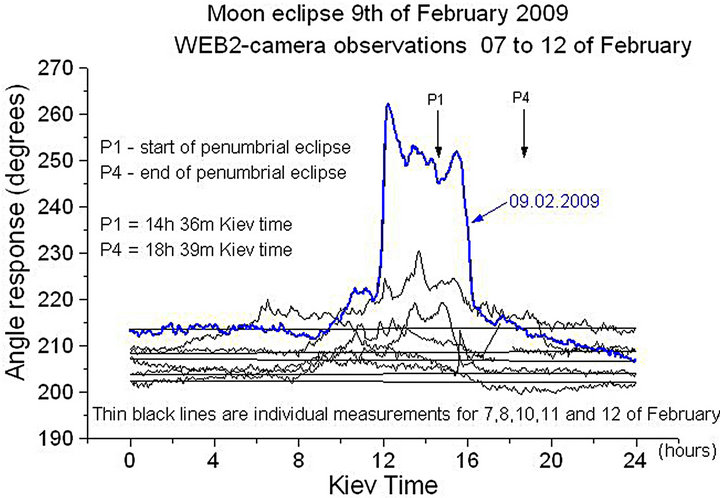
Figure 8. Lunar eclipse of 9 February, 2009.
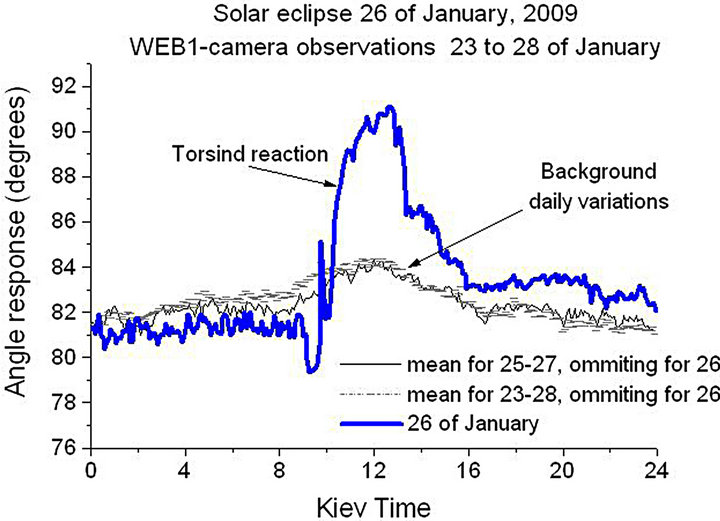
Figure 9. Solar eclipse of 26 January, 2009. Net signal after subtracting BDV is shown by the blue line.
5.4. Venus Transit
The last transit of Venus occurred June 5-6, 2012. We were observing this phenomenon during 5, 6 and 7 of June using the two torsinds—WEB_2 and WEB_3. Observation conditions remained the same.
Figure 10 shows the results of the observations, which lasted 5, 6 and 7 of June.
The first contact occurs at 22 h 09 m UT and the last one—at 04 h 49 m UT the next day.
It is obvious that almost all of the time, while the Venus was crossing the sun’s disk; the responses of both torsinds were nearly constant, except for small fluctuations. It was only 5 h 50 m after the first contact when both devices began to increase their readings at the same time. Despite the fact that the reactions of the devices were somewhat different, the most important result remains that both units have shown a reaction to this phenomenon.
6. Conclusions
It has been above shown that torsind, despite its simplic-
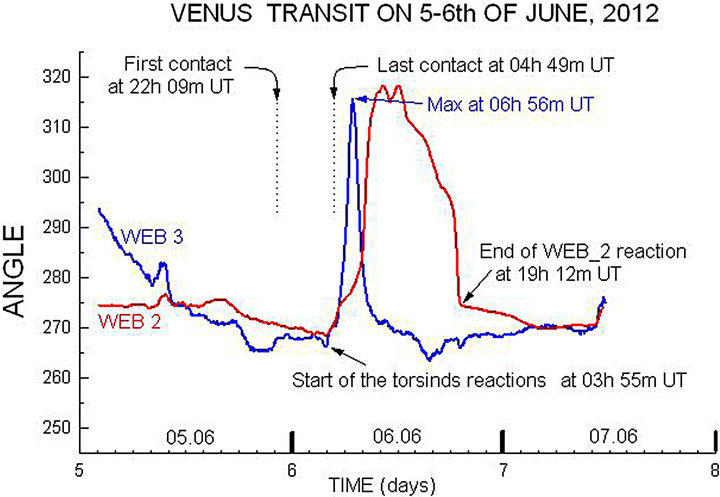
Figure 10. The torsind reaction during the Venus transit on 5-6.06.2012.
ity, has a very high sensitivity to an unexplored kind of energy, most likely associated with the Sun. The unknown energy transfers a torque; and that disk rotation is an obvious response to this phenomenon. The disk of torsind turns in one direction or another due to being affected by this energy. In many cases torsind can “feel” phenomena occurring in faraway parts of the globe very well. Furthermore, it responds to such phenomena even when installed underground [6].
The use of such devices in astronomy opens a new chapter in that science, because it gives the opportunity to study many known phenomena from a completely unknown aspect, thus deepening our understanding of the cosmos from a completely new cognitive point of view.
We do not still know what force causes the rotation of a torsind disk. But this fact should not stop us. Quite the contrary, it is possible that the force is one of the manifestations of super-weak fields. Thus the use of this device will give us the opportunity to answer the question of how this force acts and how torque is transmitted.
7. Acknowledgements
I express my gratitude to all my colleagues with whom I planned this work, prepared experiments, and discussed the results of my observations: Thomas Goodey (UK), Dimitrie Olenici (Romania), Antonio Iovane (Italy), Daniel Vorobiov (Ukraine), Lavrenty Shikhobalov (Russia) Alan Stout (USA), Jean-Bernard Deloly (France), John Francis (UK).
REFERENCES
- H. A. Munera, “Should the Laws of Gravitation Be Reconsidered?” Apeiron, Montreal, 2011, p. 448.
- A. F. Pugach, “Observations of the Astronomical Phenomena by Torsion Balance,” Physics of Consciousness and Life, Cosmology and Astrophysics, Vol. 9, No. 2, 2009, pp. 30-51.
- T. J. Goodey, A. F. Pugach and D. Olenici, “Correlated Anomalous Effects Observed during the August 1st 2008 Solar Eclipse,” Journal of Advanced Research in Physics, Vol. 1, No. 2, 2010, Article ID: 021007.
- A. F. Pugach, “Is the Maurice Allais’s Effect Exclusively Gravitational in Nature?” In: H. Munera, Ed., Should the Laws of Gravitation Be Reconsidered? Apeiron, Montreal, 2011, pp. 257-264.
- A. F. Pugach and D. Olenici, “Observations of Correlated Behavior of Two Light Torsion Balances and a Paraconical Pendulum in Separate Locations during the Solar Eclipse of 26.01.2009,” Advances in Astronomy, Vol. 2012, 2012, Article ID: 263818. doi:10.1155/2012/263818
- D. Olenici and A. F. Pugach, “Precise Underground Observations of the Partial Solar Eclipse of 1 June 2011 Using a Foucault Pendulum and a Very Light Torsion Balance,” International Journal of Astronomy and Astrophysics, Vol. 2, No. 4, 2012, pp. 204-209. doi:10.4236/ijaa.2012.24026

