International Journal of Astronomy and Astrophysics
Vol.3 No.1(2013), Article ID:29450,8 pages DOI:10.4236/ijaa.2013.31006
Change in Energy of Non-Spinning Black Holes w.r.t. the Change in Mass
1Department of Physics, Marwari College, T. M. B. U., Bhagalpur, India
2University Department of Mathematics, T. M. B. U., Bhagalpur, India
3Department of Mathematics, N. D. A., Khadakwasala, Pune, India
4Department of Physics, S. S. V. College, Kahalgaon, T. M. B. U., Bhagalpur, India
Email: dipomahto@hotmail.com
Received November 23, 2012; revised December 26, 2012; accepted January 11, 2013
Keywords: Life Time; XRBs; AGN; Energy
ABSTRACT
The present work discusses the derivation of the formula for the change in energy of non-spinning black holes with respect to the change in mass , which gives a constant quantity equal to
, which gives a constant quantity equal to  in both categories of X-ray binaries (XRBs) and Active Galactic Nuclei (AGN). This formula can be used to justify the life time of black hole given by
in both categories of X-ray binaries (XRBs) and Active Galactic Nuclei (AGN). This formula can be used to justify the life time of black hole given by 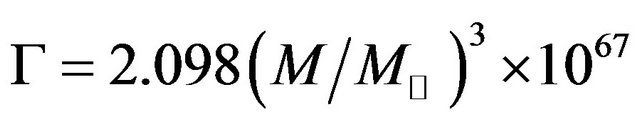 years as proposed by Stephen Hawking, where M and
years as proposed by Stephen Hawking, where M and 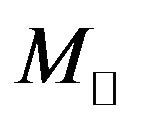 are the mass of the black hole and the sun respectively. The authors also calculate the change in energy and mass of non-spinning black holes with respect to the change in the radius of event horizon as well as
are the mass of the black hole and the sun respectively. The authors also calculate the change in energy and mass of non-spinning black holes with respect to the change in the radius of event horizon as well as 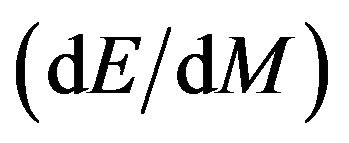 for different test non-spinning black holes in X-ray binaries (XRBs) and Active Galactic Nuclei (AGN).
for different test non-spinning black holes in X-ray binaries (XRBs) and Active Galactic Nuclei (AGN).
1. Introduction
When stars are born, they form from existing gas dust. This is called interstellar matter. When cloud of interstellar matter crosses the spiral arm of a galaxy, it begins to form clumps. The gravitational forces within the clumps cause them to contract, forming protostar. The centre of a protostar may reach a temperature of a several million of degree Celsius. At this high temperature, a fusion reaction begins. The energy released by this reaction prevents the protostar to contract. Thus, a star has been formed. There are so many stages of a star from its birth to death. The black hole is the final stage of dying star having masses 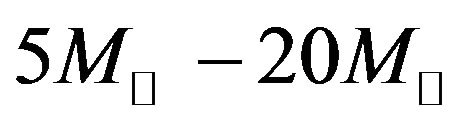 found in X-ray binaries (XRBs) and
found in X-ray binaries (XRBs) and  found in Active Galactic Nuclei (AGN) where
found in Active Galactic Nuclei (AGN) where 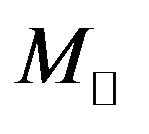 stands for the mass of the sun [1]. Like a living creature, the star takes birth and finally dies. The living creatures are very short-lived than that of the stellar bodies.
stands for the mass of the sun [1]. Like a living creature, the star takes birth and finally dies. The living creatures are very short-lived than that of the stellar bodies.
Classically, the black holes are perfect absorbers but do not emit anything; their temperature is absolute zero [2]. But in 1974, Stephan Hawking showed that quantum theory predicts that the black hole should radiate energy like a black body with a temperature proportional to the surface gravity of the black hole [3] and sometimes also after the physicists, Jacob Bekenstein who predicted that black holes should have a finite, non-zero temperature and entropy [4].
In 2010, Kanak Kumari et al derived an expression for the energy of non-spinning black holes in terms of the radius of event horizon 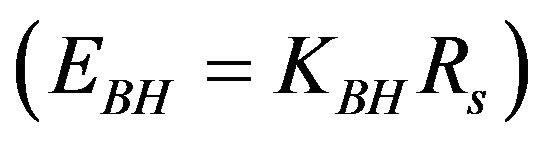 where KBH is the Black hole constant for non-spinning black holes having value equal to
where KBH is the Black hole constant for non-spinning black holes having value equal to 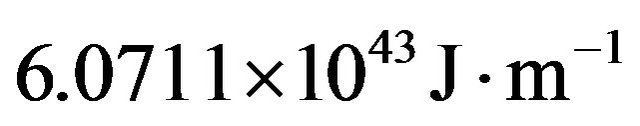 [5].
[5].
In 2011, Dipo Mahto et al derived an expression for the energy of spinning black holes in terms of the radius of event horizon 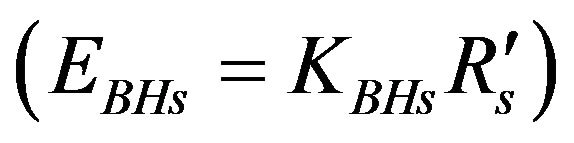 where
where 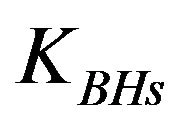 is the black hole constant for spinning black holes having value equal to
is the black hole constant for spinning black holes having value equal to 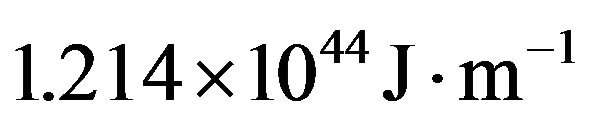 [6]. In the same year Dipo Mahto et al derived the formula for both the changes in energy
[6]. In the same year Dipo Mahto et al derived the formula for both the changes in energy 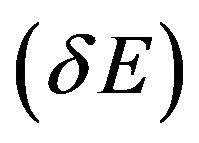 and entropy
and entropy  and calculated their values for different test non-spinning black holes in XRBs and AGN [7].
and calculated their values for different test non-spinning black holes in XRBs and AGN [7].
In the present research work, we have derived the formula for the change in energy of non-spinning black holes with respect to the change in mass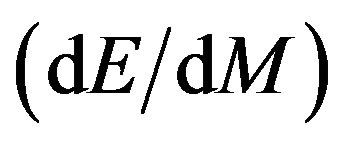 , which gives a constant quantity equal to
, which gives a constant quantity equal to 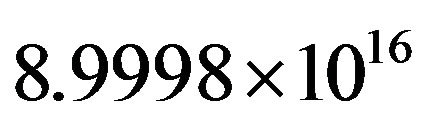 Joule/kg in both categories of X-ray binaries (XRBs) and Active Galactic Nuclei (AGN), where M and
Joule/kg in both categories of X-ray binaries (XRBs) and Active Galactic Nuclei (AGN), where M and 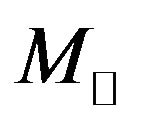 are the mass of the black hole and the sun respectively. This formula can be used to justify the life time of black hole given by
are the mass of the black hole and the sun respectively. This formula can be used to justify the life time of black hole given by 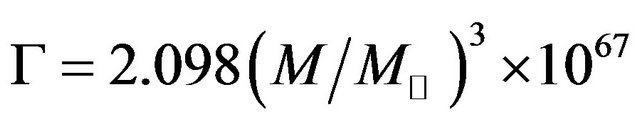 years as proposed by Stephen Hawking. We have also calculated the change in energy and mass of non-spinning black holes with respect to the change in the radius of event horizon as well as
years as proposed by Stephen Hawking. We have also calculated the change in energy and mass of non-spinning black holes with respect to the change in the radius of event horizon as well as  for different test non-spinning black holes in X-ray binaries (XRBs) and Active Galactic Nuclei (AGN).
for different test non-spinning black holes in X-ray binaries (XRBs) and Active Galactic Nuclei (AGN).
2. Discussion
2.1. Black Hole
A black hole is a solution of Einstein’s gravitational field equations in the absence of matter that describes the space time around a gravitationally collapsed star. Its gravitational pull is so strong that even light can not escape from it [8].
Hawking radiation is a thermal radiation with a black body spectrum predicted to be emitted by black holes due to quantum effects. The Hawking radiation process reduces the mass and energy of the black hole and therefore also known as black hole evaporation. The black holes that lose more matter than they gain through other means are expected to dissipate, shrink, and ultimately vanish. Smaller micro black holes are predicted to be larger net emitters of radiation than larger black holes, they tend to shrink and dissipate faster [3].
2.2. Expression for dE/dM
To discuss the loss in mass and energy of black holes, Einstein mass-energy equivalence relation can be applied with the first law of black hole mechanics. The Einstein mass-energy equivalence relation is given by [9].
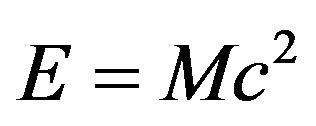 (1)
(1)
The change in energy of black holes taking place the change in their mass as
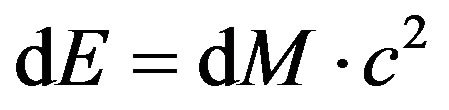 (2)
(2)
The change in energy of the black holes can be calculated when the change in mass of the black holes
can be calculated when the change in mass of the black holes 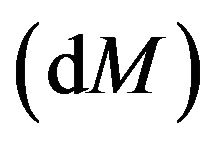 are known. For this the first law of black hole is applied such as.
are known. For this the first law of black hole is applied such as.
The first law of black hole mechanics is mass, M, angular momentum, J, and horizon area, A, of a stationary black hole when it is perturbed. To first order, the variations of these quantities in the vacuum case always satisfy [2].
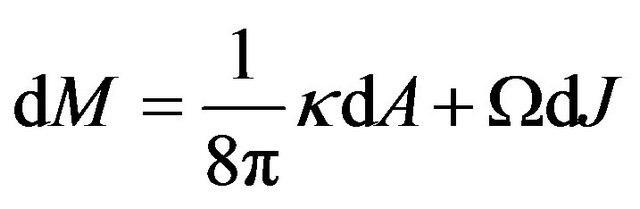 (3)
(3)
In the case of non-spinning black holes, J = 0, and hence dJ = 0 [1,7].
The Equation (3) takes its form as
 (4)
(4)
For the spherically, symmetric and stationary, or Schwarzschild black hole’s mass M, the horizon’s radius is 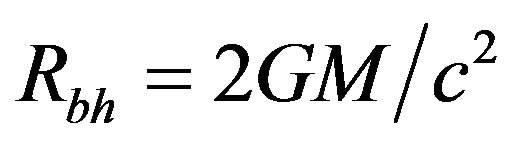 and its area is naturally given by the following relation [7,10,12].
and its area is naturally given by the following relation [7,10,12].
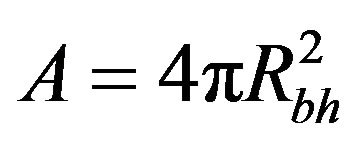 (5)
(5)
where  stands for Schwarzschild radius of horizon area of a black hole. Differentiating Equation (5), we have
stands for Schwarzschild radius of horizon area of a black hole. Differentiating Equation (5), we have
 (6)
(6)
Putting the above value in Equation (4) and solving, we have
 (7)
(7)
or
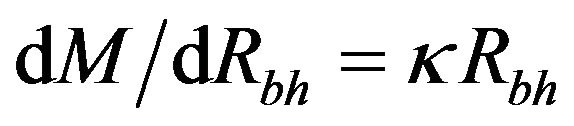 (8)
(8)
In Equation (8), the term  is the surface gravity of black holes. For the Schwarzschild case, the surface gravity
is the surface gravity of black holes. For the Schwarzschild case, the surface gravity  of a black hole is given by [11,12].
of a black hole is given by [11,12].
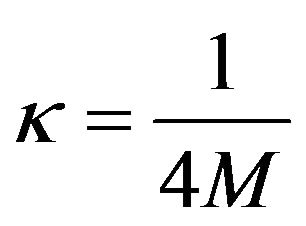 (9)
(9)
The term M stands for the mass of black holes.
From Equation (9), it is clear that the surface gravity of black hole is inversely proportional to its mass and the different black holes will have different surface gravity. Greater the mass of the black holes, smaller the surface gravity and vice-versa.
The surface gravity 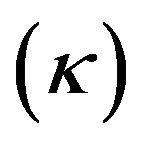 has the same role in the black hole mechanics as the temperature in the ordinary laws of thermodynamics. The zeroth law of classical black hole mechanics states that the surface gravity
has the same role in the black hole mechanics as the temperature in the ordinary laws of thermodynamics. The zeroth law of classical black hole mechanics states that the surface gravity 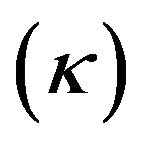 of a black hole is constant on horizon. The surface gravity tends to zero when the magnitude of charge of a black holes becomes equal to the mass of black holes [11,12] and the surface gravity
of a black hole is constant on horizon. The surface gravity tends to zero when the magnitude of charge of a black holes becomes equal to the mass of black holes [11,12] and the surface gravity 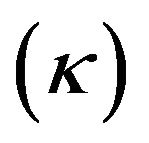 can be thought of roughly as the acceleration at horizon of black hole [8]. Putting the value of
can be thought of roughly as the acceleration at horizon of black hole [8]. Putting the value of 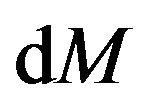 in Equation (2), we have
in Equation (2), we have
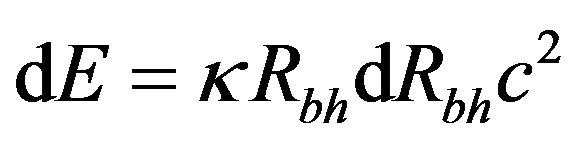 (10)
(10)
Or
 (11)
(11)
Equation (11) can be used to calculate the change in energy of black holes with respect to the radius of event horizon.
Using the Equation (9), the Equations (8) and (11) can be written as
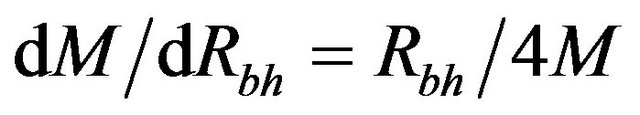 (12)
(12)
 (13)
(13)
The Equations (12) and (13) can be used to determine the change in mass and energy with respect to change in radius of event horizon of different test non-spinning black holes respectively. Now the Equation (13) is divided by Equation (12), we get
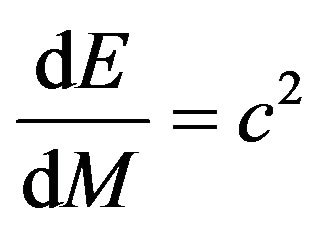 (14)
(14)
The Equation (14) shows the change in energy of different test non-spinning black holes with respect to the change in mass and has vital role to justify life time of black holes 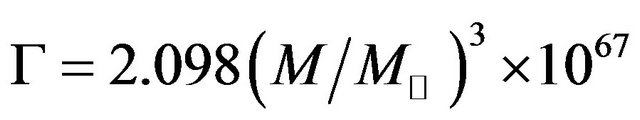 years given by Stephan Hawking.
years given by Stephan Hawking.
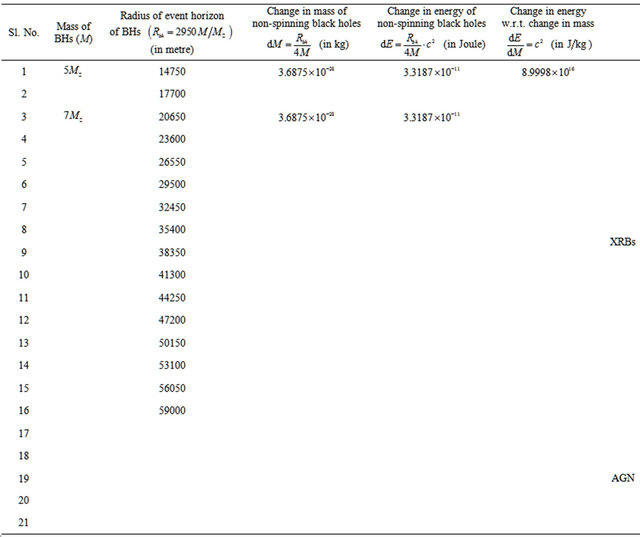
2.3. Data in Support of Mass of BHs
There are two categories of Black holes classified on the basis of their masses clearly very distinct from each other, with very different masses  for stellar—mass Black holes in X-ray binaries and
for stellar—mass Black holes in X-ray binaries and 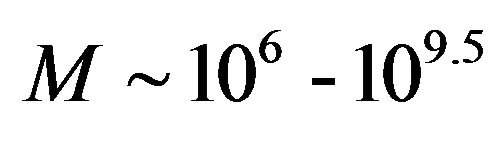
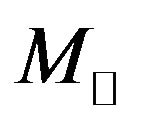 in Active Galactic Nuclei [1,11].
in Active Galactic Nuclei [1,11].
Here we have calculated the change in mass and energy with respect to the radius of event horizon using Equations (10) and (11) respectively as well as 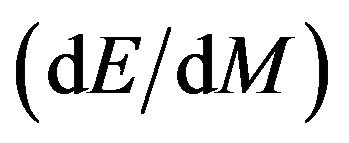 for different test Non-spinning black holes in X-ray binaries (XRBs) and Active Galactic Nuclei (AGN) listed in Table 1.
for different test Non-spinning black holes in X-ray binaries (XRBs) and Active Galactic Nuclei (AGN) listed in Table 1.
3. Result and Discussion
In the present work, we have derived the formula for the change in energy of non-spinning black holes with respect to the change in mass 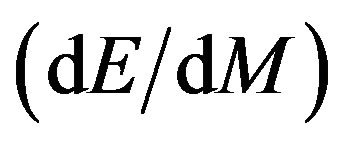 giving a constant quantity, which can be used to justify the life time of black hole in both categories X-ray binaries (XRBs) and Active Galactic Nuclei (AGN). We have calculated the change in mass
giving a constant quantity, which can be used to justify the life time of black hole in both categories X-ray binaries (XRBs) and Active Galactic Nuclei (AGN). We have calculated the change in mass 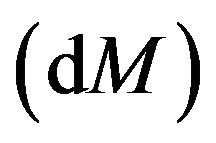 and energy
and energy 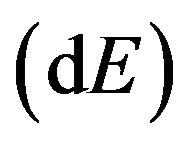 with respect to change in the radius of event horizon as well as
with respect to change in the radius of event horizon as well as 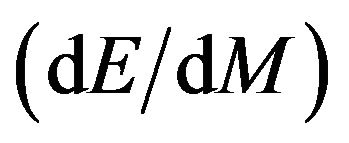 for different test non-spinning black holes in
for different test non-spinning black holes in
Table 1.  Change in energy with respect to change in mass of non-spinning black holes.
Change in energy with respect to change in mass of non-spinning black holes.
X-ray binaries (XRBs) and Active Galactic Nuclei (AGN) and the graphs have been plotted between:
1) the radius of event horizon of different test black holes and their corresponding values of change in mass in XRBs (Figure 1);
of different test black holes and their corresponding values of change in mass in XRBs (Figure 1);
2) the radius of event horizon 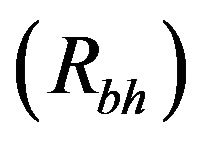 of different test black holes and their corresponding values of change in mass in AGN (Figure 2);
of different test black holes and their corresponding values of change in mass in AGN (Figure 2);
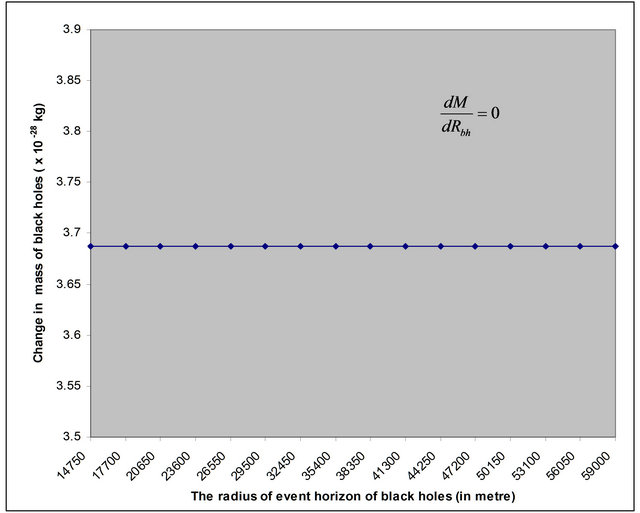
Figure 1. The graph plotted between the radius of event horizon 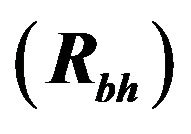 of different BHs and their corresponding values of change in mass in XRBs.
of different BHs and their corresponding values of change in mass in XRBs.
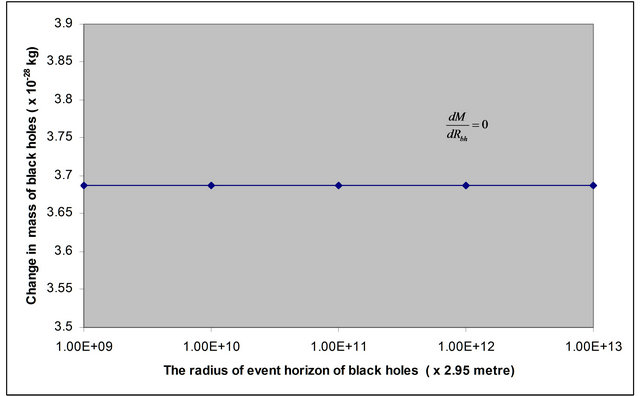
Figure 2. The graph plotted between the radius of event horizon 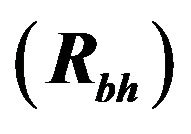 of different BHs and their corresponding values of change in mass in AGN.
of different BHs and their corresponding values of change in mass in AGN.
3) the radius of event horizon of different test black holes and their corresponding values in the change in energy in XRBs (Figure 3);
4) the radius of event horizon of different test black holes and their corresponding values in the change in energy in AGN (Figure 4);
5) the radius of event horizon of different test black holes and their corresponding values of 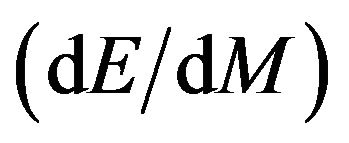 in XRBs (Figure 5);
in XRBs (Figure 5);
6) the radius of event horizon of different test black holes and their corresponding values of  in AGN (Figure 6).
in AGN (Figure 6).
The Figures 1 and 2 shows that the change in mass of non-spinning black holes remain the same with the increase the radius of event horizon of the different test non-spinning black holes in both XRBs and AGN
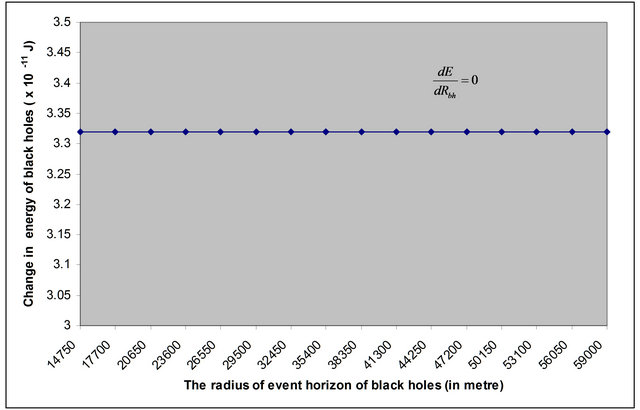
Figure 3. The graph plotted between the radius of event horizon 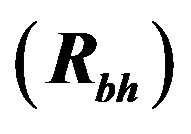 of different BHs and their corresponding values of change in mass in XRBs.
of different BHs and their corresponding values of change in mass in XRBs.

Figure 4. The graph plotted between the radius of event horizon 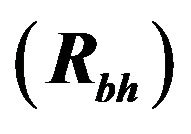 of different BHs and their corresponding values of change in mass in AGN.
of different BHs and their corresponding values of change in mass in AGN.
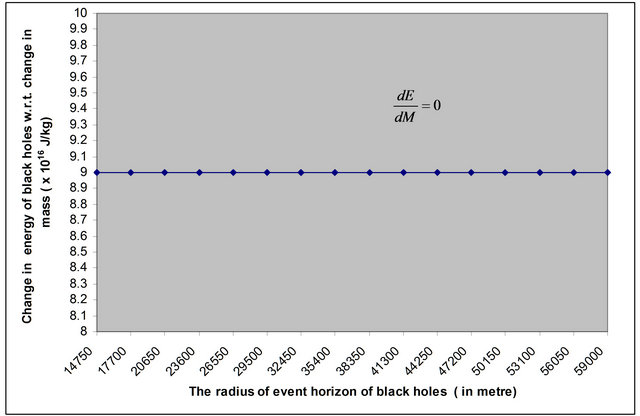
Figure 5. The graph plotted between the radius of event horizon and change in energy of black holes w.r.t. change in mass in XRBs.

Figure 6. The graph plotted between the radius of event horizon and change in energy of black holes w.r.t. change in mass in AGN.
respectively. The slope of the graph in Figures 1 and 2 shows that 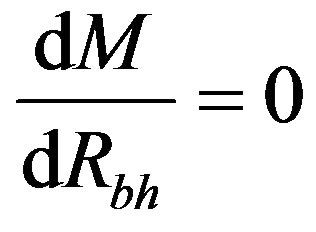 or
or 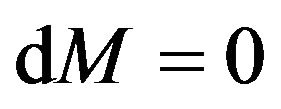 or
or 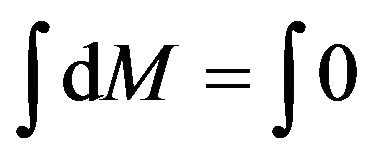 or
or
 .
.
Hence the systems like black holes obey the principle of conservation of mass.
The calculated data for the change in the mass of non-spinning black holes in each case existing either in XRBs or AGN is the same, showing the principle of conservation of mass, which is experimental fact.
The Figures 3 and 4 show that the change in energy of non-spinning black holes remain the same with the increase the radius of event horizon of the different test non-spinning black holes in both XRBs and AGN respectively. The slope of the graph in Figures 3 and 4 show that  or
or .
.
Hence the systems like black holes obey the principle of conservation of energy.
Similarly the calculated data for the change in the energy of non-spinning black holes in each case existing either in XRBs or AGN is the same showing the principle of conservation of energy, which is also experimental fact.
The Figures 5 and 6 show that the change in energy with respect to the change in mass of non-spinning black holes remains the same with the increase the radius of event horizon of the different test non-spinning black holes in both XRBs and AGN respectively. The slope of the graph in Figures 5 and 6 show that 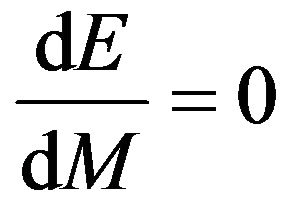 or
or 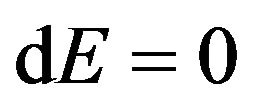 or
or 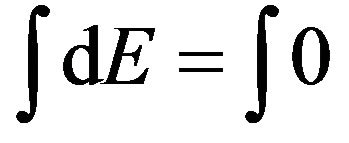 or
or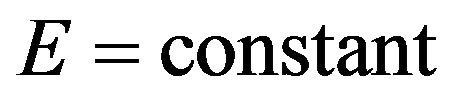 .
.
Hence the systems like black holes obey the principle of conservation of energy. Similarly the calculated data for the change in the energy of non-spinning black holes in each case existing either in XRBs or AGN is the same showing the principle of conservation of energy, which is also experimental fact.
4. Justification of Life Time of BHs
The formula for life time of the black holes as proposed by Stephen Hawking is given by
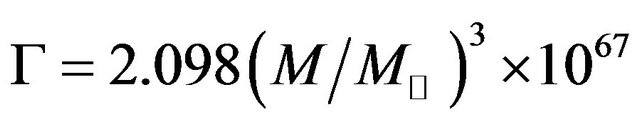 years. The equation for life time of black holes shows that the life time will be longer for heavier black holes than that of lighter black holes. In the present research work, we have shown that the rate of emission of energy with respect to mass
years. The equation for life time of black holes shows that the life time will be longer for heavier black holes than that of lighter black holes. In the present research work, we have shown that the rate of emission of energy with respect to mass 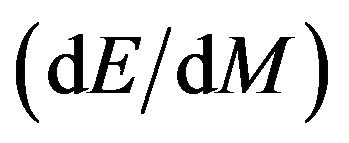 is constant for all black holes either existing in XRBs or AGN. This means that heavier and lighter black holes radiate energy in the same amount. The loss in energy of non-spinning black holes due to radiation of energy will reduce the mass of black holes according to Einstein mass-energy equivalence relation
is constant for all black holes either existing in XRBs or AGN. This means that heavier and lighter black holes radiate energy in the same amount. The loss in energy of non-spinning black holes due to radiation of energy will reduce the mass of black holes according to Einstein mass-energy equivalence relation . This results that the heavier black holes will take longer time to reduce their masses completely into energy radiated than that of the lighter black holes. Hence the heavier black holes will have longer life time than that of lighter. This result is good agreement with the formula for life time of black holes
. This results that the heavier black holes will take longer time to reduce their masses completely into energy radiated than that of the lighter black holes. Hence the heavier black holes will have longer life time than that of lighter. This result is good agreement with the formula for life time of black holes  years given by Stephan Hawking. This justifies the life time of black holes.
years given by Stephan Hawking. This justifies the life time of black holes.
5. Conclusions
In the present study of present research work, we can draw the following conclusion:
1) The change in mass calculated for each case non-spinning black hole gives the constant values equal to  in the both categories of black holes existing in XRBs and AGN leading the principle of conservation of mass;
in the both categories of black holes existing in XRBs and AGN leading the principle of conservation of mass;
2) The change in energy calculated for each case non-spinning black hole gives the constant values equal to 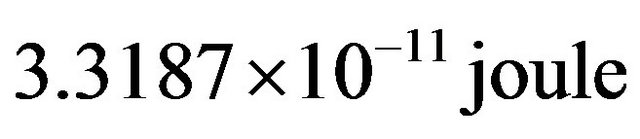 in the both categories of black holes existing in XRBs and AGN leading the principle of conservation of energy;
in the both categories of black holes existing in XRBs and AGN leading the principle of conservation of energy;
3) The change in energy with respect to change in mass 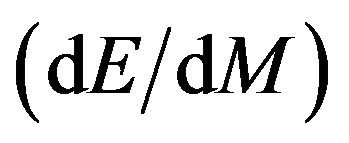 calculated for each case non-spinning black hole gives the constant values equal to
calculated for each case non-spinning black hole gives the constant values equal to 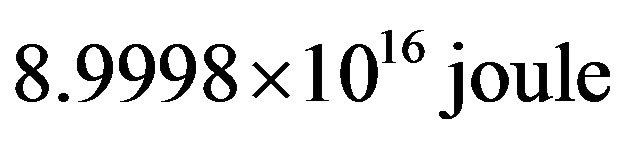 per kg in the both categories of black holes either existing in X-ray binary (XRBs) or Active Galactic Nuclie (AGN) justifying the life time of black holes that the heavier black holes will have longer life time than that of lighter. This result is good agreement with the formula
per kg in the both categories of black holes either existing in X-ray binary (XRBs) or Active Galactic Nuclie (AGN) justifying the life time of black holes that the heavier black holes will have longer life time than that of lighter. This result is good agreement with the formula  years.
years.
6. Acknowledgements
Authors acknowledge their gratitude to Dr. Gopi Kant Jha, Former Head, Department of Physics, L. N. M. U. Darbhanga (Bihar), Dr. Kamal Prasad, Dr. B. N. Singh, Dr. Ashutosh Prasad, Associate Professor, University Department of Physics, T. M. B. U. Bhagalpur and Dr. M. S. H. “John”, Principal Marwari College Bhagalpur for their stimulating discussion and motivation. Authors are also grateful to the referee for pointing out the errors in the original manuscript and making constructive suggestions.
REFERENCES
- R. Narayan, “Black Holes in Astrophysics,” New Journal of Physics, Vol. 7, No. 1, 2005, pp. 1-31.
- R. M. Wald, “The Thermodynamics of Black Holes. Living Reviews in Relativity,” 2001.
- S. W. Hawking, “A Black Hole Explosion?” Nature, Vol. 248, 1974, pp. 30-31. http://www.nature.com/nature/journal/v248/n5443/abs/248030a0.html
- C. Rose, “A Conversation with Dr. Stephen Hawking and Lucy Hawking”. http://www.charlierose.com/guest/view/6294
- K. Kumari, D. Mahto, G. Chandra, R. K. Sah and K. M. Singh, “Study of Schwarzschild’s Radius with Reference to the Non-Spinning Black Holes,” Bulletin of Pure and Applied Sciences, Vol. 29D, No. 2, 2010, pp. 183-187.
- D. Mahto, K. Kumari, R. K. Sah and V. Prakash, “Study of Schwarzschild’s Radius with Reference to the Spinning Black Holes,” Bulletin of Pure and Applied Sciences, Vol. 30D, No. 1, 2011, pp. 157-162.
- D. Mahto, K. Kumari, R. K. Sah and K. M. Singh, “Study of Non-Spinning Black Holes with Reference to the Change in Energy and Entropy,” Astrophysics and Space Science, Vol. 337, No. 2, 2011, pp. 685-691. doi:10.1007/s10509-011-0883-7
- A. Dabholkar, “Black Hole Entropy in String Theory. A Window in to the Quantum Structure of Gravity,” Current Science, Vol. 89, No. 12, 2005, p. 25.
- P. G. Bergmann, “Introduction to the Theory of Relativity,” Prentice-Hall of India, New Delhi, 1969.
- J. D. Bekenstein, “Bekenstein-Hawking Entropy,” Scholarpedia, Vol. 3, No. 10, 2008, p. 7375
- D. Mahto, V. Prakash, B. K. Singh and K. M. Singh, “Change in Entropy of Non-Spinning Black Holes w.r.t. the Radius of Event Horizon in XRBs,” Astrophysics and Space Science, Vol. 343, No. 1, 2013, pp. 153-159. doi:10.1007/s10509-012-1219-y
- J. Transchen, “An Introduction to Black Hole Evaporation,” 2000.

