International Journal of Astronomy and Astrophysics
Vol. 3 No. 2 (2013) , Article ID: 32572 , 10 pages DOI:10.4236/ijaa.2013.32013
Existence and Stability of Equilibrium Points in the Robe’s Restricted Three-Body Problem with Variable Masses
1Department of Mathematics, Faculty of Science, Ahmadu Bello University, Zaria, Nigeria
2Department of Mathematics, Statistics and Computer Science, College of Science, University of Agriculture, Makurdi, Nigeria
Email: jgds2004@yahoo.com, lekkyonix4ree@yahoo.com
Copyright © 2013 Jagadish Singh, Oni Leke. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received January 4, 2013; revised February 6, 2013; accepted February 14, 2013
Keywords: Robe’s Problem; Meshcherskii Law; GMP; Equilibruim Points
ABSTRACT
The positions and linear stability of the equilibrium points of the Robe’s circular restricted three-body problem, are generalized to include the effect of mass variations of the primaries in accordance with the unified Meshcherskii law, when the motion of the primaries is determined by the Gylden-Meshcherskii problem. The autonomized dynamical system with constant coefficients here is possible, only when the shell is empty or when the densities of the medium and the infinitesimal body are equal. We found that the center of the shell is an equilibrium point. Further, when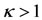 ;
; 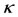 being the constant of a particular integral of the Gylden-Meshcherskii problem; a pair of equilibrium point, lying in the
being the constant of a particular integral of the Gylden-Meshcherskii problem; a pair of equilibrium point, lying in the  with each forming triangles with the center of the shell and the second primary exist. Several of the points exist depending on
with each forming triangles with the center of the shell and the second primary exist. Several of the points exist depending on ; hence every point inside the shell is an equilibrium point. The linear stability of the equilibrium points is examined and it is seen that the point at the center of the shell of the autonomized system is conditionally stable; while that of the non-autonomized system is unstable. The triangular equilibrium points on the
; hence every point inside the shell is an equilibrium point. The linear stability of the equilibrium points is examined and it is seen that the point at the center of the shell of the autonomized system is conditionally stable; while that of the non-autonomized system is unstable. The triangular equilibrium points on the 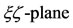 of both systems are unstable.
of both systems are unstable.
1. Introduction
The restricted three-body problem (R3BP) describes the motion of an infinitesimal mass moving under the gravitational effects of the two finite masses, called primaries, which move in circular orbits around their common center of mass on account of their mutual attraction and the infinitesimal mass not influencing the motion of the primaries. The R3BP is one of the most widely studied areas in space dynamics as well as in celestial mechanics. The studies cover both analytical and numerical aspects. The analytic aspect considered mostly the circular, planar R3BP, in which all particles are confined to a plane and the primaries are in circular orbits around their centre of mass. The numerical aspect allowed consideration of the more general problem. The applications of the R3BP span solar system dynamics, lunar theory, motion of space craft and stellar dynamics.
Generally, we assume in the classical problem that the masses of celestial bodies don’t change with time. The phenomenon of isotropic radiation or absorption in stars led scientists to formulate the restricted problem of three bodies with variable masses. During evolution, the masses of celestial bodies change, especially in a double star system were masses change rather intensively. Dufour [1] seems to have been the first to examine the astronomical phenomena of variable mass relating the secular variation of lunar acceleration with the increase of the Earth’s mass due to the impact of meteorites. Later, Gylden [2] established the differential equations of motion for the problem when the mass are subject to variation. The integrable case to this differential equation was then given by Meshcherskii [3] for a particular mass variation law. Meshcherskii [4] showed that the Gylden problem is a particular case of the problem of two bodies with variable mass under the condition that the laws of variation are the same while the relative motion of the particles separating or attaching to them is zero everywhere. This law and its following generalization are referred to as Meshcherskii law. After this contribution, the physical meaning of the problem became clear and it is known as Gylden-Meshcherskii Problem (GMP).
The GMP is a generalization of the two-body problem with constant masses; a set up wherein both masses are allowed to vary. The interest in this model arises from cometary dynamics. When orbiting the Sun, comets lose part or even all of their mass due to thermal out-gassing of volatiles and due to interaction between the solar wind and the cometary surface. It also models an isotropic change in the mass of the gravitating bodies. That is, the primaries loss mass without causing a reactive force. Beside this, the GMP is used to describe the evolution of binary stars during secular mass loss owing to photon and corpuscular activity. This problem has also received considerable attention in the restricted three-body problem. In this approach, the motion of the primaries is assumed to be determined by the GMP. Thus, one has to only study the motion of the body of infinitesimal mass which does not affect the motion of the primaries.
Gelf’gat [5] examined the restricted three-body problem of variable masses in which the primary bodies move within the framework of the GMP and established the existence of five libration points (collinear & triangular) analogous to the classical libration points. Bekov [6] found two additional equilibrium points, called the coplanar points. A few recent characterizations of the GMP were examined by Gurfil and Belyanin [7] and Singh and Leke [8]. The majority of the authors have been interested in the stellar applications of this problem than the solar system.
A new kind of the restricted three-body problem was formulated by Robe [9], in which one of the primaries of mass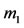 , is a rigid spherical shell, filled with homogenous, incompressible fluid of density
, is a rigid spherical shell, filled with homogenous, incompressible fluid of density , with the second mass point
, with the second mass point 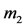 outside the shell and moving around the first primary in a Keplerian orbit; and the infinitesimal mass
outside the shell and moving around the first primary in a Keplerian orbit; and the infinitesimal mass 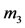 as a small solid sphere of an infinitesimal radius, and of density
as a small solid sphere of an infinitesimal radius, and of density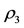 , moving inside the shell and is subject to the attraction of
, moving inside the shell and is subject to the attraction of 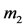 and the buoyancy force due to the fluid. He discussed the linear stability of an equilibrium point obtained in two cases; the first being the case when the orbit of
and the buoyancy force due to the fluid. He discussed the linear stability of an equilibrium point obtained in two cases; the first being the case when the orbit of 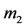 around
around 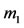 is circular and in the second case, when it is elliptic, but the shell is empty (there is no fluid inside it) or densities of
is circular and in the second case, when it is elliptic, but the shell is empty (there is no fluid inside it) or densities of 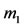 and
and 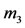 are equal. Since then, various studies under different assumptions have been carried out by some researchers (e.g., Shrivastava and Garain [10]; Hallan and Rana [11]; Hallan and Mangang [12]). The Robe’s problem can be used to study the small oscillation of the Earth inner core taking into account the Moon’s attraction and the stability of the Earth’s centre (Robe [9]).
are equal. Since then, various studies under different assumptions have been carried out by some researchers (e.g., Shrivastava and Garain [10]; Hallan and Rana [11]; Hallan and Mangang [12]). The Robe’s problem can be used to study the small oscillation of the Earth inner core taking into account the Moon’s attraction and the stability of the Earth’s centre (Robe [9]).
Modern concepts of the change in the distance between the Earth and the Moon, and the change in their masses due to, out-gassing, impact of meteorites, asteroids, comets and space dust lead to the necessity of investigating dynamics problem in the Earth-Moon system under these conditions. It is believed that the Earth gains 100,000 kilograms of mass each year from space, one million kilograms of mass every day due to in falling meteors. However, the Earth’s mass change appears to be exceedingly tiny, and seemingly, not nearly enough to change the dynamics in any significant way. Hence, in this paper, we investigate the motion of a test particle of infinitesimal mass under the set up of the Robe [9] model given that the masses of both primaries vary in proportion to each other according to the unified Meshcherskii [4] law and their motion determined by the Gylden-Meshcherskii problem (Gylden [2]; Meshcherskii [3]). The existence and the long time stability behavior of equilibrium points are investigated. This paper is a generalization of the paper by Robe [9], in the sense that the masses of the primaries are assumed to vary with time. Further, we restrict our study to the case when the shell is empty or when the densities of the medium and the infinitesimal body are equal. We found that every point inside the shell is an equilibrium point contrary to just one found at the center of the shell in the work of Robe [9].
The paper is organized as follows: Section 2 represents the equations of motion; the existence of the equilibrium points is mentioned in Section 3, while Section 4 investigates their linear stability; Section 5 discusses the obtained results; and the conclusion is drawn in Section 6.
2. The Equations of Motion
The absolute motion of a body whose mass depends on time is described by the Meshcherskii equation for a point of variable mass, (see Sommerfeld [13]) as
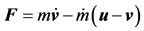 (1)
(1)
where  is the velocity of the center of mass of the absorbed mass immediately before its attachment with the body (or of the ejected mass immediately after its separation);
is the velocity of the center of mass of the absorbed mass immediately before its attachment with the body (or of the ejected mass immediately after its separation); 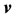 is the velocity of the point measured in an inertial coordinate and
is the velocity of the point measured in an inertial coordinate and 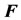 is the combined force acting on it which is also measured in an inertial coordinate system. There are two special cases of equation. However, we shall consider in the case when mass is ejected with the same velocity of the body at any moment
is the combined force acting on it which is also measured in an inertial coordinate system. There are two special cases of equation. However, we shall consider in the case when mass is ejected with the same velocity of the body at any moment , that is, mass ejection does not produce a reactive force. This case can be used to study the motion of a body ejecting matters isotropically (or radiating energy).
, that is, mass ejection does not produce a reactive force. This case can be used to study the motion of a body ejecting matters isotropically (or radiating energy).
Now, let 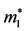 be the mass of the first primary which is a rigid spherical shell of constant radius
be the mass of the first primary which is a rigid spherical shell of constant radius  with center at
with center at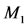 , and filled with a homogenous incompressible fluid of constant density
, and filled with a homogenous incompressible fluid of constant density 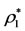 and volume
and volume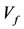 . Also, let
. Also, let  be the mass of the second primary with center at
be the mass of the second primary with center at 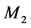 which describes a circular orbit around the first one. Both masses are assumed to vary with time due to the attachment or separation of particles to or from them. We assume that the variation in mass of the first primary occurs and does not affect the fluid inside it. Therefore, the mass of the first primary is
which describes a circular orbit around the first one. Both masses are assumed to vary with time due to the attachment or separation of particles to or from them. We assume that the variation in mass of the first primary occurs and does not affect the fluid inside it. Therefore, the mass of the first primary is
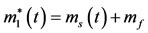 (2)
(2)
where,  is the mass of the shell;
is the mass of the shell;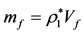 ;
;
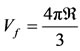 .
.
Now, if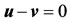 , then reactive forces are absent from Equation (1) and the relative motion is described by the GMP (Gylden [2]; Meshcherskii [3]):
, then reactive forces are absent from Equation (1) and the relative motion is described by the GMP (Gylden [2]; Meshcherskii [3]):
 (3)
(3)
where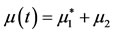 ;
;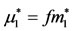 ,
,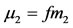 ;
; 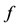 is the gravitational constant and
is the gravitational constant and  is the position vector of
is the position vector of 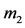 relative to
relative to .
.
Further, we let 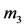 be the mass of the infinitesimal body with center at
be the mass of the infinitesimal body with center at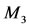 , having density
, having density 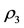 and suppose it is lying inside the spherical shell (see Figure 1). Consequently, following Robe [9] and knowing that the distances between the centers of the primaries vary with time; then, the forces acting on the third body are 1) The force of attraction of
and suppose it is lying inside the spherical shell (see Figure 1). Consequently, following Robe [9] and knowing that the distances between the centers of the primaries vary with time; then, the forces acting on the third body are 1) The force of attraction of 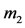 which is given by
which is given by
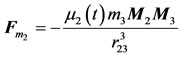 (4)
(4)
2) The gravitational force 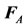 exerted by the fluid of density
exerted by the fluid of density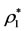 :
:
 (5)
(5)
3) The buoyancy force exerted by the fluid, which is given by
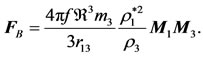 (6)
(6)
Now, the equation of motion of the third body in the inertial system taking into account the combined forces acting on it, is
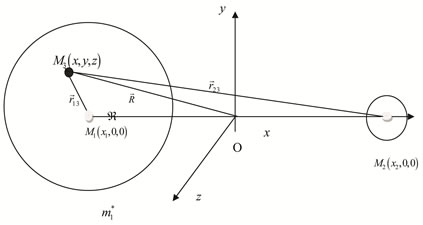
Figure 1. The Robe R3BP.
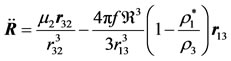 (7)
(7)
where 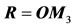
In a synodic coordinates system 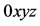 rotating with angular velocity
rotating with angular velocity 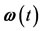 and origin at the center of mass, O, of the primaries; the equation of motion of
and origin at the center of mass, O, of the primaries; the equation of motion of 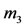 is
is
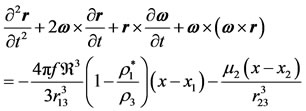 (8)
(8)
where 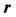 is the position vector of the third body relative to the center of mass,
is the position vector of the third body relative to the center of mass,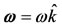 .
.
The Equation (8) in a Cartesian coordinate system, takes the form:
 (9)
(9)
where the over-dot denotes differentiation with respect to time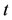 . The coordinates
. The coordinates 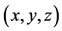 of the third body is connected with the distances between the center of the third body and centers of the primaries by the relation
of the third body is connected with the distances between the center of the third body and centers of the primaries by the relation
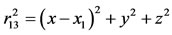 ,
, 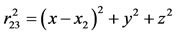
while the barycentric x-coordinates 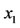 and
and  of the primaries are connected with the distance
of the primaries are connected with the distance  between them by the expressions
between them by the expressions
 (10)
(10)
Now, our aim is to transform Equation (9) to the autonomized form with constant coefficients using a Meshcherskii’s transformation; the particular solutions of the GMP and the unified Meshcherskii [4] law. However, this is possible here, only when the densities of the medium and the infinitesimal body are equal, or the shell is empty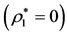 . Proceeding in this regards, using a Meshcherskii’s transformation:
. Proceeding in this regards, using a Meshcherskii’s transformation:
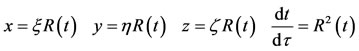 (11)
(11)
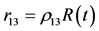 ,
,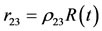 ;
;
the particular solutions of the GMP
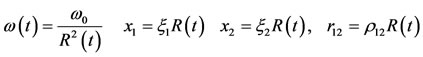 (12)
(12)
and the unified Meshcherskii [4] law:
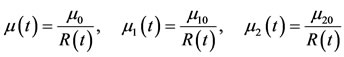 (13)
(13)
where 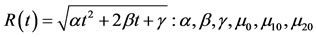 are constantsThe system of Equation (9), when the shell is empty in the autonomized forms:
are constantsThe system of Equation (9), when the shell is empty in the autonomized forms:
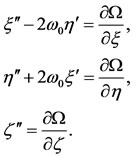 (14)
(14)
where
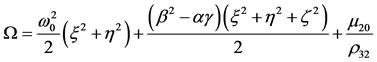
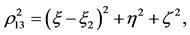
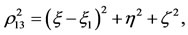
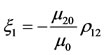 ,
,  ,
, 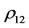 is constant and the dashes denote differentiation with respect to
is constant and the dashes denote differentiation with respect to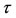 .
.
Without loss of generality, we introduce the mass parameter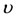 , defined as
, defined as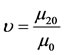 ,
,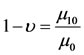 :
: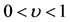 and make choice at initial time
and make choice at initial time 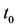 respectively for the unit of mass, distance and time such that
respectively for the unit of mass, distance and time such that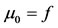 ,
,  ,
, 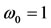 Consequently,
Consequently,
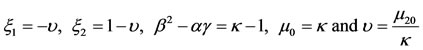 (15)
(15)
The last Equation of (15) differs from the mass ratio given in Robe [9].
The equations of motion in the dimensionless Cartesian coordinates are
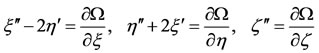 (16)
(16)
where
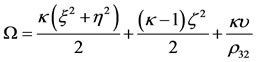
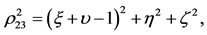
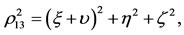
3. Equilibrium Points
The positions of the equilibrium points are the solutions of the equations
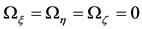 (17)
(17)
That is,
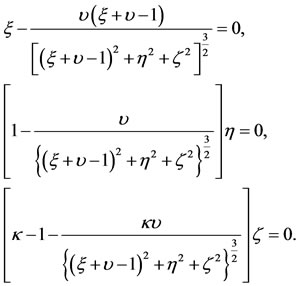 (18)
(18)
The last equation shows that if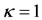 , it must have a solution
, it must have a solution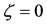 , otherwise it has a different solution. Therefore, the equilibrium points are the solutions of the following systems of equations:
, otherwise it has a different solution. Therefore, the equilibrium points are the solutions of the following systems of equations:
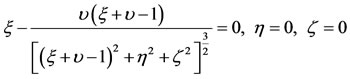 (19)
(19)
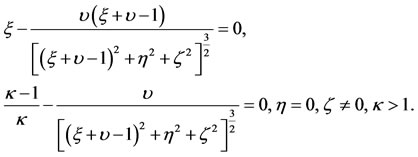 (20)
(20)
 (21)
(21)
Now, substituting the second Equation of (21) in its first one, we have
 (22)
(22)
which is not possible since 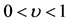 . Hence, we search for the equilibrium points on the
. Hence, we search for the equilibrium points on the  (see Figure 2).
(see Figure 2).
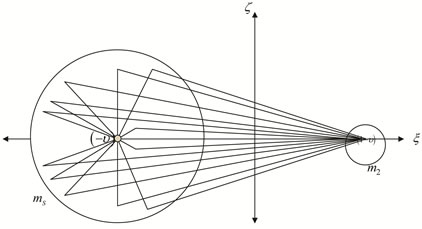
Figure 2. Equilibrium points on the 
3.1. Point at the Center of the Shell
The equilibrium point at the center of the shell is found by solving Equation (19). To do this, we denote its first equation when 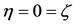 by
by , that is
, that is
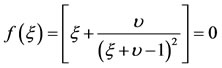 (23)
(23)
Now, 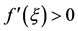 for
for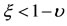 . Therefore,
. Therefore, 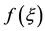 is increasing in the open interval
is increasing in the open interval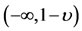 .
.
As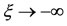 ,
, 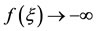 and as
and as ,
,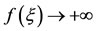 . Consequently,
. Consequently,  is zero only once in the interval
is zero only once in the interval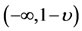 . Hence, Equation (23) has only one root in this interval. Solving it, we get
. Hence, Equation (23) has only one root in this interval. Solving it, we get
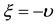 . (24)
. (24)
This gives the equilibrium point at the center of the spherical shell and is fully analogous to that obtained by Robe [9].
3.2. Triangular Points
The triangular points are found in the classical restricted three-body problem, but the existence of these points was not pointed out in the Robe [9] problem. However, the investigations concerning these points, when the shell is not empty, were carried out by Hallan and Rana [11]. The positions of the triangular equilibrium points in our case are the solutions of Equation (20). Here, we suppose that 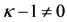 and
and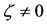 . Solving its second equation for
. Solving its second equation for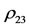 , we at once have
, we at once have
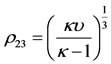 (25)
(25)
Substituting Equation (25) in the first Equation of (20), results in
 (26)
(26)
Equation (26) gives the abscissae of the triangular points, which is less than the coordinate of the second primary (i.e.,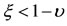 ) for
) for 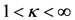 and lies within the shell.
and lies within the shell.
Now, knowing that , substituting Equations (25) and (26) in it and solving, we get
, substituting Equations (25) and (26) in it and solving, we get
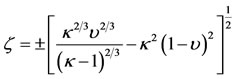 (27)
(27)
Equation (26) and (27) give the position of a pair of equilibrium points  which exist for
which exist for 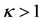 and lies in the
and lies in the 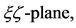 with each forming triangles with the center of the shell and the second primary; that is why we call them “triangular points” (see Figure 2: not drawn to scale and Figures 3 and 4, drawn to scale). We observe that the every point in the shell that is not collinear with the center of the shell is a triangular equilibrium points because they form triangles with the centers of both primaries, though this depends on the parameter
with each forming triangles with the center of the shell and the second primary; that is why we call them “triangular points” (see Figure 2: not drawn to scale and Figures 3 and 4, drawn to scale). We observe that the every point in the shell that is not collinear with the center of the shell is a triangular equilibrium points because they form triangles with the centers of both primaries, though this depends on the parameter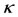 . Numerically, in the Earth-Moon system when
. Numerically, in the Earth-Moon system when  and
and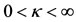 , the triangular points exist for
, the triangular points exist for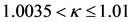 . When
. When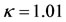 , we have
, we have 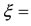 −0.0099 and
−0.0099 and 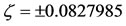 which lies inside the shell. However, when
which lies inside the shell. However, when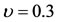 , these points exist for
, these points exist for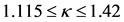 , (see Tables 1 and 2 in Section 4.2). When
, (see Tables 1 and 2 in Section 4.2). When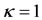 , we have
, we have 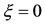 which lies outside the shell and since
which lies outside the shell and since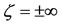 , it is seen that infinite remote equilibrium points
, it is seen that infinite remote equilibrium points 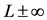 do not exist for any value of
do not exist for any value of .
.
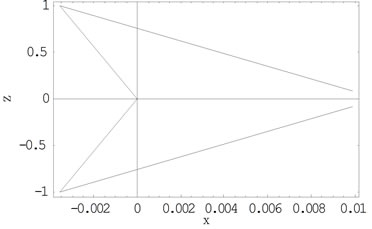
Figure 3. Equilibrium points on the  for
for 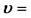
 .
.
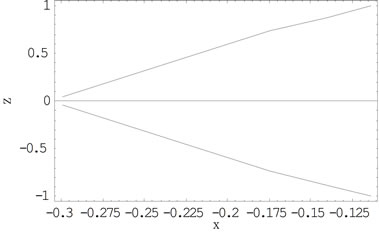
Figure 4. Equilibrium points on the  for
for .
.
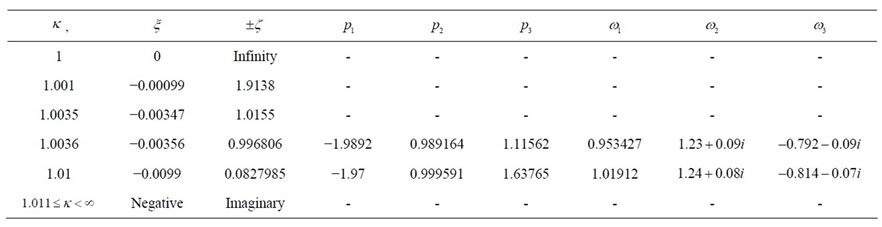
Table 1. Positions of triangular points and the characteristic roots ,
, 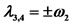 ,
, 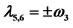 for
for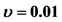 .
.
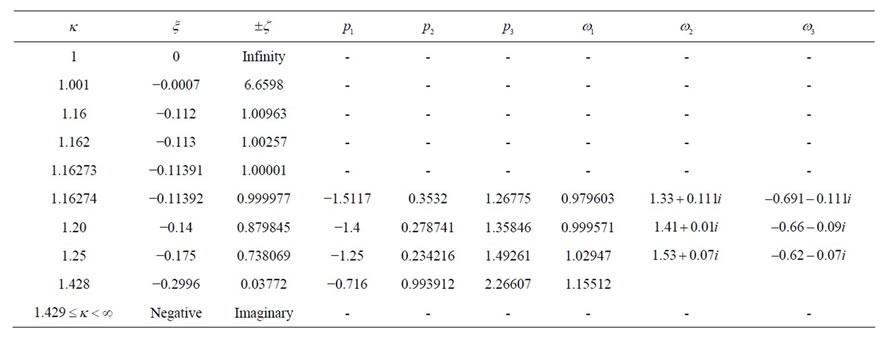
Table 2. Positions of triangular points and the characteristic roots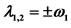 ,
, 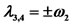 ,
, 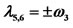 for
for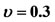 .
.
The equilibrium point at the center of the shell and the triangular equilibrium points of the system of Equation (9) when the densities of the medium and the infinitesimal body are equal, or the shell is empty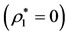 , are sought using the Meshcherskii’s [4] transformation, in the forms:
, are sought using the Meshcherskii’s [4] transformation, in the forms:
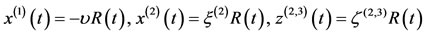 (28)
(28)
where, 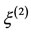 , and
, and 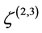 are the triangular points of the autonomized systems. The equilibrium points in this case are function of time
are the triangular points of the autonomized systems. The equilibrium points in this case are function of time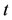 .
.
4. Stability of Equilibrium Points
Let the third body be displaced to 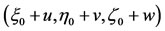 where
where 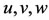 are small displacements in the coordinates of the infinitesimal mass. Then, Equation (20) in the linearized form are
are small displacements in the coordinates of the infinitesimal mass. Then, Equation (20) in the linearized form are
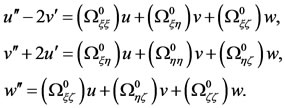 (29)
(29)
where the partial derivatives are evaluated at the equilibrium point under consideration.
4.1. Equilibrium Point at the Center of the Shell
In order to consider the motion near the equilibrium point at the center of the shell, we let solutions of the first two equations of (29) be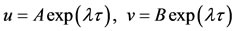 , where
, where 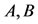 and
and 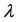 are constants. Taking first and second derivatives of the above, substituting them into the first two equations of system (29) and simplifying we obtain the matrix which has non-zero solution when
are constants. Taking first and second derivatives of the above, substituting them into the first two equations of system (29) and simplifying we obtain the matrix which has non-zero solution when
 (30)
(30)
Expanding the determinant, the characteristic equation corresponding to the variational equations when motion is considered in the 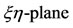 is
is
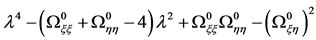 (31)
(31)
Now, the values of the second order partial derivatives computed at the equilibrium point  with the substitution,
with the substitution,  are:
are:
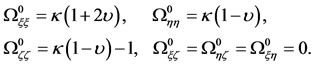 (32)
(32)
Substituting Equation of (32) in the variational Equation (29), at once results in
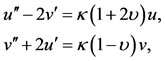 (33)
(33)
 (34)
(34)
Equation (34) is independent of Equation (33) and depicts that the motion parallel to the 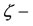 axis is stable when
axis is stable when  for
for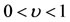 , and unstable when the converse holds.
, and unstable when the converse holds.
Now, the characteristic Equation (31) with the substitution of Equation (32) becomes
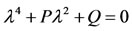 (35)
(35)
where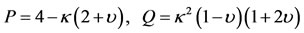 Here,
Here, 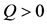 , while
, while 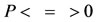 when
when 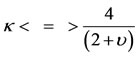 respectively.
respectively.
The roots of Equation (35) are
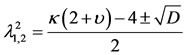 (36)
(36)
where
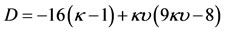 (37)
(37)
Now, when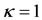 ,
,  is zero only when
is zero only when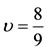 . When
. When  , the discriminant vanishes when
, the discriminant vanishes when
 (38)
(38)
where 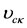 is the different values of
is the different values of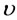 , at which the discriminant is zero.
, at which the discriminant is zero.  are the critical mass parameters which exist for different values of
are the critical mass parameters which exist for different values of . Equation (38)
. Equation (38)
exists only for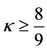 .
.
Now from Equation (37), we have
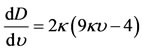 , (39)
, (39)
and is zero when 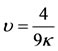 . Therefore, Equation (39) is positive when
. Therefore, Equation (39) is positive when 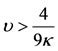 and negative when
and negative when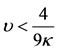 . This means that
. This means that  is strictly increasing when the former holds and strictly decreasing when the later occurs. Now, when
is strictly increasing when the former holds and strictly decreasing when the later occurs. Now, when 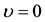 in Equation (37), we have
in Equation (37), we have
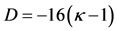 (40)
(40)
However, when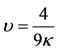 , Equation (37) reduces to
, Equation (37) reduces to
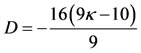 (41)
(41)
and is negative when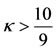 . Further, as
. Further, as 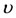 increases to
increases to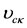 ,
, 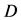 increases from the value in (41) to 0. Finallyas
increases from the value in (41) to 0. Finallyas 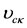 increases to 1, the discriminant increases from zero to
increases to 1, the discriminant increases from zero to
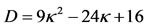 (42)
(42)
An inspection of Equation (42) reveals that for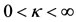 , we have
, we have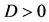 .
.
Now, since the nature of the roots depend on the nature of the discriminant, mass ratio, and the constant 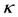 of a particular integral of the Gylden-Meshcherskii problem; we consider the three regions of Equation (37) coupled with the changes in
of a particular integral of the Gylden-Meshcherskii problem; we consider the three regions of Equation (37) coupled with the changes in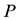 , which depends on
, which depends on 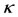 and
and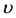 .
.
1) When simultaneously  or
or  and
and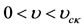 ,
, ; the roots are respectively
; the roots are respectively
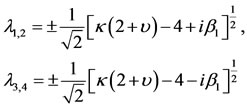 (43)
(43)
and
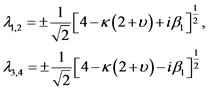
where .
.
The real parts of the two of the roots are positive and equal in both cases. Therefore, the equilibrium point is unstable.
2) When ,
,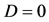 . The following cases are possible.
. The following cases are possible.
a) If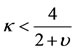 , two of the roots are real and equalwhile the other two are negative and equal as well. The equilibrium point is unstable in this case.
, two of the roots are real and equalwhile the other two are negative and equal as well. The equilibrium point is unstable in this case.
b) If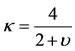 , here all the roots are zero, and the equilibrium point is unstable c) If
, here all the roots are zero, and the equilibrium point is unstable c) If , all four roots are imaginary, with two positive and equal and the other two negative and equal. In this case we have positive stable resonance.
, all four roots are imaginary, with two positive and equal and the other two negative and equal. In this case we have positive stable resonance.
3) When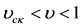 ,
, 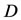 is positive. Therefore, when
is positive. Therefore, when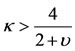 , the roots are:
, the roots are:
 (44)
(44)
where
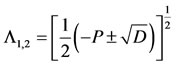
In this case both values of  are negative and all the roots are distinct and imaginary. Therefore, the equilibrium point is stable. However, for
are negative and all the roots are distinct and imaginary. Therefore, the equilibrium point is stable. However, for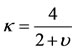 , there are two positive equal roots and two negative equal roots. When
, there are two positive equal roots and two negative equal roots. When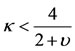 , the roots are real and distinct and the equilibrium point is unstable due to a positive root, in both cases. Hence, we conclude that the equilibrium point
, the roots are real and distinct and the equilibrium point is unstable due to a positive root, in both cases. Hence, we conclude that the equilibrium point  of the autonomized system is stable for
of the autonomized system is stable for  provided
provided 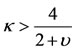 and unstable for
and unstable for 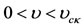 and
and 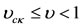 provided
provided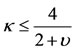 . This is characterized by the arbitrary constant
. This is characterized by the arbitrary constant 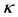 of the Gylden-Meshcherskii problem and the mass ratio
of the Gylden-Meshcherskii problem and the mass ratio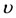 .
.
The range of the stable motion is given by
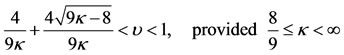 (45)
(45)
When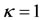 , Equation (45) becomes
, Equation (45) becomes 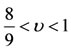 and is fully analogous to that of Robe [9], when the shell is empty and motion is circular. Hence, as
and is fully analogous to that of Robe [9], when the shell is empty and motion is circular. Hence, as 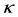 is increasing Equation (45) is approaching zero and the region of stability is increasing.
is increasing Equation (45) is approaching zero and the region of stability is increasing.
4.2. Stability of Triangular Points
For the stability of the triangular equilibrium points, we have the following values of the partial derivatives:
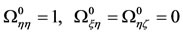 ,
,
 (46)
(46)

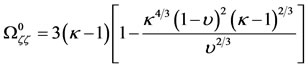
Substituting the trial solutions 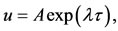
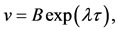
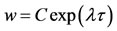 , in the variational Equations (29), and then substituting the partial derivatives (46), we obtain the characteristic equation in this case:
, in the variational Equations (29), and then substituting the partial derivatives (46), we obtain the characteristic equation in this case:
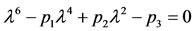 (47)
(47)
where, 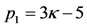
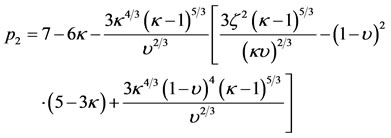
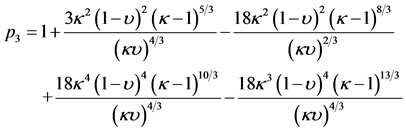
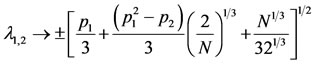
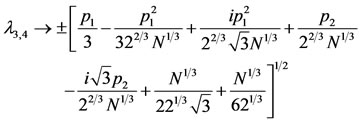 (48)
(48)
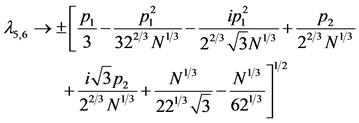
where
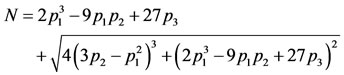
The stability of the triangular points is determined by the roots (48) of the characteristic equation. The six roots of characteristic equation and the positions of the traingular points are presented in Tables 1 and 2 numerically for 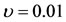 and
and 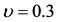 respectively with various values of the parameter
respectively with various values of the parameter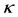 . When
. When 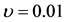 the traingular points and the characteristic roots exist only for
the traingular points and the characteristic roots exist only for , because here
, because here 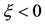 and
and 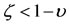 lies inside the shell. In Table 2, these points and the roots exist for values of
lies inside the shell. In Table 2, these points and the roots exist for values of  in the interval
in the interval 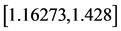 when the mass parameter
when the mass parameter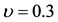 . Our numerical analysis reveals that when the triangular points exist, the coefficient
. Our numerical analysis reveals that when the triangular points exist, the coefficient 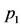 is negative,
is negative, 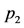 is positive and
is positive and 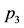 is positive in both cases of the mass parameter. It is clear from the table that for a specific set of values of the parameters at least one of the roots is real and positive or at one has a positive real part. We conclude that a positive root and positive real part of the complex roots induce instability at the triangular points. Hence the motion of the infinitesimal mass around the triangular equilibrium points is unstable.
is positive in both cases of the mass parameter. It is clear from the table that for a specific set of values of the parameters at least one of the roots is real and positive or at one has a positive real part. We conclude that a positive root and positive real part of the complex roots induce instability at the triangular points. Hence the motion of the infinitesimal mass around the triangular equilibrium points is unstable.
In the case of the stability of the solutions (28) corresponding to the equilibrium point at the center of the shell, on the basis of Lyapunov’s definition of stable solution (Krasnov et al. [14]), we have
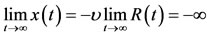 (49)
(49)
Equation (49) proves the instability of the equilibrium point at the center of the shell varying with time according to the Lyapunov’s theorem as they tend to infinity as time  is tending to infinity, which is however not possible in reality. However, when
is tending to infinity, which is however not possible in reality. However, when  is tending to infinity,
is tending to infinity, 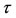 is approaching a finite value (Singh and Leke [8]) and the Lyapunov Characteristic Numbers are positive for solutions with negative exponents, negative for solutions with positive exponents and zero for solutions with oscillatory and constant solutions. We conclude that solutions with positive exponents which are unstable induce instability to the solutions. This also applies in the case of the triangular solutions. Hence, the equilibrium points of the non autonomous system of equations are unstable with respect to time.
is approaching a finite value (Singh and Leke [8]) and the Lyapunov Characteristic Numbers are positive for solutions with negative exponents, negative for solutions with positive exponents and zero for solutions with oscillatory and constant solutions. We conclude that solutions with positive exponents which are unstable induce instability to the solutions. This also applies in the case of the triangular solutions. Hence, the equilibrium points of the non autonomous system of equations are unstable with respect to time.
5. Discussion and Conclusion
We have derived the equations of motion of the infinitesimal mass under the effects of the buoyancy force exerted by the fluid, the gravitational attraction of the fluid and the attraction of the second primary; when the masses of the primaries vary with respect to time in the absence of reactive forces. We have found that the equations of motion can be transformed, when the motion of the primaries is determined by the GMP, to the autonomized forms, only when the shell is empty.
One equilibrium point which lies on the center of the spherical shell and fully analogous to that of Robe [9] exists. Further, the existence of two or more triangular points is found which depends on the mass ratio provided , and if the points lie within the shell. Numerically, when
, and if the points lie within the shell. Numerically, when 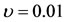 and
and , there are two triangular point positioned at
, there are two triangular point positioned at 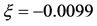 and
and 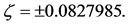 However, for
However, for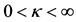 , there is more than just a pair of these points. When
, there is more than just a pair of these points. When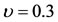 , infinitely many triangular points exist depending on the value of the constant of the GMP in the interval
, infinitely many triangular points exist depending on the value of the constant of the GMP in the interval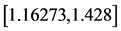 . These equilibrium points are different from those of restricted three-body problem with variable masses and those of Robe [9].
. These equilibrium points are different from those of restricted three-body problem with variable masses and those of Robe [9].
The linear stability of the equilibrium points obtained has been studied and it is seen that the triangular points of the autonomized and time dependent systems are unstable. The point on the center of the shell of the autonomized systems is stable under some certain conditions, while that dependent on time is unstable. The masses of celestial bodies are changing with time; therefore it is hoped that the results of this paper will be useful in the study of the dynamics problem in the Earth under the attraction of the Moon.
REFERENCES
- M. Dufour, “Ch.: Comptes Rendus Hebdomadaires de L’,” Accademie de Sciences, Amsterdam, 1886, pp. 840-842.
- H. Gylden, “Die Bahnbewegungen in Einem Systeme von zwei Körpern in dem Falle, dass die Massen Ver NderunGen Unterworfen Sind,” Astronomische Nachrichten, Vol. 109, 1884, 1884, pp. 1-6.
- I. V. Meshcherskii, “Ueber die Integration der Bewegungsgleichungen im Probleme zweier Körper von ver nderlicher Masse,” Astronomische Nachrichten, Vol. 159, No. 15, 1902, pp. 229-242. doi:10.1002/asna.19021591502
- I. V. Meshcherskii, “Works on the Mechanics of Bodies of Variable Mass,” GITTL, Moscow, 1952, p. 205.
- B. E. Gelf’gat, “Modern Problems of Celestial Mechanics and Astrodynamics,” Nauka, Moscow, 1973, p. 7.
- A. A. Bekov, “Liberation Points of the Restricted Problem of Three Bodies of Variable Mass,” Soviet Astronomy, Vol. 32, 1988, pp. 106-107.
- P. Gurfil and S. Belyanin, “The Gauge-Generalized Gylden-Meshcherskii Problem,” Advances in Space Research, Vol. 42, No. 8, 2008, pp. 1313-1317. doi:10.1016/j.asr.2008.01.019
- J. Singh and O. Leke, “Stability of the Photogravitational Restricted Three-Body Problem with Variable Masses,” Astrophysics and Space Science, Vol. 326, 2010, pp. 305- 314.
- H. A. G. Robe, “A New Kind of Three Body Problem,” Celestial Mechanics and Dynamical Astronomy, Vol. 16, No. 3, 1977, pp. 343-351. doi:10.1007/BF01232659
- A. K. Shrivastava and D. N. Garain, “Effect of Perturbation on the Location of Libration Point in the Robe Restricted Problem of Three Bodies,” Celestial Mechanics and Dynamical Astronomy, Vol. 51, No. 1, 1991, pp. 67- 73. doi:10.1007/BF02426670
- P. P. Hallan and N. Rana, “The Existence and Stability of Equilibrium Points in the Robe’s\Estricted Problem ThreeBody Problem,” Celestial Mechanics and Dynamical Astronomy, Vol. 79, No. 2, 2001, pp. 145-155. doi:10.1023/A:1011173320720
- P. P. Hallan and K. B. Mangang, “Existence and Linear Stability of Equilibrium Points in the Robe’s Restricted Three Body Problem When the First Primary Is an Oblate Spheroid,” Planetary and Space Science, Vol. 55, No. 4, 2007, pp. 512-516. doi:10.1016/j.pss.2006.10.002
- A. Sommerfeld, “Mechanics,” Academic Press, New York, 1952.
- M. L. Krasnov, A. I. Kiselyov and G. I. Makarenko, “A Book of Problems in Ordinary Differential Equations,” MIR Publications, Moscow, 1983, p. 255.

