International Journal of Astronomy and Astrophysics
Vol. 2 No. 2 (2012) , Article ID: 19746 , 4 pages DOI:10.4236/ijaa.2012.22014
Quantum Cosmology Explains the General Galaxy-Black Hole Correlation
Cosmo-One Group, Fairbanks Court, New York, USA
Email: cosmo.one@hotmail.com
Received March 9, 2012; revised April 18, 2012; accepted April 28, 2012
Keywords: Dark Matter and Energy; Quantum Physics of the Universe; Cosmology
ABSTRACT
The symmetric quantum physics of the Universe demonstrates that the massive black holes developing in the post-inflation big-bang prompt the formation of the host galaxies around them. A general correlation between the variety of galaxies and black holes develops, a specific example of which is the celebrated (but not understood) mass correlation between the host elliptical galaxies and their core black holes. The elucidations and predictions in this exposition are inclusive and far-reaching, resolving a myriad of yet unsolved problems and quandaries in the evolving Universe, among which are: how the general galaxy-black hole correlations are established; what is the role of the dark matter and energy in the formation of galaxies and stars; how the spiral galaxies with less predominant black holes are formed; how the early star forming globular cluster emerged with sparse dark matter; why some galaxy mergers give rise to the starbursts, while other mergers switch the star flourishing galaxies off into grave yards; and how could the Universe have wound up as sheets and filaments of galaxy clusters encompassing great voids.
1. Introduction
Based on the symmetric quantum physics [1], this paper explicates the general correlations developing between the variety of host galaxies and the core black holes in the post-inflation big bang. This is the culminate unraveling for the current preoccupation; its special case, among others, explains the observationally purported mass correlation between the core black hole mass, Mb, and the host elliptical galaxy mass, Mg, in the approximation [2],
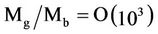 (1)
(1)
The standard theory, on the other hand, submits that the stellar black holes—whose masses range up to O(30 )—in the early Universe, working along their host galaxies in mass correlation, grow incrementally over some billions of years to the ultra-massive size of
)—in the early Universe, working along their host galaxies in mass correlation, grow incrementally over some billions of years to the ultra-massive size of 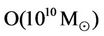 in the expanding Universe through mergers, accretions, and AGN processes [3].
in the expanding Universe through mergers, accretions, and AGN processes [3].
However, those assertions of the standard theory are refuted by the experimental observations and theoretical analysis. Most of all, the size of the core black holes is negligibly small as compared with the spread of the host galaxies, and the major portion of the galaxies in the expanding Universe lies at a far enough distance to be immune from the influence of the core black holes. It has also been shown that the AGN processes could not have been a part of the proposed development [4].
A dearth of intermediate black holes is found from the mass  to the mass
to the mass 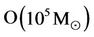 [5]; to overleap such a large gap, impossible O(1,000) simultaneous black hole mergers would in effect be required. Moreover, black holes of mass range 2 × (109
[5]; to overleap such a large gap, impossible O(1,000) simultaneous black hole mergers would in effect be required. Moreover, black holes of mass range 2 × (109 -1010
-1010 ) have also been found in the dawn of time [6,7]. Obviously, the standard theories have no systematic mechanism that could create such behemoth black holes from the foot-loose matters in the open early Universe [8], giving support to the direct collapses, rather than the alleged mergers, for their formations.
) have also been found in the dawn of time [6,7]. Obviously, the standard theories have no systematic mechanism that could create such behemoth black holes from the foot-loose matters in the open early Universe [8], giving support to the direct collapses, rather than the alleged mergers, for their formations.
Inside the post-inflation big-bang, on the other hand, the situation seems to be designed for that particular chore of the early formation of galaxies and black holes.
The big-bang expands with its average (visible matter) density decreasing for a period of time to match those black holes from 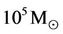 to
to 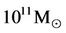 inside the Schwarzschild radius. With the propitious propensity for gravitational collapse, the (visible) matter in the spheres are ready-made seeds for the black hole formation in the post-inflation big-bang (see §3). In fact, the news of observations of the black holes forming far earlier than expected, and the appearance of the large galaxies at much larger distance than anticipated in the standard theory are mounting with increasingly rapid strides [9]. These early galaxies and black holes must have in fact been formed even in seconds of the post-inflation big-bang [10,11].
inside the Schwarzschild radius. With the propitious propensity for gravitational collapse, the (visible) matter in the spheres are ready-made seeds for the black hole formation in the post-inflation big-bang (see §3). In fact, the news of observations of the black holes forming far earlier than expected, and the appearance of the large galaxies at much larger distance than anticipated in the standard theory are mounting with increasingly rapid strides [9]. These early galaxies and black holes must have in fact been formed even in seconds of the post-inflation big-bang [10,11].
The cardinal postulate of dark matter interacting solely by gravitational attraction in the standard theory still remain the unmitigated conjecture. The experimental observations that repudiate this incredulous prescript has been mounting [12], and the symmetric quantum physics [1] predicted that the dark matter interaction generates repulsive force via the dark energy production (see § 2)—the dark matter distending propensity, rebounding at compression—which was incorrectly conjectured to be the fifth force [14].
The above findings causes a variety of eminent consequences, for example, the unfolding of the dark matter into the galactic halo, instead of amassing toward the core. This is now unequivocally verified by the observation that the dark matter spread smoothly over the dwarf galaxies [15], the implication of which is paraphrased by Penarrubia [16]: “If a dwarf galaxy were a peach, the standard model says we should find a dark matter ‘pit’ at the center. Instead, the dwarf galaxies are found to be like pitless peaches.”
The basic premisses of the standard theories are untenable, undermining their foundation, including their formation mechanisms for galaxies (see §6) and stars (see §7). The reason for the complete failure of the standard theory to explain the dark matter and energy (nonobservable to humans)—after several decades of excruciating efforts with thousands of papers being published with haughty claims—in turn becomes self-explanatory.
It is now imperative to call for the theory of generalized posture—the symmetric quantum physics of the Universe [1,17,18]—which enables to elucidate, among many others, the general galaxy-black hole correlations that can explain not only the obstinate mass correlation puzzle, Equation (1), as a subsidiary contingency, but also the various developing mechanisms of the Universe, comprehensively elucidating many problems that are unable to be solved by the standard theories.
2. Cosmology of the Quantum Symmetric Physics [1; see the Footnote 1]
The nature in essence is simple and often structured in symmetry. But the symmetry is not always obvious, one half of it being predisposed for classical interpretation, while the other half requires non-archetypal elaboration. Niels Bohr emphasized the importance of this cryptic symmetry in his principle of complementarity [19]: “The opposite of a profound truth may well be another profound truth.” This truth was aptly demonstrated in the physics of Dirac’s negative energy states that, after being dismissed to be physically meaningless, had led to the matter-antimatter symmetry in physics. The (non-physical) negative energy state turned out to be really a (physical) positive energy antimatter, indicating that incidental symmetries in mathematics do matter in physics.
In a simple analogy [19; see p. 132], the Dirac’s matter-antimatter symmetry physics arises from the signs of square root of the square of the (positive) energy E, i.e.,
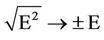 (2)
(2)
The next level symmetry arises from the square root sequel of Equation (2) for momentum p,
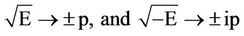 (3)
(3)
This is the basis for the physics of Hermitean-antiHermitean symmetry; the universal principle that is expounded in the quantum theory textbooks [20].
The standard theory a priori limits its exploration to the Hermitean physics—where the energy is positive with real momentum, making the things observable (to humans). For the time being, this classical physics version of cosmology seems to be more than sufficient to describe the prevailing Universe. The antiHermitian physics, where the implied energy is negative with imaginary momentum (in the perspective of the Hermitian physics)—turning objects non-observable—is to be scrapped as being nonphysical. But could there be a higher level ramification of Dirac’s escapade for these non-observables (to humans)? As if in retort, the so-called dark matter and energy—the non-observables (to humans)— emerged in the major (96%) constituents of the Universe.
With this phenomenal divulgence, the relevance of the Hermitean-antiHermitean symmetry physics in the quantum theory version of cosmology is firmly established, rendering the standard theory like trying to explain quantum phenomena by classical physics. The history is repeating itself. The once seemingly self-sufficient classical physics needed to be expanded into the quantum physics to explain the atomic phenomena. Now, the classic physics version of cosmology needs to be expanded into the quantum physics version of cosmology, commensurately incorporating the quantum symmetric counter part, the (non-observable to human) antiHermitean physics that goes hand in hand with (non-observable to human) dark matter and energy.
According to the cosmology of symmetric quantum physics, the Hermitean physics and antiHermitian physics in the generalized space-time are generically equivalent with their observability roles reversible, leading to the symmetric edifice of two Universes—the RHS Universe and the LHS Universe in unbiased terms [1]. The antiHermitian physics of the imaginary momentum (i.e. negative energy) in the RHS Universe switches to the Hermitean physics of the real momentum (i.e. positive energy) in the LHS Universe, the non-observable dark matter and energy (to humans) in the RHS Universe becoming not only observable (in accord with the archetypal physical law—e.g., the Lorentz transformation—to the putative observers) but also interacting in the LHS Universe.
The dark constituents of the quantum cosmology have now staked their claim, and there are similarities and purposeful differences in nature and the processes are implemented in the two Universes. For example, the dark matter charge interaction creates the dark energy in the LHS Universe in symmetry with a phenomenon in the RHS Universe, viz, the charged particle interactions that create the electromagnetic energy.
The dark matter (and energy) are the permanently coupling baryon plasma with its unique interaction mechanisms in the LHS Universe, whereupon the primary dark energy productions arise from the pair annihilation and the charge clumping of the dark matter in the expanding Universe [1]. With the dark matter interaction that produces the repulsive dark energy in the normal setting of the expanding Uinverse, the dark matter distending propensity—intensifying into the rebounding propensity at local dark matter compressions—is one of the inevitable consequences in the symmetric quantum physics [1]. In the abnormal circumstance of, for example, the galaxy cluster collisions, the strained head-on collision of dark matter could lead to an anomalous consequence predicted [1], and so observed in the intricacy of the Abell 520 [21].
The interactions gradually transform the dark matter into the dark energy in conservation of matter/energy, and simulates the Cosmological Constant at precisely observed value [1, also see §8]. The standard theory, on the other hand, continues to hinge on the vacuum energy that is too large by the catastrophic factor of 10120. Moreover, there is no evidence that the vacuum fluctuations exist to fill the entire Universe in the absence of matter [22].
There is a clear division of labor between the visible and dark families of matter and energy with complementary roles in the governing of the Universe. For one, the big-bang inflation in the quantum cosmology was entirely powered by the intense concentration of repulsive dark energy generated by the dark matter interaction. The dark energy is reabsorbed by the dark matter during the inflation, which naturally slowed down. By contrast, the standard theory postulates an unseemly two-fold (or more) scalar field interaction, one for the inflation, and the other for flagging it down [23; see p. 77]..
3. The Black Hole and Hard Globule
For a black hole of mass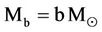 , its Schwarzschild radius is [24,25],
, its Schwarzschild radius is [24,25],
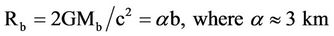 (4)
(4)
Its average (visible) mass density rvm (g/cc) corresponding to mass Mb,
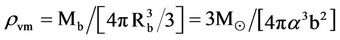 yields,
yields,
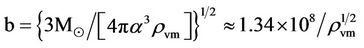 (5)
(5)
From the assortment of estimates [e.g., 26], the b in terms of  along with the average dark matter density
along with the average dark matter density 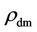 and dark energy density
and dark energy density 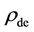 as function of the post-inflation big-bang time t (=10f second) are shown in Figure 1 [see Equation (11) for rdm and
as function of the post-inflation big-bang time t (=10f second) are shown in Figure 1 [see Equation (11) for rdm and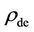 ].
].
The post-inflation big-bang expansion follows, and the 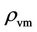 decreases, incidentally matching the average earmark densities of the black holes,
decreases, incidentally matching the average earmark densities of the black holes, 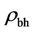 The gravity of the matter and energy inside the presumably homogeneous big-bang is neutral. When the inertia of the big-bang expansion in the extreme high temperature can be bested without causing implosion, the visible matter portion
The gravity of the matter and energy inside the presumably homogeneous big-bang is neutral. When the inertia of the big-bang expansion in the extreme high temperature can be bested without causing implosion, the visible matter portion 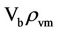 equal to the black hole mass of
equal to the black hole mass of 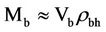 is apt to act by its propensity for the gravitational collapse into the black hole in its Schwarzschild volume
is apt to act by its propensity for the gravitational collapse into the black hole in its Schwarzschild volume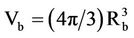 .
.
The residual matter and energy in the volume Vb would come alive, acting as a “hard globule” with its effective mass in ratio k to the impending black hole mass to be determined by the Einstein-Friedmann Equation [27], i.e.,
 (6)
(6)
The hard globule now establishes its own Schwarzschild sphere of radius,
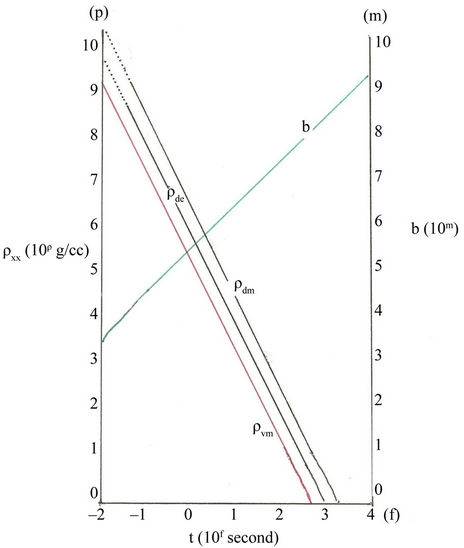
Figure 1. The average densities {rvm , rdm, rde} and b in the big-bang.
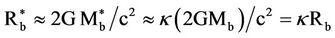 (7)
(7)
The mass and energy inside the sphere of radius 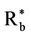 are trapped to form the host galaxy—lying outside the hard globule of radius Rb—without suffering a gravitational collapse.
are trapped to form the host galaxy—lying outside the hard globule of radius Rb—without suffering a gravitational collapse.
The collapsing visible matter toward the destined black hole core would inflame the dark matter rebounding propensity in radial course and, for certain range of f (in the big-bang time t = 10f), the dark matter and energy (that are perpetually coupled [1]) would swerve and hurtle out of the hard globule. The visible matter inside the sphere of radius Rb then completes its collapse into a black hole, while the trapped matter and energy inside the sphere of radius 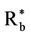 form the embryonic galaxy around it. Based on this proposition—the “hard globule model,” derived from the the symmetric quantum physics of the Universe [1], not conjectured—this paper explicates not only the general galaxy-black hole correlation, but also the variety of confounding phenomena shrouding the subject.
form the embryonic galaxy around it. Based on this proposition—the “hard globule model,” derived from the the symmetric quantum physics of the Universe [1], not conjectured—this paper explicates not only the general galaxy-black hole correlation, but also the variety of confounding phenomena shrouding the subject.
The dark matter and energy so emanating out of the hard globule would tarry around the black hole and exert to it a portentous influence, by enhancing the gravity and rotational torque, on the developing accretion dynamics. In time, the trapped dark matter in the galaxy, driven by the distending propensity, redistributes to form the galactic halo, explaining why the black hole and the dark matter halo at the early epoch grew together, but why the standoffish dark matter halo would not subsequently influence the evolving of the black hole. Here, the formation of black holes and galaxies (with stars) is simple and straightforward, and resolves—with appropriate inferences—the exigent puzzles: “downsizing problem”, “invariant galaxy problem”, “core-cusp problem”, “dark matter emergence problem,” “missing satellite problem,” and more.
4. Development of the Galaxy-Black Hole Correlation
The dark matter and energy in the Universe at 380,000 year is determined to be [1],
 (8)
(8)
whereupon
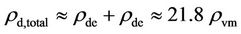 (9)
(9)
This total dark matter and energy at 380,000 year was verified by the QUaD data [28].
The densities in Equation (8) at 380,00 year change to the prevailing data [29],
 (10)
(10)
which also give the same 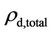 of Equation (9). The rdm thus gradually transforms into
of Equation (9). The rdm thus gradually transforms into , changing from those of Equation (8) to those of current Equation (10), with the conservation of the total dark matter and energy through the history of the expanding Universe.
, changing from those of Equation (8) to those of current Equation (10), with the conservation of the total dark matter and energy through the history of the expanding Universe.
On the other hand, the tempering of 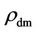 and
and 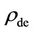 of Equation (8) at 380,000 year by Equation (6) could give the impression of [1],
of Equation (8) at 380,000 year by Equation (6) could give the impression of [1],
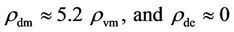 (8A)
(8A)
as in fact so determined by the five (and three)-year WMAP data [29]. Between the WMAP data in Equation (8A) at 380,000 year and those in Equation (10) of today blatantly violates the total dark matter and energy conservation in the Universe. Moreover, the dark matter dominated dynamics without dark energy is inadequate to administer the intricate primordial Universe (see §6).
According to Equation (8), the dark energy is so plentiful and pervasive that the (visible) photons released upon recombination around 380,000 year would be largely homogenized, the mark of the unfolding galaxies delicately imprinted on the CMB.
In the standard theory, the galaxy formations is yet to begin from the nigh homogeneous footloose gasses, whereupon the dark matter rebounding propensity would make the task difficult, taking billions of years for the chore in variance with the observation.
The approximation by extrapolation indicates that 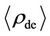 in Equation (8) arose mainly from the dark matter pair annihilation energy density of
in Equation (8) arose mainly from the dark matter pair annihilation energy density of  at the inflation termination point of the big-bang, supplemented by the density
at the inflation termination point of the big-bang, supplemented by the density 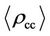 that evolved from the onward charge clumping of the dark matter [1]. Although no scrupulous estimates are possible at this time, the adjustments back into the post-inflation big-bang renders to surmise the possible average densities of
that evolved from the onward charge clumping of the dark matter [1]. Although no scrupulous estimates are possible at this time, the adjustments back into the post-inflation big-bang renders to surmise the possible average densities of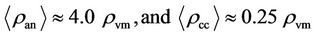 providing the density approximation in the post-inflation big-bang,
providing the density approximation in the post-inflation big-bang,
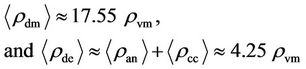 (11)
(11)
The densities of Equation (11) yield in terms of Equation (6) with the equation of state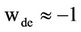 ,
,
 (12)
(12)
The size ratio of the developing black hole and the nascent galaxy manifested by Equation (7) is remarkably small—“a jack ball: a basketball”—and the gravitational force of the hard globule could forcefully reach out to its Scwartschild radius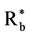 , and wrest the matter/energy in it intact to form the host galaxy around the black hole.
, and wrest the matter/energy in it intact to form the host galaxy around the black hole.
The rapidly rotating embryonic galaxies, being culled off from the environs, would eventually establish their dynamic stability in the expanding Universe.
The predicted mini-sized primordial quark black hole [30] has never been realized. However, the observation of the dark dwarf galaxy of mass 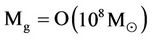 indicates that the post-inflation big-bang dynamics according to Figure 1 may become amenable to the black hole formations of
indicates that the post-inflation big-bang dynamics according to Figure 1 may become amenable to the black hole formations of 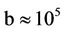 around
around 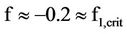 [31, 32] with excessive
[31, 32] with excessive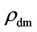 . This explains why the black holes of mass
. This explains why the black holes of mass 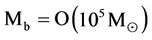 along the dwarf galaxies of mass
along the dwarf galaxies of mass  with overabundant
with overabundant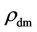 , emerge after their incipient stage absence. The black holes of b > 105 [in f > fl, crit] along the dwarf galaxies then follow with gradually decreasing rdm. With the time increasing to
, emerge after their incipient stage absence. The black holes of b > 105 [in f > fl, crit] along the dwarf galaxies then follow with gradually decreasing rdm. With the time increasing to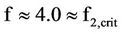 , a likely critical value, b increases and, through the super-massive black holes, the ultra-massive black holes of
, a likely critical value, b increases and, through the super-massive black holes, the ultra-massive black holes of  would in principle be realized with correspondingly large host galaxies in mass correlation, but with much lower
would in principle be realized with correspondingly large host galaxies in mass correlation, but with much lower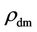 .
.
What really happens in the post-inflation big-bang, however, might not be that simple and categorical as projected above. The increasing number of large galaxy-black hole duos would disturb the post-inflation big-bang ambiance for , and gradually subdue their additional autonomous formations. The galaxy-black hole duo production efficiency then could peak, say, around
, and gradually subdue their additional autonomous formations. The galaxy-black hole duo production efficiency then could peak, say, around  (or
(or ), building up to it from
), building up to it from 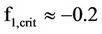 (or
(or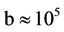 ), then tapering off from it toward
), then tapering off from it toward 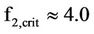 (or
(or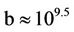 ). It is possible that some additionally heavier duos might have been produced via mergers of those autonomous duos. Because the Equation (13) is independent of b, the mergers of the duos that increase their size would maintain their indigenous mass correlation ratio. This guarantees the realization of the observed super-massive and ultra-massive black holes in the early Universe [6,7].
). It is possible that some additionally heavier duos might have been produced via mergers of those autonomous duos. Because the Equation (13) is independent of b, the mergers of the duos that increase their size would maintain their indigenous mass correlation ratio. This guarantees the realization of the observed super-massive and ultra-massive black holes in the early Universe [6,7].
The similar aberration might also happen earlier in reverse time direction from 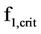 as well. If the looming black hole-hard globule interaction in the big-bang buckles prematurely in the very high density configuration in f < f1,crit , the electric resistivity of the dark plasma matter in the hard globule would skyrocket, precipitously piling up the dark energy [1]. The hard globule would implode.
as well. If the looming black hole-hard globule interaction in the big-bang buckles prematurely in the very high density configuration in f < f1,crit , the electric resistivity of the dark plasma matter in the hard globule would skyrocket, precipitously piling up the dark energy [1]. The hard globule would implode.
The implosions at the extreme high densities {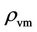 ,
, 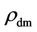 ,
, 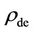 } in the earlier part of this duration (perhaps, around f » -1.5) would be so powerful that the impending galaxy portion could be swept away with the incipient core black hole in the upheaval disarranging to form the globular clusters, the comparatively simple, yet very poorly understood phenomenon in the standard theory. This solves the mystery of why the globular clusters, really the wrecks of inchoate (visible matter) black holes, do not contain much dark matter [33,34] , emerging with high density visible matter. Moreover, the globular clusters that stopped short of becoming the black hole before the formation of the dark dwarf galaxies with black hole mass of
} in the earlier part of this duration (perhaps, around f » -1.5) would be so powerful that the impending galaxy portion could be swept away with the incipient core black hole in the upheaval disarranging to form the globular clusters, the comparatively simple, yet very poorly understood phenomenon in the standard theory. This solves the mystery of why the globular clusters, really the wrecks of inchoate (visible matter) black holes, do not contain much dark matter [33,34] , emerging with high density visible matter. Moreover, the globular clusters that stopped short of becoming the black hole before the formation of the dark dwarf galaxies with black hole mass of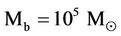 , would have (see Figure 1) total visible masses in the range of (105 - 104)
, would have (see Figure 1) total visible masses in the range of (105 - 104) 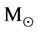 as so in fact observed [35].
as so in fact observed [35].
The destructive effect of the implosion would mitigate in time as f → f 1,crit , and the scuffling inside the hard globule could disarray the prospect black hole and the galaxy into globular clusters, harboring massive core (like M15) [36]. This may explains why the globular clusters, their boundary becoming disconcerted, act in ways like the compact dwarf galaxies [37], along the way providing the sporadic exposition of the intermediate-mass black holes [5].
The globular clusters that emerged as very high density congregations of the visible matter could form the stars in the primordial time (see §7). This explains why the globular clusters are observed at high enough redshifts even to appear to be 15 billion years old (as if older than the age of the Universe [38]), saliently verifying that they must in fact have been born in the post-inflation big-bang.
The globular clusters so created would roam the space to be subsequently pulled into the nearby galactic spaces—sometimes pulled from dwarf galaxies to larger galaxies—in numbers proportional to the gravitational pull from the galaxy mass which is correlated to the black hole mass. This explains why the globular clusters spread in the galactic space in numbers proportional to the black hole mass [39]. The fact that globular clusters are produced independent of the large galaxies is confirmed by the observation that about half (40%) of them are moving independently in opposite direction from the Milky Way Galaxy rotation [40].
5. Baseline Mass Correlation
The trapped visible matter inside the Schwarzschild radius  would manifest the host galaxy, yielding for the (elliptical) galaxy-black hole mass correlation,
would manifest the host galaxy, yielding for the (elliptical) galaxy-black hole mass correlation,
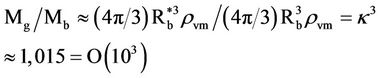 (13)
(13)
Equation (13) agrees with the observed ratio of Equation (1), which must be more than a fortuitous coincidence, providing the validity to the density estimations of Equation (8) as well as Equation (11).
The observable masses both in the black holes and galaxies are immutable and, aside from the accretion effect from the surroundings, the mass correlation lasts.
The dark matter, however, transforms into dark energy, changing from 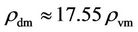 (and
(and ) of Equation (11) in the post-inflation big-bang to the present day
) of Equation (11) in the post-inflation big-bang to the present day 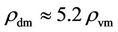 (and
(and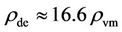 ) of Equation (10). Moreover, the transformation rate of
) of Equation (10). Moreover, the transformation rate of  varies depending on the size of the galaxies, and the mass relation between the black hole and dark matter halo could in time lose its consistency.
varies depending on the size of the galaxies, and the mass relation between the black hole and dark matter halo could in time lose its consistency.
The Universe eventually partitions into the serial number of galaxies,
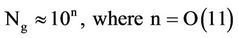 (14)
(14)
whereupon each galaxy would harbor the average number of stars, ns » 10s with a galaxy mass , where on average
, where on average
s = O(11)(15)
With b » 10m, Equations (14) & (15) lead to
 (16)
(16)
establishing, in terms of the total number of stars in the Universe Ng n s » 1022,
 (17)
(17)
The baseline mass correlation between the black hole and the (elliptical) galaxy duos is shown in Figure 2 for {s} = {2.5, 3.0, 3.5} corresponding to
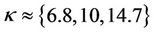 (18)
(18)
6. The General Galaxy-Black Hole Correlation
The discrepancies between the densities in Equation (8)
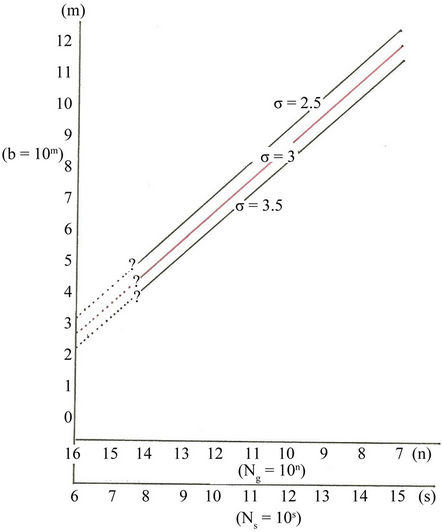
Figure 2. Baseline mass correlation for the black hole of (b » 10m ) with the galaxies of (ns » 10s) for the correlation exponents s » {2.5, 3, 3.5}.
and Equation (8A) are large.
The dynamic environ of the galaxy forming post-inflation big-bang may actually subject it to a significant time (and location) dependent diversification from the specific densities of Equation (8) and Equation (11). This is important, because a conversion from the dark matter to dark energy by 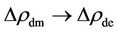 causes an amplified shift of
causes an amplified shift of  in
in , rendering a consequential alteration in the culminating dynamics.
, rendering a consequential alteration in the culminating dynamics.
This is shown in Table 1 for the possible range of moderation factor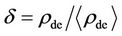 , where
, where  of Equation (11). The Fpull and Fpush here represent, respectively, the forces pulling inward and pushing outward in the forming galaxies.
of Equation (11). The Fpull and Fpush here represent, respectively, the forces pulling inward and pushing outward in the forming galaxies.
With d » 1, the galaxies would be primarily elliptical [41] to give the special mass correlation of Equation (1). The correlations would be generalized with the inclusive 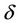 that embraces all possible situation in the post-inflation big-bang. For d > 1, likely during the later period in the big-bang, the ratio Mg/Mb in Table 1 is very sensitive to the modification in d, indicating that a small local tweak in
that embraces all possible situation in the post-inflation big-bang. For d > 1, likely during the later period in the big-bang, the ratio Mg/Mb in Table 1 is very sensitive to the modification in d, indicating that a small local tweak in 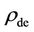 in the big-bang turmoil could reduce Mg/Mb by a large ratio. This trend might be enhanced because, with a weaker Fpull/Fpush, the enfolding of the matter to the galaxy would be weakened. This dumbfounding prediction has been verified by the observations of the unusually small Mg/Mb » 30 [42] as well as the super-massive black holes in the small galaxies [43].
in the big-bang turmoil could reduce Mg/Mb by a large ratio. This trend might be enhanced because, with a weaker Fpull/Fpush, the enfolding of the matter to the galaxy would be weakened. This dumbfounding prediction has been verified by the observations of the unusually small Mg/Mb » 30 [42] as well as the super-massive black holes in the small galaxies [43].
With the ongoing turmoil of galaxy-black hole duos formation in the post-inflation big-bang in the later time, the repulsive dark energy in Fpull/Fpush → 1.0 could expel the significant portion of dark matter along with a certain portion of the visible matter out of the galaxy. This in effect could generate new genre of low dark matter density dwarf galaxies in stark contrast to the regular dwarf galaxies produced earlier with high dark matter density. This low dark matter dwarf galaxies would bear a certain resemblance in the star formation to the much smaller globular clusters formed in earlier time with sparse dark matter in it (see §7).
The imbalance in the the forces Fpull and Fpush over the extent of  in the formation stage may cause the torque Ftorq in proportion to k2(Fpull/Fpush). The Ftorq normalized to 1 at
in the formation stage may cause the torque Ftorq in proportion to k2(Fpull/Fpush). The Ftorq normalized to 1 at 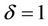 is given in Table 1. The main mover to the supernova spin was determined to be the core-collapse process itself [44], and the cause of fast rotation of a star proved to be its heavy mass at its formation [45]. The rapid increase of Ftorq as
is given in Table 1. The main mover to the supernova spin was determined to be the core-collapse process itself [44], and the cause of fast rotation of a star proved to be its heavy mass at its formation [45]. The rapid increase of Ftorq as 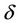 decreases from
decreases from 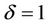 would cause the observed faster rotations to the newly forming, very heavy galaxies.
would cause the observed faster rotations to the newly forming, very heavy galaxies.
With rapid rotation, because of the centrifugal force, the vertical radius of rotating visible matter around the rotational axis can be stabilized. While the dark matter overall settles in the halo by the distending propensity,

Table 1. The galaxy framework with modified dark energy density r de;mod.
the visible matter would be pulled inward by gravity parallel to the rotational axis. The visible matter would in time flatten out perpendicular to the rotational axis, forming the spiral disks. But the increase of the visible matter density toward the disk also locally attract and enhance dark matter density, whereupon its rebounding propensity would slow and stop the further contraction of the disk thickness.
The foregoing establishes the long searched-after mechanism for the formation of the spiral galaxies, including the Milky Way Galaxy that, with considerably larger than the typical Mg/Mb of Equation (1), had led a relatively quiet existence at least for about 10 billions year [46]. This course of spiral galaxy formation may explain why the rotation velocity of the stars in the inner regions is comparable to that at much larger distance where the dark matter dominates, solving “the Disk-halo Conspiracy problem” [47].
During the earlier period in the post-inflation big-bang when the black hole size was relatively small, a reduction in d could also have made a sensitive change in the culminating spiral galaxy configurations. The galaxy bulges here are generated mostly by the visible matter portion inside the filing column of radius Rb that moves toward the core parallel to the rotational axis. The bulge size, Mg,bulge, would thus be only a portion of the galaxy mass Mg. Because the increased centrifugal force would push the matter outwards, the Mg,bulge may become prostrated as the galaxy rotational velocity increases, and the spiral galaxy with modest bulges could be formed with certain mid-weight black holes.
The culminating agglomeration of the visible matter toward the core would be hardier for a larger black hole, eventually leading to spirals that wrap around the black hole tighter as so observed [48]. With high Fpull/Fpush, the trend could be enhanced with greater accretion of intergalactic gasses into the galaxies.
The standard theory densities of Equation (8A) with 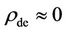 in essence provides the one variable (
in essence provides the one variable (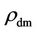 ) dynamics for the early Universe, and fails to deftly describe the observed correlation for the galaxy-black hole development. The densities of Equation (8) with substantial dark energy sojourning as determined by the symmetric quantum physics [1], in contrast, tender the two-variable (
) dynamics for the early Universe, and fails to deftly describe the observed correlation for the galaxy-black hole development. The densities of Equation (8) with substantial dark energy sojourning as determined by the symmetric quantum physics [1], in contrast, tender the two-variable (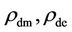 ) dynamics to aptly explicate the observed generalized galaxy-black hole development. The analysis here is primarily exploratory (at the most using the hand calculator), yet it can explain practically every aspect of the pertinent dynamics (the criterion for a correct theory), the details of which can be worked out from the germane framework physics established here (likely using the super-computers.)
) dynamics to aptly explicate the observed generalized galaxy-black hole development. The analysis here is primarily exploratory (at the most using the hand calculator), yet it can explain practically every aspect of the pertinent dynamics (the criterion for a correct theory), the details of which can be worked out from the germane framework physics established here (likely using the super-computers.)
7. Formation of the Stars
With the dark matter of solely attractive gravity as conjectured in the standard theories, the star formation in the dark galaxy VIRGOHI21 would be quickly completed in the earlier Universe with its visible matter of  along with the maximal amount of dark matter in it. The globular clusters with sparse dark matter in them, on the other hand, would be very tardy in the star formation.
along with the maximal amount of dark matter in it. The globular clusters with sparse dark matter in them, on the other hand, would be very tardy in the star formation.
What actually happens is completely antithetical. The globular clusters devoid of dark matter have largely completed the star formation, while the dark galaxy flooded with dark matter has failed to form stars [49]. This again indicates that the dark matter is not the primary agency in the star formation; the stars can not only be formed without much aid of the dark matter [33], but its profuse presence may hinder their formation.
The observed particulars in the star formation in fact proved to be not a fueling question so much as a collection puzzle, the “fizzle problem” [50]. The physics behind this aberration in the star formation is the dark matter rebounding propensity: although the appropriate density dark matter can aid the collection of the visible matter for star formations, the compression of it into denser than certain limit of it could divert the process with more production and local trapping of the repulsive dark energy.
The visual matter thus cools and, if the dark matter rebounding propensity is not pervasive, its self-gravity could become the primary force for the star formations.
The formation of stars in the galaxies would thus require
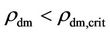 (19)
(19)
where  is a critical dark matter density in the local domain. This stipulation for the formation of the stars in the galaxies—unthinkable in terms of the standard theory—has actually been upheld by the recent experimental observation [51], where the galaxies need only one-tenth of the dark matter to sustain star formation than predicted by the standard theories.
is a critical dark matter density in the local domain. This stipulation for the formation of the stars in the galaxies—unthinkable in terms of the standard theory—has actually been upheld by the recent experimental observation [51], where the galaxies need only one-tenth of the dark matter to sustain star formation than predicted by the standard theories.
In the large galaxies with low rdm (see Figure 1), the condition Equation (19) is satisfied in the early Universe, and the primary star formations are in the main consummated.
In the dwarf galaxies of high dark matter densities, the star formation is initially prevented because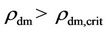 Although the expansion of the Universe dilutes ρdm toward
Although the expansion of the Universe dilutes ρdm toward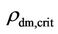 , they would take time to cross over to satisfy condition Equation (19).
, they would take time to cross over to satisfy condition Equation (19).
The dark and regular dwarf galaxies with very high initial dark matter densities may still loiter in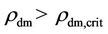 . As a dwarf galaxy in
. As a dwarf galaxy in  encounters another galaxy, however, the dark matter in it may suffer a sudden dispersion, switching over to satisfy the condition Equation (19). The dwarf galaxy then lights up in starburst. This might be how the Messier 82 shines even though it is relatively puny in both size and mass compared to its big partner Messier 81 [52].
encounters another galaxy, however, the dark matter in it may suffer a sudden dispersion, switching over to satisfy the condition Equation (19). The dwarf galaxy then lights up in starburst. This might be how the Messier 82 shines even though it is relatively puny in both size and mass compared to its big partner Messier 81 [52].
The star formation depletes the free gas in the galaxies, and continuation of it requires enough gas to remain in
 (20)
(20)
where is an indigenous critical visible matter density. The pervasive dark matter would decide whether to promote or impede the star formation according to Equations (19) and (20), or with appropriately low
is an indigenous critical visible matter density. The pervasive dark matter would decide whether to promote or impede the star formation according to Equations (19) and (20), or with appropriately low in their combination.
in their combination.
Relevance of the criterion of Equations (19) and (20) is further born out in variety of vicissitudes, beginning from the notorious globular clusters—the defaulted black holes with sparse 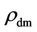 and high
and high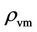 —by producing the stars as old as the big-bang.
—by producing the stars as old as the big-bang.
The dwarf galaxies of low dark matter densities produced in d > 1 (see § 6) with moderately high  are the other paradigm. They are roughly same size with high dark matter density dwarf galaxies, but they could facilely move to satisfy the criterion of Equations (19) and (20) with expansion of the Universe. This enables them to start forming the stars at very high rate earlier, solving the observed puzzle of why the newly found dwarf galaxies of low dark matter densities were making batches of stars at much more intense rate than the simulated results [53].
are the other paradigm. They are roughly same size with high dark matter density dwarf galaxies, but they could facilely move to satisfy the criterion of Equations (19) and (20) with expansion of the Universe. This enables them to start forming the stars at very high rate earlier, solving the observed puzzle of why the newly found dwarf galaxies of low dark matter densities were making batches of stars at much more intense rate than the simulated results [53].
While the dark matter mass gradually decreases by transforming into dark energy, the visible matter mass remains the same, and 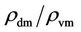 decreases in time. For
decreases in time. For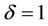 , where the galaxies are elliptical, the
, where the galaxies are elliptical, the 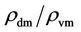 was already low in the early Universe, and the star formation began earlier. For
was already low in the early Universe, and the star formation began earlier. For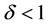 , where the galaxies are likely spiral, the pervading rdm itself is higher, and the star formation (on the average) might be delayed until
, where the galaxies are likely spiral, the pervading rdm itself is higher, and the star formation (on the average) might be delayed until 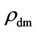 is reduced to allow the star formation.
is reduced to allow the star formation.
A merger of two inactive galaxies of 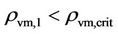 and
and 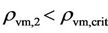 with
with 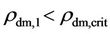 and
and  into
into 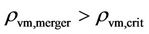 and
and  could restart the star formation in terms of Equations (19) and (20). On the other hand, a merger of two star forming galaxies of
could restart the star formation in terms of Equations (19) and (20). On the other hand, a merger of two star forming galaxies of 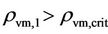 and
and  with
with  and
and 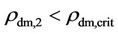 into
into  and
and 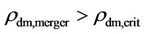 could in the same vein stop the star formation cold. These stipulations resolve the puzzle of why most galaxy mergers give rise to the starbursts, while other mergers switch off the star flourishing galaxies into grave yards of stars [54]. The beauty of the cogent criteria, Equations (19) and (20), is their simplicity in the extremely complicated situations that requires further ramification.
could in the same vein stop the star formation cold. These stipulations resolve the puzzle of why most galaxy mergers give rise to the starbursts, while other mergers switch off the star flourishing galaxies into grave yards of stars [54]. The beauty of the cogent criteria, Equations (19) and (20), is their simplicity in the extremely complicated situations that requires further ramification.
8. Observational Supports and Reflections
It has been shown that the dark matter was not the primal agency for the formation of black holes and galaxies in the open Universe as assumed by the standard theory, but the “hard globules” in the post-inflation big-bang were. It is no surprising that the comparable blunders persist into the star formation, where it was experimentally determined that—as betokened by Equation (19)—only one tenth of dark matter is required for the star formation than the amount determined to be needed by the standard theory [51].
The observational verifications of the predictions by the symmetric quantum physics are mounting in wide range of subject matters. The prolific number of supermassive black holes [55-57] along with large galaxies [9,11,58,59] have been observed to emerge as if they came straight out of the big-bang. The age of the metalpoor star HE1523-0901 is 13.2 billion years, nearly as old as the Universe itself [60].
The evidence is reinforced by the recent observations of the luminous quasar in a very early Universe [6] and the galaxy cluster in early Universe that is unexpectedly mature [61].
The robust star-burst galaxies with SFR of up to 4,000 stars per year are also observed in the early Universe [62]. At this rate, the galaxies need only 50 million years to grow into those equivalent to the most massive ones observed today. Moreover, opposite to what is conventionally expected, the stellar birthrate in the early baby-boom galaxies is much higher in the centers of the galaxies than at the edges [63], indicating the dark matter distending propensity in action for the early realization of the dark matter halo.
For all that, some of the extremely massive galaxyblack hole duos could have been formed through the mergers of the large (but relatively smaller) seed duos, maintaining the indigenous mass correlation. A sizable portion of matter and energy must also have emerged from the big-bang undifferentiated. It has been observed that a substantial amount of intergalactic gasses have been drawn into the galaxies during the long history of the expanding Universe, and this may help resolve the paradox of why today’s large galaxies haven’t yet run out of the gas for the belated star formation.
The Universe in the standard theory emerges from the big-bang as the most uniform, homogenized, consistent, and smooth soup of matter conceivable [64], and the galaxy formations would take billions of years. Moreover, with the densities of Equation (8A) in the early Universe—of the low dark matter distribution with the zero vacuum derived dark energy—it is impossible that the Universe could make the dynamic shifts to end up today as sheets and filaments of galaxy clusters encompassing great voids.
On the other hand, the predictions by symmetric quantum physics of the Universe [1] have been verified by the observation of the massive galaxies in the fog of time and distance in the primordial Universe, seemingly formed quickly but surprisingly peacefully, without having to invoke much violent mergers and galaxy interactions [65]. And the bountiful dark matter and energy of Equation (8) could again be the viable rejoinder for the governing dynamics in the primordial Universe.
The seeds of galaxies produced in close proximity of each other in the compact post-inflation big-bang would maintain the gravitational linkages in clusters. The pulling (visible and hesitant dark) matter would heap toward the heavier core. The repulsive dark energy along the distending dark matter, deliberately being dispelled to the fringe of diluted matter densities, would in time form a halo around the clusters. This mass polarization would in turn generate the power polarization, the dark energy pushing the galaxies from outside to make the clusters stay together [66], while visible matter and a significant portion of dark matter compacting in the inner side, some spreading into the safe-haven around the cluster core [67].
The dark energy halo around the clusters, gradually intensified, institutes a unremitting space mobility toward the massively congregating neighbors to shuffle the early Universe into the swarming clusters. Such an uneven clumping of the dark energy (at least in the early Universe) is not completely ruled out [68]. The innately repulsive dark energy (of the equation of state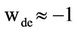 ) would in time spread out in the expanding Universe without an over-and-above energy enervation, simulating the Cosmological Constant [1].
) would in time spread out in the expanding Universe without an over-and-above energy enervation, simulating the Cosmological Constant [1].
Almost everything in the cosmos, including the galaxy clusters, seems to be rotating way too fast [69]. The origin of the rotation must be in their formation, their overall rotations in the Universe balancing out, one portion rotating one way, the other portion in the opposite direction. Certain lateral thrusts, something like the Magnus force [70], could cause the rotation aligned clusters to proceed toward the same area in the early Universe, potentially eventuating—working along the gravity and the polarizing mobile dark energy forces—in the amazingly constricted structure observed today in the Universe.
9. The Incidental Predictions for Globular Clusters
There are many observationally established results that the standard theory cannot consistently explain. While there are vast research literature (derived via super computers) claiming success on individual problems based on situation specific artifices, the large pictures is usually not addressed; the cross-referencing of particular solution to other problems is rarely if ever successfully attempted [71]. To validate a theory, however, all related phenomena should be inclusively elucidated from a basic proposition.
The general galaxy-black hole correlation based on the “hard globule model” derived from the symmetric quantum physics of the Universe [1], in contrast, works inclusively, elucidating even those extraneous subjects as well, e.g., the globular clusters. Their existence was incidentally emanated in this paper with following anomalous properties in agreement with the observation:
1) What are the globular clusters?
2) How the globular clusters are created with such high stellar density?
3) Why dark matter is sparse in the globular clusters?
4) How the globular cluster without the dark matter (whose gravity is considered to be instrumental for creating the stars in the standard theory) created stars almost as old as the Universe itself?
5) Why globular clusters act in ways like the dwarf galaxies, especially those low dark matter density dwarf galaxies?
6) Why globular clusters are primarily in the mass range of (104 - 105)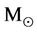 ?
?
7) Why the globular clusters are spread in the galaxies, its number crudely in proportion to the core black hole mass?
8) Why the nearly half of the globular clusters are on the retrograde orbits of the Milky Way Galaxy rotation?
10. Conclusion
Based on the cosmology of the symmetric quantum physics, the general galaxy-black hole correlations are developed, providing remarkably inclusive and far-reaching elucidations and predictions on the developing Universe in agreement with the experimental data. Such consistent accordance in the wide range of subject matters cannot be fortuitous coincidences, and this paper concludes that the neophyte theory has proved itself to be fundamentally true and correct.
11. Acknowledgements
The author thanks Drs. Milton Hoenig, Mike Stauber, and Jerry Padawer, and Jonathan Suh and Daniel Russ for their support.
REFERENCES
- P. Suh, “The Symmetric Physics of the Universe,” Apeiron, Vol. 18, No. 2, 2011, pp. 84-145.
- A. Marconi and L. Hunt, “The Relation between Black Mass and Bulge Mass,” The Astrophysical Journal Letters, Vol. 589, No. 1, 2003, pp. L21-L24. doi:10.1086/375804
- S. Nadis, “Exploring the Galaxy-Black Hole Connection,” Astronomy, Vol. 38, No. 5, 2010, pp. 28-33.
- K. Schawinski, S. Virani, B. Simmons, et al., “Do Moderate-Luminosity Active Galactic Nuclei Suppress Star Formation?” The Astrophysical Journal Letters, Vol. 692, No. 1, 2009, pp. L19-L23. doi:10.1088/0004-637X/692/1/L19
- T. Creighton and R. Price, “Supermassive Black Hole,” Scholarpedia, Vol. 3, No. 1, 2008, p. 4277. doi:10.4249/scholarpedia.4277
- D. Mortlock, S. Warrwen, B. Venemans, et al., “A Luminous Quasar at Redshift z = 7.085,” Nature, Vol. 474, 2011, pp. 616-619. doi:10.1038/nature10159
- N. McConnell, C. Ma, K. Gebhaedt, et al., “Two TenBillion-Solar-Mass Black Holes at the Center of Giant Elliptical Galaxies,” Nature, Vol. 480, 2011, pp. 215-218. doi:10.1038/nature10636
- J. Greene, “Goldlocks Black Holes,” Vol. 306, No. 1, 2012, pp. 40-47.
- J. Richard, J. Kneib, H. Ebeling, et al., “Discovery of a Possibly Old Galaxy at z = 6.027, Multiply Imaged by the Massive Cluster Abell 383,” Monthly Notices of the Royal Astronomical Society: Letters, Vol. 414, No. 1, 2011, pp. L31-L35. doi:10.1111/j.1745-3933.2011.01050.x
- J. Trefil, “The Moment of Creation,” Charles Scribner, New York, 1983.
- E. Treister, K. Schawinski, et al., “Black Hole Growth in the Early Universe is Self-Regulating and Largely Hidden from View,” Nature, Vol. 474, 2011, pp. 356-358.
- L. Battison, “Dark Matter Theory May Be Wrong,” Space & Astronomy, 19 September 2011.
- X. Hernandez and W. Lee, “An Upper Limit to the Central Density of Dark Matter Halo,” Monthly Notices of the Royal Astronomical Society: Letters, Vol. 404, 2010, pp. L6-L10.
- J. Simon, A. Bolatto, A. Leroy, et al., “High-Resolution Measurement of the Halos of Four Dark Matter-Dominated Galaxies: Deviations from a Universal Density Profile,” The Astrophysical Journal, Vol. 621, No. 2, 2005, pp. 757-778. doi:10.1086/427684
- M. Walker and J. Penarrubia, “A Method for Measuring the Mass Profiles of Dwarf Spheroidal Galaxies,” The Astrophysical Journal, Vol. 742, No. 1, 2011, p. 20. doi:10.1088/0004-637X/742/1/20
- L. Kruesi, “Dark Matter Grows More Mysterious,” Astronomy, Vol. 40, No. 2, 2012, p. 13.
- K. S. Suh, “Partially Latent Interaction in the Elementary Particle Formation,” International Journal of Theoretical Physics, Vol. 3, No. 5, 1970, pp. 359-366. doi:10.1007/BF00671865
- P. Suh, “On Dark Matter and Energy,” American Physical Society Spring Meeting, 2007-2009.
- J. Baker, “50 Physics Ideas You Really Need to Know,” Quercus, London, 2007.
- D. Bohm, “Quantum Theory,” Dover Publications, New York, 1989.
- M. Jee, A. Mahdavi, H. Hoekstra, et al., “A Study of the Dark Core in A520 with Hubble Space Telescope, the Mystery Deepens,” The Astrophysical Journal, Vol. 747, No. 2, 2012, p. 96.
- D. Harris, “Vacuum Packed,” The New Scientist, Vol. 213, No. 2852, 2012, pp. 34-37. doi:10.1016/S0262-4079(12)60435-7
- J. Vacca, “The World’s 20 Greatest Unsolved Problems,” Prentice Hall, Upper Saddle River, 2005.
- I. Nicolson, “Unfolding Our Universe,” Cambridge University Press, Cambridge, 1999. doi:10.1017/CBO9780511584626
- J. Webber, “General Relativity and Gravitational Waves,” Dover Publications, New York, 2004.
- T. Herter, “Cosmology IV: The Early Universe,” Cornell University Astronomy, 2011.
- A. Friedmann, “On the Possibility of a World with Constant Negative Curvature of Space,” General Relativity and Gravitation, Vol. 31, No. 12, 1999, pp. 2001-2008. doi:10.1023/A:1026755309811
- M. Brown, P. Ade, J. Bock, et al., “Improved Measurement of the Temperature and Polarization of the Cosmic Background from QUaD,” The Astrophysical Journal, Vol. 705, No. 1, 2009, pp. 978-999. doi:10.1088/0004-637X/705/1/978
- G. Hinshaw, et al., “Five-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations,” Astrophysical Journal Supplement Series, Vol. 180, pp. 225-245, 2009.
- G. Bouldoul and A. Barrau, “Primordial Black Holes,” 2002. http://arXiv/astro-ph/0212225
- R. Minchin, J. Davies and M. Disney, “A Dark Hydrogen Cloud in the Virgo Cluster,” The Astrophysical Journal, Vol. 622, No. 1, 2005, pp. L21-L24. doi:10.1086/429538
- R. Lovett, “Dark Matter Galaxy Detected: Hidden Dwarf Lurks Nearby?” National Geographic News, 4 January 2011.
- C. Conry, A. Leob, D. Spergel, et al., “Evidence Against Dark Matter Halos Surrounding the Globular Clusters MGC1 and NGC2419,” The Astrophysical Journal, Vol. 741, No. 2, 2011, p. 72. doi:10.1088/0004-637X/741/2/72
- K. Freeman and G. McNamara, “In Search of Dark Matter,” Springer, UK, 2006.
- J. Talpur, “A Guide to Globular Clusters,” Keele Universiry Report, 1997.
- J. Gerssen, R. van der March, K. Gebhardt, et al., “HST Search for an Intermediate-Mass Black Hole in Globular Cluster M15-II,” The Astronomical Journal, Vol. 124, No. 6, 2002, p. 3270. doi:10.1086/344584
- S. van den Bergh, “Globular Cluster and Dwarf Spheroidal Galaxies,” Monthly Notices of the Royal Astronomical Society: Letters, Vol. 385, No. 1, 2007, pp. L20-L22.
- A. Navabi and N. Riazi, “Is the Age Problem Resolved?” Journal of Astrophysics and Astronomy, Vol. 24, No. 1-2, 2003, pp. 3-10.
- L. Gretchen, H. Harris and W. Harris, “The Globular Cluster/Central Black Hole Connection,” 2010. http://ArXiv:1008.4748v1
- B. Dauphole, M. Geffet, J. Colin, et al., “The Kinematics of Globular Clusters, Apocentric Distances and a Halo Metallicity Gradient,” Astronomy and Astrophysics, Vol. 313, 1996, pp. 119-128.
- J. Kormendy and R. Bender, “Supermassive Black Holes Do Not Correlate with Disks or Pseudobulges,” Nature, Vol. 469, No. 7330, 2011, pp. 374-376. doi:10.1038/nature09694
- C. Carilli and D. Riechers, “Black Holes Were Born before Galaxies,” 213th American Astronomical Society Meeting, Long Beach, 4-8 January 2009.
- J. Trump, B. Weiner, C. Scarlata, et al., “A Candels WFC3 Grism Study of Emission-Line Galaxies at z~2: A Mix of Nuclear Activity and Low-Metallicity Star Formation,” The Astrophysical Journal, Vol. 743, No. 2, 2011, p.144.
- K. Ferron, “What Is One of the Current ‘Big Ideas’ about Black Holes?” Astronomy, Vol. 39, No. 9, 2011, p. 20.
- S. Meibom, S. Barnes, D. Latham, et al., “The Kepler Cluster Study: Stellar Rotation in NGC68111,” The Astrophysical Journal Letters, Vol. 733, No. 1, 2011, p. L9.
- V. Allevato, F. Finoguenov, N. Cappelluti, et al., “The XMM-Newton Wide Field Survey in the Cosmo Field,” The Astrophysical Journal, Vol. 736, No. 2, 2011, p. 99. doi:10.1088/0004-637X/736/2/99
- T. van Albada, J. Bahcall, K. Begeman, et al., “Distribution of Dark Matter in the Spiral Galaxy NGC3198,” The Astrophysical Journal, Vol. 295, 1985, pp. 305-313. doi.org/10.1086/163375
- D. Benningfield, “Black Hole May ‘Wind Up’ Spiral Galaxies,” StarDate, June/July 2008.
- K. Cooper, “Galaxy Evolution Model Comes under Fire,” Astronomy Now, Vol. 22, 2005, p. 24.
- T. Plotner, “Messsier 90,” Unuiverse Today, 21 December 2009.
- A. Amblard, C. Asantha, P. Serra, et al., “Sub-Millimeter Halos with Masses Greater than 3E11 Solar Mass,” Nature, Vol. 470, 2011, pp. 510-512. doi:10.1038/nature09771
- P. Eisenhardt, T. Jarrett, R. Overzor, et al., “Merging Galaxies Trigger a Star Burst,” American Astronomical Society Press Release, 13 January 2011.
- A. van der Wel, A. Stranghn, H. Rix et al., “Extreme Emission-Line Galaxies in Candels,” The Astrophysical Journal, Vol. 742, No. 2, 2011, p. 111. doi:10.1088/0004-637X/742/2/111
- L. Grossman, “Galaxy Graves Are Growing Bigger,” Science News, 9 December 2009.
- F. Meelia, “The Black Hole at the Center of our Galaxy,” Princeton University, Princeton, 2003.
- B. McNamara, P. Nulsen, M. Wise, et al., “The Heating of Gas in Galaxy Cluster by X-Ray Cavities and Large-Scle Shock Fronts,” Nature, Vol. 433, 2005, pp. 45-47. doi:10.1038/nature03202
- Y. Shen, M. Strauss, M. Oguri, et al., “Clustering of High-Redshift (z > 2.9) Quasars from Sloann Digital Sky Survey,” The Astrophysical Journal, Vol. 133, 2007, pp. 2222-2241.
- W. Zheng, H. Ford, L. Infante, et al., “Bright Candidate of Galxies at Redshift 7 - 8 in the ACS Cluster Field,” American Astronomical Society Meeting, Calcary, June 2006.
- M. Iye, O. Kazuaki, N. Kashikawa, et al., “A Galaxy at Red-Shift z = 6.96,” Vol. 443, 2006, pp. 186-188.
- [61] A. Frebel, N. Christlieb, J. Norris, et al., “Discovery of HE1523-0901, a Strongly r-Process-Enhanced Metal Poor Star with Detected Uranium,” The Astrophysical Journal Letters, Vol. 660, No. 2, 2007, pp. L117-L120. doi:10.1086/518122
- [62] R. Gobat, E. Daddi, M. Onodera, et al., “A Mature Cluster with X-Ray Emission at z = 2.07,” Astronomy & Astrophysics, Vol. 526, 2011, p. A133. doi:10.1051/0004-6361/201016084
- [63] P. Capak, C. Carilli, N. Lee, et al., “Spectroscopic Confirmation of an Extremely Starburst at Redshift 4.547,” The Astrophysical Journal Letters, Vol. 681, No. 2, 2008, pp. L53-L56. doi:10.1086/590555
- [64] K. Tran, C. Papvich, A. Saintonge, et al., “Reversal of Fortune: Confirmation of an Increasing Star Formulation Density in a Cluster at z = 1.62,” The Astrophysical Journal Letters, Vol. 719, No. 2, 2010, p. L126. doi:10.1088/2041-8205/719/2/L126
- [65] S. Singh, “Big Bang,” Harper Collins, New York, 2004.
- [66] G. Cresci, F. Mannucci, R. Maiolino, et al., “Gas Accretion as the Origin of Chemical Abundance Gradients in the Distant Galaxies,” Nature, Vol. 467, 2010, pp. 811- 813. doi:10.1038/nature09451
- [67] E. Baldwin, “Old Galaxies Stick Together,” Astronomy Now, Vol. 22, 2005, p. 24.
- [68] D. Coe, N. Benitez, T. Broadhurst, et al., “A High-Resolution Mass Map of Galaxy Cluster Substructure,” Nature, Vol. 722, 2010, pp. 1-25.
- [69] F. Perrotta and C. Baccigalupi, Physical Review D, Vol. 65, No. 12, 2002.
- [70] H. Hwang and M. Lee, “Searching for Rotating Galaxy Cluster in SDSS and 2dFGRS,” The Astrophysical Journal, Vol. 662, No. 1, 2007, pp. 236-249. doi:10.1086/514328
- [71] A. Omar, “A Possibility of Magnus Effect on Disk Galaxies,” Current Science, Vol. 100, No. 9, 2011, pp. 1391- 1393.
- [72] P. Kroupa and M. Pawlowski, “Dark Matter Crisis,” Spectrum/der Wissenschaft, 2011.

