International Journal of Astronomy and Astrophysics
Vol.1 No.4(2011), Article ID:16376,22 pages DOI:10.4236/ijaa.2011.14027
A Numerical Characterization of the Gravito-Electrostatic Sheath Equilibrium Structure in Solar Plasma
1Department of Physics, Tezpur University, Assam, Bharat
2Ved-Vijnanam Pravartanam Samitihi, Pratapgarh (Awadh), Bharat
E-mail: pkk@tezu.ernet.in, jagatpurdwivedi@gmail.com
Received October 3, 2011; revised November 7, 2011; accepted November 25, 2011
Keywords: Sun, Solar Wind Plasma, Gravito-Electrostatic Coupling Processes, Inhomogeneity Scale Lengths, Solar Interior Plasma, Gravito-Electrostatic Sheath, Solar Models, Electromagnetic Sun
Abstract
This article describes the equilibrium structure of the solar interior plasma (SIP) and solar wind plasma (SWP) in detail under the framework of the gravito-electrostatic sheath (GES) model. This model gives a precise definition of the solar surface boundary (SSB), surface origin mechanism of the subsonic SWP, and its supersonic acceleration. Equilibrium parameters like plasma potential, self-gravity, population density, flow, their gradients, and all the relevant inhomogeneity scale lengths are numerically calculated and analyzed as an initial value problem. Physical significance of the structure condition for the SSB is discussed. The plasma oscillation and Jeans time scales are also plotted and compared. In addition, different coupling parameters, and electric current profiles are also numerically studied. The current profiles exhibit an important behavior of directional reversibility, i.e., an electrodynamical transition from negative to positive value. It occurs beyond a few Jeans lengths away from the SSB. The virtual spherical surface lying at the current reversal point, where the net current becomes zero, has the property of a floating surface behavior of the real physical wall. Our investigation indicates that the SWP behaves as an ion current-carrying plasma system. The basic mechanism behind the GES formation and its distinctions from conventional plasma sheath are discussed. The electromagnetic properties of the Sun derived from our model with the most accurate available inputs are compared with those of others. These results are useful as an input element to study the properties of the linear and nonlinear dynamics of various solar plasma waves, oscillations and instabilities.
1. Introduction
The well known standard solar model (SSM) basically assumes a single neutral gas approximation under hydrostatic equilibrium description of the Sun [1-6]. This model ignores the Coulomb property of the solar plasma constituents and the role of coulomb interactions on binary and collective scales. This can be physically justified as because the quasi-neutral property of the solar plasma is well satisfied on the Jeans scale lengths. Consequently, the possible role of space charge electrical action due to plasma wall interactions is also absent. Nevertheless, a few curious minds [7-9] took an interest to investigate the possible effect and semi-empirical estimation of the electrical forces on the pressure in a star shown to have a net electrical charge on the surface. In an attempt made to determine the suspected electric field by the measurements of the Stark effect [10], no field could be detected below an upper limit of 100 V/cm. Gunn endeavored to indicate the importance of the electric fields and calculated its value using Pannekoek model for charge separation [10]. It amounts to 0.015 V/cm, a value which is too small to be measured by Stark effect. Afterwards the idea of electric field in the solar/stellar interior and exterior regions could not gather much momentum for further research. In these electrical models the problem of the origin mechanism and maintenance of the electric field still remains as an open question. Moreover, these models do not find out exact solutions of the basic structure equations, but provide empirical and simple theoretical estimations of the solar and stellar specific values.
Dwivedi, Karmakar and Tripathy in 2007 proposed a simple model of gravito-electrostatic sheath (GES) formation [11] around the solar surface boundary (SSB). This GES ranging from the bounded to unbounded scales is similar to the pre-sheath region of the laboratory scale plasma bounded by physical wall. It is normally believed that the terms plasma and sheaths were introduced in 1928-29 by Irving Langmuir in the study of electrical discharges in gases [12,13]. The continuous emission of the subsonic solar interior plasma (SIP) and its acceleration to the supersonic speed seems to be a necessity for sustaining the dynamically bounded GES-type of equilibrium of the Sun as a coupled system of two different plasmas. We wish to provoke that the gravitational squeezeing causes surface charge polarization due to excessive flux emissions of the electrons at successive spherical surfaces lying at variable radial points relative to the heliocentre. We can thus easily think that the successive surfaces will develop negative charges varying with radial position, being the highest at the SSB. Finally, a global scale charge polarization in the bulk SIP will be reflected on the SSB and beyond on Jeans scale length order. Thus one can understand and explain the interior origin of the solar wind plasma (SWP) and its supersonic acceleration due to space charge electrical field action in terms of the basic principles of plasma-wall interaction process. The existence of a spherical floating surface is an outcome of the GES theory. To say much more about its physical significance, we need more and more thinking and investigation.
This model provides an integrated and unique view of a self-consistently coupled system of the solar interior and exterior plasmas. Consideration of a two-fluid (one for the SIP, and the other, SWP) solar plasma model offers a new physical insight for describing the equilibrium hydrodynamic structure and space charge electrical state of the Sun and its atmosphere. In fact, the concept of a single neutral fluid model suffers deficiency of hiding the role of the Coulomb interactions on the binary and collective scales both. Hence it lacks in the complete description of the equilibrium properties of the solar plasma on both the bounded and unbounded scales. The bounded scale solar plasma is termed as the SIP, whereas the unbounded scale solar plasma is called the SWP. Both are of the same origin, but different on the basis of the dynamical behaviors. They are mutually interconnected and are sustained self-consistently as a steady state hydrodynamic equilibrium of a single unit of the self-gravity confined solar plasma and its own atmosphere. The GES concept allows the role of plasma-wall interaction physics to cause the origin of space charge electric field effect to play an important role in the selfgravitational confinement of the solar (stellar) plasma. It is sustained by the surface emission mechanism of the solar (stellar) wind plasma in general in a steady state (time-stationary) hydrodynamic configuration.
From the basic knowledge of a bounded plasma behavior on laboratory scale [14-16], one knows that the quasi-neutral property of the plasma is violated near the boundary wall. A non-zero and nonlinear space charge electric field (called plasma sheath or Debye sheath) develops near the wall surface and extends its impact over a few Debye lengths inside the confined plasma. This localized electrostatic field, nonlinear in space, confines the bulk quasi-neutral plasma enclosed within a solid boundary wall. In the case of a completely absorbing physical wall the loss of more flux of thermal electrons to the wall than that of the ions causes the origin of space electric field in the bulk plasma. The space charge electric field thus arising due to plasma-wall interaction process evolves and gets localized within a region of a few Debye lengths width [14-16].
In the case of solar plasma, there is no solid physical boundary wall located at some specified radial position as such, but the solar self-gravity itself acts as a gravitational potential wall having variable strengths in radial direction with the maximum strength at the SSB. The self-gravitational wall strength at any radial point is measured by the escape velocity of the plasma fluid at that point. This means that ion fluid requires certain minimum threshold velocity in supersonic range to cross over the gravitational barrier created and maintained by the entire solar plasma mass distribution itself.
This is to furthermore note that the wall strength in laboratory-produced plasma is a constant and is located at some fixed position with respect to our reference point in the plasma. In the case of the solar self-gravity confined plasma, on the other hand, it is continuous with variable strength at different radial positions from the heliocentre. The radial distribution of the solar selfgravity wall strength having the maximum value on the SSB is describable by the gravitational Poisson equation. Applying the basic conceptual knowledge of plasma-wall interaction physics in the GES model, we predict the existence of a concentric virtual spherical wall with floating surface potential away from the SSB. Our model offers a precise definition of the SSB and its associated electromagnetic properties. This also offers an alternate approach to understand the basic physics of the solar surface origin of the SWP and its supersonic transition through the transonic equilibrium. This physical model illustrates the idea of an internal origin of the SWP by plasma-boundary interaction processes and cross-border effects. This is in contrast to all the other proposed models reported so far as discussed above in earlier part of the introduction.
Many other authors [17-20] also discuss about the Sun and SWP physics. Moreover, the thermodynamics of the Sun and its non-ideal interior are well understood with a proper equation of state for the composing ionized matter based on the free energy minimization principle [26]. This is to acknowledge that the ideas of electric field, magnetic field, solar surface charge, etc. were known earlier [7-10]. But this is to comment that the exact solutions of the basic model equations were missing. The degree of accuracy on theoretical results requires accuracy in problem formulation, mathematical strategy, methodological calculations, and mathematical-physical consistency. For example, in our model calculation the inclusion of electrostatic Poisson term in further calculation of the space charge electric field arising at Jeans scale length order becomes redundant. This is well justified due to very wide range difference of the solar plasma Debye length and Jeans length scales. This simply implies that the quasi-neutral property holds well on the bounded and unbounded scales of the solar plasmas associated with fields and electric currents. As a result, consideration of electrostatic Poisson term in charge density to mass density ratio estimation as done earlier [8] leads to zero values of ~10–36 on a normalized scale length on Jeans order. So, to describe the property of the space charge electric field on Jeans scale length order, it seems inconsistent to include the electrostatic Poisson term in the theoretical analysis and quantitative estimation of the solar or stellar plasma electric field.
Our model calculation questions the earlier idea of the solar surface origin of the SWP and suggests its origin from deep inside the Sun i.e. in the core. One of the most important results of this model calculation is the flow of electric current inside the Sun and beyond the SSB in the solar atmosphere with current reversal property. In this research contribution, we derive and discuss the basic physics of the GES formation in detail, its existennce condition compared to other models [7-10], all the relevant characteristic lengths as well as the electrical and magnetic state of the Sun and its atmosphere.
Apart from the “Introduction” part described in Section 1 above, this paper is structurally organized in a usual simple format as follows. Section 2 includes the basic ideas and approximations of the model along with the mathematical formulations of the problem. In Section 3, we present the basic physical concept of the solar self-gravitational wall and existence condition of the GES formation. Section 4 describes the numerical results of the different physical parameters associated with the GES equilibrium structure in three added subsections. Subsections 4.1, 4.2 and 4.3 present the numerical results for the bounded SIP, unbounded SWP, and relative comments, respectively. Lastly, in Section 5, possible conclusions are drawn briefly and tentative future scopes with astrophysical importance are discussed to extend the problem further in more realistic astrophysical situations.
2. Physical Model and Formulations
A simplified ideal two-fluid plasma model is adopted to study the solar plasma equilibrium under the GES model framework on the bounded and unbounded scales in a field-free hydrodynamic equilibrium configuration. For mathematical simplicity, no collisions of any type are included and no magnetic field effect is considered. Applying the spherical capacitor charging model, the coulomb charge on the SSB comes out to be 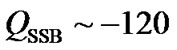 C. For rotation frequency of the solar surface corresponding to the mean angular frequency about the centre of the system
C. For rotation frequency of the solar surface corresponding to the mean angular frequency about the centre of the system 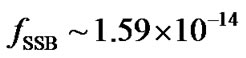 Hz [9], the mean value of the strength of the solar magnetic field at the SSB in our model analysis is estimated as
Hz [9], the mean value of the strength of the solar magnetic field at the SSB in our model analysis is estimated as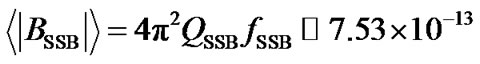 T. This is negligibly small for producing any significant effects on the dynamics of the solar plasma particles. Thus the effects of the magnetic field are not realized by the particles due to the weak Lorentz force, which is now estimated to be
T. This is negligibly small for producing any significant effects on the dynamics of the solar plasma particles. Thus the effects of the magnetic field are not realized by the particles due to the weak Lorentz force, which is now estimated to be 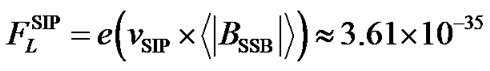 N corresponding to a subsonic flow speed
N corresponding to a subsonic flow speed  cm/s. Thus the Lorentz force has a very weak effect on the plasma particles and hence, neglected. It justifies the convective and circulation dynamics being neglected as well. Therefore our unmagnetized plasma approximation is well justified in our GES model configuration. All types of kinetic effects are also ignored to avoid complications of mathematics and physics both. An estimated value
cm/s. Thus the Lorentz force has a very weak effect on the plasma particles and hence, neglected. It justifies the convective and circulation dynamics being neglected as well. Therefore our unmagnetized plasma approximation is well justified in our GES model configuration. All types of kinetic effects are also ignored to avoid complications of mathematics and physics both. An estimated value 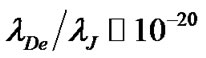 of the ratio of the solar plasma Debye length and the Jeans length of the total solar mass justifies the quasi-neutral behavior of the solar plasma on both the bounded and unbounded scales. The confining wall of the solar plasma looks like a spherically symmetric surface boundary of non-rigid and non-physical nature. The solar plasma is assumed to consist of a single component of Hydrogen ions and electrons. The electrons are assumed to have Maxwellian density distribution with gravitational potential term ignored due to zero mass approximation of the electrons. Ions follow the full inertial dynamics in one dimension of simplified radial degree of freedom.
of the ratio of the solar plasma Debye length and the Jeans length of the total solar mass justifies the quasi-neutral behavior of the solar plasma on both the bounded and unbounded scales. The confining wall of the solar plasma looks like a spherically symmetric surface boundary of non-rigid and non-physical nature. The solar plasma is assumed to consist of a single component of Hydrogen ions and electrons. The electrons are assumed to have Maxwellian density distribution with gravitational potential term ignored due to zero mass approximation of the electrons. Ions follow the full inertial dynamics in one dimension of simplified radial degree of freedom.
The basic sets of dynamical evolution equations relevant for the bounded and unbounded solar plasma description and characterization are given and discussed in separate subsections as follows.
2.1. Basic Equations for SIP Scale Equilibrium
The basic autonomous coupled set of mathematical equations for the investigation of the SIP equilibrium properties is given below. All the equations are normalized and the normalizations are defined in our previous publication [11].
Solar self-gravity Poisson equation:
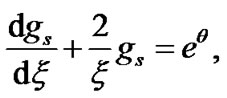 (1)
(1)
Ion continuity equation:
 (2)
(2)
Ion momentum equation:
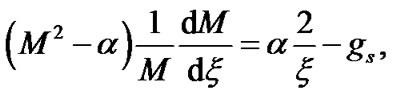 (3)
(3)
where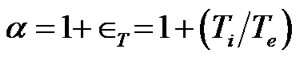 ,
, 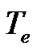 is the thermal electron temperature and
is the thermal electron temperature and 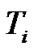 is the inertial ion temperature for the bounded solar plasma on the SIP scale (each in eV). Equations (2) and (3) are simplified by using the Maxwellian population density distribution for the electrons of the solar plasma system. In fact Equation (1) defines and describes the physical nature (strength and its radial variation) of the solar self-gravitational wall. The gravitational potential energy corresponding to the solar self-gravity at any given radial position quantifies the physical strength of the gravitational wall at that radial position. This is also expressible in the form of the escape velocity of the solar plasma ions as shown in Figures 9(a)-(c).
is the inertial ion temperature for the bounded solar plasma on the SIP scale (each in eV). Equations (2) and (3) are simplified by using the Maxwellian population density distribution for the electrons of the solar plasma system. In fact Equation (1) defines and describes the physical nature (strength and its radial variation) of the solar self-gravitational wall. The gravitational potential energy corresponding to the solar self-gravity at any given radial position quantifies the physical strength of the gravitational wall at that radial position. This is also expressible in the form of the escape velocity of the solar plasma ions as shown in Figures 9(a)-(c).
The mathematical notations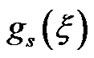 ,
, 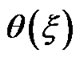 , and
, and 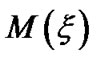 as usual represent the equilibrium solar self-gravity, GES associated electrostatic potential and Mach number in normalized forms, respectively. Let us mention that the solar self-gravity is normalized by the solar free-fall (heliocentric) gravitational strength
as usual represent the equilibrium solar self-gravity, GES associated electrostatic potential and Mach number in normalized forms, respectively. Let us mention that the solar self-gravity is normalized by the solar free-fall (heliocentric) gravitational strength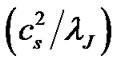 . The GESassociated electrostatic potential is normalized by the electron thermal potential
. The GESassociated electrostatic potential is normalized by the electron thermal potential . The ion flow velocity is normalized by solar plasma sound speed
. The ion flow velocity is normalized by solar plasma sound speed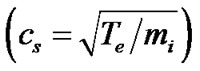 . Moreover, the independent variables like time
. Moreover, the independent variables like time 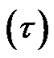 and space
and space  are normalized with Jeans time
are normalized with Jeans time 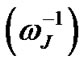 and Jeans length
and Jeans length 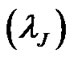 scales, respectively. Appendix may be useful to offer an instant and quick reference of the standard physical values [6-21] purposeful for solar plasma calculations for any reader of the paper conveniently. The equilibrium values of the relevant normalization parameters (/constants) useful for our work along with plasma parameters are estimated and enlisted in Appendices 2 and 3, respectively. Here we take
scales, respectively. Appendix may be useful to offer an instant and quick reference of the standard physical values [6-21] purposeful for solar plasma calculations for any reader of the paper conveniently. The equilibrium values of the relevant normalization parameters (/constants) useful for our work along with plasma parameters are estimated and enlisted in Appendices 2 and 3, respectively. Here we take 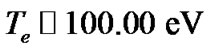 and
and 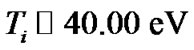 so that
so that 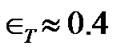 for both the SIP and SWP. This is found to be the best choice for which the hydrodynamic condition is fulfilled. Other formulae, constants and mathematical expressions of the relevant plasma parameters are directly adopted from NRL Plasma Formulary [21].
for both the SIP and SWP. This is found to be the best choice for which the hydrodynamic condition is fulfilled. Other formulae, constants and mathematical expressions of the relevant plasma parameters are directly adopted from NRL Plasma Formulary [21].
Astrophysical inhomogeneity scale lengths in the case of accretion disks have been derived and discussed in detail [22,23]. Applying the same methodologies in the Sun, the normalized forms of inhomogeneity scale lengths for self-gravity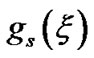 , electrostatic potential
, electrostatic potential , Mach number
, Mach number , population density
, population density 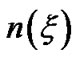 and electric current density
and electric current density 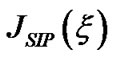 are respectively defined as,
are respectively defined as,
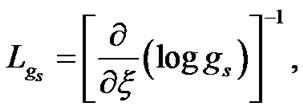 (4)
(4)
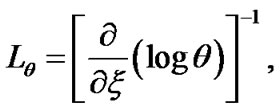 (5)
(5)
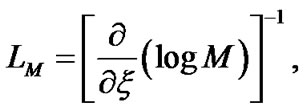 (6)
(6)
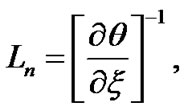 (7)
(7)
 (8)
(8)
Furthermore, the normalized forms of the gravitothermal coupling coefficient for electrons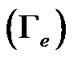 , gravitothermal coupling coefficient for ions
, gravitothermal coupling coefficient for ions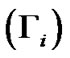 , and gravitoacoustic coupling coefficient for ions
, and gravitoacoustic coupling coefficient for ions  are, respectively, expressed as follows
are, respectively, expressed as follows
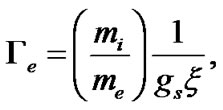 (9)
(9)
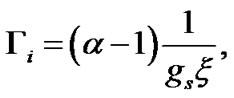 (10)
(10)
and
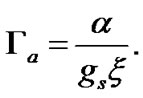 (11)
(11)
The expression for the SIP electric current density with ion thermal contribution included is written as follows in the form of Equation (12),
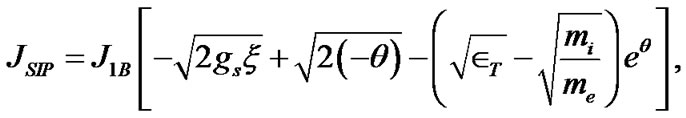 (12)
(12)
where  defines the equilibrium ion Bohm current density for the SIP and
defines the equilibrium ion Bohm current density for the SIP and 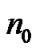 specifies the mean SIP equilibrium population density.
specifies the mean SIP equilibrium population density.
Additional interesting properties of the SIP are electron Debye length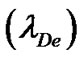 , Jeans frequency
, Jeans frequency , Jeans length
, Jeans length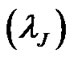 , electron plasma oscillation time scale
, electron plasma oscillation time scale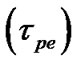 , ion plasma oscillation time scale
, ion plasma oscillation time scale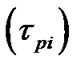 , SIP ion escape velocity
, SIP ion escape velocity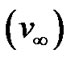 , etc. Their expressions are derived and given as follows
, etc. Their expressions are derived and given as follows
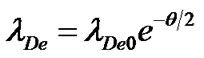 where
where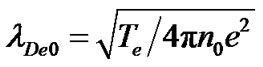 , (13)
, (13)
 where
where , (14)
, (14)
 where
where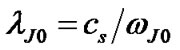 , (15)
, (15)
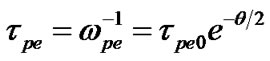 where
where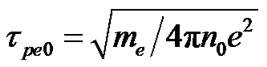 , (16)
, (16)
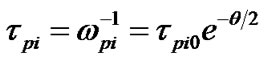 where
where , (17)
, (17)
and
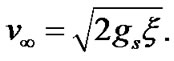 (18)
(18)
Again when these time scales are normalized with Jeans time scales, the same expressions will read as
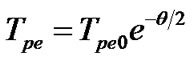 (19)
(19)
where 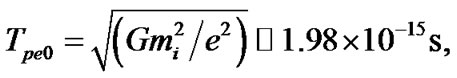 and
and
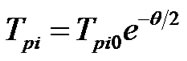 (20)
(20)
where 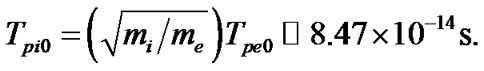
Again the SIP ions get energized under the influence of the electric field associated with the GES. The electric field-induced source velocity of the ions without thermal correction  (for cold ions) and electric field-induced velocity with thermal correction
(for cold ions) and electric field-induced velocity with thermal correction 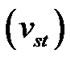 (for relatively hot ions) associated with the SIP flow dynamics are respectively derived and given as follows
(for relatively hot ions) associated with the SIP flow dynamics are respectively derived and given as follows
 , (21)
, (21)
and
 . (22)
. (22)
2.2. Basic Equations for SWP Scale Equilibrium
While exploring the SWP properties on an unbounded scale, this should be kept in mind that the self-solar gravity is switched off by electrical screening of the solar self-gravitational field. Now the Sun as a whole acts as a source of an external gravity, and it controls and monitors the dynamics of the SWP. The basic autonomous coupled set of the governing equations for the SWP equilibrium properties, as described on the SIP scale, is cast as follows
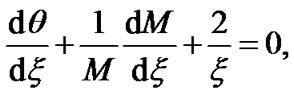 (23)
(23)
and
 (24)
(24)
where 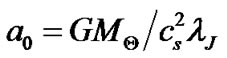 is a normalization coefficient and
is a normalization coefficient and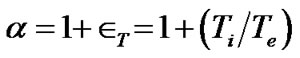 ,
, 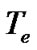 is the solar plasma thermal electron temperature and
is the solar plasma thermal electron temperature and 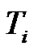 is the inertial ion temperature as defined before. The normalized forms of the inhomogeneity scale lengths for electrostatic potential
is the inertial ion temperature as defined before. The normalized forms of the inhomogeneity scale lengths for electrostatic potential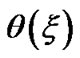 , Mach number
, Mach number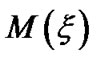 , population density
, population density 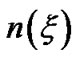 and electric current density
and electric current density  are, respectively, defined on the unbounded SWP scale as follows,
are, respectively, defined on the unbounded SWP scale as follows,
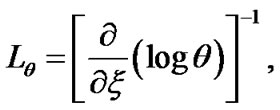 (25)
(25)
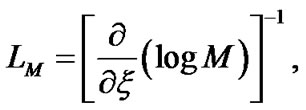 (26)
(26)
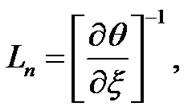 (27)
(27)
and
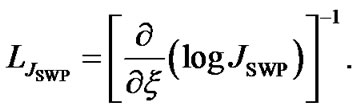 (28)
(28)
The gravito-thermal coupling coefficient of the electrons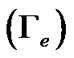 , gravito-thermal coupling coefficient of the ions
, gravito-thermal coupling coefficient of the ions , and gravito-acoustic coupling coefficient of the ions
, and gravito-acoustic coupling coefficient of the ions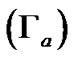 , respectively, are derived on the SWP scale and presented as follows
, respectively, are derived on the SWP scale and presented as follows
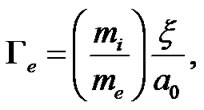 (29)
(29)
 (30)
(30)
and
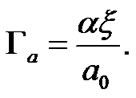 (31)
(31)
Expression for the SWP carrying electric current with the ion thermal contribution taken into account is written as follows
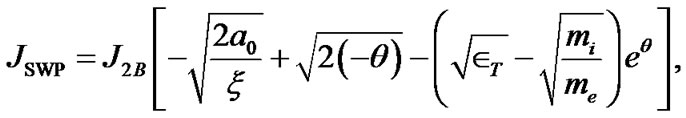 (32)
(32)
where 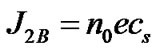 is defined as the usual equilibrium Bohm current density on the SWP scale and
is defined as the usual equilibrium Bohm current density on the SWP scale and 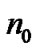 specifies the SWP equilibrium population density.
specifies the SWP equilibrium population density.
Moreover, some additional interesting physical properties of the SWP are electron Debye length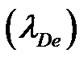 , Jeans frequency
, Jeans frequency , Jeans length
, Jeans length , electron plasma oscillation time scale
, electron plasma oscillation time scale , ion plasma oscillation time scale
, ion plasma oscillation time scale , SWP ion escape velocity
, SWP ion escape velocity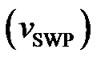 , etc. Normalized expressions for escape velocity of the SWP ions
, etc. Normalized expressions for escape velocity of the SWP ions , electric filed-induced velocity without thermal correction
, electric filed-induced velocity without thermal correction 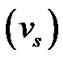 (for cold ions) and electric filed-induced velocity with thermal correction
(for cold ions) and electric filed-induced velocity with thermal correction 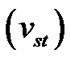 (for relatively hot ions) associated with the SWP flow dynamics are respectively given as follows
(for relatively hot ions) associated with the SWP flow dynamics are respectively given as follows
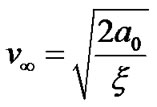 , (33)
, (33)
 , (34)
, (34)
and
 . (35)
. (35)
3. Conditions for the GES Formation
In the case of laboratory plasma the Bohm criterion [14] must be satisfied for the formation of Debye sheath near the wall boundary. This implies that the inertial ions must enter the non-neutral space charge layer known as the Debye sheath or simply plasma sheath with velocity exceeding the sonic velocity. Now, a presheath region must exist to accelerate the ions to acquire the requisite velocity as dictated by the Bohm criterion. In the case of completely absorbing wall the potential of the wall is raised to some maximum negative value so as to equalize the electron and ion particle flux densities received by the wall surface. Thus for such condition of the wall, no net electric current is drawn by the wall and hence, it is called the floating wall. To understand the basic physical process of plasma sheath formation in laboratory plasma, the following arguments are advanced. In an initial stage of the physically confined plasma the wall receives more thermal electron particle flux density than that of the inertial ions. This occurs due to the assumption of the zero electron-inertia with respect to heavier inertial ions. As a result, the wall acquires excess negative charge leaving an ion excess charge region inside the whole of the bulk plasma volume.
Now the wall-induced space charge polarized electric field comes into action that accelerates the bulk plasma ions towards the wall. Hence a dynamical process of space charge electric field evolution sets in and continues till the electron and ion fluxes are equalized at the wall. This is termed as the floating condition of the wall confining any simple two-component plasma. Initially produced space charge electrostatic potential extending over the entire plasma volume shrinks and localizes near the wall over a distance on the order of few Debye lengths. This distance is known as plasma sheath width. This is how the formation mechanism of plasma sheath in laboratory confinement of plasma is understood. This nonneutral space charge layer acts as an electrostatic fencing which confines quasi-neutral bulk plasma and protects it from any external influence. There are some recent theoretical reportings [24,25] about the existence of subsonic plasma sheaths too in the case of a predominant electron current flowing through the wall. Kinetic description of the plasma is used to arrive at this conclusion where the conventional Bohm criterion [14-16] is not able to describe the sheath edge transition.
Let us now discuss the basic physics of the GES formation in a self-gravitational confinement of solar plasma. The solar plasma creates its own confining boundary wall of gravitational potential barrier by virtue of Jeans collapse process of an interstellar dust cloud where the Sun is born. In the process of Jeans collapse of dust cloud, an excessive heating of the self-gravitationally collapsing matter converts it into a plasma state of matter. Now the plasma interacts with the solar self-gravitational field that acts as a squeezing agent to squeezing out the electrons from the gravitational wall surfaces producing thereby surface space charge polarization. The structure and strength of the gravitational wall is defined and described by the gravitational Poisson equation as expressed in Equation (1). The maximization of the solar self-gravity dictates the condition for the creation of a boundary wall confining the SIP. Any boundary, of course, may be defined as the one where physical field variables become extremum. This is to note that the gravitational wall has a variable structure and strength with the maximum value defining the wall boundary. This is important to note from Equation (1) that the maximization of the solar self-gravity does not occur in a plane geometry approximation.
In fact the lighter electrons are squeezed out of the successive spherical surfaces due to solar self-gravity acting on the bulk interior plasma leaving the heavier ions to compress radially inward. This leads to an enhancement of ions population inside the compressed volume with an enhancement of thermal electron flux emitted out of the successive spherical surfaces at different radial positions. As a result space charge polarization on the Jeans scale length order comes into action to accelerate the SIP ions against the solar self-gravity. The ions are then continuously accelerated radially outwards, but the self-gravity suppresses the bulk plasma flow. As a net effect, the bulk plasma leaks through the SSB with some minimum possible velocity of a few cm/sec. In fact, at the SSB the solar self-gravity effect is cancelled out by the space charge electric field. Consequently, the SIP leak velocity is controlled and monitored by the compressibility of the ion fluid flow and curvature effect acting at equal level. Thus the formation of the GES could be well understood in terms of physical phenomenon occurring on the laboratory scale plasma due to plasma-wall interaction process in the vicinity of some physical wall.
In the case of laboratory plasma the rigidity of the wall prevents the physical movement of the ions and electrons both across the wall. In the case of gravitationally confined plasma like solar plasma with solar self-gravity confinement, the electrons and ions are not equally hindered to prevent the motion across any spherical surface in the SIP. The electrostatic field strength is decided by the solar self-gravitational wall strength of the bounded SIP system. With these analytical arguments in mind, we denote the maximum value 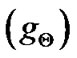 of solar self-gravity at some radial position
of solar self-gravity at some radial position 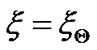 where
where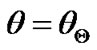 . Applying the necessary condition for
. Applying the necessary condition for  being the maximum at some radial position
being the maximum at some radial position 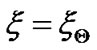 as
as  in Equation (1), one yields
in Equation (1), one yields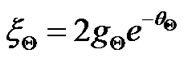 . However, it is not sufficient to justify the occurrence of the maximum value of
. However, it is not sufficient to justify the occurrence of the maximum value of 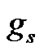 until and unless the second derivative of
until and unless the second derivative of 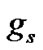 is shown to possess some negative value at this specific radial point. To derive the sufficient condition for the maximum value of
is shown to possess some negative value at this specific radial point. To derive the sufficient condition for the maximum value of 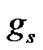 at
at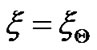 , let us once spatially differentiate Equation (1) to yield the following
, let us once spatially differentiate Equation (1) to yield the following
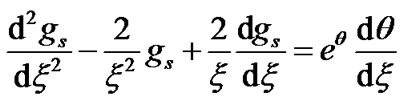 . (36)
. (36)
Now let us derive mathematical condition for sufficiency of 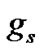 being the maximum at
being the maximum at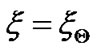 . Using the exact hydrostatic equilibrium approximation given by
. Using the exact hydrostatic equilibrium approximation given by 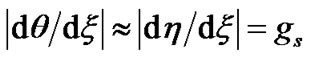 for the gravito-electrostatic force balancing near the SSB, following inequality is obtained,
for the gravito-electrostatic force balancing near the SSB, following inequality is obtained,
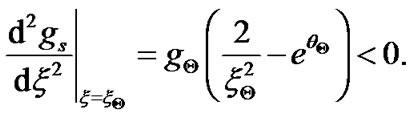 (37)
(37)
The necessary condition for the maximum  -value, which is the requirement for any self-gravitating bounded plasma system, from Equation (1) can analytically be expressed by the following relation,
-value, which is the requirement for any self-gravitating bounded plasma system, from Equation (1) can analytically be expressed by the following relation,
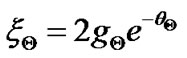 . (38)
. (38)
Again these two above Conditions (37) and (38) can be combined together to derive a single simplified condition for a bounded solution of the SIP to exist as
 (39)
(39)
If we define escape velocity as , the above Inequality (39) could be rewritten in the form of gravitational wall strength defined in terms of the SIP escape velocity as,
, the above Inequality (39) could be rewritten in the form of gravitational wall strength defined in terms of the SIP escape velocity as,
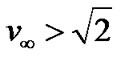 . (40)
. (40)
This means that the strength of the solar self-gravitational wall must be such that the ions could not overcome the barrier and the wall could bear with the ram pressure of the supersonic bulk plasma flow. This is now to comment that like the usual Bohm condition, there exists a similar criterion for a bounded GES solution to exist in case of self-gravitating solar plasma in spherical geometry. Here the escape velocity given by Equation (18) measures the physical strength of the gravitational wall at the SSB. Figure 6 depicts the validity of the existential condition of the GES. This is also to note that the solar self-gravity wall is bounded, whereas the electrostatic potential field is unbounded and extends over many hundreds of Jeans length beyond the SSB (Figures 1 and 10). The virtual floating surface wall is found to exist at a distance on the order of seven times of Jeans length beyond the SSB (Figure 12(c)). This is again interestingly noted that the major electrostatic potential drop occurs beyond the SSB (Figures 10(a) and (b)).
This may be worth-mentioning that the 1st term on R.H.S. of the Inequation (37) arises due to the spherical geometry of the gravitational wall and represents the rate of spatial change (decrease) in curvature effect (in selfgravity). The 2nd term on R.H.S. of inequation (37) represents the rate of spatial change (decrease) in solar plasma density due to plasma-wall interaction process with wall acquiring negative potential. The location of the maximum solar self-gravity defines the SSB. As the strength of the gravitational wall increases with increase in radial position from heliocentre outward, the electrostatic potential as well as the electrostatic electric field too increases in magnitude. For a bounded solution of the wall to exist, the rate of spatial change (decrease) in solar plasma density (2nd term) must exceed the rate of spatial change (decrease) in curvature effect (1st term) on R.H.S. of Equation (37).
Defining the boundary as a point where an exact balancing of the gravito-electrostatic force occurs, Equation (3) reduces into a simplified form written as follows
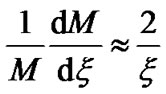 . (41)
. (41)
This is clear from Equation (41) that the unbounded supersonic SWP outflow is the transformed outcome of the bounded subsonic SIP in presence of curvature (geometrical) effect. Moreover, for a plane-geometry approximation , one gets
, one gets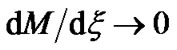 . Thus there will be no acceleration of the subsonic SIP into SWP by gravito-acoustic coupling processes. It, therefore, implies that the subsonic GES formation is not possible under a plane-geometry approximation even in presence of self-gravity. This indeed is an astrophysical reality in a self-gravitating plasma system under nonplaner geometry applicable for the theoretical description of the fundamental issues of the self-gravitationally confined solar plasma flow dynamics.
. Thus there will be no acceleration of the subsonic SIP into SWP by gravito-acoustic coupling processes. It, therefore, implies that the subsonic GES formation is not possible under a plane-geometry approximation even in presence of self-gravity. This indeed is an astrophysical reality in a self-gravitating plasma system under nonplaner geometry applicable for the theoretical description of the fundamental issues of the self-gravitationally confined solar plasma flow dynamics.
4. Discussions of Numerical Results
In order to get a detailed picture of the hydrodynamic GES equilibrium features, we have used the well-known fourth order Runge-Kutta method (RK-IV method) for numerical analyses of the solar plasma system. The two scale equilibrium structures of the coupled solar plasma system are governed by Equations (1)-(3) for the bounded SIP, and Equations (23)-(24) for the unbounded SWP. Two different sets of realistic initial values of the relevant solar physical variables are specified for numerical solutions of the basic governing equations. The first set of realistic initial values for the SIP description is analytically specified by nonlinear stability analysis, which falls within the solar core region. The values of these physical variables at the SSB are the natural outcomes of the nonlinear dynamical solutions of the SIP Equations (1)-(3) as an initial value problem. Now the numerically calculated values of these physical variables at the SSB forms the second set of realistic initial values for the SWP description as carried out in our earlier work [11]. In fact, this is the way we have solved the nonlinearly coupled governing dynamical equations of the two-layer GES model description. These two sets of realistic initial values are listed in Table 1 as follows.
4.1. Numerical Results for Bounded SIP
The coupled structure Equations (1)-(22) for the GES characterization are numerically simulated with the initial values as tabulated in Table 1 on the SIP scale. Figures 1-9 describe the profile structures of the SIP equilibrium in terms of the GES physical parameters. As given in Table 3 the values of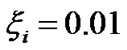 ,
, 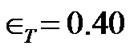 and
and 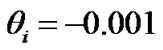 are kept fixed as already specified in our earlier paper [11] for all the numerical plots for the SIP scale description. The other fixed initial values obtained by nonlinear stability analyses for the concerned characterization here are
are kept fixed as already specified in our earlier paper [11] for all the numerical plots for the SIP scale description. The other fixed initial values obtained by nonlinear stability analyses for the concerned characterization here are  and
and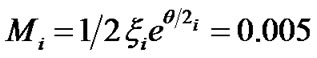 . Figure 1 contains the plots of the normalized solar selfgravity, its gradient and associated inhomogenity scale length (scaled down by division with 20) at various radial positions from the initial location. It is clear from Figure 1 that
. Figure 1 contains the plots of the normalized solar selfgravity, its gradient and associated inhomogenity scale length (scaled down by division with 20) at various radial positions from the initial location. It is clear from Figure 1 that 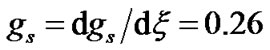 at
at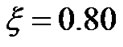 . Near the maximum value of the solar self-gravity associated with the SIP, i.e., near the SSB, the gradient indeed becomes zero which justifies the necessary condition for the maximization of the solar self-gravity. Moreover, near the SSB, the scale length becomes infinitely larger. The rate of spatial change of the solar self-gravity increases initially and then decreases to zero value as one approach the SSB. This means that the gravitational wall strength increases initially up to
. Near the maximum value of the solar self-gravity associated with the SIP, i.e., near the SSB, the gradient indeed becomes zero which justifies the necessary condition for the maximization of the solar self-gravity. Moreover, near the SSB, the scale length becomes infinitely larger. The rate of spatial change of the solar self-gravity increases initially and then decreases to zero value as one approach the SSB. This means that the gravitational wall strength increases initially up to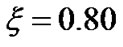 . These profiles are physically quite consistent to each others.
. These profiles are physically quite consistent to each others.
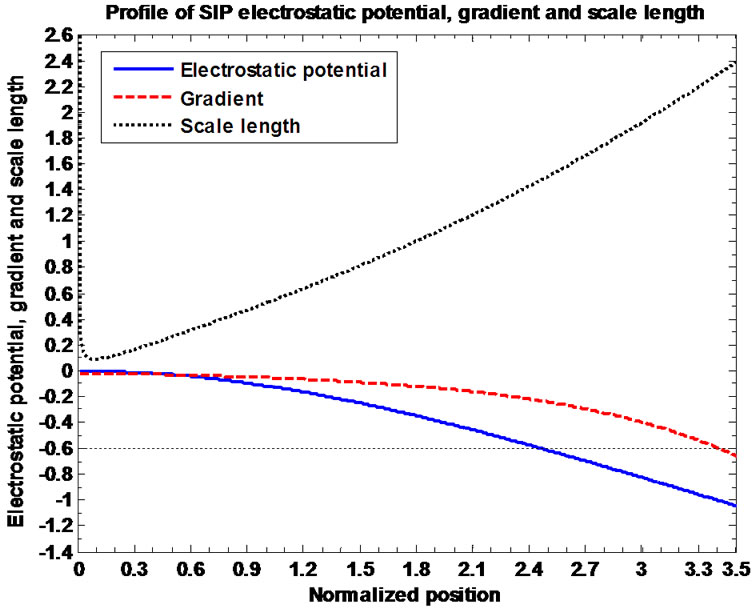
Figures 2(a) and (b) depict the plots of the GES-associated normalized electrostatic potential, its gradient and associated inhomogeneity scale length. The scale length profile is non-monotonous in nature and exhibits a sudden decrease in the vicinity of the initial position and then increases rapidly. There is a minimum normalized scale length of the electrostatic potential variations of the order of 0.1. The basic features of Figure 2 near the initial location can obviously be understood from Figure 2(b), which is the enlarged view of Figure 2(a). This is interestingly noted from Figure 2(b) that 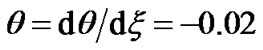 at
at 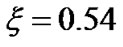 beyond which
beyond which 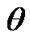 increases at a faster rate (more negative value). This is found from Figures 1 and 2 that
increases at a faster rate (more negative value). This is found from Figures 1 and 2 that 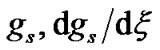 and
and  intersect approximately within the region defined by
intersect approximately within the region defined by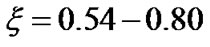 . This means that
. This means that  and
and 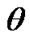 behave dynamically as exponentially varying functions of
behave dynamically as exponentially varying functions of 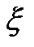 as
as  and
and 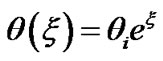 in this region particularly, respectively. This, in turn, helps the bounded solar plasma to leak through the self-gravitational potential barrier without overflowing through it.
in this region particularly, respectively. This, in turn, helps the bounded solar plasma to leak through the self-gravitational potential barrier without overflowing through it.
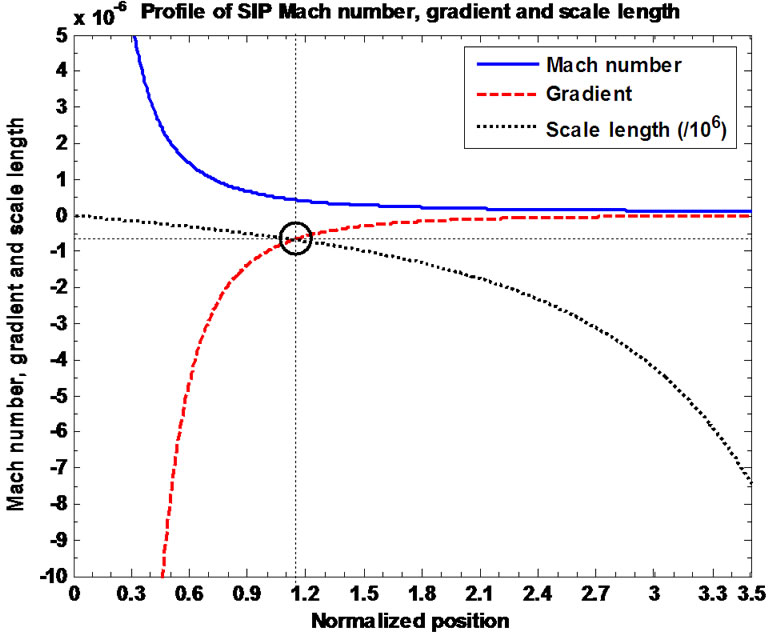
When the self-gravitational potential barrier height increases, the initial bulk flow of the SIP is drastically reduced to the minimum possible values at the SSB as shown in Figures 3(a) and (b). Figures 3(a) and (b) depict the plots of the ion Mach number, gradient and scale length (scaled down by division with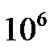 ). These plots exhibit monotonous behaviors having two scales of faster and slower regions of Mach number variations, respectively. Similarly, Figures 4(a) and (b) portray the plots
). These plots exhibit monotonous behaviors having two scales of faster and slower regions of Mach number variations, respectively. Similarly, Figures 4(a) and (b) portray the plots

Table 1. Initial and boundary GES values.
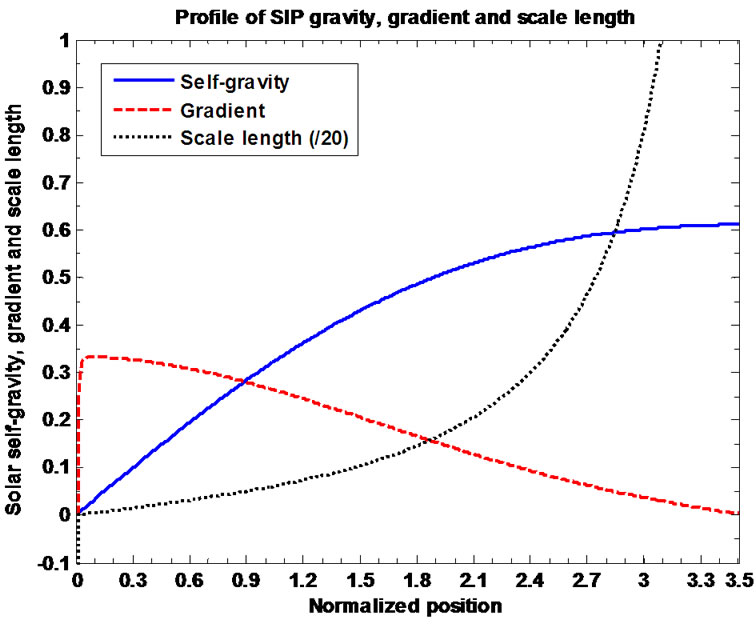
Figure 1. Variation of the normalized values of solar selfgravity 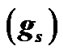 (solid blue line), self-gravity gradient
(solid blue line), self-gravity gradient  (red dashed line) and self-gravity scale length
(red dashed line) and self-gravity scale length
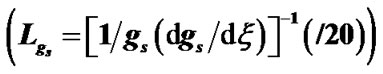 (black dotted line) associated with the SIP flow dynamics with normalized position
(black dotted line) associated with the SIP flow dynamics with normalized position 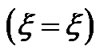 from the heliocentre
from the heliocentre . The initial values
. The initial values ,
, 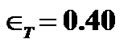 and
and 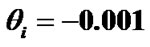 are kept fixed. The other fixed initial values by nonlinear stability analyses are
are kept fixed. The other fixed initial values by nonlinear stability analyses are 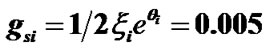 and
and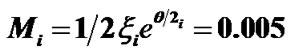 .
.
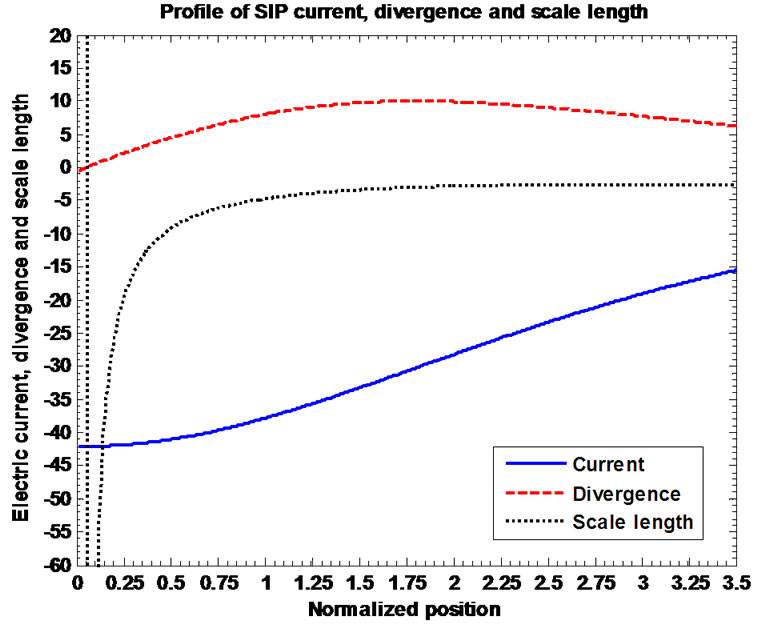
of solar plasma current density, its divergence and scale length. The gradient profile clearly shows the non-divergent behavior of the electron dominated current flowing through the gravitational wall of the SIP. From conventional viewpoint, the direction of current flow is towards the helio-centre. The magnitude of the current decreases as one moves from heliocentre to the SSB. The enlarged description of Figure 4(a) is given in Figure 4(b) showing the electrodynamics of the solar electric current near the heliocentre. This is found from Figure 4(b) that 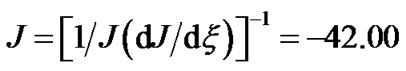 at both
at both 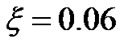 and
and . But at the position
. But at the position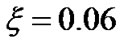 , it is seen that
, it is seen that , approximately.
, approximately.
Figure 5 exhibits the plots of the normalized solar plasma (population) density, its gradient and scale length. Figure 6 depicts the numerical plot of the second order differential derivative of the solar self-gravity and exhibits the validity of the condition for sufficiency of the maximization of the solar self-gravity at the SSB. Figure 7 exhibits the profiles of the normalized time scales for electron oscillations (scaled up by division with ), SIP ion oscillation (scaled up by division with
), SIP ion oscillation (scaled up by division with ) and Jeans collapse. It is clear to note that the Jeans time scale is quite larger by several orders of magnitude relative to each of the rest. Figure 8 depicts the plots of the
) and Jeans collapse. It is clear to note that the Jeans time scale is quite larger by several orders of magnitude relative to each of the rest. Figure 8 depicts the plots of the
 (a)
(a)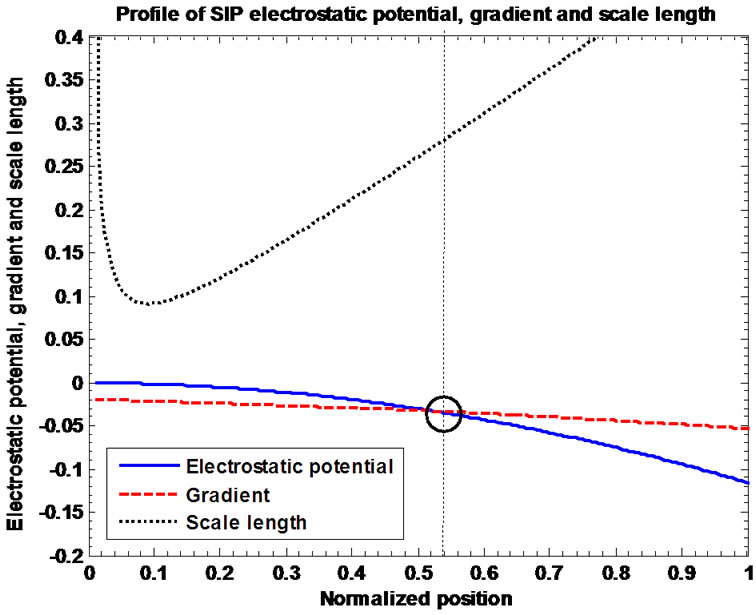 (b)
(b)
Figure 2. (a) Variation of the normalized values of electrostatic potential 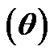 (solid blue line), potential gradient
(solid blue line), potential gradient 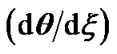 (red dashed line) and potential scale length
(red dashed line) and potential scale length
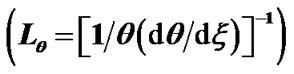 (black dotted line) associated with the SIP flow dynamics with normalized position
(black dotted line) associated with the SIP flow dynamics with normalized position 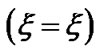 from the heliocentre
from the heliocentre  under the same initial conditions as in Figure 1; (b) Same as Figure 2(a), but in a magnified form.
under the same initial conditions as in Figure 1; (b) Same as Figure 2(a), but in a magnified form.
normalized coupling constants for the gravito-thermal coupling for the SIP electrons, gravito-thermal coupling for the SIP ions and gravito-acoustic coupling for the SIP ions.
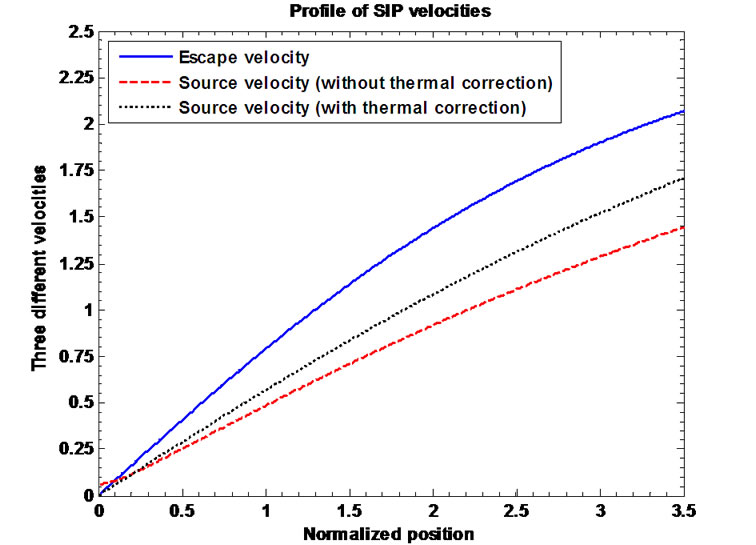
Lastly, Figures 9(a)-(c) depict the profiles of the normalized escape velocity needed for the ions to cross over the gravitational wall. They also depict the electric field induced velocities’ (source velocities) profiles without and with thermal correction for the inertial ions. Simi-
 (a)
(a) (b)
(b)
Figure 3. (a) Variation of the normalized values of Mach number  (solid blue line), Mach number gradient
(solid blue line), Mach number gradient  (red dashed line) and Mach number scale length
(red dashed line) and Mach number scale length
 (black dotted line) associated with the SIP flow dynamics with normalized position
(black dotted line) associated with the SIP flow dynamics with normalized position 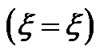 from the heliocentre
from the heliocentre 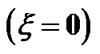 under the same initial conditions as in Figure 1; (b) Same as Figure 3(a) but in a magnified form.
under the same initial conditions as in Figure 1; (b) Same as Figure 3(a) but in a magnified form.
larly, as before, Figures 9(b) and (c) show the enlarged and more enlarged views of Figure 9(a) near the Heliocentre, respectively. This is now observed that 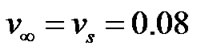 at
at 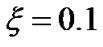 and
and 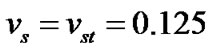 at
at 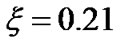 showing the intersecting dynamics near the heliocentre. This is to note that the bulk SIP leaks through the self-gravitational wall by plasma-boundary interaction and finally emerges out in the form of the
showing the intersecting dynamics near the heliocentre. This is to note that the bulk SIP leaks through the self-gravitational wall by plasma-boundary interaction and finally emerges out in the form of the
 (a)
(a)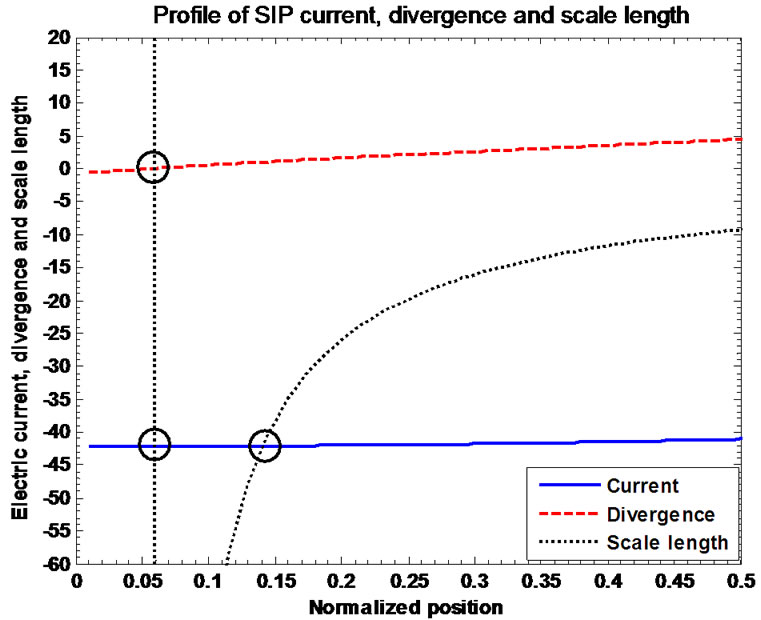 (b)
(b)
Figure 4. (a) Variation of the normalized values of electric current density 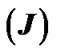 (solid blue line), divergence of current density
(solid blue line), divergence of current density 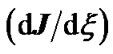 (red dashed line) and current density scale length
(red dashed line) and current density scale length  (black dotted line)
(black dotted line)
associated with the SIP flow dynamics with normalized position  from the heliocentre
from the heliocentre  under the same initial conditions as in Figure 1; (b) Same as Figure 4(a), but in a magnified form.
under the same initial conditions as in Figure 1; (b) Same as Figure 4(a), but in a magnified form.
subsonic SWP at the SSB due to gravitational squeezing of the electron flux as discussed earlier.
4.2. Numerical Results for Unbounded SWP
Similar to the bounded SIP analyses, here too, we simulate the coupled dynamical evolution Equations (23)-(35) on the SWP scale with the numerically pre-obtained initial values as shown in Table 1. Figures 10-16 describe
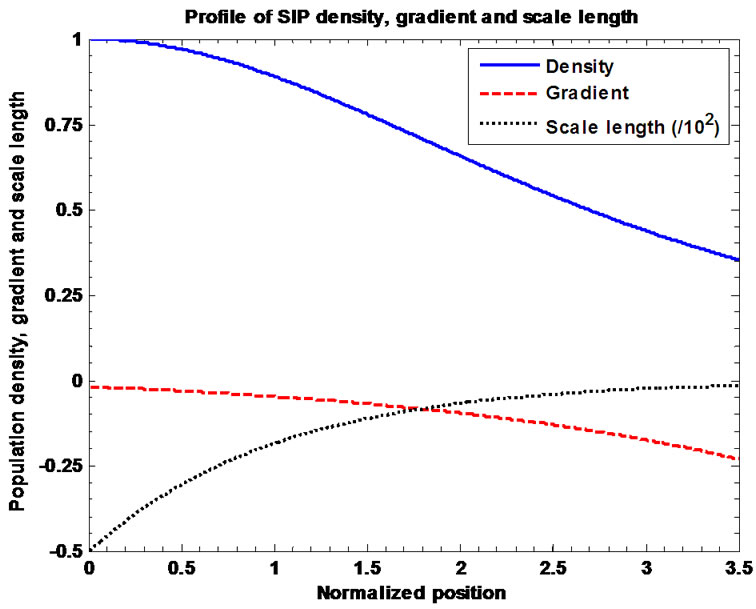
Figure 5. Variation of the normalized values of population density 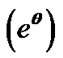 (solid blue line), density gradient
(solid blue line), density gradient 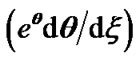 (red dashed line) and density scale length
(red dashed line) and density scale length 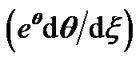
 (black dotted line) associated with the SIP flow dynamics with normalized position
(black dotted line) associated with the SIP flow dynamics with normalized position  from the heliocentre
from the heliocentre  under the same initial conditions as in Figure 1.
under the same initial conditions as in Figure 1.
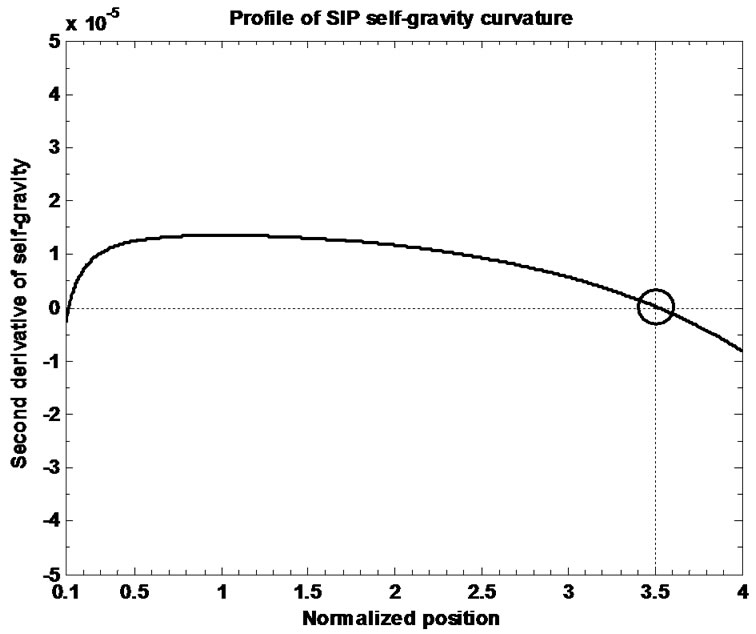
Figure 6. Variation of the normalized value of the second derivative of self-gravity  (solid black line) associated with the SIP flow dynamics with normalized position
(solid black line) associated with the SIP flow dynamics with normalized position  from the heliocentre
from the heliocentre  under the same initial conditions as in Figure 1.
under the same initial conditions as in Figure 1.
the profile structures of the SWP equilibrium in terms of the proposed GES plasma parameters. The predetermined values of the physical variables for the SSB, viz.,  ,
,  ,
,  ,
, 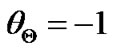 , and
, and 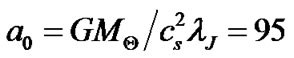 are kept fixed throughout. Figures 10(a) and (b) depict the equilibrium profiles of the normalized electrostatic potential, its gradient (scaled up
are kept fixed throughout. Figures 10(a) and (b) depict the equilibrium profiles of the normalized electrostatic potential, its gradient (scaled up

Figure 7. Variation of the normalized values of electron oscillation time scale 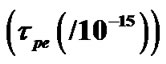 (blue solid line), ion oscillation time scale
(blue solid line), ion oscillation time scale 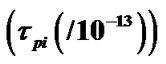 (red dashed line) and Jeans time scale
(red dashed line) and Jeans time scale 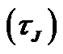 (black dotted line) associated with the SIP flow dynamics with normalized position
(black dotted line) associated with the SIP flow dynamics with normalized position 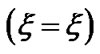 from the heliocentre
from the heliocentre 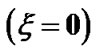 under the same initial conditions as in Figure 1.
under the same initial conditions as in Figure 1.

Figure 8. Variation of the normalized values gravitothermal coupling coefficient for electrons 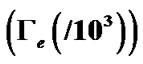 (blue solid line), gravito-thermal coupling coefficient for ions (
(blue solid line), gravito-thermal coupling coefficient for ions ( ) (red dashed line) and gravito-acoustic coupling coefficient for ions
) (red dashed line) and gravito-acoustic coupling coefficient for ions  (black dotted line) associated with the SIP flow dynamics with normalized position
(black dotted line) associated with the SIP flow dynamics with normalized position  from the heliocentre
from the heliocentre  under the same initial conditions as in Figure 1.
under the same initial conditions as in Figure 1.
by multiplication with 10) and scale length (scaled down by division with ) associated with the GES on the SWP scale. Figure 10(b) shows the same plot as shown in Figure 10(b), but in a magnified form.
) associated with the GES on the SWP scale. Figure 10(b) shows the same plot as shown in Figure 10(b), but in a magnified form.
 (a)
(a)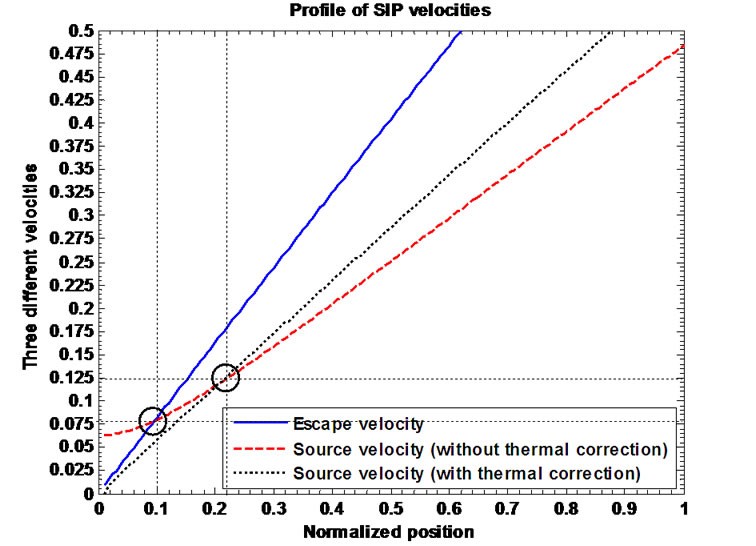 (b)
(b)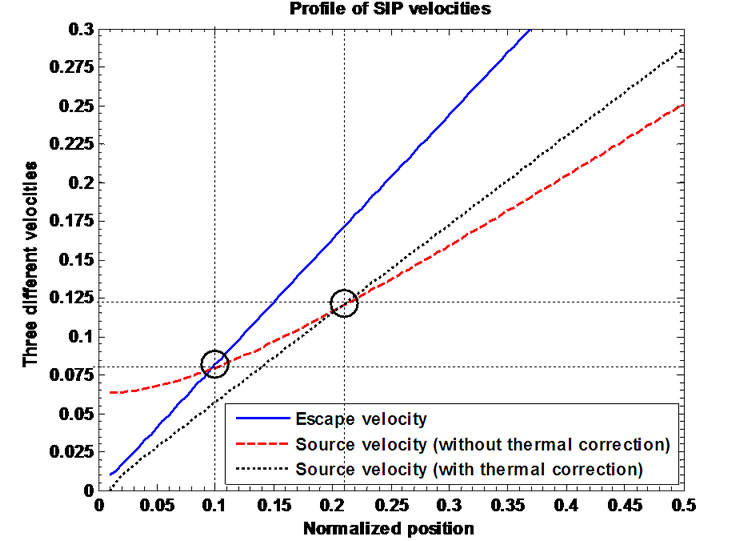 (c)
(c)
Figure 9. (a) Variation of the normalized values of escape velocity of ions 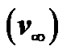 (blue solid line), source velocity without thermal correction of ions
(blue solid line), source velocity without thermal correction of ions 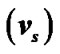 (red dashed line) and source velocity with thermal correction of ions
(red dashed line) and source velocity with thermal correction of ions 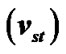 (black dotted line) associated with the SIP flow dynamics with normalized position
(black dotted line) associated with the SIP flow dynamics with normalized position  from the heliocentre
from the heliocentre  under the same initial conditions as in Figure 1; (b) Same as Figure 9(b), but in a magnified form; (c) Same as Figure 9(a), but in a more magnified form.
under the same initial conditions as in Figure 1; (b) Same as Figure 9(b), but in a magnified form; (c) Same as Figure 9(a), but in a more magnified form.
 (a)
(a) (b)
(b)
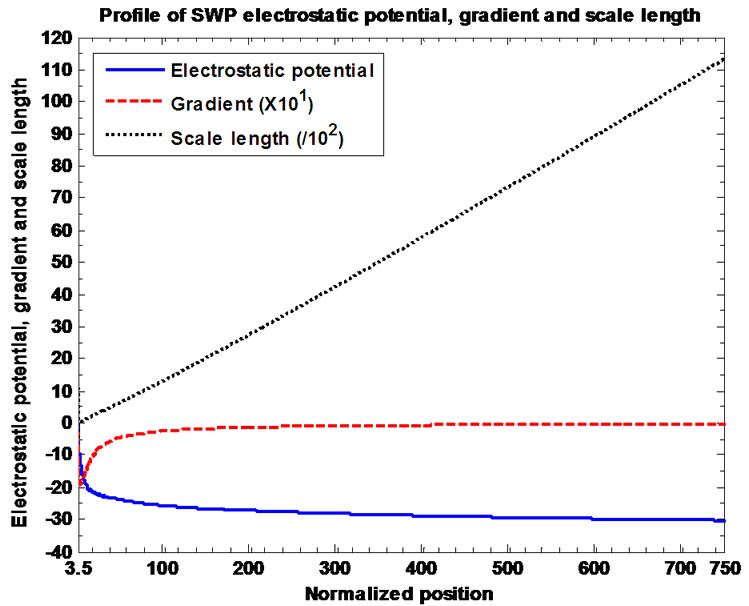
Figure 10. (a) Variation of the normalized values of electrostatic potential  (solid blue line), potential gradient
(solid blue line), potential gradient  (red dashed line) and potential scale length
(red dashed line) and potential scale length  (black dotted line) associated with the SWP flow dynamics with normalized position
(black dotted line) associated with the SWP flow dynamics with normalized position 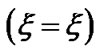 from the SSB
from the SSB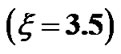 . The predetermined SSB parameter values
. The predetermined SSB parameter values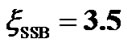 ,
,  ,
,  ,
, 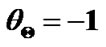 , and
, and  are kept fixed; (b) Same as Figure 10(a), but in a magnified form.
are kept fixed; (b) Same as Figure 10(a), but in a magnified form.
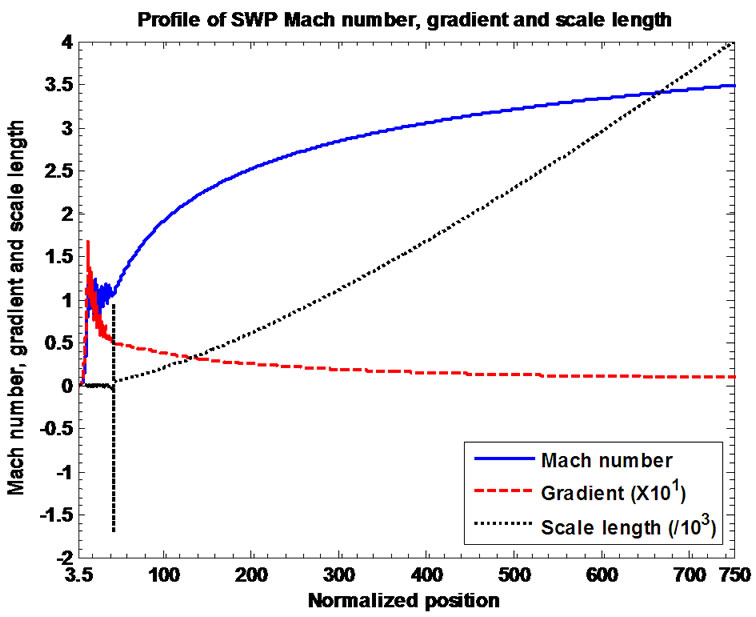
Figures 11(a) and (b) depict the equilibrium profile structures of the SWP Mach number, gradient (scaled up by multiplication with 10) and scale length (scaled down by division with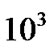 ). This is clear from Figure 11(b) that in the entire sonic zone,
). This is clear from Figure 11(b) that in the entire sonic zone, 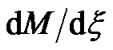 decreases with
decreases with 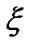 asymptotically. This can be justified by the binomial simplification of the L.H.S. of Equation (24) near the singular sonic point as defined by
asymptotically. This can be justified by the binomial simplification of the L.H.S. of Equation (24) near the singular sonic point as defined by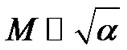 . Under the condition
. Under the condition , we reduce equation (24) to
, we reduce equation (24) to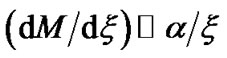 . This immediately implies
. This immediately implies
 (a)
(a)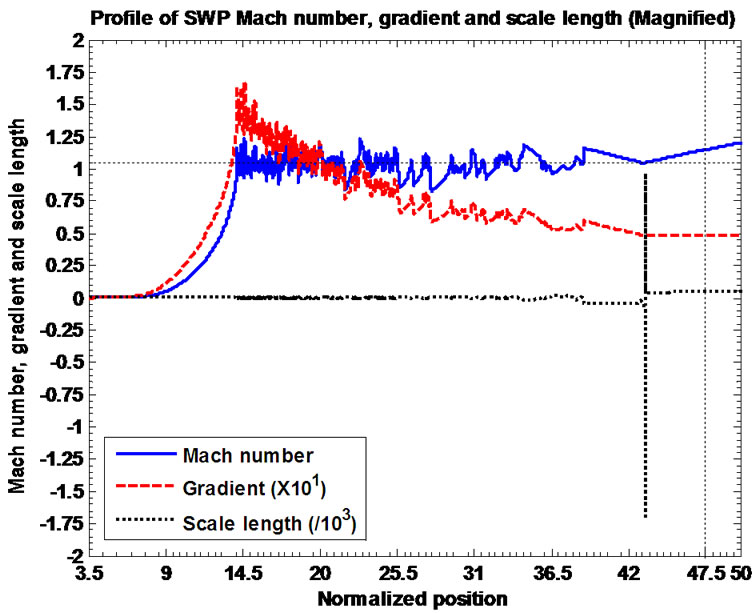 (b)
(b)
Figure 11. (a) Variation of the normalized values of Mach number 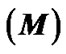 (solid blue line), Mach number gradient
(solid blue line), Mach number gradient  (red dashed line) and Mach number scale length
(red dashed line) and Mach number scale length 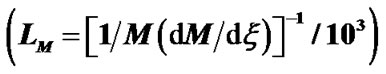 (black dotted line) associated with the SWP flow dynamics with normalized position
(black dotted line) associated with the SWP flow dynamics with normalized position  from the SSB
from the SSB 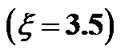 under the same initial conditions as in Figure 10(a); (b) Same as Figure 11(a), but in a magnified form.
under the same initial conditions as in Figure 10(a); (b) Same as Figure 11(a), but in a magnified form.
that the supersonic/ hypersonic unbounded SWP outflow is the outcome of the curvature (geometrical) effect of the spherically bounded subsonic SIP mass distribution. Figure 11(b) shows the same plot as shown in Figure 11(a), but in a magnified form depicting the vivid picture of the sonic zone associated and followed with the onset of the supersonic/ hypersonic SWP flow dynamics.
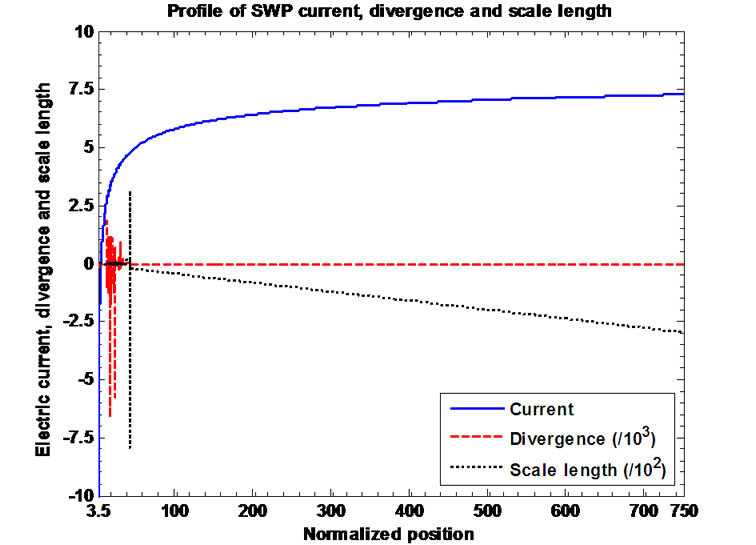
Figures 12(a)-(c) describe the profile structure of the normalized SWP current, divergence (scaled down by division with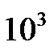 ) and scale length (scaled down by
) and scale length (scaled down by
 (a)
(a)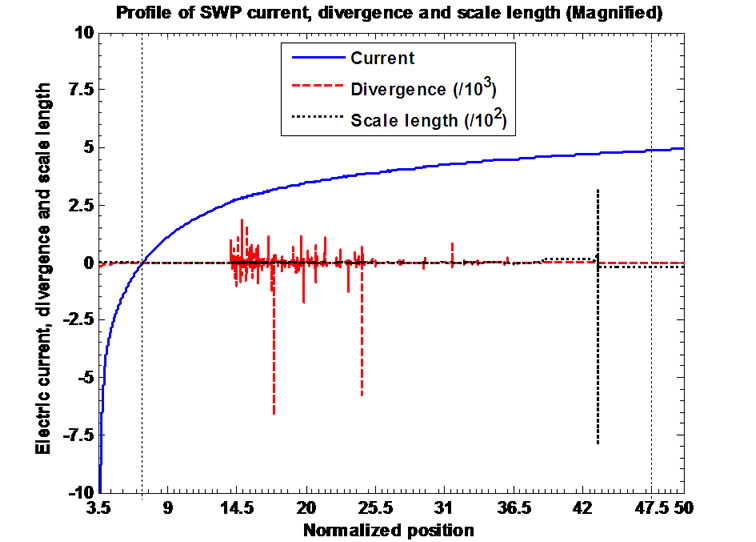 (b)
(b)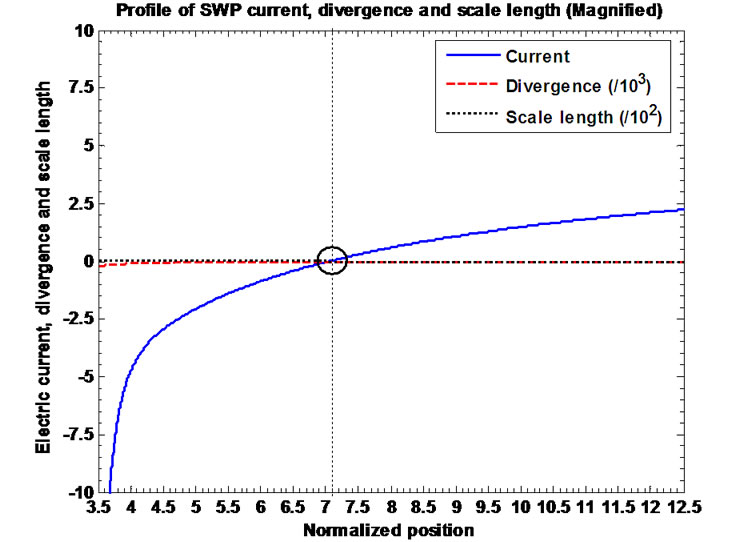 (c)
(c)
Figure 12. (a) Variation of the normalized values of electric current density  (solid blue line), divergence of current density
(solid blue line), divergence of current density 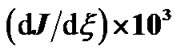 (red dashed line) and current density scale length
(red dashed line) and current density scale length 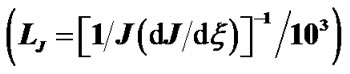 (black dotted line) associated with the SWP flow dynamics with normalized position
(black dotted line) associated with the SWP flow dynamics with normalized position 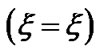 from the SSB
from the SSB 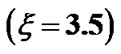 under the same initial conditions as in Figure 10(a); (b) Same as Figure 12(a), but in a magnified form; (c) Same as Figure 12(a), but in a more magnified form.
under the same initial conditions as in Figure 10(a); (b) Same as Figure 12(a), but in a magnified form; (c) Same as Figure 12(a), but in a more magnified form.
division with ). Figure 12(b) shows the same plot as shown in Figure 12(a), but in a magnified form. Furthermore, Figure 12(c) depicts the same plot as shown in Figure 12(a), but in a more magnified form describeing the characteristics of the floating conditions. This is found from Figure 12(c) that the floating condition
). Figure 12(b) shows the same plot as shown in Figure 12(a), but in a magnified form. Furthermore, Figure 12(c) depicts the same plot as shown in Figure 12(a), but in a more magnified form describeing the characteristics of the floating conditions. This is found from Figure 12(c) that the floating condition  exists at
exists at , and the corresponding floating potential from Figure 10b is numerically found to be
, and the corresponding floating potential from Figure 10b is numerically found to be . The spherical floating surface around the heliocentre is thus characterized with radius
. The spherical floating surface around the heliocentre is thus characterized with radius  (on Jeans length) and biasing voltage
(on Jeans length) and biasing voltage 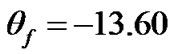 (on electron thermal potential). But analytically, as in our earlier work [11], the floating potential at
(on electron thermal potential). But analytically, as in our earlier work [11], the floating potential at 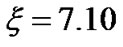 is estimated to be
is estimated to be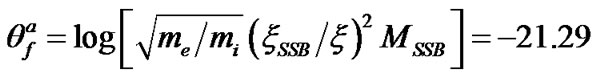 . Thus there is a floating potential deviation by about
. Thus there is a floating potential deviation by about  over the calculated value, which seems to be over estimated. This is due to ion thermal contribution taken into account here to model the SWP, which was neglected earlier. It is however found that the divergence of the SWP current remains zero over the entire unbounded scale.
over the calculated value, which seems to be over estimated. This is due to ion thermal contribution taken into account here to model the SWP, which was neglected earlier. It is however found that the divergence of the SWP current remains zero over the entire unbounded scale.
Figure 13 contains the profile of the normalized SWP density (scaled up by division with ), gradient (scaled up by division with
), gradient (scaled up by division with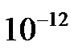 ) and scale length. Figure 14 contains the profile structures of the normalized time scales for the SWP electron oscillations (scaled up by division with
) and scale length. Figure 14 contains the profile structures of the normalized time scales for the SWP electron oscillations (scaled up by division with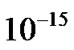 ), SWP ion oscillation (scaled up by division with
), SWP ion oscillation (scaled up by division with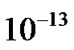 ) and Jeans collapse. It is clear to note immediately that the Jeans time scale is quite large
) and Jeans collapse. It is clear to note immediately that the Jeans time scale is quite large
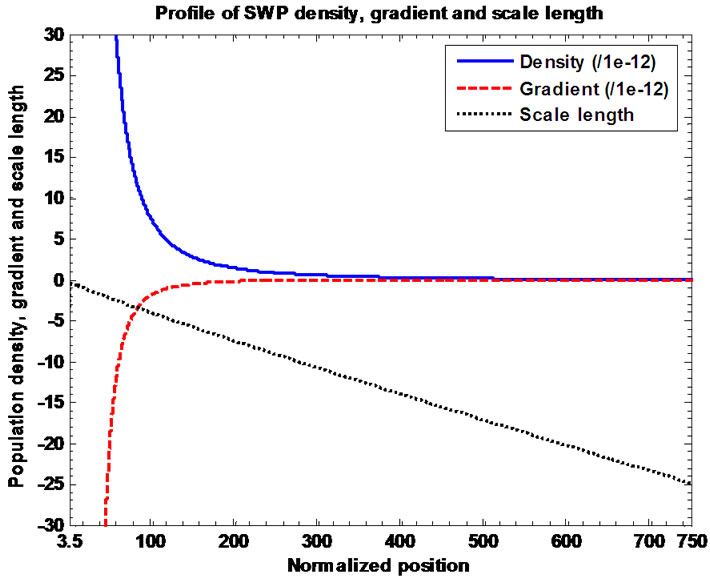
Figure 13. Variation of the normalized values of population density 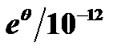 (solid blue line), density gradient
(solid blue line), density gradient 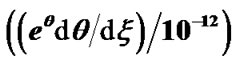 (red dashed line) and density scale length
(red dashed line) and density scale length 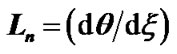 (black dotted line) associated with the SWP flow dynamics with normalized position
(black dotted line) associated with the SWP flow dynamics with normalized position 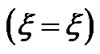 from the SSB
from the SSB 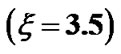 under the same initial conditions as in Figure 10(a).
under the same initial conditions as in Figure 10(a).
by several orders of magnitude relative to each of the rest on the unbounded SWP scale too. Figure 15 contains the plots of the normalized coupling constants of the gravitothermal coupling for the SWP electrons (scaled down by
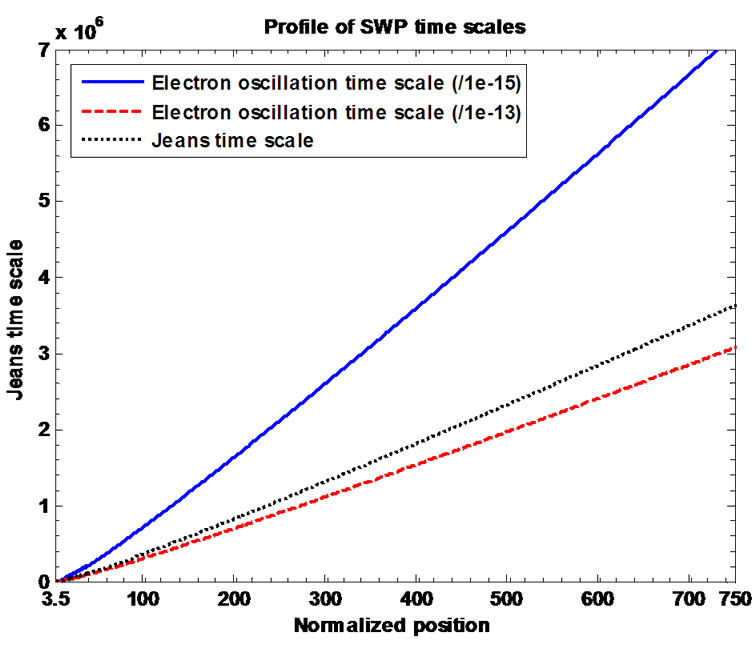
Figure 14. Variation of the normalized values of electron oscillation time scale 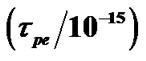 (blue solid line), ion oscillation time scale
(blue solid line), ion oscillation time scale 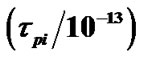 (red dashed line) and Jeans time scale
(red dashed line) and Jeans time scale  (black dotted line) associated with the SWP flow dynamics with normalized position
(black dotted line) associated with the SWP flow dynamics with normalized position  from the SSB
from the SSB  under the same initial conditions as in Figure 10(a).
under the same initial conditions as in Figure 10(a).

Figure 15. Variation of the normalized values of gravitothermal coupling coefficient for electrons  (blue solid line), gravito-thermal coupling coefficient for ions
(blue solid line), gravito-thermal coupling coefficient for ions 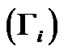 (red dashed line) and gravito-acoustic coupling coefficient for ions
(red dashed line) and gravito-acoustic coupling coefficient for ions 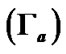 (black dotted line) associated with the SWP flow dynamics with normalized position
(black dotted line) associated with the SWP flow dynamics with normalized position 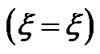 from the SSB
from the SSB  under the same initial conditions as in Figure 10(a).
under the same initial conditions as in Figure 10(a).
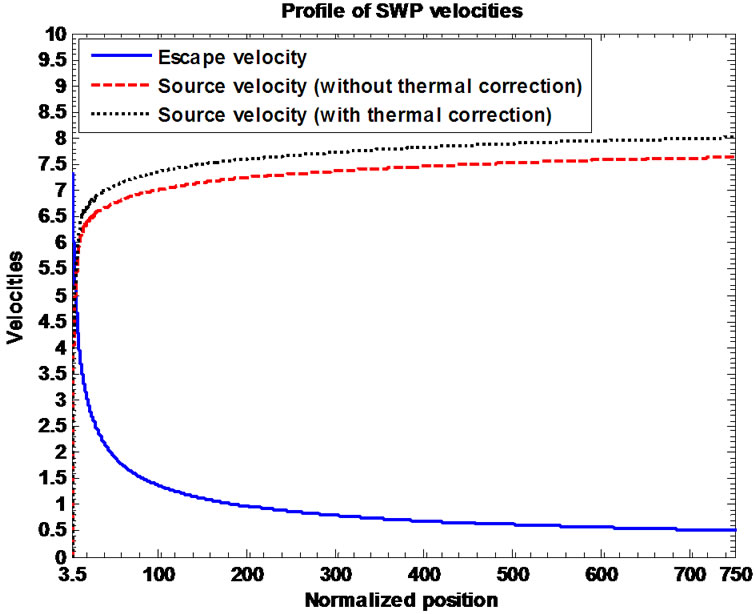
division with ), gravito-thermal coupling for the SWP ions and gravito-acoustic coupling for the SWP ions. Figures 16(a) and (b) depict the profile structures of the normalized escape velocity needed for the SWP ions to cross over the barrier of the solar external gravity, electric field induced source velocities with and without thermal corrections for the SWP ions. Lastly, Figure 16(b) shows the same plot as shown in Figure 16(a), but in a magnified form to speculate the hidden portion thereof. This is observed that
), gravito-thermal coupling for the SWP ions and gravito-acoustic coupling for the SWP ions. Figures 16(a) and (b) depict the profile structures of the normalized escape velocity needed for the SWP ions to cross over the barrier of the solar external gravity, electric field induced source velocities with and without thermal corrections for the SWP ions. Lastly, Figure 16(b) shows the same plot as shown in Figure 16(a), but in a magnified form to speculate the hidden portion thereof. This is observed that  at
at
 (a)
(a)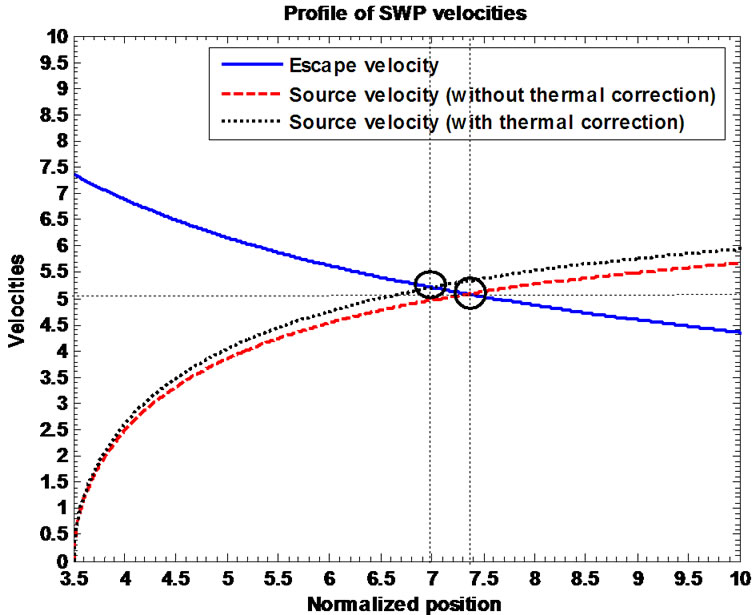 (b)
(b)
Figure 16. (a) Variation of the normalized values of escape velocity of ions  (blue solid line), source velocity without thermal correction of ions
(blue solid line), source velocity without thermal correction of ions  (red dashed line) and source velocity without thermal correction of ions
(red dashed line) and source velocity without thermal correction of ions 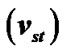 (black dotted line) associated with the SWP flow dynamics with normalized position
(black dotted line) associated with the SWP flow dynamics with normalized position  from the SSB
from the SSB 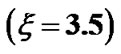 under the same initial conditions as in Figure 10(a); (b) Same as Figure 16(a), but in a magnified form.
under the same initial conditions as in Figure 10(a); (b) Same as Figure 16(a), but in a magnified form.
 and
and 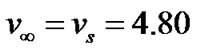 at
at 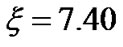 showing the intersecting dynamics beyond the SSB. From Figures 12(c) and 16(b), one can interestingly notice that the floating condition of net zero electric current is satisfied at the radial point (relative to the heliocentre) where the SWP ions are considerably energized enough to escape the gravitational barrier of the solar external gravity.
showing the intersecting dynamics beyond the SSB. From Figures 12(c) and 16(b), one can interestingly notice that the floating condition of net zero electric current is satisfied at the radial point (relative to the heliocentre) where the SWP ions are considerably energized enough to escape the gravitational barrier of the solar external gravity.
4.3. Comparative Results
Theoretical and numerical analyses are carried out in detail to describe the properties of the GES equilibrium structure. It is interestingly found that the GES equilibrium structure is of inhomogeneous nature. One finds variable local gradients and scale lengths of different physical variables associated with it. The details of the GES equilibrium are highly needed for normal mode analyses of the fluctuations on both the bounded and unbounded scales of the solar plasma system. The quantitative estimation of the solar current provides a good scope for the characterization of a field-free quasi-neutral self-gravitating plasma in a quasi-hydrostatic type of global equilibrium configuration. Although quite idealized, simplified and unmagnetized, the GES-based physical model for solar plasma may offer a new scope for understanding the basic physics of the inter-connected interplay between the SIP and SWP, and their coupled dynamics.
Applying the spherical capacitor charging model, the coulomb charge on the SWP at a distance of ~1 AU comes out to be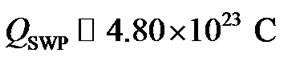 . For rotation frequency of the solar plasma system corresponding to the mean angular frequency about the centre of the system
. For rotation frequency of the solar plasma system corresponding to the mean angular frequency about the centre of the system 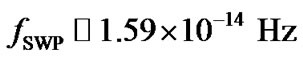 [9], the mean value of the strength of the solar magnetic field associated with the SWP in our model analysis is estimated as
[9], the mean value of the strength of the solar magnetic field associated with the SWP in our model analysis is estimated as  . This is obviously considerably higher for producing any significant effects on the dynamics of the SWP particles. Thus the effects of the magnetic field are not ignorable for the SWP particles dynamics due to the significantly strong Lorentz force, which is now estimated to be
. This is obviously considerably higher for producing any significant effects on the dynamics of the SWP particles. Thus the effects of the magnetic field are not ignorable for the SWP particles dynamics due to the significantly strong Lorentz force, which is now estimated to be 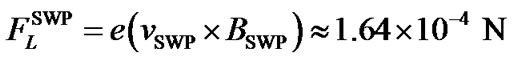 corresponding to a supersonic flow speed
corresponding to a supersonic flow speed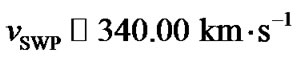 . Thus the Lorentz force may have some remarkable effects on the SWP particles as compared to that for the SIP particles for
. Thus the Lorentz force may have some remarkable effects on the SWP particles as compared to that for the SIP particles for  and hence, may not justifiably neglected for the unbounded SWP scale description. It justifies the convective and circulation dynamics to be considered in that context. Therefore our unmagnetized plasma approximation may not prove well justified in our GES model configuration for the SWP flow dynamics description.
and hence, may not justifiably neglected for the unbounded SWP scale description. It justifies the convective and circulation dynamics to be considered in that context. Therefore our unmagnetized plasma approximation may not prove well justified in our GES model configuration for the SWP flow dynamics description.
Although collision processes are dominant in the realistic solar interior [26-28], collisionless models [18,30] are also equally useful for the solar plasma description. Thus our collisionless model approximation for mathematical simplicity may be justified here. In our GES model, the calculated values of the mean free paths for the solar plasma electrons,  and for ions,
and for ions,  justify the collisionless model approximation on the bounded SIP scale calculation scheme. This approximation holds good justifiably under the fulfillment of the validity condition
justify the collisionless model approximation on the bounded SIP scale calculation scheme. This approximation holds good justifiably under the fulfillment of the validity condition 
From our model calculations, it is clear that high electric current flows on both the bounded and unbounded scales. The occurrence of current reversal indicates the existence of a virtual floating surface with net zero current (where electrons and ions driven electric currents are balanced). Tables 4 and 5 give a glimpse of scale lengths for solar self-gravity, electrostatic potential and ion flow associated with the GES equilibrium at some well defined locations of the heliocentre, the SSB and at a distance of 1.00 AU . The various normalized inhomogeneity scale lengths of the relevant SIP parameters of physical interest thus numerically obtained as already discussed above, are summarized and shown in Table 2 as follows.
. The various normalized inhomogeneity scale lengths of the relevant SIP parameters of physical interest thus numerically obtained as already discussed above, are summarized and shown in Table 2 as follows.
The various normalized inhomogeneity scale lengths of the relevant SWP parameters of astrophysical interest obtained similarly as already mentioned above, are shown in Table 3 as follows.

Table 2. Inhomogeneity scale lengths of relevant SIP parameters.

Table 3. Inhomogeneity scale lengths of relevant SWP parameters.
The main distinctions between laboratory plasma sheath, i.e., Debye plasma sheath (DPS) and gravitoelectrostatic sheath (GES) are tabulated in Table 4" target="_self"> Table 4 as shown below. Of course, although both are formed by a common origin of plasma-wall interaction processes as already mentioned earlier, they indeed differ a lot in their characteristics.
The obtained results and equilibrium plasma properties, of course, may be found to have some experimental support as well, although qualitatively, in accordance with the observation by the Solar and Heliospheric Observatory (SOHO) spacecraft [1-20]. For an example, the inhomogeneous nature of the solar plasma equilibrium has already been in situ observed [1-2] and hence, we may apply nonlocal formalism [22,23] for solar fluctuation analyses in future. The main features of our dynamical observations based on our numerical analyses may further be discussed as follows. Although pointed out above, the main distinctive comparisons between the standard solar model (SSM) and gravito-electrostatic sheath (GES) model are now explored, summarized and tabulated in Table 5 as follows. It is clear here that the SSM and GES are quite different in terms of their basic physics and model approaches. The former deals with a neutral fluid treatment, whereas the latter, an idealistic plasma-based fluid model. Thus the disparity in the different set of the characteristic values obtained by them, we must admit at

Table 4. Distinctions between DPS and GES.
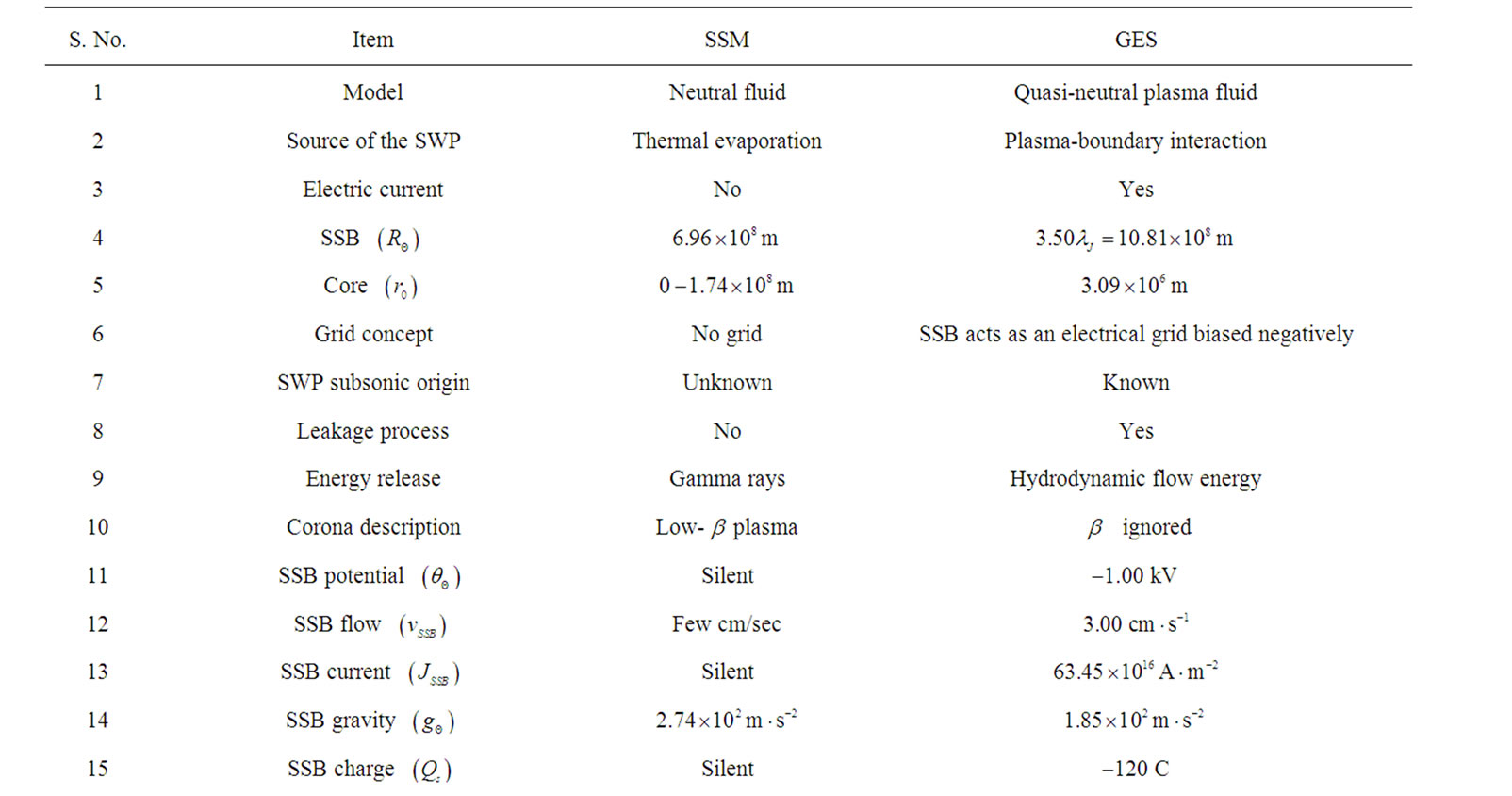

Table 5. Standard solar model (SSM) versus gravito-electrostatic sheath (GES) model.
the outset, may be somewhat different due to the attributed difference in the primary approaches with the plasma boundary interaction processes involved for precisely locating and describing the SSB in the latter.
In fact the ideas of electric field effect and of the electromagnetic state of the Sun, like stars and their atmospheres were already introduced empirically by S. Rosseland, R. Gunn and R. G. Athay et al. [8,9,26] in the past. Let us term their models collectively as the electrical solar model (ESM). The separation of electrical charge inside the Sun has been understood with the help of ionization and diffusion processes [7,27]. The solar dynamo mechanism with rotational dynamics taken into account to yield electrical energy is, however, an interesting area to be investigated more [26-31] and excluded for the present. The electrical model, however, has not pointed out anything on the gravito-acoustic coupling, plasma-boundary wall interaction processes and governing basic physical insights. As already mentioned above, the basic charge separation mechanism inside the Sun according to the GES model is the plasma-boundary interaction processes. The relevant solar parameters of electromagnetic significance are calculated under the light of the GES model at different radial points and compared with those obtained by applying the ESM.
These important results on the solar (or, some other like stellar objects) electromagnetic parameterization in our simplified model approach are obtained in detail to understand the associated electromagnetic characteristics. These are summarized, compared and tabulated in Table 6 as follows.
This is important to note that a wide range discrepancy exists in the numerical values of the electromagnetic characteristics of the Sun as estimated by us and by others [9]. This is also found that the solar surface charge calculated by us matches with that the Pannekoek model [7] as mentioned in the paper by Gunn [9] within a factor of magnitude 3. A wide range disparity noticed in other electromagnetic properties may be due to exact theoretical calculations by us (in the presence of gravito-electrostatic interaction process) and empirical formulations
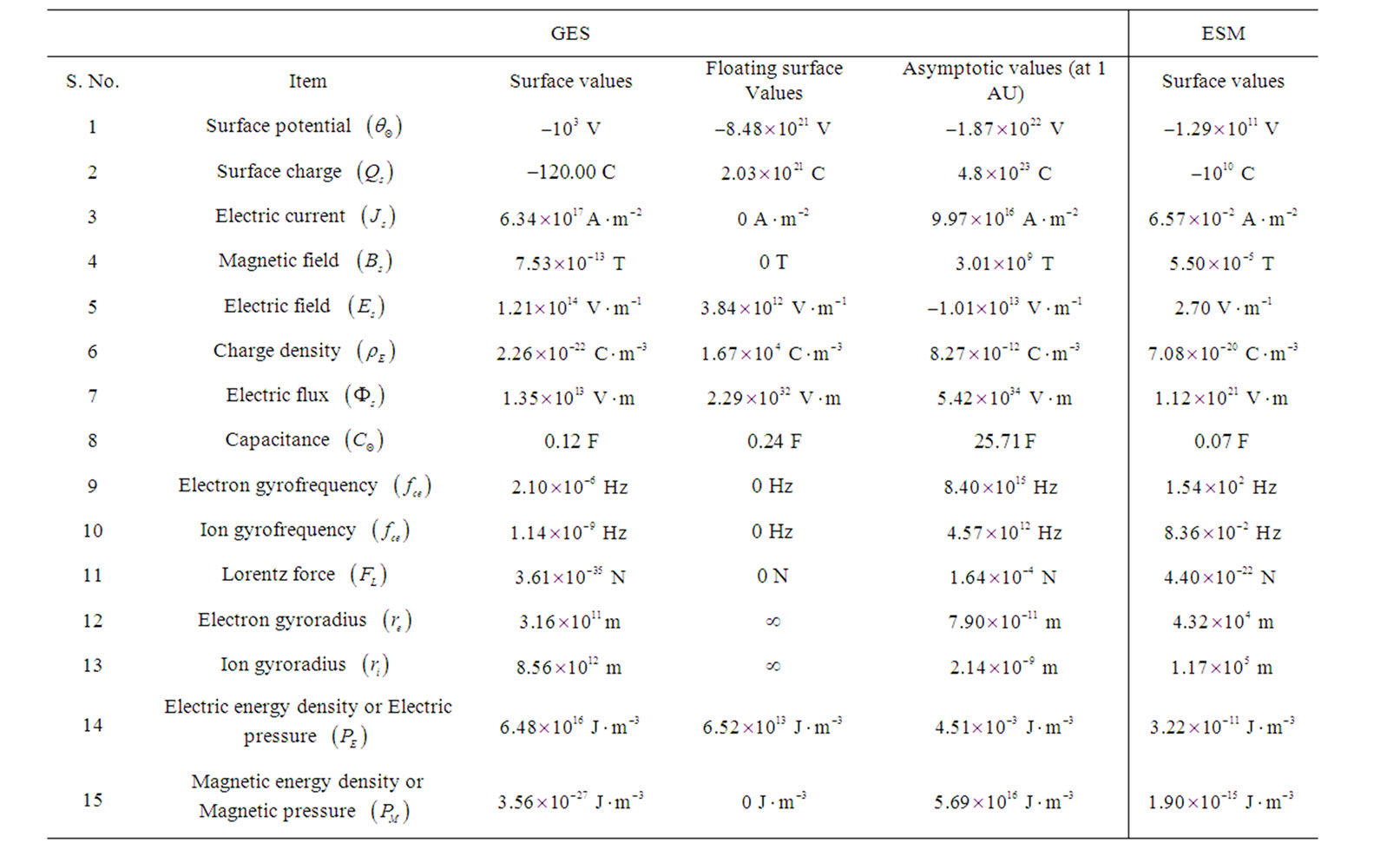
Table 6. Gravito-electrostatic sheath (GES) model versus electrical solar model (ESM).
by others (in the absence of any boundary interaction effect). This, however, is an open question to be resolved in future in the light of more and more observations on the solar plasma system.
5. Conclusions
A detailed qualitative, quantitative and comparative study of the solar plasma equilibrium structure and associated relevant physical parameters under our GES model is carried out to describe the distinct structural features of the solar interior, exterior and its coupled atmosphere relative to other solar models. A relative idea of the plasma and Jeans time scales is given so as to identify and describe the dominant role of solar plasma wave, instability and oscillation dynamics. Quantitative characterizations of the different possible coupling coefficients are also presented to identify the dominant bulk forces that are active on the SIP and SWP scales. This piece of research work forms an initial elementary input about the solar plasma equilibrium structure and associated various characteristics, which is an essential building block for the investigative study of the self-gravitating (solar) plasma oscillations, waves and instabilities in more realistic astrophysical situations.
Numerical analyses of the solar plasma equilibrium on bounded and unbounded scales reveal a unique result of finite non-zero electric current generation that flows through the boundary wall. Beyond the SSB, a new feature of electric current reversal occurs. Moreover, we find that on the SIP scale, a negative electron current dominates which is not divergence free. This poses a problem of the electromagnetic Maxwell equations to be satisfied until and unless a non-divergent sink term is proposed to exist. On the SWP scale, ion dominated current flows, which is divergence free. Thus the SWP offers an example of unmagnetized ion current carrying plasma with supersonic flow motion without any substantial electric field, source, collisions etc. Our theoretical model of the GES provides physical explanation for the solar interior origin of the subsonic SWP and its acceleration up to the supersonic/hypersonic velocity. It seems that the SIP leaks through the solar self-gravitational potential wall continuously and emerges out of the SSB in the form of the natural high-speed SWP.
The solar plasma density profiles obtained from our GES calculations do not match with the observed values [15-21]. This could be attributed to omitting the actual temperature profiles of the solar plasma. Hence a proper inclusion of temperature profile through an appropriate heat transport equation requires an additional improvement of the GES theory to make it more realistic, useful, and practical. One can infer that the solar plasma near the heliocentre is in a near zero-gravity condition, and hence it escapes and leaks through the solar self-gravitational potential boundary layer of variable strength. Solar plasma oscillation time scales are found to be smaller than the Jeans time scale by many orders of magnitude. This compels to speculate that a wide range of gravitoelectrostatic fluctuation modes are more likely to describe the solar plasma wave and oscillation dynamics. The frequencies of these modes are supposed to be ranging from pure Jeans mode (larger wavelength) to pure plasma sound mode (shorter wavelength). The non-uniformity of the GES equilibrium profiles indicates the presence of some natural sources and sinks to excite or suppress these modes of waves and oscillations.
The two-scale structure of the GES equilibrium for the Sun and its atmosphere is found to give a two-scale dynamical coupling system of the GES waves and oscillations. The surface modes on the SSB are likely to provide coupling in between the bulk modes of the SIP and SWP. The future course of our work on the GES theory is to study the natural normal mode properties of the coupled GES-induced waves and oscillations. The mathematical method adopted here may be applicable to other similar types of gravitational plasma characterization under both equilibrium and fluctuation model approaches [26-31]. The two-layer theory of the GES model may give a more suitable physical picture to understand the equilibrium structure of the Sun and its atmosphere.
In brief, we can argue that our present calculation gives quantitative estimations of the GES-associated equilibrium parameters. Under our GES model calculations, we find that the Sun is surrounded by a virtual floating spherical boundary at about a distance of seven times Jeans length apart from the SSB. This is the entrance point of the SWP acceleration zone, which extends up to a distance of 14.5 times Jeans length apart from the SSB. It is followed with sonic (from 14.5 up to about 43 times Jeans length) and supersonic (extending from 43 times Jeans length up to 1 AU, and beyond to infinity) zones. Our model could further be useful as an important element to offer new perspectives in the study of the properties of the helioseismic and asteroseismic dynamics of the Sun and other stars extensively from plasma-based framework [17-20].
6. Acknowledgements
The valuable comments, specific remarks and precise suggestions by an anonymous referee, to refine the prerevised original manuscript into the present post-revised improved form, are very gratefully acknowledged. Moreover, authors appreciatively acknowledge the support, help and cooperation received during academic visits from Dr. Manohar Lal, Associate Professor, Dr. K. S. Krishnan Geomagnetic Research Laboratory (KSKGRL), Indian Institute of Geomagnetism, Leelapur Road, Near Chamanganj (Jhunsi), Hanumanganj, Allahabad-221505, U. P. (Bharat). Last but not least, the investigative support from the Department of Science and Technology (DST) of New Delhi, Bharat Sarkar, extended to PKK through the SERC Fast Track Project (Grant No. SR/FTP/PS-021/2011) is also thankfully recognized for carrying out this small piece of exploration.
7. References
[1] J. Christensen-Dalsgaard, “Helioseismology,” Reviews of Modern Physics, Vol. 74, No. 4, 2002, pp. 1073-1129. doi:10.1103/RevModPhys.74.1073
[2] S. R. Cranmer, “Coronal Holes and the High-Speed Solar Wind,” Space Science Reviews, Vol. 101, No. 3-4, 2002, pp. 229-294. doi:10.1023/A:1020840004535
[3] J. W. Chamberlain, “Interplanetary Gas. II. Expansion of a Model Solar Corona,” Astrophysical Journal, Vol. 131, 1960, pp. 47-56. doi:10.1086/146805
[4] J. W. Chamberlain, “Interplanetary Gas. III. A Hydrodynamic Model of the Corona,” Astrophysical Journal, Vol. 133, 1961, pp. 675-687. doi:10.1086/147070
[5] J. Lemaire and V. Pierrard, “Kinetic Models of Solar and Polar Winds,” Astrophysics and Space Science, Vol. 277, No. 1-2, 2001, pp. 169-180. doi:10.1023/A:1012245909542
[6] R. Dendy, “Plasma Physics: An Introductory Cours,” Cambridge University Press, Cambridge, 1993, pp. 267-289.
[7] A. Pannekoek, “Ionization in Stellar Atmospheres,” Bulletin of the Astronomical Institutes of the Netherlands, Vol. 1, No. 19, 1922, pp. 107-118.
[8] S. Rosseland, “Electrical state of a Star,” Monthly Notices of the Royal Astronomical Society, Vol. 84, No. 308, 1924, pp. 720-728.
[9] R. Gunn, “The Electrical State of the Sun,” Physical Review, Vol. 37, No. 8, 1931, pp. 983-989. doi:10.1103/PhysRev.37.983
[10] G. E. Hale and H. D. Babcock, “An Attempt to Measure the Free Electricity in the Sun’s Atmosphere,” Proceedings of the National Academy of Sciences (USA), Vol. 1, No. 3, 1915, pp. 123-127. doi:10.1073/pnas.1.3.123
[11] C. B. Dwivedi, P. K. Karmakar and S. C. Tripathy, “A Gravito-Electrostatic Sheath Model for Surface Origin of Subsonic Solar Wind Plasma,” Astrophysical Journal, Vol. 663, No. 2, 2007, pp. 1340-1353. doi:10.1086/511409
[12] I. Langmuir, “Oscillations in Ionized Gases,” Proceedings of the National Academy of Sciences (USA), Vol. 14, No. 8, 1928, pp. 627-637. doi:10.1073/pnas.14.8.627
[13] I. Langmuir, “The Interaction of Electron and Positive Ion Space Charges in Cathode Sheaths,” Physical Review, Vol. 33, No. 6, 1929, pp. 954-989. doi:10.1103/PhysRev.33.954
[14] D. Bohm, “The Characteristics of Electrical Discharges in Magnetic Fields,” McGraw-Hill, New York, 1949, p.77.
[15] K.-U. Riemann, “The Bohm Criterion and Sheath Formation”, Journal of Physics D: Applied Physics, Vol. 24, No. 4, 1991, pp. 493-518. doi:10.1088/0022-3727/24/4/001
[16] K.-U. Riemann, “The Influence of Collisions on the Plasma Sheath Transition,” Physics of Plasmas, Vol. 4, No. 11, 1997, pp. 4158-4166. doi:10.1063/1.872536
[17] J. Christensen-Dalsgaard, “Seismological Challenges for Stellar Structure,” Astronomische Nachrichten, Vol. 331, No. 9-10, 2010, pp. 866-872. doi:10.1002/asna.201011416
[18] I. Zouganelis, M. Maksimovic, N. Meyer-Vernet, H. Lamy and K. Issautier, “A Transonic Collisionless Model of the Solar Wind,” Astrophysical Journal, Vol. 606, No. 1, 2004, pp. 542-554. doi:10.1086/382866
[19] M. P. D. Mauro, “Helioseismology,” Astrophysics and Space Sciences Transactions, Vol. 4, No. 1, 2008, pp. 13- 17. doi:10.5194/astra-4-13-2008
[20] W. J. Chaplin, “Challenges and Opportunities for Helioand Asteroseismology,” Astronomische Nachrichten, Vol. 331, No. 9-10, 2010, pp. 1090-1094. doi:10.1002/asna.201011464
[21] J. D. Huba, “Fundamental Plasma Parameters,” NRL Plasma Formulary, Naval Research Laboratory, Washington DC, 2000, pp. 28-40. doi:10.1002/asna.201011464
[22] S. C. Tripathy, C. B. Dwivedi, A. C. Das and A. R. Prasanna, “Plasma Instability at the Inner Edge of the Accretion Disk-I,” Journal of Astrophysics and Astronomy, Vol. 14, No. 2, 1993, pp. 103-114. doi:10.1007/BF02702252
[23] S. C. Tripathy, C. B. Dwivedi, A. C. Das and A. R. Prasanna, “Plasma Instability at the Inner Edge of the Accretion Disk-II,” Journal of Astrophysics and Astronomy, Vol. 14, No. 3-4, 1993, pp. 167-179. doi:10.1007/BF02702366
[24] J. Loizu, P. Ricci and C. Theiler, “Existence of Subsonic Plasma Sheaths,” Physical Review E, Vol. 83, No. 1, 2011, pp. 016406(1)-016406(4).
[25] L. A. Gougam and M. Tribeche, “Debye Shielding in a Nonextensive Plasma,” Physics of Plasmas, Vol. 18, No. 6, 2011, pp. 062102(1)-062102(5).
[26] R. G. Athay, B. C. Low and O. R. White, “The Solar Interior-Atmospheric System,” ASP Conference Series, Vol. 383, 2008, pp. 315-326.
[27] S. L. Bi, M. P. Di Mauro and J. Christensen-Dalsgaard, “An Improved Equation of State under Solar Interior Conditions,” Astronomy and Astrophysics, Vol. 364, 2000, pp. 879-886.
[28] C. J. Cannon and R. N. Thomas, “The Origin of Stellar Winds: Subatmospheric Nonthermal Storage Modes versus Radiation Pressure,” Astrophysical Journal, Vol. 211, No. 3, 1977, pp. 910-925. doi:10.1086/155003
[29] V. M. Nakariakov and E. Verwichte, “Coronal Waves and Oscillations,” Living Reviews in Solar Physics, Vol. 2, 2005, pp. 3-65. http://livingreviews.org/lrsp-2005-3
[30] E. Marsch, “Kinetic Physics of the Solar Corona and Solar Wind,” Living Reviews in Solar Physics, Vol. 3, 2006, pp. 1-100. http://livingreviews.org/lrsp-2006-1
[31] A. Nordlund, R. F. Stein and M. Asplund, “Solar Surface Convection,” Living Reviews in Solar Physics, Vol. 6, 2009, pp. 2-117. http://livingreviews.org/lrsp-2009-2
Appendix

Table A1. Standard values of various useful astrophysical constants.
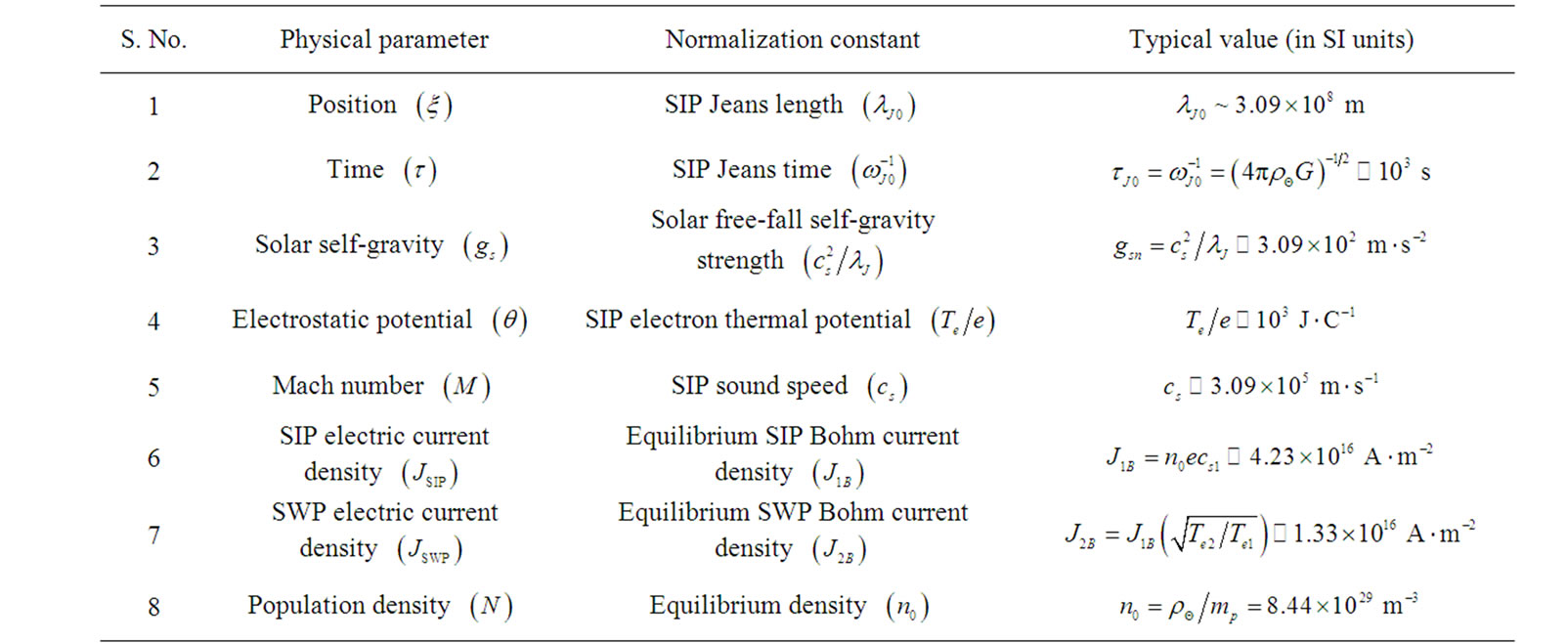
Table A2. Various normalization constants for physical parameters.

Table A3. Various normalization constants for plasma parameters.

