International Journal of Astronomy and Astrophysics
Vol.2 No.4(2012), Article ID:26110,5 pages DOI:10.4236/ijaa.2012.24029
Cosmic String in Bianchi Type-III Space-Time with Bulk Viscosity and Magnetic Field
Department of Mathematics, Government Vidarbha Institute of Science and Humanities, Amravati, India
Email: *spkandalkar2004@yahoo.com
Received May 10, 2012; revised June 12, 2012; accepted June 22, 2012
Keywords: Bulk Viscosity; Magnetic Field; String Cosmological
ABSTRACT
We investigate some locally rotationally symmetric (LRS) Bianchi type-III string cosmological model in the presence of bulk viscosity and magnetic field, where an equation of state 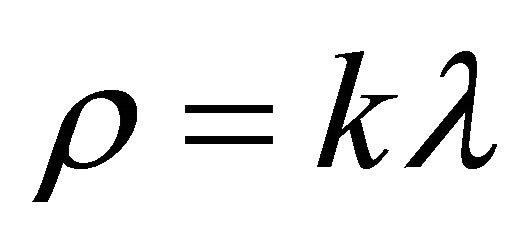 and relation between metric potential
and relation between metric potential 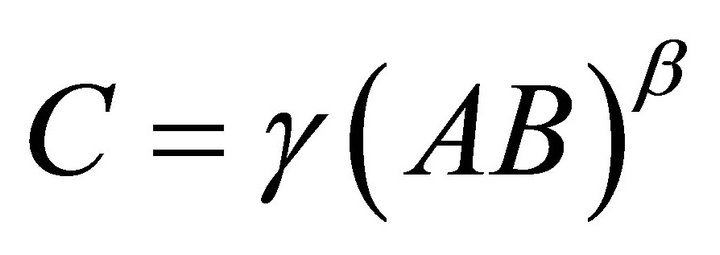 are considered. The solution describes a shearing and non-rotating model with big-bang start. In the absence of magnetic field it reduces to a string model with bulk viscosity, where the relation between the coefficient of bulk viscosity and the energy density is
are considered. The solution describes a shearing and non-rotating model with big-bang start. In the absence of magnetic field it reduces to a string model with bulk viscosity, where the relation between the coefficient of bulk viscosity and the energy density is 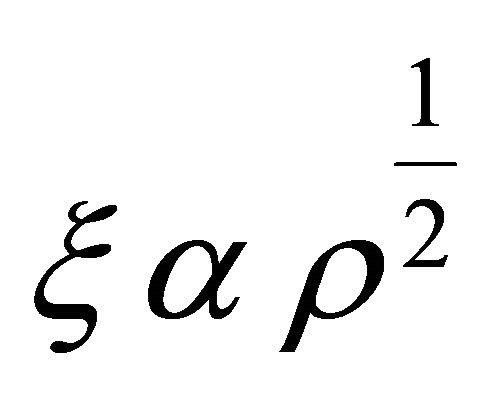 for α = 0.
for α = 0.
1. Introduction
It is a challenging problem to determine the exact physical situation at the early stages of formation of our universe. Strings are well-known and very important topological defect [1,2] which occurs during the phase transition at the early stages of the universe. The existence of a large scale network of string in the early universe does not contradict the present day observation of the universe and further the galaxy formation can be explain by the density fluctuation [3] generated by a vacuum strings. As gravitation is the only range force binding the contents of the universe and Einstein theory of gravitation is the sole theory for understanding the nature and evolution of large-scale structure of the universe, so it may be interesting to study the gravitational effects, which arises due to string within the framework of Einstein gravity. In fact, the general relativistic treatment of strings was initiated by Letelier [4] and Satchel [5]. This model has been used as source for Bianchi Type I and Kantowski-Sachs cosmologies by Letelier [4]. Afterwards, the Krori et al. [6] and Wang [7] have discussed the solutions of Bianchi types II, VI, VIII and IX for a cloud string. Tikekar and Patel [8] and Chakraborty and Chakraborty [9] have presented the exact solutions of Bianchi type III and spherically cosmology respectively for a cloud string.
On the other hand, the matter distribution is satisfactorily described by perfect fluids due to the large scale distribution of galaxies in our universe. However, a relativistic treatment of the problem requires the consideration of material distribution other than the perfect fluid. It is well known that when neutrino decoupling occurs, the matter behaves as a viscous fluid in an early stage of the universe. Viscous fluid cosmological model of early universe have been widely discussed in the literatures [10,11]. Recently, Bali and Dave [12] have discussed Bianchi type III string cosmological models with bulk viscosity, where the constant coefficient of bulk viscosity is considered.
Moreover, the magnetic field has important role of the cosmological scale and is present in galactic and intergalactic spaces. The importance of the magnetic fluid for various astrophysical phenomena has been studied in many papers. Further Melvin [13] has pointed out that during the evolution of the universe a large part of the history of evolutions matter was highly ionized, smoothly coupled with the field and subsequently forming neutral matter during the expansion of the universe. Therefore considering the presence of magnetic field in cloud string universe is not unrealistic and has been investigated by many authors [14-17]. Magnetized bulk viscous string cosmological models have been investigated by Yadav et al. [18]. Recently Bali et al. [19] has studied Bianchi type VIo magnetized bulk viscous massive string cosmological model in general relativity.
In the present paper, we study string cosmology with bulk viscosity and magnetic fluid for Bianchi type III. An equation of state 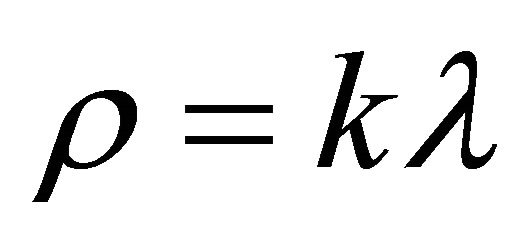 and relation between metric potential are considered.
and relation between metric potential are considered.
2. The Metric and Field Equations
We consider the space-time of general Bianchi III-type with the metric
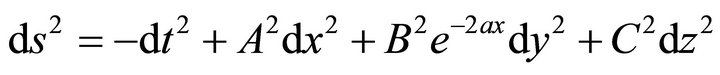 (1)
(1)
where A, B, C are functions of “t” and “a” is constant.
The energy momentum for a cloud of string with bulk viscosity and magnetic field is ([13,20])
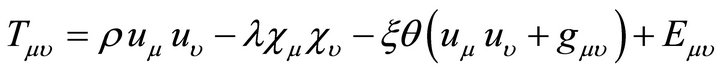 (2)
(2)
where 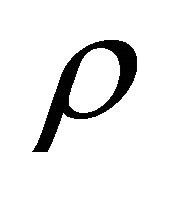 is the rest energy density of the cloud of strings with particles attached to them,
is the rest energy density of the cloud of strings with particles attached to them, 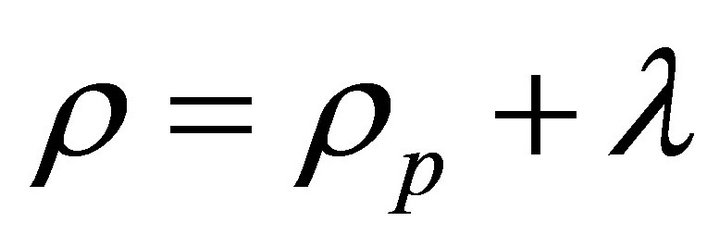 , with
, with  being the rest energy density of particles,
being the rest energy density of particles, 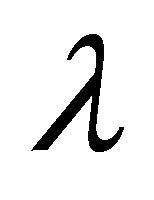 the tension density of the cloud of strings,
the tension density of the cloud of strings, 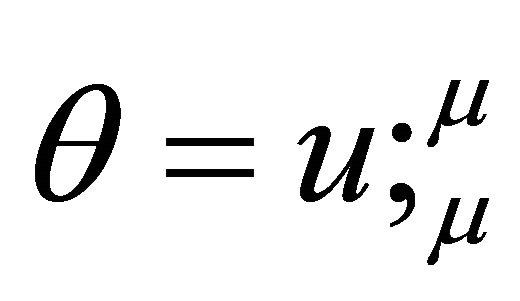 is the scalar expansion, and
is the scalar expansion, and  the coefficient of bulk viscosity. As pointed out by Letelier [4], the energy density for the coupled system
the coefficient of bulk viscosity. As pointed out by Letelier [4], the energy density for the coupled system 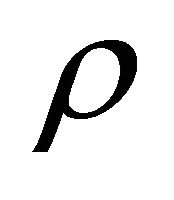 and
and 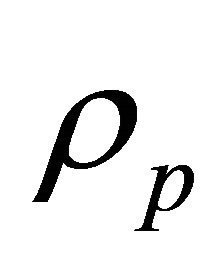 is restricted to be positive, while the tension density
is restricted to be positive, while the tension density 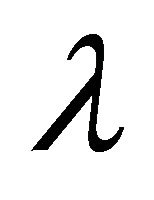 may be positive or negative. The vector represents
may be positive or negative. The vector represents 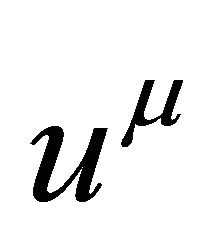 describes the cloud four velocities and
describes the cloud four velocities and 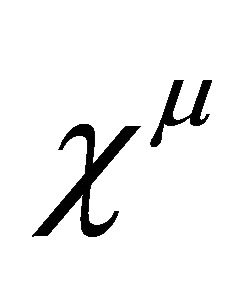 represent a direction of anisotropy that is the direction of string, satisfy the standard relation [21].
represent a direction of anisotropy that is the direction of string, satisfy the standard relation [21].
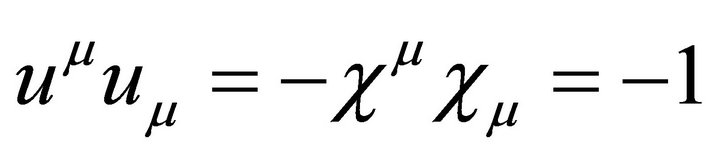 and
and  (3)
(3)
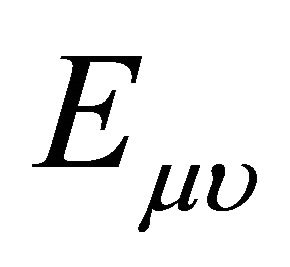 is the energy momentum for magnetic field,
is the energy momentum for magnetic field,
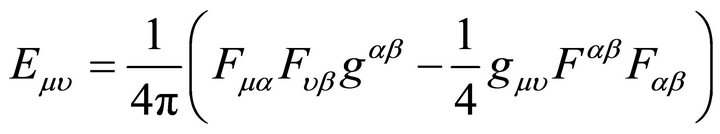 (4)
(4)
where, 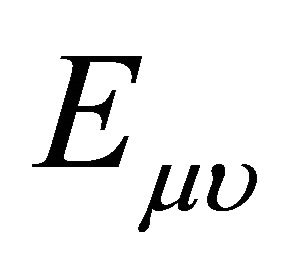 is the electromagnetic field tensor, which satisfies the Maxwell equations are,
is the electromagnetic field tensor, which satisfies the Maxwell equations are,
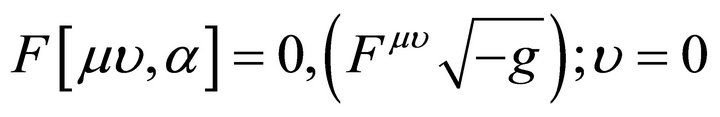 (5)
(5)
In co-moving coordinates, the incident magnetic field is taken along z-axis, with the help of Maxwell Equation (5), the only non-vanishing component of 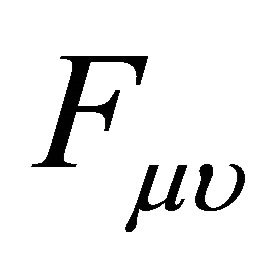 is,
is,
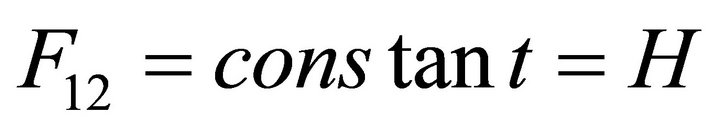 (6)
(6)
Einstein’s equation, we consider here is
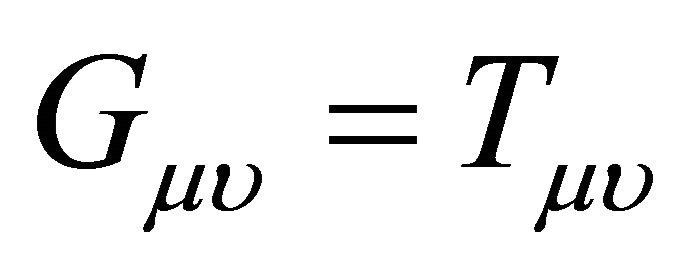 (7)
(7)
where 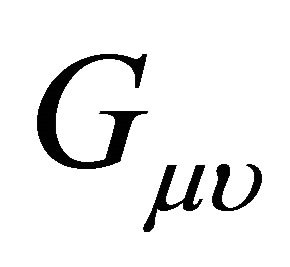 is Einstein tensor and we choose unit such that,
is Einstein tensor and we choose unit such that,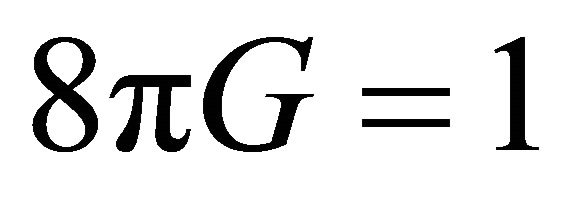 .
.
With the help of Equations (1)-(6), Einstein’s Equation (7) can be written as
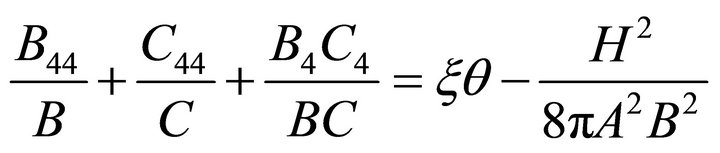 (8)
(8)
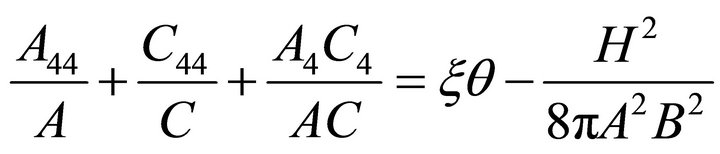 (9)
(9)
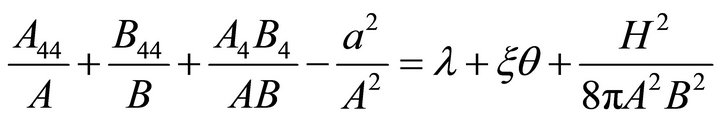 (10)
(10)
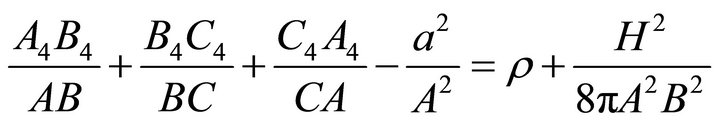 (11)
(11)
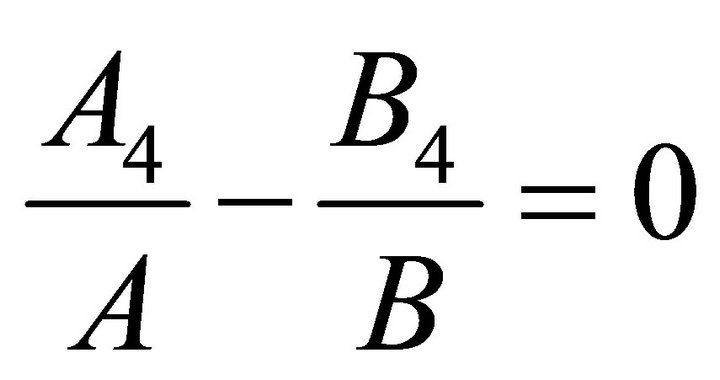 (12)
(12)
where the suffix 4 at the symbols A, B and C denotes ordinary differentiation with respect to “t”.
Here we have, five field equations connecting six unknown quantities A, B, C,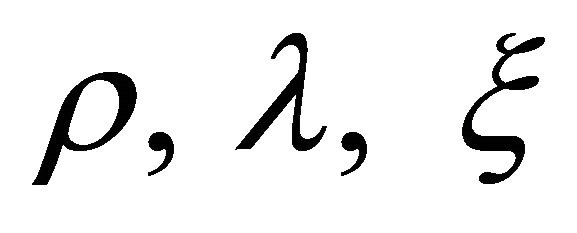 . Therefore, in order to obtain exact solutions we must need one more relation connecting the unknown quantities. We consider Takabayasi’s [20] equation of state
. Therefore, in order to obtain exact solutions we must need one more relation connecting the unknown quantities. We consider Takabayasi’s [20] equation of state
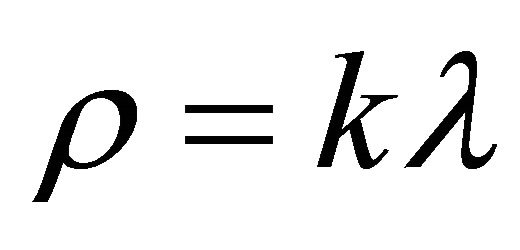 (13)
(13)
where k is a constant.
One should note that we also assumed the relation [9]
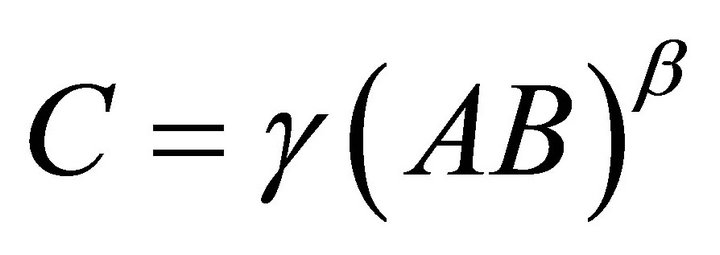 (14)
(14)
where 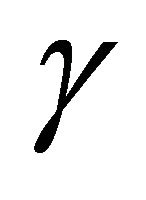 and
and  are arbitrary constants. Equation (12) leads to
are arbitrary constants. Equation (12) leads to
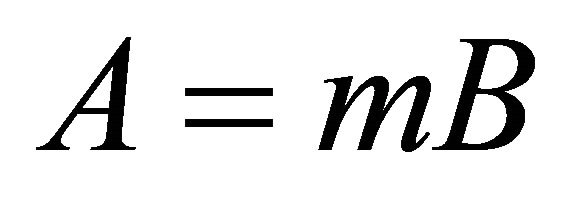 (15)
(15)
where m is an integrating constant. From (14) and (15), we obtain
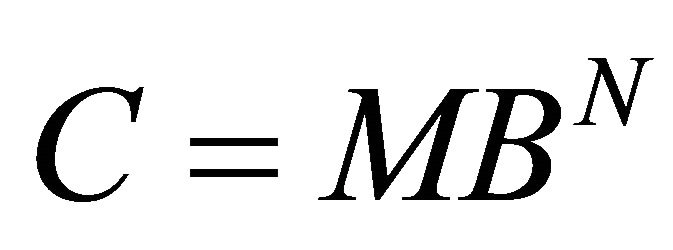 (16)
(16)
where
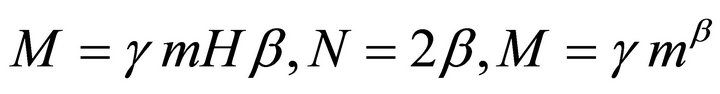 (17)
(17)
From field Equations (8), (10) and (11), with the help of Equation (13), eliminating  and
and , we obtain
, we obtain
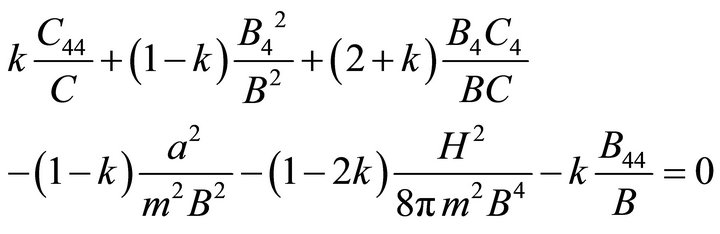 (18)
(18)
Substituting Equation (16) into Equation (18), we get
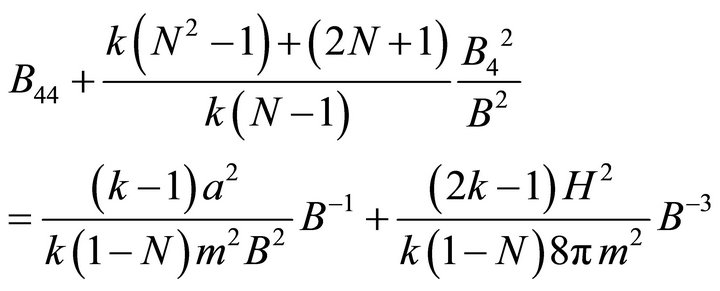 (19)
(19)
To solve Equation (19), we denote 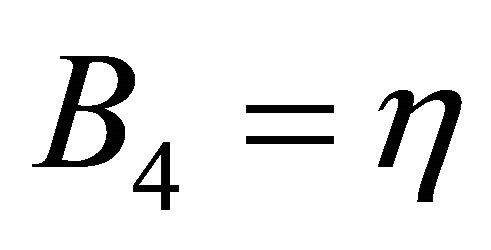 then Equation (19) can be reduced to a first order differential equation as follows,
then Equation (19) can be reduced to a first order differential equation as follows,
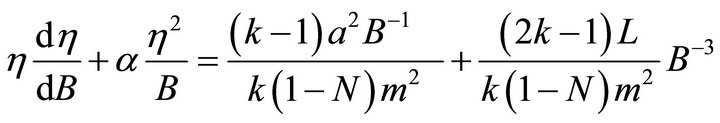 (20)
(20)
where
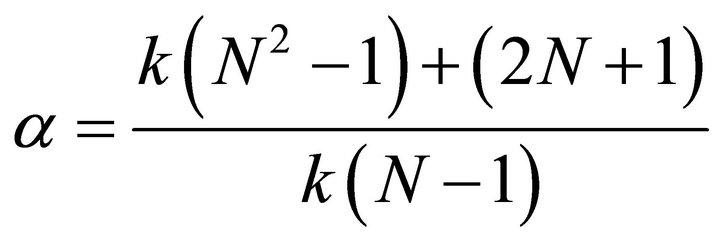 (21)
(21)
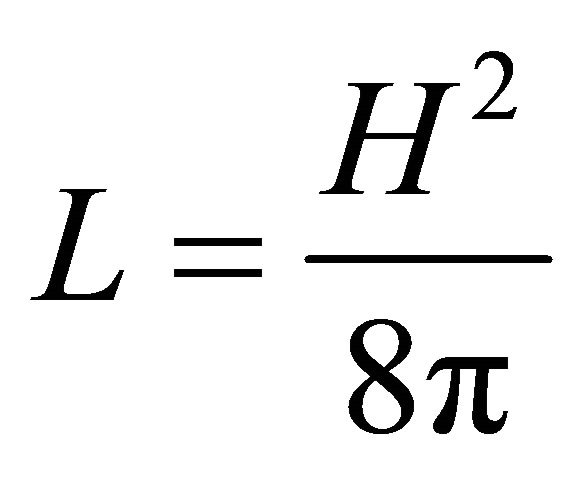 (22)
(22)
Equation (20) can further be written as
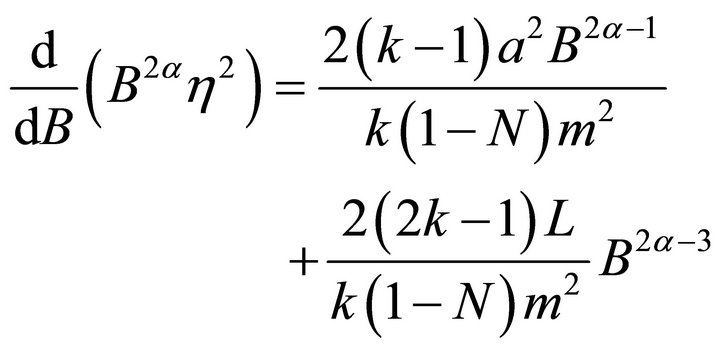 (23)
(23)
From Equation (23), we obtain
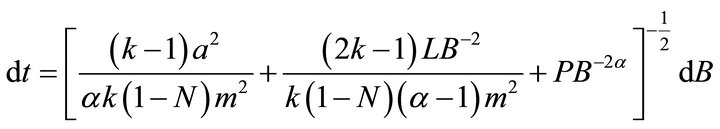 (24)
(24)
where P is the constant of integration.
For this solution, the geometry of the universe is described by the line-element
 (25)
(25)
Using suitable transformation of coordinates, the metric (25) can be reduced to the form
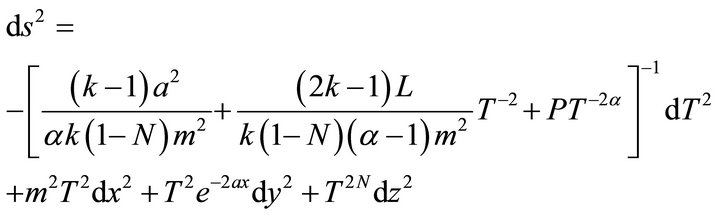 (26)
(26)
For the model of Equation (26), the other physical and geometrical parameters can be easily obtained. The expressions for the energy density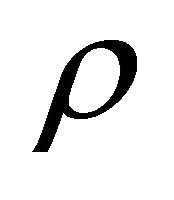 , the string tension
, the string tension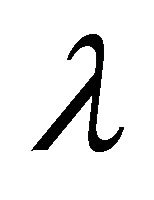 , the particle density
, the particle density 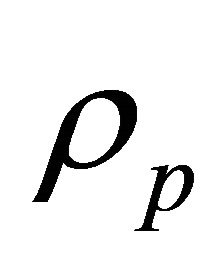 and the coefficient of bulk viscosity
and the coefficient of bulk viscosity  are respectively as follows.
are respectively as follows.
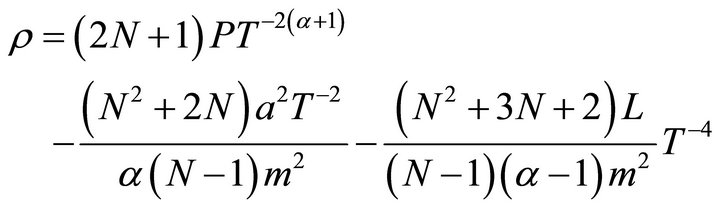 (27)
(27)
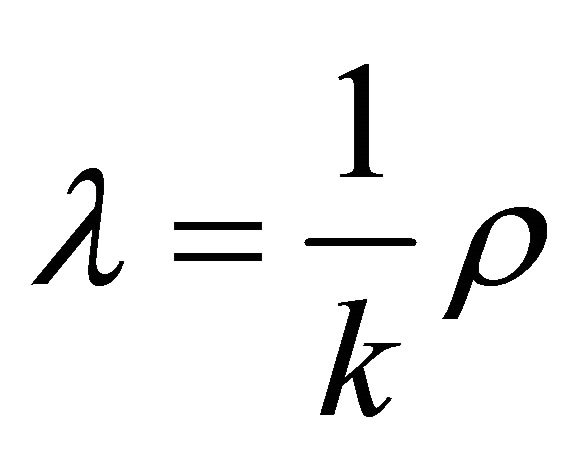 (28)
(28)
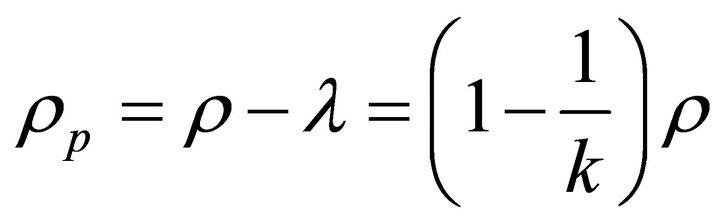 (29)
(29)
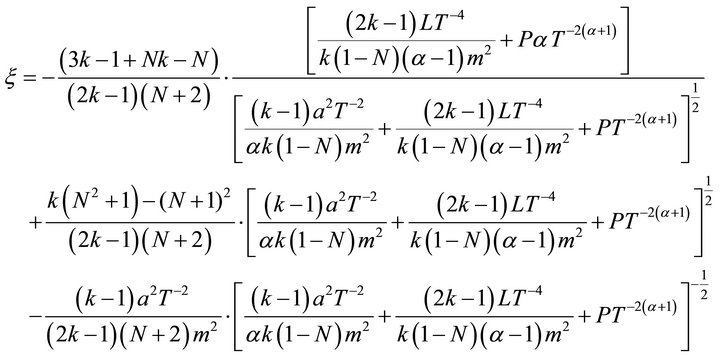 (30)
(30)
The scalar of expansion , the shear
, the shear 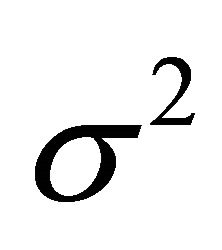 and the spatial volume V, are given by
and the spatial volume V, are given by
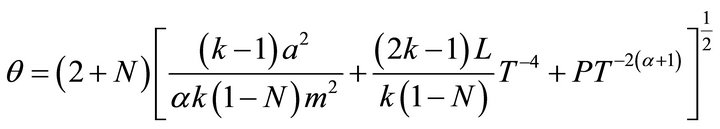 (31)
(31)
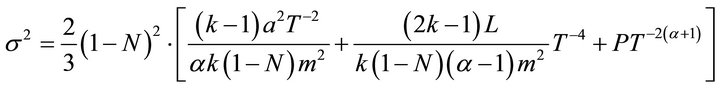 (32)
(32)
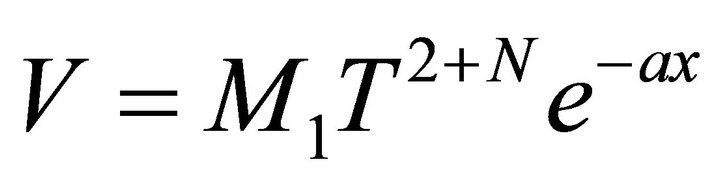 (33)
(33)
In the absence of magnetic field (i.e. L = 0), we obtain a string model with bulk viscosity and in this case the metric (26) reduces to the form
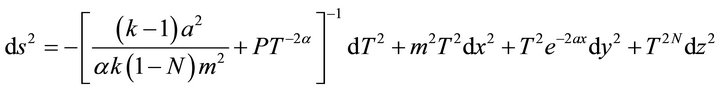 (34)
(34)
For the model (34), the physical and geometric parameters can be easily obtained. The expressions for the energy density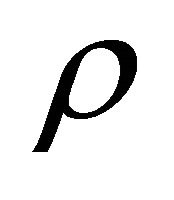 , the string tension density
, the string tension density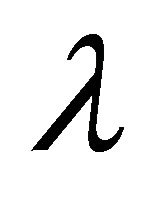 , the particle density
, the particle density 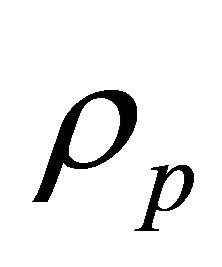 and the coefficient of bulk viscosity
and the coefficient of bulk viscosity  are respectively as follows,
are respectively as follows,
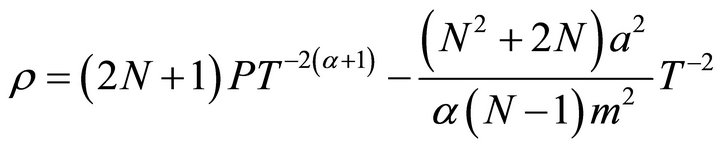 (35)
(35)
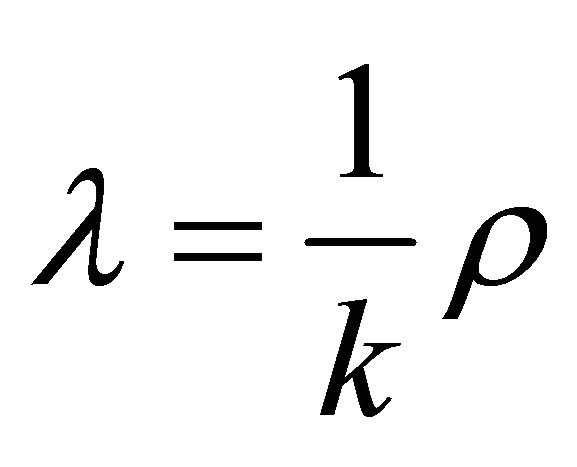 (36)
(36)
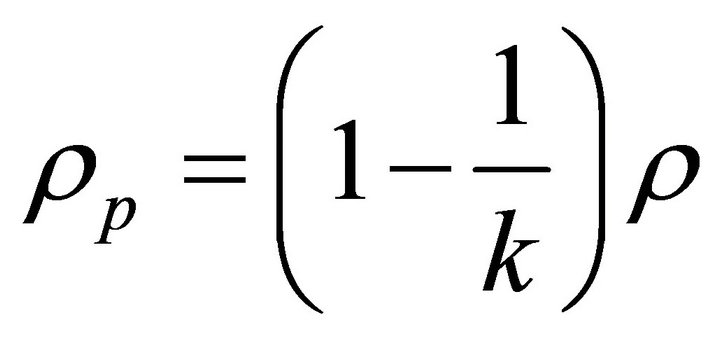 (37)
(37)
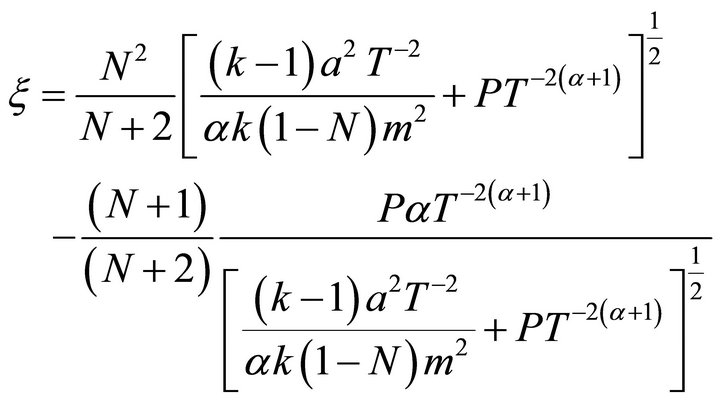 (38)
(38)
The scalar of expression , the shear
, the shear 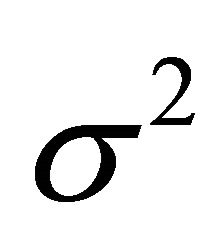 and the spatial volume V, are given respectively by
and the spatial volume V, are given respectively by
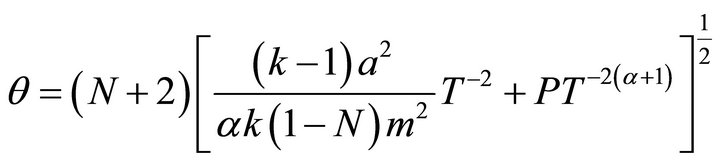 (39)
(39)
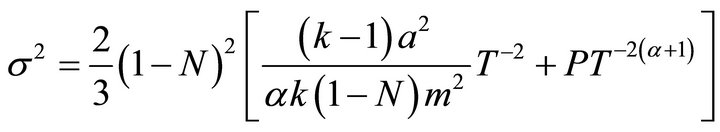 (40)
(40)
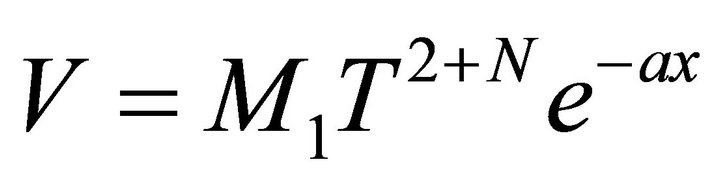 (41)
(41)
3. Conclusions
We have discussed LRS Bianchi type III cosmological model for a cloud of string with bulk viscosity and magnetic field and a model (26) is constructed. We observed from the Equation (27) that if we choose suitable values for constants the energy condition 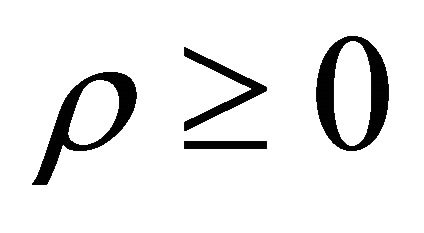 is satisfied.
is satisfied.
For example, if we choose 0 < N < 1, 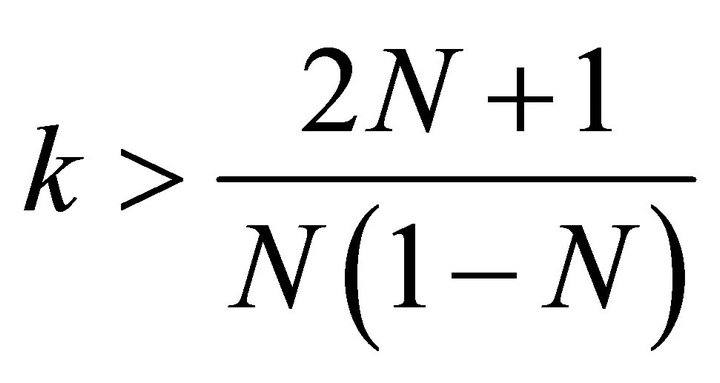 it is shown that all the coefficient in the expression of energy density (
it is shown that all the coefficient in the expression of energy density (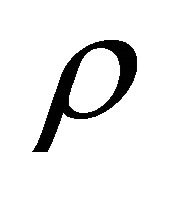 ) given by Equation (27) are positive. In the absence of magnetic field the model (34) is constructed. In this case, from Equation (35), the energy condition
) given by Equation (27) are positive. In the absence of magnetic field the model (34) is constructed. In this case, from Equation (35), the energy condition 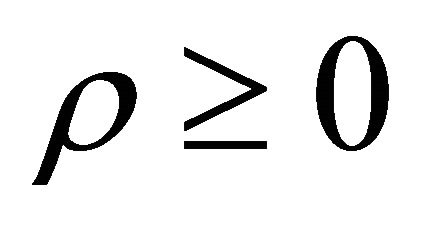 can be fulfill provided 0 < N < 1. Further the solutions can be reduced to a string model with bulk viscosity where
can be fulfill provided 0 < N < 1. Further the solutions can be reduced to a string model with bulk viscosity where 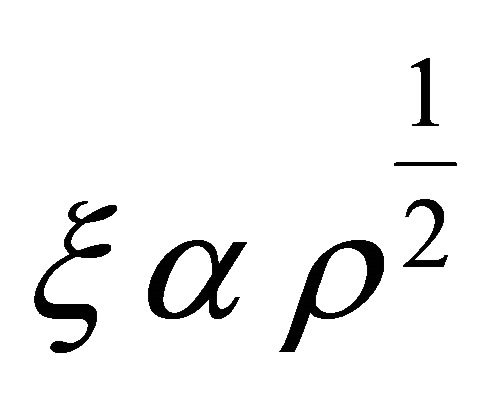 for a = 0.
for a = 0.
For the models (26) and (34), the scale of expansion ( ) is infinite at
) is infinite at 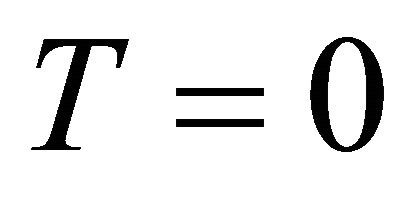 and
and  when
when , provided
, provided 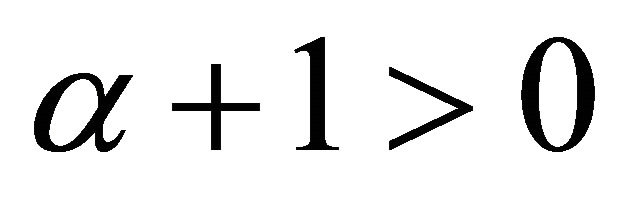 thus the models represent shearing and non-rotating universe with a big-bang start. Also the spatial volume
thus the models represent shearing and non-rotating universe with a big-bang start. Also the spatial volume  when
when  and when
and when 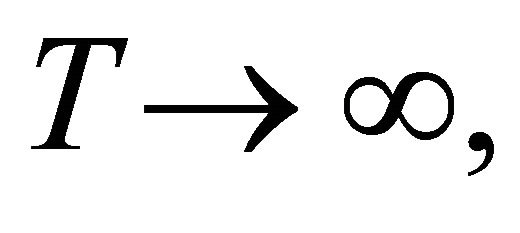
 whereas
whereas 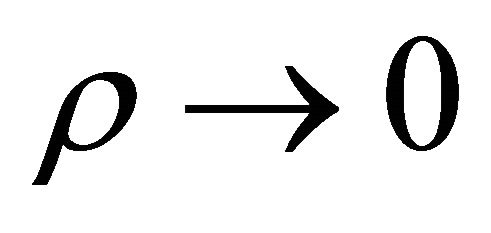 as
as , thus the models tends empty universe when
, thus the models tends empty universe when  and does not approach isotropy for large value of
and does not approach isotropy for large value of 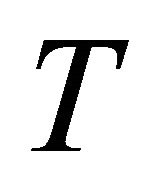 as
as 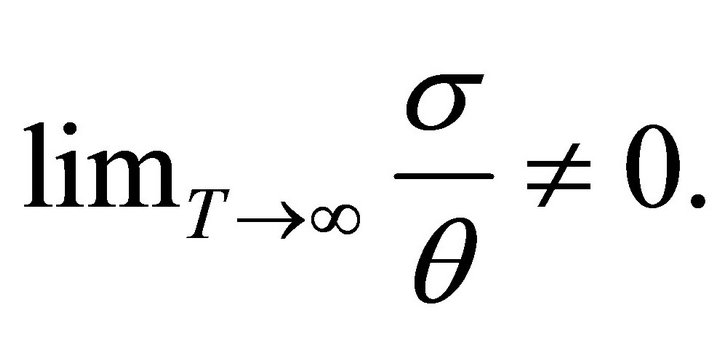
Further when k > 2 or k < 0, we have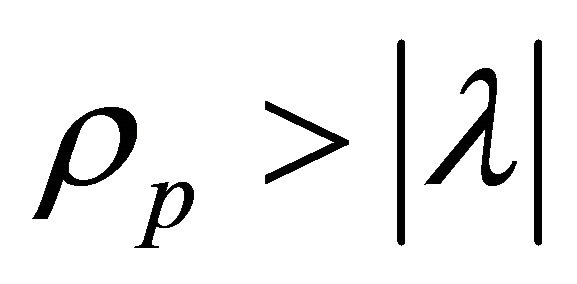 , therefore, in these cases, the massive string dominates the universe in the process of universe. However, when 1 < k < 2, we have
, therefore, in these cases, the massive string dominates the universe in the process of universe. However, when 1 < k < 2, we have 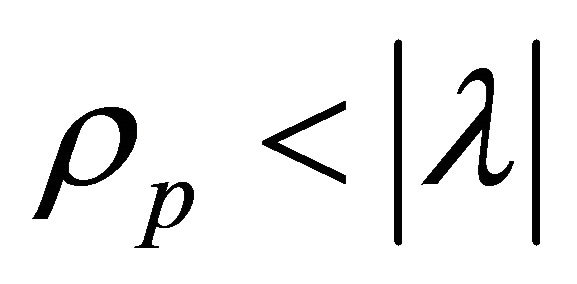 and hence the string dominate over the particles.
and hence the string dominate over the particles.
4. Acknowledgements
The authors are thankful to the referee for valuable comments and suggestions.
REFERENCES
- T. W. B. Kibble, “Topology of Cosmic Domains and Strings,” Journal of Physics, Vol. 9, No. 8, 1976, pp. 1387-1398.
- A. Vilenkin, “Cosmic Strings and Other Topological Defects,” Physical Review, Vol. 121, 1985, pp. 263-296.
- Ya. B. Zel’dovich, “Cosmological Fluctuations Produced Near a Singularity,” Monthly Notices of the Royal Astronomical Society, Vol. 192, 1980, pp. 663-668.
- P. S. Letelier, “String Cosmologies,” Physical Review D, Vol. 28, 1983, pp. 2414-2419.
- J. Stachel, “Thickening the String. I. The String Perfect Dust,” Physical Review D, Vol. 21, 1980, pp. 2171-2181.
- K. D. Krori, T. Chaudhary, C. R. Mahanta and A. Muzumdar, “Some Exact Solution in String Cosmology,” General Relativity Gravitation, Vol. 22, No. 2, 1990, pp. 123-130.
- X. X. Wang, “Exact Solutions for String Cosmology,” Chinese Physics Letters, Vol. 20, No. 5, 2003, pp. 615-617. doi:10.1088/0256-307X/20/5/307
- R. Tikekar and L. K. Patel, “Some Exact Solutions of String Cosmology in Bianchi III Space-Time,” General Relativity Gravitation, Vol. 24, No. 4, 1992, pp. 397-404.
- S. Chakraborty and A. K. Chakraborty, “String Cosmology in Spherically Symmetric Space Time,” Journal of Mathematical Physics, Vol. 33, No. 3, 1992, pp. 2336- 2338.
- K. D. Krori and A. Mukherjee, “Bianchi Cosmologies with Particle Creation and Bulk Viscosity,” General Relativity Gravitation, Vol. 32, No. 8, 2000, pp. 1429- 1438.
- T. Singh and A. Beeshan, “Bulk Viscous Cosmological Models with variable G and Lambda,” General Relativity Gravitation, Vol. 30, 1998, pp. 573-578.
- R. Bali and S. Dave, “Bianchi Type-III String Cosmological Models with Bulk Viscous Fluid in General Relativity,” Astrophysics and Space Science, Vol. 282, No. 1, 2002, pp. 461-467.
- M. A. Melvin, “Homogeneous Axial Cosmologies with Electromagnetic Fields and Dust,” Annals of the New York Academy of Sciences, Vol. 262, No. 2, 1975, pp. 253-274.
- A. Banerjee, A. Sanyal and S.Chakraborty, “String Cosmology in Bianchi I Space-Time,” Pramana, Journal of Physics, Vol. 34, No. 1, 1990, pp. 1-11.
- G. P. Singh and J. Singh, “String Cosmological Models with Magnetic Field,” General Relativity Gravitation, Vol. 31, No. 3, 1999, pp. 371-378. doi:10.1023/A:1026644828215
- R. Bali and R. D. Upadhaya, “L.R.S. Bianchi Type I String Dust Magnetized Cosmological Models,” Astrophysics and Space Science, Vol. 283, No. 1, 2003, pp. 97-108.
- S. K. Tripathy, S. K. Sahu and T. R. Routray, “String Cloud Cosmologies for Bianchi Type-III with Electromagnetic Field,” Astrophysics and Space Science, Vol. 315, No. 1-4, 2008, pp. 105-110.
- M. K. Yadav, A. Pradhan and S. K. Singh, “Some Magnetized Bulk Viscous String Cosmological Models in General Relativity,” Astrophysics and Space Science, Vol. 311, No. 4, 2007, pp. 423-429.
- R. Bali, R. Banerjee and S. K. Banerjee, “Bianchi Type VIo Magnetized Bulk Viscous Massive String Cosmological Model in General Relativity,” Astrophysics and Space Science, Vol. 317, No. 2, 2008, pp. 21-26.
- T. Takabayasi, “Theory of One-Dimensional Relativistic Elastic Continuum for the Model of Particles and Resonances,” Mathematical Physics and Applied Mathematics, Vol. 1, No. 1, 1976, pp. 179-216.
- R. Bali and K. Sharma, “Bianchi Type I Bulk Viscous Stiff Fluid Tilted Cosmological Model in General Relativity,” Astrophysics and Space Science, Vol. 275, No. 4, 2001, pp. 485-497.
NOTES
*Corresponding author.

