Journal of Sensor Technology
Vol.04 No.02(2014), Article ID:47414,16 pages
10.4236/jst.2014.42010
A Quaternion Scaled Unscented Kalman Estimator for Inertial Navigation States Determination Using INS/GPS/Magnetometer Fusion
Wassim Khoder1, Bassem Jida2
1Faculty of Economics and Business Administration, Lebanese University, Tripoli, Lebanon
2Faculty of Science, Lebanese University, Tripoli, Lebanon
Email: wassim.khoder@hotmail.com, bassemjida@hotmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 30 April 2014; revised 26 May 2014; accepted 26 June 2014
ABSTRACT
This Inertial Navigation System (INS), Global Positioning System (GPS) and fluxgate magnetometer technologies have been widely used in a variety of positioning and navigation applications. In this paper, a low cost solid state INS/GPS/Magnetometer integrated navigation system has been de- veloped that incorporates measurements from an Inertial Navigation System (INS), Global Posi- tioning System (GPS) and fluxgate magnetometer (Mag.) to provide a reliable complete navigation solution at a high output rate. The body attitude estimates, especially the heading angle, are fun- damental challenges in a navigation system. Therefore targeting accurate attitude estimation is considered a significant contribution to the overall navigation error. A better estimation of the body attitude estimates leads to more accurate position and velocity estimation. For that end, the aim of this research is to exploit the magnetometer and accelerometer data in the attitude estima- tion technique. In this paper, a Scaled Unscented Kalman Filter (SUKF) based on the quaternion concept is designed for the INS/GPS/Mag integrated navigation system under large attitude error conditions. Simulation and experimental results indicate a satisfactory performance of the newly developed model.
Keywords:
Inertial Navigation System, Inertial Sensor Model, GPS, Magnetometer, Quaternion Attitude Parameterization, Rotation Vector, Scaled Augmented Unscented Kalman Filter

1. Introduction
The principal software functions executed in the Inertial Navigation System (INS) computer are the angular rate and linear acceleration signals. The angular rate signals is integrated to compute the attitude data (denoted as at- titude algorithm). The attitude information is used to transform the linear acceleration signal into a suitable na- vigation coordinate frame where it is double integrated in order to obtain the velocity and position states (de- noted as velocity and position algorithms). Thus three integration functions (INS algorithm) are involved: atti- tude, velocity, and position. Each of which requires high accuracy to assure negligible error compared to inertial sensors’ accuracy requirements. Since acceleration from the accelerometers and angular rate from the rate gyros are generally susceptible to various measurement noise sources, the accuracy of position, velocity and attitude information degrades with time [1] -[4] . Recent research has shown that the growth of numerical errors in Inertial Measurement Units (IMUs) navigation with time can be prevented by using external aiding sensors such as the Global Positioning System (GPS) [5] - [7] , and the magnetometer [8] [9] . The magnetometers are susceptible to magnetic disturbances, which corrupt their measurements of the earth magnetic field. These errors typically known as Hard-iron and Soft-iron effects are calibrated out once the system is installed in its final mounting po- sition. The benefits of this integration are well known. The supporting sensors (GPS and magnetometers) pro- vide the earth-fixed position, velocity, and earth magnetic field measurements which the filter uses to calculate corrections to the trajectory state and estimate inertial sensor errors. This fusion of multiple sensors allows for a wide variety of sensor characterizations including bias, scale factor, and unit mounting misalignment. The larg- est error in attitude and heading propagation is associated with the gyro bias terms. Without a filter structure and separate independent measurements, the attitude information would diverge from the true trajectory. Since in INS algorithm, the accuracy of attitude information governs the accuracy of velocity and position estimation, the most researched topic for the INS integration functions has been primarily focused on the design of algorithms for the attitude integration function and initial alignment. Several parameterizations have been used to represent the attitude, such as Euler angles, Direct Cosine Matrix, Quatemions, Rotation vector, Rodrigues parameters, etc. The detailed discussion on each par metrization for attitude estimation is found in [7] [10] [11] . The Extended Kalman Filter (EKF) is widely used nonlinear filtering method for attitude estimation [12] . The Unscented Kal- man Filter (UKF) is an extension of the classical Kalman filter to nonlinear process and measurement models and has been proposed for attitude estimation, which is more robust than the EKF for large initial attitude-error conditions [6] [7] [10] [11] . The quatemion’s method is advantageous since it requires less computation, gives better accuracy, avoids singularity and the kinematics equation is bilinear [13] [14] . However, the quatemion must obey a normalization constraint, which can be violated in many nonlinear quatemion filtering approaches. In fact, if the state vector is quatemion, the predicted quaternion mean should be calculated in the rotational space to preserve the nonlinear nature of unit quatemion. To directly utilize UKF formulation built in vector space and to avoid a mean computation problem of quatemions, a modified method employing the combination of the quaternion with the generalized Rodrigues parameters is used in [7] [10] [11] . This method converts a qu- atemion to a Rodrigues parameter and converted Rodrigues parameters are used to compute the predicted mean, the covariance and cross-relation matrix since Rodrigues parameters are unconstrained. Rodrigues parameters are converted back to quaternion be-ause this method uses the inertial quaternion for state propagation. An UKF in a unit quaternion space is possible when a weighted mean of quaternions produces a unit quaternion estimate, and the predicted covariance computation and quaternion guarantees that quaternion in filter lies on unit sphere. As an additional development, an alternative formulation for the square root version of the UKF is developed and presented in this paper for the integrated INS navigation, GPS and magnetometer. This version is based on a generalized unconstrained three component attitude-error vector to represent the quaternion error vector, where no parameter conversion is required, such as transformation between quaternions and Rodrigues parameters. A multiplicative quaternion-error is used for predicted covariance computation of the quaternion because it represents the distance from the predicted mean quaternion, and the unit quaternion is not closed for subtraction, guaranteeing that the quaternion in filter lies in unit quaternion space. The quaternion multiplication is used to perform the updates. Since quaternion process noise finally results in an increase of the uncertainty in attitude orientation, we treat then the quaternion error vector as a rotation vector. No small angle assumption is made in the model development.
2. Mathematical model of Integrated INS/GPS/Mag System
In an INS, specific forces and angular rates from an Inertial Measurement Unit (IMU) are transformed into posi- tion, velocity and attitude by solving a set of differential equations called INS mechanization. On the other hand, GPS and magnetometer deliver positions, velocities and earth magnetic field measurements with relatively low accuracy but with a bounded error. INS, GPS and magnetometer have complementary properties and are there- fore well suited for integration. There are different modes of integration [15] - [17] . In this work, a loosely coupled INS/GPS/Mag system has been implemented [18] [19] . This means primarily that GPS positions and velocities information are used as inputs to the navigation filter rather than pseudo-ranges measurements.
2.1. Process Model
The state vector 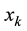 is composed of quaternion, velocity, position and sensor errors (bias, scale factor and mi- salignments errors). The state model is a nonlinear system process represented by
is composed of quaternion, velocity, position and sensor errors (bias, scale factor and mi- salignments errors). The state model is a nonlinear system process represented by
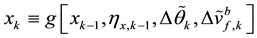 (1)
(1)
The system process model 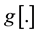 describes the effect of the compensation of the inertial sensor measurement
describes the effect of the compensation of the inertial sensor measurement
on the navigation terms computation (position, velocity and attitude). It refers to the overall INS navigation al- gorithm which is described below.
2.1.1. Navigation error Model Compensation
The compensation of inertial sensor measurement is accomplished to express the true integrated inertial sensor measurement, as follows:
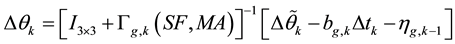 (2)
(2)
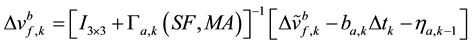 (3)
(3)
where, 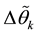 due to the angular rates and
due to the angular rates and 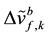 due to the specific forces represent the incremental angle and
due to the specific forces represent the incremental angle and
velocities measured by the inertial sensors respectively. 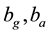 represent the gyro and the accelerometer biases,
represent the gyro and the accelerometer biases,
respectively. 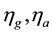 represent the gyro and the accelerometer measurement noises.
represent the gyro and the accelerometer measurement noises. 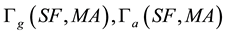
are the 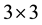 matrices of gyro and accelerometer scale factors (SF)/misalignments (MA) [16]. The sensor error model can be applied as follows:
matrices of gyro and accelerometer scale factors (SF)/misalignments (MA) [16]. The sensor error model can be applied as follows:
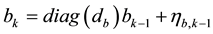 (4)
(4)
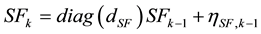 (5)
(5)
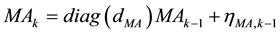 (6)
(6)
where 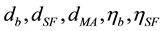 and
and 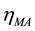 are the parameters that can represent the random walk, the random con-
are the parameters that can represent the random walk, the random con-
stant and the first-order Gauss-Markov processes.
2.1.2. Navigation Digital Attitude quaternion integration
The digital attitude quaternion integration model, 
dated as follows [12] :


where 
orientation at time 

lows [fusion]:

where 

The attitude quaternion
tation at time 


where 


where 






2.1.3. Digital velocity integration
The digital velocity integration model, 

The velocity increment, due to the specific force, 

where 

gravity and Coriolis correction term 



with components of the angular velocity 
2.1.4. Digital position integration
The INS computes position vector by integrating velocity vector [3] [12] [13] . The general position can be up- dated as follows

where 

the midway and 
2.2. Measurement Model
The position and velocity, inclination angles and magnetic field obtained from GPS, the 3 accelerometers of INS and magnetometer respectively, are considered as the measurements set in the Kalman filter.
2.2.1. GPS measurement model
Since the GPS antenna and the INS cannot be installed at the same place in the host vehicle, the position of the
INS is different from that of the GPS, which is known as the lever-arm effect
position and velocity measurements is written as:


where 








The position vector in the e-frame 



where 



2.2.2. Accelerometer Measurement model
The difference between the estimates, at time


The tilt angles estimated by the inertial navigation system can be determined by the following equation:

where 

meters can be determined by the following equation [22] :


where 




where 



2.2.3. Magnetometer measurement model
A three-axes magnetometer measures the Earth magnetic field 
sensors, magnetometer measurement errors can be compensated by using the following measurement model:

where 





where 

pensated Earth magnetic field vector is used to correct the yaw angle or heading compensation. The basic idea for yaw angle compensation is as follows. The residual quantity in the measurement of a declination angle will be the same as the residual of a yaw angle. Hence, we first compute the residual value of the declination which
is the difference between the ideal declination angle given by the world magnetic model 2005 [23] , 
and the measured declination angle

where 
gation frame. Then this residual is used to compensate for the yaw angle in the framework of the unscented Kalman filter. The following measurement model is used for the yaw angle measurement:

3. The Quaternion Scaled Unscented Kalman Filter (Q-SUKF)
In order to fuse aiding GPS and Magnetometer measurements with the INS navigation algorithm to guarantee the accuracy of attitude information, the Unscented Kalman Filter (UKF) based on a quaternion parametrization is used. A description of the UKF can be found in [24] - [26] . The UKF is based on the unscented transformation which is referred to the procedure of obtaining a set of deterministically chosen points, called the sigma points, to represent the untransformed mean and covariance of the variable to be estimated [27] . By choosing appropri- ate weights, which obey the constraint that the sum of the weights is equal to 1, the weighted average and the weighted outer product of the transformed points give the mean and covariance of the transformed distribution. This is true when the state vector elements lie in a vector space. However, if the state vector is quaternion, the predicted quaternion mean should be calculated in the rotational space to preserve the nonlinear nature of unit quaternion. The straightforward implementation of the UKF with quaternions is possible when a weighted mean of quaternions produces a unit quaternion estimate, and the predicted covariance computation and quaternion guarantees that quaternion in filter lies on unit sphere. Generally, the number of sigma points is (2p + 1) (aug- mented state dimension p). However, in the reduced sigma point filter, a set of (p + 2) sigma points can be con- structed that fully captures all of the known statistics of the distribution [26] . In this paper the spherical simplex scaled sigma points are utilized to implement the UKF with quaternions because it generates better numerical properties [28] .
Let us consider the general nonlinear system process and measurement dynamic models:


where











We begin by defining the following state vector, where the superscript “+” denotes an update:

where 







meter biases, respectively, 

tively, and 

step is the initialization of the augmented state 


where 



where 


around 

parameter 






With 



the ith scaled sigma point. The augmented system state square-root matrix 

where 
in [28] . Note that the elements of 

(30.a). If we interpret the sigma points as a set of disturbed state vectors, then Equation (34.d) describes how
these disturbed state vectors are build from the set
closed for addition and subtraction. The sigma points for the quaternion are also quaternions satisfying the nor- malization constraints and should be scattered around the current quaternion estimate on the unit sphere. There- fore, the quaternion sigma points are generated by multiplying the error quaternion by the current quaternion es- timate. Then the set of p + 1 scaled sigma points is split up and constructed as

where 

scaled sigma points corresponding to the rest part of the augmented state-vector and 


where 

where we have denoted the components of sigma points which correspond to actual state variables and process
noise with matrices 


compensated outputs of the gyro and the accelerometer, respectively, defined in Equation (2), Equation (3). The system process model 
Propagation stage is completed, the predicted state vector 
the propagated sigma points, 

However, the weighted sum of unit quaternions is generally not a quaternion of unit norm because the unit quaternion is not mathematically closed for addition and scalar multiplication. Therefore, the predicted attitude quaternion 

As in averaging attitude quaternions, the predicted covariance of posterior quaternions cannot be directly computed because the unit quaternion is not closed for subtraction. We can use the quaternion-error for pre- dicted covariance computation because it represents the distance from the predicted mean quaternion

Let 

Since 





In additive noise case, the process noise is directly added to the state variables, but other forms of noise effect are now also allowed. Once the predicted state and covariance are computed, the sigma points need to be rege- nerated using Equation (36) in the update stage. Next, the sigma points are transformed through the measure- ment model:

where we have denoted the component of sigma points corresponding to measurement noise with matrix


The predicted covariance of the measurement 

With
using:

The Kalman gain matrix 

Finally, the estimated state vector 



With 
should be updated using quaternion multiplication. Then, the estimated quaternion 

where 

4. Numerical simulation and Experimental Results
The quaternion scaled unscented Kalman filter (Q-SUKF) developed in this paper is demonstrated using the ex- perimental results in this section for a moving vehicle’s attitude, position and velocity, as well as the initial sen- sors biases, scale factors. We assume that the misalignment errors of the initial sensors are considered equal to zeros in our case. The experimental platform consists of an INS aided by GPS and magnetometer sensors. The approach corresponds to a loosely integrated INS/GPS/magnetometer system. The experiment was conducted using car driving (reference trajectory) for 10 mimutes. This reference trajectory and their incremental angles and velocities at each moment was generated by the functions “progencar, gendv and genthet” of INS toolbox version 3.0 created by GPSoft. Its motion is described in the navigation frame coordinates with origin (point of
interest) location at 


assume that the rotations about x-axis and y-axis are very small. The initial attitude is given by the quaternion

and
lerometer noises and integrated through the mechanization equations to give the inertial navigation sates. The integration of white noise components of the gyroscopes and accelerometers increase the uncertainty of the po- sition, velocity and attitude of INS. The figures (figure 1), (figure 2) and (figure 3) show the drift over time of attitude, velocity and position of the inertial navigation system trajectory.
The gyro and accelerometer biases are considered as Random Walks and are given by their spectral densitity


modeled as Random Constants and are equals to 

the gyros and accelerometers are given by 10 deg/hr and 0.003 m/s2 respectively, for each axis. The GPS data was generated by adding to the true positions and velocities of the reference trajectory a white Gaussian noise. The initial standard deviation of the horizontal position expressed in geographic coordinates and vertical posi- tion are equal to 8 × 10?7 rd and 5 m respectively. The initial standard deviation of the horizontal and vertical velocities expressed in the navigation frame is equal to 15 m/s and 3 m/s respectively. The sampling frequency of the GPS is 10 Hz (100 ms). Simulated data of Earth’s magnetic field in the navigation frame were generated by the World Magnetic Model 2005 (WMM-2005) that uses the geographic position of the vehicle to determine its components. This reference magnetic field is transformed into the body frame and corrupted by a Gaussian white noise of zero-mean and standard deviation equal to 0.02 Gauss/s1/2. During the experiment, the raw data of the inertial navigation system (incremental angles and velocities) are provided at 200 Hz (5ms) whereas the magnetometer data (magnetic field) is supplied at 50 Hz (20 ms). To test the robustness of the Q-SUKF an ini- tial attitude error of 60 degrees is given in each axis. The diagonal terms of initial covariance matrix represent variances or mean squared errors. The off-diagonal terms are set to be zeros. The parameters used in the Q-SUKF developed are given by scaling parameters 





Figure 1. position errors of INS.
Figure 2. velocity errors of INS.
Figure 3. angle errors of INS.
shows the root mean square errors (RMSE) of the components of attitude, velocity and position resulting from the two hybridizations.
So we can already conclude that the integration of the magnetometer with the inertial navigation system and GPS provided a better behavior of the convergence of Euler angles, which in turn lead to a better estimate of the velocity and position. All these results indicate that the algorithm Q-SUKF proposed is able to provide a reliable information of the inertial navigation states when it is aided by GPS data (position and velocity) and magneto- meter data whatever the initial values on the attitude angles.



Figure 4. (a) Q-SUKF performance (Longitude error); (b) Q-SUKF performance (Latitude error); (c) Q-SUKF performance (Height error).



Figure 5. (a) Q-SUKF performance (North velocity error); (b) Q-SUKF performance (Est velocity error); (c) Q-SUKF performance (Downt velocity error).



Figure 6. (a) Q-SUKF performance (Roll angle error); (b) Q-SUKF performance (Pitch angle error); (c) Q- SUKF performance (Yaw angle error).
Table 1. states navigation RMSE.
5. Conclusion
Since the behavior and the accuracy of an INS navigation algorithm are strongly influenced by INS errors, this paper develops an integrating Inertial Navigation aided by GPS and magnetometer measurements for large atti- tude errors using quaternion parameterization of the attitude, velocity and position. Differing from other quater- nion models, the weighted mean computation for quaternions is derived in rotational space as a barycentric mean with renormalization and a multiplicative quaternion-error is used for predicted covariance computation of the quaternion because it represents the distance from the predicted mean quaternion. The updates are performed using quaternion multiplication which guarantees that quaternion normalization is maintained in the filter. Since the quaternion process noise resulted in increase of the uncertainty in attitude orientation, it is modeled as a rotation vector. The Q-SUKF solves the multi-rate sensor fusion problem in which a series of aiding sensor data with different measurement vector size and different update-rate are fused with high-rate IMU sensor measurements. Numerical simulation results showed that attitude, velocity and position accuracy can be achieved using the proposed approach for large attitude errors.
References
- Grewal, M.S., Weill, L.R. and Andrews, A.P. (2001) Global Positioning Systems, Inertial Navigation, and Integration. John Wiley & Sons, Inc., Hoboken.
- Rogers, R.M. (2003) Applied Mathematics in Integrated Navigation Systems. 2nd Edition, AIAA Education Series, Reston.
- Salychev, O. (2004) Applied Inertial Navigation: Problems and Solutions. BMSTU Press, Moscow.
- Titterton, D.H. and Weston, J.L. (2004) Strapdown Inertial Navigation Technology. 2nd Edition, AIAA Education Se- ries, Reston. http://dx.doi.org/10.1049/PBRA017E
- Kong, X. (2004) INS Algorithm Using Quaternion Model for Low Cost IMU. Robotics and Autonomous Systems, 46, 221-246. http://dx.doi.org/10.1016/j.robot.2004.02.001
- Shin, E.-H. (2005) Estimation Techniques for Low-Cost Inertial Navigation. UCGE Reports Number 20219. The University of Calgary, Calgary.
- Crassidis, J.L. (2006) Sigma-Point Kalman Filtering for Intagrated GPS and Inertial Navigation. IEEE Transactions on Aerospace and Electronic Systems, 42, 750-756. http://dx.doi.org/10.1109/TAES.2006.1642588
- Ali, S. and El-Sheimy, N. (2013) Low-Cost MEMS-Based Pedestrian Navigation Technique for GPS-Denied Areas. Hindawi Publishing Corporation. Journal of Sensors, 2013, Article ID: 197090. http://dx.doi.org/10.1155/2013/197090
- Zhang, P., Gu, J., Milios, E.E. and Huynh, P. (2005) Navigation with IMU/GPS/Digital Compass with Unscented Kal- man Filter. Proceedings of the IEEE International Conference on Mechatronics & Automation, Niagara Falls, July 2005, Vol. 3, 1497-1502. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=1626777
- Shuster, M.D. (1993) A Survey of Attitude Representations. Journal of the Astronautical Sciences, 41, 439-517.
- Crassidis, J.L. and Markley, F.L. (2003) Unscented Filtering for Spacecraft Attitude Estimation. Journal of Guidance, Control, and Dynamics, 26, 536-542. http://dx.doi.org/10.2514/2.5102
- Markley, F.L. (2003) Attitude Error Representations for Kalman Filtering. Journal of Guidance, Control, and Dynam- ics, 26, 311-317. http://dx.doi.org/10.2514/2.5048
- Miller, R.B. (1983) A New Strapdown Attitude Algorithm. Journal of Guidance and Control, 6, 287-291. http://dx.doi.org/10.2514/3.19831
- Waldmann, J. (2002) Attitude Determination Algorithms, Computational Complexity, and the Accuracy of Terrestrial Navigation with Strap down Inertial Sensors. 14th Congress Brasileiro de Automatica, Natal-RN, 2-5 September 2002, 2367-2373.
- Hiliuta, A., Landry Jr., R. and Gagnon, F. (2004) Fuzzy Correction in a GPS/INS Hybrid Navigation System. IEEE Transactions on Aerospace and Electronic Systems, 40, 591-600. http://dx.doi.org/10.1109/TAES.2004.1310007
- Khoder, W. (2010) Contribution à la navigation linéaire par filtrage non linéaire et approche floue. Ph.D. Dissertation, ULCO University, Calais.
- He, X., Chen, Y. and Iz, H.B. (1998) A Reduced-Order Model for Integrated GPS/INS. IEEE AES Systems Magazine, 40-45.
- Touil, K. and Ghadi, A. (2012) Bayesian Bootstrap Filter Approach for GPS/INS Integration. International Journal of Networks and Systems, 1.
- Gautier, J.D. (2003) GPS/INS Generalized Evaluation Tool (GIGET) for the Design and Testing of Integrated Naviga- tion Systems. Ph.D. Dissertation, Department of Aeronautics and Astronautics, Stanford University, Stanford.
- Khoder, W., Fassinut-Mombot, B. and Benjelloun, M. (2008) Inertial Navigation Attitude Velocity and Position Algo- rithms Using Quaternion Scale Unscented Kalman Filtering. The 34 Annual Conference on Information of the IEEE Industrial Electronics Society, 10-13 November 2008, Orlando, 1754-1759.
- Khoder, W., Fassinut-Mombot, B. and Benjelloun, M. (2008) Quaternion Unscented Kalman Filtering for Integrated Inertial Navigation and GPS. The 11th International Conference on Information Fusion, Cologne, 30 June-3 July 2008, 1-8.
- Vasconcelos, J.F., Calvário, J., Oliveira, P. and Silvestre, C. (2004) GPS Aided IMU Unmanned Air Vehicles. Pro- ceedings of the 5th IFAC/EURON Symposium on Intelligent Autonomous Vehicles, Instituto Superior Técnico, Lisboa, 5-7 July 2004, 1-6.
- Oh, S.M. (2007) Nonlinear Estimation Techniques for Vision-Based Air-to-Air Tracking. School of Aerospace Engi- neering, Georgia Institute of Technology, Atlanta.
- Julier, S.J. and Uhlmann, J.K. (1997) A New Extension of the Kalman Filter to Nonlinear Systems. Multi Semsor Fusion, Tracking and Resource Management, II SPIE, Orlando, April 1997, Vol. 3068, 182-193.
- Wan, E.A. and van der Merwe, R. (2001) The Unscented Kalman Filter. In: Haykin, S., Ed., Kalman Filtering and Neural Networks, Wiley, New York, 221-280.
- Julier, S.J. and Uhlmann, J.K. (2004) Reduced Sigma Point Filters for the Propagation of Means and Covariances through Nonlinear Transformations. Proceedings of the IEEE, 92, 401-422. http://dx.doi.org/10.1109/JPROC.2003.823141
- Julier, S.J., Uhlmann, J.K. and Durrant-Whyte, H.F. (2000) A New Method for the Nonlinear Transformation of Means and Covariances in Filters and Estimators. IEEE Transactions on Automatic Control, 45, 477-482. http://dx.doi.org/10.1109/9.847726
- Julier, S.J. (2003) The Spherical Simplex Unscented Transformation. Proceedings of the American Control Conference (ACC ‘03), Denver, 4-6 June 2003, Vol. 3, 2430-2434.







