Journal of Signal and Information Processing
Vol. 3 No. 3 (2012) , Article ID: 22123 , 9 pages DOI:10.4236/jsip.2012.33042
An Efficient Nonuniform Cosine Modulated Filter Bank Design Using Simulated Annealing
![]()
1Department of Electronics and Communication Engineering, Netaji Subhash Engineering College, Kolkata, India; 2Department of Electronics and Tele-Communication Engineering, Jadavpur University, Kolkata, India.
Email: sdhabal@ieee.org, pvwn@ieee.org
Received June 27th, 2012; revised July 25th, 2012; accepted August 6th, 2012
Keywords: NPR; CMFB; FIR Filter; Optimization
ABSTRACT
In this paper, a new approach for the design of non-uniform frequency spacing filter bank using Simulated Annealing has been presented. The filter bank structure is obtained by merging the relevant bands of a uniformly shifted filter bank with integer sampling factors. The design problem is formulated as a single objective unconstrained optimization problem for reducing the amplitude distortion of the overall filter bank for a specified pass-band ripple and stop-band attenuation of the prototype filter. The prototype filter coefficients are optimized using block update method to reach global optimum very quickly and the near perfect reconstruction of the filter bank is also preserved. Simulation results demonstrate that the linear-phase non-uniform filter banks designed by the proposed method have small amplitude distortions and aliasing distortions. Using this technique to minimize design objective is suitable for filter banks applied in sub-band filtering because linear phase property is assured here.
1. Introduction
This Non-uniform Filter Banks (NUFBs) are used in several applications such as audio and image signal processing, biomedical signal processing, hearing aid instruments because of their flexibility in partitioning subbands and better performance [1-3]. Based upon the frequency spacing between bands, filter banks are broadly classified into two categories i.e. uniform band and non-uniform band filter bank. Most of the surveys focus on uniform frequency bandwidth in which incoming signals are split with same sampling rate [4-6]. But in few applications having different incoming data rates and different quality of service non-uniform filter bank is required. For example, to approximate the critical bands sensed by the human ear, non-uniform designs of filter bank using all pass frequency transformation shows better performance than uniform one [7]. Although few methods already have been reported in the literature using constrained or unconstrained optimization techniques, still efficient solutions to the direct design of non-uniform filter banks have yet to be developed [8]. This nonlinear arrangement of frequency bands is necessary when the signal energy exhibits bandwidth dependent distribution. The basic structure of uniform filter bank is shown in Figure 1, where the input signal  is decomposed by M analysis filters
is decomposed by M analysis filters 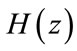 and then outputs are decimated by a factor of M to obtain M sub-band signals. In the synthesis section, the decimated signals are up-sampled by same factor M before passing through the synthesis bank
and then outputs are decimated by a factor of M to obtain M sub-band signals. In the synthesis section, the decimated signals are up-sampled by same factor M before passing through the synthesis bank  and finally sub-band signals are added together to reconstruct the original signal. The theory and design procedure of Perfect Reconstruction Filter Bank (PRFBs) have been extensively studied in the formerly reported literature [4-6]. Among them Cosine Modulated Filter Bank (CMFB) is an efficient technique, where all filters of analysis and synthesis bank are obtained by simply cosine modulation of a single prototype filter.
and finally sub-band signals are added together to reconstruct the original signal. The theory and design procedure of Perfect Reconstruction Filter Bank (PRFBs) have been extensively studied in the formerly reported literature [4-6]. Among them Cosine Modulated Filter Bank (CMFB) is an efficient technique, where all filters of analysis and synthesis bank are obtained by simply cosine modulation of a single prototype filter.
The implementation and design complexities of CMFB are very low compared with other general purpose PRFBs due to the modulation. Thus the design procedure of the complete filter bank reduces to that of the prototype filter and modulation overhead. When the polyphase components of the prototype filter assure some pair-wise power complementary conditions the filter bank will be worked as perfect reconstruction filter bank. But in that case the optimization of the prototype filter coefficients is highly nonlinear. Due to the nonlinear optimization, designing general purpose PRFBs is a complicated problem, particularly for filter banks with rigid frequency specifications such as sharp cutoff, high stopband attenuation in case of large number of channels.
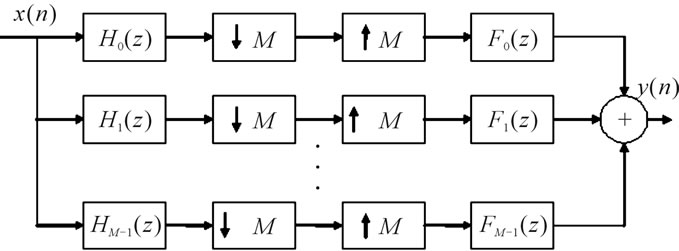
Figure 1. Structure of uniform filter bank.
Consequently, filter banks that structurally satisfy the nearly perfect reconstruction conditions have received considerable attention in recent times [5,6].
Filter banks are broadly classified into two groups, i.e. Perfect Reconstruction (PR) banks and Nearly Perfect Reconstruction (NPR) banks. In PR filter banks the output signal is only delayed version of the input signal and in case of NPR filter banks the output signal approximately characterize the input signal due to small reconstruction error that is acceptable in most applications. By appropriate choice of the prototype filter this inaccuracy can be minimized and many approaches have been reported to the design of uniform or non-uniform filter bank with perfect reconstruction and nearly PR. In our proposed method, the prototype filter is designed using Simulated Annealing (SA) in which to reduce the overall complexity of the prototype filter, optimum numbers of coefficients have been optimized and performance of the non-uniform bank is evaluated. The non-uniform bank is obtained by merging some relevant bands of the corresponding uniform one so that all desirable characteristics of the uniform bank are also preserved. Therefore the design procedure is reduced to the design of optimized prototype filter for the design of uniform bank and thereafter by merging appropriate bands using tree structure method [8-11].
The remaining of this paper is organized as follows: Sections 2 and 3 describe the theory of Uniform and Non-uniform filter bank respectively. Two performance parameters of filter bank are formulated in Section 4. The background of SA has been discussed in details in Section 5. Section 6 describes the design procedure of the prototype filter using SA. Proposed design method is presented in Section 7. Two separate examples have been carried out using proposed method in Section 8 and finally conclusions and future scope are given in Section 9.
2. Uniform Modulated Filter Bank
The basic structure of M-channel maximally decimated filter bank is shown in Figure 1. The reconstructed output signal 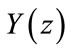 can be stated in terms of the input signal
can be stated in terms of the input signal  as follows [4-6]:
as follows [4-6]:
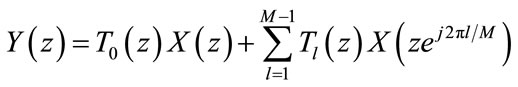 (1)
(1)
where 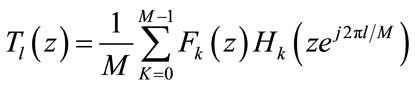
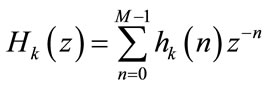 and
and 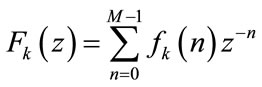
Here  indicates the overall amplitude distortion and
indicates the overall amplitude distortion and ,
, 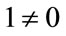 is the aliasing transfer function. To cancel aliasing and attain perfect reconstruction, it is required that
is the aliasing transfer function. To cancel aliasing and attain perfect reconstruction, it is required that
 (2)
(2)
where 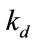 is a positive integer that represents the reconstruction delay of the overall system.
is a positive integer that represents the reconstruction delay of the overall system.
The impulse responses of the analysis bank filters  and synthesis bank filters
and synthesis bank filters  are obtained by simply cosine modulation of the prototype filter
are obtained by simply cosine modulation of the prototype filter  given as:
given as:
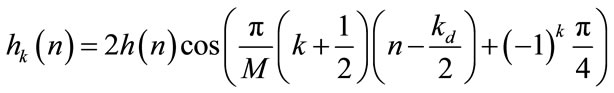 (3a)
(3a)
 (3b)
(3b)
for  and
and  where
where  is the impulse response of the N-length prototype filter
is the impulse response of the N-length prototype filter .
.
Due to narrow transition width of analysis/synthesis section filters and high stop-band attenuation, the overlap between nonadjacent filters is insignificant. Major aliasing component arises for overlapping between adjacent bands that can be cancelled by selecting 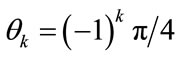 [6]. In most practical applications, the requirement of perfect reconstruction can be relaxed by allowing small amount of errors and the filter banks that closely approximate the perfect reconstruction property can be utilized. Such filter banks are known as nearly perfect reconstruction filter bank are advantageous from arithmetic complexity point of view and VLSI implementation is also possible.
[6]. In most practical applications, the requirement of perfect reconstruction can be relaxed by allowing small amount of errors and the filter banks that closely approximate the perfect reconstruction property can be utilized. Such filter banks are known as nearly perfect reconstruction filter bank are advantageous from arithmetic complexity point of view and VLSI implementation is also possible.
3. Non-Uniform Modulated Filter Bank
In case of uniform filter banks the frequency range  rad/sec is subdivided into M parallel channels of equal bandwidth of
rad/sec is subdivided into M parallel channels of equal bandwidth of  and the maximum decimation or interpolation factor for each band is also M. The frequency response for
and the maximum decimation or interpolation factor for each band is also M. The frequency response for 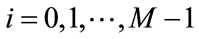 channels are given by [1]:
channels are given by [1]:
 (4)
(4)
Now we consider the design of non-uniform CMFB which is derived from a uniform bank by merging adjacent analysis and synthesis filters [9,10]. We define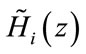 ,
,  to be the filters obtained by merging the
to be the filters obtained by merging the 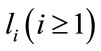 adjacent analysis filters
adjacent analysis filters 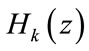 for
for 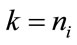 through
through  in a uniform M-channel filter bank shown in Figure 2.
in a uniform M-channel filter bank shown in Figure 2.
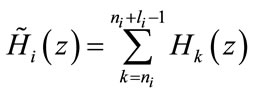 ,
, (5)
(5)
Similarly we define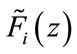 ,
, 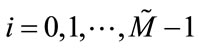 to be the filters of synthesis section obtained by merging the
to be the filters of synthesis section obtained by merging the  adjacent synthesis filters
adjacent synthesis filters  for
for 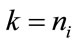 through
through  in a uniform M-channel filter bank.
in a uniform M-channel filter bank.
 ,
,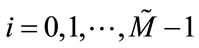 (6)
(6)
Then 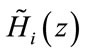 and
and ,
,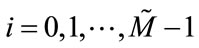 form a new set of analysis and synthesis filters in the
form a new set of analysis and synthesis filters in the  channel non-uniform filter bank. The bandwidth of the analysis filters becomes
channel non-uniform filter bank. The bandwidth of the analysis filters becomes 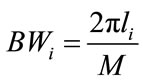 for
for . Here
. Here 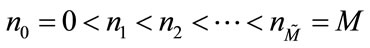 and
and
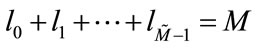 . The maximum factor of decimaltion and interpolation for the
. The maximum factor of decimaltion and interpolation for the 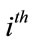 channel of the nonuniform bank is given by
channel of the nonuniform bank is given by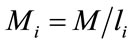 ,
, 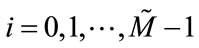 which are not same for all the channels. To obtain integer decimation factor M should be divisible by
which are not same for all the channels. To obtain integer decimation factor M should be divisible by 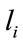 [1,11].
[1,11].
4. Performance Parameters of Filter Bank
Generally three types of errors appear at the reconstructed output waveform i.e. amplitude, phase and aliasing distortion. Assuming high stop-band attenuation for prototype filter reduces aliasing distortion but reconstruction error is increased. The peak to peak reconstructtion and the peak aliasing errors are defined as follows [5,6]:
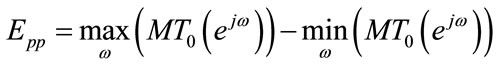 (7)
(7)
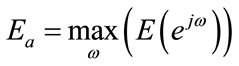 (8)
(8)
where 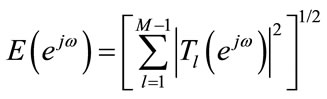
In NPR filter bank, aliasing is eliminated and the amplitude distortion of the overall system is a delay only approximately. Assuming the prototype filter 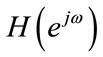 has linear phase response, the conditions for approximate reconstruction can be stated as follows:
has linear phase response, the conditions for approximate reconstruction can be stated as follows:
 for
for  (9)
(9)
 where
where 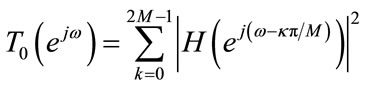 (10)
(10)
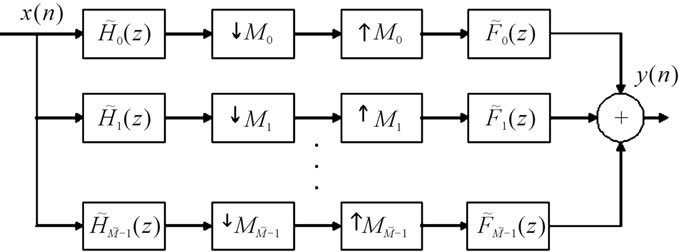
Figure 2. Structure of non-uniform filter bank.
The accurateness of (9) reduces aliasing error and for (10) amplitude distortion is reduced. The phase error can be eliminated completely by using linear phase prototype filter. All three distortion parameters can be reduced greatly with proper choice of optimization technique. Therefore to eliminate amplitude distortion 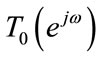 must be constant for all frequencies. To obtain high quality reconstruction in filter bank, the low-pass prototype
must be constant for all frequencies. To obtain high quality reconstruction in filter bank, the low-pass prototype  must satisfy as much as possible two following two conditions:
must satisfy as much as possible two following two conditions:
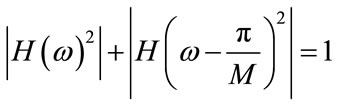 for
for  (11)
(11)
and
 for
for 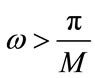 (12)
(12)
The amplitude distortion is eliminated in the combined analysis/synthesis section if (11) is satisfied exactly, while if (12) is satisfied, there is no aliasing between nonadjacent bands. Aliasing between adjacent bands is also eliminated by selecting appropriate phase factors in the modulation. Unfortunately, a finite length filter can not satisfy both the constraints precisely, so it is customary to design one that approximately satisfies them. By combining them into a single cost function and then minimized using the Hooke’s and Jeave’s optimization algorithm near perfect reconstruction can be achieved. Now iteratively change the pass-band frequency to minimize the cost function given by [6]:
 (13)
(13)
The cost function given in (13) is convex with respect to the pass-band/cut-off frequency and any reasonable optimization method will converge to the same global minima value regardless of the starting value of passband frequency.
5. Simulated Annealing Approach
Simulated annealing (SA) is a heuristic random search global optimization method, analogous to complex physical process of heating up a solid metal above melting temperature and then cooling down slowly such that the highly excited atoms can freeze into minimum energy single crystal structure without getting trapped in local minima [12-17]. This method proposed by Kirkpatrick to solve highly nonlinear optimization problem with many constraints [12]. The main advantages over other local search methods are its flexibility and its ability to approach global minimum point regardless of any restricttive properties of the system. As this is a meta-heuristic method, a suitable choice of initial solution is required to turn it into a robust optimization technique. In this approach the quality of the solutions obtained is far better although a long time require to obtain global minima due to its stochastic nature. In the process of finding optimum solution, SA not only accepts optimization solution but also accept deterioration solution in certain degree according to random acceptance criteria (Metropolis criteria) [13]. In addition, the probability to accept deterioration solution tends to 0 gradually, and this make it possible to jump out from local extreme area and then find the global optimum solution, so to ensure the convergence of the algorithm. Simulated Annealing consists of four functional relationships [14]:
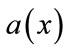 : The probability for accepting a new value given the just previous value.
: The probability for accepting a new value given the just previous value.
 : The cost function to be optimized.
: The cost function to be optimized.
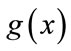 : The probability density function of the state space
: The probability density function of the state space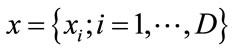 .
.
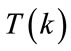 : An annealing temperature schedule in annealing-time for k steps that modifies the instability or fluctuations of one or both of the two previous probability densities.
: An annealing temperature schedule in annealing-time for k steps that modifies the instability or fluctuations of one or both of the two previous probability densities.
5.1. Initialization
A simple local search method starts with an arbitrary initial solution  and a new solution
and a new solution 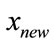 is generated using
is generated using  in the neighborhood of this solution for which the objective function
in the neighborhood of this solution for which the objective function 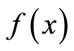 is also calculated. If reduction in
is also calculated. If reduction in 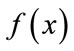 is achieved then new solution
is achieved then new solution 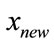 is updated else the current solution is retained and the process is repeated until no further reduction in the objective function is obtained. In this case the searching process may terminate with a local minimum, which may not be the true global optimum. In SA, instead of this policy, the algorithm attempts to avoid being trapped in a local minimum by sometimes accepting even the worse move. The acceptance and rejection of the worse move is controlled by probability function
is updated else the current solution is retained and the process is repeated until no further reduction in the objective function is obtained. In this case the searching process may terminate with a local minimum, which may not be the true global optimum. In SA, instead of this policy, the algorithm attempts to avoid being trapped in a local minimum by sometimes accepting even the worse move. The acceptance and rejection of the worse move is controlled by probability function . The probability of accepting a move, which causes an increased
. The probability of accepting a move, which causes an increased  in
in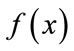 , is called the acceptance function. It is normally set to
, is called the acceptance function. It is normally set to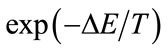 , where T is a control parameter, which corresponds to the temperature in analogy with the physical annealing. This acceptance function implies that the small increase in
, where T is a control parameter, which corresponds to the temperature in analogy with the physical annealing. This acceptance function implies that the small increase in 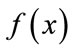 is more likely to be accepted than a large increase in
is more likely to be accepted than a large increase in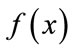 . When T is high most uphill moves are accepted, but as T approaches to zero, most uphill moves will be rejected. Initially, the temperature T is large, and a new point is accepted roughly half the time. The algorithm progresses by attempting a certain number of moves at each temperature, T is reduced, thus lowering the chances that the acceptance function will accept a new point if its functional value is greater than that of the current point.
. When T is high most uphill moves are accepted, but as T approaches to zero, most uphill moves will be rejected. Initially, the temperature T is large, and a new point is accepted roughly half the time. The algorithm progresses by attempting a certain number of moves at each temperature, T is reduced, thus lowering the chances that the acceptance function will accept a new point if its functional value is greater than that of the current point.
5.2. Temperature Reductions
SA also requires a suitable cooling schedule for successful optimization that can be developed by trial and error method and the choice of annealing schedule depends not only on optimization problem but also on specific problem. In case of filter design problems coefficients are chosen from a D-dimensional search space with different finite ranges, bounded by several physical constraints [16]. Boltzmann’s Annealing (BA) and Cauchy’s or Fast Annealing (FA) has infinite ranges of sample distributions and there is no possibility of accepting the differences between each parameter dimension [15]. This problem can be overcome using modified form of Very Fast Simulated Re-annealing (VFSR) known as Adaptive Simulated Annealing (ASA) which is a faster global optimization method [17]. ASA is completely deal with randomly chosen parameter space rather than utilizing deterministic approaches and temperature reduction schedule exponentially decreases which is much faster than BA and FA algorithm. In BA to obtain global optimum of a given cost function the temperature is selected to be not faster than  whereas in FA that is replaced by
whereas in FA that is replaced by . In ASA approach the annealing schedule is chosen as
. In ASA approach the annealing schedule is chosen as . Another important feature of ASA is its ability to perform quenching in a systematic manner and using this approach annealing schedule can be redefined as [18]:
. Another important feature of ASA is its ability to perform quenching in a systematic manner and using this approach annealing schedule can be redefined as [18]:
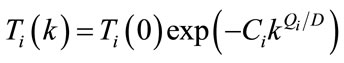 (14)
(14)
5.3. Searching Method
SA is based on iterative random search and calculation of derivative is not required i.e. the cost function does not need to be continuous in the searching domain. Although the function may have many local extremum due to random walk of each independent variables of the cost function and other important features of SA, trapping from the local minimum are possible. Starting with an arbitrary initial guess 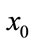 confined in the domain of interest, the initial energy
confined in the domain of interest, the initial energy 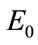 is evaluated using cost function
is evaluated using cost function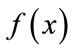 . Now a random walk is taken by perturbation of parameters of
. Now a random walk is taken by perturbation of parameters of 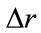 that produces the new point
that produces the new point  for which new energy
for which new energy 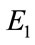 is obtained. Then observe the change in energy caused by random movement of variables from
is obtained. Then observe the change in energy caused by random movement of variables from 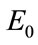 to
to  as follows:
as follows:
 (15)
(15)
Based on Metropolis criterion [13] the newly generated point  is accepted as a new starting point if
is accepted as a new starting point if  i.e. if random walk would bring the system to a lower energy state otherwise
i.e. if random walk would bring the system to a lower energy state otherwise  is chosen to be a new starting point with probability of
is chosen to be a new starting point with probability of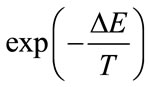 . Mathematically that can be defined as
. Mathematically that can be defined as
 (16)
(16)
where T is current “temperature” of the system that controls the rejection of new point. Now take a random number 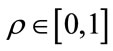 and if
and if ,
,  is accepted as a new starting point and update
is accepted as a new starting point and update . Otherwise, the new point
. Otherwise, the new point 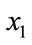 is rejected and starting point remains same as
is rejected and starting point remains same as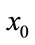 . Here
. Here  indicates the acceptance probability of selecting
indicates the acceptance probability of selecting 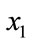 as a new starting point with unity probability if cost function decreases after random movement. On the other hand, if
as a new starting point with unity probability if cost function decreases after random movement. On the other hand, if 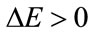 the point
the point  can be chosen as starting point with a probability
can be chosen as starting point with a probability
 . For large values of T, most of the time
. For large values of T, most of the time 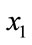 is accepted and to obtain best performance the value of T should satisfy approximately
is accepted and to obtain best performance the value of T should satisfy approximately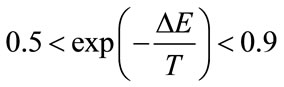 because when probabilities close to 1 most of the point would be accepted and below 0.5 require unnecessary function assessment to escape from local minima [19]. The step size
because when probabilities close to 1 most of the point would be accepted and below 0.5 require unnecessary function assessment to escape from local minima [19]. The step size  should be chosen properly such that it can escape from local minima within short period hence initially chosen a large value. But as the iteration number increases step size
should be chosen properly such that it can escape from local minima within short period hence initially chosen a large value. But as the iteration number increases step size  should be reduced otherwise
should be reduced otherwise 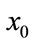 may cross over the point which corresponds to the global minimum. Therefore finally smaller step size is required to reach closer to global minimum.
may cross over the point which corresponds to the global minimum. Therefore finally smaller step size is required to reach closer to global minimum.
5.4. Stopping Criterion
To minimize execution time and computational effort a well constructed stopping criterion is required. The stopping criterion can be defined based on objective function value or on final temperature or maximum no of iterations. When the cost function attains a minimum value of objective function set by the designer based on system performance the searching process may terminate. Another way is starting with a high temperature select and the process will freeze until no change in the objective function is observed or the temperature falls below the minimum value. The procedure may also run for predefined no of iterations after which the optimization routine automatically terminates.
6. FIR Filter Design Using Simulated Annealing
The frequency response of an FIR filter with impulse response 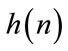 is the Z-transform of the sequence evaluated on the unit circle:
is the Z-transform of the sequence evaluated on the unit circle:
 ,
,  (17)
(17)
Depending upon the polarity and symmetrical the linear phase FIR filter can be classified into 4 types among which type 1 and type 2 is considered here to design with SA.
Type 1: positive symmetrical impulse response with odd length
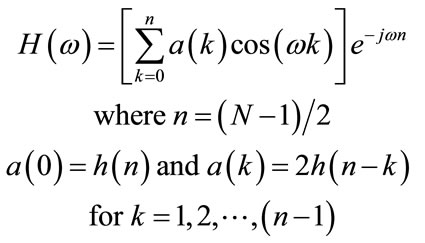 (18)
(18)
Type 2: positive symmetrical impulse response with even length
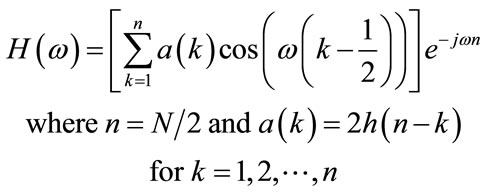 (19)
(19)
Therefore to obtain the desired response using symmetric property only n variables instead of N need to optimized using SA. The overall filter bank can be constructed using the following objective function:
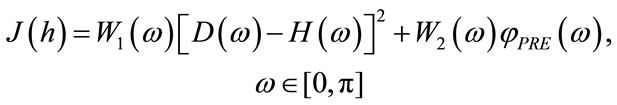 (20)
(20)
where 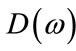 is the desired frequency response,
is the desired frequency response, 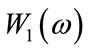 and
and 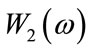 are the weighting functions,
are the weighting functions,  indicates the cost function to reduce the PRE. Now apply SA to minimize the maximum weighted difference given in (20) using the procedure, as given below in pseudo code format [17-19]:
indicates the cost function to reduce the PRE. Now apply SA to minimize the maximum weighted difference given in (20) using the procedure, as given below in pseudo code format [17-19]:
Step 1: Make an initial guess of the solution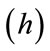 , lower bound
, lower bound , upper bound
, upper bound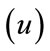 , maximum number of iterations
, maximum number of iterations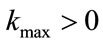 , the quenching factor
, the quenching factor 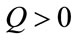 i.e. taken as small value for slow quenching and large for fast one and the minimum tolerance of function
i.e. taken as small value for slow quenching and large for fast one and the minimum tolerance of function  that can be assumed as very small value.
that can be assumed as very small value.
Step 2: Let  and
and 
Step 3: For  to
to 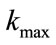

Generate 1 × N uniform random vector to make 
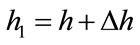

If 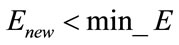 then
then
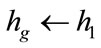 and
and 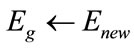
exit from the loop;
end;
If  then
then
 and
and 
else
Generate a uniform random number 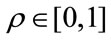
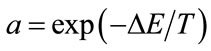
if  then
then
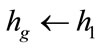 and
and 
else
No action and reject the solution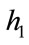 .
.
end
end
The corresponding flow chart of the modified Simulated Annealing is given in Figure 3.
7. Proposed Design Method
1) Assume number of bands (M), transition width ( ) and stop-band attenuation (As). Initialize step value, search direction, flag, toll and initial value of objective function (20).
) and stop-band attenuation (As). Initialize step value, search direction, flag, toll and initial value of objective function (20).
2) Set the while loop with flag = 0 (Design prototype filter).
a) Design the prototype filter 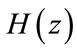 using Simulated Annealing assuming pass-band frequency
using Simulated Annealing assuming pass-band frequency , stop-band edge at
, stop-band edge at 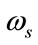 satisfying pass-band as well as stop-band specifications and also minimize the cost function (20). Determine the maximum absolute value of objective function using current filter coefficients. And compare the current value of objective function with previous or initial value.
satisfying pass-band as well as stop-band specifications and also minimize the cost function (20). Determine the maximum absolute value of objective function using current filter coefficients. And compare the current value of objective function with previous or initial value.
b) If the current value greater than previous value step becomes half and change search directions then go step (2d).
c) If the difference between current value and previous value less than or equal to toll, then flag becomes set to “1”, come out from the loop, and go to step (3).
d) Modify the value of pass-band frequency as ( ) and now current value of objective function becomes previous value and go to step (2a).
) and now current value of objective function becomes previous value and go to step (2a).
End of the loop.
3) Calculate the value of peak to peak reconstruction
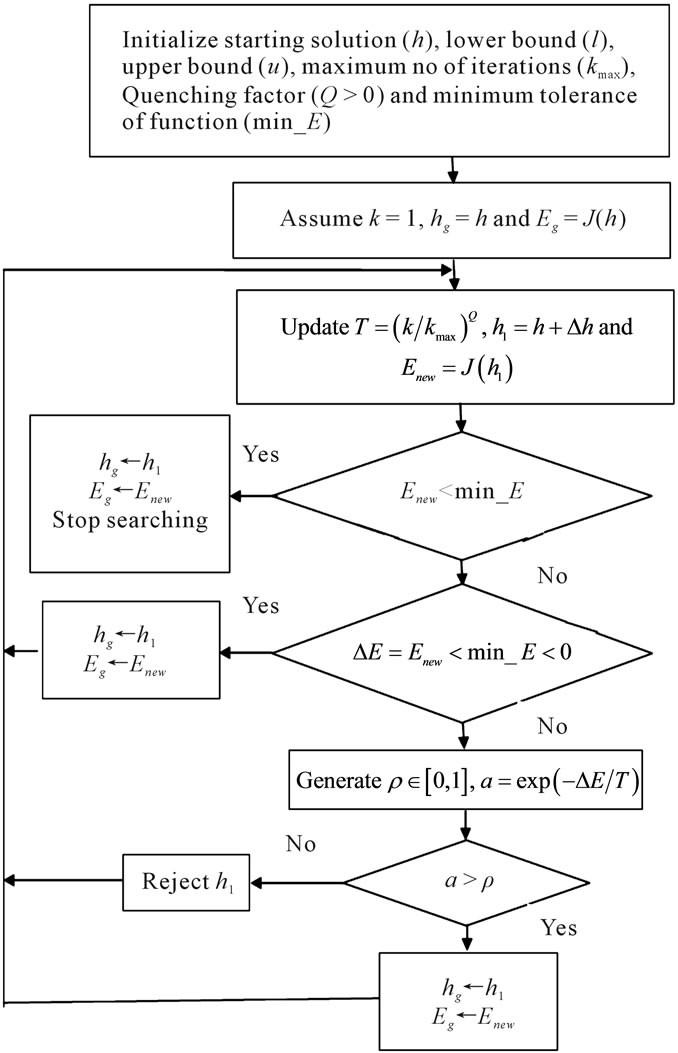
Figure 3. FIR filter design using SA.
and the peak aliasing errors using (7) and (8) for minimum value of objective function obtained above. Then plot peak to peak reconstruction and peak aliasing errors in log scale.
8. Design Examples
Example 1: In this example a 3-channel NUFB has been designed using SA with the same specifications as given in [9,10], using SA. The sampling factor for three channels is 4, 4, 2 respectively. To design the prototype filter for stop-band attenuation of As = 100 dB the obtained values of filter taps is N = 63, 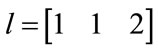 and
and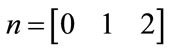 . The magnitude response of the analysis bank is shown in Figure 4. The band-edge frequencies are
. The magnitude response of the analysis bank is shown in Figure 4. The band-edge frequencies are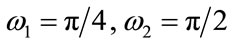 . The variation of amplitude distortion in the whole frequency range is given in Figure 5. Figure 6 describes the minimization of cost function using the robust algorithm. From this plot it is observed that within 15,000 iterations the cost function attains the minimum value. The obtained value of maximum amplitude distortion is
. The variation of amplitude distortion in the whole frequency range is given in Figure 5. Figure 6 describes the minimization of cost function using the robust algorithm. From this plot it is observed that within 15,000 iterations the cost function attains the minimum value. The obtained value of maximum amplitude distortion is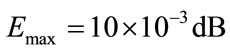 .
.
Example 2: Here a 5 channel NUFB is designed using

Figure 4. Amplitude responses of the analysis filters.
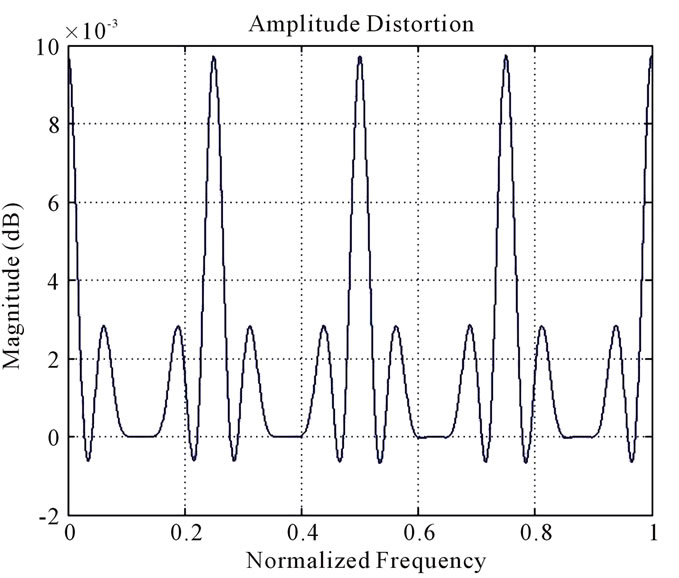
Figure 5. Variation of amplitude distortion.
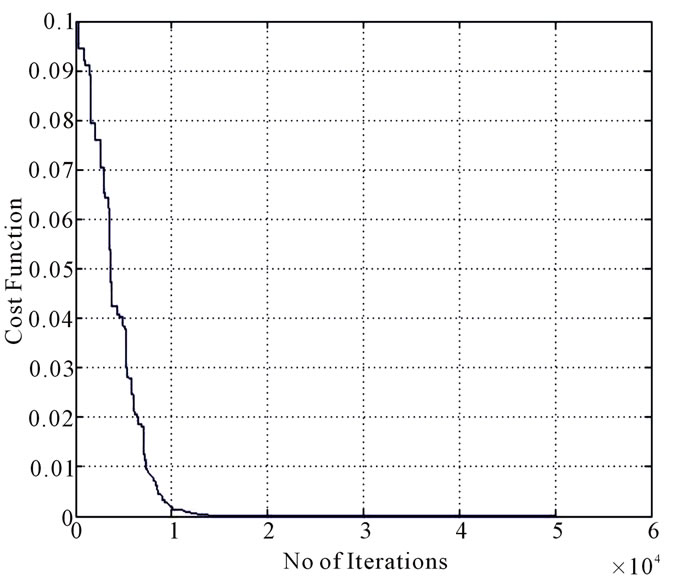
Figure 6. No of iterations vs. cost function.
the same method with the following specifications as given in [3,8]. The decimation factors for all five channels are chosen as (2, 2, 1, 1, 2). The design specifications of the filter are: As = 50 dB, N = 163, 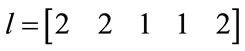 and
and . The band-edge frequencies are
. The band-edge frequencies are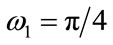 ,
, 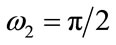 ,
, 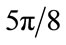
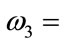 ,
, . The obtained value of maximum amplitude distortion is
. The obtained value of maximum amplitude distortion is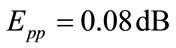 . Figure 7 and Figure 8 shows the magnitude response of analysis bank and amplitude distortion plot respectively. The objective function attains the minimum value within 60,000 iterations shown in Figure 9.
. Figure 7 and Figure 8 shows the magnitude response of analysis bank and amplitude distortion plot respectively. The objective function attains the minimum value within 60,000 iterations shown in Figure 9.
9. Conclusion
Here the prototype filter is designed using modified SA and all filters of the bank are obtained by modulation and merging of adjacent bands of prototype filter. Two sepa-
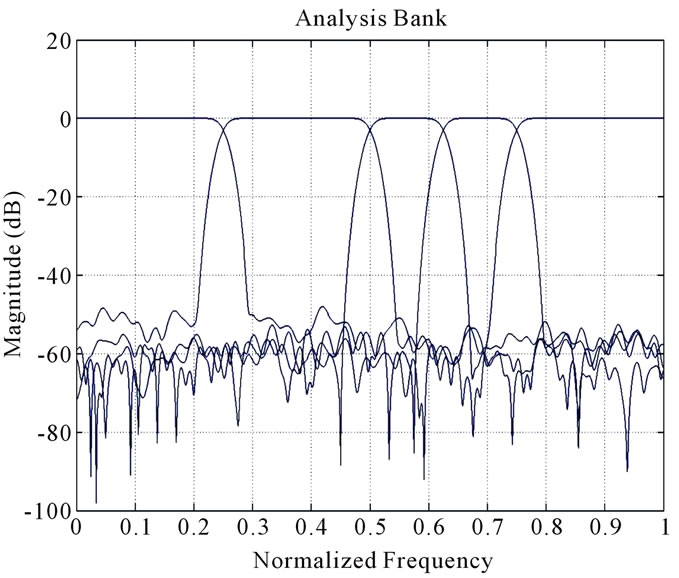
Figure 7. Amplitude responses of the analysis filters.

Figure 8. Variation of amplitude distortion.

Figure 9. No of iterations vs. cost function.
rate examples have been carried out using the proposed method. From the obtained results it is obvious that with the increase of filter taps the convergence procedure becomes slow i.e. large no of iterations are required to optimize the parameters. In case of 3 channel bank only 15,000 iterations are required whereas for 5 band 60,000 evaluations. The sampling factors for the different channels are assumed as integer value. Here the assumed cost function always reaches the global minimum regardless of the initial parameter selection. Further reduction in amplitude distortion can be obtained with suitable design of objective function. The closed form design of the system matrices may lead to fast convergence of the above algorithm. The obtained filter coefficients show linear phase response hence always stable.
REFERENCES
- S. Wada, “Design of nonuniform division multirate FIR filter banks,” IEEE Transactions on Circuits and Systems II: Analog and Digital Signal Processing, Vol. 42, No. 7, 1995, pp. 115-121. doi:10.1109/82.365350
- J. Princen, “The design of nonuniform modulated filter banks,” IEEE Transactions on Signal Processing, Vol. 43, No. 11, 1995, pp. 2550-2560. doi:10.1109/78.482106
- J. Lee and B. G. Lee, “A design of nonuniform cosine modulated filter banks,” IEEE Transactions on Circuits and Systems II: Analog and Digital Signal Processing, Vol. 42, No. 11, 1995, pp. 732-737. doi:10.1109/82.475253
- H. H. Kha, H. D. Tuan and T. Q. Nguyen, “Efficient Design of Cosine Modulated Filter-banks via Convex Optimization,” IEEE Transactions on Signal Processing, Vol. 57, No. 3, 2009, pp. 966-976. doi:10.1109/TSP.2008.2009268
- R. Bregovic and T. Saramaki, “An efficient approach for designing nearly perfect-reconstruction low delay Cosine-Modulated filter banks,” IEEE International Symposium on Circuits and Systems, Vol. 1, 2002, pp. 825- 828.
- S. Dhabal, S. M. L. Chawdhury and P. Venkateswaran, “A Novel Low Complexity Multichannel Cosine Modulated Filter Bank Using IFIR Technique for Nearly Perfect Reconstruction,” 2012 1st International Conference on Recent Advances in Information Technology (RAIT), Dhanbad, 15-17 March 2012, pp. 208-213.
- A. Petrovsky, M. Parfieniuk and K. Bielawski, “Psychoacoustically Motivated Nonuniform Cosine Modulated Polyphase Filter Bank,” 2nd International Workshop on Spectral Methods and Multirate Signal Processing, France, September 2002, pp. 95-101.
- Z. J. Zhang and Y. Yang, “A Simple Design Method for Nonuniform Cosine Modulated Filter banks,” International Symposium on Microwave, Antenna, Propagation and EMC Technologies, Hangzhou, 16-17 August 2007, pp. 1052-1055.
- X. M. Xie, X. Y. Chen and G. M. Shi, “A Simple Design Method of Linear Phase Nonuniform Filterbanks with Integer Decimation Factors,” Proceedings of International Symposium on Circuit and System, Vol. 1, 7-10 August 2005, pp. 724-727.
- J. Li, T. Q. Nguyen and S. Tantaratana, “A Simple Method for Near-Perfect-Reconstruction Nonuniform Filter banks,” IEEE Transactions on Signal Processing, Vol. 45, No. 8, 1997, pp. 2105-2109. doi:10.1109/78.611222
- X. M. Xie, S. C. Chan and T. I. Yuk, “A Class of Perfect Reconstruction Nonuniform Cosine-Modulated Filter Bank with Dynamic Recombination,” Proceedings of 11th European Signal Processing Conference, Vol. 2, 2002, pp. 549-552.
- S. Kirkpatrick, C. D. Gelatt Jr. and M. P. Vecchi, “Optimization by Simulated Annealing,” Science, vol. 220, no. 4598, 1983, pp. 671-680. doi:10.1126/science.220.4598.671
- N. Metropolis, A. Rosenbluth, M. Rosenbluth, A. Teller and E. Teller, “Equation of state calculations by fast computing machines,” Journal of Chemical Physics, Vol. 21, No. 6, 1953, pp. 1087-1090. doi:10.1063/1.1699114
- B. Rosen, “Function optimization based on advanced simulated annealing,” www.ingber.com
- L. Ingber, “Adaptive simulated annealing (ASA): Lessons learned,” journal of Control and Cybernetics, Vol. 25, 1996, pp. 33-54. www.ingber.com
- N. Benvenuto, M. Marchesi and A. Uncini, “Applications of Simulated Annealing for the design of Special Digital Filters,” IEEE Transactions on Signal Processing, Vol. 40, No. 2, 1992. pp. 323-332. doi:10.1109/78.124942
- L. Ingber, “Very fast simulated re-annealing,” Mathematical and Computer Modelling, Vol. 12, No. 8, 1989, pp. 967-973.
- H. A. Oliveira Jr., A. Petraglia and M. R. Petraglia, “Frequency Domain FIR Filter Design Using Fuzzy Adaptive Simulated Annealing,” IEEE International Symposium on Signal Processing and Information Technology, Giza, 15- 18 December 2007, pp. 884-888. doi:10.1109/ISSPIT.2007.4458181
- B. W. Jung, H. J. Yang and J. Chun, “Finite Wordlength Digital Filter Design Using Simulated Annealing,” 2008 42nd Asilomar Conference on Signals, Systems and Computers, Pacific Grove, 26-29 October 2008, pp. 546-550.

