Journal of Signal and Information Processing
Vol.3 No.2(2012), Article ID:19558,4 pages DOI:10.4236/jsip.2012.32023
Robust Image Registration Based on Mutual Information Measure
![]()
1Faculty of Computer Science, Polish-Japanese Institute of Information Technology, Warszawa, Poland; 2Institute of Mechanics and Applied Computer Science, Kazimierz Wielki University, Bydgoszcz, Poland.
Email: wkos@pjwstk.edu.pl, me@pawelmichalak.com, piotr.gut@stylex.pl
Received November 23rd, 2011; revised March 10th, 2012; accepted April 8th, 2012
Keywords: Image Registration; Mutual Information; Entropy; Affine Transformation; Medical Images
ABSTRACT
A new implementation of the image registration algorithm based on the mutual information is presented for the case of medical images. The registration is achieved if the maximum of the mutual information is attained. In this maximization process optimal values of five parameters of an affine transformation are searched.
1. Introduction
The issue of image registration is everywhere where there is a need for common analysis, presentation of two images of the same object, and showing other aspects of it. This is due to the fact that the images can be recorded using different techniques at other times, in different conditions and different perspectives of providing complementary information. Data (images) provided by various types of data acquisition systems are called multimodal data.
Multimodal image registration can be viewed as the task of integrating information from multiple sources. It consists of transformation of the overlayed image to the reference image coordinate system by means of appropriate transformations. Those transformations are based on specific characteristics of the multimodal data. Common presentation, usually visual, registered images creates the opportunity to see fuller details of the analyzed object. An important role the image registration is played in medical imaging [1], which allows detect diseases, monitoring of the patient, planning and assessment the quality of treatment (radiotherapy, surgery, etc.) and supports doctors in these tasks. To date, several methods of image registration were developed [2-4].
From the medical image registration point of view, a very important element is the selection of appropriate image features under which the image registration will be made. It is so important that it can play a very important role in the treatment of a patient. Sometimes one uses even the most uncomfortable for the patient’s invasive methods consisting in fixing the patient’s body elements, where the outside markups are placed, used later in the image registration. This can be done using screws driven in shallow drilled holes e.g. the skull, or by means of special pins. Also, one can find a less invasive method consisting of placing on the patient’s skin special characters in certain places.
In this article we present a method of mutual information in medical imaging, which is a fully automated method. The advantage of this method is that it benefits from features, which are all pixels from registration images. Features’ identification, in this case, is completely non-invasive. It does not require any pre-processing of images, which could produced already at this stage cause errors; it does not use any markups. It is very convenient for the patient and medical team, which makes the method very useful in the clinical treatment.
Organization of the paper is as follows. In Section 2 the concept of mutual information is introduced. It is based on the concept of entropy which shortly presented in Section 3. The basis for its definition which is shortly presented the histogram about which Section 4 treats. Here the optimization technique based on Powell’s method with the golden search method is quoted. Tests performed on pairs of images CT-MRI and MRI-PET are presented in Section 5. The paper ends with conclusions.
2. Mutual Information
Mutual information is a statistical measure that originates from the information theory. It measures statistical dependence of two random variables and presents how much information one random variable provides about another random variable.
Research on mutual information as an image registration measure has its beginning in the early nineties. In 1993 D. L. G. Hill used a feature space that presents all the combinations of corresponding pixels intensities in a pair of images. The feature space changes along with the alignment of images. If the images are correctly registered corresponding anatomical structures could be identified as specific groups in the feature space. In the case of mis-registration the structures in the first image do not match to their corresponding pixels in the second image. This creates not existing pairs of intensities in the feature space and affects its dispersion. This property of the feature space allowed to apply dispersion as a registration measure. Small amount of dispersion in the feature space means that the pair of images is aligned correctly.
As a result in 1995 A. Collignon and C. Studholme proposed entropy as a registration measure. Entropy measures the dispersion of the probability distribution function. It reaches its minimum when there is one main element in the distribution and has its maximum in the case of equal probability of occurrence of each of the elements. Therefore finding transformations that minimize the entropy leads to correct registration of the images.
Shortly after use of entropy in image registration A. Collignon and P. Viola with W. M. Wells presented a mutual information as a new image registration measure [5]. Soon it became one of the leading methods of multimodal images registration [6].
Mutual information could be presented in many ways. The most common formulas are based on Shannon’s entropy and Kullback-Leibler distance measure between two probability distributions. By means of Shannon’s entropy the mutual information could be presented. It will be done in the next sections.
3. Entropy
Let H(A) and H(B) be the entropies of random variables A and B, respectively, while H(A,B) is their joint entropy, and 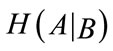 and
and 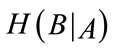 are the entropies of A given B and of B given A, respectively. In particular
are the entropies of A given B and of B given A, respectively. In particular
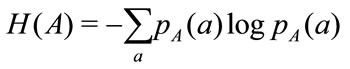
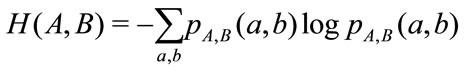
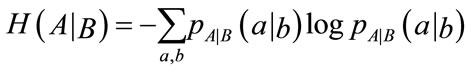
Then mutual information could be presented in terms of entropy
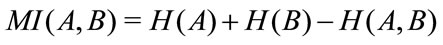 (1)
(1)
Here H(A) is Shanon’s entropy of the image A calculated from the probability distribution of its pixels’ intensities, while 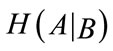 is a conditional entropy based on the conditional probability
is a conditional entropy based on the conditional probability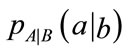 , which could be interpreted as a probability that for given pixel intensity a in the image A the corresponding pixel in the image B will have intensity value b. In this case mutual information could be defined as a measure of information that one image contains about another. It is assumed that images are registered correctly when their mutual information is maximal, in other words when the amount of information they contain about each other is maximal.
, which could be interpreted as a probability that for given pixel intensity a in the image A the corresponding pixel in the image B will have intensity value b. In this case mutual information could be defined as a measure of information that one image contains about another. It is assumed that images are registered correctly when their mutual information is maximal, in other words when the amount of information they contain about each other is maximal.
If the images are regarded as two models, then one can naturally require that one model be predictable from another. Predictability is closely related to the concept of entropy. A predictable random variable has low entropy, while an unpredictable random variable has high entropy.
Another popular definition of the mutual information is based on Kullback-Leibler distance measure between two probability distributions (A and B):
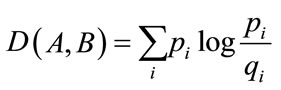 (2)
(2)
If we assume pixels’ intensities in a pair of images as random variables we can apply any statistical measure. Then the mutual information, denoted by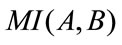 , measures the degree of dependence of A and B by estimating the distance between the joint distribution
, measures the degree of dependence of A and B by estimating the distance between the joint distribution 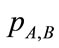 and the distribution in the case of a complete independence
and the distribution in the case of a complete independence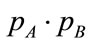 . The formal expression for
. The formal expression for 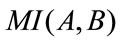 is
is
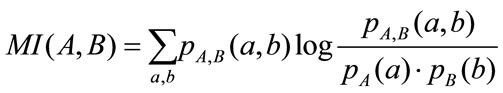 (3)
(3)
Let us recall that two random variables: A and B, with marginal probability distributions, 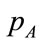 and
and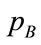 , and joint probability distribution,
, and joint probability distribution, 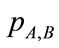 , are statistically independent if
, are statistically independent if
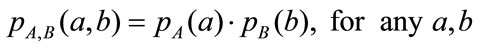
They are maximally dependent if they are related by a mapping T such that
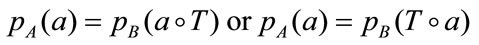 (4)
(4)
where the symbol 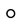 denotes the function composition (superposition).
denotes the function composition (superposition).
Now we can see why the mutual information becomes a tool in the multimodal image registration. Therefore in the case of images the mutual information could be interpreted as some measure of the dependence between pixels’ intensities in images. Maximal dependence exists when the images are correctly aligned [6,7]. Estimation of probability distributions 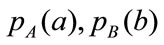 and joint probability distribution
and joint probability distribution 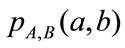 of pixels intensities are crucial elements of the mutual information based image registration. It could be achieved by the normalization of a joint histogram
of pixels intensities are crucial elements of the mutual information based image registration. It could be achieved by the normalization of a joint histogram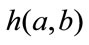 .
.
4. Histogram
Considering a pair of intensity values 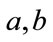 of a pair of images, as random variables A and B. It is possible to estimate marginal
of a pair of images, as random variables A and B. It is possible to estimate marginal 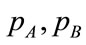 and joint distributions
and joint distributions 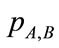 by normalization of the marginal and joint histograms
by normalization of the marginal and joint histograms 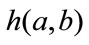 of the images:
of the images:
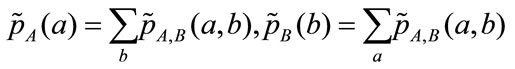 (5)
(5)
with
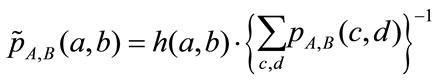
Joint histogram 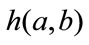 is the object feature of two images: reference and floating
is the object feature of two images: reference and floating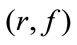 , and it is based on their pixels intensities. Value at the point
, and it is based on their pixels intensities. Value at the point 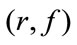 means how many times intensity f in floating image covered intensity r in reference image. For example every time a pixel of intensity 204 in floating image B covers a pixel of intensity 181 in reference image A the value at the point (181, 204) increases by 1 [7], cf. Figure 1.
means how many times intensity f in floating image covered intensity r in reference image. For example every time a pixel of intensity 204 in floating image B covers a pixel of intensity 181 in reference image A the value at the point (181, 204) increases by 1 [7], cf. Figure 1.
Dispersion of the joint histogram is correlated with mis-registration of the images. The smallest dispersion could be observed in case of correct images alignment.
In the example, cf. Figure 2, the same MRI image was a reference and a floating one. The image was displaced by 20 pixels. There is a visible dispersion of the joint histogram before registration. Because of the fact that the images are identical corresponding pixels intensities create a diagonal line after the registration. The process of the mutual information based image registration refers to solving the optimization problem. The aim of the optimization is to find transformation parameter 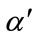 for which the mutual information MI of two given images is maximal in which optimal transformation parameters is searched. We can write
for which the mutual information MI of two given images is maximal in which optimal transformation parameters is searched. We can write
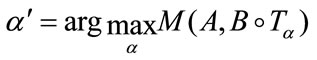 (6)
(6)
where 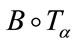 denotes the composition appearing on RHS of (4).
denotes the composition appearing on RHS of (4).
Our main assumptions are:
• Intensities a and b could be related by a geometric transformation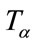 , i.e.
, i.e.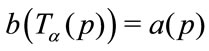 , where
, where 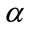
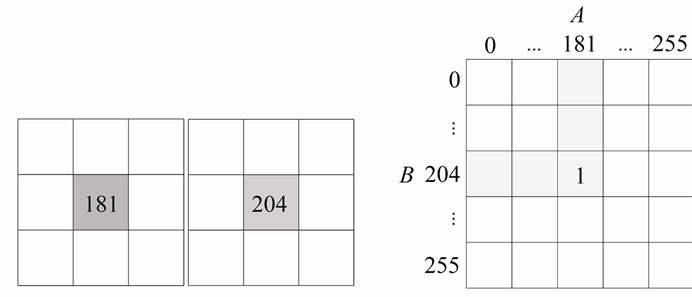
Figure 1. Formation of joint histogram of images A and B.

Figure 2. MRI image, and joint histograms before and after registration.
is the registration vector-valued parameter at the pixel location p. It describes: translation in the x direction, translation in the y direction, angle of rotation and scaling.
• Images are correctly aligned by the transformation 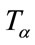 when their mutual information
when their mutual information 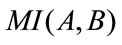 from (3), with substitution from (5) is maximal in (6).
from (3), with substitution from (5) is maximal in (6).
• The process of the image registration refers to solving the optimization problem in which optimal parameter 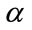 is searched.
is searched.
• The optimization problem can be solved using Powell’s method.
Choice of optimization method is crucial for the accuracy and duration of the registration process. The most common techniques include such methods as Powell’s method, Nelder-Mead simplex method or steepest descent method. Thanks to the proven performance of the Powell’s method that was the choice for the test implementation. Powell’s method allows to simplify multidimensional problem to one dimensional optimization task. Each of the iterations of the algorithm consists of n one dimensional searches along defined directions. To find the optimum for each of the directions any linear optimization method such as golden section search method could be used. Each direction is responsible for one of the transformation parameters. Powell’s method is simple to implement and it does not require computation of gradient what might computationally be expensive [8]. Powell’s method is a non-gradient numerical technique (zero-order method) for unconstrained optimization problems.
The number of searched parameters depends on the type of transformation and its number of degrees of freedom. For the test implementation of the method affine transformations with five degrees of freedom were used— translation in the x and y directions, rotation around center of the image and scaling in x and y. In that case the optimization of a function of five variables was performed.
5. Examples
Two images A and B present MRI and CT images. Third image is the absolute difference after the registration, cf. Figure 3.
Below two images A and B present PET and MRI images. Third image is the absolute difference after the
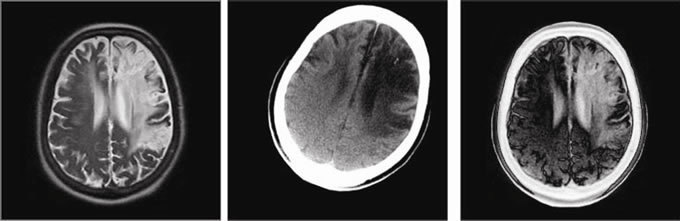
Figure 3. MRI and CT images, and absolute difference after registration.
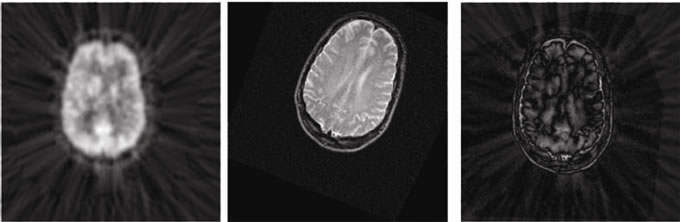
Figure 4. PET and MRI images, and absolute difference after registration.
registration.
Test implementation proved that the mutual information is a highly reliable and effective method of the multimodal images registration. Tests performed on pairs of images CT-MRI and MRI-PET showed the general registration performance and the accuracy as well as the reliability of the mutual information function in the case of a possible image degradation caused by acquisition errors. Most of the tests were completed successfully.
6. Conclusion
Mutual information is a highly effective method for multimodal medical images registration. No assumption concerning particular relationship between pixel intestines in images is needed. Without any prior feature extraction (or prior feature segmentation) or preprocessing of the images the mutual information proved to be the highly accurate and robust method of multimodal medical images registration, cf. Figure 4.
REFERENCES
- I. N. Bankman, Ed., “Handbook of Medical Imaging— Processing and Analysis,” Academic Press, London, 2000.
- L. G. Brown, “A Survey of Image Registration Techniques,” ACM Computing Surveys, Vol. 24, No. 4, 1992, pp. 325-376. doi:10.1145/146370.146374
- C. R. Mauer and J. M. Fitzpatrick, “A Review of Medical Image Registration,” In: R. J. Maciunas, Ed., Interactive Image Guided Neurosurgery, American Association of Neurological Surgeons, 1993, pp. 17-44.
- P. A. van den Elsen, E. J. D. Pol and M. A. Viergever, “Medical Image Matching—A Review with Classification,” IEEE Engineering in Medicine and Biology, Vol. 3, 1993, pp. 26-39. doi:10.1109/51.195938
- P. Viola and W. M. Wells III, “Alignment by Maximization of Mutual Information,” International Journal of Computer Vision, Vol. 24, No. 2, 1997, pp. 137-154. doi:10.1023/A:1007958904918
- L. Chmielewski, J. L. Kulikowski and A. Nowakowski, Eds., “Biomedical Imaging (in Polish),” In: M. Nałecz, Ed., Series Biocybernetics and Biomedical Engineering, Vol. 8, Akademicka Oficyna Wydawnicza EXIT, Warsaw, 2003.
- K. Kuczyński and P. Mikołajczak, “Mutual Information Based Registration of Brain Images,” Journal of Medical Informatics and Technologies, Vol. 3, No. 3, 2002, pp. 213-219.
- F. Maes, A. Collignon, D. Vandermeulen, G. Marchal and P. Suetens, “Multimodality Image Registration by Maximization of Mutual Information,” IEEE Transactions on Medical Imaging, Vol. 16, No. 2, 1997, pp. 187-198. doi:10.1109/42.563664

