International Journal of Geosciences
Vol.07 No.04(2016), Article ID:65828,10 pages
10.4236/ijg.2016.74040
Prediction of Tight Sand Reservoir with Multi-Wavelet Decomposition and Reconstructing Method
Lifang Cheng, Yanchun Wang, Zhiguo Li, Fuxiu Gong
School of Geophysics and Information Technology, China University of Geosciences, Beijing, China

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 February 2016; accepted 22 April 2016; published 25 April 2016
ABSTRACT
Special reservoir or fluid has an abnormal response to some certain frequencies, so that seismic decomposition and reconstruction are used to highlight the seismic reflection at certain frequencies useful to identify special geological bodies. Because seismic wavelets are time-varying and spatial-variable in the propagation, synthetic traces based on single wavelet make some weak but useful information lost, and make artifacts form. However, Morlet wavelet aggregation with mathematical analytical expression is able to fully and correctly reflect the variations of wavelet in the propagation of underground medium. The matching pursuit algorithm on the basis of Morlet wavelet improves the calculating efficiency in decomposition and reconstruction greatly. This method is applied to the actual study area to do conjoint analysis of single well and well-tie multi- wavelet decomposition. It is found that frequencies sensitive to interest reservoirs range from 8 to 34 Hz. Reconstructing the wavelets at those special frequencies and analyzing the reconstructed seismic data, it is pointed out that interest reservoirs have abnormal characteristics with respectively strong RMS amplitude in the reconstructed data. Crossplot of gamma value at wells and reconstructed RMS amplitude suggests that anomalies caused by interest reservoirs are well separated from the background anomalies when the reconstructed RMS amplitude is greater than 3650. Quantitative prediction results of interest reservoirs distribution in the study area reveal that interest reservoirs of western and northern study area are distributed annularly and bandedly, while most contiguous sandstone in eastern regions appears sporadically.
Keywords:
Morlet Wavelet, Matching Pursuit, Decomposition and Reconstruction, Tight Sandstone, Reservoir Prediction

1. Introduction
With the objects of seismic exploration and development transiting form the conventional structural reservoirs to the subtle reservoirs including low relief structure, thin interbedded reservoirs, upward dipping formation and lithological pinch out, the conventional post-stack seismic data cannot meticulously describe various geological anomalies [1] . Especially the thickness of thin reservoir is a few or decade meters which is far less than a quarter of seismic wavelength, so the reflected waves of thin sandstone interbedded with thin mudstone are interfered with each other, and it makes seismic identification more difficult. Therefore, it’s necessary to use some special frequency information of seismic signals to highlight the certain geological anomalies. Multi-wavelet seismic decomposition and reconstruction is proposed to decompose the seismic traces to multiple wavelet with linear superposition firstly, and then determine the interest frequencies according to geological anomalies having responses at some certain frequencies by means of time-frequency transform method, and linearly reconstruct the wavelets at those given frequencies finally to get new seismic data meeting the research purposes [1] .
Multi-wavelet concept was first proposed by Geronimo, Hardin and Massopust, et al. [2] in 1994, then Lilly and Park [3] developed a new technology called multi-wavelet transform in 1995. Lots of researchers improved the multi-wavelet decomposition technology based on this principle afterward. Nowadays there are many methods to achieve multi-wavelet decomposition and reconstruction, and one of them is Matching Pursuit (MP) algorithm first proposed by Mallat and Zhang et al. [4] in 1993. It is on the basis of Gabor wavelet dictionary, but is characterized by greed reducing the computation efficiency. Later Liu J. (2004) and Marfurt (2005) et al. [5] [6] successively proposed new matching pursuit algorithm based on Ricker wavelet and Morlet wavelet to decrease the scale of wavelet dictionary. On top of that, these two researchers put forward the dynamic matching pursuit algorithm [7] to improve the calculating speed greatly. Many other researchers at home such as Song Weiqi (2007), Chen Lin (2008), Feng Lei (2009), and Zhang Xianwen (2010) et al. improved MP algorithm to one degree or another and obtained good application effects [8] - [11] . However, it is still very rare that applying the matching pursuit algorithm to the development stage to predict the interest sandstone associations and to guide the deployment of development wells.
Since that the reservoir in the research area is tight thin sandstone with low porosity and low permeability and that the sandstones vary quickly in lateral direction, the general reservoir prediction method cannot identify the distribution of interest reservoirs. Therefore, this paper intends to use matching pursuit decomposition based on Morlet wavelet to decompose the seismic data volume into data at single frequencies, and pick out the frequencies at which the interest reservoirs have an obvious abnormality combined with well data analysis. The data at interest frequencies are planned to be reconstructed to obtain a new seismic data volume at which the seismic attributes and well data analysis are applied to predict the distribution of interest reservoirs.
2. Method Principle
2.1. Multi-Wavelet Convolution Model
The convolution model of common seismic interpretation has an assumption that the wavelet is unique and constant [12] [13] . The convolution formula is shown in Formula (1).
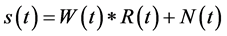 (1)
(1)
where 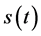 is synthetic record,
is synthetic record,  is the seismic wavelet,
is the seismic wavelet,  is formation reflection coefficient, and
is formation reflection coefficient, and 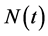 is noise. However, in fact, because of the existing factors such as energy diffusion, earth filtering, mul-
is noise. However, in fact, because of the existing factors such as energy diffusion, earth filtering, mul-
tiple reflection, interference and other aspects, the wavelet morphology is time-varying and spatial-variable in the propagation. Above assumption differs significantly from the actual situation, which may lead to the loss of some weak effective information and generating several artifacts. Thus, the wavelets with different frequencies and amplitudes are used in convolution respectively and superimposed finally, and the convolution results are much closer to the real seismic data [12] [14] . The multi-wavelet convolution formula is pointed out in Formula (2).
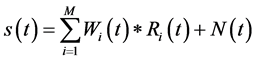 (2)
(2)
where  represents a wavelet aggregation including different spectral characteristics, and
represents a wavelet aggregation including different spectral characteristics, and 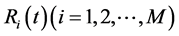 is non-zero reflection coefficient series. Seismic wavelet morphology is arbitrary from the
is non-zero reflection coefficient series. Seismic wavelet morphology is arbitrary from the
theoretical model analysis, while it has a definite morphology after exciting the source wavelet in fact. Although various factors in the propagation make the wavelet morphology change, the performance of this change is mostly a relatively high frequency component attenuation increasing and a relatively low frequency attenuation decreasing. The basic shape of those wavelets with different morphologies are similar, so that it is considered to use a mathematical analytical expression to describe those wavelets aggregation. For example, Morlet wavelet function has a clear mathematical analytical form in time and frequency domains, and it is able to characterize the energy attenuation and velocity dispersion of seismic waves in the propagation of underground medium [15] [16] . Its mathematical expressions in time and frequency domains respective are
 (3)
(3)
and
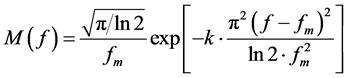 (4)
(4)
where f is frequency, 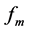 is mean or main frequency, and k is a constant acting on the Gauss part of wavelet
is mean or main frequency, and k is a constant acting on the Gauss part of wavelet
functions to modulate the wavelet morphology. The higher k value is, the more serious wave compression is, the less side lobe gets, and the narrower wavelets becomes.
2.2. Wavelet Decomposition and Reconstruction
The basic principle of multi-wavelet decompositionand reconstruction is decomposing the seismic traces into various wavelets with different frequencies and amplitudes in mathematical methods, which is shown in Figure 1(a). Since the decomposition is linear, those wavelets are superimposed again to get back into the original seismic traces [17] - [20] . By analyzing the variations of decomposed single frequency data in the interest formations, the useful wavelets are picked out and superimposed again with maintaining its position unchanged to form new seismic traces, which is called seismic reconstruction shown is Figure 1(b). In new seismic data after decomposition and reconstruction, the interference waves are suppressed as much as possible and the useful information as highlighted.
2.3. Matching Pursuit
During various mathematical algorithms of wavelet decomposition and reconstruction such as shot-term Fourier transform (STFT), wavelet transform (WT), matching pursuit (MP) and so on [12] , the last one are adapted in this study. Its basic thinking is decomposing the seismic signals via iterative algorithm into a series of Gabor wavelet function aggregation matching with time-frequency characteristics of seismic signals. But this method only considers the optimal matching level locally, and makes the calculation greedy [12] [21] . Fortunately, the matching pursuit based on Morlet wavelet uses the instantaneous attribute information of complex seismic traces to decrease the wavelet dictionary as well as time of searching for the best wavelet and improve the computa-
tional efficiency greatly [6] . The principle of this technology is that seismic signal 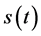 is band-limited and can be expressed a s a linear combination of M Morlet wavelets, as in
is band-limited and can be expressed a s a linear combination of M Morlet wavelets, as in

Figure 1. Schematic diagram of multi-wavelet decomposition (a) and reconstruction (b).
 . (5)
. (5)
where 







where 



and

and

respectively. Wherein instantaneous frequency is the derivative of instantaneous phase versus time.
3. Examples
3.1. Geological Background
The H area is located on a faulted anticline structure of Turpan-Hami basin, China. It’s almost 10 km2 (Figure 2), and the main gas-bearing reservoir is the second member of Sanjianfang formation, Jurassic system, whose lithology primarily consists of fine sandstone, siltstone and argillaceous sandstone. The thickness of sandstone is mostly less than 5 meters, so that the reservoir is thin interbed. There are totally 36 wells (Figure 2) and various well data in the study area. By doing statistics of sandstone layers at wells in J2s2 member, the lithological associations of H area are classified into three categories which is shown in Figure 3. The first kind is single thin sandstone, the second type is thin interbedded sandstone, and the last class is large thick sandstone. The interest associations are both of the second and last class, which is to say the associations with high sand-to-formation ratio is the interest reservoir.
Figure 2. Structural map with well distributions in research area.
Figure 3. Lithological correlation of J2s2 member between H1, H2, H3, H4 and H5 well in H area. In the legend, 1 is yellow fine sandstone, 2 is yellow siltstone, 3 is yellow argillaceous siltstone, 4 is gray slity mudstone, 5 is gray mudstone, 6 is green mudstone, 7 is red-brown mudstone, 8 is variegated mudstone, 9 is black carbonaceous mudstone, and 10 is black coal seam. The colors of 1, 2 and 3 are changed to yellow from gray to highlight their lithology.H1 and H6 wells are classified as Class I according to the lithological association, and H3 and H5 wells are classified as Class II as well as both H2 and H4 wells being classified as Class III.
3.2. Application Analysis
Using different lithology and fluid having various responses to different frequencies, multi-wavelet decomposition and reconstruction are applied to J2s2 member of the study area on reservoir prediction. Analysis are from point to line and then to surface. Figure 4 shows the decomposed wavelet dictionary of seismic trace near H1 well and the corresponding amplitude spectrum. The figure points out that this seismic trace is decomposed into lots of Morlet wavelet, and points out that the main frequency ranges from 15 to 30 Hz.
Transforming multi-wavelet decomposition results of seismic trace near wells into the amplitude spectrum shown in Figure 5, it is found that the spectrum characteristics of coal bed is strong energy, high frequency and broad bandwidth, and that of both of thin interbedded sandstone and large thick sandstone is medium-to-strong energy and medium-to-high frequency as well as that of single thin sandstone being characterized by weak energy, low frequency and narrow bandwidth. The main frequency of energy group the is the corresponding frequency at the strongest energy in the time-frequency spectrum, and oblateness is the ratio of bandwidth of energy group to time thickness. Results of statistics and analyzing on time-frequency spectrum of all wells in the study area reveals that the main frequency has a fitting relation of power function with oblateness, which is shown in Figure 6. The fitting formula is as follows,

where O and f is the oblateness and main frequency of energy group respectively, and R represents the correlation coefficient between fitting formula and scatter data. The closer to 1 the 
The original seismic records are decomposed into plenty of data at single frequency ranging from 0 to 90 Hz via multi-wavelet matching pursuit decomposition method. Seismic well-tie sessions of Figure 7(a) and Figure 7(b) are original data and single frequency data at 26 Hz respectively. In the former figure, the amplitude difference among different lithological associations is not very obvious and unable to be distinguished visually, while in the latter one, the amplitude difference of each wells are amplified, wherein amplitude of both H2 and H4 wells is relatively strong, while that of H3 and H5 wells is relativelyweak, and that of H1 and H6 wells cen-

Figure 4. Decomposition wavelet dictionary (a) and its spectrum (b) of seismic trace near H1 well.
Figure 5. Multi-wavelet time-frequency spectrum of seismic traces near H1 well.
Figure 6. Crossplot of main frequency and flattening of seismic traces near wells in H area. The blue line is the trend line, and the black boxes represent the main frequency interval.


Figure 7. Energy difference of different lithologic association between original seismic data (a) and single frequency data at 26 Hz (b).
tered. Thus, responses of different lithological associations to particular frequencies varies greatly. Observing the characteristic responses of different lithological associations at frequencies ranging from lower frequency of 10 Hz to higher one of 50 Hz, it is found that sandstone in the second class is characterized by enhanced energy at low frequencies which is less than 20 Hz, and that sandstone of the third class performs enhanced energy at middle frequencies from 20 to 34 Hz, and that sandstone of the first class has stronger energy at high frequencies more than 35 Hz. From the above analysis, it shows that frequencies of energy anomalies reflected by the interest second and third classes is both low and medium frequency bands which is less than 35 Hz.
Considering the analysis results of single well and well-tie multi-wavelet decomposition, it is suggested that the interest frequencies of the study area in interest reservoirs range from 8 to 34 Hz. Then wavelets of those frequencies are linearly superimposed by multi-wavelet matching pursuit reconstruction to obtain new reconstructed seismic data which is shown in Figure 8. H2, H3, H4 and H5 wells with interest lithological associations have respectively strong amplitude in the reconstructed data.
During all 36 wells in the study area, there are only a quarter having lithological data. For this, comparing the gamma value of wells without lithology data in interest reservoirs with gamma value of wells with lithology data, and combining with gamma characteristics of different lithological associations, the wells without lithology information are classified according to lithological associations. The crossplot of mean gamma values in interest reservoirs and RMS amplitude at wells extracting from reconstruction data is shown in Figure 9. When the RMS amplitude is greater than 3650, 63% wells with interest lithological associations are distributed within this range, while 78% wells beyond interest associations are eliminated. Therefore, the distribution with RMS amplitude greater than 3650 is the potential area of interest reservoirs, and the prediction is shown in Figure 10. The prediction results suggest that the interest sandstone in interest reservoirs are mainly in the west of the study area. Wherein southwestern sandstone is characterized by annular high amplitude anomalies, and sandstone of western and northern areas demonstrate large-scale and banded distribution, and contiguous sandstone in eastern regions appears sporadically.
Figure 8. Reconstruction data at frequency from 8 to 34 Hz of J2s2 member in study area.
Figure 9. Crossplot of both mean GR values and RMS amplitude of reconstruction data in J2s2 member among all wells of study area.
Figure 10. Prediction of interest reservoir distribution of J2s2 member in H area.
4. Conclusion
In summary, multi-wavelet decomposition and reconstruction technology break through the limitations caused by the single wavelet assumption in conventional seismic convolution, and Morlet wavelet function greatly describes frequency attenuation and velocity dispersion of seismic wavelet in the propagation. Matching pursuit decomposition and reconstruction technology based on Morlet wavelets decomposes the original seismic traces into multiple Morlet wavelet linearly superimposing. By analyzing the sensitive frequencies where geological bodies generate anomalies, wavelets at those frequencies are picked out and linearly reconstructed to obtain new seismic data where reservoir predictions are well done. Application of this method to H area in Turpan-Hami basin shows that multi-wavelet decomposition and reconstruction technology greatly describes the lateral discontinuity of reservoirs, provides strong support for reservoir geology and geophysical interpretation.
Cite this paper
Lifang Cheng,Yanchun Wang,Zhiguo Li,Fuxiu Gong, (2016) Prediction of Tight Sand Reservoir with Multi-Wavelet Decomposition and Reconstructing Method. International Journal of Geosciences,07,529-538. doi: 10.4236/ijg.2016.74040
References
- 1. Wang, Z. (2012) The Application and Study of Spectral Decomposition Technology on Channel Sand Body Description. Master Thesis, China University of Petroleum (East China), Qingdao. (In Chinese)
- 2. Geronimo, J.S., Hardin, D.P. and Massopust, P.R. (1994) Fractal Functions and Wavelet Expansions Based on Several Scaling Functions. Journal of Approximation Theory, 78, 373-401.
http://dx.doi.org/10.1006/jath.1994.1085 - 3. Lilly, J.M. and Park. J. (1995) Multiwavelet Spectral and Polarization Analyses of Seismic Records. Geophysical Journal International, 122, 1001-1021.
http://dx.doi.org/10.1111/j.1365-246X.1995.tb06852.x - 4. Mallat, S.G. and Zhang, Z.F. (1993) Matching Pursuit with Time-Frequency Dictionaries. IEEE Transactions on Signal Processing, 41, 3397-3415. http://dx.doi.org/10.1109/78.258082
- 5. Liu, J.L., Wu, Y.F., Han, D.H. and Li, Z.G. (2004) Time-Frequency Decomposition Based on Ricker Wavelet. SEG Technical Program Expanded Abstracts of the 74th SEG Annual International Meeting, Denver, 10-15 October 2004, 1937-1940.
http://dx.doi.org/10.1190/1.1851176 - 6. Liu, J.L. and Marfurt, K.J. (2005) Matching Pursuit Decomposition Using Morlet Wavelets. SEG Technical Program Expanded Abstracts of the 75th SEG Annual International Meeting, Houston, 6-11 November 2005, 786-789.
http://dx.doi.org/10.1190/1.2148276 - 7. Liu, J.L. and Marfurt, K.J. (2007) Instantaneous Spectral Attributes to Detect Channels. Geophysics, 72, 23-31.
http://dx.doi.org/10.1190/1.2428268 - 8. Song, W.Q., Zhu, W.X. and Sun, Y.J. (2007) Identify Bed Layer Sandbody by Complex Wavelet Matching Algorithm. Progress in Geophysics, 22, 1796-1801. (In Chinese)
- 9. Chen, L. and Song, H.B. (2008) Extraction of Seismic Time-Frequency Attribute Based on Morlet Wavelet Match Tracing Algorithm. Oil Geophysical Prospecting, 43, 673-679. (In Chinese)
- 10. Fen, L. and Jiang, Z.X. (2009) Spectral Decomposition Based on Matching Pursuit and its Application. Progress in Exploration Geophysics, 32, 33-36. (In Chinese)
- 11. Zhang, X.W., Han, L.G., Wang, Y. and Shan, G.Y. (2010) Seismic Spectral Decomposition Fast Matching Pursuit Algorithm and Its Application. Geophysical Prospecting for Petroleum, 49, 1-6. (In Chinese)
- 12. Qiu, N. (2012) Research on Seismic Wavelet Decomposition and Reconstruction Technology. Master Thesis, Ocean University of China, Qingdao. (In Chinese)
- 13. She, G., Zhou, X.Y. and Wang, J.B. (2013) Prediction of Sand Reservoir with Multi-Wavelet Seismic Trace Decomposition and Reconstruction. Journal of Southwest Petroleum University (Science & Technology Edition), 35, 19-27. (In Chinese)
- 14. Liu, X., Chen, C., Zhao, Y.T. and Wang, X. (2015) Multi-Wavelet Decomposition and Reconstruction Based on Matching Pursuit Algorithm Fast Optimized by Particle Swarm. Journals of Jilin University (Earth Science Edition), 45, 1856-1861. (In Chinese)
- 15. Morlet, J., Arens, G, Fourgeau, E. and Giard, D. (1982) Wave Propagation and Sampling Theory-Part II: Sampling Theory and Complex Waves. Geophysics, 47, 222-236.
http://dx.doi.org/10.1190/1.1441329 - 16. Xu, T.J., Shen, Z.M. and Wen, X.K. (2010) Research and Application of Multi-Wavelet Decomposition and Reconstruction Technology. Journal of Chengdu University of Technology (Science & Technology Edition), 37, 660-665. (In Chinese)
- 17. Dai, S.H., Chen, Z.G., Yu, J.B., et al. (2011) Application of Multi-Wavelet Decomposition and Reconstruction Technique in Reservoir Characterization in TKT-NGS Oilfield, Algeria. Oil Geophysical Prospecting, 46, 103-109. (In Chinese)
- 18. Huang, Y., Xu, D. and Wen, X.K. (2013) Optimization of Wavelets in Multi-Wavelet Decomposition and Reconstruction Method. Geophysical Prospecting for Petroleum, 52, 17-22. (In Chinese)
- 19. Chen, S., Ouyang, Y.L., Zeng, Q.C., Bao, S.H., Li, X.Y. and Yang, Q. (2014) Application of Matching Pursuit Wavelet Decomposition and Reconstruction Technique to Reservoir Prediction and Gas Detection. Lithologic Reservoirs, 26, 111-119. (In Chinese)
- 20. Wang, Y., Feng, X.Y., Qin C., et al. (2015) Application of Wavelet Decomposition and Reconstruction Technique for Identification of CBW in Zhengzhuang of Shanxi. China Petroleum Exploration, 20, 78-83. (In Chinese)
- 21. Li, C.H. (2012) Fast Matching Pursuit Decomposition and Instantaneous Spectral Analysis of Seismic Signals. Master Thesis, China University of Petroleum (East China), Qingdao. (In Chinese)
- 22. Shen, Y.Q. (2013) Signal Sparse Decomposition Based on the Improved Matching Pursuit Algorithm. Master Thesis, Zhejiang University, Hangzhou. (In Chinese)
- 23. Zhang, L.G. (2010) Research and Application of Signal Self-Adaptive Decomposition Based on Matching Pursuit (MP) Algorithm. Master Thesis, Central South University, Changsha. (In Chinese)









