Received 19 September 2015; accepted 27 October 2015; published 30 October 2015

ABSTRACT

When we study and process magnetotelluric data, the earth’s interior structure is usually equated with isotropic medium in the existing approaches. When the underground structure is complex, there is serious resistivity anisotropy in macroscopic view, and then the traditional processing and interpretation methods often produce wrong results. For that we must establish the study method based on the anisotropy in order to explain the measured data exactly. In this paper, by considering the change of resistivity in three electrical spindle directions, we deduce two-dimen- sional magnetotelluric variational equation for vertical anisotropy. The study region is divided into many rectangular units, and it is dealt with linear interpolation in each of them. By comparing with former achievements including the results of the isotropic and anisotropic models, it demonstrates the validity of the program. The pseudosection map of vertical anisotropic body shows that we can’t ignore the anisotropy effect and provides a solid foundation for the further inversion study.

Keywords:

Vertical Anisotropy, Magnetotelluric Method, Isotropy, Anisotropy Effect

1. Introduction

Magnetotelluric method which is based on natural alternating electromagnetic field source is the main geophysical prospecting method to study the earth’s crust and upper mantle electrical structure through observing orthogonal electric field and magnetic field components on the ground. Magnetotelluric method compared with other means of exploration has many advantages such as great exploration depth, low cost and convenient field work, and then it is widely used in various fields. There are several aspects to cause the earth medium anisotropy, including tectonic stress field of the earth, rock fracture, geological deposition, the earth medium deformation and pore water, etc. With the improvement of field exploration precision and the more knowledge of the nature of the interior of the earth, the anisotropic problem gradually caused the attention of people.

The study of one-dimension anisotropy [1] and two-dimension isotropy [2] [3] forward and inversion problems is quite mature, but for two-dimension anisotropic problem, international and domestic academics mostly do the study of symmetrical anisotropic medium, such as Xu (1985) [4] , Yang (1997) [5] , etc. In 1997, Pek used the finite difference method to achieve the general research of anisotropy [6] and in 2002 Li systematically expounded the general anisotropic formula by finite element method [7] . Huo and Qin also did the research about the two-dimensional anisotropic problem [8] -[11] .

Previous studies have shown that the anisotropic problems cannot be ignored, but there is no related literature in the field of two-dimensional magnetotelluric doing the study about the difference between vertical anisotropy and isotropy. In this paper, based on the research status quo, by using the rectangular element subdivision and linear interpolation in each element, the study of the vertical anisotropic medium and vertical anisotropy is done, and the comparison with the results of isotropic body shows that we can’t ignore the anisotropy effect.

2. Method Theory

The study region is shown in Figure 1, in which x is the advancing direction, y is the horizontal direction and z is the vertical direction. For the underground geological medium, the permeability is m » m₀ and the permittivity is e » e₀, and only the conductivity is changed. For the magnetotelluric method, the time factor is, the equation of the electromagnetic field is:

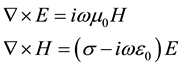. (1)

The conductivity is a scalar quantity in an isotropic medium, and is a tensor in an anisotropic medium. We then consider the influence of the anisotropy. The vertical anisotropy means that anisotropy principal axis is overlap with measurement principal axis, but in three principal axes the conductivity is different.

As is shown in Figure 1 in the coordinate system, the tensor of conductivity is:

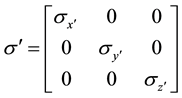. (2)

For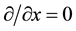, and then expanding the Formula (1) we can get:

(3)

And then from the Formula (3) we can get the fowling variational equation:

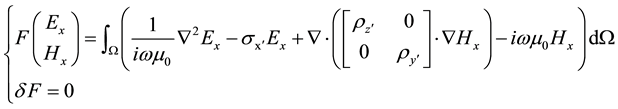. (4)

The left and right boundary conditions and the bottom boundary condition are based on one-dimensional anisotropic solution, and the inner boundary condition is automatically satisfied. Two sets of magnetic and electric field values which are got by one-dimensional anisotropic solution are used as the upper boundary condition. For the study region rectangular element and linear interpolation are used. By bringing two sets of initial values and solving the equation, we can get two sets of solutions:, 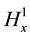and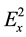,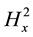. According to Formula (3) we can get the corresponding auxiliary field values: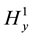, 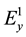and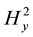,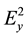. And then we can get the following impedance formula:

(5)

The corresponding apparent resistivity and impedance phase are:

. (6)

3. Model Examples

3.1. Model 1

Model 1 is shown in Figure 2, and the model is an isotropic medium model, which means the three axes have the same resistivity. And then by using the vertical anisotropic program to calculate the model and comparing the result with MARE2DEM from Kerry Key, from that we can verify the correctness of the program for isotropic medium model. The model is set as three sections, and the resistivity from left to right is 10 Ω∙m, 1 Ω∙m and 50 Ω∙m. The width of middle section is 5 km. The finite element grid consisted of 106 elements horizontally ´ 51 elements vertically (including 14 air grids). The task is to compare the apparent resistivity and impedance phase at all stations for the 0.1 Hz.

The contrast diagram of isotropic medium is shown in Figure 3. The circle is the calculation result of this paper and the line is the result of Kerry Key. From that we can see the apparent resistivity and impedance phase have good matches, and that also verify the correction of the program in calculating the isotropic medium model in both xy and yx cases. And in the same time the curves also well show the differences of the fault in resistivity.

3.2. Model 2

Model 2 is shown in Figure 4, and the model is a vertical anisotropic medium model. Comparing the result with MARE2DEM from Kerry Key can verify the correctness of the program for vertical anisotropic medium model. The model is set as three sections, and the resistivity in both sides is 40 Ω∙m, 100 Ω∙m and 50 Ω∙m in three axes separately. The width of middle section is 5 km and the resistivity is 3 Ω∙m, 10 Ω∙m and 20 Ω∙m in three axes separately. The finite element grid consisted of 106 elements horizontally ´ 51 elements vertically (including 14 air grids). The task is to compare the apparent resistivity and impedance phase at all stations for the 0.1 Hz.

The contrast diagram of vertical anisotropic medium is shown in Figure 5. The circle is the calculation result of this paper and the line is the result of Kerry Key. From that we can see the apparent resistivity and impedance phase have good matches, and that also verify the correction of the program in calculating the vertical anisotropic medium model in both xy and yx cases. For the model is symmetric the curves are symmetric and then well distinguish the fault boundary.

3.3. Model 3

Model 3 is shown in Figure 6, and the model is a vertical anisotropic body in the isotropic medium. The resistivity of the isotropic medium is 100 Ω・m, and the body in three axes is 3 Ω∙m, 10 Ω∙m and 20 Ω∙m separately. And in the same time setting the body as isotropic body, the resistivity is set as 3 Ω∙m, 10 Ω∙m and 20 Ω∙m. The task was to compare the pseudosection map of the apparent resistivity and impedance phase in the four cases from 0.1 Hz to 1000 Hz under xy and yx cases. The finite element grid consisted of 50 elements horizontally ´ 92 elements vertically (including 14 air grids).

The pseudosection maps are got on the base of the function of SURFER software. The simulating results of anisotropic body are shown in Figure 7(a) for xy case and Figure 8(a) for yx case. The calculating results of isotropic body are shown in Figure 7(b) (3 Ω∙m), Figure 7(c) (10 Ω∙m), Figure 7(d) (20 Ω∙m) for xy case and Figure 8(b) (3 Ω∙m), Figure 8(c) (10 Ω∙m), Figure 8(d) (20 Ω∙m) for yx case. From the Figure 7 the pseudosection map

of ρ_xy and φ_xy we can see that the apparent resistivity and impedance phase of the vertical anisotropic body are different with the isotropic body in three cases, but it is close to the isotropic body in the y axis direction which is shown in Figure 7(a) and Figure 7(c). It is insensitive to the z axis that is shown in Figure 7(a) and Figure 7(d). Form the Figure 8 the pseudosection map of ρ_yx and φ_yx we can see that the apparent resistivity and impedance phase of the vertical anisotropic body is like the isotropic body whose resistivity is 3 Ω∙m. The phenomenon shows that in this case it is the same as the isotropic body in x axis. Those indicate that we can’t ignore the anisotropy effect of vertical anisotropic body.

4. Conclusion

In this paper, by simulating two-dimensional magnetotelluric finite element method for vertical anisotropy and comparing the calculating results with Kerry Key, we can verify the correctness of the program. By simulating the pseudosection map of apparent resistivity and impedance phase for anisotropic body in xy and yx cases, we can illustrate that there is a big difference in xy case, but it is simulate to the isotropic body in y axis and is insenstivitive to z axis. In yx case, it is the same as the isotropic body in x axis. Above all, we can’t ignore the anisotropy effect of vertical anisotropy. On the base of the forward research, we need to do inversion study in the future to solve the vertical anisotropic problem and get more accurate interpreting results.

Cite this paper

Miao-XinYang,Han-DongTan,MaoWang,HuanMa, (2015) Two-Dimensional Magnetotelluric Forward Research for the Vertical Anisotropy. International Journal of Geosciences,06,1166-1172. doi: 10.4236/ijg.2015.610091

References