International Journal of Geosciences
Vol.06 No.05(2015), Article ID:56759,32 pages
10.4236/ijg.2015.65041
Brief Review of Numerical Simulation Applied to Solve Oil Extraction Problems
M. M. Onofre-Ramos, L. Castañeda*, E. Austria-Aguilar, E. E. Hernández-Martínez, A. Oropeza-Osornio
Escuela Superior de Ingeniería Mecánica y Eléctrica Unidad Ticomán, Instituto Politécnico Nacional, México D. F., México
Email: monofrer0900@alumno.ipn.mx, *luiscas@cablevision.net.mx, eaustria@ipn.mx, euhernandezm@ipn.mx, aoropeza@ipn.mx
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 24 March 2015; accepted 25 May 2015; published 28 May 2015
ABSTRACT
In the last decades, the numerical analysis has abridged the time and cost of oil extractive operations, and thus their implementation has been promoted so much that today is used to solve a large number of phenomena that occur during the extraction of hydrocarbons, not only economizing the operation, but also shedding light to the phenomenon, and helping to have a better understanding. Nevertheless in spite of the success of the applications of numerical simulations, it has been until today, looking for their optimization, because the discretization methods of the domain and the model are through meshes, which require modifying the physics of the problem so that this matches the numerical method, and not in backwards.
Keywords:
Numerical Simulation, Oil Reservoir, Smooth Particle Hydrodynamics

1. Introduction
To achieve a broad state of the art and get a good understanding of the subject, it is necessary to explain generally the main techniques used to analyse, simulate and exploit the oil reservoirs and in what do they consist, reporting a briefly explanation of the more important development points. The aim of this review is to present a summary of numerical simulations used in Oil Extraction industry, which will help to select the best solution- schema that provides more chance of improvement in means of time processing and computational resources.
2. Numerical Simulation of Geothermal Reservoirs
Two main goals can be identify history matching and forecast of future scenarios (consequent to the exploitation of the reservoir). History matching is usually done to check the reliability of a model and evaluate the sustainability level in retrospect. It is the analysis of an exploitation history according to the data log until present time or during a particular time interval. This also allows to check the numerical model in a “feedback loop” and calibrate or adapt it to what is reported in the history data (in order to improve future scenarios forecast). This is practically done by assigning temperature and mass flow rate of both, the geo fluid extracted and re-injected, and any other useful historical data recorded that can be translated into thermo-physical parameters or boundary/initial conditions. Some phenomena which affect the behaviour of field utilization could not be put into a simulation in a proper way, without knowing about them from the history (natural recharge, natural change of the pathways of circulation into the rock formations, losses of pressure, etc.). If a model is considered to be reliable, it can be used to study how the durability of the resource changes depending on different: extraction rates, reinjection temperatures, wells siting, and fractures. A productive strategy can be based on the results of a model simulation. This is true for both power plants and thermal energy direct uses. Some general and macroscopic aspects of the application of numerical simulation to the geothermal energy study are listed here:
o Equations describing the phenomena considered (circulation, energy/mass transport).
o Estimation of the main thermo-physical parameters.
o Boundary conditions (BC).
o Geothermal potential assessment.
o Coupling between the power/thermal utilization and reservoir.
2.1. Characterization of the Geothermal Source Potential
The final goal of the potential assessment is the sustainable utilization prediction of the resource. It involves the complete characterization of the field, energy stored, maximum fluid rate, useful temperatures and chemical parameters of the fluid (to determine the minimum temperature for reinjection). This evaluation is surely important for each kind of water dominant geothermal field.
During the running of a plant the productivity (and wells deliverability) can show some remarkable variations (in terms of flow rate, fluid chemistry and specific enthalpy of geo fluid). These changes can be addressed to reservoir pressure decline because of excessive fluid production. The reservoir fluid pressure is also another important parameter, linked both to the productivity of the well and the scaling phenomena. High pressure in the geo fluid pipes can keep the scaling phenomena under controlled rates.
2.2. Reinjection Strategy and Geofluid Chemistry
When reinjection is practiced, the geothermal energy is being used as a renewable energy source. The practice of reinjection avoids temperature and pressure decline in a geothermalfield. For the binary power plants it is a basic approach for resource management and it appears to be compulsory. The task is the optimization and enhancement of the durability of the resource [1] .
The objectives of this methodarethe efficient restitution of the geo fluid to the reservoir (to optimize the recharge in terms of enthalpy and flow rate), and choosing the correct siting and depth of the wells (to guarantee a sustainable use of the resource). The optimum reinjection strategy is a quite complex task and it strongly depends on the type of geothermal system (Kaya et al. [2] ). In general the minimum temperature values are in the range between 60˚C and 80˚C. The siting of production and reinjection well and their mutual interference are the main issues of the strategy. A correct reinjection strategy has to take into account the thermodynamic and chemical problems of the scaling phenomena, which in many cases increase with lowering of the temperature. A study of the geothermal system is fundamental, in order to avoid the worst consequences of fouling, corrosion and clogging of the parts of the plant, of the piping’s, and the “tapping” of the wells.
3. Numerical Simulation of Geothermal Reservoirs: An Integrated Approach to Sustainable Design
Numerical simulation of geothermal reservoirs allows to understand the hydrogeological behaviour and heat transport into the reservoir under a certain utilization rate. It is possible to study the geothermal reservoir by solving the balance equations of mass, momentum and energy in the particular volume in which hydro-thermal circulation of fluid occurs. The constitutive laws are peculiar for each kind of reservoir, while the numerical analysis issues are also important in order to achieve a reliable solution. The hydrogeological issues linked to the geothermal exploitation (knowledge of the geological structures and of the groundwater system) must be connected with the engineering tasks of the design and optimization of the energy conversion system. The development of the numerical model itself has to follow two main directions:
a. The unperturbed (or undisturbed) natural state.
b. The utilization scenarios (during the exploitation).
Different phases in the development of the model can be identified. A first “block-structure” has to be built together with the data of the parameters which best fit what it is expected by the conceptual model. This first step model should reproduce:
a. Geological structure of the reservoir.
b. Geometrical features of wells and fractures.
c. Hydraulic, Thermal, Mechanic and Chemical conditions (HTMC).
3.1. Conceptual Model and Numerical Model
The conceptual scheme for the realization and simulation of a geothermal reservoir model is represented in Figure 1 [3] . An important step of “interpretation” and appropriate data collection must be pursued firstly, for the elaboration of the conceptual model (Huenges [4] ). This first step model should reproduce: geological structure of the reservoir; geometrical features of wells and fractures; Hydraulic, Thermal, Mechanic and Chemical conditions (HTMC).
The model should then pass a further step of calibration and refinement. It is an iterative process ruled by the conceptual and physical model, in which the parameters and boundary conditions should be adjusted. Some
Figure 1. Conceptual scheme for the elaboration of a numerical model of a geothermal reservoir.
thermo-physical properties (permeability, thermal conductivity, porosity, specific heat capacity) change with siting, depth and hydrothermal alteration. Their value can be adjusted and the mesh can be refined at this step.
A first model of the unperturbed state is the result of execute these steps. The simulation time interval should be very large, between 80 - 100 years, in order to verify the model stability and convergence. Exploitation and energy utilization scenarios can be then run starting from the unperturbed state simulation as initial conditions. In particular, temperature and pressure should be kept stable in the reservoir as much as possible.
If chemical properties are known, scaling and chemical deposition phenomena can be also introduced in the calculations, in a multi-physics simulation environment. The models can couple different transport equations, referring to mass, heat and chemicals. From the simulation, some useful data for the plant design must be extracted.
It is important to remark that building a numerical model of a geothermal reservoir is not easy, a reservoir cannot be practically measured in all its features. Its evolution can be studied, and a model can represent a way of behaviour prediction only if it is based on reliable data. In Figure 2 [5] a conceptual scheme about how the development of numerical models can help the sustainability assessment is shown. The size of the geothermal area must be known, the geometric domain must be big enough to comprehend every interesting mass/energy transfer boundary or spot, but also small enough to reach a proper calculation time.
Once the geometry and mesh have been set up, the equation parameters (and constitutive law) must then be considered. The constitutive law (e.g. Darcy Law) is typical for each phenomena, the conceptual model must arrange and properly describe the transport phenomena occurring in the geological system. Thermo-physical parameters should then be put into the simulation.
One single value of a significant parameter like porosity or permeability is assigned to a layer, or element. Often is not possible to assigning tensors or directional parameters (e.g. preferential directions for circulation), as they derive from very accurate measurements and interpretations. Calibration is a good tool, as it allows addressing parameter values matching with real temperature and pressure data. Anyway, it is possible only when reliable measured data are available. The main parameters to be assigned are essentially:
o Porosity (ϕ, defined as the ratio between the voids and the total volume considered) and effective porosity (taking into account all the “interconnected” voids, allowing then the fluid circulation).
o Permeability (k), being property of both the rock and the circulating fluid, giving an idea of the productivity of such a rock formation.
o Density (ρ, its distribution derives from accurate measurements and usually it is approximated with a single value for each rock formation).
o Thermal conductivity (of both rock and fluid).
o Specific thermal capacity (of both rock and fluid).
Figure 2. Information flow and prospect for the sustainable assessment through the use of the numerical simulation of the reservoir.
The mathematical and engineering 7 physical background is a fundamental part of this very complex process, but is not necessary always to develop a new algorithm, is better first to try with a well-known algorithm. A proper time scale should be identified, considering both economic lifetime (20 - 50 years for new fields and 80 - 100 years to recovery operations) and natural (or induced) renewability of the resource itself.
Different strategies can be adopted, in order to keep the utilization sustainable. It is very important to define the size of the installation (power plant) only after the simulation and complete resource assessment. Oversizing or resource fast depletion (reservoir cooling, wrong reinjection) can be some consequences of incorrect sizing.
3.2. Mathematical and Physical Background
From a mathematical point of view, in studies about transport, the task is to understand the response of a porous or fractured system when a hydraulic gradient is applied. The hypothesis and the real situation of the field should be compared very carefully. The basic calculations executed by the software’s for numerical simulation substantially deal with the resolution of the flow into porous and/or fractured media. The mathematical tools used by the software’s are: constitutive laws and conservation equations. The constitutive laws deal with the particular phenomenon involved. The following conservation equations are usually solved: mass, momentum, energy, concentration of pollutant (or chemicals) dissolved.
Geothermal reservoirs fluid flow can be generally studied according to the Darcy Law about porous media, the Darcy fluid velocity q is de fined as (Saeid et al. [6] )
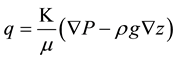
where k is the intrinsic permeability, being proportional to the hydraulic conductivity K according to the definition (in [6] ):

In which ρ is the density, g is the acceleration of gravity and μ is the viscosity, p is the pressure and z is the vertical coordinate. One thing to be considered is that in case of anisotropy and hydraulic conductivity tensor K can be defined:
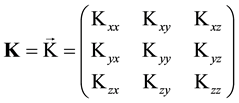
This element is important in order to consider the complexity of the phenomena involved. Average scalar values of the hydraulic conductivity or permeability are often assigned, but the real behaviour of rock formations can be very different from an averaged parameter. For example, porosity also changes with pressure and depth, it is important to understand which assumption must be done when assigning an average value to an extended rock body (having for example an unknown fractures field). The fractures are particularly difficult to reproduce in a numerical model, their accurate description is important if their spatial extension is to be compared to the rock formation size, otherwise average properties can be considered. In the most common reservoir simulation software’s, like for example TOUGH2 [7] , it is also possible to define different models for the relative permeability (Rl) as a function of the liquid saturation in the mixture (geothermal fluid) (Petrasim Manual [8] ). Let us now consider a single phase (liquid) flow in a geothermal system. According to Rybach and Muffler [9] the following assumptions have to be considered:
o Rock matrix is homogeneous and isotropic, in particular referring to porosity, permeability and thermal con- ductivity (supposed to be independent by temperature).
o Incompressible fluid; with density (ρ) and kinematic viscosity (v) dependent by temperature according to the laws:
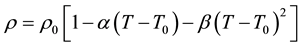

with ρ0, v0, α, β and T0 being opportune constants, while s(T) is a function of T. Pressure work and dissipations due to viscosity can be neglected, internal energy of liquid (l) and solid matrix (r) being
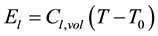

with cl,vol and cr,vol specific volumetric heat capacities of rock and liquid. Under these assumptions the balance equations of mass, momentum and energy can be written respectively as (according to [9] ):
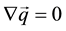

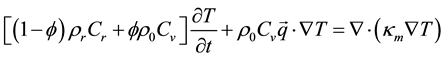
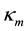 being the thermal conductivity of the mixture solid liquid.
being the thermal conductivity of the mixture solid liquid.
A double phase system, in which the vapour phase is also considered, is described by similar equations [9] . The following assumptions about porosity have to be done in this case:
o Porosity ϕ only depends on local pressure of fluid.
o Liquid and vapour phases are in local thermal equilibrium.
The equation of conservation (respectively) of mass, momentum (liquid and vapour) and energy can be then written as follows:
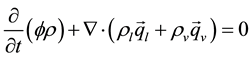
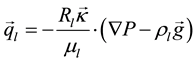
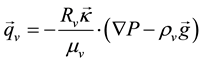
where E is the internal energy of the liquid vapour mixture, k is the permeability tensor and Rl is the relative permeability of the ith phase (I = l/g liquid or vapour). Some fundamental differences between the flow in porous and coherent media than in fractured media must then be taken into account ( [9] [10] ):
a. Permeability induced by fracturing is generally higher than average formation permeability.
b. Fracturing permeability is usually anisotropic (it depends on fracturing preferential direction).
c. The permeability due to fracturing is considerably more dependent on pressure and tension field in the rock with respect to rock matrix permeability.
In the recent paper by Zeng et al. [11] a discussion about the methods for fractured systems simulation is given. Geothermal fracture systems can be represented essentially in two ways:
1. Discrete fracture network method (fracture orientation, spacing and mechanical properties).
2. Equivalent continuous porous media method (the fracture system is seen as an equivalent continuous media, with similar methodologies as for double porosity and double permeability).
In Fox et al. [12] an analytical and numerical model for fractured reservoirs (multi-fractured EGS) is presented and simulated. In the following Figure 3 an example of simplified scheme of fluid circulation into the fractures is shown (b being the fracture size and xs the fractures mutual spacing). There is also the possibility of coupling thermal-flow problems with chemical or geomechanics problems into the same numerical simulation. It is the case of some models presented in literature, like for example the case of a fully-coupled flow and geo- mechanical model by Hu et al. [13] .
Figure 3. Conceptual scheme for multi-fracture vertical geothermal system (xs is the spacing between fractures, b is the fracture aperture).
4. Hot Dry Rock (HDR) Reservoirs
Hot Dry Rock geothermal energy extraction [14] : has come to mean the forced circulation of water between injection and recovery boreholes through a naturally fractured rock mass. In such reservoirs, typically developed in granitic or similar crystalline basement, the intact rock usually has very low permeability and porosity. Heat extraction is controlled by conduction through the intact rock blocks towards water conducting fractures whose apertures may have been artificially increased, where advection transports thermal energy towards the recovery well(s).
Fluid flow rates in fractures are strongly dependent on the fracture aperture, typically the fluid velocity in response to a given pressure gradient is proportional to the square of the fracture aperture. This relation is commonly expressed in terms of the parallel plate laminar flow solution (Reynolds equation), using a hydraulic aperture related to the mean mechanical fracture aperture. The hydraulic aperture is a non-linear function of effective normal stress, the fracture morphology, material properties and its history. Shear displacement of the fracture wall, caused by engineering interventions such as high-pressure fluid injection (“stimulation”), or chemical deposition/solution may alter the hydraulic aperture irreversibly and change the reservoir properties. HDR systems, therefore, respond non-linearly, and sometimes irreversibly, to changes in operational parameters.
HDR field experiments (reservoir stimulation and circulation), are expensive to execute and cannot be repeated indefinitely from the same borehole due to progressive irreversible changes in the system under study. Numerical experimentation provides a mean to demonstrate understanding of the available experimental results and to extend that understanding to other conditions. This leads to a predictive capability, support to design and operational planning.
The HDR modelling task is, in some aspects, more demanding than that faced by the underground storage or hydrocarbon industries. This stems firstly from the strong dependence of reservoir flow properties on the fluid pressures encountered during high pressure injection and secondly from the lack of field data sufficient to adequately characterise the rock mass. Modelling for underground radioactive waste isolation is aided by detailed measurements made in in situ rock laboratories, whilst hydrocarbon reservoir modelling benefits from rock mass imaging using seismic and the possibility of direct measurement of the critical parameters of interest (porosity, permeability, wettability) from core recovery, often from many wells. In contrast, within the HDR community there is little opportunity for direct measurement of many of the parameters of critical interest, such as in situ fracture compliance, shear behaviour or fracture length distributions. Furthermore, in the absence of extensive operational experience of HDR systems, modelling plays a critical role in assessing design and performance expectations. In order to carry out these tasks effectively the HDR community needs to achieve a level of confidence in its modelling methods and also predictive capabilities consistent with the investment needed for commercial prototypes.
The objectives of HDR models are to attempt one or more of the following, but at present no model manages to achieve all five objectives.
a. To help understand the performance of actual field experimental systems and to help design measures to improve inadequate system performance (e.g. re-drilling, secondary stimulations, sealant treatments).
b. To predict/simulate the effects of different reservoir creation strategies; mainly high pressure fluid injections and proppant placement (stimulation models).
c. To predict the thermal performance with time of an engineered reservoir under a given operating strategy (thermal drawdown curve).
d. To predict the hydraulic performance of an engineered reservoir under a given operating strategy (impedance, water loss).
e. To optimise well placement and operating strategy in relation to both reservoir creation and circulation
HDR reservoir models can be examined in the light of their treatment of the coupling of fluid mechanical, rock mechanical, thermal, chemical and hydraulic processes within the reservoir [15] - [24] , together with their representation of the geometry of the underground system [25] - [27] . The way in which these two aspects, coupling and geometry, are approached will be the result of compromises between the objectives of the model and the resources available. Typically, strong coupling can be placed in geometrically reduced or abstract models, whilst geometrically “realistic” models require excessive computational resources to support strong coupling. Thus, at the present time, it is likely that the best approach to HDR modelling will be made through optimisation of the compromises required, rather than through efforts to simulate with exactitude all processes and the complex geometry of fractured rock within a single model.
The commonly observed distinction between models of stimulation and circulation is a natural one. There is a change from rapidly evolving fluid-rock mechanical coupling on the scale of hours to days during stimulation, to thermal-mechanical-chemical coupling over a time scale measured in years during circulation. HDR field experiments to date indicate that circulation through a virgin rock mass does not appear viable, therefore there is a necessity for models of heat extraction (i.e. circulation) to combine with, or use the results of, stimulation models, to show how the required starting conditions for potentially economic reservoirs may be engineered.
4.1. Modelling of Governing Factors
Rock stress and joint mechanical properties: Knowledge of in-situ stress and fluid pressure are critical for modelling reservoir behaviour. The interaction between stress, pressure, fracture orientation and fracture friction angles determines the fluid pressure that has to be applied to start the stimulation processes. The region activated by hydraulic stimulation often appears to be an ellipsoid with the major axis almost coinciding with the direction of maximum compressive stress. The vertical effective stress gradient determines the migration direction of the stimulation (upward or downward) [28] . The fracture mechanical properties, i.e. joint normal stiffness, shear stiffness and shear dilation rate (broadly determined by the roughness at wavelengths comparable to the displacement), are the key factors inducing the nonlinear coupling among the fluid pressure, fracture aperture and rock stress.
Flow within fractures: Corey-type relative permeability is usually assumed. When the reservoir is highly frac- tured, overall permeability is dependent on the characteristics and spatial distribution of the fractures. Niibori and Chida [29] , investigated the effect of the fracture distribution on the relative permeability. Channelling of flow on fracture surfaces is to be expected [30] . Channelling reduces the overall flow impedance compared to uniform flow in equivalent mechanical apertures. However, the heat exchange area will be reduced by channelling. Channelling may be treated stochastically by using a model of fracture aperture composed of mated fractal fracture surfaces [31] . Simulation of fluid flow through such a fracture is possible, but at this time it is numerically impractical for field-size fractures and approximate treatments are required. Turbulent, or at least non-lin- ear flow, has been suggested to occur in the experimental reservoir at Soultz [32] - [38] . The contrast in permeability between the intact rock and fractures is large in HDR reservoirs. Numerical calculations are difficult and special modelling is required [39] if both fracture and intact rock permeability are to be represented explicitly.
Heat transfer: It is common for models to assume that the mean temperature of the fluid within a fracture element is equal to the mean temperature of the fracture surface. But, this assumption may not be appropriate when the flow rate is large or fluid flow is channelled. An experimental study [40] on the heat transfer from the fracture surface to the fluid has provided surface heat transfer coefficients at fracture surfaces. Such considerations are only likely to be important in a small volumetric fraction of HDR reservoirs.
The heat transfer effect of flow channelling within fractures needs further consideration in HDR reservoir models. In most reservoir-scale models, the individual fractures are modelled as uniform aperture discs or polygons. Within models suitable for PCs further small-scale resolution of flow channelling is not possible on computational grounds. Therefore, there is a need for simplified representation of the effect. Channelling on a scale of less than a few meters probably does not have to be spatially modelled provided local time-smearing on the scale of a few months is accepted. This time resolution is quite adequate for modelling long-term heat production. A simple lumped-parameter model should be sought to cover the heat transfer effects of channelling for use at such a geometric scale. Channelling makes it harder for heat to leave the rock mass. The effect could be modelled by the introduction of a layer of “virtual rock” lining each fracture. Such a layer of virtual rock would mimic the effective reduced heat transfer area near the fracture, but would be given no thermal mass. Effectively it would become a large-scale heat transfer coefficient.
4.2. Structure of Reservoirs as Derived from Field Observations
Drilling noise measurement and acoustic emission (AE) reflection techniques can give information on reflecting layers that seem to be closely related to the larger subsurface structures. These can be used for modelling in the first stages of exploitation, i.e. before hydraulic stimulation.
Models to estimate the local transmissivity distribution within the reservoir by using AE magnitude through the usual approach of estimating the slip area and magnitude of slip movement have been proposed [41] - [46] . By the use of the “collapsing technique” [47] and “doublet analysis” [48] , both of which are methods for refining the internal structure of clouds of AE, structures that may be predominant fluid flow paths can be delineated from the AE clouds recorded during hydraulic stimulation. In subsequent circulation simulation, these main flow paths could be taken into account. This is important, because the evaluation of the behaviour of reservoirs during circulation and heat extraction is highly dependent on the condition of reservoirs at the start of circulation and heat extraction.
Almost always aseismic regions are found within the AE cloud detected during hydraulic stimulation. It is not known whether these regions are accepting fluid or are mostly mechanically and hydraulically inactive. In order to overcome this difficulty, new approaches to acquiring information on the flow paths are needed. The AE tomography method [49] and Electrical Resistance Tomography could be used to acquire images of fluid flow paths and of changes of the flow paths with time, but remain dependent on experimental data acquisition opportunities.
Tracers can be used to indirectly assess the state of a reservoir. Although tracers have been used for a long time, their full potential for understanding HDR/HWR reservoirs has not yet been realized. Reactive tracers (those that thermally degrade in a controlled way and those that attach themselves to the crack surface) could be used to monitor the cooling of the reservoir and the surface area of the reservoir. By using tracers repeatedly during operation, a measure of the dynamic changes occurring in a reservoir could be obtained. It may even be possible to use controlled diameter particles to measure joint opening during reservoir operations.
Models must be developed to ensure that they reflect the reservoir’s heterogeneity as revealed by increasingly sophisticated field data processing, whilst at the same time recognizing that interpretational ambiguities remain.
4.3. Overall Modelling of Reservoir Performance
The modelling of a reservoir, including all interactions between fracture/channel flow paths and the host rock, all geometric irregularities and all changes in the flow paths during stimulation, development and operation, is a challenging problem. This is, of course, the original problem, which was posed more than 20 years ago.
Willis-Richards and Wallroth (1995) [25] - [27] classified models using six categories for the representation of reservoir geometry: one abstract geometry class, four reduced geometry model classes and one realistic geometry class. All lumped-parameter models fall into the category of abstract geometry models. Single planar fracture models, such as PKN and CGDD models, fall into the category of reduced geometry. Network models with regular grids also fall into this category. Realistic geometry models use computer-generated fracture networks. In this review, we classify models into three categories: lumped-parameter models, continuum models and network models.
Lumped-parameter models: Lumped-parameter models [25] - [27] [50] , proposed two simple models, based on standard analytic solutions for the mechanical behaviour of cracks combined with a simple representation of the frictional properties of fracture surfaces. The two models describe the stimulation and circulation of HDR reservoirs in a naturally-fractured basement. Hyodo [50] applied a simple model, which used an analogy to an electrical circuit, to the data from the Hijiori experiments. The model consists of the wellbore impedance, reservoir impedance, loss impedance and reservoir capacitance. All these are set to be dependent on the flow rate, and system parameters can be estimated by simple field experiments, such as step-rate tests.
Continuum modelling approach: In continuum modelling, using either finite difference or finite element approaches, fractures are represented as lying between volumes of matrix rock. These rock masses may be permeable, thermally conducting and/or elastic according to the situation under examination. A variant on this approach has recently been proposed by Vychytil and Horii [51] based on micromechanics. The main input data are joint spacing and preferred orientation of joint sets. It can take into account the aperture change of joints due to slippage along them and is very effective from the view point of the trade-o between the computing time and the geometric reality of the model, especially in the very early stage of exploitation during which information on subsurface structure is very restricted. Three-dimensional simulation is performed fairly easily. The model was successfully applied to data from the Fenton Hill site.
Fracture network modelling: Computer-generated fracture networks conditioned by field data could be used to simulate the operation of the whole reservoir. However, there still remain some problems including this, which need to be solved. For example, the active and the stimulated networks in a HDR reservoir do not correspond exactly to the pre-stimulation (i.e. undisturbed) fracture network. The mechanical and hydraulic processes of stimulation determine which network members can become activated through shear movement and fracture dilation. The additional thermal, chemical and long-term mechanical effects during operation determine their further development. Thus, accurate representation of initial conditions and good representations of the relevant mechanisms are required. Furthermore, whether a statistically accurate realization is sufficient for most purposes has not yet been adequately explored. Also, it is difficult to introduce rock-fracture interactions into a fracture network model without modelling the host rock matrix in at least the same degree of detail mechanically with considerable computational burden ensuing. It is possible to constrain the generated network to ®t the observations in the near field of the access wells. The far field is necessarily treated statistically.
In recent years, it has become apparent that fracture-size distributions are fractal [45] [52] [53] ; or at least close to fractally distributed, although it is commonly assumed that spatial distribution of fractures is random. The undisturbed aperture-fracture size relationship is not known at the scale of geothermal reservoirs. This is potentially critical, because the fluid flow resistance primarily depends on a high power of the aperture. Transmissivity, tortuosity and storage are common field data relating to aperture.
4.4. Simulation Codes
Many simulation codes have been developed and each has its own merit. It is helpful to summarize, classify and show which code is applicable to each of the four stages of exploration, stimulation, circulation and heat extraction. Table 1 [14] summarizes codes for this purpose. In the table, the column “coupling of processes” represents the coupling between fundamental processes (Tsang, 1987, 1991), i.e. H-M, rock stresses responding to fluid pressure changes; T-M, rock stresses responding to temperature changes; M-H, fracture flow apertures responding to stress change; H-T, heat transfer by fluid flow water; and T-H, viscosity and flow patterns changing with temperature. DEM, FEM, FDM and BIM stand for Discrete Element Method, Finite Element Method, Finite Difference Method and Boundary Integral Equation Method, respectively. There are no simulation codes included in Table 1 for water/rock chemical interaction. Indeed, the review paper by Willis-Richards and Wallroth (1995) has cited only two papers by Robinson and Pendergrass (1989) and by Shoji et al. (1989), both of which are for a one-dimensional crack, which cover such interactions.
5. Foam Dynamics in Porous Media and Its Applications in Enhanced Oil Recovery
Foam is a mix of gas, water and a foamer, and consists of liquid films/lamellae and Plateau borders (Schramm
Table 1. Program codes for numerical simulation of hydraulic simulation and heat extraction.
and Wassmuth, [54] ; Vikingstad, [55] ). A plateau border is the connection point of three lamellae, at an angle of 120˚ (Figure 4). Foam is a special case of two-phase (gas-liquid) flow. For gas-liquid flow in porous media without foam, the gas phase resides in the center of the large pores occupying the main paths of flow, while the liquid phase fills the small pores and coats walls of the large pores. Existence of foam affects this diffusivity mechanism. The gas phase in foam will be trapped by films of the liquid lamellae. As a result the gas velocity decreases and gas and liquid phases will move together at the same velocity if a case of stable foam has been achieved. This section briefs mechanisms of generating, stability, and flow regimes of foam in porous media.
5.1. Generation of Foam in Porous Media
Ransohoff and Radke [56] observed three mechanisms lead to foam generation in porous media; snap-off, leave- behind, and lamella division. Figure 5 shows these mechanisms.
5.2. Snap-Off Mechanism
Roof [57] showed that when oil emerges from a water-wet constriction into a water-filled pore, the interfacial forces are such that a leading portion of the oil may separate into a droplet (snap off). The same mechanism occurs during invasion of gas to pores filled with liquid. It takes place regardless of the presence or absence of surfactant, but if a stabilizing surfactant is not present, snapped off bubbles quickly coalesce (Kovscek and Radke, [58] ). The snap-off process is a result of the difference in the capillary pressure between the pore body and pore throat. Thus occurrence of the process is a function of ratio of the body-to-throat equivalent diameters. Kovscek and Radke [58] , and Li [59] - [61] presented details of the snap-off process.
Figure 4. Sketch of a foam system.
Figure 5. Mechanisms of foam generation in porous media.
5.3. Leave-Behind Mechanism
The leave behind mechanism also occurs during invasion of a gas phase to a porous medium saturated with a liquid phase. Foams generated solely by leave-behind give approximately a five-fold reduction in steady-state gas permeability (Ransohoff and Radke, [56] ; Kovscek and Radke, [58] ), whereas discontinuous-gas foam created by snap-off resulted in a several-hundred fold reduction in gas mobility (Persoff et al., [62] ; Ettinger and Radke, [63] ; Kovscek and Radke, [58] ). This indicates that the strength of foam (i.e. number and stability of lamellae) is affected by the dominant mechanism of foam generation.
5.4. Lamella Division Mechanism
Increasing number of lamellae or bubbles by lamella division mechanism can be existed when mobile foam bubbles are pre-existed in the porous medium. When a moving lamella train encounters a branch in the flow path, it may split into two, one in each branch of the path (Tanzil et al., [64] ). Lamella division is thought to be the primary foam-generation mechanism in steady gas-liquid flow (Gauglitz et al., [65] ; Li, [59] - [61] ).
5.5. Stability of Foam in Porous Media
Foam in porous media can be in a stable state at a certain value of the capillary pressure, called the limiting capillary pressure (Pc*) (Khatib et al., [66] ). The limiting capillary pressure is a function of the surfactant formulation and concentration, gas velocity, permeability of the porous medium, and presence of oil. The corresponding liquid saturation of (Pc*) is (Sw*).
Flow regimes of foam in porous media (Osterloh and Jante [67] ) showed that two flow regimes of foam in porous media can be identified; high-quality (dry) regime in which steady-state pressure gradient is independent of gas flow rate and low quality (wet) regime in which pressure gradient is independent of liquid flow rate. The transition zone between the two regimes was characterized by a specific value of gas fractional flow (gas velocity divided by total velocity) (fg*). Alvarez et al. [68] confirmed conclusions of Osterloh and Jante [67] and showed that this behaviour of foam flow is general by using data of foam flow with a variety of porous media and surfactant formulations, over a range of flow rates. There is a critical pressure gradient that must be exceeded to generate a high-quality regime of foam during the flow of surfactant solution and gas through homogeneous porous media (Li et al., 2008). Figure 6 shows a schematic plot of parameters of the foam flow in porous media.
5.6. Factors Affecting Foam Dynamics in Porous Media
Experimental studies that investigated factors affecting foam dynamics in porous media have been reviewed and their important conclusions have been highlighted. The studies investigated different types of surfactant (anionic, non-ionic, cationic, and amphoteric surfactants) with types of porous media consisted of steel wool packs, sand packs, crush cores, and sandstone and carbonate cores. The used methodologies included static and flow tests (pre-prepared foam injection, co-injection of surfactant solution and gas, and SAG injection) at conditions ranged from room to reservoir conditions and in absence and presence of oil. The progress of foam front was monitored by measuring of the differential pressure. To identify the liquid saturation and propagation of foam in porous media, some studies used X-ray computed tomography e.g. Apaydin and Kovscek [69] and Nguyen [70] , or Gama ray e.g. Persoff et al. [71] . The investigated factors include; surfactant, injection parameters, permeability and heterogeneity of porous media, and presence of oil.
5.7. Surfactant
The surfactant has an important role in generation and stability of the foam in porous media. It affects the interfacial forces between the gas and liquid which in turn affects value of Pc*. The proper surfactant should have the following properties: be capable of generating ample, lasting foam at the reservoir conditions, should have low adsorption and decomposition losses, should increase the sweep efficiency and the oil recovery, in addition it should be commercially available and inexpensive (Casteel and Djabbarah, [72] ). Foam is readily formed during a drainage process (displacing the liquid phase by the gas phase) whenever the porous medium is pre-saturated with a surfactant solution (Chou, 1991). The reduction of surfactant concentration below the Critical Miscelle Concentration (CMC) caused a shift of the transition zone of the flow regimes to lower values of fg* and Pc* (Alvarez et al., 1999). Foam coalescence forces are inversely proportional to surfactant concentration, thus the foam weakens and the displacement efficiency decreases as the surfactant concentration decreases (Apaydin and Kovscek, [73] ). Friedmann and Jensen [74] showed that size of foam bubbles inside porous media slightly decreases with increasing of the surfactant concentration. Li [59] - [61] found that higher velocity is required to create foam when the surfactant concentration is reduced. Adsorption of the surfactant on the reservoir rock reduces the surfactant concentration in the injected fluid. The adsorption is a function of the surfactant formulation, reservoir fluids, reservoir lithology, and reservoir conditions (Casteel and Djabbarah, [72] ). For
Figure 6. Schematic plot of parameters of the foam flow in porous media.
unconsolidated sand cores at temperatures ranging from 50˚C (122˚F) to 150˚C (302˚F) it was found that the surfactant adsorption decreases with increasing the temperature, and increases with the presence of clays in the core (Novosad et al., [75] ). Grigg and Mikhalin [76] showed that the adsorption is a function of state of the fluid movement beside the other parameters, and the density of adsorption of the surfactant on the rock is best described as a function of the surfactant available in the system (concentration plus volume), rather than by surfactant concentration only. In experiments on carbonate cores, Liu et al. [59] - [61] observed that the presence of gas with the surfactant solution in the rock does not affect the surfactant adsorption.
5.8. Injection Parameters
5.8.1. Pre-Prepared Foam Injection and Co-Injection of Surfactant and Gas
The injection flow rate affects foam dynamics strongly. Faster flow rate produces foam with smaller and more uniform bubble sizes, and the foam formed at the higher pressure is more stable (Friedmann and Jensen, [74] ). The relationship between the gas fractional flow (also called foam quality, fg) and gas mobility is characterized by two straight lines intersecting at a critical foam quality (fg*) (Khatib et al., [66] ; Liu et al., [59] - [61] ), as shown in Figure 7. At values of fg slightly below fg*, gas mobility slightly decreases or remains constant with increasing of fg, which indicates a stable state of foam texture (high-quality regime). While at higher fg (above fg*) the gas mobility increases with increasing of fg which indicates an unstable state of the foam texture (low- quality regime). Persoff et al. [62] [71] found that during the transient foam flooding, the flow characteristics vary from characteristic of free gas to that of strong, fine-textured foam. Nguyen [70] showed that before the breakthrough the foam displaces the liquid in a piston-like manner and after the breakthrough a stage of strong secondary liquid de-saturation initiates in central portion of the porous medium and propagates towards the inlet and the outlet.
5.8.2. SAG Injection
Since foam is readily formed during drainage process whenever the porous medium is pre-saturated with a surfactant solution (Chou, [77] ), thus SAG injection is a favourite method to create in-situ foam in porous media. (Xu, [78] ) proved that the SAG injection can produce stable and persistent foam. Li et al. [79] [80] pointed that foam generated in situ by SAG injection can be a substitute for polymer drive in the alkaline-surfactant-polymer EOR process. Gas mobility in SAG injection is higher than that in co-injection of surfactant and gas [59] - [61] . This makes SAG injection more favourite than co-injection to overcome problem of the injectivity reduction that accompanies foam applications in EOR processes.
5.9. Permeability and Heterogeneity of the Porous Media
The foam propagation rate in porous media is significantly affected by rock permeability (Friedmann and Jensen, [74] ). The minimum pressure gradient required for triggering foam generation in steady flow through porous
Figure 7. Schematic plot for the relationship between fg and gas mobility.
media varies with the permeability (Rossen et al., [81] ). As permeability increases, the pressure gradient and gas velocity required for foam generation decrease (Li, [59] - [61] ), and value of fg* is much higher in the high-per- meability medium (Alvarez et al., 1999). In SAG injection, gas breakthrough is much faster in a high-perme- ability bead-pack than in a low-permeability pack (Li, 2006). Khatib et al. [66] concluded from their experiments on porous media with permeability range of 69.09 to 8882.31 µm2 (70 to 9000 Darcies) that Pc* decreases with increasing of the permeability, and there is a straight line relationship between Pc* and logarithm of permeability. This conclusion needs to be verified for low permeability porous media. Siddiqui et al. (1997) stated that the dependence of foam mobility on the injection parameters is different for the low-permeability porous media than that of higher-permeability porous media. (Rossen et al., [81] ) showed that the relation between the minimum pressure gradient required for creating foam and permeability is more complex in consolidated media. Casteel and Djabbarah [72] conducted an interesting experiment to optimize oil recovery from parallel layers have different permeabilities. The result was the foam is more effective to improve oil recovery if it is conducted after the recovery by gas injection. This result agrees with findings of Apaydin et al. [82] where they showed that in heterogeneous layers the foam fronts move at identical rates in all layers if the layers are in capillary communication and cross flow is allowable, but if the cross flow is prohibited between the layers, foam partially plugs the high permeability zone and diverts flow into the low permeability zone. Based on that, it can be concluded that the stage of using foam in EOR should be after a stage of gas flooding alone to get the maximum oil recovery. Thus, foam injection must be the fourth stage of the recovery after primary recovery, water flooding, and gas flooding.
5.10. Presence of Oil
For simplicity most of the experimental studies have been conducted in the absence of oil (Sayegh and Girard, [83] ; Liu, [84] ; Persoff et al., [71] ; Apaydin et al., [82] ; Schramm and Kutay, [85] ; Apaydin and Kovscek, [69] [73] ; Dong, [86] ; Xu, [78] ; Nguyen, [70] ; Xu and Rossen, [87] ; Kutay and Schramm, [88] ; Du et al., [89] ; Kim et al., [90] [91] ; Li, [59] - [61] ; Liu et al., [61] ; Li, [79] [80] ). Success without oil is a precondition to success with oil (Ashoori and Rossen, [92] ). But presence of oil has important effects on foam flow in porous media. Presence of oil represents an additional phase to the gas phase and the surfactant solution phase in the porous medium. This will affect the interfacial tension between phases and the saturations of the phases in the porous medium. Nikolov et al. [93] showed that brine concentration, and surfactant type and concentration affect directly the stability of emulsion and foam films. Oil saturation has a stronger effect on foam than the variances in properties of oil (Jensen and Friedmann, [94] ), and behaviour of foam to displace oil is not the same for all the surfactants (Novosad et al. [95] [96] ). Effect of the presence of oil on the propagation of foam in porous media is strongly surfactant-specific, this was confirmed by Jensen and Friedmann [94] , Novosad et al. [95] [96] , Mannhardt et al. [97] , and Vikingstad and Aarra [98] . For instance Friedmann and Jensen [74] found that presence of oil greater than 20% saturation is detrimental to both foam generation and to propagation of preformed foam, while with different porous medium, oil, and surfactant Vassenden et al. [99] showed that in presence of oil even at very low saturation (5%), gas and surfactant solution were found to flow together without forming foam, and a low-mobility foam zone was found to propagate from the inlet significantly slower than the gas and surfactant fronts. This high difference in the critical oil saturation at which presence of oil be a detrimental factor for propagation and stability of foam indicates that results of experiment of the foam flooding are very restricted to the used type of porous medium, type and saturation of oil, and type and concentration of surfactant, i.e. it is difficult to develop generalized correlations for predicting performance of foam in oil reservoirs.
6. Smooth Particle Hydrodynamics (SPH) Method
6.1. Introduction
Smooth Particle Hydrodynamics (SPH) method will be explained and developed in its original form based on updated Lagrangian formalism. SPH is a relatively new numerical technique for the approximate integration of partial differential equations. It is a meshless Lagrangian method that uses a pseudo-particle interpolation method to compute smooth field variables. Each pseudo-particle has a mass, Lagrangian position, Lagrangian velocity, and internal energy; other quantities are derived by interpolation or from constitutive relations.
The advantage of the meshless approach is its ability to solve problems that cannot be effectively solved using other numerical techniques. It does not suffer from the mesh distortion problems that limit Lagrangian approaches based on structured mesh when simulating large deformations. As it is a Lagrangian method it naturally tracks material history information, such as damage, without the diffusion that occurs in Eulerian approaches due to advection.
Gingold [100] and Lucy [101] initially developed SPH in 1977 for the simulation of astrophysics problems. Their breakthrough was a method for the calculation of derivatives that did not require a structured computational mesh. Review papers by Benz [102] and Monaghan [103] cover the early development of SPH. Libersky and Petchek [104] extended SPH to work with the full stress tensor in 2D. This addition allowed SPH to be used in problems where material strength is important. The development SPH with strength of materials continued with extension to 3D [105] , and the linking of SPH with existing finite element codes [106] [107] .
The introduction of material strength highlighted shortcomings in the basic method: accuracy, tensile instability, zero energy modes and artificial viscosity. These shortcomings were identified in a first comprehensive analysis of the SPH method by Swegle [108] , and Wen [109] . The problems of consistency and accuracy of the SPH method, identified by Belytschko [110] , were addressed by Randles and Libersky [111] and Vignjevic and Campbell [112] . This resulted in a normalised first order consistent version of the SPH method with improved accuracy. The attempts to ensure first order consistency in SPH led to the development of a number of variants of the SPH method, such as Element Free GalerkinMehod (EFGM) [113] [114] , Reproducing Kernel Particle Method (RKPM) [56] [57] , Moving Least Square Particle Hydrodynamics (MLSPH) [12] , Meshless Local PetrovGalerkin Method (MLPG) [115] . These methods allow the restoration of consistency of any order by means of a correction function. It has been shown by Atluri [115] [116] that the approximations based on corrected kernels are identical to moving least square approximations. The issue of stability was dealt with in the context of particle methods in general by Belytschko [117] , and independently by Randles [118] . They reached the same conclusions as Swegle [108] in his initial study.
In spite of these improvements, the crucial issue of convergence in a rigorous mathematical sense and the links with conservation have not been well understood. Encouraging preliminary steps in this direction have already been put forward very recently by Ben Moussa [119] , who proved convergence of their meshless scheme for non-linear scalar conservation laws; see also [120] . This theoretical result appears to be the first of its kind in the context of meshless methods. Furthermore, Ben Moussa proposed an interesting new way to stabilise normalised SPH and allow for treatment of boundary conditions by incorporating upwinding, an approach usually associated with finite volume shock-capturing schemes of the Godunov type, see [121] - [123] . The task of designing practical schemes along these lines is pending, and there is scope for cross-fertilisation between engineers and mathematicians and between SHP specialists and Godunov-type schemes specialists.
The improvements of the methods in accuracy and stability achieved by kernel re-normalisation or correction, have not, however, come for free; now it is necessary to treat the essential boundary conditions in a rigorous way. The approximations in SPH do not have the property of strict interpolants so that in general they are not equal to the particle value of the dependent variable, i.e.
Consequently it does not suffice to impose zero values for uI at the boundary positions to enforce homogeneous boundary conditions.
The treatment of boundary conditions and contact was neglected in the conventional SPH method. If the imposition of the free surface boundary condition (stress free condition) is simply ignored, then conventional SPH will behave in an approximately correct manner, giving zero pressure for fluids and zero surface stresses for solids, because of the deficiency of particles at the boundary. This is the reason why conventional SPH gives physically reasonable results at free surfaces. Contact between bodies occurs by smoothing over all particles, regardless of material. Although simple, this approach gives physically incorrect results.
Campbell [124] made an early attempt to introduce a more systematic treatment of boundary condition by re-considering the original kernel integral estimates and taking into account the boundary conditions through residual terms in the integral by parts. Probably the most sophisticated work on boundary conditions in SPH is due to Takeda et al. [125] , who have applied SPH to a variety of viscous flows. A similar approach has also been used to a limited extent by Libersky [104] [105] with the ghost particles added to accomplish a reflected symmetrical surface boundary condition. In, Belytschko, Lu and Gu [113] the essential boundary conditions were imposed by the use of Lagrange multipliers leading to an awkward structure of the linear algebraic equations, which are not positive definite. Krongauz and Belytschko [126] proposed a simpler technique for the treatment of the essential boundary conditions in meshless methods, by employing a string of finite elements along the essential boundaries. This allowed for the boundary conditions to be treated accurately, but reintroduced the short- comings inherent to structured meshes.
Randles et al. [111] [118] were first to propose a more general treatment of boundary conditions based on an extension of the ghost particle method. In this, the boundary is considera surface one-half of the local smoothing length away from the so-called boundary particles. A boundary condition is apply to a field variable by assigning the same boundary value of the variable to all ghost particles. A constraint isimpose on the boundary by interpolating it smoothly between the specified boundary particle value and the calculated values on the interior particles. This serves to communicate to the interior particles the effect of the specific boundary condition. There are two main difficulties in this:
o Definition of the boundary (surface normal at the vertices).
o Communication of the boundary value of a dependent variable from the boundary to internal particles.
A penalty contact algorithm for SPH was developed at Cranfield by Campbell and Vignjevic [112] . This algorithm was tested on normalised SPH using the Randles approach for free surfaces. The contact algorithm considered only particle-particle interactions, and allowed contact and separation to be correctly simulated. However tests showed that this approach often excited zero-energy modes.
Another unconventional solution to the SPH tensile instability problem was first proposed by Dyka [127] in which the stresses are calculated at the locations other than the SPH particles. The results achieved in 1D were encouraging but a rigorous stability analysis was not performed. A 2D version of this approach was investigated by Vignjevic [112] , based on the normalised version of SPH. This investigation showed that extension to 2D was possible, although general boundary condition treatment and simulation of large deformations would require further research.
To utilise the best aspects of the FE and SPH methods it was necessary to develop interfaces for the linking of SPH nodes with standard finite element grids [107] [128] and contact algorithms for treatment of contact between the two particles and elements [129] .
From the review of the development of meshless methods, given above, the following major problems can be identified: consistency, stability and the treatment of boundary conditions.
6.2. Basic Formulations
The spatial discretisation of the state variables is provided by a set of points. Instead of a grid, SPH uses a kernel interpolation to approximate the field variables at any point in a domain. For instance, an estimate of the value of a function f(x) at the location x is given in a continuous form by an integral of the product of the function and a kernel (weighting) function.
where: the angle brackets denote a kernel approximation, h is a parameter that defines size of the kernel support known as the smoothing length, and x' is new independent variable.
The kernel function usually has the following properties: Compact support, which means that it’s zero everywhere but on a finite domain inside the range of the smoothing length 2h:
Normalised:
These requirements, formulated by Lucy [101] , ensure that the kernel function reduces to the Dirac delta function when h tends to zero:
Therefore, it follows that:
If the function f(x) is only known at N discrete points, the integral of equation 1 can be approximated by a summation:
where mj/ρj is the volume associated to the point or particle j. In SPH literature, the term particles is misleading as in fact these particles have to be thought of as interpolation points rather than mass elements.
The last equation constitutes the basis of SPH method. The value of a variable at a particle denoted by superscript is calculate by summing the contributions from a set of neighbouring particles (Figure 8), denoted by superscript j and for which the kernel function is not zero:
6.3. Conservation Equations
The conservation equations in Lagrangian framework are given by:
The subscripts α and β denote the component. These equations are the forms proposed by Monaghan [130] . The kernel interpolation allows the derivation of the basic SPH form of these conservation equations as:
Figure 8. Set of neighbouring particles.
All the equations above contain integrals of the form:
Using a development in a Taylor series about x' = x, it follows:
As W is an even function, the terms containing odd powers of x' - x vanish. Neglecting second and higher order terms, which is consistent with the overall order of the method, gives:
Using the last relation:
All equations include kernel approximations of spatial derivatives:
Integrating by part gives:
The first term of the second member can be rewritten:
Using Greens theorem, it follows:
The surface integral is zero if the domain of integration is larger than the compact support of W or if the field variable assumes zero value on the boundary of the body (free surface). If none of these conditions is satisfied, modifications should be to make to account for boundary conditions.
One should note that in equations:
The spatial derivatives of the field variables are substitute by the derivatives of the kernel:
It follows:
The final step is to convert the continuous volume integrals to sums over discrete interpolation points. Finally, after a few arrangements in order to improve the consistency between all equations, the most common form of the SPH discretised conservation equations are obtain:
6.4. Kernel Function
To complete the discretisation one has to define the kernel function. Numerous possibilities exist. A large number of kernel function types are discuss in literature, ranging from polynomial to Gaussian. The most common is the B-spline kernel that was propose by Monaghan [130] :
D is the number of dimensions of the problem (i.e. 1, 2 or 3).
C is the scaling factor, which depends on the number of dimensions and ensures that the consistency conditions 2 and 3 are satisfied:
6.5. Variable Smoothing Length
If large deformations occur, particles can largely separate from each other. If the smoothing length remains constant, the particle spacing can become so large than particles will no more interact. On the other hand, in compression, many particles might enter in the neighbouring of each other, which can significantly slow down the calculation. In order to avoid these problems, Benz [102] proposed the use of a variable smoothing length. The intent was to maintain a healthy neighbourhood as continuum deforms. The equation for evolution of h derived by [102] is:
where h0 and ρ0 are initial smoothing length, and density and n is the number of dimensions of the problem.
Another frequently used equation of evolution based on conservation of mass is:
where div(v) is the divergence of velocity.
6.6. Neighbour Search
An important step in the SPH computation is the neighbour search. This task can be extremely time consuming. The neighbour search routine lists the particles that are inside the neighbourhood of each particle at each time step. A direct search between every particle is particularly inefficient. A bucket sort algorithm is more efficient. In this method, an underlying grid of side 2 h is generated and the particles are sorted according to the box in which they are located (Figure 9). Then for each particle, the neighbours are searched among the particles
Figure 9. Bucket sort and neighbour search.
contained in the same box and the surrounding boxes. This allows the computational time to be cut down from a default time proportional to N2 for a direct search to N*log (N), where N is the total number of particles.
6.7. SPH Shortcomings
The basic SPH method has shown several problems when used to model a solid body:
o Consistency.
o Tensile instability.
o Zero-energy modes
6.7.1. Consistency
The SPH method in its continuous form is inconsistent within 2 h of the domain boundaries due to the kernel support incompleteness. In its discrete form the method loses its 0th order consistency not only in the vicinity of boundaries but also over the rest of the domain if particles have an irregular distribution. Meglicki [131] showed that node disorder results in a systematic error. Therefore, a proper SPH grid should be as regular as possible and not contain large discrepancies in order to perform most accurate simulation.
The first order consistency of the method can be achieve in two ways. Firstly, by correcting the kernel function, second, by correcting the discrete form of the convolution integral of the SPH interpolation. Johnson [132] uses this correction procedure, and proposed the Normalised Smoothing Function. Vignjevic [112] also implemented a kernel normalisation and correction to lead to a Corrected Normalised Smooth Particle Hydrodynamics (CNSPH) method which is first order consistent. The full derivation of this correction is given below. In SPH methods based on a corrected kernel, it is no-longer possible to ignore boundary conditions. In basic SPH, free surface boundary conditions are not imposed and are simply ignored as variables tends to zero at boundaries because of the deficiency of neighbour particles.
Derivation of normalised corrected gradient SPH formula
The approximation of fields using a Normalised Corrected SPH (NCSPH) interpolation has been published [112] [118] [133] . Some authors have chosen to use properties of the integrals of motion (linear and angular momentum) to derive Normalisation and Gradient Correction for kernel interpolation, see [133] . This approach lacks generality and does not provide the insight into the origin and the nature of the problem. A full derivation of the correction proposed by Vignjevic [112] , which has not been published before, is given below. The derivation is based on the homogeneity and isotropy of space, the space properties, which have as a consequence conservation of linear and angular momentum, see [134] . The mixed correction insures that homogeneity and isotropy of space are preserved in the process of spatial discretisation.
An interpolation technique should not affect homogeneity of space. One way of demonstrating this is to prove that the interpolation of the solution space itself is independent of a translation of the coordinate axes. In order to express this statement mathematically one can start by writing the general expression for the SPH interpolation of a vector field:
If the field to be interpolated is the solution space then:
And the last equation becomes:
In a different, translated coordinate system, this equation is:
where X′ is the coordinate vector in the new coordinate system. If the translation vector by which the origin of the coordinate system was move is defined as ∆X then the relationship between X and X′ is:
If the interpolated coordinates of a point are independent of the translation of coordinate axes then the following should hold:
By substituting the last two equations, for both Xi and X′I one obtains:
Alternatively:
By comparison between:
It is clear that the discretised space will only be homogeneous if the following condition is satisfied:
Similarly, an interpolation technique should not affect isotropy of space. One way of demonstrating this is to prove that the interpolation of the solution space itself is independent of a rotation of the coordinate axes. The same holds for the SPH approximation. The change in coordinates due to a rotation of the coordinate axes is:
where C is the rotation matrix. For small rotations, this can also be write as:
where ∆φ is the rotation vector.
If one wants to ensure that, the SPH approximation does maintain the fact that space is isotropic then the approximation has to satisfy the following condition:
This means that the rotation matrix has to be approximate exactly.
In order to develop this equation one can start by rewriting:
where 
This means that, for small rotations, the rotation matrix is given by:
The approximation of the rotated coordinates is:
This means that the requirement on the interpolation is:
Expanding this expression leads to:
Therefore to preserve space isotropy:
The following condition has to be satisfied.
The form of the normalised kernel function and the approximation of the first order derivatives which provides first order consistency is given in Table 2 below.
Using the NCSPH approximations, the conservation equations assume the following form:
6.7.2. Tensile Instability
A Von Neumann stability analysis of the SPH method was conducted Swegle [108] and Balsara [135] separately. This has revealed that the SPH method suffers from a tensile instability. This instability manifests itself as a clustering of the particles, which resembles fracture and fragmentation, but is in fact a numerical artefact. Swegle [108] concluded that the instability does not result from the numerical time integration algorithm, but rather
Table 2. Corrected forms of the kernel function and its gradient.
from an effective stress resulting from a non-physical negative modulus being produce by the interaction between the constitutive relation and the kernel interpolation. In other words the kernel interpolation used in spatial discretisation changes the nature of original partial differential equations.
These changes in the effective stress amplify, rather than reduce, perturbations in the strain. From Swegle’s stability analysis, it emerged that the criterion for stability was that:
where W'' is the second derivative of W with respect to its argument and σ is the stress, negative in compression and positive in tension.
This criterion states that instability can also occur in compression, not only in tension. Indeed, if the slope of the derivative of the kernel function is positive, the method is unstable in tension and stable in compression and if the slope is negative, it is unstable in compression and stable in tension.
The fact that this instability manifests itself most often in tension can be explain. Figure 10 shows the stability regime for the B-spline kernel function. The minimum of the derivative is situated at u = 2/3 h. In standard configurations, the particle spacing is equal to the smoothing length, u = h. Thus, standard configurations are unstable in tension. This explains why this unstable phenomenon is generally observe in tension and hence, it is misleading name “tensile instability”.
In order to remedy this problem several solutions have been propose. Guenther [136] and Wen [109] have proposed a solution, known as Conservative Smoothing. Randles and Libersky [111] proposed adding dissipative terms, which is relate to conservative smoothing. Dyka [127] proposed an original solution by using a non- collocated discretisation of stress and velocity points. At one set of points, the stresses are evaluate, while the momentum equation is calculated at another set of points. The “stress” points are equivalent to the Gauss quad- rature points in FE, the other set of points is equivalent to the element nodes. This approach was extende to two dimensions, in combination with kernel normalisation, by Vignjevic and Campbell [112] . Other solutions were proposed, for instance see [137] . The former proposes a corrective SPH method by enforcing higher order con- sistency, while the latter proposes the addition of an artificial force to stabilise the computation. Recently Randles and Libersky combined MLS interpolation with the stress and velocity point approach. They called this approach the Dual Particle Dynamics method [138] .
The conservative smoothing and the artificial repulsive forces methods have limited applicability and have to be use with caution because they affect the strength of material being modelled. At present, the most promising approach is non-collocational spatial discretisation. This problem is in the focus of attention of a number of researchers working on mesh-less methods.
Figure 10. Stability regimes for the B-spline kernel function [108] .
6.7.3. Zero-Energy Modes
Zero-energy modes are a problem that is not unique to particle methods. These spurious modes, which correspond to modes of deformation characterised by a pattern of nodal displacement that produces zero strain energy, can also be find in the finite difference and finite element methods.
Swegle [108] was first to show that SPH suffers from zero energy modes. These modes arise from the nodal under integration. The fundamental cause is that all field variables and their derivatives are calculate at the same locations (particle positions). For instance, for an oscillatory velocity field, illustrated in Figure 1, the kernel approximation would give negligible gradients and consequently stresses at the particles. These modes of deformation are not resist and can be easily excite by rapid impulsive loading. Another explanation can be find in the origin of the kernel approximation. As the kernel approximation, which is the basis of SPH, is an interpolation of a set of discrete data, a constant field, can be fitted with a sinusoidal curve/surface if the order of the interpolation is high enough.
Figure 11 illustrates this spurious mode for a field in 1D SPH. If one would approximate the derivative of the field shown in Figure 4 with a central difference formula:
Then one would obtain:
At all points. Hence, this mode cannot be detect, and can grow unhindered. This means that this mode could grow to a level where it dominates the solution.
Zero energy or spurious modes are characterised by a pattern of nodal displacement that is not a rigid body but produces zero strain energy.
One of the key ideas to reduce spurious oscillations is to compute derivatives away from the particles where kernel functions have zero derivatives. Randles [118] proposed a stress point method. Two sets of points are create for the domain discretisation, one carries velocity, and another carries stress. The velocity gradient and stress are compute on stress points, while stress divergence is sample at the velocity points using stress point neighbours. According to [108] , these spurious modes can be eliminate by replacing the strain measure by a non-local approximation based on gradient approach. Beissel [139] proposed another way to stabilise nodal integration, the least square stabilisation method.
7. Summary
Smoothed particle hydrodynamics (SPH) is a meshfree particle method, which not only uses particles as the computational frame for interpolation or differencing, but also uses the particles to carry the material properties.
Figure 11. Zero energy modes.
In this survey, the smoothed particle hydrodynamics method, and its recent development in numerical algorithms and applications have been reviewed. In methodology and numerical approximation, the basic concepts of kernel and particle approximations as well as the main technique for developing SPH formulation have been addressed. Some smoothing kernel functions have been reviewed with constructing conditions provided.
The emphasis is on the consistency problem, which traditionally limits the accuracy of the SPH method. The general definition of consistency has been surveyed. Several important numerical topics have been investigated, including boundary treatment, solid obstacles, material interface treatment and tensile instability.
The last decades have witnessed the great success of SPH developments in methodology and applications, and there are still many remaining tasks and challenges. To achieve a reliable solution, the computational accuracy, consistency, efficiency, stability and convergence need to incorporate into good SPH algorithms. In general, SPH has great potential in many problems in engineering and science. It has salient advantages over traditional grid based numerical models in treating large deformation, tracking free surfaces, moving interfaces, and deformable boundaries, resolving moving discontinuities such as cracks and shock waves.
The attraction of the SPH method has been showcased not only by saving time and computational resources, but also for its use in diversified applications. One obvious advantage is that the SPH method provides a feasible physical model for non-continuum, as it has some same features as the classic molecular dynamics method and the dissipative particle dynamics method. Therefore, it would be very attractive to apply the SPH method to simulating problems where the main concern of the object is a set of discrete physical particles rather than a continuum, e.g. environmental flows with solid and fluid particles such as landslide, mudslide and multiphase flow in an oil reservoir.
Acknowledgements
L. Castañeda gratefully acknowledges the financial support from the Escuela Superior de Ingeniería Mecánica y Eléctrica Unidad Ticomán, Instituto Politécnico Nacional, through Project no. 20150465. L. Castañeda also thanks Angel Maldonado Austria for useful discussions.
References
- Vaccaro, M. (2013) Multidisciplinary Approach for the Sustainable Utilization of Medium-Low Temperature Geothermal Resources. Ph.D. Thesis, University of Pisa, Pisa. http://etd.adm.unipi.it/
- Kaya, E., Zarrouk, S.J. and O’Sullivan, M.J. (2011) Reinjection in Geothermal Fields: A Review of Worldwide Experience. Renewable Sustainable Energy Reviews, 15, 47-68. http://dx.doi.org/10.1016/j.rser.2010.07.032
- Ungemach, P., Papachristou, M. and Antics, M. (2007) Renewability versus Sustainability. A Reservoir Management Approach. Proceedings of European Geothermal Congress, Unteraching, 30 May-1 June 2007, Paper No. 216.
- Huenges, E. (2010) Geothermal Energy Systems: Exploration, Development, and Utilization. Wiley-VCH, Weinheim.
- Franco, A. and Vaccaro, M. (2014) Numerical Simulation of Geothermal Reservoirs for the Sustainable Design of Energy Plants. Renewable and Sustainable Energy Reviews, 30, 987-1002. http://dx.doi.org/10.1016/j.rser.2013.11.041
- Saeid, S., Al-Khoury, R. and Barends, F. (2013) An Efficient Computational Model for Deep Low-Enthalpy Geothermal Systems. Computers Geosciences, 51, 400-409. http://dx.doi.org/10.1016/j.cageo.2012.08.019
- Pruess, K., Oldenburg, C. and Moridis, G. (1999) TOUGH2 User’s Guide, Version 2.1. Earth Sciences Division. Lawrence Berkeley National Laboratory University of California, Berkeley. http://dx.doi.org/10.2172/751729
- Thunder Head Engineering, Petra Sim 5 User Manual. http://www.thunderheadeng.com/petrasim/
- Rybach, L. and Muffler, P. (1981) Geothermal Systems: Principles and Case Histories. John Wiley and Sons, Hoboken.
- Stefánsson, V. (1997) Geothermal Reinjection Experience. Geothermics, 26, 99-139. http://dx.doi.org/10.1016/S0375-6505(96)00035-1
- Zeng, Y.C., Su, Z. and Wu, N.Y. (2013) Numerical Simulation of Heat Production Potential from Hot Dry Rock by Water Circulating through Two Horizontal Wells at Desert Peak Geothermal Field. Energy, 56, 92-107. http://dx.doi.org/10.1016/j.energy.2013.04.055
- Fox, D.B., Sutter, D., Beckers, K.F., Lukawski, M.Z., Koch, D.L., Anderson, B.J., et al. (2013) Sustainable Heat Farming: Modeling Extraction and Recovery in Discretely Fractured Geothermal Reservoirs. Geothermics, 46, 42-54. http://dx.doi.org/10.1016/j.geothermics.2012.09.001
- Hu, L., Winterfield, P.H., Fakcharoenphol, P. and Wu, Y.S. (2013) A Novel Fully-Coupled Flow and Geomechanics Model in Enhanced Geothermal Systems. Journal of Petroleum Science and Engineering, 107, 1-11. http://dx.doi.org/10.1016/j.petrol.2013.04.005
- Willis-Richards, J. and Wallroth, T. (1995) Approaches to the Modelling of HDR Reservoirs: A Review. Geothermics, 24, 307-332. http://dx.doi.org/10.1016/0375-6505(95)00011-E
- Cook, N.G.W. (1987) Coupled Processes in Geomechanics. In: Tsang, C.F., Ed., Coupled Processes Associated with Nuclear Waste Repositories, 39-65. http://dx.doi.org/10.1016/B978-0-12-701620-7.50010-6
- Fairhurst, C. (1987) Comments on the Modelling of Coupled Thermo-Mechanical-Fluid Flow Behaviour of Rock Masses. In: Tsang, C.F., Ed., Coupled Processes Associated with Nuclear Waste Repositories, 713-731. http://dx.doi.org/10.1016/B978-0-12-701620-7.50055-6
- Noorishad, J. and Tsang, C.F. (1990) Development and Verification of a Numerical Technique for Coupled Hydromechanical Phenomena in Rocks. Proceedings of International Symposium on Rock Joints, Loen, 673-679.
- Rutqvist, J., Ljunggren, C., Stephansson, O., Noorosjad, J. and Tsang, C.F. (1990) Theoretical and Field Investigations of Fracture Hydromechanical Response under Fluid Injection. Proceedings of International Symposium on Rock Joints, Loen, 557-564.
- Tsang, C.F. (1991) Coupled Hydromechanical-Thermomechanical Processes in Rock Fractures. Reviews of Geophysics, 29, 537-551. http://dx.doi.org/10.1029/91RG01832
- Tsang, C.F. (1987) Coupled Processes Associated with Nuclear Waste Repositories. Academic Press, Waltham.
- Tsang, Y.W. and Witherspoon, P.A. (1985) Effects of Fracture Roughness on Fluid Flow through a Single Deformable Fracture. Proceedings of International Association of Hydrogeologists Conference on Hydrogeology of Rocks of Low Permeability, Tucson, 683-694.
- Tsang, C.F., Noorishad, J. and Witherspoon, J. (1985) The Effect of Deformability on Fluid Flow through a Fractured Porous Medium. Proceedings of International Association of Hydrogeologists Conference on Hydrogeology of Rocks of Low Permeability, Tucson, 676-682.
- Wang, J.S.Y., Tsang, C.F. and Sterbentz, R.A. (1983) The State of the Art of Numerical Modelling of Thermohydrologic Flow in Fractured Rock Masses. Environmental Geology, 4, 133-199.
- Witherspoon, P.A., Tsang, Y.W., Long, J.C.S. and Noorishad, J. (1981) New Approaches to Problems of Fluid Flow in Fractured Rock Masses. Proceedings of 22nd US Rock Mechanics Symposium, MIT, Cambridge, 1-20. http://dx.doi.org/10.1007/BF02380512
- Kruger, P., Hicks, T.W. and Willis-Richards, J. (1992) The Potential for Thermal Energy Extraction from Cornish Granite. Transactions on Geothermal Resources Council, 16, 465-472.
- Willis-Richards, J. (1992) Review of HDR Modelling. Report of CSM Associates Ltd., Report IR02/07 for AEA Technology E/5A/164/2873.
- Willis-Richards, J. (1995) Evaluation of HDR Reservoir Performance Using Stochastic Techniques and Scalabitity. Geothermics, 24.
- Pine, R.J. and Batchelor, T. (1984) Downward Migration of Shearing in Jointed Rock during Hydraulic Injections. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstract, 21, 244-263. http://dx.doi.org/10.1016/0148-9062(84)92681-0
- Niibori, Y. and Chida, T. (1989) Estimations of Apparent Relative Permeabilities Considered Distribution of Saturation. Journal of the Geothermal Research Society of Japan, 11, 251-268.
- Glover, P.W.J., Matsuki, K., Hikima, R. and Hayashi, K. (1996) Fluid Flow in Fractally Rough Synthetic Fractures. Geophysical Research Letters, 20, 1803-1806.
- Matsuki, K., Sakaguchi, K. and Li, S. (1999) Fractal Nature of Crack Surfaces, Characteristics of Fluid Flow through a Crack and Interfacial Stiffness Induced by Contact between Two Crack Surfaces. Geothermal Science and Technology, 6, 113-139.
- Evans, K.F., Kohl, T., Hopkirk, R.J. and Rybach, L. (1992) Modelling of Energy Production from Hot Dry Rock Systems. Final Report to Swiss National Energy Research Fund on Project No. NEFF 359, ETH Zuèrich/Polydynamics Ltd.
- Kohl, T. and Hopkirk, R.J. (1995) “FRACTure”―A Simulation Code for Forced Fluid Flow and Transport in Fractured, Porous Rock. Geothermics, 24, 333-343. http://dx.doi.org/10.1016/0375-6505(95)00012-F
- Kohl, T., Evans, K.F., Hopkirk, R.J. and Rybach, L. (1992) Modelling of Coupled Hydraulic, Thermal and Mechanical Processes in the Simulation of Hot Dry Rock Reservoir Behaviour. Proceedings of International Conference on Jointed and Fractured Rock Masses, Lake Tahoe, 535-542.
- Kohl, T., Evans, K.F., Hopkirk, R.J. and Rybach, L. (1995) Coupled Hydraulic, Thermal and Mechanical Considerations for the Simulation of Hot Dry Rock Reservoirs. Geothermics, 24, 345-359. http://dx.doi.org/10.1016/0375-6505(95)00013-G
- Kohl, T., Evans, K.F., Hopkirk, R.J. and Rybach, L. (1997) Observation and Simulation of Non-Darcian Flow Transients in Fractured Rock. Water Resources Research, 3, 407-418. http://dx.doi.org/10.1029/96WR03495
- Kohl, T., Hopkirk, R.J., Evans, K.F. and Rybach, L. (1993) Coupled Processes in Heat Extraction by HDR-Systems. Proceedings of Second HDR International Forum, Yamagata, Paper H-1.
- Kohl, T., Jung, R., Hopkirk, R.J. and Rybach, L. (1996) Non-Linear Flow Transient in Fractured Rock Mass―The 1995 Injection Experiment in Soultz. Proceedings of 25th Workshop on Geothermal Reservoir Engineering, Stanford University, SGP-TR-151.
- Kimura, S., Masuda, Y. and Hayashi, K. (1991) An Efficient Numerical Method Based on Double Porosity Model to Analyse Heat and Fluid Flows in Fractured Rock Formation. Transactions of the Japan Society of Mechanical Engineers, 57, 157-161.
- Ogino, F. and Yamamura, K. (1999) Pressure Drop of Water Flow through a Crack and Heat Transfer from Hot Dry Rock to Water―Owing through a Crack. Geothermal Science and Technology, 6, 139-162.
- Yamamoto, T., Fujimitu, Y. and Ohnishi, H. (1995) Hot Dry Rock 3D Simulation of the Ogachi Site. Transactions on Geothermal Resources Council, 19, 284-287.
- Yamamoto, Y., Kitano, K., Tanaka, N. and Ohnishi, H. (1996) Hot Dry Rock 3D Simulation of the Ogachi Site II. Transactions on Geothermal Resources Council, 20, 467-474.
- Willis-Richards, J. (1995) Assessment of HDR Reservoir Stimulation and Performance Using Simple Stochastic Models. Geothermics, 24, 385-402. http://dx.doi.org/10.1016/0375-6505(95)00016-J
- Willis-Richards, J. and Wallroth, T. (1995) Approaches to the Modelling of HDR Reservoirs: A Review. Geothermics, 24, 307-332. http://dx.doi.org/10.1016/0375-6505(95)00011-E
- Willis-Richards, J., Watanabe, K. and Takahashi, H. (1996) Progress toward a Stochastic Rock Mechanics Model of Engineered Geothermal System. Journal of Geophysical Research, 101, 17481-17496. http://dx.doi.org/10.1029/96JB00882
- Willis-Richards, J., Watanabe, K., Yamaguchi, T., Sato, Y. and Takasugi, S. (1995) HDR Reservoir Analysis Incorporating Acoustic Emission Data. Proceedings of 20th Workshop on Geothermal Reservoir Engineering, Stanford University.
- Stewart, R., Jones, R., Niitsuma, H., Sasaki, S. and Kaieda, H. (1996) A Re-Examination of Micro Seismic Data from the Hijiori HDR Project. Proceedings of 3rd International HDR Forum.
- Moriya, H., Niitsuma, H., Rutledge, J.T. and Fehler, M. (1997) Estimation of Regional In-Situ Stress Field Controlling Subsurface Fracture System by Using Microseismic Multiplets. In: Sugawara, K. and Obara, Y., Eds., Rock Stress, Balkema, 247-252.
- Block, L.V., Cheng, C.H., Fehler, M.C. and Philips, W.S. (1994) Seismic Imaging Using Microearthquakes Induced by Hydraulic Fracturing. Geophysics, 59, 102-112.
- Hyodo, M., Shinohara, S., Takasugi, S., Wright, C.A. and Conant, R.A. (1995) An HDR System Hydraulics Model and Detailed Analysis of the 1991 Circulation Test at the Hijiori HDR Site, Japan. Geothermal Resources Council Transactions, 19, 263-268.
- Vychytil, J. and Horii, H. (1999) Constitutive Modelling and Numerical Simulation of the Hot Dry Rock Reservoir Stimulations. Geothermal Science and Technology, 6, 259-280.
- Shoji, T., Watanabe, K. and Takahashi, H. (1989) Long Term Performance of Geothermal Circulation System Significance of Water Rock Interaction. Proceedings of International Hot Dry Rock Geothermal Energy Conference, Camborne School of Mines, 436-445.
- Watanabe, K. and Takahashi, H. (1995) Fractal Geometry Characterization of Geothermal Reservoir Fracture Networks. Journal of Geophysical Research, 100, 521-528. http://dx.doi.org/10.1029/94JB02167
- Schramm, L.L. and Wassmuth, F. (1994) Foams: Basic Principles. In: Schramm, L.L., Ed., Foams: Fundamentals and Application in the Petroleum Industry, American Chemical Society, Washington DC. http://dx.doi.org/10.1021/ba-1994-0242.ch001
- Vikingstad, A.K. (2006) Static and Dynamic Studies of Foam and Foam-Oil Interactions. Ph.D. Dissertation, University of Bergen, Norway.
- Ransohoff, T.C. and Radke, C.J. (1988) Mechanisms of Foam Generation in Glass-Bead Packs. Journal of Reservoir Engineering of Society of Petroleum Engineers, 3, 573-585. http://dx.doi.org/10.2118/15441-pa
- Roof, J.G. (1970) Snap-Off of Oil Droplets in Water-Wet Pores. Journal of Society of Petroleum Engineers, 10, 85-90. http://dx.doi.org/10.2118/2504-PA
- Kovscek, A.R. and Radke, C.J. (1993) Fundamentals of Foam Transport in Porous Media. Topical Report Prepared, Earth Sciences Division of Lawrence Berkeley Laboratory and Department of Chemical Engineering/University of California, Berkeley. http://www.osti.gov/bridge/purl.cover.jsp;jsessionid=26234ECD11F647ABA6CAC0C2F0FB734E?purl=/101 92736-ecob6j/
- Li, B., Hirasaki, G.J. and Miller, C.A. (2006) Upscaling of Foam Mobility Control to Three Dimensions. Paper Presented at the SPE/DOE Symposium on Improved Oil Recovery, 2-26 April 2006, Tulsa, SPE 99719.
- Li, Q. (2006) Foam Generation and Propagation in Homogeneous and Heterogeneous Porous Media. Ph.D. Dissertation, University of Texas at Austin, USA.
- Liu, Y., Grigg, R.B. and Svec, R.K. (2006) Foam Mobility and Adsorption in Carbonate Core. Paper Presented at the SPE/DOE Symposium on Improved Oil Recovery, Tulsa, 2-26 April 2006, SPE 99756.
- Persoff, P., Radke, C.J., Pruess, K., Benson, S.M. and Witherspoon, P.A. (1991) A Laboratory Investigation of Foam Flow in Sandstone at Elevated Pressure. Journal of Reservoir Engineering of Society of Petroleum Engineers, 6, 365- 371. http://dx.doi.org/10.2118/18781-pa
- Ettinger, R.A. and Radke, C.J. (1992) Influence of Foam Texture on Steady Foam Flow in Berea Sandstone. Journal of Reservoir Engineering of Society of Petroleum Engineers, 7, 83-90.
- Tanzil, D., Hirasaki, G.J. and Miller, C.A. (2002) Conditions for Foam Generation in Homogeneous Porous Media. Paper Presented at the SPE/DOE Improved Oil Recovery Symposium, Tulsa, 13-17 April 2002, SPE 75176.
- Gauglitz, P.A., Friedmann, F., Kam, S.I. and Rossen, W.R. (2002) Foam Generation in Homogeneous Porous Media. Journal of Chemical Engineering Science, 57, 4037-4052. http://dx.doi.org/10.1016/S0009-2509(02)00340-8
- Khatib, Z.I., Hirasaki, G.J. and Falls, A.H. (1988) Effects of Capillary Pressure on Coalescence and Phase Mobilities in Foam Flowing through Porous Media. Journal of Reservoir Engineering of Society of Petroleum Engineers, 3, 919- 926. http://dx.doi.org/10.2118/15442-pa
- Osterloh, W.T. and Jante, M.J. (1992) Effects of Gas and Liquid Velocity on Steady-State Foam Flow at High Temperature. Paper Presented at the SPE/DOE Enhanced Oil Recovery Symposium, Tulsa, 22-24 April 1992, SPE 24179.
- Alvarez, J.M., Rivas, H.J. and Rossen, W.R. (1999) Unified Model for Steady-State Foam Behavior at High and Low Foam Qualities. Paper Presented at the Annual Technical Conference and Exhibition of Society of Petroleum Engineers, Houston, 3-6 October 1999, SPE 56825.
- Apaydin, G.O. and Kovscek, A.R. (2000) Surfactant Concentration and End Effects on Foam Flow in Porous Media. SUPRI TR-120 Report, DEFC26-00BC15311, U.S. Department of Energy. http://pangea.stanford.edu/ERE/research/supria/publications/public/tr120.pdf
- Nguyen, Q.P. (2004) Dynamics of Foam in Porous Media. Ph.D. Dissertation, Delft University of Technology, Netherlands.
- Persoff, P., Radke, C.J., Pruess, K., Benson, S.M. and Witherspoon, P.A. (1991) A Laboratory Investigation of Foam Flow in Sandstone at Elevated Pressure. Journal of Reservoir Engineering of Society of Petroleum Engineers, 6, 365- 371. http://dx.doi.org/10.2118/18781-pa
- Casteel, J.F. and Djabbarah, N.F. (1988) Sweep Improvement in CO2 Flooding by Use of Foaming Agents. Journal of Reservoir Engineering of Society of Petroleum Engineers, 3, 1186-1192. http://dx.doi.org/10.2118/14392-pa
- Apaydin, G.O. and Kovscek, A.R. (2000) Surfactant Concentration and End Effects on Foam Flow in Porous Media. SUPRI TR-120 Report, DEFC26-00BC15311, U.S. Department of Energy. http://pangea.stanford.edu/ERE/research/supria/publications/public/tr120.pdf
- Friedmann, F. and Jensen, J.A. (1986) Some Parameters Influencing the Formation and Propagation of Foams in Porous Media. Paper Presented at the California Regional Meeting of Society of Petroleum Engineers, Oakland, 2-4 April 1986, SPE 15087.
- Novosad, J., Maini, B.B. and Huang, A. (1986) Retention of Foam-Forming Surfactants at Elevated Temperature. Journal of Canadian Petroleum Technology, 25, 2-46. http://dx.doi.org/10.2118/86-03-04
- Grigg, R.B. and Mikhalin, A.A. (2007) Effects of Flow Conditions and Surfactant Availability on Adsorption. Paper Presented at the International Symposium on Oilfield Chemistry of Society of Petroleum Engineers, Houston, 28 February-2 March 2007, SPE 106205.
- Chou, S.I. (1991) Conditions for Generating Foam in Porous Media. Paper Presented at the Annual Technical Conference and Exhibition of Society of Petroleum Engineers, Dallas, 6-9 October 1991, SPE 22628.
- Xu, Q. (2003) Theoretical and Experimental Study of Foam for Enhanced Oil Recovery and Acid Diversion. Ph.D. Dissertation, University of Texas at Austin, USA.
- Li, R.F., Yan, W., Liu, S., Hirasaki, G.J. and Miller, C.A. (2008) Foam Mobility Control for Surfactant EOR. Paper Presented at the Improved Oil Recovery Symposium of Society of Petroleum Engineers, Tulsa, 19-23 April 2008, SPE 113910. http://dx.doi.org/10.2118/113910-ms
- Li, Z. (2008) Experimental Study and Modeling of Gas Trapping in Foam Flow in Porous Media Using Tracer Technique. Ph.D. Dissertation, University of Texas at Austin, USA.
- Rossen, W.R., Chen, M., Yortsos, Y.C., Kim, J.S., Dong, Y., Nguyen, Q.P., Zitha, P.L.J., Currie, P.K., Xu, Q., Cox, S.J., Neethling, S., Schleifenbaum, W., Schmidt-Wellenburg, P., Cilliers, J.J., van Duijn, C.J., Shan, D., Kam, S.I., Li, Q., Bruining, J., Frenier, W.W., Davies, S.N., Gauglitz, P.A., Friedmann, F., Cheng, L., Delshad, M., Mamun, C.K., Rong, J.G., Liljestrand, H.M., Alvarez, J.M. and Rivas, H. (2005) Mechanistic Studies of Improved Foam EOR Processes. Final Report DE-FC2601BC15318, Center for Petroleum and Geosystems Engineering, The University of Texas at Austin, USA. http://www.netl.doe.gov/technologies/oil-gas/publications/EP/BC15318_Final.pdf
- Apaydin, O.G., Bertin, H., Castanier, L.M. and Kovscek, A.R. (1998) An Experimental Investigation of Foam Flow in Homogeneous and Heterogeneous Porous Media. SUPRI TR-112 Report, DE-FG22-96BC14994, U.S. Department of Energy. http://pangea.stanford.edu/ERE/research/supria/publications/public/tr112.pdf
- Sayegh, S.G. and Girard, M. (1989) The Mobility of Carbon Dioxide Foams in Porous Media. Paper Presented at the 40th Annual Technical Meeting of the Petroleum Society of Canadian Institute of Mining, Banff, 28-31 May 1989, Paper No. 89-40-30. http://dx.doi.org/10.2118/89-40-30
- Liu, D. (1991) Transient Foam Flow in Porous Media with CAT Scanner. Ph.D. Dissertation, Stanford University, USA.
- Schramm, L.L. and Kutay, S.M. (2000) Structure/Performance Relationships for Surfactant Stabilized Foams in Porous Media. Paper Presented at the Petroleum Society’s Canadian International Petroleum Conference, Calgary, 4-8 June 2000, Paper No. 2000-64. http://dx.doi.org/10.2118/2000-064
- Dong, Y. (2001) Experimental Study of CO2 Foam Flow in Porous Media and Application of Fractional-Flow Method to Foam Flow. M.Sc. Thesis, University of Texas at Austin, USA.
- Xu, Q. and Rossen, W.R. (2004) Experimental Study of Gas Injection in a Surfactant-Alternating-Gas Foam Process. Journal of Reservoir Evaluation & Engineering of Society of Petroleum Engineers, 7, 438-448. http://dx.doi.org/10.2118/84183-PA
- Kutay, S.M. and Schramm, L.L. (2004) Structure/Performance Relationships for Surfactant and Polymer Stabilized Foams in Porous Media. Journal of Canadian Petroleum Technology, 43, 19-28. http://dx.doi.org/10.2118/04-02-01
- Du, D., Zitha, P.L.J. and Uijttenhout, M.G.H. (2005) Carbon Dioxide Foam Rheology in Porous Media: A CT Scan Study. Paper Presented at the International Improved Oil Recovery Conference in Asia Pacific of Society of Petroleum Engineers, Kuala Lumpur, 5-6 December 2005, SPE 97552.
- Kim, J.S., Dong, Y. and Rossen, W.R. (2005) Steady-State Flow Behavior of CO2 Foam. Journal of Society of Petroleum Engineers, 10, 405-415. http://dx.doi.org/10.2118/89351-pa
- Rossen, W.R., Chen, M., Yortsos, Y.C., Kim, J.S., Dong, Y., Nguyen, Q.P., Zitha, P.L.J., Currie, P.K., Xu, Q., Cox, S.J., Neethling, S., Schleifenbaum, W., Schmidt-Wellenburg, P., Cilliers, J.J., van Duijn, C.J., Shan, D., Kam, S.I., Li, Q., Bruining, J., Frenier, W.W., Davies, S.N., Gauglitz, P.A., Friedmann, F., Cheng, L., Delshad, M., Mamun, C.K., Rong, J.G., Liljestrand, H.M., Alvarez, J.M. and Rivas, H. (2005) Mechanistic Studies of Improved Foam EOR Processes. Final Report DE-FC2601BC15318, Center for Petroleum and Geosystems Engineering, The University of Texas at Austin, USA. http://www.netl.doe.gov/technologies/oil-gas/publications/EP/BC15318_Final.pdf
- Ashoori, E. and Rossen, W.R. (2010) Can Formation Relative Permeabilities Rule out a Foam EOR Process? Paper Presented at the Annual Technical Conference and Exhibition of Society of Petroleum Engineers, Florence, 19-22 September 2010, SPE 134906.
- Nikolov, A.D., Wasan, D.T., Huang, D.W. and Edwards, D.A. (1986) The Effect of Oil on Foam Stability: Mechanisms and Implications for Oil Displacement by Foam in Porous Media. Paper Presented at of the 61st Annual Technical Conference and Exhibition of Society of Petroleum Engineers, New Orleans, 5-8 October 1986, SPE 15443.
- Jensen, J.A. and Friedmann, F. (1987) Physical and Chemical Effects of an Oil Phase on the Propagation of Foam in Porous Media. Paper Presented at the California Regional Meeting of Society of Petroleum Engineers, Ventura, 8-10 April 1987, SPE 16375.
- Mannhardt, K., Novosad, J.J. and Schramm, L.L. (1998) Foam/Oil Interactions at Reservoir Conditions. Paper Presented at the SPE/DOE Improved Oil Recovery Symposium, Tulsa, 19-22 April 1998, SPE 39681.
- Novosad, J., Maini, B.B. and Huang, A. (1986) Retention of Foam-Forming Surfactants at Elevated Temperature. Journal of Canadian Petroleum Technology, 25, 42-46. http://dx.doi.org/10.2118/86-03-04
- Mannhardt, K., Novosad, J.J. and Schramm, L.L. (1998) Foam/Oil Interactions at Reservoir Conditions. Paper Presented at the SPE/DOE Improved Oil Recovery Symposium, Tulsa, 19-22 April 1998, SPE 39681.
- Vikingstad, A.K. and Aarra, M.G. (2009) Comparing the Static and Dynamic Foam Properties of a Fluorinated and an Alpha Olefin Sulfonate Surfactant. Journal of Petroleum Science and Engineering, 65, 105-111. http://dx.doi.org/10.1016/j.petrol.2008.12.027
- Vassenden, F., Holt, T., Moen, A. and Ghaderi, A. (2000) Foam Propagation in the Absence and Presence of Oil. Paper Presented at the SPE/DOE Improved Oil Recovery Symposium, Tulsa, 3-5 April 2000, SPE 59284.
- Gingold, R.A. and Monaghan, J.J. (1977) Smoothed Particle Hydrodynamics: Theory and Application to Non-Spheri- cal Stars. Monthly Notices Royal Astronomical Society, 181, 375-389. http://dx.doi.org/10.1093/mnras/181.3.375
- Lucy, L.B. (1977) A Numerical Approach to the Testing of Fusion Process. Astronomical Journal, 88, 1013-1024. http://dx.doi.org/10.1086/112164
- Benz, W. (1990) Smooth Particle Hydrodynamics: A Review. In: Buchler, J.R., Ed., The Numerical Modelling of Non- linear Stellar Pulsatations, Kluwer Academic Publishers, Berlin, 269-288. http://dx.doi.org/10.1007/978-94-009-0519-1_16
- Monaghan, J.J. (1982) Why Particle Methods Work. SIAM Journal on Scientific and Statistical Computing, 3, 422-433. http://dx.doi.org/10.1137/0903027
- Libersky, L.D. and Petschek, A.G. (1990) Smooth Particle Hydrodynamics with Strength of Materials. Advances in the Free Lagrange Method, Lecture Notes in Physics, 395, 248-257.
- Libersky, L.D., Petschek, A.G., Carney, T.C., Hipp, J.R. and Allahdadi, F.A. (1993) High Strain Lagrangian Hydrodynamics: A Three-Dimensional SPH Code for Dynamic Material Response. Journal of Computational Physics, 109, 67- 75. http://dx.doi.org/10.1006/jcph.1993.1199
- Attaway, S.W., Heinstein, M.W. and Swegle, J.W. (1994) Coupling of Smooth Particle Hydrodynamics with the Finite Element Method. Nuclear Engineering and Design, 150, 199-205. http://dx.doi.org/10.1016/0029-5493(94)90136-8
- Johnson, G.R. (1994) Linking of Lagrangian Particle Methods to Standard Finite Element Methods for High Velocity Impact Computations. Nuclear Engineering and Design, 150, 265-274. http://dx.doi.org/10.1016/0029-5493(94)90143-0
- Swegle, J.W., Attaway, S.W., Heinstein, M.W., Mello, F.J. and Hicks, D.L. (1994) An Analysis of Smooth Particle Hydrodynamics. Sandia Report SAND93-2513.
- Wen, Y., Hicks, D.L. and Swegle, J.W. (1994) Stabilising SPH with Conservative Smoothing. Technical Report SAND94-1932.
- Belytschko, T., Krongauz, Y., Organ, D., Fleming, M. and Krysl, P. (1996) Meshless Methods: An Overview and Recent Developments. Computer Methods in Applied Mechanics and Engineering, 139, 3-47. http://dx.doi.org/10.1016/S0045-7825(96)01078-X
- Randles, P.W. and Libersky, L.D. (1996) Smoothed Particle Hydrodynamics: Some Recent Improvements and Applications. Computer Methods in Applied Mechanics and Engineering, 139, 375-408. http://dx.doi.org/10.1016/S0045-7825(96)01090-0
- Vignjevic, R., Campbell, J. and Libersky, L. (2000) A Treatment of Zero Energy Modes in the Smoothed Particle Hydrodynamics Method. Computer Methods in Applied Mechanics and Engineering, 184, 67-85. http://dx.doi.org/10.1016/S0045-7825(99)00441-7
- Belytschko, T., Lu, Y.Y. and Gu, L. (1994) Element-Free Galerkin Methods. International Journal for Numerical Methods in Engineering, 37, 229-256. http://dx.doi.org/10.1002/nme.1620370205
- Krongauz, Y. and Belytschko, T. (1997) Consistent Pseudo Derivatives in Meshless Methods. Computer Methods in Applied Mechanics and Engineering, 146, 371-386. http://dx.doi.org/10.1016/S0045-7825(96)01234-0
- Atluri, S. and Zhu, T. (2000) A New Meshless Local Petrov Galerkin (MLPG) Approach in Computational Mechanics. Computational Mechanics, 22, 117-127. http://dx.doi.org/10.1007/s004660050346
- Atluri, S., Kim, H.G. and Cho, J.Y. (2000) A Critical Assessment of the Truly Meshless Local Petrov Galerkin (MLPG) and Local Boundary Integral Equation (LBIE). Computational Mechanics, 24, 348-372. http://dx.doi.org/10.1007/s004660050457
- Belytschko, T. and Xiao, S. (2002) Stability Analysis of Particle Methods with Corrected Derivatives. http://www.tam.northwestern.edu/xiaop/stable.html
- Randles, P.W., Libersky, L.D. and Petschek, A.G. (1999) On Neighbors, Derivatives, and Viscosity in Particle Codes. Proceedings of ECCM Conference, Munich, 31 August-3 September 1999.
- Moussa, B. (2000) Meshless Particle Methods: Recent Developments for Non-Linear Conservation Laws in Bounded Domain. In: Toro, E.F., Ed., Godunov Methods: Theory and Applications, Kluwer Academic/Plenum Publishers, Berlin.
- Moussa, B. and Vila, J.P. (2000) Convergence of the SPH Method for Scalar Nonlinear Conservation Laws. SIAM Journal of Numerical Analysis, 37, 863-887. http://dx.doi.org/10.1137/S0036142996307119
- Toro, E.F. (1991) A Linearised Riemann Solver for the Time Dependent Euler Equations of Gas Dynamics. Proceedings of the Royal Society of London A, 434, 683-693. http://dx.doi.org/10.1098/rspa.1991.0121
- Toro, E.F. (1995) Direct Riemann Solvers for the Time-Dependent Euler Equations. Shock Waves, 5, 75-80. http://dx.doi.org/10.1007/BF02425037
- Toro, E.F. (1999) Riemann Solvers and Numerical Methods for Fluid Dynamics. 2nd Edition, Springer Verlag, Berlin. http://dx.doi.org/10.1007/978-3-662-03915-1
- Campbell, P.M. (1989) Some New Algorithms for Boundary Value Problems in Smooth Particle Hydrodynamics. Technical Report DNA-TR-88-286, Mission Research Corporation.
- Takeda, H.T., Miyama, S.M. and Sekiya, M. (1994) Numerical Simulation of Viscous Flow by Smooth Particle Hydrodynamics. Progress of Theoretical Physics, 92, 939-960. http://dx.doi.org/10.1143/ptp/92.5.939
- Krongauz, Y. and Belytschko, T. (1996) Enforcement of Essential Boundary Conditions in Meshless Approximations Using Finite Elements. International Journal for Numerical Methods in Engineering, 131, 133-145. http://dx.doi.org/10.1016/0045-7825(95)00954-x
- Dyka, C.T. and Ingel, R.P. (1995) An Approach for Tension Instability in Smoothed Particle Hydrodynamics (SPH). Computers and Structures, 57, 573-580. http://dx.doi.org/10.1016/0045-7949(95)00059-P
- Johnson, G.R., Petersen, E.H. and Stryk, R.A. (1993) Incorporation of an SPH Option in the EPIC Code for a Wide Range of High Velocity Impact Computations. International Journal of Impact Engineering, 14, 385-394. http://dx.doi.org/10.1016/0734-743X(93)90036-7
- Vignjevic, R., De Vuyst, T. and Gourma, M. (2001) Interpolation Techniques in Meshless Methods. Computer Modelling in Engineering and Science Journal, 2, 319-337.
- Monaghan, J.J. and Gingold, R.A. (1983) Shock Simulation by the Particle Method SPH. Journal of Computational Physics, 52, 374-389. http://dx.doi.org/10.1016/0021-9991(83)90036-0
- Meglicki, Z. (1998) Analysis and Application of Smoothed Particle Magnetohydrodynamics. Ph.D. Thesis, Australian National University, Acton.
- Johnson, G.R., Stryk, R.A. and Beissel, S.R. (1996) SPH for High Velocity Impact Computations. Computer Methods in Applied Mechanics and Engineering, 139, 347-373. http://dx.doi.org/10.1016/S0045-7825(96)01089-4
- Bonet, J. and Kulasegaram, S. (1999) Correction and Stabilization of Smooth Particle Hydrodynamics Methods with Application in Metal Forming Simulation. International Journal of Numerical Methods Engineering, 47, 1189-1214. http://dx.doi.org/10.1002/(SICI)1097-0207(20000228)47:6<1189::AID-NME830>3.0.CO;2-I
- Landau, L.D. and Lifshitz, E.M. (1960) Mechanics, Course of Theoretical Physics. Vol. 1, Pergamon Press, Oxford.
- Balsara, D.P. (1995) Von Neumann Stability Analysis of Smoothed Particle Hydrodynamics―Suggestions for Optimal Algorithms. Journal of Computational Physics, 121, 357-372. http://dx.doi.org/10.1016/S0021-9991(95)90221-X
- Guenther, C., Hicks, D.L. and Swegle, J.W. (1994) Conservative Smoothing versus Artificial Viscosity. Technical Report SAND94-1853.
- Monaghan, J.J. (2002) SPH without a Tensile Instability. Journal of Computational Physics, 159, 290-311. http://dx.doi.org/10.1006/jcph.2000.6439
- Randles, P.W. and Libersky, L.D. (2000) Normalized SPH with Stresspoints. International Journal for Numerical Methods in Engineering, 48, 1445-1462. http://dx.doi.org/10.1002/1097-0207(20000810)48:10<1445::AID-NME831>3.0.CO;2-9
- Beissel, S. and Belytschko, T. (1996) Nodal Integration of the Element-Free Galerkin Method. Computational Methods Applied Mechanical Engineering, 139, 49-71. http://dx.doi.org/10.1016/S0045-7825(96)01079-1
NOTES
*Corresponding author.



























































































