International Journal of Geosciences
Vol.5 No.2(2014), Article ID:43199,6 pages DOI:10.4236/ijg.2014.52019
A Computer-Assisted Method for Depositional Model Determination
Mapathe Ndiaye1, Eric Davaud2, Stéphan J. Jorry31Laboratoire de Mécanique et Modélisation, University of Thies, Thies, Senegal
2Section of Earth and Environmental Sciences, University of Geneva, Geneva, Switzerland
3IFREMER, Department of Marine Geosciences, Brest, France
Email: mapathe.ndiaye@univ-thies.sn
Copyright © 2014 Mapathe Ndiaye et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Mapathe Ndiaye et al. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received January 5, 2014; revised February 4, 2014; accepted February 21, 2014
Keywords:Depositional Model; Sequence; Log; Markov Chain; Transition Matrix; Walker; Harper; Turk; El Garia Formation
ABSTRACT
A software has been developed to overcome the difficulties related to depositional model determination in Geosciences. The implemented methods, Walker, Harper and Turk methods, based on Markov process and Markov chain analysis, have been used in a case study. The results of the analysis are consistent with previous works. The analysis shows also that the results are accurate and do not rely on the used method. Therefore, the obtained depositional sequence is suitable to build a depositional model on which reliable sequence stratigraphic studies can be based.
1. Introduction
The determination of the depositional model remains a key step for sequence stratigraphy studies. A commonly used method is based on the comparison with present day analogous model that allows retrieving the depositional sequence of facies and deducing the depositional model. In this case, the main difficulties are linked to the size of the data (large variation of forming facies, length and number of stratigraphic logs, etc.) [1]. Another major difficulty of depositional model determination remains for the deposits without known present-day analogous model [2].
Several depositional model determination methods aiming to overcome the lack of present-day facies counterparts have been developed. These methods are mainly based on Markov process and Markov chain analysis [3-8].
Markov chain based facies model methods have been widely adopted by quantitative stratigraphers [9-11]. However, the use of these methods is still limited by the complexity of involved probabilistic concepts and the tediousness of multiple computing steps.
These difficulties motivated the development of Stratisignal, a standalone software that performs all the steps of depositional sequence determination using Markov chain based methods, from the stratigraphic log to the facies relationship diagram that expresses the most probable depositional sequence. To validate the software, we carried out a case study analyzing stratigraphic logs from the Eocene El Garia Formation, Central Tunisia, and compared the results with a previous sequence stratigraphy study [12]. Strati-signal is available for free at: http://archive-ouverte.unige.ch/vital/access/manager/Repository/unige:717
2. Material and Method
We used 16 stratigraphic logs from El Garia Formation, Kesra Plateau, Central Tunisia [12,13]. El Garia Formation is formed by carbonate facies dominated by Nummulites large benthic foraminifera, for which no presentday analogous is known. We used transition matrix methods based on Markov chain to analyze the data aiming to retrieve the depositional sequence.
Transition matrix (TM), as a method for quantitative stratigraphy, has been advocated for the first time by Walker [6], following the works of Read [3], Gingerich [4] and Selley [5]. The method supposes that the succession of facies in a set of stratigraphic logs can be considered as a Markov process. A Markov process is defined as a succession of states or events where the occurrence of a given state depends on the previous one [14].
In this case study, we used the three TM methods implemented in Strati-signal: Walker [6], Harper [7] and Turk methods [8]. In fact, each one of these three methods used separately may suffice to retrieve a deposit sequence. The purpose of diversifying the used methods is to test the sensibility of the obtained results to the chosen method, given that the two first and the third methods use very different approaches. The difference between these three methods resides in the processing steps, to separate significant transitions from random transitions between facies.
All TM methods start with the facies transition matrix definition. It consists of storing in a two-way table, the number of transitions between every couple of the facies present in the stratigraphic logs (Table 1). The depositional sequence will be defined based on the statistically significant transitions.
The simplest TM routine is Walker method (Figure 1). The depositional sequence is obtained by comparing the observed probability of transition between facies with randomly occurring transitions.
An improvement of Walker method has been suggested by Harper [7] advocating that, transitions probabilities greater than random must be tested for statistical significance. Harper argued that, we could not consider a transition as significant if we cannot rule out the null hypothesis of its randomness. Thus, an objective procedure is to choose a given significance level and, for each transition between two facies, compute the probability of having at least the observed number of successions in N trials. This corresponds to the binomial probability. Considering the null hypothesis that a transition occurs at random, it can be rejected if the binomial probability is greater than or equal to the chosen level of significance. To reduce the risk of null hypothesis rejection while it is true, the level of significance must be chosen considerably low [15].
Later, Turk [16] suggested instead, splitting the transition matrix into noise and signal matrix. It returns to isolating the part of the matrix responsible of non-randomness. The “filtering” is performed iteratively (Figure 2) based on a priori hypothesis provided by knowledge, intui tion or a posteriori hypothesis based on residual analysis.
In fact, Turk method uses a signal-processing approach and is, in this way very different from Walker and Harper methods. Its principle consists of performing a chi square test on the remaining matrix after the retrieval of the signal corresponding cells. The truncated cells are restored using iterative proportional fitting [8,17].
Several iterations are often necessary to isolate these two disjoint matrices. The final result, the Guided Transition matrix, is computed using the difference between the observed and the random matrix and is used to draw the facies relationship diagram.

Table 1. Transition matrix of El Garia Formation, showing all the transitions in the 16 stratigrahic logs.

Figure 1. Flow chart of walker transition matrix method.
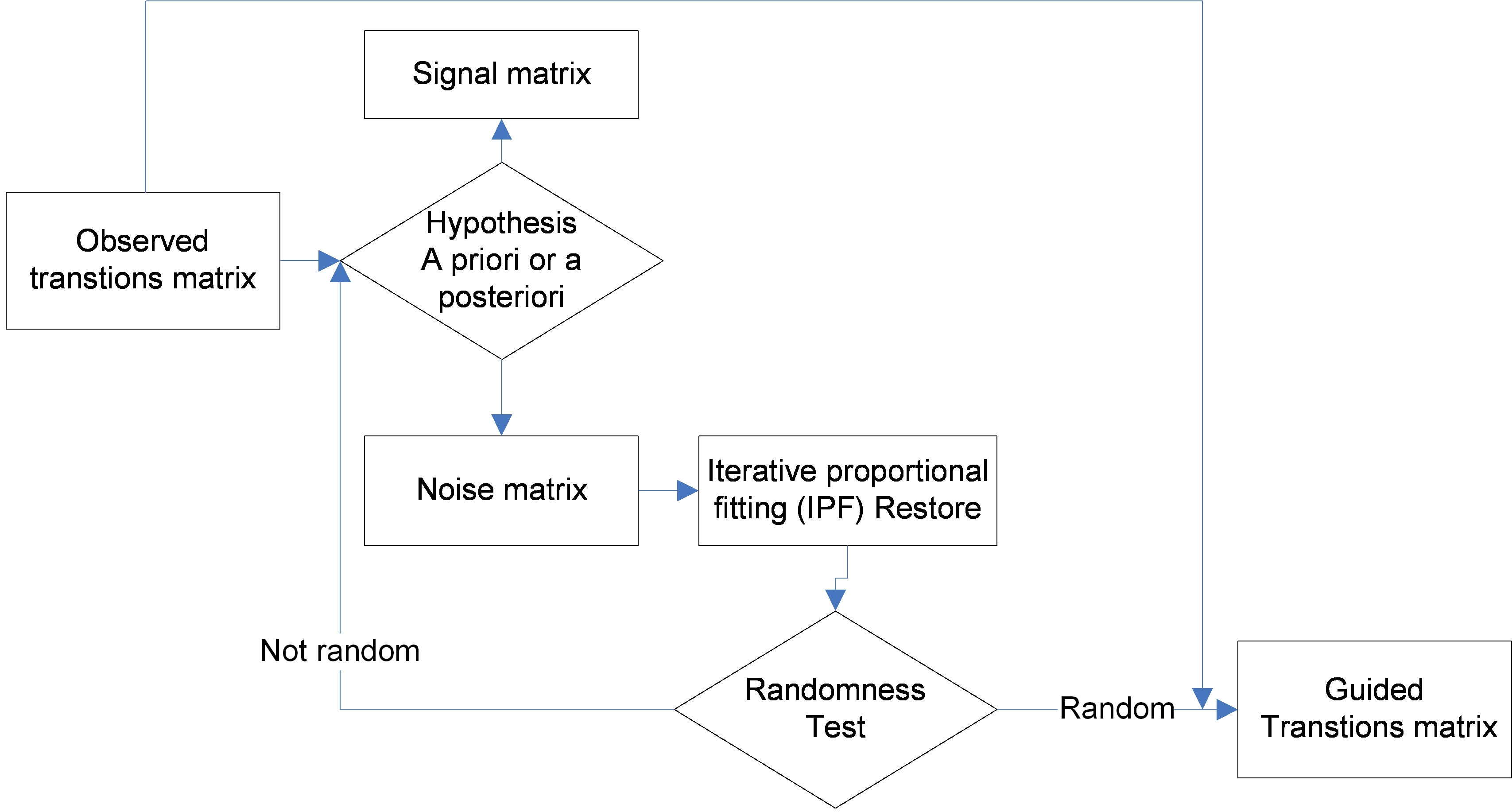
Figure 2. Flow chart of Turk transition matrix method.
3. Case Study
Based on field observations, on nummulites morphology and on petrographic thin sections analysis, nine facies have been distinguished within the 16 stratigraphic logs of the El Garia Formation [12]:
Ÿ Facies F1: Large robust nummulite grainstone.
Ÿ Facies F2: Small robust nummulite grainstone.
Ÿ Facies F3: Large flat nummulite grainstone.
Ÿ Facies F4: Small flat nummulite packstone.
Ÿ Facies F5: Operculina and nummulithoclastic packstone.
Ÿ Facies F6: Nummulithoclastic packstone.
Ÿ Facies F7: Argilaceous wackestone.
Ÿ Facies F8: Nautiloid packestone-wackestone.
Ÿ Facies F9: Bioturbated glauconitic marls.
The 16 stratigraphic logs are loaded as text files (one file per log) in Strati-signal “Log generator” module (Figure 3).
This module allows stratigraphic log creation using a very simple text written syntax. For instance, a line F1 = 10; creates a log with an F1 layer, 10 units thick. If we are only interested in transitions between facies, the thickness of the layer could be neglected, we write simply F1;
Each log is shown in a tabbed pane. When the user hits the “Create log” button, the logs are automatically generated. One can choose to customize layer facies rendering changing color, texture or erosional profile.
Generated stratigraphic logs are shown in the “Log properties” window. “Log properties” is a tool of the “Log analysis” module.
In the next step, we use “Log analysis” module, especially “Facies analysis” tool that extracts automatically the transition matrix (Table 1).
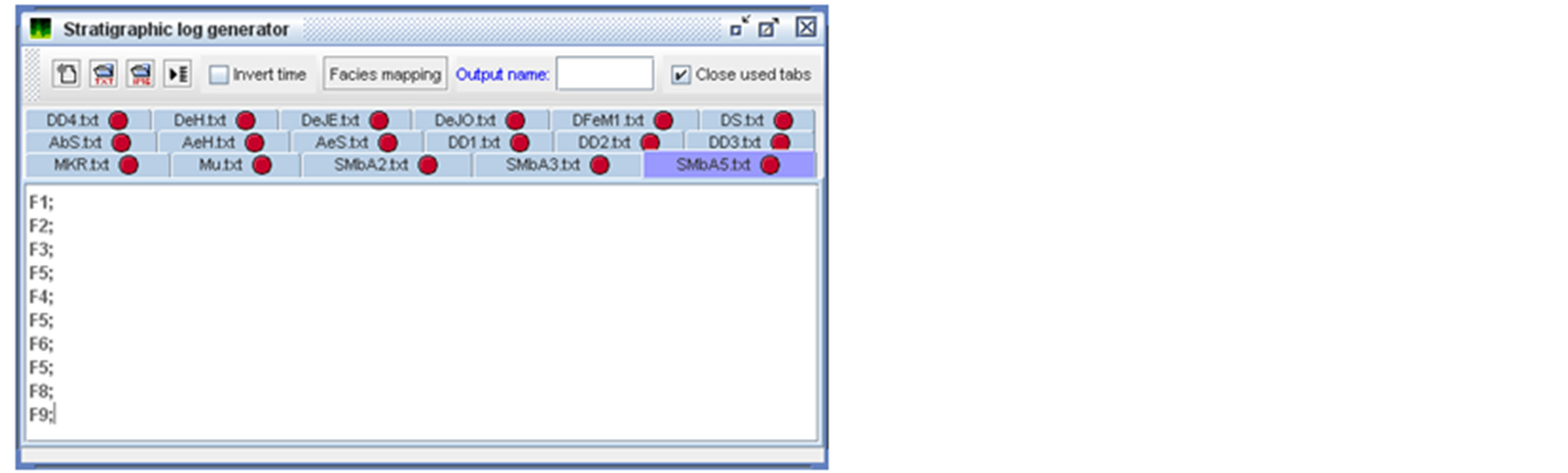
Figure 3. “Log generator” module showing the 16 stratigraphic logs of the El Garia Formation.
The transition matrix can be tested for randomness using the quasi-independence model. In fact, there is no point in looking for patterns in the transition matrix when the data are random [18]. As the computed chi-square exceeds the critical chi-square, the data do not appear to be random (Figure 4).
The final step consists in analyzing the data using successively Walker, Harper and Turk methods (Figure 5). To proceed, the user has to select the stratigraphic logs to be involved in the analysis. In this case we select the “All logs” option.
By default, the sampling step is set to zero. It means that, only transitions from two different facies are considered. An embedded transition matrix is therefore generated. If the user opts for a non-embedded matrix (considering the transition from a facies to itself), he has to specify a sampling step. It is worth noticing that embedded matrices are more common in stratigraphic studies. Non-embedded matrices result in autocorrelation of the thicker facies with themselves and thus, mask important
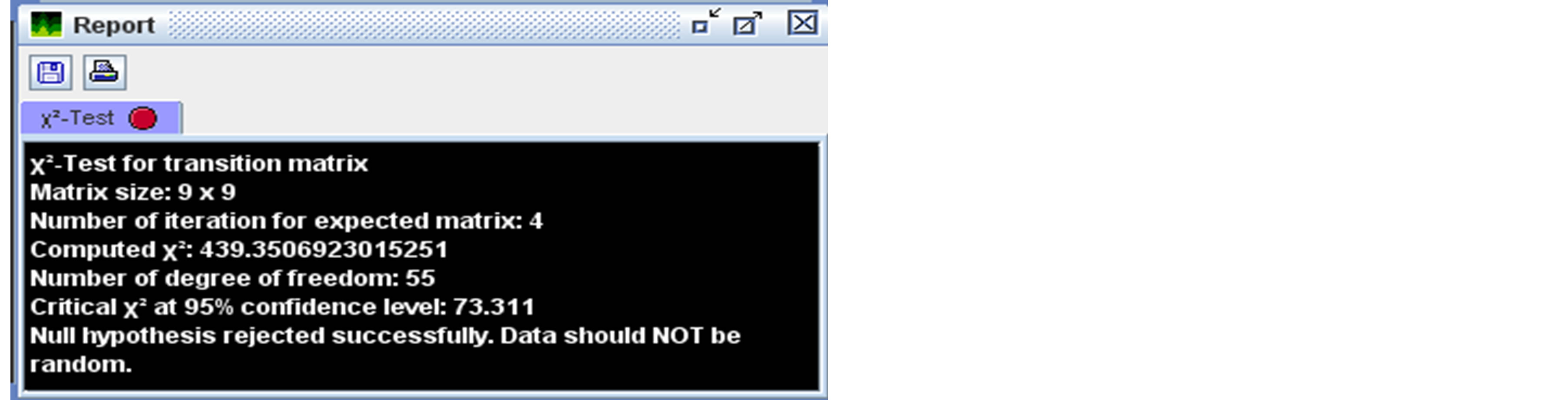
Figure 4. Report of transition matrix test for randomness.
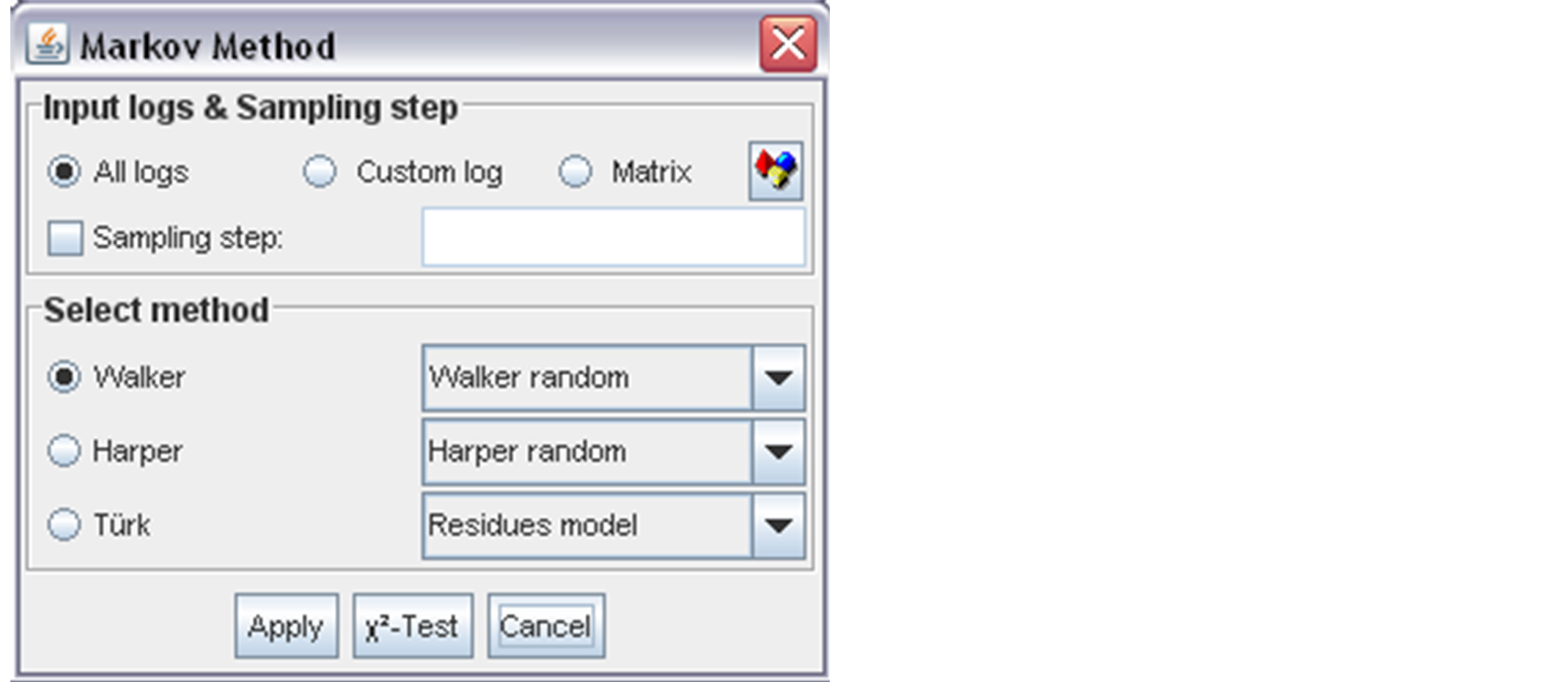
Figure 5. Transition matrix method selection.
transition probabilities between different facies [19].
For Walker and Harper methods, the user can specify the random matrix computation method. The difference between the two given methods resides in whether rows or columns sum is used to estimate a facies number of occurrences. Nevertheless, the use of default options is recommended as far as the user does not have specific needs.
In the case of Turk method, the user can also specify random matrix determination method. Two models are proposed: Residues and Custom models. In the case of “residues model”, the random matrix is computed automatically by the analysis of residues [16]. In the case of the “custom model”, the user has to specify manually the matrix entries corresponding to non-random cells, delete them or replace them by zeros. In this case, the user can get help from the half normal plot of the median tetrads [7,20]. The median tetrad estimates the amount by which an observed score deviates from that expected if there were no interaction [21]. The half normal plot of the median tetrads allows the visualization of outliers generally responsible of non-randomness. Strati-signal allows plotting and navigating through the tetrads to target those deviating from normality. It is worth noticing that the custom model requires a good a priori knowledge of the transition matrix under study.
The results are always shown in a new tabbed pane titled with the used method (e.g. “Harper method”). For each method, the most relevant matrices are displayed on the left side of the facies relationship diagram (FRD).
4. Results and Discussion
Analysis of the El Garia Formation data using Walker method at the 99% confidence level gives the facies relationship diagram shown on Figure 6.
On the Walker FRD, each facies or state present in the stratigraphic logs is represented. Two given facies are linked with an arrow showing the probability, greater than random, to pass from one facies to another. When transitions are simultaneously from A to B and from B to A, we say that A-B transition is cyclical. The Walker FRD shows an “F9-F8-F6-F7-F5-F4-F3-F2-F1” sequence. In other words, from the F9 facies, we can follow the arrows to F8, then to F6 until we reach F1. For each transition represented by an arrow, a value representing the transition probability greater than random is represented. In the following, we will refer to this sequence as the F91 sequence. The Walker FRD shows that the transition F4-F3 can be cyclical before passing to F2. More rarely, the transition can be direct from F4 to F2 skipping F3. A cyclicity can be also observed in F6-F5 transition and F7 can be skipped.
The analysis of the El Garia Formation data using Harper method at the 99% confidence level gives the facies relationship diagram shown on Figure 7. Here, the represented facies or states are linked with arrows containing the binomial probability, which is the probability of having at least the observed number of transitions in N trials, N being the total number of transitions.
We notice that, at the 99% confidence level, the Harper method substantiates Walker results and shows the F91 sequence; Nevertheless F2-F1 transition is no more
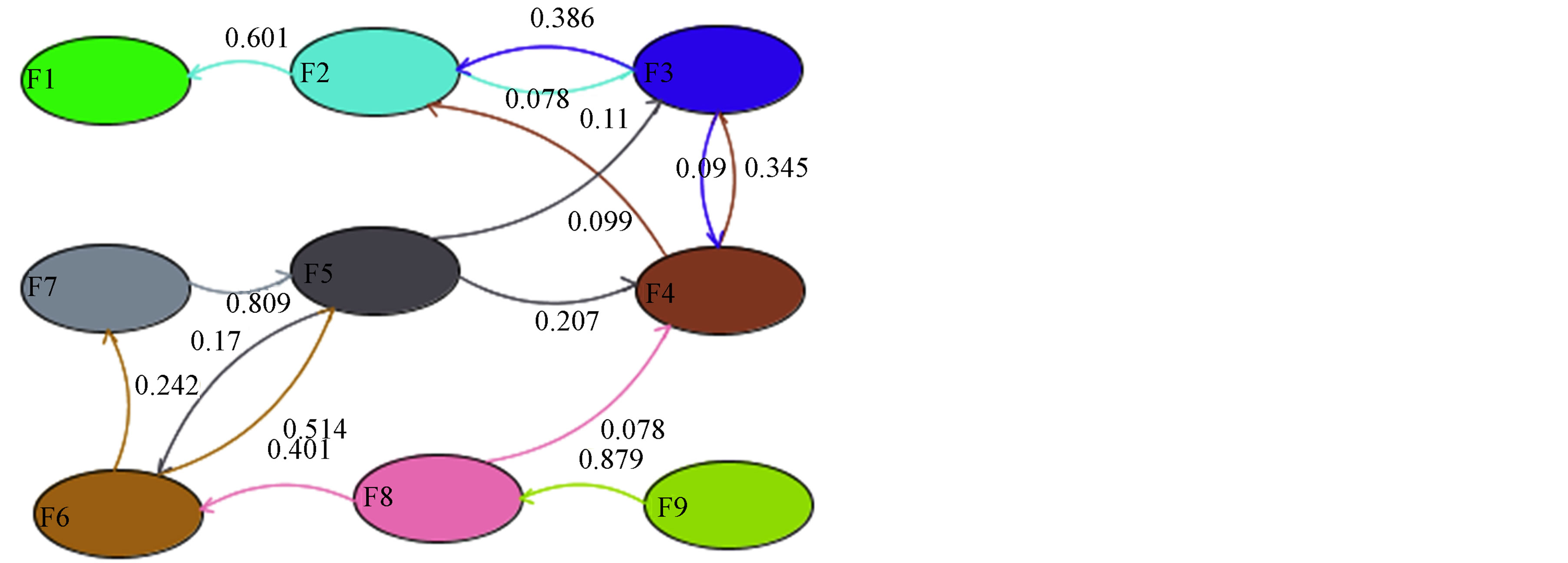
Figure 6. Facies relationship diagram of El Garia Formation using walker method that considers transition probabilities greater than random as significant.
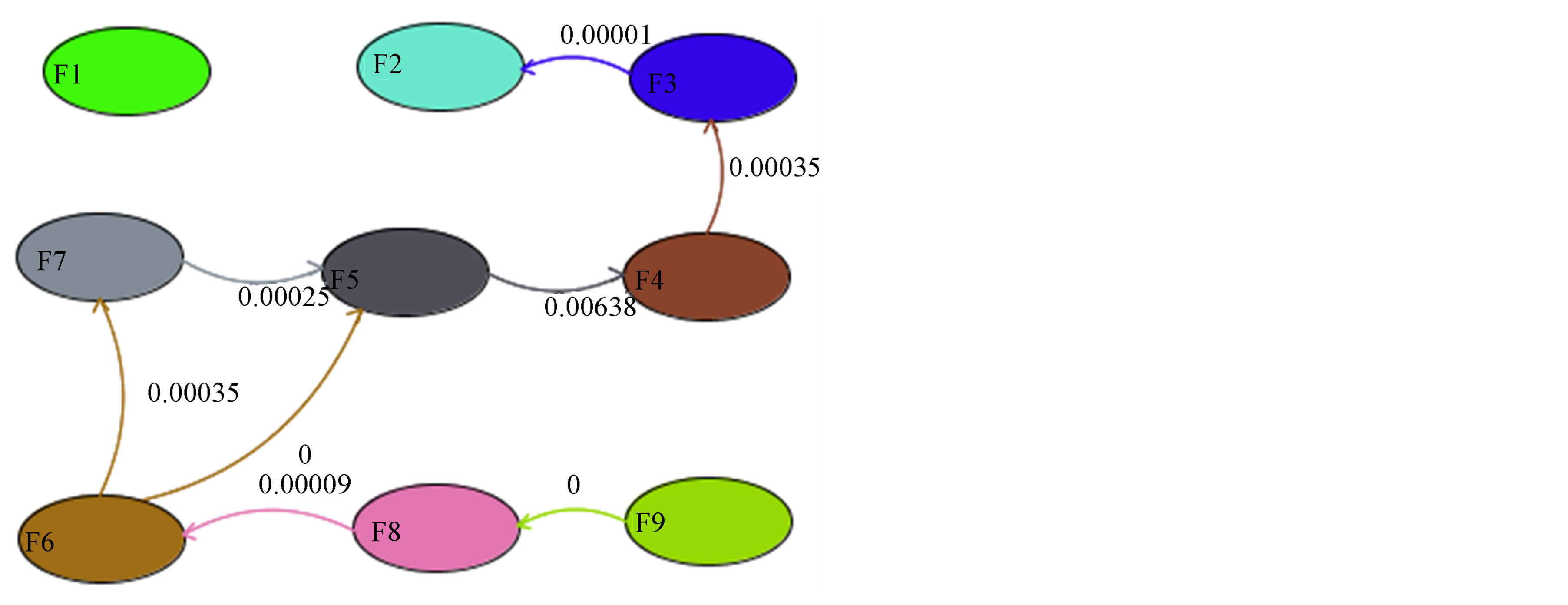
Figure 7. Facies relationship diagram of El Garia Formation using Harper method that considers transition probabilities greater than random and tested for statistical significance.
significant meaning that, according to Harper, F2-F1 transition should be random and F4-F3 cycle has disappeared, which also means that F3-F4 transition should be random. Therefore, we notice that two transitions (F2-F1 and F3-F4) considered as not random for Walker method should be random according to Harper It can be concluded that the Harper method seems to be more restrictive in randomness determination than Walker method. Finally, the analysis of the El Garia Formation using the Turk method with the residues model shows, at the 99% confidence level the facies relationship diagram shown on Figure 8. On this FRD, the facies or states forming the El Garia stratigraphic logs are shown and linked with arrows showing the guided transition values. The guided transition is the non-random part of observed transitions between two given facies. We notice many similarities with the results of Walker and Harper methods. In fact, Turk method substantiates the F91 sequence with F6-F5 cycle. But an F2-F3 cycle is also noticed.
The analysis of the El Garia Formation using Walker, Harper and Turk transition matrix methods gives very similar results. All the results show an F91 sequence. In this case, the different approach between Walker-Harper on one side and Turk methods on the other, strengthens the reliability of the F91 sequence. In fact, these two types of methods can give, in the case, where the nonrandomness of the transitions is weak or null, completely different results [16]. The difference between the results consists in the apparition of short depositional cycles that are different from a method to another. These minor dissimilarities, according to the size of the data (F2-F3 is 3.8% of the transitions and F3-F4 is 4.4%), are linked to randomness determination that is specific to each method.
5. Conclusions
Analysis of the El Garia Formation using Strati-signal
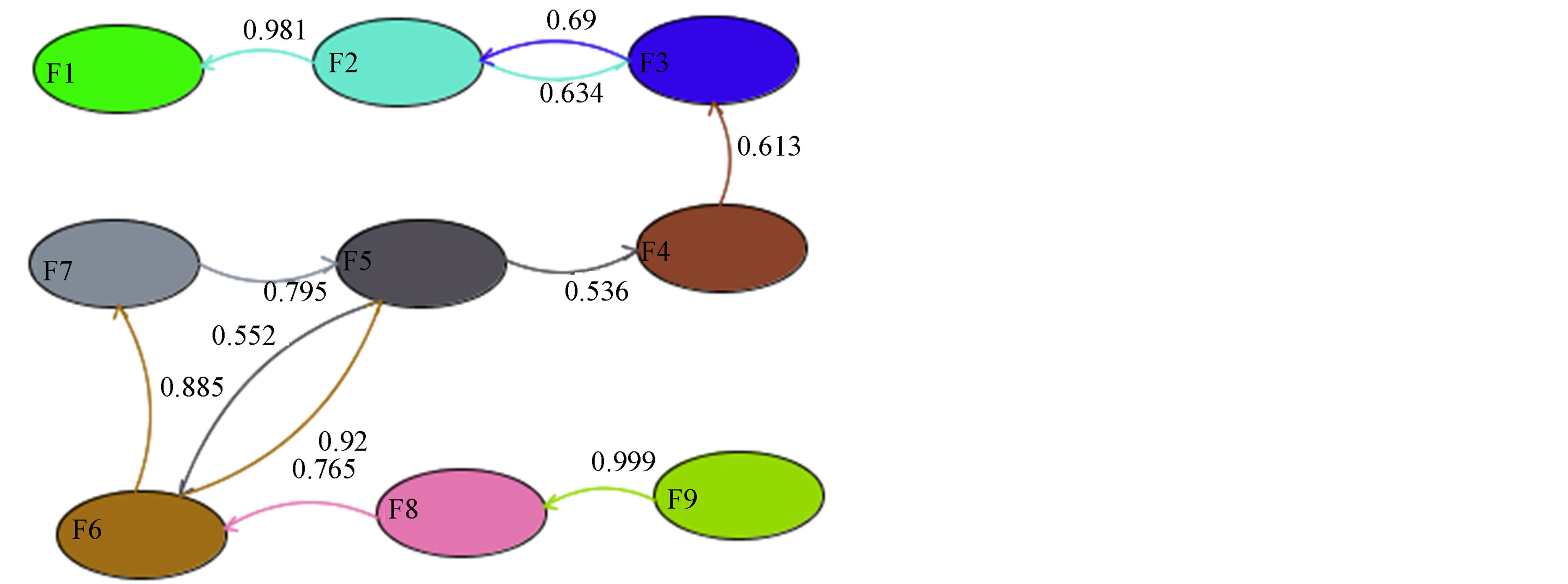
Figure 8. Facies relationship diagram of El Garia Formation using Turk method that considers guided transitions obtained after removing the random part from the bulk transition.
facies transition module reveals the presence of a depositional sequence F91 at 99% confidence level. Moreover, the obtained facies sequence does not rely on the used transition method. This strengthens the reliability of the obtained sequence to define the depositional model. The obtained results are consistent with previous analysis of the El Garia Formation [12].
In the analysis, we used transition between states based on the lithology, but sometimes, mainly in cyclostratigraphic studies, it is worth using other existing stratigraphic surfaces as aerial exposure, erosional surface that carry information similar to lithologic facies.
REFERENCES
[1] P. Enos and E. Samankassou, “Lofer Cyclothems Revisited (Late Triassic, Northern Alps, Austria),” Facies, Vol. 38, No. 1, 1998, pp. 207-227. http://dx.doi.org/10.1007/BF02537366
[2] C. W. J. Harper, “Improved Methods of Facies Sequence Analysis, Facies Models: Response to Sea Level Change,” Geological Association of Canada, Reprint Series 1, 1984, pp. 11-13.
[3] W. A. Read, “Analysis and Simulation of Namurian Sediments in Central Scotland Using a Markov-Process Model,” Mathematical Geology, Vol. 1, No. 2, 1969, pp. 199-219. http://dx.doi.org/10.1007/BF02048562
[4] P. D. Gingerich, “Markov Analysis of Cyclic Alluvial Sediments,” Journal of Sedimentary Research, Vol. 39, No. 1, 1969, pp. 330-332. http://dx.doi.org/10.1306/74D71C4E-2B21-11D7-8648000102C1865D
[5] R. C. Selley, “Studies of Sequence in Sediments Using a Simple Mathematical Device,” Quarterly Journal, Vol. 125, 1969, pp. 557-581.
[6] R. G. Walker, “Facies and Facies Models: General Introduction,” In W. R. G., Ed., Facies Models, Geological Association of Canada, Second Edition, 1979, pp. 1-7.
[7] C. W. J. Harper, “Facies Model Revisited: An Examination of Quantitative Methods,” Geoscience Canada, Vol. 11, No. 4, 1984, pp. 203-207.
[8] G. Turk, “Transition Analysis of Structural Sequences: Discussion,” Geological Society of America Bulletin, Vol. 90, No. 10, 1979, pp. 989-991. http://dx.doi.org/10.1130/0016-7606(1979)90<989:TAOSSD>2.0.CO;2
[9] T. R. Carr, “Log-Linear Models, Markov Chains and Cyclic Sedimentation,” Journal of Sedimentary Petrology, Vol. 52, No. 3, 1982, pp. 905-912.
[10] G. S. Weissmann and G. E. Fogg, “Multi-Scale Alluvial Fan Heterogeneity Modeled with Transition Probability Geostatistics in a Sequence Stratigraphic Framework,” Journal of Hydrology, Vol. 226, No. 1-2, 1999, pp. 48-65. http://dx.doi.org/10.1016/S0022-1694(99)00160-2
[11] M. Fenerci-Massea, J. P. Massea and E. Pernarcic, “Quantitative Stratigraphy Next Term of Rudist Limestones and Its Bearing on Spatial Organisation of Rudist Communities: The Late Barremian, Urgonian, Sequences of Provence (S.E. France),” Palaeogeography, Palaeoclimatology, Palaeoecology, Vol. 215, No. 3-4, 2005, pp. 265-284. http://dx.doi.org/10.1016/j.palaeo.2004.09.008
[12] S. Jorry, E. Davaud and B. Caline, “Controls on the Distribution of Nummilite Facies: A Case Study from the Late Ypresian El Garia Formation (Kesra Plateau, Central Tunisia),” Journal of Petroleum Geology, Vol. 26, No. 3, 2003, pp. 283-306. http://dx.doi.org/10.1111/j.1747-5457.2003.tb00031.x
[13] S. Jorry, “The Eocene Nummulite Carbonates (Central Tunisia and NE Libya): Sedimentology, Depositional Environments and Application to Oil Reservoirs,” Terre & Environnement, Vol. 45, 2004, 230 p.
[14] D. W. Powers and R. G. Easterling, “Improved Methodology for Using Embedded Markov Chains to Describe Cyclical Sediments,” Journal of Sedimentary Petrology, Vol. 52, No. 3, 1982, pp. 913-923.
[15] H. Xu and I. A. J. MacCarthy, “Markov Chain Analysis of Vertical Facies Sequences Using a Computer Software Package (SAVFS): Courtmacsherry Formation (Tournaisian), Southern Ireland,” Computers and Geosciences, Vol. 24, No. 2, 1998, pp. 131-139. http://dx.doi.org/10.1016/S0098-3004(97)00086-1
[16] G. Turk, “Comment on ‘Markov Chain Analysis of Vertical Facies Sequences Using a Computer Software Package (SAVFS): Courtmacsherry Formation’ by H. Xu and I. A. J. MacCarthy,” Computers & Geosciences, Vol. 28, No. 3, 2002, pp. 427-429. http://dx.doi.org/10.1016/S0098-3004(02)00002-X
[17] L. A. Goodman, “The Analysis of Cross-Classified Data: Independence, Quasi Independence and Interactions in Contingency Tables with or without Missing Entries,” Journal of The American Statistical Association, Vol. 63, No. 324, 1968, pp. 1091-1131.
[18] A. R. H. Swan and M. Sandilands, “Introduction to Geological Data Analysis,” Blackwell Science, 1995, 446 p.
[19] S. Holm, I. Isaksson and R. Stevens, “A Test of Independence for Stratigraphic Sequences with Respect to Embedded Markov Chains,” Mathematical Geology, Vol. 18, No. 6, 1986, pp. 551-561. http://dx.doi.org/10.1007/BF00914255
[20] D. Bradu and D. M. Hawkins, “Location of Multiple Outliers in Two-Way Tables, Using Tetrads,” Technometrics, Vol. 24, No. 2, 1982, pp. 103-108. http://dx.doi.org/10.1080/00401706.1982.10487730
[21] J. K. M. Brown, G. H. J. Kema, H.-R. Forrer, E. C. P. Verstappen, L. S. Arraiano, P. A. Brading, E. M. Foster, P. M. Fried and E. Jenny, “Resistance of Wheat Cultivars and Breeding Lines to Septoria Tritici Blotch Caused by Isolates of Mycosphaerella graminicola in Field Trials,” Plant Pathology, Vol. 50, No. 3, 2001, pp. 325-338. http://dx.doi.org/10.1046/j.1365-3059.2001.00565.x

