Open Journal of Optimization
Vol.05 No.01(2016), Article ID:64516,9 pages
10.4236/ojop.2016.51006
A Regularized Newton Method with Correction for Unconstrained Convex Optimization
Liming Li, Mei Qin*, Heng Wang
College of Science, University of Shanghai for Science and Technology, Shanghai, China

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 17 January 2016; accepted 12 March 2016; published 15 March 2016
ABSTRACT
In this paper, we present a regularized Newton method (M-RNM) with correction for minimizing a convex function whose Hessian matrices may be singular. At every iteration, not only a RNM step is computed but also two correction steps are computed. We show that if the objective function is LC2, then the method posses globally convergent. Numerical results show that the new algorithm performs very well.
Keywords:
Regularied Newton Method, Correction Technique, Trust Region Technique, Unconstrained Convex Optimization

1. Introduction
We consider the unconstrained optimization problem [1] -[3]
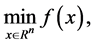 (1.1)
(1.1)
where  is twice continuously differentiable, whose gradient
is twice continuously differentiable, whose gradient 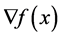 and Hessian
and Hessian 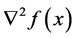 are denoted by
are denoted by  and
and  respectively. Throughout this paper, we assume that the solution set of (1.1) is nonempty and denoted by X, and in all cases
respectively. Throughout this paper, we assume that the solution set of (1.1) is nonempty and denoted by X, and in all cases  refers to the 2-norm.
refers to the 2-norm.
It is well known that 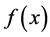 is convex if and only if
is convex if and only if 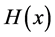 is symmetric positive semidefinite for all
is symmetric positive semidefinite for all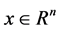 . Moreover, if
. Moreover, if 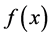 is convex, then
is convex, then 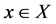 if and only if x is a solution of the system of nonlinear equations
if and only if x is a solution of the system of nonlinear equations
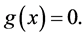 (1.2)
(1.2)
Hence, we could get the minimizer of  by solving (1.2) [4] -[8] . The Newton method is one of efficient solution methods. At every iteration, it computes the trial step
by solving (1.2) [4] -[8] . The Newton method is one of efficient solution methods. At every iteration, it computes the trial step
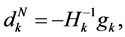 (1.3)
(1.3)
where 






To overcome the difficulty caused by the possible singularity of

where I is the identity matrix. 
Now we need to consider another question, “how to choose the regularized parameter
Fukushima [10] chose 
with 

Inspired by the regularized Newton method [13] with correction for nonlinear equations, we propose a modified regularized Newton method in this paper. At every iteration, the modified regularized Newton method first solves the linear equations

to obtain the Newton step


to obtain the approximate Newton step
It is easy to see

Then it solves the linear equations

to obtain the approximate Newton step
The aim of this paper is to study the convergence properties of the above modified regularized Newton method and do a numerical experiment to test its efficiency.
The paper is organized as follows. In Section 2, we present a new regularized Newton algorithm with correction by trust region technique, and then prove the global convergence of the new algorithm under some suitable conditions. In Section 3, we test the regularized Newton algorithm with correction and compared it with a regularized Newton method. Finally, we conclude the paper in Section 4.
2. The Algorithm and Its Global Convergence
In this section, we first present the new modified regularized Newton algorithm by using trust region technique, then prove the global convergence. First, we give the modified regularized Newton algorithm.
Let 






Define the actual reduction of 

Note that the regularization step 
If we let
then it can be proved [4] that 
By the famous result given by Powell in [14] , we know that

By some simple calculations, we deduce from (1.7) that
so, we have

Similar to

but also a solution to the trust region problem
where

Based on the inequalities (2.2), (2.3) and (2.4), it is reasonable for us to define the new predicted reduction as

which satisfies

The ratio of the actual reduction to the predicted reduction

plays a key role in deciding whether to accept the trial step and how to adjust the regularized parameter.
The regularized Newton algorithm with correction for unconstrained convex optimization problems is stated as follows.
Algorithm 2.1
Step 1. Given




Step 2. If
Step 3. Compute
Solve

to obtain
Solve

to obtain 
Solve

to obtain 
Step 4. Compute

Step 5. Choose 

Set 
Before discussing the global convergence of the algorithm above, we make the following assumption.
Assumption 2.1. 




and

It follows from (2.14) that

The following lemma given below shows the relationship between the positive semidefinite matrix and symmetric positive semidefinite matrix.
Lemma 2.1. A real-valued matrix A is positive semidefinite if and only if 
Proof. See [4] . ♢
Next, we give the bounds of a positive definite matrix and its inverse.
Lemma 2.2. Suppose A is positive semidefinite. Then,
and
hold for any
Proof. See [13] . ♢
Theorem 2.1. Under the conditions of Assumption 2.1, if f is bounded below, then Algorithm 2.1 terminates in finite iterations or satisfies

Proof. We prove by contradiction. If the theorem is not true, then there exists a positive 


Without loss of generality, we can suppose

Now we will analysis in two cases whether T is finite or not.
Case (1): T is finite. Then there exists an integer 
By (2.11), we have
Therefore by (2.12) and (2.17), we deduce

Since


Duo to (1.7), we get
From (2.10), we obtain

where 
It follows from (2.1) and (2.5) that

Moreover, from (2.6), (2.17), (2.13) and (2.19), we have

for sufficiently large k.
Duo to (2.21) and (2.22), we get

which implies that


Case (2): T is infinite. Then we have from (2.6) and (2.17) that

which implies that

The above equality together with the updating rule of (2.12) means

Similar to (2.20), it follows from (2.25) and (2.26) that
for some positive constant
This equality together with (2.24) yields
which implies that

It follows from (2.8), (2.27), (2.26) and (2.20) that

Since 
which means

By the same analysis as (2.23) we know that

Hence, there exists a positive constant 

3. Numerical Experiments
In this section, we test the performance of Algorithm 2.1 on the unconstrained nonlinear optimization problem, and compared it with a regularized Newton method without correction. The function to be minimized is

where 



The Hessian 
where


singular as the sum of every column is zero. Since the Hessian 
The aims of the experiments are as follows: to check whether Algorithm 2.1 converges quadratically as stated in Section 3 and also to see how well the technique of correction works. We set






Table 1 reports the norms of 







We may observe that the whole sequence 

We also ran the regularized Newton algorithm (RNA) without correction, that is, we do not solve the linear equations (2.9)-(2.10) and just set the solution of (2.8) to be the trial step. Then, we tested the regularized Newton algorithm without correction and Algorithm 2.1 for various of n, 









Table 1. Results of Algorithm 2.1 to test quadratic convergence.
Table 2. Results of RNA and Algorithm 2.1.
Moreover, we can see for the same

4. Concluding Remarks
In this paper, we propose a regularized Newton method with correction for unconstrained convex optimization. At every iteration, not only a RNM step is computed but also two correction steps are computed which make use of the previous available Jacobian instead of computing the new Jacobian. Numerical experiments suggest that the introduction of correction is really useful.
Acknowledgements
This research is supported by the National Natural Science Foundation of China (11426155) and the Hujiang Foundation of China (B14005).
Cite this paper
LimingLi,MeiQin,HengWang, (2016) A Regularized Newton Method with Correction for Unconstrained Convex Optimization. Open Journal of Optimization,05,44-52. doi: 10.4236/ojop.2016.51006
References
- 1. Yang, W.W., Yang, Y.T., Zhang, C.H. and Cao, M.Y. (2013) A Newton-Like Trust Region Method for Large-Scale Unconstrained Nonconvex Minimization. Abstract and Applied Analysis, 2013.
- 2. Polyak, R.A. (2009) Regularized Newton Method for Unconstrained Convex Optimization. Mathematical Programming Series B, 120, 125-145.
http://dx.doi.org/10.1007/s10107-007-0143-3 - 3. Shen, C.G., Chen, X.D. and Liang, Y.M. (2012) A Regularized Newton Method for Degenerate Unconstrained Optimization Problems. Optimization Letters, 6, 1913-1933.
http://dx.doi.org/10.1007/s11590-011-0386-z - 4. Sun, W. and Yuan, Y. (2006) Optimization Theory and Methods. Springer Science and Business Media, LLC, New York.
- 5. Zhou, W. and Li, D. (2008) A Globally Convergent BFGS Method for Nonlinear Monotone Equations without Any merit Functions. Mathematics of Computation, 77, 2231-2240.
http://dx.doi.org/10.1090/S0025-5718-08-02121-2 - 6. Argyros, I.K. and Hilout, S. (2012) On the Convergence of Damped Newton Method. Applied Mathematics and Computation, 219, 2808-2824.
http://dx.doi.org/10.1016/j.amc.2012.09.011 - 7. Nashed, M.Z. and Chen, X. (1993) Convergence of Newton-Like Method for Singular Operator Equations Using Outer Inverses. Numerische Mathematik, 66, 235-257.
http://dx.doi.org/10.1007/BF01385696 - 8. Kelley, C.T. (1999) Iterative Methods for Optimization. In: Frontiers in Applied Mathematics, Vol. 18, SIAM, Philadelphia, 2.
http://dx.doi.org/10.1137/1.9781611970920 - 9. Sun, D. (1999) A Regularization Newton Method for Solving Nonlinear Complementarity Problems. Applied Mathematics and Optimization, 40, 315-339.
http://dx.doi.org/10.1007/s002459900128 - 10. Li, D.H., Fukushima, M., Qi, L. and Yamashita, N. (2004) Regularized Newton Methods for Convex Minimization Problems with Singular Solutions. Computational Optimization and Applications, 28, 131-147.
http://dx.doi.org/10.1023/B:COAP.0000026881.96694.32 - 11. Fan, J.Y. and Yuan, Y.X. (2005) On the Quadratic Convergence of the Levenberg-Marquardt Method without Nonsingularity Assumption. Computing, 74, 23-39.
http://dx.doi.org/10.1007/s00607-004-0083-1 - 12. Fan, J.Y. and Pan, J.Y. (2009) A Note on the Levenberge-Marquardt Parameter. Applied Mathematics and Computation, 207, 351-165.
http://dx.doi.org/10.1016/j.amc.2008.10.056 - 13. Fan, J.Y. and Yuan, Y.X. (2014) A Regularized Newton Method for Monotone Nonlinear Equations and Its Application. Optimization Methods and Software, 29, 102-119.
http://dx.doi.org/10.1080/10556788.2012.746344 - 14. Powell, M.J.D. (1975) Convergence Properties of a Class of Minimization Algorithms. In: Mangasarian, O.L., Meyer, R.R. and Robinson, S.M., Eds., Nonlinear Programming, Vol. 2, Academic Press, New York, 1-27.
http://dx.doi.org/10.1016/b978-0-12-468650-2.50005-5
NOTES
*Corresponding author.





























