Received 14 May 2015; accepted 26 September 2015; published 29 September 2015

ABSTRACT

Necessary conditions for optimality are proved for smooth infinite horizon optimal control problems with unilateral state constraints (pathwise constraints) and with terminal conditions on the states at the infinite horizon. The aim of the paper is to obtain strong necessary conditions including transversality conditions at infinity, which in many cases lead to a set of candidates for optimality containing only a few elements, similar to what is the case in finite horizon problems. However, strong growth conditions are needed for the results to hold.

Keywords:

Infinite Horizon, Optimal Control, State Constraints

1. Introduction

The aim of this paper is, in a control problem with unilateral state constraints and terminal conditions at infinity, to obtain necessary conditions, with a full set of transversality conditions at infinity, which frequently make it possible to narrow down the set of candidates for optimality to only a few, or sometimes a single one. In infinite horizon problems without unilateral state constraints (pathwise constraints), with or without terminal conditions on the states at the infinite horizon, there exist various types of necessary conditions for optimality, and examples are [1] (without a transversality condition), and a number of results with certain limited types of transversality conditions, for example [2] , slightly generalized in [3] . See the latter paper and [4] for several further references (see also [5] ). The limited types of transversality conditions mentioned are in problems with several states-often insufficient if one wishes to avoid getting an infinite number of candidates. With strong growth conditions there exist necessary conditions, with a full set of transversality conditions at infinity, which in many cases make it possible to narrow down the set of candidates to only a few, or sometimes a single one, see Theorem 16, p. 244¹ in [5] . For nonsmooth problems with a full set of transversality conditions in the infinite horizon case, see [6] . For such problems, see also [7] .

The novelty of the results in this paper is hence the establishment of necessary conditions that include a full set of transversality conditions at infinity in an infinite horizon problem with both terminal constraints at the infinite horizon and unilateral state constraints (constraints of the form 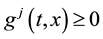for all t). Strong growth conditions are needed for the results to hold.

For Michel-type necessary condition in the case of unilateral state constraints, sees [8] .

The growth conditions used below, ((11), (12), (13)) are more demanding than the conditions applied in [9] for the case of no unilateral state constraints and no terminal constraints (problems with a dominant discount). In later work the authors use even more general conditions, see [10] (see also [11] , and [12] for problems with a special structure).

The results below are of especial interest in the case where not all states are completely constrained at infinity. In the opposite case, generalizations of Halkin’s infinite horizon theorem in [1] to problems with unilateral state constraints where no transversality conditions appear, like Theorem 9, p. 381 in [6] , frequently yield enough information for determining one or a few candidates for optimality. When not all states are completely constrained at infinity, transversality conditions related to the terminal conditions are needed, unless one can accept the possibility of an infinite number of candidates for optimality.

In certain cases there is a danger of degeneracy of multipliers. See the early review in [13] and [14] . We have added conditions that secure nondegeneracy of multipliers in some such cases, in particular in the case where unilateral constraints are satisfied as equalities by the initial state (the state at time zero). See [15] -[17] for a presentation of similar conditions in the finite horizon case, as well as for a number of references for this case (see for example [18] -[22] ).

2. The Control Problem, Necessary Conditions, and Examples

Consider the problem

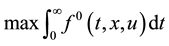(1)

where 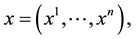subject to

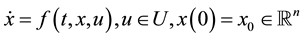(2)

(3)

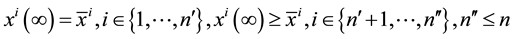(4)

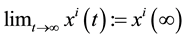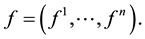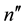
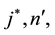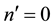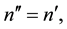where we require that exists for and where Here, and n are given natural numbers, and we allow for the case where there are no equality constraints or no inequality constraints in (4) (in which cases and so and/or 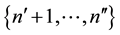are empty sets). Furthermore, are fixed entities, u the control. It is possible that

in which case is replaced by We want to maximize the objective in (1) over the set

of all measurable functions taking values in U and being bounded on bounded time intervals, subject

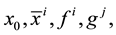
to (2)-(4). When the solution corresponding to such a satisfies (2)-(4), we call admissible. Below will be a given optimal admissible pair, assumed to exist.

We assume that is continuous in that is measurable in continuous in with derivatives and, where is continuous in x and is continuous in

We also assume, for any bounded sets and that

and that for any x, These assumptions are called the basic smoothness

assumptions. At various points some strengthening of these assumptions are added.

The following definitions are needed: let

let be the resolvent of the equation

(I the identity map), if

In Theorem 1, in addition to the basic assumptions, assumptions (5)-(15) below are needed. It is assumed that for all

(5)

We shall make use of some constraint qualifications, (6) and (8) below, related to Define ,

,

(6)

((6) holds vacuously if).

(7)

(8)

(9)

Either²

(10)

The following growth conditions are also needed: For some

(11)

and there exist some positive constants such that

(12)

(13)

where. In (10) (g), we also need that for some for all

Assume finally that, for all j

(14)

(15)

Define The following necessary conditions for optimality holds.

Theorem 1. (Necessary condition, infinite horizon) Assume (5)-(8), (11)-(15) and the basic smoothness as

sumptions. There exist a number vectors, bounded vector functions and nondecreasing and right continuous on, such that if ³ satisfies, for, the equation

(16)

then (the limit does exist), is left continuous on and satisfies (16) for (the integrals exist), and

(17)

Moreover,

(18)

(19)

(20)

Finally, for some and if (6) fails, then (18) must be replaced by ,

Remark 1. For the growth condition in (13) can be weakened to : For some for all (where still satisfies). ,

In the sequel three trivial examples with rather obvious optimal controls will be presented, but to illustrate the use of the necessary conditions, we derive the form of the optimal controls from these conditions.

Example 1., free, free.

Solution:

Evidently and, because by necessity, for all t. For from (16) we get Then The maxi- mum condition is that

(21)

Consider first the case that we might have Let satisfy

Now, for means that for t close to T,

see the expression for so for t close to T. But this surely continues back to (see

the expression for again). So even for (for such t, in fact,

when). Let be the smallest such that for Consider first the subcase Then and by the expression for, and By the maximum condition for for We must have in order to obtain we get

for for so For (an arbitrary constant). Using we get hence Thus, , with k satisfying i.e. so (By the way, note here that as satisfies the equation for we would know that for some constant C, but would not determine the constant. This shows the usefulness of the formula) The subcase is impossible, then and The case is impossible, then for t close to T, so for such t and then for all t (see the expression for). In fact, when so for all t, implying and a contradiction. Consider finally Then, by (18), so and then for t close to T, so for such t, in fact for all t (see the expression for), and Hence, for all t, which gives and contradicting ,

Remark 2. (Further non-triviality properties)

a) Replace (6) by the assumption that either is empty, or (if not), for some some for any there exists a such that for all where is assumed to exist. Assume also that and are bounded⁴. Then

b) Assume in addition that, for any either is empty, or (if not), there exists a such that for all and, in case that for each u, is continuous, that is left continuous at each and has a limit when Then ,

For finite horizon normality conditions, see [23] and [24] .

The main reason for including the next theorem is that it forms a basis for obtaining Theorem 1, but it has some interest of its own.

It contains necessary conditions for the case where (14) and/or (15) fail, in particular where also depends on We then need three conditions, see (25)-(27) below, that automatically hold if (14) and (15) are satisfied.

Theorem 2. In the situation of Theorem 1, with (5), (6), (8), (14), and (15) deleted, assume that the three conditions (25), (26), (27) below are satisfied. Then the following necessary conditions hold: for some for some vector and some bounded nonnegative finitely additive set functions vanishing on sets of Lebesgue measure zero, for a.e. s, for all

(22)

where (and the integrals exist). Moreover, satisfying (20). Finally, defining we have

(23)

(24)

If (7) and (8) hold, Moreover,

if, for some and some positive when for all Finally, if both the last condition and (7) and (8) hold, then

,

As before when is replaced by

Assume, for some arbitrarily large that the conditions (25)-(27) hold

(25)

Let be a solution on of for given. For some positive second order term (i.e.), if then, for all j, for all

(26)

Moreover, for any given number and any given positive second order term a positive second order term exists such that the following property holds. Let be a solution on of

for given,. Then, if

(27)

As an example in which (25)-(27) hold, consider a case where (11) and (12) hold for where f

is concave in x, and where, for some positive is and convex, and all j, (For in a short

hand notation

where which means that, a.e., so If then and then

Remark 3. For Theorem 2 to hold, we can weaken (7) and the basic assumptions on and as follows: the derivatives and exist at for all t and the three conditions on below are satisfied: For all

(28)

(29)

(30)

Moreover in the growth conditions (12) and (13), roughly speaking, the inequalities need not hold for states x that cannot possibly occur, more precisely, the conditions can be modified as follows. Define for each t,

the solution of (2) corresponding to. Then (12), (13) need only hold for some for such that In (10)(g) we must add the assumptions that, for some is differentiable in at uniformly in with a derivative at this point bounded uniformly in

Finally, U can be replaced by a time dependent subset where , continuous, we then require all control functions to satisfy We assume and in case in (9), we require Then the maximum conditions (17) and (22) hold only for (The set U can even be replaced by with (17) and (22) holding for We must then still require and, in (9), In the proof below, the perturbations of the optimal control have to belong to. ,

Example 2.

for all t,

free. It is convenient to replace by (Then (25)-(27) will be satisfied). Choose as the largest possible such that for If and even, for some for all t, then so by the maximum condition

(31)

and, contradicting the last inequality. Consider now the case where

Let be the set of time points s for which (31) holds. Now, implies the existence of some for which ⁵, (see the state equation). If can be chosen arbitrarily large, if can be chosen arbitrarily close to. Now, so If then (use (31) for), implying contradicting Hence, (Note that this

argument would not work if we had replaced by, say,). For by (31),

and because is strictly decreasing on (is con-

stant on), in fact on in fact on all by (31). Hence, on

so is finite and and It is easily seen by a similar argument that on

: to see this, having on an interval, assuming that is as large as

possible, is impossible: Let and define Now, leads to on which is impossible, and both for and and for and certain time points in close to (i.e. arbitrarily large if) exist at which but then in by (31), as is strictly decreasing in. But in

contradicts in. Hence, on, by (31), so or on (can be represented by an integrable function here). If we put, we have a valid proposal for the multipliers (It can be seen that is even necessary, compare (89(ii)) on p. 333 in [6] ).

Example 3.

, free. It is convenient to replace by The maximum condition is

(32)

Again, assuming, for some that for all t, and (in the opposite case) both yield contradictions. So Now, in (32) is impossible, so all the time. But, due to the constraint then all the time (see the state equation). Let The maximum condition (32) yields , for Now,. The general solution is To have the initial condition and satisfied we need and hence

Remark 4. Assume in the problem (1)-(7), (11)-(15), that is convex and that there are given additional constraints in the problem of the form (Perhaps In this case, here and below, replace by.) Assume that is optimal in this problem. We assume for that is continuous and depends only on , that and exist, that that

is continuous in uniformly in t and that

is in and measurable in t. We assume, for some positive constants for all

that for and for and for and, for that and for and for Define {: For all such that }. Assume that and that (8) holds, for for

in (9). Write Then, in addition to and satisfying (20), (23), and (24), there exist bounded non-

negative finitely additive set functions also vanishing on Lebesgue null sets, such that (22) holds

for, summing now over Moreover, for for all

(33)

(34)

(and the integrals exist). Furthermore, for we have on and on for all Finally, where (If (6) fails, then the last property must be replaced by).

When for some vectors, the following properties hold: the maxi-

mum condition (17) holds for, together with

(35)

for all where now

(36)

and where, for some nonnegative , , for and for if or if for Moreover, and in (36), for can be

represented by a bounded nondecreasing right-continuous function and, finally,

(If (6) fails, then this property must be replaced by).

When, in addition, for some some for all the inequality holds for all t, then for and, for in both (36) and (35), can be represented by a nonnegative function in (replace by) and, moreover, (If (6) fails, then this property must be replaced by). Finally, in this case, for a.e. t, for all

,

3. Proofs of the Results

Proof of Theorem 2. To simplify the notation, instead of the criterion (1), we can and shall assume that is the criterion to be maximized, that is free, hence is not required to be equal to The proof will be carried out under the assumptions of Theorem 2, allowing for the weakening of these assumptions in Remark 3.

Overview of the proof. A rough outline of the proof is as follows. We are going to make a number of strong (needleshaped) perturbations of This gives rise to first order variations of the optimal trajectory (the - functions below). We introduce a convex subset of these variations (below) consisting of variations satisfying a first order version of the unilateral constraint. We then introduce the convex set of endpoints (at infinity) of these variations as is standard in traditional proofs of the maximum principle, and show that it has to be separated from the set of “better, first order admissible” points, the set { for if } (The endpoints we consider consist actually only of the first components of the state). The separation argument (carried out in) consists of a standard use of the Brouwer fixed point theorem combined with the fact the endpoints are “good” first order approximations of the endpoints of the exact solutions following from the perturbations. We need the fact that these exact solutions satisfy the unilateral state constraint, and this is shown first. The separating functional (-vector) is denoted. Another separation argument, carried out in -space’ gives the multipliers related to the unilateral state constraints.

Detailed proof. To avoid certain problems connected with coinciding perturbation time points, the following construction is helpful (we then avoid coinciding perturbation time points). Let be a countable dense set in

and let be the set of right Lebesgue points of and all in

Then choose some set of full measure (i.e. meas),

such that for each a subset of exists with the property that if and then and with the property that for each each there exists a sequence such

that and For any given let be the collection of -tuples of the type

and for all such that belongs

to and belongs to (This means that for any if then which implies). The separate treatment of the case where we can have several perturbations at the same time, is useful for obtaining nondegeneracy results (i.e. informative necessary conditions). Below is varying

Let and for define

(37)

and

where a sum over an empty set is put equal to zero. For

Let and note that is convex⁶. Define to be the convex subset of consisting of functions that satisfy: For some

(38)

where

The linear variations are the ones that will appear in the necessary conditions that will be obtained (see (53), (54) below). These variations are jumping at each perturbation time points, so, near these points, they do not approximate (to the first order) the corresponding (continuous) exact solutions. Yet, we are able to show that the latter solutions satisfy the unilateral constraints when belongs to. To show this, the “better”, continuous, approximations are used.

3.1. Satisfaction of the Unilateral Constraints by Perturbed Solutions

Fix a pair such that satisfies (38) for certain numbers

. Let be some number for which (25), (26) and (27) hold. There exists a so small that

(39)

To see this, choose such that (39) is satisfied in this manner both for and (by using (25)) for Then, for satisfies

(40)

For some positive for for all, when then and are disjoint for all and, moreover, if

(is closed). Let be the set of points in for which

(41)

Now,

(42)

by (40) because in Let and define inductively by the for

mula (). Let and, for let

(see (37) for). Then, assuming right continuity at, (see (9)⁷), it is easily seen that

(43)

is small when is small, uniformly in See the arguments connected with (74) below. For

let for let for (recall that these intervals are disjoint when the left ends differ and that

), and elsewhere. Let be the corresponding solution. Define

Now, for small, for hence by (43) and the Lebesgue point property of and at is of the second order in uniformly in and Let We want to prove that for some

(44)

Because is bounded by assumption (25), and is of the second order, is of the second order, uniformly in Moreover, is of the second order, uniformly in by the boundedness of Hence, by (41), for some positive for

(45)

Next, it is well-known that

(46)

uniformly in (see Lemma D in Appendix). Moreover, by the differentiability assumption on at ((28)), for some positive second order term, we have

(47)

for all (because is of the first order in). Hence, for some positive second order term for

(48)

both for all by boundedness of on (combine (46) and (47)) and for all (com-

bine (27) and (26)). Then, by (45), for some positive

for Moreover,

for some positive for for all t, by (48),

and (by (25)), uniformly in so uniformly for

(49)

Hence, (44) has been shown, and in particular, (see (42))

(50)

So far, we have only used the basic assumptions and the first of the three conditions on in Remark 3, namely (28). The other two properties, (30) and (29), will be used in what follows.

We want to show that when Now, implies for close to (recall). Thus, by (40), for and For small (),when (by continuity, is small, when is small). Note that if for some, is a convex combination of and (the former one has weight). Hence, for any belongs to the segment between and hence for

So far, we have proved (44) for recall that if then for, (in particular this holds for so for (44) holds for all).

Finally, let us prove (44) for We can assume that is so small that

if So consider the case where,

Then the right derivative First

consider the subcase where and (only one). By (39),

Combining the two last weak inequalities we get Then so for for small ().

Consider next the subcase where contains several pairs ,

Using (43), it is easily seen that

When and we have that Now, by (39), so Hence we again get for for small ().

Thus, when satisfies (38), then

(51)

3.2. Local Controllability at Infinity

Observation 1. Define and { for for all with if }. Note that by Lemma B in Appendix, for all and,

and exist. Let be the convex set

(for see (38)). If, then for some positive, some where each equals linearly independent. Let Then

for some vector In fact, for each there is a unique such that evidently depends linearly on z, note that extends linearly to all. Let and let consist of all for

the moment we allow the pairs in to be doubly indexed, (and the time points not to be ordered). Then

where (as we have double

indices on, we have double indices on the components of). Note that

Of course, we can re-index the pairs in (and so also the entities) by using a

single index, with the time points in the pairs in increasing order. Let be the number of pairs We use also as the name of the vector of reindexed pairs, and for the vector consisting of all entities reindexed in the same manner as the pairs in. Then for

linear.

The following result should surprise nobody, a proof however is given in Appendix.

Lemma 1. Assume that for linear,. Then there exist some first order term (i.e.) and some such that for each for some some , ,

3.3. Separation Arguments That Yield the Multipliers

By optimality, for all To see this, assume, by contradiction the opposite,

that for some Then by Observation 1 and Lemma 1, for and small,

for some and satisfies the unilateral time constraint (3), see (51) (because and). The last equality gives that satisfies the terminal constraint (4) for small, and that This contradicts the optimality of. Thus the sets and are disjoint (this is trivial if). Thus these sets can be separated⁸: there exists a nonzero vector such that As this inequality gives that

(52)

Define {: for all j, for some positive, , when }. Recall that for all see (25), and write. Note that (for, see (38)) has to be disjoint from the convex body in otherwise the inequality is contradicted. By separation, for some continuous linear functional on and some number

(53)

for all all Evidently, by this inequality, and are nonnegative on, with for all Each can be represented by a bounded

finitely additive nonnegative set function vanishing on sets of Lebesgue measure zero. Evidently, va-

nishes on for all in particular vanishes on The inequality (53) gives that, for), for all pairs (still fixed in) and for all pairs and

(54)

where (To obtain (54), in (53) let). Moreover, (54) also holds for, for for any given

Let us now choose a sequence converging to zero when such that (54) holds in the manner

described for for certain multipliers In particular (54) holds for

for any given Let us fix such a sequence assuming it to be bounded. We can assume that (we extend to by letting). Using the weak* topology on there exists a cluster point of the sequence satisfying

(55)

(for some subsequence ). (by the cluster point property, so the last

equality holds). The cluster point is a bounded nonnegative finitely additive set function that vanishes on Lebesgue null sets. It is furthermore easily seen that (54) holds for and, for, and for

, both for equal to the cluster point ⁹ as well as for provided this limit exists, for any for any given

Now is nondecreasing and bounded. Let be the continuity points in of For any and for any a sequence exists, such that and (see the very beginning of this proof), and because (54) holds for it is easily seen by taking limits that (54) holds for and ¹⁰.

Finally, let us extract an additional property. If for all t in some interval and then, for some for when which by (55) implies and hence. Thus

(56)

for (say) ¹¹_.

3.4. Further Information on the Multipliers in Special Cases

Let us prove the results concerning the multipliers in the three last sentences in Theorem 2 in the case where is maximized.

Define

(57)

Now, assume (9) and (10) (a), with We may assume of the sequence used above that for the single (there exists a sequence such that). Here (29) was used. Let satisfy the inequality in (9), define and assume that Then, by (30), for some for close to 0, which combined with the previous inequality gives So any given cluster point of. We can assume that (54)

holds for this cluster point, for

Evidently, for all t close to 0. Now, if and for all then for any From we get, for all close to zero, that which gives for close to zero, and so a contradiction. Hence,

When and 0 is a right Lebesgue point of (i.e. (10) (b) holds), we can choose the sequence Evidently, by (29), when so again and we get the same conclusion regarding (with again) and in this case, (as well as in the case that is differentiable,

i.e. (10) (g), see Appendix), we don’t need the assumption that contains a single element¹². In fact,

when (8) holds, in Theorem 2, we can assume

Define Note that, by (23), for large enough if Assume that a and positive numbers and exist such that

(58)

(see the end of Theorem 2). For

Assume for the moment that Choose a sequence such that Letting in the preceding inequality, and using (see Appendix, Lemma A), we get so

Can? No, we have shown that then, and then so a contradiction. So when (58) holds

(59)

Finally, assume that both (58) and (8) are satisfied. By contradiction assume now that

Then (Þand, so a contradiction. So (58) and (8) imply

(60)

Proof of Theorem 1.

We still keep the assumption that is maximized. Using lemmas in Appendix, note that (25)-(28) are implied by the basic smoothness assumptions, the growth conditions (11)-(13), (7), (14) (i.e. depends only

on,), and (15) implying that is differentiable at 0, uniformly in t ((27) follows from Lemma E in Appendix). Moreover, also (29), (30) evidently follow. So all the above results also hold in the situation of Theorem 1. Using the definition (57) the maximum condition (54) can be written

(61)

Now, Using (5) and (14), when Then, by (57), also exists, and Hence, when

Let Let be the continuity points of all Write for the moment

and Then¹³, for and then With (occurring in the definition of) it is well-known that satisfies (16)¹⁴. Evidently, (61) yields

(62)

In Theorem 1, we have written and instead of and.

Note that (6) implies that (58) holds, as,. Thus, (60) holds, which means that

in the situation of Theorem 1, because then exists and equals.

Proof of Remark 2. We give a proof for the case where is maximized. Note that

for for where is a set of Lebesgue points of of full measure. The inequality holds for all in case of left continuity of.

Proof of a)

Let and recall Assume Assume by contradiction that Then, for all large enough

(the last term is all square brackets when). Then which is a contradiction because for So cannot be when. Hence implies

Proof of b) Assume by contradiction that

If then for some arbitrary large we must have For for all j, for large the left hand side is i.e. it does not change much if is replaced by. Hence, for (whether or =1), for large, for as in a),

Using the vectors in a), for large we then have Because when s large, we finally get when is large. When s is large means Using and (22) (which even holds for ), for large, we get Hence, both for and for for some (large) s.

Next, let By contradiction, assume Let where has the property that for see b). By continuity, for any and close to

(63)

There exist and arbitrarily close to such that for . If for all j, the left hand side is so for close to for all whether or Combining this inequality with (63), we get for s close to that for ¹⁵. From this, we finally get, by Lipschitz continuity of on, uniformly in s, that there exists a and close to such that when and can be chosen so close to that when The last inequality and (22) then yields which gives both for and for and so for all j. Evidently we cannot have so Thus contradicting Hence

Proof of Remark 4. We construct an auxiliary problem: assume for given functions that we want to maximize subject to

(64)

measurable. Here are auxiliary states, governed by where are auxiliary controls. Write For define { if }, , and let Below, is so small that Given any measurable control functions let be the solutions of (64) and corresponding to . For any there exists a such that if and then for all t, by Lemmas B and C in Appendix, hence, by continuity of at uniformly in t, for some for when and (and perhaps dependent on). In the auxiliary problem the constraints are the terminal constraints (4), for all for for all for Hence, if is admissible in the auxiliary problem, we have seen that is admissible in the original problem when We assume that is (for see the beginning of Remark 4, then and then, for the property related to in Remark 3 is satisfied in the auxiliary problem for). So, in the auxiliary problem, are optimal in the set of controls { }. The arguments in the proof of Theorem 2 apply also in the present situation, with one modification: For the inequality in for automatically holds for Hence the arguments in the section between (50) and (51) are not needed¹⁶ (and do not work) for

The necessary conditions in Theorem 2 are now applied to this auxiliary system (they apply even when admissible controls are restricted as above, see the inequalities involving and even for replaced by see the end of Remark 3¹⁷. In the auxiliary system, the linearized system is where is the transposed of The resolvent of the linearized system becomes

(65)

where From Lemma A in Appendix, we get that

(66)

for some constant Q, independent of t and, where is the i’th row of B and (to apply Lemma A, note that for in an obvious notation, where ). Note that (22), or actually (54), applied to the auxiliary system, holds for for the limit point given, any given element in (see remarks subsequent to (55)). From this we get, for and and that

(67)

From now on assume in (67). Moreover, for from (54) applied to the auxiliary system, we get that (54) holds as written. Finally, defined below.

Let consist of all pairs such that satisfies (52) and satisfies for all and (56) for with Let consist of all pairs such that (67) holds for the given and (54) are satisfied for all for a.e. s, in particular for and any given

cluster point of any given sequence, each corresponding to some collection from.

Let consist of all finite set We have just proved that for each, is nonempty, so by compactness is nonempty (the weak* topology is applied on the m’s ). Let be any given element in the latter intersection. Then, for, both

(67) holds for all and (54) is satisfied for for a.e. s. (To obtain this last property, preferably the set of point s for which (54) holds should be independent of the’s in each, one can use that (54) now holds for, for for, and hence by earlier limit arguments (54) holds for, for all, for a.e. s). We also have that (54) is satisfied by for for any given cluster point for any given sequence, each corresponding to some

for some.

The proof of is the same as the proof for the analogous condition in the case noting that for some means for some for t near 0 (so again leads to a contradiction in the same way as before)¹⁸. Similarly, has essentially the same proof as before. To show in case holds, we now assume and we replace by in the definition of where Then from (66), we get

(68)

Using the inequality

(69)

(i.e. (67)), we get

(70)

Note that So, from (68), (70) and, it follows that Then

(note the -norm on). But then, can be

represented by nonnegative functions in in fact in because is bounded.

Let us finally show that when exists. By (66), for independent of and So, for , By this inequality, there exists a such that, for for Next, for some, for for. To see this, for k chosen such that for note that when By (67) and the two inequalities involving for, and for for any

But then because was arbitrary. A contradiction of has arisen, so

4. Conclusion

The paper establishes necessary conditions for optimality in a smooth infinite horizon optimal control problem with unilateral state constraints and terminal constraints at the infinite horizon. The necessary conditions include a complete set of transversality conditions at infinity. The specific growth conditions placed upon the system in this paper can easily be modified, but strong growth conditions are in any case needed for the full set of necessary conditions to hold.

Acknowledgements

I was deeply grateful to the referees. Their detailed comments made it possible to correct omissions and improve the exposition.

Cite this paper

AtleSeierstad, (2015) A Maximum Principle for Smooth Infinite Horizon Optimal Control Problems with State Constraints and with Terminal Constraints at Infinity. Open Journal of Optimization,04,100-130. doi: 10.4236/ojop.2015.43012

References

Appendix

Below, for any matrix .

Lemma A. Let let

where, in, the matrices in the first row are respectively and and in the second row and, and, in, is and is all entries being measurable functions of and locally integrable. Assume that for some positive numbers Write for the solution on, , of for given. Define Then for some positive number Q, only dependent on

Hence

Lemma B. Let and be measurable in t, and with, and Lipschitz continuous with Lipschitz constants, , and, respectively, Write

There exists a positive number such that the following properties hold: let

and be two solution on of for, respectively given, assumed to exist. Then for all t, and, so which implies that exists if exists. ,

Note that and do exist whenever and are integrable.

The proofs of the lemmas A and B are of a standard type and omitted in order to save space.

Let be given and let Let

Lemma C. Let be a family of functions such that all are Lipschitz

continuous in with a common Lipschitz rank integrable, and with measurable. Let

be a solution of and given (assumed to exist). Assume that all

are bounded by a common constant. Then a constant exists such

that for any for any given, a solution of exists, and

for all.

Proof of Lemma C. Note that so by Gronwall’s inequality,

Lemma D. Let be a family of functions all Lipschitz continuous in x with a

common Lipschitz rank, integrable, and with measurable. Let be a given function in and let be a solution of, given (assumed to exist). We assume that all

are bounded by a common constant. We also assume that is differentiable at for a.e. t. For let be a solution of given. Then, for some for all t, when Moreover, for some and some second order term for all t, all all all f such that where is the solution of given (it does exist).

Proof of Lemma D. The proof of follows from Lemma C. Let and let on We have that and, by differentiability of at we have that for some second order increasing term, so for

for a.e. t. Dividing by d, we get

By Lebesgue’s dominated convergence theorem, when. As

then

and then by Gronwall’s inequality,

where a second order term in d, equals

Lemma E. In the situation of Lemma B, let be differentiable at where is a given solution on of given, assumed to exist. For each let be a solution on of given (it does exist), and let be a solution of given. Assume that, for some K, for all a second order term in d. Then for some second order term,

Proof of Lemma E. By Lemma D, for some term being of the second order in d, when is of the second order. For some for Hence, by Lemma B, for some constants we have that so

By Lebesgue’s dominated convergence theorem the conclusion in the lemma follows if we can prove that for

each t, when To obtain the latter fact, let

and note that

where the second order term

Proof of Lemma 1.

Consider the map for d any number in. Let and note that, by Lemma C, and are continuous in Then, by Lemma B, and are continuous in Let be a Lipschitz rank of and. For let the second order term satisfy

when

for the existence of see Lemmas D and E. Recall that and that when for some second order term, see an argument preceding (44) and Lemma A. Hence, for,

when

Note that for we have as, and for d small (for some), Fix such a. Now, is continuous in and has a fixed point here, by Brouwer’s fixed point theorem. As and Then let to obtain Lemma 1.

Observation A. On the space of continuous real-valued functions on with compact support, furnished with the sup-norm, can be represented by a nondecreasing bounded function such that for all bounded continuous with compact support. In fact, we can let , (right continuous for). Let be the continuity points in of Then for any hence for and so is also left continuous at s. For piecewise constant functions with bounded support, jumping only at points in evidently By approximating continuous function (or even piecewise continuous functions jumping only at points in) by such piecewise constant functions, one see that the same equality holds for continuous functions (or such piecewise continuous functions) with bounded support.

Note that if uniformly (continuous, with a common bounded support), and then: Assuming for simplicity (say), this follows from

Let arbitrary. For large, hence, for any Thus for Hence, when If is bounded and continuous, but with unbounded support, evidently, by the last inequality, so exists. As also (), exactly the same argument works for the latter limit written

Proof of (10) (g) Þ

Assume again that is maximized and postulate the conditions in Theorem 2 (allow even for the conditions in Remark 3), in particular postulate (10) (g). For simplicity, assume for for We want to replace each condition by two conditions, for for It can be done by requiring that holds for and, by adding new constraints required to hold on, where for. We now first assume both that, is independent of t, and that is independent of t for. Assume that there exist, (see (9)) such that

(71)

Then, for some both

(72)

and, for

(73)

Let have the property that and for Let

be a first order term (i.e. when), such that

when for all, i. As we did in connection with (43), let and define inductively . Let. Choose a partition of such that. Define It is easily seen that for

(74)

for any To see this, note that for the left hand side vanishes, while for the left hand side is smaller that Let Define Let be any given number, such that and when.

Let Moreover, let Then when as. So when

Consider the following auxiliary control problem on. Define Let and introduce the two state equations , free, and let and be the controls. We require on for and

on for and described below. The end conditions on are as before. Then and (on) are optimal in this problem, see below. Applying Theorem 2 to this problem, with and as costates corresponding to and, gives

for all for and the maximum condition (22), i.e. (a.e.)

,

where

,

In particular, because when see (72), then

(75)

Assume by contradiction both that and that where which by necessity means that Then, fo r

,

for for

for which gives and for and for. Also, by (73). As, using (74), we have, for,

contradicting for (as is optimal).

The optimality of follows from the following argument: Let be an arbitrary admissible quadruple in the auxiliary problem. Let If let for let for and let, for Next, let Then

and hence Moreover,

So is a solution in the original system evidently satisfying the end restrictions, and for Because for and then for Finally, on as we shall see in a moment, so for hence for all For let in which case is automatically an original solution.

From (74) and for we get

(76)

Using when for

Then, by (72), (73), (76), for all all all

¹⁹In case we have constraints, , (in which case, is required), then for and small, for, , as.

As then for Moreover, for for some positive small enough, when (For there is nothing to prove.)

Now, for so belongs to the set of admissible pairs in the original problem. We have hence are optimal in the auxiliary problem¹⁹.

Let now where and let and be corresponding multipliers, satisfying the normalization We put Now, has a cluster point satisfying (22), (55), and (56). Assume now that . Then there exist some such that and hence Hence, which leads to a contradiction, as was shown above. Thus,.

We can extend this result to problems that are nonautonomous on, by using t as a new state variable, say z, governed by with x governed by provided that is jointly differentiable in at for all t, and that is differentiable in at uniformly in with a derivative at this point bounded uniformly in

NOTES

¹In that theorem, correct the inequality by replacing it by.

²A right Lebesgue point s of any integrable function means a point s such that. If in (9) even belongs to and (10) (b) holds, then the right continuity in (9) can be weakened to 0 being a right Lebesgue point of for all.

³ always exists, and is left continuous on .

⁴For it suffices that when, , note that for, for some C.

⁵Or even, an observation needed in the next example.

⁶One may consult Observation 1 below at this point.

⁷Only when there are more than one perturbation at right continuity is needed to obtain (43). If there is a single perturbation at, (i.e. for all, = some) it suffices that is a right Lebesgue point of. Finally, if, then we shall throughout assume a single perturbation at.

⁸If and, then K and can be separated. If, then for some nonzero, , and can be chosen such that.

⁹For simplicity, assume that. Then, for any, for all n large enough, for all for, so, by (25); for, , for any; for all n large enough, for all. As, , so, which converges to zero at least for a subsequence of.

¹⁰If U is replaced by as in Remark 3, we asume that. The perturbations will belong to, because in the proof we now require the’s to belong to and then for t in, for d small. Then (54) holds for a.e. s for (Þfor n) and also for, for any given cluster point of any given bounded sequence where, , In addition, (54) holds for for all limits of all such sequences that are convergent. In particular, (54) holds for a given cluster point of a given sequence, where, given points in,.

¹¹In case, it can be assumed that, for all j, and, as said before, we then assume that for all P, , some arbitrarily given element in (in in case U is replaced by, for n large).

¹²If (8) holds only for a subset of then it is easily seen that the collection, , , is nonzero (at least one entity is nonzero).

¹³Observation A in Appendix may be consulted at this point.

¹⁴Compare e.g. Section 9.5 in [16] .

¹⁵As an alternative to the left continuity assumption on in Remark 2 (for), we may assume that, if in the necessary conditions, then these conditions imply left continuity of on.

¹⁶Thus we don’t need (and often don’t have!) differentiability of for.

¹⁷The growth conditions related to are of the same type as those related to in problem (1)-(4). Note that the perturbations now belong to.

¹⁸We can again let, also in the present case, (67) does not change for this change of.