Advances in Remote Sensing
Vol.05 No.04(2016), Article ID:72608,19 pages
10.4236/ars.2016.54023
Improvement of Bare Soil Semi-Empirical Radar Backscattering Models (Oh and Dubois) with SAR Multi-Spectral Satellite Data (X-, C- and L-Bands)
Rémy Fieuzal, Frédéric Baup
Centre d’Études de la BIOsphère (CESBIO), Université de Toulouse, CNES/CNRS/IRD/UPS, Toulouse, France

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: October 18, 2016; Accepted: December 4, 2016; Published: December 7, 2016
ABSTRACT
The objective of this study is to improve the performance of semi-empirical radar backscatter models, which are mainly used in microwave remote sensing (Oh 1992, Oh 2004 and Dubois). The study is based on satellite and ground data collected on bare soil surfaces during the Multispectral Crop Monitoring experimental campaign of the CESBIO laboratory in 2010 over an agricultural region in southwestern France. The dataset covers a wide range of soil (viewing top soil moisture, surface roughness and texture) and satellite (at different frequencies: X-, C- and L-bands, and different incidence angles: 24.3˚ to 53.3˚) configurations. The proposed methodology consists in identifying and correcting the residues of the models, depending on the surface properties (roughness, moisture, texture) and/or sensor characteristics (frequency, incidence angle). Finally, one model has been retained for each frequency domain. Results show that the enhancements of the models significantly increase the simulation performances. The coefficient of correlation increases of 23% in mean and the simulation errors (RMSE) are reduced to below 2 dB (at the X and C-bands) and to 1 dB at the L-band, compared to the initial models. At the X- and C-bands, the best performances of the modified models are provided by Dubois, whereas Oh 2004 is more suitable for the L-band (r is equal to 0.69, 0.65 and 0.85). Moreover, the modified models of Oh 1992 and 2004 and Dubois, developed in this study, offer a wider domain of validity than the initial formalism and increase the capabilities of retrieving the backscattering signal in view of applications of such approaches to strongly- contrasted agricultural surface states.
Keywords:
Semi-Empirical Backscatters Model, Oh Model, Dubois Model, Multi-Frequency (X-, C-, L-Band), Microwave, TerraSAR-X, Radarsat-2, Alos-PALSAR

1. Introduction
The backscattering electromagnetic models of bare soils aim to reproduce the interactions between the electromagnetic wave and the surface. They are considered a useful tool to understand the processes (single, multi-or volume scattering) in the backscattering coefficient that microwave antennas record, in perspective of the inversion of soil parameters such as the top soil moisture, texture, and surface roughness [1] [2] [3] [4] . Their use over agricultural surfaces involves the identification of an approach that faithfully reproduces the radar signals while reconciling the constraints of the landscape and those inherent to satellite remote sensing (i.e., a large observed area with contrasted surface conditions) [5] [6] . In this context, approaches based on the exact solution of Maxwell equations (or exact models) are not a relevant response at the scale of an agricultural region. Indeed, these methods, which are known as “method of moments” or the “finite difference time domain method”, require high computing time and rely on many input variables (difficult to collect at a large scale) [7] [8] . Conversely, the approximate and semi-empirical models provide an alternative method because they require a limited number of surface descriptors, which are easily measurable in situ.
The most commonly used approximate models based on a physical description of the backscattering processes are the small-perturbation model, Kirchhoff model, which is declined using two approximations according to the roughness level (geometric optic or physical optic for low or high roughness, respectively), and Integral Equation Model (IEM) [9] - [15] . As in the case of physical based models, they are site dependent and limited to specific soil conditions. Finally, the most used semi-empirical models [16] [17] [18] have a simple formalism as the main advantage, which facilitates their implementation and combined use with satellite images.
With the availability of satellite SAR data that have been acquired over the past 20 years in the L-band (Alos 1 or 2), C-band (Ers 1 or 2, Radarsat 1 or 2, Envisat, Sentinel- 1a/b…), and X-band (TerraSAR-X, Tandem-X, Cosmo-skymed constellation…), it is now possible to independently evaluate and improve these semi-empirical models (developed at least 12 years ago) in different wavelength domains in terms of the estimation of surface soil parameters (moisture, texture or roughness).
In this context, the objective of this study is to address the performances of three semi-empirical models (Oh 1992, Oh 2004 and Dubois) over a wide range of soil surface conditions and propose an improvement of the models using an original method based on the reduction of their residues. Initially developed and applied in mathematics and statistic domains, the analyze and the reduction of the residues is fundamental in modeling approaches and can significantly improve the performances of models by removing the effect of physical characteristics non-taken into account in the initial formalism. The application of such method on backscattering model (used in remote sensing) is unique, especially regarding the surface descriptors and/or satellite characteristics.
This work is based on the multi-spectral SAR satellite images acquired by TerraSAR-X, Radarsat-2 and Alos-PALSAR over agricultural surfaces, which are characterized by their specific top soil moisture, surface roughness and texture [19] . The second section of the paper presents the study site with the SAR satellite images and ground measurements. The methodology focuses on the formalism of the semi-empirical models and their domains of validity before describing different steps of the statistical analysis (section 3). The results (section 4) present the performances of the models for different SAR configurations (from X- to L-bands and for multi-angular acquisitions). The improved models are presented and evaluated in the identical conditions. Finally, the conclusions and perspectives are presented in Section 5.
2. Materials
2.1. Study Area
The study area is located in southwestern France near Toulouse (Figure 1) over an area of 420 km² centered at the following coordinates: 43˚29'36''N, 01˚14'14''E. The network of monitored fields is mainly located in the alluvial plain of Garonne. The region is governed by a temperate climate with an annual rainfall of approximately 600 mm and a mean daily air temperature of a few degrees in winter and 25˚C in summer. Agricultural activities occupy 90% of the landscape, where surfaces are dedicated to crops (56.8%), forests (7.9%), urban areas (2.4%), grasslands (32.1%) and water bodies (0.8%) [20] .
2.2. In Situ Data
The top soil moisture, surface roughness and texture were measured over a network of 37 agricultural fields when the soils were bare [21] (Figure 1). The sizes and local slopes of these fields were 1.4 - 38.2 hectares and 0.04˚ - 5.31˚, respectively.
The dielectric constant of the soil was measured at each satellite overpass using mobile theta probe sensors. The volumetric soil moisture of the first five centimeters was derived from the in situ calibration function of [21] (R² = 0.75, RMSE = 4.1%, n = 403). For each field, the mean values of the Top Soil Moisture (TSM) were averaged from at least 15 measurements per field. The TSM values were collected during contrasted conditions, which ranged from dry to saturated soil, with values of 2.4% - 35.3% m3・m−3 (Figure 2(a)).
The soil roughness was measured using a 2 m pin profilometer at each change of surface state (e.g., transition from a prepared soil to a harrowed or plowed soil), that is, 1 - 6 times on the surveyed fields depending on the agricultural practices. Two profiles were collected in the directions parallel and perpendicular to the tillage orientation. The two standard statistical parameters (i.e., the standard deviation of roughness heights and the autocorrelation length, abbreviated as hrms and lc, respectively) were calculated from each profile. During the experiment, 117 roughness measurements were collected over the surface states that ranged from smooth (after the soil preparation for the crop sowing) to highly rough conditions (after a deep plowing). The roughness values in the semi-empirical model (abbreviated as khrms, where k corresponds to the wave number) were 0.55 - 12.57 (Figure 2(b)).
The soil texture measurements included sampling the surface (0 - 25 cm depth) in a
Figure 1. Location of the study site in southwestern France. The network of the surveyed fields is highlighted in purple and superimposed on a color-composed TerraSAR-X image (Red: 02/21/2010, Green: 03/26/2010, Blue: 05/09/2010).
circle of 15 meters radius, with 16 sub-samples. Along the transect of the soil moisture, 2 - 8 samples were obtained depending on the length of the transect and the observed behavior of the top soil moisture. Over the study area, the soil content was dominated by silt, whose mean value was 52%, followed by the fractions of clay and sand (24%). Nevertheless, a high variability was observed, and the 146 measurements show that the clay, silt and sand contents were 9% - 58%, 22% - 77%, and 4% - 53%, respectively (Figure 2(c) and Figure 2(d)). They fill three classes of the European Soil Map [22] texture classification system (i.e., Fine, Medium and Medium Fine).
2.3. Multi-Spectral SAR Data
Table 1 summarizes the satellite images acquired when the soils were bare. During this period, regular high-spatial-resolution images (less than 20 m) were provided by



Figure 2. Histograms of soil parameters values considered as input variables in the semi-empi- rical models: top soil moisture (a), standard deviation of roughness heights (khrms) (b), fractions of clay (c) and sand (d).
TerraSAR-X (TS-X, 29 images), Radarsat-2 (RS-C, 22 images), and Alos-PALSAR (AP-L, 3 images), which operate in the X-band (f = 9.65 GHz, λ = 3.1 cm), C-band (f = 5.405 GHz, λ = 5.5 cm) and L-band (f = 1.27 GHz, λ = 23.6 cm), respectively. The TerraSAR- X images were acquired with HH polarization at incidence angles of 27.3˚ - 53.3˚ using two beam modes (StripMap (SM) and SpotLight (SL)), which were characterized by a pixel spacing of approximately 3 and 1.5 m, respectively [23] . The Radarsat-2 images were acquired with the full quad-polarization mode (Fine Quad-Pol), which delivers images at HH, VV, HV, and VH polarizations [24] . The incidence angles were 24˚ - 41˚ with a pixel spacing of 5 m. The Alos-PALSAR images were acquired at the same incidence angle of 38.7 using the fine-beam single polarization (FBS at the HH polarization) and fine-beam dual polarization (FBD, at HH and HV polarizations). The pixel spacings of the FBS and FBD products were 6.25 and 12.5 m, respectively [25] . All radar images were calibrated and geo-referenced using ortho-photos (with a resolution of 50 cm) provided by the French National Geographic Institute [23] [26] .
3. Methodology
3.1. Description of the Backscattering Models
3.1.1. Oh et al. 1992 Model
The model is based on the relationships that calculate the backscattering coefficients in HH, VV and HV polarizations from the polarization ratios (denoted p and q), sensor characteristics and surface parameters (Equations (1) - (8)).
Table 1. TerraSAR-X, Radarsat-2 and Alos PALSAR image configurations.
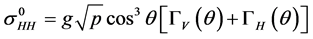 (1)
(1)
 (2)
(2)
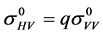 (3)
(3)
where 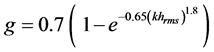
The ratio p refers to the co-polarizations (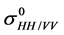 ), whereas the ratio q considers the co-and cross-polarizations (
), whereas the ratio q considers the co-and cross-polarizations (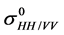 ). The backscattering coefficients are related to the angle of incidence (θ), wave number (k), standard deviation of roughness heights (hrms), and Fresnel reflection from the surface at nadir (Г0) by non-linear relationships.
). The backscattering coefficients are related to the angle of incidence (θ), wave number (k), standard deviation of roughness heights (hrms), and Fresnel reflection from the surface at nadir (Г0) by non-linear relationships.
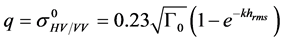 (4)
(4)
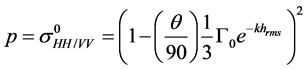 (5)
(5)
The Fresnel coefficients (Г0, ГH and ГV) are derived from the dielectric constant values of the soil (εr) (Equations (6) - (8)), which are derived from the top soil moisture and texture measurements (clay, silt and sand contents) using the relationships described by [27] .
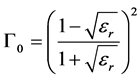 (6)
(6)
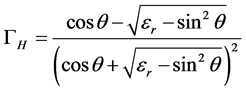 (7)
(7)
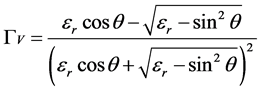 (8)
(8)
3.1.2. Oh et al. 2004 Model
In their study of 2004, [18] proposed a variation in the expression of the polarization ratios, enabling the relationships proposed by [27] (and consequently the texture data) and Fresnel reflection to be overcome. The ratio p and the cross-polarization are a function of the angle of incidence (θ), wave number (k), standard deviation of roughness heights (hrms), top soil moisture (mv). Based on a larger dataset than that available in 1992, the authors show that the expression of ratio q is independent of the surface moisture [28] (Equations (9) - (13)).
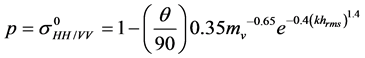 (9)
(9)

The backscattering coefficients are calculated according to the following relationships:



3.1.3. Dubois et al. 1995 Model
The formalism proposed by [17] differs from the Oh models (no polarization ratios or cross-polarization backscattering coefficients) and describes the behavior of the co-po- larized backscattering coefficients (



3.1.4. Domain of Validity of the Models
In previous studies, the authors define the range of values for which the performance of the models is optimal (Table 2). Regarding the roughness parameter, the extent of the confidence interval is a function of the wave number (k) and consequently of the microwave frequency considered. In Table 2, the equivalence between the khrms values (proposed by the author) and hrms in the X-, C- and L-bands are provided (X-hrms, C-hrms and L-hrms, respectively, which correspond to the TerraSAR-X, Radarsat-2 and Alos-PALSAR data). The confidence intervals regarding the surface roughness are notably similar for the two models proposed by Oh (slightly larger in the case of Oh 2004) and significantly wider than the model of Dubois, which is limited to low roughness levels (with values of khrms less than 2.5). In contrast, a wider confidence interval of the top soil moisture is associated with the model of Dubois, 35% m3・m−3, followed by Oh 2004 (25.1% m3・m−3) and Oh 1992 (22% m3・m−3). According to the incidence angle, the domain of validity is 10˚ - 70˚ regarding the models proposed by [16] and [18] , whereas the relationships presented by [17] are valid for incidence angles above 30˚.
3.2. From Model Performances Analysis to Their Improvement
The method of evaluation and improvement of semi-empirical backscattering models is presented in Figure 3. First, the three models (Dubois, Oh 1992 and 2004) were evaluated over all available field data for HH polarization and the three considered frequencies (X-, C-, and L-bands) (Section 4.1). Then, the residues of the models were analyzed (i.e., difference between 



Table 2. Domains of validity of the semi-empirical models.
Figure 3. Flowchart of the methodology to evaluate the performances and improve the semi- empirical models.
to improve the models. The equations of the modified models are described and evaluated in the last section (4.2). The models were implemented and evaluated on two independent databases. From a random selection, one half of the samples was used for training (STRAINING), and the remainder was used for validation (SVALIDATION) (except in the L-band because of the limited quantity of data).
4. Results and Discussion
4.1. Evaluation of the Performances of the Semi-Empirical Models
4.1.1. Comparison of the Global Performances
The semi-empirical models exhibit a wide range of performances, as illustrated by the values of the coefficient of correlation (0.31 - 0.80) (Figure 4). The results obtained in the X- and C-bands are poor, with r less than 0.59 and 0.45, respectively. In contrast, the results in the L-band are intermediate, with values of r exceeding 0.71 and RMSE less than 2.6 dB. For the X- or C-band, the RMSE values are lower for the two Oh models (RMSE < 2.72 dB) and, more important, for the Dubois model (RMSE < 4.48 dB), as noticed in previous studies over different study sites in Canada, France and Tunisia [29] [30] [31] . In the L-band, the results are more accurate with the Oh 2004 model, which is consistent with the literature [18] .
Figures 5(a)-5(c) illustrate the best result of the comparison between simulated and estimated backscattering coefficients for the X-, C- and L-bands. The simulations in the domains of validity (as defined by the authors) are shown in black; otherwise, they are in blue. In those examples, the theoretical domains of validity limit the applicability of the model to 59% (n = 168, in the X-band), 78% (n = 174, in the C-band) and 66% (n = 10, in the L-band) of the observed surface conditions. Nevertheless, the distinction of the simulations based on the domains of validity appears difficult, particularly in the case of Oh’s models, where the two sets of points (blue or black) have fairly similar dispersions. Regarding the model of Dubois, the simulations inside or outside the domain
Figure 4. Coefficient of correlation and RMSE estimated between simulated and observed backscattering coefficients for the two Oh models and Dubois model in the three frequency domains (X-, C- and L-bands).


Figure 5. Examples of the comparison between the observed and simulated backscattering coefficients in the X-, C- and L-bands ((a), (b) and (c)), respectively. The black and blue dots represent the simulations performed inside or outside the domain of validity of the models.
of validity are clearly separable and associated with an underestimation or overestimation of the backscattering coefficient values, respectively (the results in the X- and C- bands are not shown here).
4.1.2. Analysis of Residues of the Models
The behaviors of the residues of the models (

Those sensitive parameters were corrected in the modified version of the three models (displayed in red in Figure 6).
Figure 6. Summary of the sensitivities observed between the residues of the models and the input variables, expressed in dB for khrms, dB by % m3・m−3 for Top Soil Moisture, dB by % for Clay or Sand, and dB−1 for Incidence Angle.
As an example, Figure 7 presents two observed residue behaviors with respect to the incidence angle or khrms and the Dubois model. The behaviors of the model residues are not necessarily homogenous and linear, as in the case of the relationship between the incidence angle and the residues of the Dubois model in the X-band (Figure 7(a)). Indeed, a non-linear decrease (relationship between khrms and the residues, Figure 7(b)) is observed. These specific behaviors are integrated in the semi-empirical models to improve their representativeness of bare agricultural soils.
4.2. Improvement of the Semi-Empirical Models
4.2.1. Statistical Performances of the Modified Models
The modified semi-empirical models were statistically evaluated on validation samples, which represent 50% of the total samples (Figure 8). The increase in r and the RMSE values demonstrate the improvement of the simulations of different models regardless


Figure 7. Examples of relationships observed between the residues of the models and the input variables: residues observed in the X-band with the Dubois model versus the incidence angle (a) or standard deviation of the roughness heights (b). The black and gray dots represent the samples used for the training and validation, respectively.
Figure 8. Coefficient of correlation and RMSE estimated between simulated and observed backscattering coefficients for the three modified models in the three frequency domains (X-, C- and L-bands).
of the considered frequency. In the X-band, the coefficient of correlation is 0.69 for the models proposed by Oh in 1992 and Dubois (versus 0.59 before the modification), and the errors on the backscattering coefficients are equal to 1.47 and 1.41 dB, respectively (2.33 and 4.79 dB before the correction). In the C-band, different models show similar performances, where r is approximately 0.64 (they were 0.32 - 0.45), and the RMSE is less than 2 dB (20% in relative value). These errors were 2.16 - 3.66 dB depending on the considered model (Figure 4). The simulations performed with the best modified model (from Dubois) in the X- and C-bands are shown in Figure 9(a) and Figure 9(b), respectively (black dots), which illustrate the reduction of scattering compared to the initial version of the model (gray dots).
In the L-band, the coefficient of correlation also increases (r is larger than 0.84 for the models proposed by Oh, whereas it is 0.80 before the correction) (Figure 9(c)). The associated RMSE of the backscattering coefficients is reduced to values below 1 dB and 1.30 dB for the model proposed by Dubois.
In the following sections, only the best modified models are described for each wavelength (Dubois in the X- and C-bands; Oh 2004 in the L-band).
4.2.2. Equations of the Best Modified Models
In the X-band, three correction functions (denoted C1-Dubois =f (θ), C2-Dubois = f (TSM) and C3-Dubois = f (khrms)) were applied to the initial Dubois model to reduce the error from the incidence angle, top soil moisture and standard deviation of roughness heights (Equations (16) - (19)):




Figure 9. Examples of the comparison between the backscattering coefficients simulated by the initial (gray) and modified (black) versions of the models and those observed from the satellite in the X-, C- and L-bands ((a), (b) and (c)), respectively.


In the C-band, the errors from the incidence angle, top soil moisture and standard deviation of roughness heights were also reduced by applying three correction functions to the initial Dubois model (denoted C1-Dubois = f (θ), C2-Dubois = f (TSM) and C3-Dubois = f (khrms)) (Equations (20) - (23)):




In the L-band, the Oh 2004 model was modified (C1-Oh2004 = f (TSM) and C2-Oh2004 = f (khrms)) according to the sensitivities observed with the top soil moisture and standard deviation of roughness heights (Equations (24) - (26)):






Figure 10. Domains of validity of the initial (gray) and modi- fied (black) semi-empirical models regarding the incidence angle (a), top soil moisture (b), and standard deviation of rough- ness heights (c) in the microwave bands (X, C and L).
4.2.3. Extending of the Domains of Validity of the Modified Models
The domains of validity of the three modified models were extended according to khrms, the top soil moisture and the incidence angle point of view (Figure 10). In the X-band, the domain of validity increases by a factor 5 according to the khrms values for the modified Dubois model. Initially, limited to values below 2.50, the modified model can be applied over a larger range of roughness (to 12.57, which corresponds to an hrms of 6.22 cm). It is slightly improved regarding the incidence angle (27.3˚ - 70.0˚ instead of 30.0˚ - 70.0˚) and not improved in terms of the surface soil moisture. In the C-band, the domain of validity of khrms for the modified Dubois model also strongly increased (limited now to 9.72, compared to 2.50 initially). No difference was observed for the domain of validity of the top soil moisture, but the lower limit of incidence angle is now 24.3˚ instead of 30.0˚. The increase of the domain of validity widens the possibilities of applications of the semi-empirical models to various agricultural surface states observed after tillage practices [32] [33] [34] .
Finally, unlike the X- and C-bands, the limited sampling in the L-band (n = 15) does not enable the extension of the domain of validity of the models. Indeed, the observed roughness levels, with khrms values of 0.33 - 1.44, are circumscribed within the limits defined by the authors (0.13 - 6.98). Regarding the incidence angle, all images were acquired at a single value of 38.7˚. Only the top soil moisture had a slightly larger range of values than the initial Oh 2004 model: 3.8-33.3% instead of 4.0% - 29.1%.
5. Conclusions
This study aimed to improve the performances of three semi-empirical models (Oh 1992, Oh 2004 and Dubois) using a SAR multi-frequency (X-, C- and L-bands) database, which was acquired over an agricultural area with a wide variability of bare soil surface states. The proposed methodology consisted in identifying and correcting the residues of the models, depending on the surface properties (roughness, moisture, texture) and/or sensor characteristics (frequency, incidence angle). The results show that the correction of the residues is significant, especially regarding to the incidence angle, top soil moisture and soil roughness, for which the signal sensitivity is equal to 0.13 dB by, 0.06 dB by % m3・m−3 and 1.25 dB by m m−1 in mean, respectively. Finally, the modified models perform better than the initial formalisms, and the best modified model has been retained for each frequency domain: Dubois for X- and C-bands, and Oh 2004 for L-band. After correction of the residues, the correlations were improved between simulations and observations (from 0.59 to 0.69 in the X-band, from 0.44 to 0.65 in the C-band, and up to 0.84 in the L-band), whereas the RMSE and biases were reduced (RMSE < 2 dB in the C- and X-bands and 1 dB in the L-band), highlighting the pertinence of the method. Moreover, the domains of validity were strongly increased for the modified models because the original formalism did not consider all information carried by the main input variables (standard deviation of roughness heights and top soil moisture) to simulate the backscattering coefficients, which explains the poor initial results. The extension of the domains of validity is particularly notable in the X- and C-bands with maximum khrms values of 12.57 and 9.72 for the Dubois model, which corresponds to an increase by a factor 5 and 4, respectively.
The results offer new perspectives for the inversion of soil parameters from microwave models, particularly with the ongoing and future satellite missions (Sentinel-1A/ B, Alos-2, Terrasar-X…). In a near future, this approach could be extended to physical-based models such as the IEM (Integral Equation model) widely used in microwave remote sensing.
Acknowledgements
The authors wish to thank the ESA (European Space Agency), DLR (German Space Agency), CSA (Canadian Space Agency), JAXA (Japan Aerospace eXploration Agency), SOAR Project and CNES (Centre National des Etudes Spatiales) for their support, funding and satellite images (proposal HYD0611 and SOAR-EU and Categorie-1 ESA project no. 6843). In addition, the authors wish to thank the farmers (Mr. Blanquet, Mr. Bollati, Mr. Brardo, Mr. Pavan and Mr. Peres) for their time and precious discussion and the people who helped for collecting the ground data.
Cite this paper
Fieuzal, R. and Baup, F. (2016) Improvement of Bare Soil Semi-Empirical Radar Backscattering Models (Oh and Dubois) with SAR Multi-Spectral Satellite Data (X-, C- and L-Bands). Advances in Remote Sensing, 5, 296-314. http://dx.doi.org/10.4236/ars.2016.54023
References
- 1. Paloscia, S., Pampaloni, P., Pettinato, S. and Santi E. (2008) Comparison of Algorithms for Retrieving Soil Moisture from ENVISAT/ASAR Images. IEEE Transactions on Geoscience and Remote Sensing, 46, 3274-3284.
https:/doi.org/10.1109/TGRS.2008.920370 - 2. Rahman, M.M., Moran, M.S., Thoma, D.P., Bryant, R., Holifield Collins, C.D., Jackson, T., Orr, B.J. and Tischler, M. (2008) Mapping Surface Roughness and Soil Moisture Using Multi-Angle Radar Imagery without Ancillary Data. Remote Sensing of Environment, 112, 391-402.
https:/doi.org/10.1016/j.rse.2006.10.026 - 3. Zribi, M., Baghdadi, N., Holah, N., Fafin, O. and Guérin, C. (2005) Evaluation of a Rough Soil Surface Description with ASAR-ENVISAT Radar Data. Remote Sensing of Environment, 95, 67-76.
https:/doi.org/10.1016/j.rse.2004.11.014 - 4. Zribi, M., Kotti, F., Lili-Chabaane, Z., Baghdadi, N., Ben Issa, N., Amri, R., Amri, B. and Chehbouni, A. (2012) Soil Texture Estimation over a Semiarid Area Using TerraSAR-X Radar Data. IEEE Geoscience and Remote Sensing Letters, 9, 353-357.
https:/doi.org/10.1109/LGRS.2011.2168379 - 5. Kalluri, S., Gilruth, P. and Bergman, R. (2003) The Potential of Remote Sensing Data for Decision Makers at the State, Local and Tribal Level: Experiences from NASA’s Synergy Program. Environmental Science & Policy, 6, 487-500.
https:/doi.org/10.1016/j.envsci.2003.08.002 - 6. Seelan, S.K., Laguette, S., Casady, G.M. and Seielstad, G.A. (2003) Remote Sensing Applications for Precision Agriculture: A Learning Community Approach. Remote Sensing of Environment, 88, 157-169.
https:/doi.org/10.1016/j.rse.2003.04.007 - 7. Hasting, F.D., Schneider, J.B. and Broschat, S.L. (1995) A Monte Carlo FDTD Technique for Rough Surface Scattering. IEEE Transactions on Antennas and Propagation, 43, 1183-1191.
https:/doi.org/10.1109/TAP.1995.481168 - 8. Soriano, G. and Saillard, M. (2001) Scattering of Electomagnetic Waves from Two Dimensional Rough Surfaces with Impedance Approximation. Journal of Optical Society of America, 18, 124-133.
https:/doi.org/10.1364/JOSAA.18.000124 - 9. Ulaby, F.T., Moore, R.K. and Fung, A.K. (1982) Microwave Remote Sensing: Active and Passive, Volume II, Radar Remote Sensing and Surface Scattering and Emission Theory.
- 10. Fung, A.K., Li, Z. and Chen, K.S. (1992) Backscattering from a Randomly Rough Dielectric Surface. IEEE Transactions on Geoscience and Remote Sensing, 30, 356-369.
https:/doi.org/10.1109/36.134085 - 11. Fung, A.K. (1994) Microwave Scattering and Emission Models and Their Applications. Artech House Inc., Norwood, MA.
- 12. Chen, K.S., Wu, T.D., Tsay, M.K. and Fung, A.K. (2000) A Note on the Multiple Scattering in an IEM Model. IEEE Transactions on Geoscience and Remote Sensing, 38, 1 249-256.
https:/doi.org/10.1109/36.823917 - 13. Baghdadi, N., Holah, N. and Zribi, M. (2006) Calibration of the Integral Equation Model for SAR Data in C band and HH and VV Polarizations. International Journal of Remote Sensing, 27, 805-816.
https:/doi.org/10.1080/01431160500212278 - 14. Baghdadi, N., Chaaya, J.A. and Zribi, M. (2011) Semiempirical Calibration of the Integral Equation Model for SAR Data in C-Band and Cross Polarization Using Radar Images and Field Measurements. IEEE Geoscience and Remote Sensing Letters, 8, 14-18.
https:/doi.org/10.1109/LGRS.2010.2050054 - 15. Baghdadi, N., Zribi, M., Paloscia, S., Verhoest, N.E.C., Lievens, H., Baup, F. and Mattia, F. (2015) Semi-Empirical Calibration of the Integral Equation Model for Co-Polarized L-Band Backscattering. Remote Sensing, 7, 13626-13640.
https:/doi.org/10.3390/rs71013626 - 16. Oh, Y., Sarabandi, K. and Ulaby, F.T. (1992) An Empirical Model and an Inversion Technique for Radar Scattering from Bare Soil Surfaces. IEEE Transactions on Geoscience and Remote Sensing, 30, 370-381.
https:/doi.org/10.1109/36.134086 - 17. Dubois, P.C., van Zyl, J. and Engman, T. (1995) Measuring Soil Moisture with Imaging Radars. IEEE Transactions on Geoscience and Remote Sensing, 33, 915-926.
https:/doi.org/10.1109/36.406677 - 18. Oh, Y. (2004) Quantitative Retrieval of Soil Moisture Content and Surface Roughness from Multipolarized Radar Observations of Bare Soil Surfaces. IEEE Transactions on Geoscience and Remote Sensing, 42, 596-601.
https:/doi.org/10.1109/TGRS.2003.821065 - 19. Fieuzal, R. (2013) Apports des données radar pour l’estimation des paramètres biophysiques des surfaces agricoles. Sciences de la Terre. Université Toulouse III-Paul Sabatier, Francais.
- 20. Marais Sicre, C., Baup, F. and Fieuzal, R. (2014) Determination of the Crop Row Orientations from Formosat-2 Multi-Temporal and Panchromatic Images. ISPRS Journal of Photogrammetry and Remote Sensing, 94, 127-142.
https:/doi.org/10.1016/j.isprsjprs.2014.04.021 - 21. Baup, F., Fieuzal, R., Marais-Sicre, C., Dejoux, J.F., le Dantec, V., Mordelet, P., Claverie, M., Hagolle, O., Lopes, A., Keravec, P., Ceschia, E., Mialon, A. and Kidd, R. (2012) MCM’10: An Experiment for Satellite Multi-Sensors Crop Monitoring from High to Low Resolution Observations. IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Munich, 22-27 July 2012, 4849-4852.
https:/doi.org/10.1109/igarss.2012.6352527 - 22. European Soil Bureau Working Group. HYdraulic PRoperties of European Soils (HYPRES). Texture Classes. HYPRES Website.
http://www.macaulay.ac.uk/hypres/hypressoil.html - 23. Breit, H., Fritz, T., Balss, U., Lachaise, M., Niedermeier, A. and Vonavka, M. (2010) TerraSAR-X SAR Processing and Products. IEEE Transactions on Geoscience and Remote Sensing, 48, 27-40.
https:/doi.org/10.1109/TGRS.2009.2035497 - 24. Morena, L.C., James, K.V. and Beck, J. (2004) An Introduction to the RADARSAT-2 Mission. Canadian Journal of Remote Sensing, 30, 221-234.
https:/doi.org/10.5589/m04-004 - 25. Rosenqvist, A., Shimada, M., Ito, N. and Watanabe, M. (2007) ALOS PALSAR: A Pathfinder Mission for Global-Scale Monitoring of the Environment. IEEE Transactions on Geoscience and Remote Sensing, 45, 3307-3316.
https:/doi.org/10.1109/TGRS.2007.901027 - 26. NEST. Next ESA SAR Toolbox.
http://nest.array.ca/web/nest - 27. Hallikainen, M.T., Ulaby, F.T., Dobson, M.C., El-Rayes, M.A. and Lil-Kun, W. (1985) Microwave Dielectric Behavior of Wet Soil—Part 1: Empirical Models and Experimental Observations. IEEE Transactions on Geoscience and Remote Sensing, 23, 25-34.
https:/doi.org/10.1109/TGRS.1985.289497 - 28. Oh, Y., Sarabandi, K. and Ulaby, F.T. (2002) Semi-Empirical Model of the Ensemble-Averaged Differential Mueller Matrix for Microwave Backscattering from Bare Soil Surfaces. IEEE Transactions on Geoscience and Remote Sensing, 40, 1348-1355.
https:/doi.org/10.1109/TGRS.2002.800232 - 29. Baghdadi, N. and Zribi, M. (2006) Evaluation of Radar Backscatter Models IEM, OH and Dubois Using Experimental Observations. International Journal of Remote Sensing, 27, 3831-3852.
https:/doi.org/10.1080/01431160600658123 - 30. Baghdadi, N., Saba, E., Aubert, M., Zribi, M. and Baup, F. (2011) Evaluation of Radar Backscattering Models IEM, Oh, and Dubois for SAR Data in X-Band Over Bare Soils. IEEE Geoscience and Remote Sensing Letters, 8, 1160-1164.
https:/doi.org/10.1109/LGRS.2011.2158982 - 31. Baup, F., Fieuzal, R., Mingam, B., Lopes, A., Fjortoft, R., Marais Sicre, C., Dejoux, J.F., Zribi, M., Baghdadi, N. and Ceschia, E. (2011) Contribution of ALOS, RADARSAT-2 and TerraSAR-X Radar Data for Monitoring Agricultural Surfaces. IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Vancouver, 24-29 July 2011, 4 p.
- 32. Jackson, T.J., McNairn, H., Weltz, M.A., Brisco, B. and Brown, R. (1997) First Order Surface Roughness Correction of Active Microwave Observations for Estimating Soil Moisture. IEEE Transactions on Geoscience and Remote Sensing, 35, 1065-1069.
https:/doi.org/10.1109/36.602548 - 33. Davidson, M.W.J., Le Toan, T., Mattia, F., Satalino, G., Manninen, T., and Borgeaud, M. (2000) On the Characterization of Agricultural Soil Roughness for Radar Remote Sensing Studies. IEEE Transactions on Geoscience and Remote Sensing, 38, 630-640.
https:/doi.org/10.1109/36.841993 - 34. Callens, M., Verhoest, N.E.C. and Davidson, M.W.J. (2006) Parameterization of Tillage-Induced Single-Scale Soil Roughness from 4-M Profiles. IEEE Transactions on Geoscience and Remote Sensing, 44, 878-888.
https:/doi.org/10.1109/TGRS.2005.860488










