International Journal of Nonferrous Metallurgy
Vol. 2 No. 2 (2013) , Article ID: 30479 , 7 pages DOI:10.4236/ijnm.2013.22009
Developing a Thermodynamical Method for Prediction of Activity Coefficient of TBP Dissolved in Kerosene
1Department of Mining and Metallurgical Engineering, Amirkabir University of Technology, Tehran, Iran
2Research Center for Materials and Mining Industries Technology, Amirkabir University of Technology, Tehran, Iran
3Department of Materials Science and Engineering, Sharif University of Technology, Tehran, Iran
Email: alamdari@aut.ac.ir, sadrnezh@sharif.ac.ir
Copyright © 2013 Eskandar Keshavarz Alamdari, Sayed Khatiboleslam Sadrnezhaad. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received December 31, 2012; revised February 13, 2013; accepted February 20, 2013
Keywords: Thermodynamics; Activity; Activity Coefficient; Kerosene; TBP; Organic Solution
ABSTRACT
Results of the experimental measurements on the partial molar volume of kerosene used as a medium for dissolving TBP are utilized to determine the activity of TBP in the binary kerosene-TBP solution through the application of Gibbs-Duhem equation. The treatment is based on combination of the experimental data with the thermodynamic values available on the compressibility factor of pure kerosene at room temperature. It is shown that the activity of TBP in kerosene has a positive deviation from ideality with an activity coefficient derived as follows: 1) at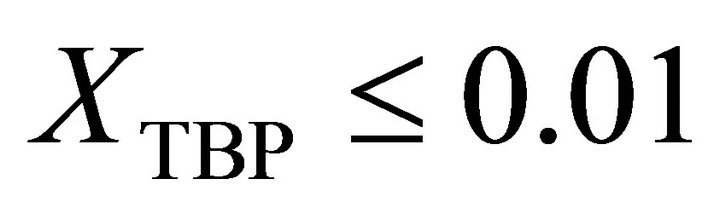 :
: , 2) at the
, 2) at the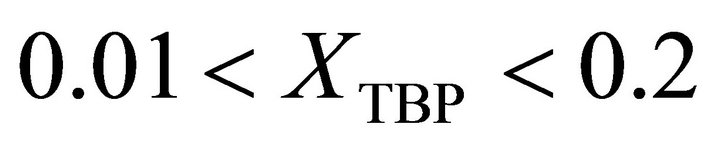 :
: 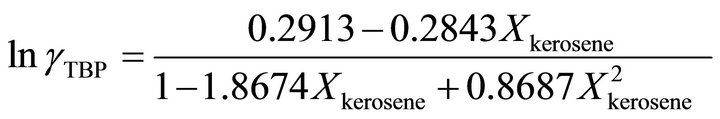 3) at higher TBP concentrations
3) at higher TBP concentrations :
:  and 4) at TBP Raoultian concentrations
and 4) at TBP Raoultian concentrations . These quantities can be utilized at temperature closed to 298 K.
. These quantities can be utilized at temperature closed to 298 K.
1. Introduction
Activities of the spices dissolved in organic aromatic solutions are of the important information required for understanding of the thermodynamics of the solvent extraction regimes usually utilized in production of the nonferrous metals. It has been reported that the activity coefficients of involved components in the extraction reaction of metals during extraction processes are usually equal to one [1-10]. However, the activities in the real component values are significantly different from the ideal state. The activity coefficient of components (especially components in aqueous media) was estimated by using some conventional thermodynamic models such as Debye-Hückel or Pitzr Equation [11]. On the other hand, due to the physicochemical interaction of organic components, the mathematical models could be used in some special cases. By applying the correct value of the activity coefficients in the extraction equations, a correct mathematical model can predict an acceptable value for extracted metals.
The thermodynamic evaluation of the distribution ratio of metals, for instance, becomes much easier if the activity of coefficient tri-n-butyl phosphate (TBP) dissolved in kerosene becomes precisely known. There is, however, no data available in the literature on the activity coefficient of different spices dissolved in such aromatic or aliphatic solutions as kerosene.
TBP is a common organic material which uses as extractant and/or modifier in the presence of some aliphatic diluents such as kerosene. Therefore, developing an analytical method for the prediction of the activity coefficients of organic component could be useful for future investigations. In this paper, an analytical method for determination of the activity and the activity coefficient of TBP dissolved in kerosene is developed and presented.
2. Thermodynamical Parameters and Prediction of the Activity and the Activity Coefficients
It is shown that the excess partial molar Gibbs free energy of the spices i depends on the composition of the solution. The difference between the partial molar Gibbs free energy of the spices i and the molar Gibbs free energy of pure i is the change in the Gibbs free energy accompanying the formation of one mole of i dissolved in the solution; 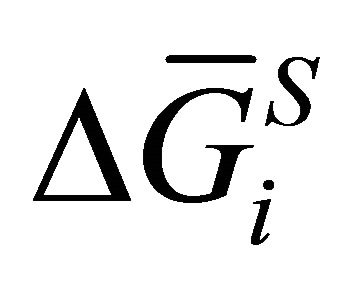 [12-15]. Thus:
[12-15]. Thus:
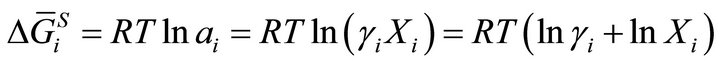 (1)
(1)
on the other hand:
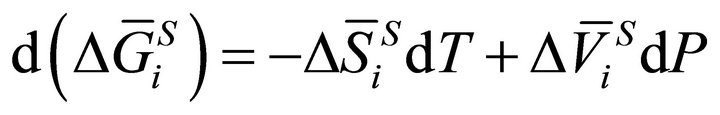 (2)
(2)
where 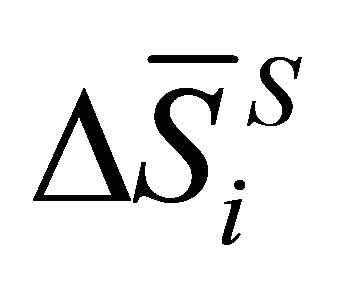 and
and 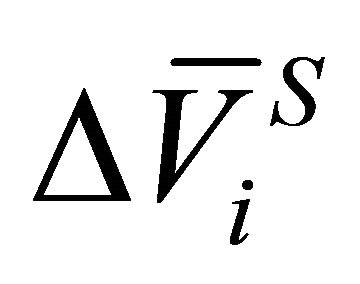 are the partial molar entropy and the partial volume change of the dissolution reaction, respectively. In the isothermal condition, Equation (2) is rewritten as:
are the partial molar entropy and the partial volume change of the dissolution reaction, respectively. In the isothermal condition, Equation (2) is rewritten as:
 (3)
(3)
The molar volume of a multi component solution is defined by:
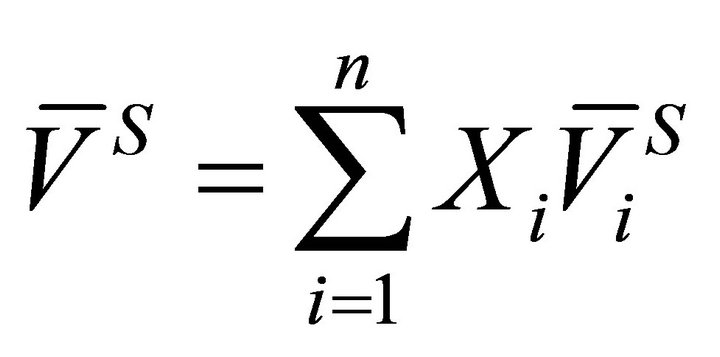 (4)
(4)
The molar volume of the mechanical mixture can similarly be defined by:
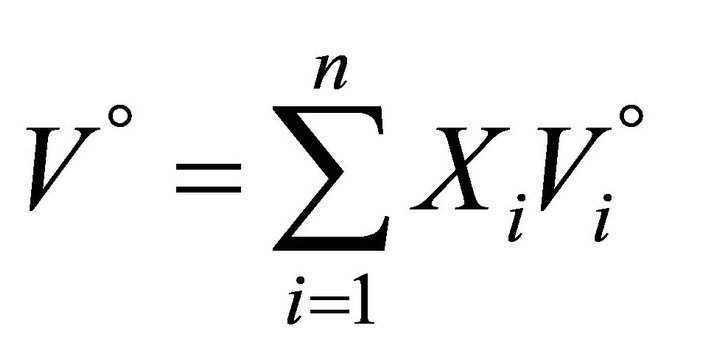 (5)
(5)
The volume change due to the formation of the solution is, thus, given by:
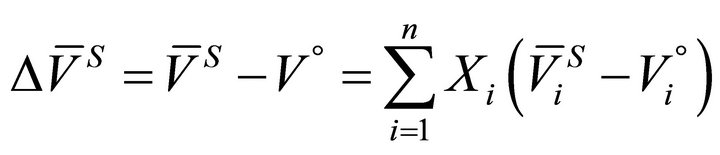 (6)
(6)
The value of 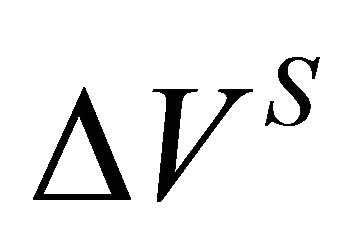 for a binary solution, which exhibits negative deviation from ideality, is less than zero. Based on known thermodynamic relationships available [12-15], the volume change of the species A in a binary A-B system can be obtained from:
for a binary solution, which exhibits negative deviation from ideality, is less than zero. Based on known thermodynamic relationships available [12-15], the volume change of the species A in a binary A-B system can be obtained from:
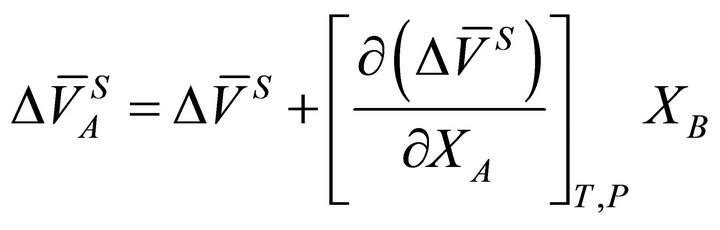 (7)
(7)
Also, the isothermal compressibility of a substance, or a system, is defined as:
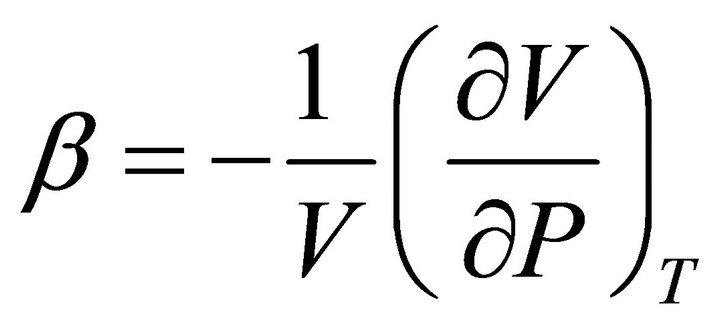 (8)
(8)
This is the fractional decrease in the volume of the system for unit increase in pressure at constant temperature. For pure A, the isothermal compressibility is defined as:
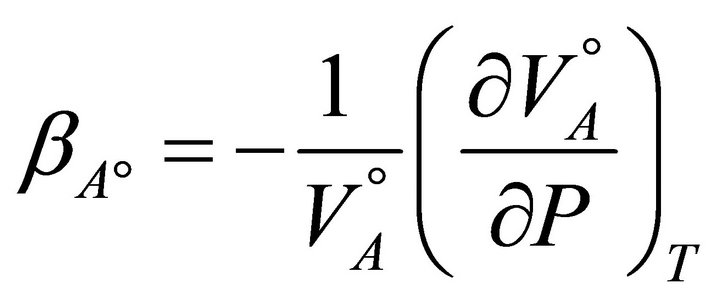 (9)
(9)
and for species A of the binary solution:
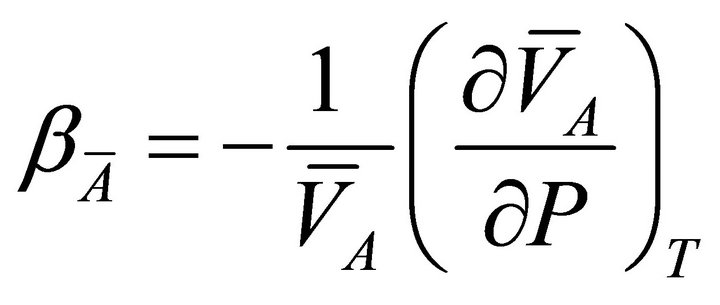 (10)
(10)
if we assume that:
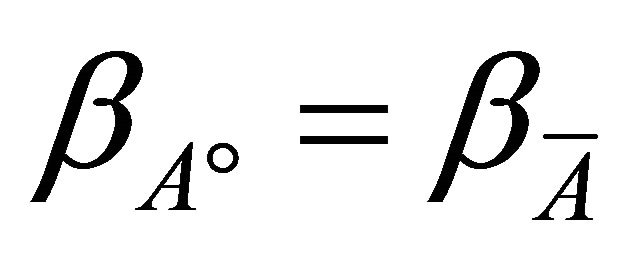 (11)
(11)
then from Equations (9) and (10):
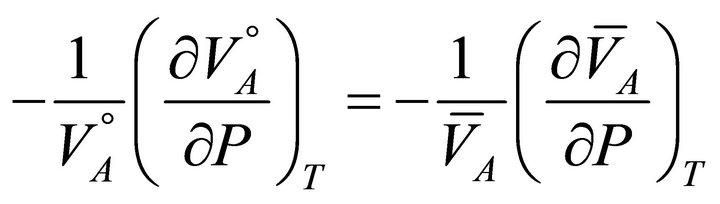 (12)
(12)
hence at a constant temperature, we have:
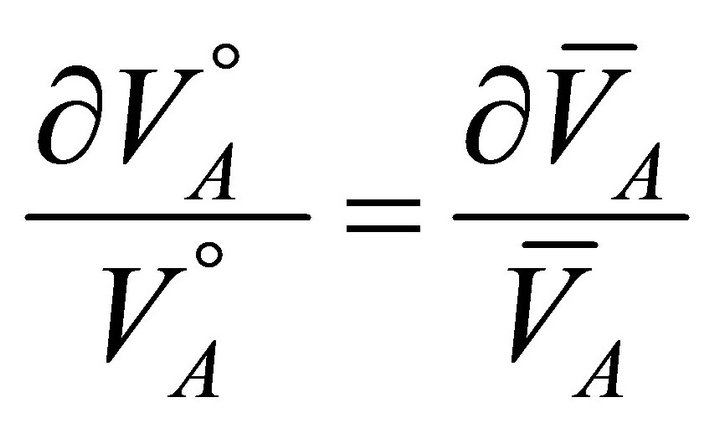 (13)
(13)
or:
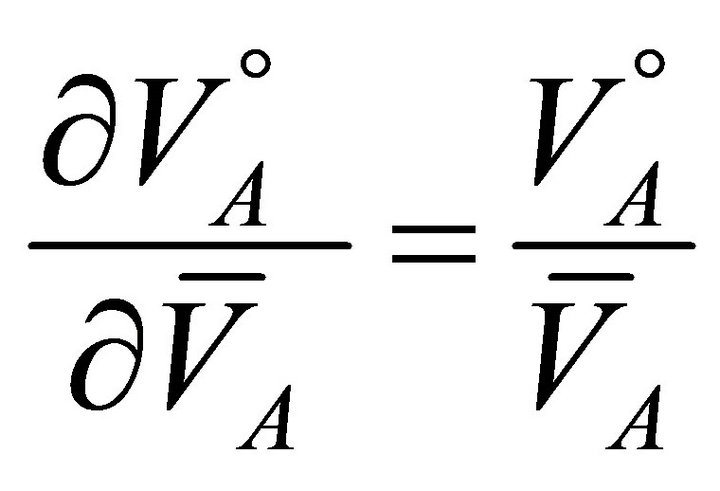 (14)
(14)
and also:
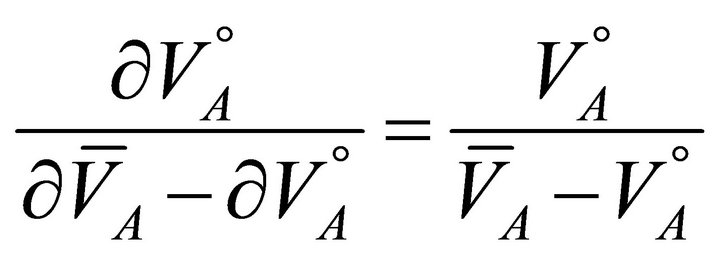 (15)
(15)
or:
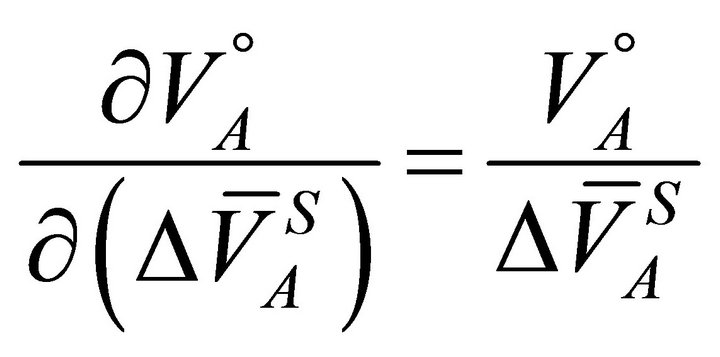 (16)
(16)
then:
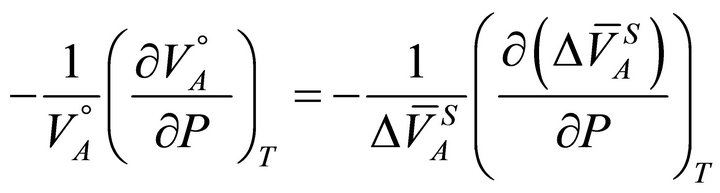 (17)
(17)
hence:
 (18)
(18)
At a constant temperature, Equation (18) can be rearranged as:
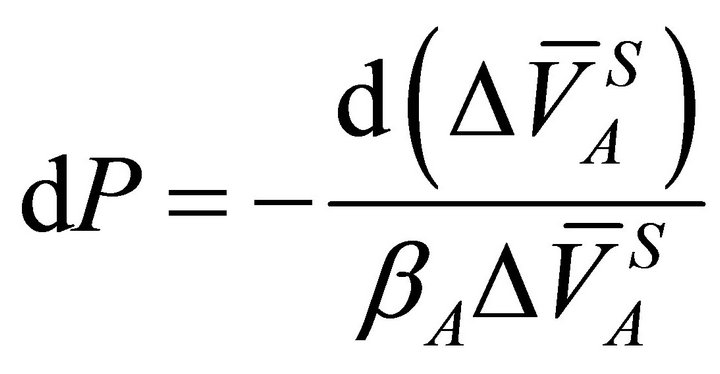 (19)
(19)
by substituting the value of (dP) from Equation (19) into Equation (3), we have:
 (20)
(20)
and from Equation (1), we obtain:
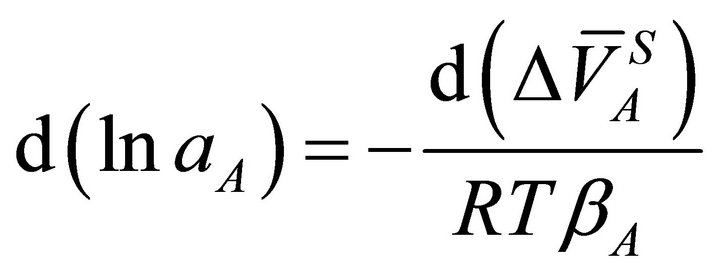 (21)
(21)
Integrating Equation (21) from the initial condition where XA = 1 and , one can write:
, one can write:
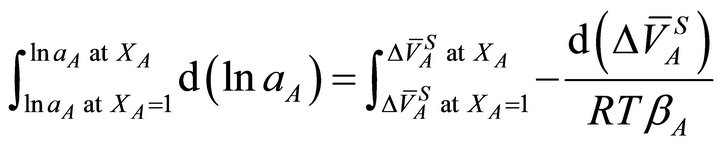 (22)
(22)
or:
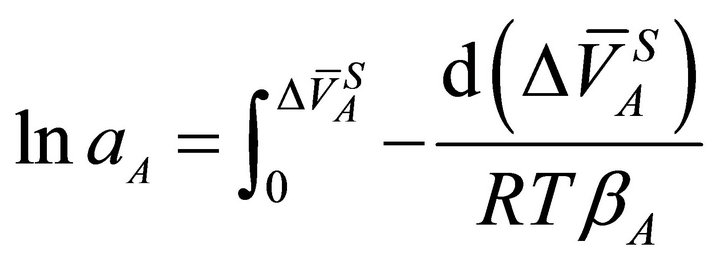 (23)
(23)
The value of the right hand side at Equation (23) can graphically be obtained by plotting the quantity of
 vs
vs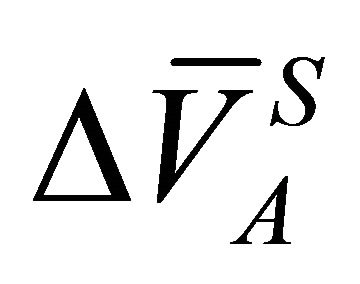 , and determining the area under the curve. The activity coefficient of the species A of binary solution can thus be obtained from:
, and determining the area under the curve. The activity coefficient of the species A of binary solution can thus be obtained from:
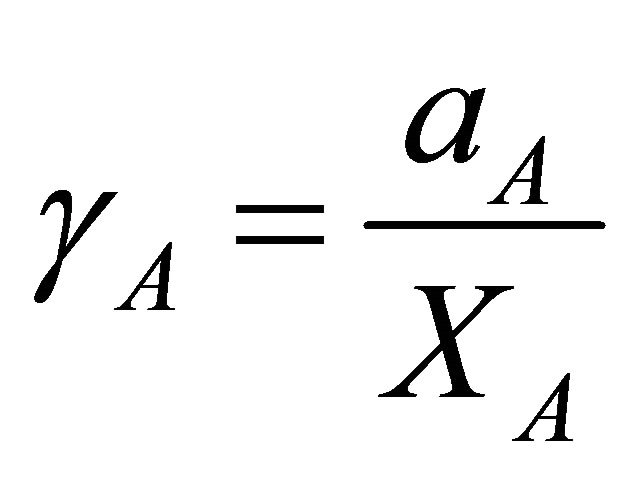 (24)
(24)
The activity coefficient of the second component of the solution can be determined by integration the GibbsDuhem equation [12-15]:
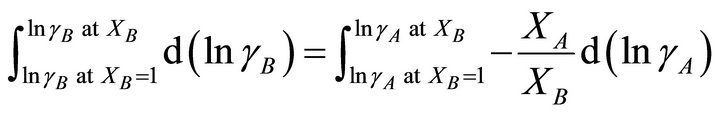 (25)
(25)
At the boundary condition where  and
and  are equal to one,
are equal to one, 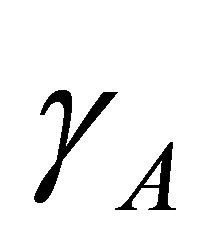 equals to
equals to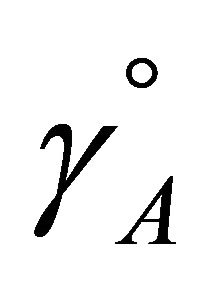 , thus:
, thus:
 (26)
(26)
The activity of species B is, thus, determined from:
 (27)
(27)
3. Material and Methods
Both TBP and kerosene, which were used, were of analytical grade from Fluka AB., Switzerland. Small quantity of TBP weighted with a mettler 240 balance system was added to a calibrated 100-ml. Kerosene was instilled to the 100-ml flask and the solution was mixed thoroughly. The solution was then retained for five to ten minutes to absorb the required heat for reaching to chemical equilibrium. The total weight of the solution was then measured.
The experiments were carried out at constant room temperature (298 K). The molecular weight of the pure TBP was equal to 263.32 gr/mole. The molecular weight of the used kerosene was determined by the gas chromatography and the change of the melting point methods. In the latter, the melting temperature change was measured by analytical grade phenol with a molecular weight of 94.11 gr/mole .The molecular weight of kerosene was the determined from [16,17]:
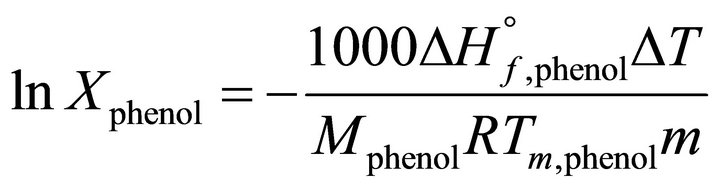 (28)
(28)
where  is mole fraction of phenol in dilute phenol-kerosene solution,
is mole fraction of phenol in dilute phenol-kerosene solution, 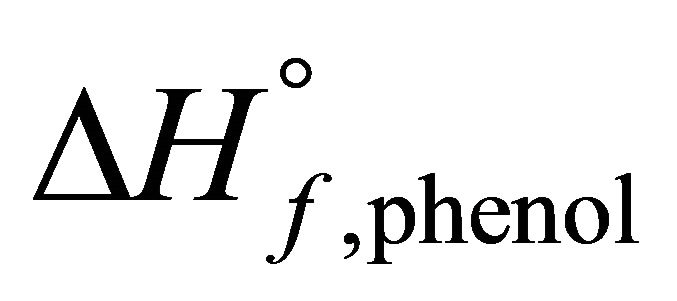 is the latent heat of melting of phenol in its melting point
is the latent heat of melting of phenol in its melting point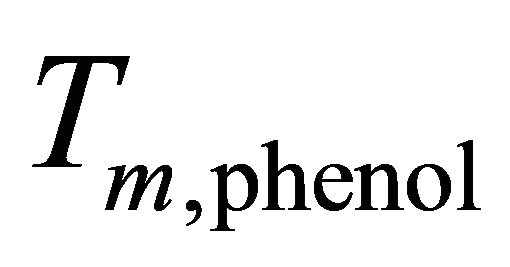 ,
, 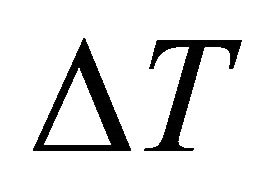 is the change of melting point of solution when the molality of kerosene in dilute solution is m and
is the change of melting point of solution when the molality of kerosene in dilute solution is m and 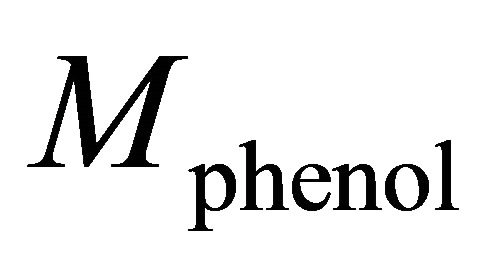 is the molecular weight of phenol. The result was equal to 173.3 gr/mole.
is the molecular weight of phenol. The result was equal to 173.3 gr/mole.
With the experimental data, the integral molar volume of the solution 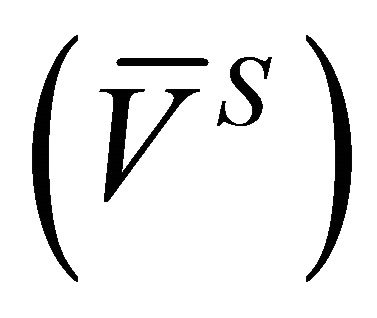 and the integral molar volume change of the solution
and the integral molar volume change of the solution 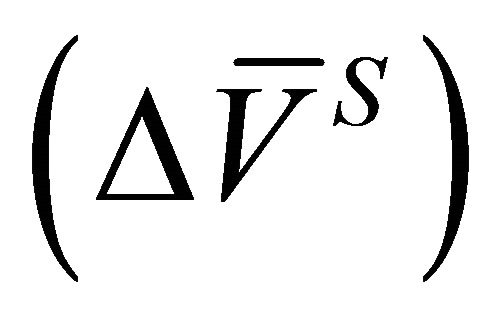 were determined from Equations (4) and (6).
were determined from Equations (4) and (6). 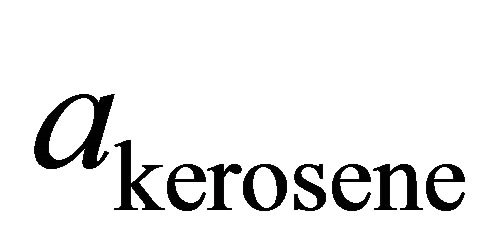 (Equation (23)),
(Equation (23)),  (Equation (24)),
(Equation (24)), ![]() (Equation (26)) and
(Equation (26)) and ![]() (Equation (27)) were then evaluated.
(Equation (27)) were then evaluated.
4. Results and Discussion
There is not much known of the physical properties of TBP. Determination of the activity and the activity coefficient of TBP is, therefore, derived from the corresponding quantities for kerosene. The isothermal compressibility of kerosene at 298 K and 1 atm pressure is known to be 1.45 ´ 10−4 atm−1 [18]. Applying this value to Equation (23), the activity of kerosene is, therefore, being determined.
Figure 1 shows the integral molar volume of the binary kerosene-TBP solution as a function of the kerosene mole fraction; Xkerosene. As shown in this figure, the integral molar volume of the solution has a positive deviation from the ideal behavior (dashed line). This quantity is defined by Equation (4). Figure 2 illustrates the relative molar volume of the binary solution 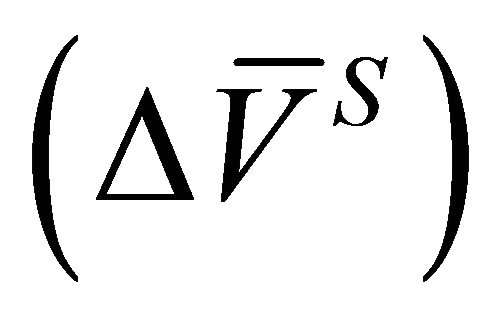 versus kerosene mole fraction. It is seen from this figure that, the molar volume of the formation of the binary solution has a positive deviation from ideality and has a maximum near
versus kerosene mole fraction. It is seen from this figure that, the molar volume of the formation of the binary solution has a positive deviation from ideality and has a maximum near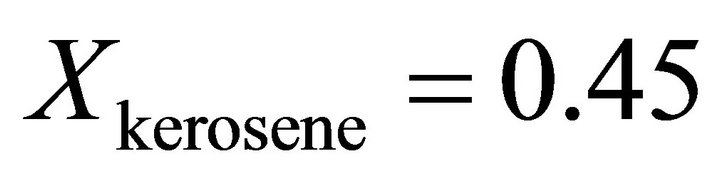 . The predicted value of the
. The predicted value of the
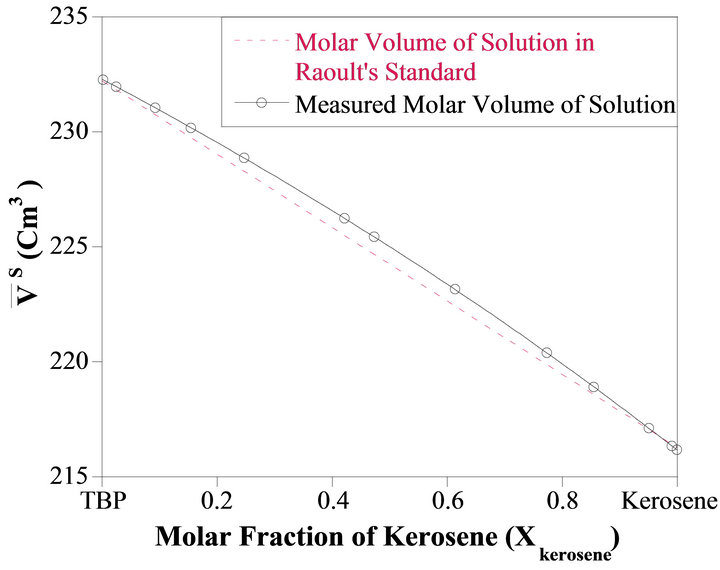
Figure 1. The integral molar volume of TBP-kerosene binary solution as a function of measured  at room temperature.
at room temperature.
volume change has a correlation with the experimental data:
 (29)
(29)
The molar volume change of the kerosene dissolved in the binary solution is determined from Equation (7) as a function of . Figure 3 illustrated the partial molar volume change of kerosene
. Figure 3 illustrated the partial molar volume change of kerosene  as a function of
as a function of . The partial molar volume changes of the kerosene in the pure TBP
. The partial molar volume changes of the kerosene in the pure TBP  and in the pure kerosene
and in the pure kerosene  are equal to infinity and zero, respectively.
are equal to infinity and zero, respectively.
Based on Equation (14), the activity of kerosene can be determined by using a graphical method. Figure 4
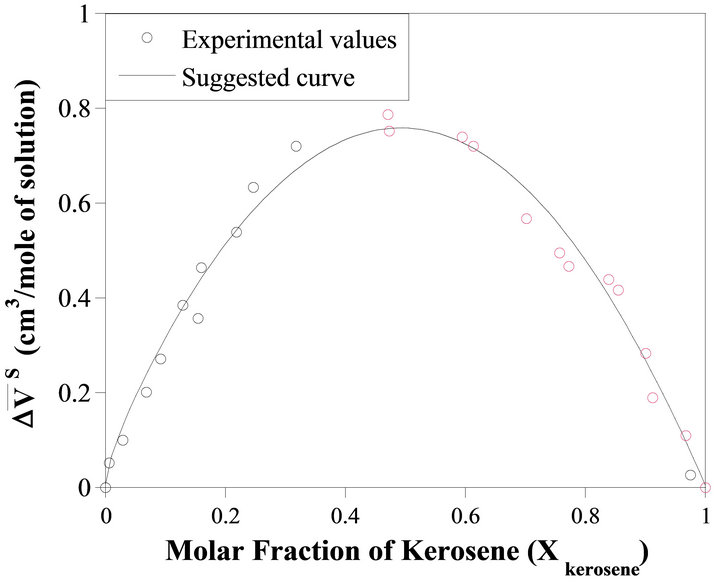
Figure 2. The relative integral molar volume of the kerosene-TBP solution versus the solution composition.
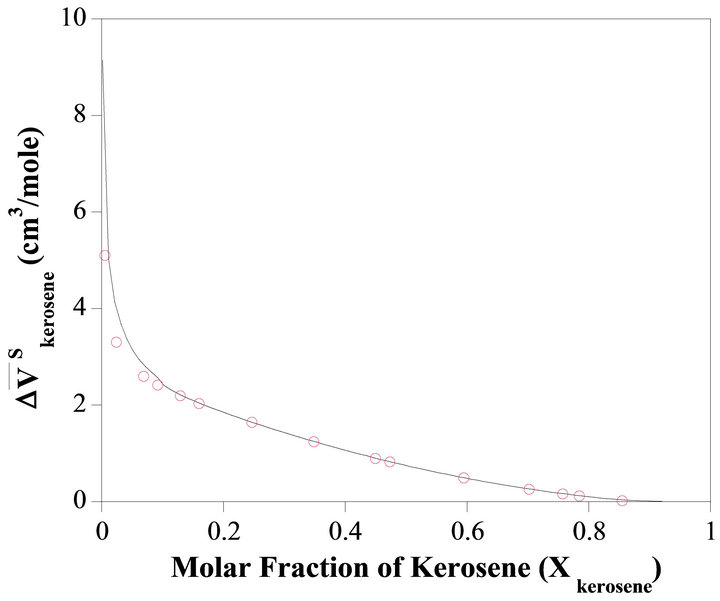
Figure 3. The relative partial molar volume of kerosene as a function of composition.
illustrates that the change of 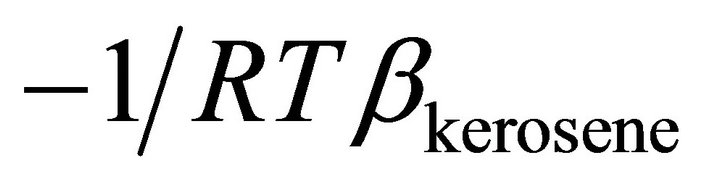 vs
vs  at the constant temperature 298˚K. we have assumed that the isothermal compressibility constant of the kerosene at every composition of binary solution is constant and that the compositional change has no significant effect on its value. So the activity of the kerosene is determined from the area under the curve plotted in Figure 4, as was stated by Equation (23). The results are given in Figure 5 (solid line). As shown in this figure, the activity of the kerosene indicates a very positive deviation from ideality, especially at low concentrations. A curve fitting method can be used to determine the activity of the kerosene at
at the constant temperature 298˚K. we have assumed that the isothermal compressibility constant of the kerosene at every composition of binary solution is constant and that the compositional change has no significant effect on its value. So the activity of the kerosene is determined from the area under the curve plotted in Figure 4, as was stated by Equation (23). The results are given in Figure 5 (solid line). As shown in this figure, the activity of the kerosene indicates a very positive deviation from ideality, especially at low concentrations. A curve fitting method can be used to determine the activity of the kerosene at
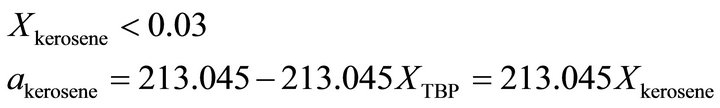 (30)
(30)
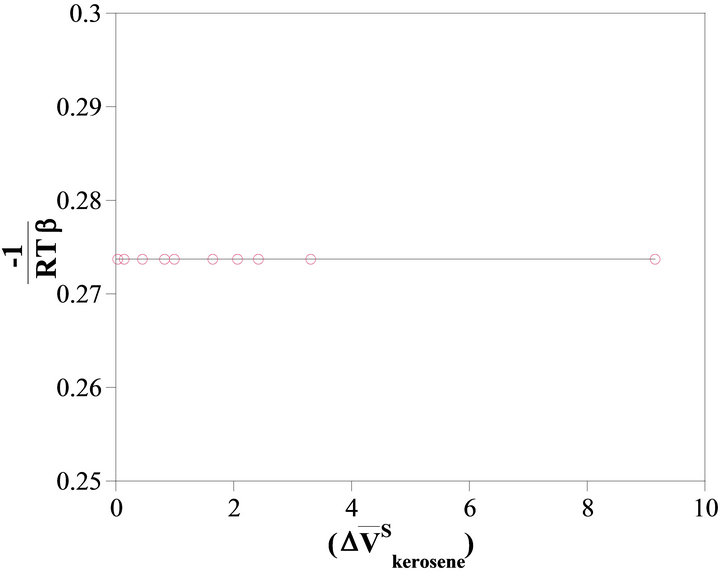
Figure 4. The value of  vs molar volume change of kerosene in binary kerosene-TBP solution.
vs molar volume change of kerosene in binary kerosene-TBP solution.
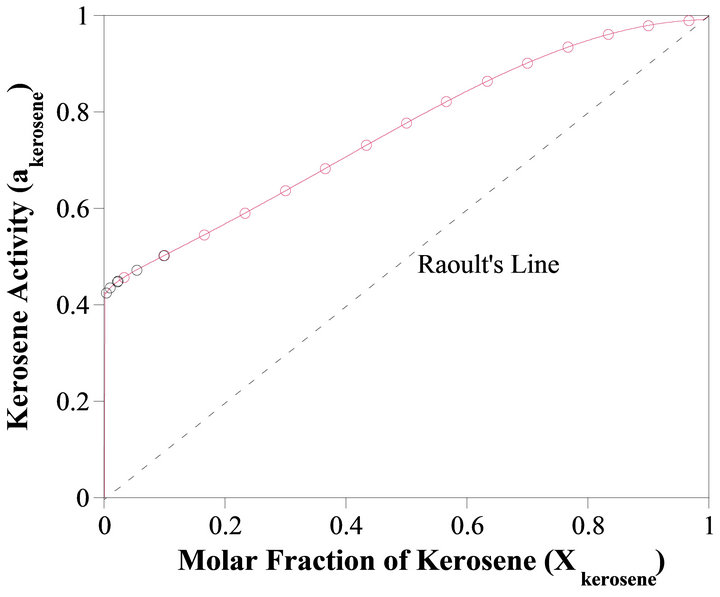
Figure 5. Activity of kerosene as a function of composition of the solution.
and at the higher kerosene concentration, the activity of kerosene is determined by:
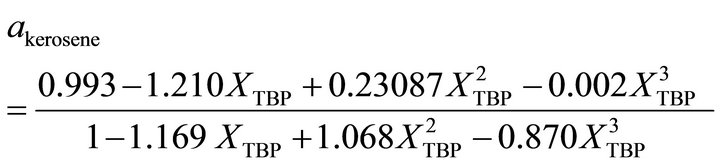 (31)
(31)
The activity coefficient of kerosene is determined from Equation (24). Figure 6 shows the change of  as a function of
as a function of . With the method of curve fitting, the activity coefficient of the kerosene at
. With the method of curve fitting, the activity coefficient of the kerosene at  is determined by:
is determined by:
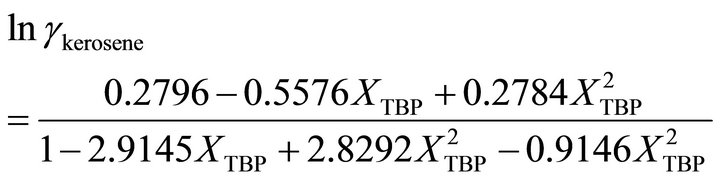 (32)
(32)
at the higher kerosene concentrations , the activity coefficient of kerosene is determined by:
, the activity coefficient of kerosene is determined by:
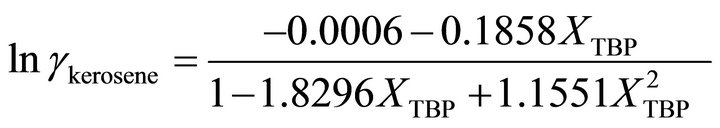 (33)
(33)
The Henry’s constant for the kerosene  is determined by:
is determined by:
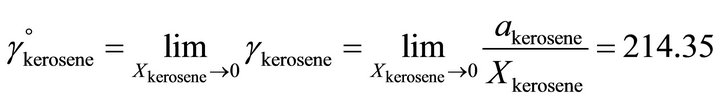 (34)
(34)
The Gibbs-Duhem Equation and its results (Equations (23) and (26)) help to determine the activity coefficient of the TBP with a graphical method. Figure 7 shows the value of  vs
vs . The results of the calculations are shown in Figure 8. With the curve fitting method, the activity coefficient of the TBP at
. The results of the calculations are shown in Figure 8. With the curve fitting method, the activity coefficient of the TBP at
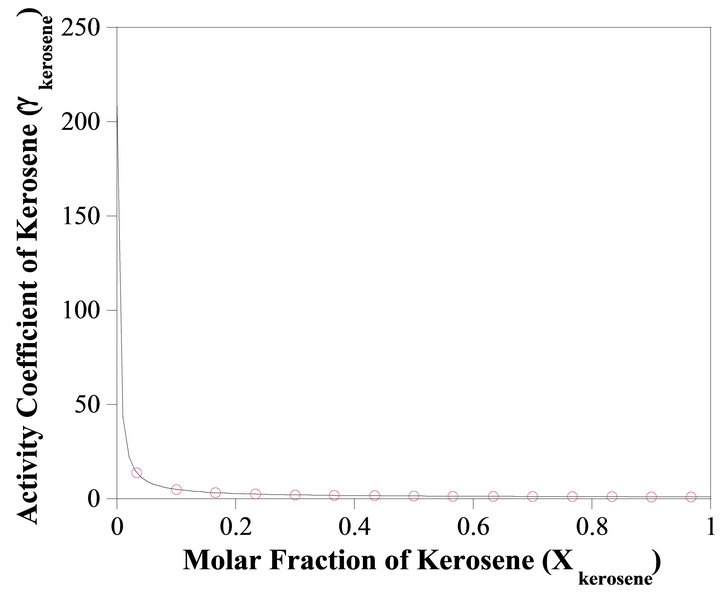
Figure 6. Activity coefficient of kerosene as a function of concentration.
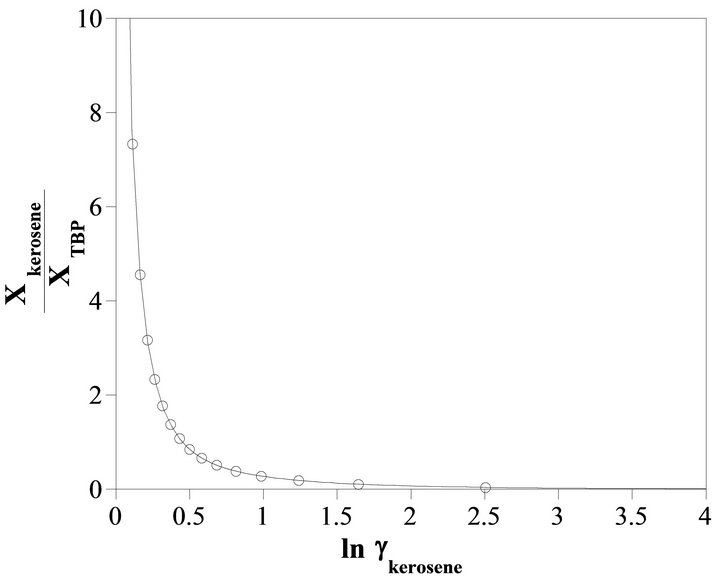
Figure 7. The value of 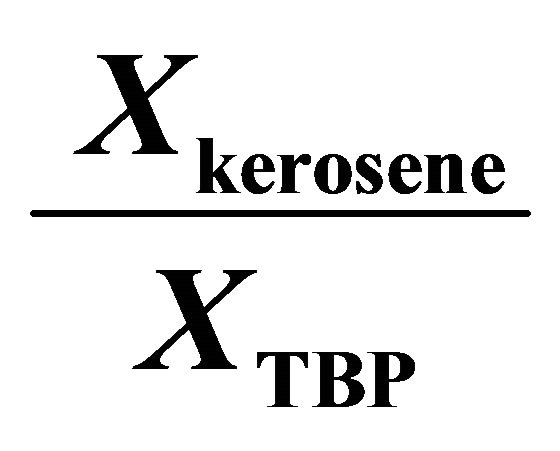 vs
vs .
.
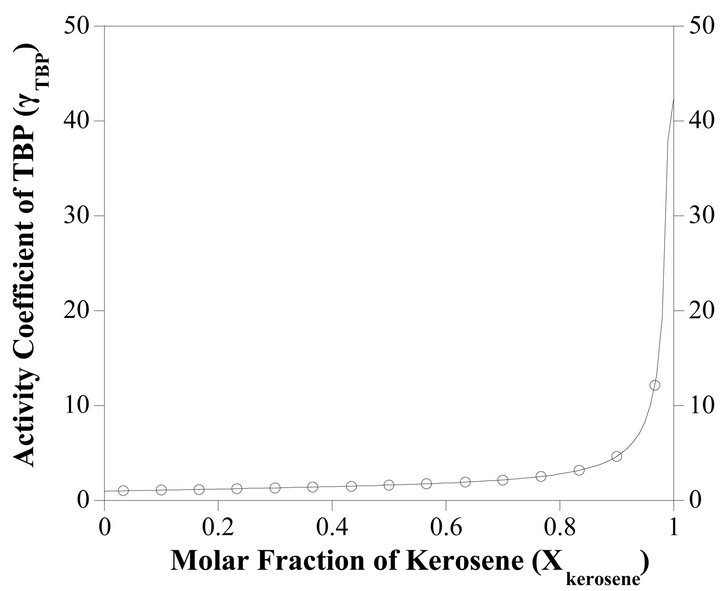
Figure 8. The activity coefficient of TBP as a function of the molar fraction of the kerosene.
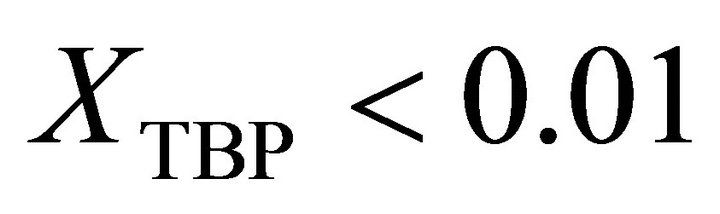 is determined by:
is determined by:
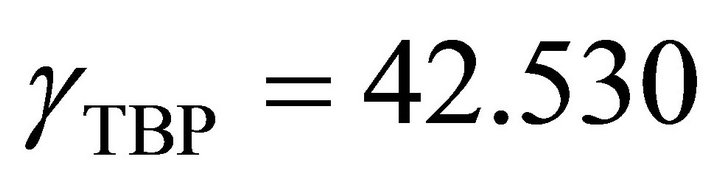 , (35)
, (35)
at 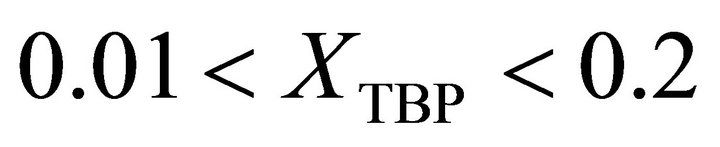 is given by:
is given by:
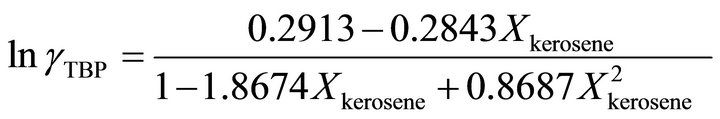 (36)
(36)
and at the higher TBP concentrations , the activity coefficient of TBP is evaluated by:
, the activity coefficient of TBP is evaluated by:
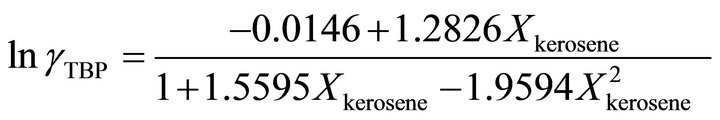 (37)
(37)
So the Henry’s constant for the TBP is equal to 42.530. The values of the activity of the TBP evaluated from an equation similar to Equation (24) are shown in Figure 9. The activity of the TBP has a very positive deviation
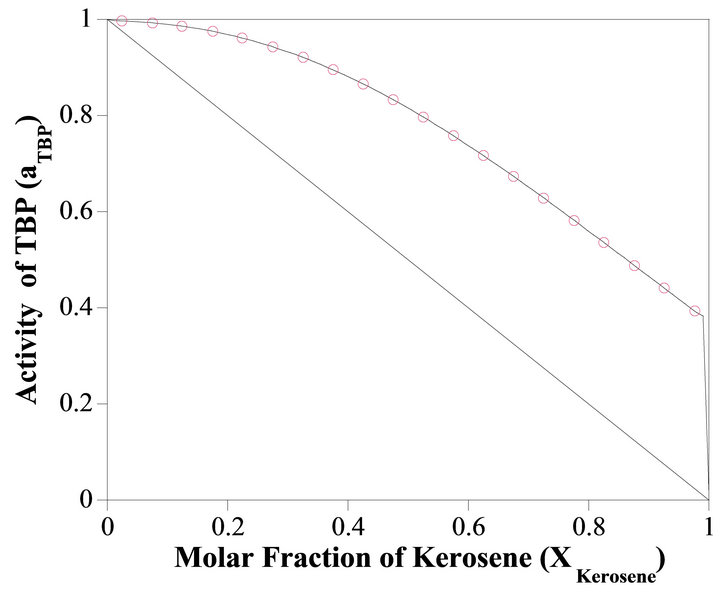
Figure 9. The activity of TBP vs Xkerosene.
from ideality. With the curve fitting method, the activity of the TBP at  is determined by:
is determined by:
 , (38)
, (38)
at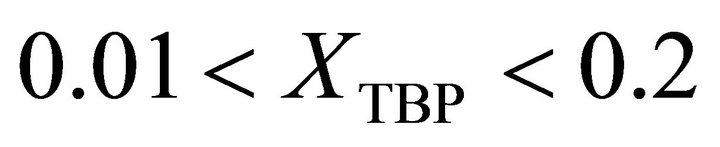 . It is evaluated by:
. It is evaluated by:
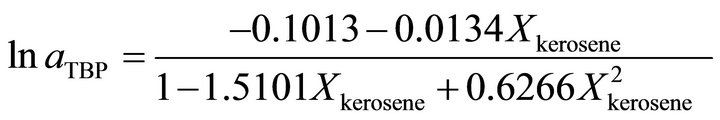 (39)
(39)
at the higher TBP concentration , the activity of TBP is determined by:
, the activity of TBP is determined by:
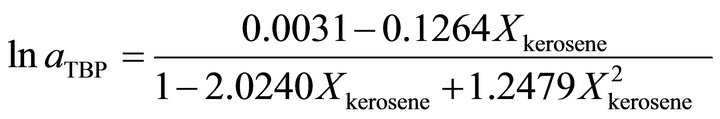 (40)
(40)
and at Raoultian range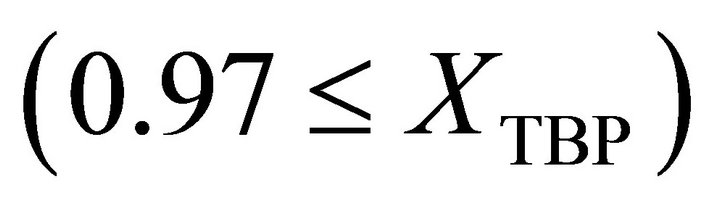 :
: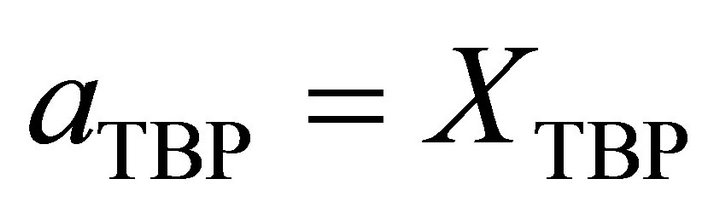 .
.
5. Summary
An analytical method is presented in this paper for determination of the activity of the TBP dissolved in the kerosene through a simple physical property measurement. The results show that the binary solution of the kerosene with the TBP has a positive deviation from the Raoult’s law behavior. The Henry’s constant of very dilute TBP in kerosene is equal to 42.350. This constant for very dilute kerosene in TBP is equal to 214.35. The activity coefficient of the TBP at 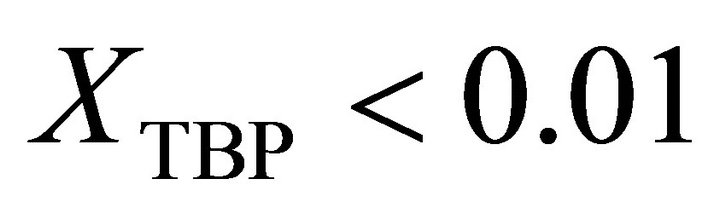 is determined by:
is determined by: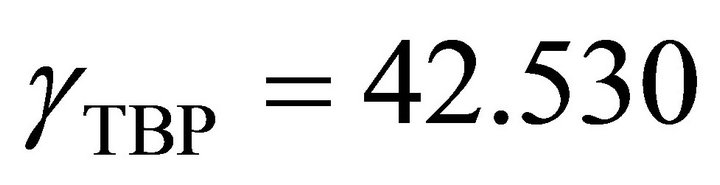 , at
, at  is given by:
is given by:

and at the higher TBP concentrations the activity coefficient of the TBP is determined by:
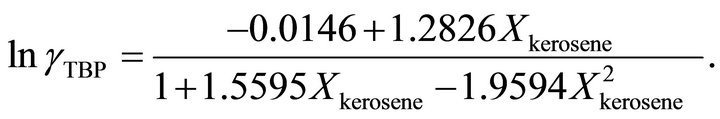
Also the activity of TBP at 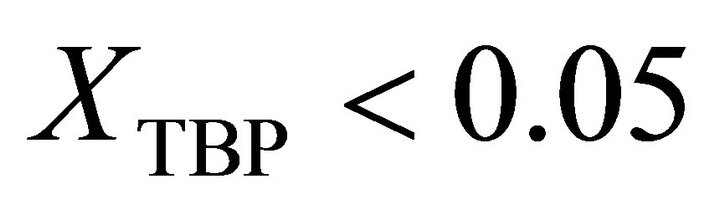 is determined by:
is determined by:
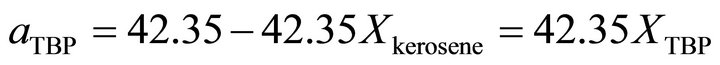
at 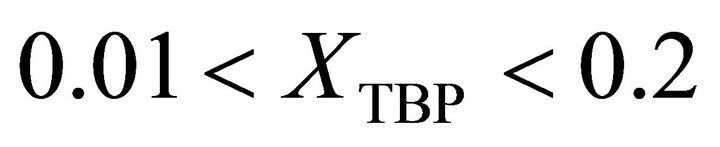 is given by:
is given by:
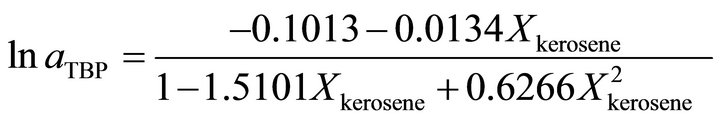
and at the higher TBP concentrations the activity of TBP is determined by:
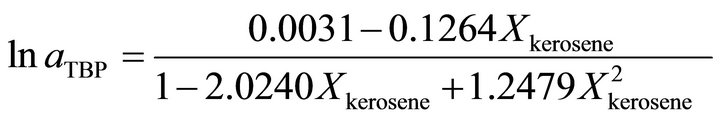 .
.
REFERENCES
- E. Keshavarz Alamdari, D. Darvishi, D. F. Haghshenas, N. Yousefi and S. K. Sadrnezhaad, “Separation of Re and Mo from Roasting-Dust Leach-Liquor Using Solvent Extraction Technique by TBP,” Separation and Purification Technology, Vol. 86, 2012, pp. 143-148. doi:10.1016/j.seppur.2011.10.038
- D. Darvishi, D. F. Haghshenas, E. Keshavarz Alamdari and S. K. Sadrnezhaad, “Extraction of ZN, MN and CO from ZN-MN-CO-CD-NI Containing Solution Using D2EHPA, Cyanex® 272 and Cyanex® 302,” International Journal of Engineering, Transactions B: Applications, Vol. 24, No. 2, 2011, pp. 183-192.
- D. F. Haghshenas, D. Darvishi, S. Etemadi, A. R. Eivazi Hollagh, E. Keshavarz Alamdari and A. A. Salardini, “Interaction between TBP and D2EHPA during Zn, Cd, Mn, Cu, Co and Ni Solvent Extraction: A Thermodynamic and Empirical Approach,” Hydrometallurgy, Vol. 98, No. 1-2, 2009, pp. 143-147.
- D. F. Haghshenas, D. Darvishi, H. Rafieipour, E. Keshavarz Alamdari and A. A. Salardini, “A Comparison between TEHA and Cyanex 923 on the Separation and the Recovery of Sulfuric Acid from Aqueous Solutions,” Hydrometallurgy, Vol. 97, No. 3-4, 2009, pp. 173-179. doi:10.1016/j.hydromet.2009.02.006
- D. Darvishi, D. F. Haghshenas, S. Etemadi, E. Keshavarz Alamdari and S. K. Sadrnezhaad, “Water Adsorption in the Organic Phase for the D2EHPA-Kerosene/Water and Aqueous Zn2+, Co2+, Ni2+ Sulphate Systems,” Hydrometallurgy, Vol. 88, No. 1-4, 2007, pp. 92-97. doi:10.1016/j.hydromet.2007.02.010
- D. Darvishi, D. F. Haghshenas, E. Keshavarz Alamdari, S. K. Sadrnezhaad and M. Halali, “Synergistic Effect of Cyanex 272 and Cyanex 302 on Separation of Cobalt and Nickel by D2EHPA,” Hydrometallurgy, Vol. 77, No. 3-4, 2005, pp. 227-238. doi:10.1016/j.hydromet.2005.02.002
- E. Keshavarz Alamdari, D. Moradkhani, D. Darvishi, M. Askari and D. Behnian, “Synergistic Effect of MEHPA on Co-Extraction of Zinc and Cadmium with DEHPA,” Minerals Engineering, Vol. 17, No. 1, 2004, pp. 89-92. doi:10.1016/j.mineng.2003.10.003
- S. K. Sadrnezhaad and E. Keshavarz Alamdari, “Thermodynamics of Extraction of Zn2+ from Sulfuric Acid Media with a Mixture of DEHPA and MEHPA,” International Journal of Engineering, Transactions B: Applications, Vol. 17, No. 2, 2004, pp. 191-200.
- R. E. Blanco, C. A. Blake Jr., W. Davis Jr. and R. H. Rainey, “Survey of Recent Developments in Solvent Extraction with Tri-Butyl-Phosphate,” Oak Ridge National Laboratory (ORNL), 1963. www.ornl.gov/info/reports/1963/3445605494266.pdf
- W. Davis Jr., “Thermodynamics of Extraction of Nitric Acid by Tri-N-Butyl Phosphate—Hydrocarbon Diluent Solutions I. Distribution Studies with Tbp in Amsco 125-82 at Intermediate and Low Acidities,” Oak Ridge National Laboratory (ORNL), 1961. www.ornl.gov/info/reports/1963/3445605700033.pdf
- X. Liu, D. Fang, J. Li, J. Yang and S. Zang, “Thermodynamics of Solvent Extraction of Thallium(I),” Journal of Phase Equilibria and Diffusion, Section I: Basic and Applied Research, Vol. 26, 2005, pp. 342-346. doi:10.1361/154770305X56791
- D. R. Gaskell, “Introduction to the Thermodynamics of Materials,” 5th Edition, Taylor & Francis Publisher, New York, 2008.
- D. V. Ragon, “Thermodynamics of Materials,” John Wiley & Sons Inc., New York, 1995.
- R. T. Dehoff, “Thermodynamics in Materials Science,” 2nd Edition, Mc Graw-Hill, New York, 1993.
- J. B. Hudson, “Thermodynamics of Materials,” John Wiley & Sons Inc., New York, 1996.
- F. Daniels, J. W. Williams, P. Bender, R. A. Alberty and C. D. Cornwell, “Experimental Physical Chemistry,” 7th Edition, McGraw Hill, New York, 1970.
- G. W. Castellan, “Physical Chemistry,” 3rd Edition, Addison-Wesley, Menlo Park, 2004.
- R. H. Perry, “Perry’s Chemical Engineers’ Handbook,” 7th Edition, McGraw Hill, New York, 1997.

