Crystal Structure Theory and Applications
Vol. 2 No. 2 (2013) , Article ID: 33492 , 13 pages DOI:10.4236/csta.2013.22011
Method to Study the Primary Nucleation for Solid Solution: Application to Uranium-Neodymium Oxalate Coprecipitation
1Commissariat à l’Energie Atomique et aux Energies Alternatives, Radiochemistry and Process Department, Bagnols-sur-Cèze, France
2Reactions and Chemical Engineering Laboratory-CNRS, Nancy, France
Email: murielle.bertrand@cea.fr
Copyright © 2013 Delphine Parmentier et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received November 7, 2012; revised January 2, 2013; accepted January 10, 2013
Keywords: Coprecipitation; Solid Solution; Thermodynamics; Kinetics; Supersaturation; Nucleation; Uranium
ABSTRACT
Actinides co-precipitation is currently investigated in order to synthesize solid solutions of actinides mixed oxalates. This paper deals with the thermodynamic and kinetic study of the precipitation of uranium-neodymium oxalate system. Based on an analysis of the theories developed in the literature, a new expression for the determination of the supersaturation ratio for the solid solutions is presented. An experimental study of the nucleation kinetics was performed on the mixed uranium-neodymium oxalates. Homogeneous and heterogeneous primary nucleation laws are obtained using a specific stopped flow apparatus. The experimental results are consistent with the classical behaviour of nucleation phenomena. The values of the kinetic parameters for the solid solution point out that the formation of the uraniumneodymium mixed oxalates is kinetically favoured compared with the simple uranium and neodymium oxalates.
1. Introduction
Current concepts for future nuclear systems aim at improving the fuel cycle with the co-management of actinides in order to enhance the fuel performance and to reduce the proliferation risk. The actinide co-conversion processes, such as COEXTM process [1], play an important role by producing mixed actinide compounds used as starting materials for fuel re-fabrication. The co-conversion of actinides into oxide can be achieved by different processes such as oxalic co-precipitation, thermal co-denitration or co-gelation. The Oxalic co-precipitation is one investigated way to synthesize solid solutions of actinide mixed oxalates which have to meet strict requirements [2]. Thus to support the process development, the determination of mechanisms and kinetic laws associated with the co-precipitation appears to be a key issue. This article focuses on the kinetic study in order to determine the primary nucleation rate for the uranium-neodymium oxalate system, which simulates the uranium-actinide system behaviour.
Compared with simple salts, mechanisms involved in the formation of mixed crystals are much more complex and remain poorly understood. The phenomenological theories are not still clarified in the literature. Equilibrium conditions for a solid solution-aqueous solution (SS-AS) system can be described using the approach developed by Lippmann who proposes an extension of the solubility product concept [3]. Several both experimental and theoretical studies have recently focused on the thermodynamics of mixed crystals [4-13] contrary to the kinetic studies which are reported in very few papers only [14,15]. The key point in the precipitation of solid solutions is the definition of the driving force. All authors agree to describe the difficulty in determining a rigorous expression of the supersaturation which is a fundamental crystallization parameter. The difficulty arises from the need to express supersaturation using the chemical potentials of components in both solid and aqueous solutions which are mutually independent. The way that the driving force should be defined is still controversial [16,17]. Shtukenberg et al. [11] propose to evaluate the supersaturation using Lippmann’s approach, whereas Astilleros et al. [8] developed two formulations, the first one based on the stoichiometric saturation concept [18] and the second one based on the actual activity concept [8].
This study focuses on the uranium(IV)-neodymium(III) oxalate solid solutions described by the following precipitation reaction, where can vary from 0 to 0.5 [2]:
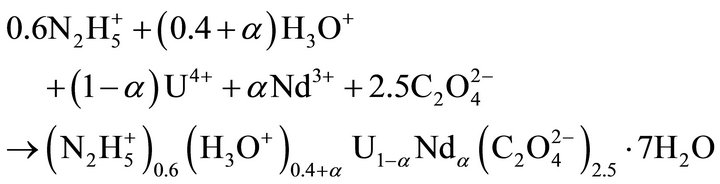 (1)
(1)
The solid solutions composed of U(IV)-Nd(III) oxalates are complex as the stoichiometric coefficients are different for each component. Solid solutions usually described in the literature have simple formula such as (Ba, Sr)SO4 or (Ba, Sr)CO3 [19-21] where cations and anions have the same charge, while in our case (see Equation (1)) the formation of the solid solution is much more complex and needs a more profound investigation not previously encountered in the literature. Thus, the aim of this work is to study experimentally the formation of this kind of complex solid solutions and to find adequate nucleation rate expressions in order to use them in modelling of precipitation processes in nuclear industry. The first part of this paper is concerned with the discussion of the Lippmann model in the case of complex solid solutions. A new suitable expression for the relative supersaturation ratio is then presented. Section 3 describes the experimental study of the nucleation kinetics performed on the mixed uranium-neodymium oxalate. The experimental results obtained are presented in section 4 and are confronted with the new model of the supersaturation.
2. Supersaturation Concept in SS-AS Systems
In precipitation, the supersaturation concept describes in a quantitative way the deviation of a given aqueous solution from the equilibrium state. For a pure solid of the form BA, the solubility product is defined as the product of activities of species in solution at equilibrium conditions:
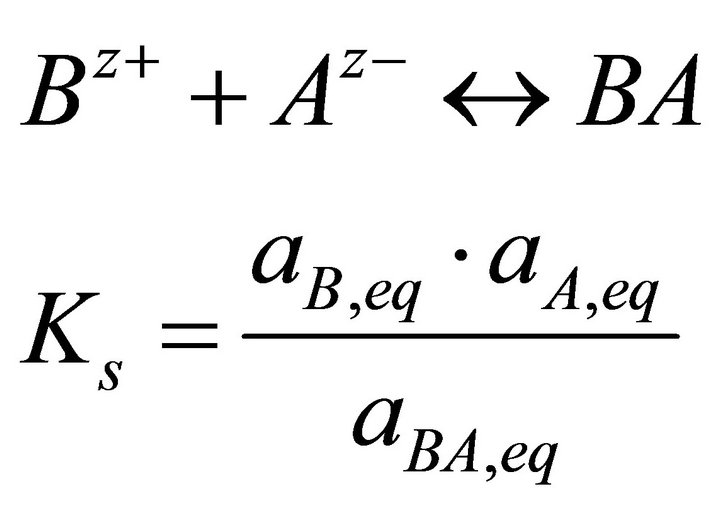 (2)
(2)
where Ks is the solubility product of BA, aA and aB the activity of the ions Az− and Bz+ in the liquid phase, aAB the activity of BA in the solid phase and z the positive and negative charge of ions, eq means at equilibrium state.
The driving force of the nucleation process, the relative supersaturation ratio, can be calculated by the wellknown general expression:
 [19] (3)
[19] (3)
where S is the supersaturation ratio, 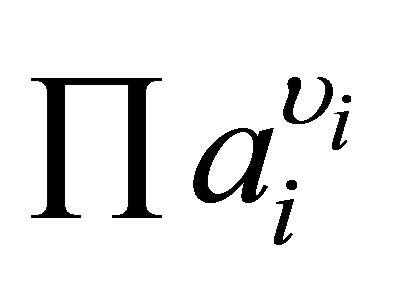 the product of the ionic activities and υi the stoichiometric number of ion i.
the product of the ionic activities and υi the stoichiometric number of ion i.
Regarding the solid solutions, the application of the supersaturation concept (for example in the case of the coprecipitation of BA and CA compounds, see Equations (4) and (5)) requires first to define the equilibrium conditions.
2.1. Lippmann’s Approach
Lippmann [3] proposed to extent the solubility product concept to the solid solution based on an analogy to liquid-vapour systems. We consider a solid solution-aqueous solution system where the cations Bz+ and Cz+ and the anions Az− are presented in the aqueous phase and react to lead to the solid solutions 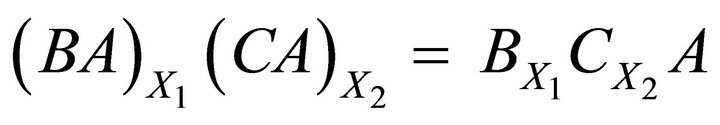
formed by the pure end-members BA and CA. The equilibrium conditions between the solid solution and the aqueous solution are given by two expressions provided by the following reaction schemes:
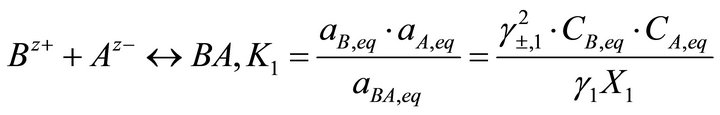 [3] (4)
[3] (4)
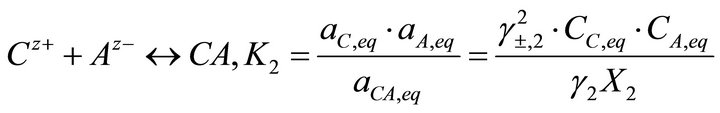 [3] (5)
[3] (5)
where K1 and K2 are the solubility product of the endmembers, X1 and X2 the molar fractions of endmembers in the solid solution, aA, aB and aC the activities of the ions Az−, Bz+ and Cz+ in the aqueous solution, aBA and aCA the activities of BA and CA in the solid solution, CA, CB and CC the concentrations of the ions Az−, Bz+ and Cz+, γ1 and γ2 the activity coefficients in the solid phase and γ±1 and γ±2 the mean activity coefficients in the liquid phase.
These reactions are coupled only through the mass balance that implies:
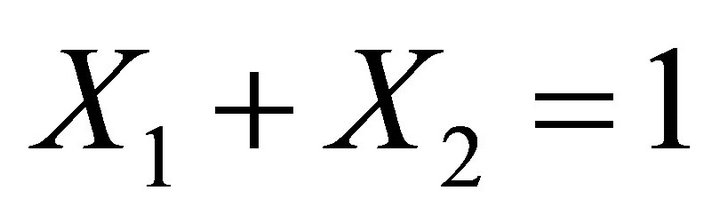 [3] (6)
[3] (6)
We note BA the endmember 1 and CA the endmember 2 with conventionally 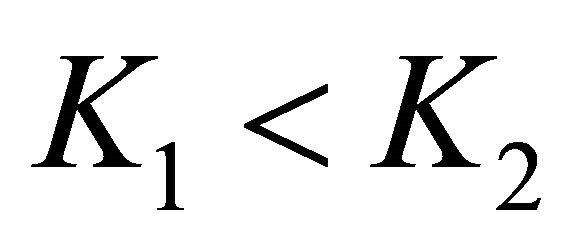 [3].
[3].
According to Lippmann, in the same way as the total vapour pressure of a liquid mixture is the sum of the partial vapour pressure of each component, the total solubility product can be defined as the sum of the partial solubility products of each endmember of the solid solution:
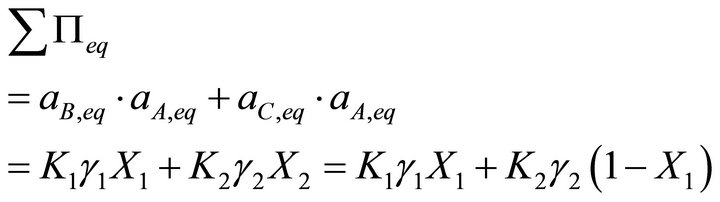 [3] (7)
[3] (7)
where  is the total solubility product.
is the total solubility product.
The products 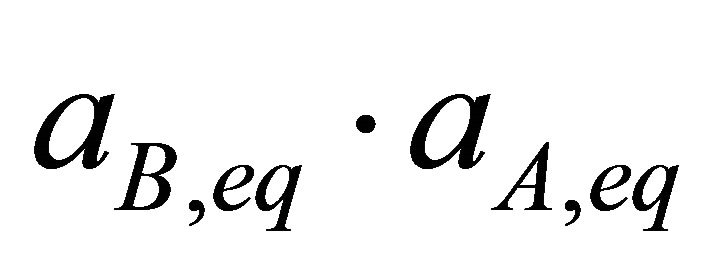 and
and 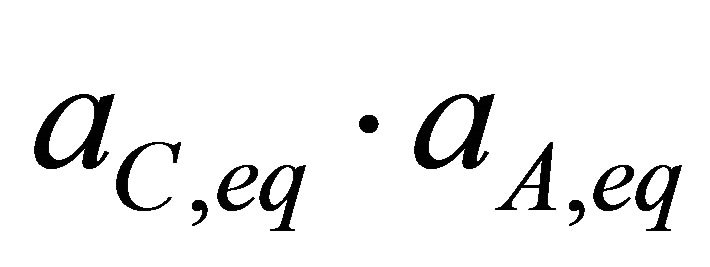 are analogous to partial pressures of a vapour pressure diagram of a binary system and can be assimilated to partial solubility products.
are analogous to partial pressures of a vapour pressure diagram of a binary system and can be assimilated to partial solubility products.
The total solubility product as a function of the solid solution composition 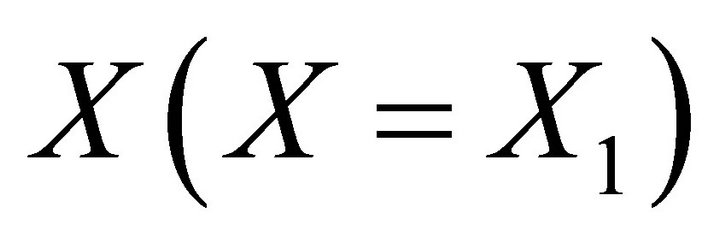 leads to the Lippmann solidus equation. Similarly, the total solubility product as a function of the aqueous solution composition
leads to the Lippmann solidus equation. Similarly, the total solubility product as a function of the aqueous solution composition 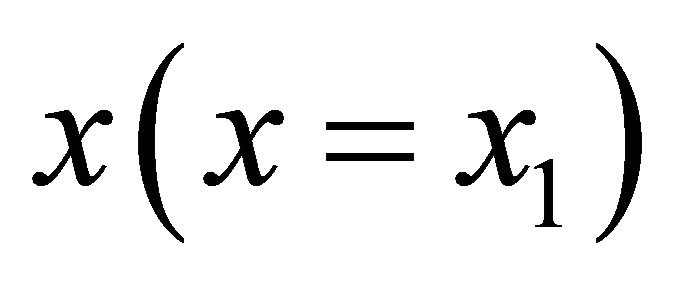 leads to the Lippmann solutus equation.
leads to the Lippmann solutus equation.
Therefore a phase diagram is obtained by analogy to the vapour pressure diagram.
Using the Lippmann approach, the driving force can be expressed as follows [11]:
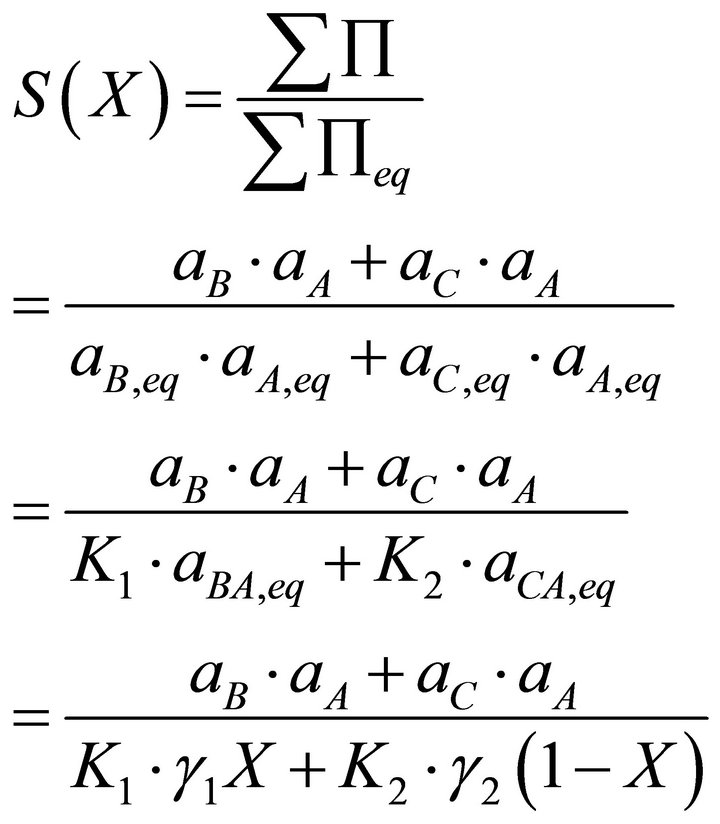 [11] (8)
[11] (8)
where S is the supersaturation ratio depending on X.
In the literature, this approach described by Lippmann was applied by several authors for bivalent cations and anions and the considered systems can thus be described by Equations (4) and (5) where . The classical systems studied were (Ba, Sr)SO4, (Ba, Sr)CO3, (Ca, Mg)CO3, etc. There are however more complex solid solutions in which the endmembers present different stoichiometric coefficients: this specially applies to the nuclear industry where different actinide solid solutions are formed by coprecipitation [22-24].
. The classical systems studied were (Ba, Sr)SO4, (Ba, Sr)CO3, (Ca, Mg)CO3, etc. There are however more complex solid solutions in which the endmembers present different stoichiometric coefficients: this specially applies to the nuclear industry where different actinide solid solutions are formed by coprecipitation [22-24].
For solid systems with endmembers of different stoichiometry, the Lippmann formalism needs to be adjusted. To illustrate these cases, we consider now a simple SSAS system where the cations B+ and C2+ and the anion A2− are presented in the aqueous phase and react to lead to solid solutions 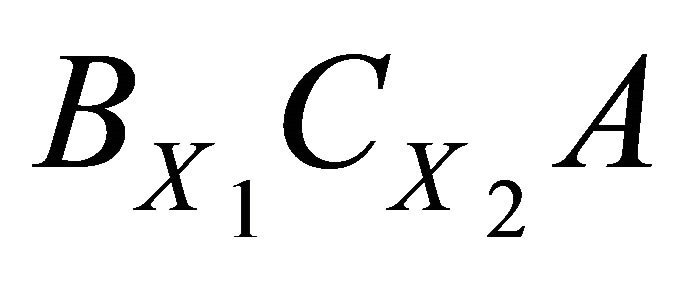 formed by the pure endmembers B2A and CA. The equilibrium conditions of this binary system are as follows:
formed by the pure endmembers B2A and CA. The equilibrium conditions of this binary system are as follows:
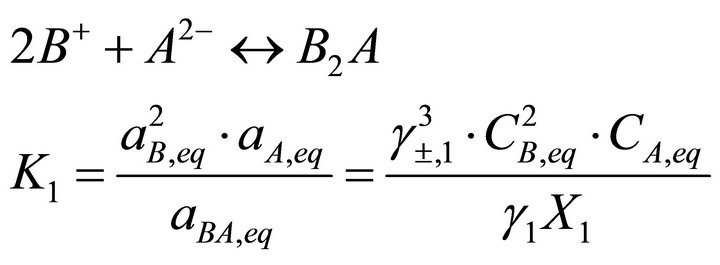 (9)
(9)
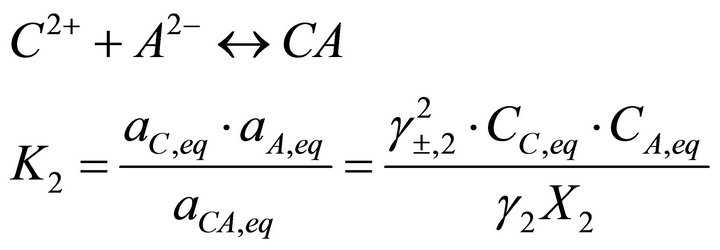 (10)
(10)
According to the Lippmann proposition, the total solubility product would be obtained by adding Equations (9) and (10):
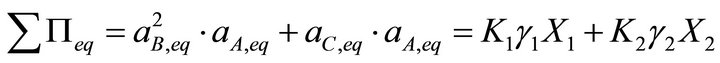 (11)
(11)
This equation is not adequate as it is composed of terms with different dimensionalities: the first endmember solubility product K1 is expressed in (mol·m−3)3, whereas the second endmember solubility product K2 is in (mol·m−3)2. This example points out that the Lippmann model for a complex solid solution cannot be directly applicable since it fails to satisfy the fundamental dimensionality principle. To our opinion, the Lippmann theoretical approach is right, but his mathematical approach needs to be generalized. We accept the Lippmann similarity between liquid phase-vapour phase equilibrium and solid solution-aqueous solution equilibrium, but a new mathematical expression consistent with equilibrium relations can be proposed. For a liquid-vapour equilibrium, assuming a thermodynamically ideal liquid solution, the total vapour pressure is given as follows:
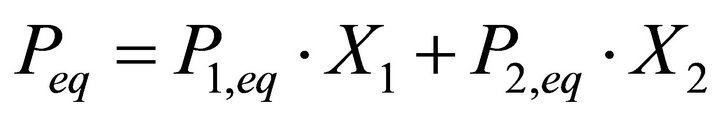 (12)
(12)
while Equation (7) proposed by Lippmann is equivalent to the following expression:
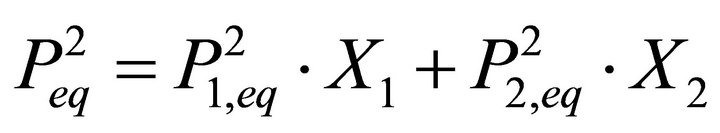 (13)
(13)
which is not a correct equation.
In these equations, 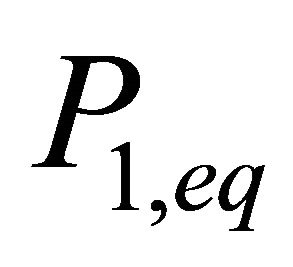 and
and ![]() are the partial vapour pressure, X1 and X2 the molar fractions of the components and Peq the total vapour pressure of the liquid mixture. Whatever the system considered, the terms added in Equation (12) have always the same dimensionality as a pressure. The concentration dimensionality is directly proportional to a pressure. Therefore, to be consistent with the vapour-liquid system, the total equilibrium term should have always the same dimensionality as a concentration and should be defined as the sum of terms with a concentration dimensionality (in thermodynamics, in the domain of multi-component phase equilibrium, only terms having pressure or concentration dimensionalities in power 1 can be additional terms).
are the partial vapour pressure, X1 and X2 the molar fractions of the components and Peq the total vapour pressure of the liquid mixture. Whatever the system considered, the terms added in Equation (12) have always the same dimensionality as a pressure. The concentration dimensionality is directly proportional to a pressure. Therefore, to be consistent with the vapour-liquid system, the total equilibrium term should have always the same dimensionality as a concentration and should be defined as the sum of terms with a concentration dimensionality (in thermodynamics, in the domain of multi-component phase equilibrium, only terms having pressure or concentration dimensionalities in power 1 can be additional terms).
In addition, if we consider the expression of the supersaturation ratio defined by Shtukenberg et al. [11] (see Equation (8)), we can notice that for the pure endmembers this expression doesn’t converge to the general expression of the supersaturation ratio (see Equation (3)).
2.2. New Expression
Based on these considerations, we propose a new expression to determine the total solubility term at equilibrium. For a system defined by Equations (4) and (5), the new formulation is:
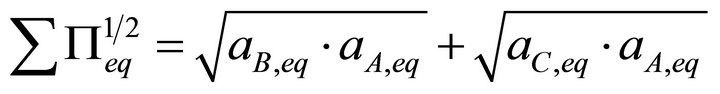 (14)
(14)
Based on equilibrium Equations (4) and (5), it follows:
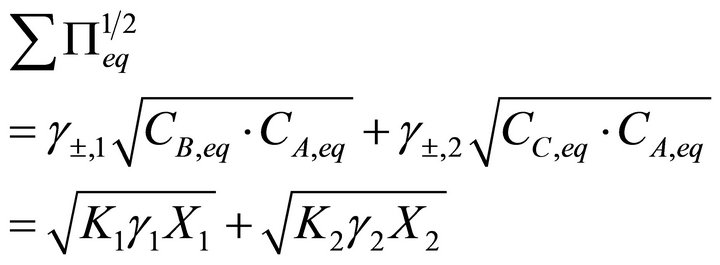 (15)
(15)
Therefore, the absolute supersaturation will be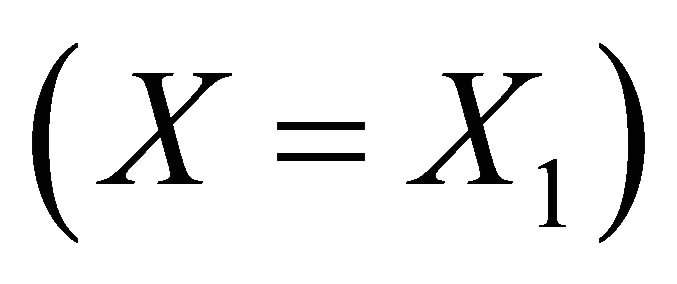 :
:
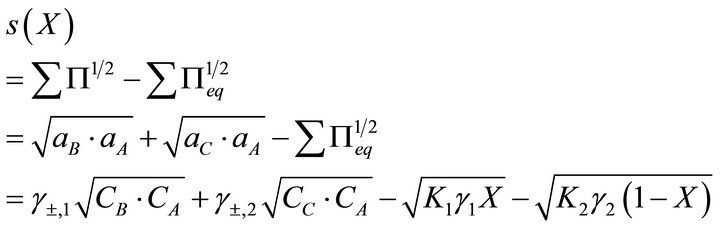 (16)
(16)
and the supersaturation ratio:
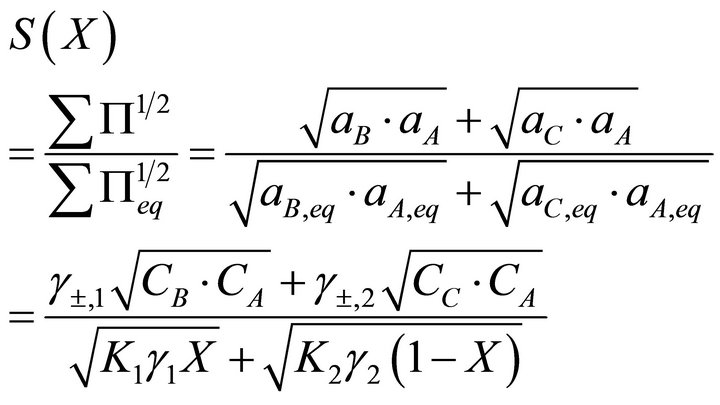 (17)
(17)
We can also note that the Expressions (16) and (17) converge to the right expressions for the single component systems when 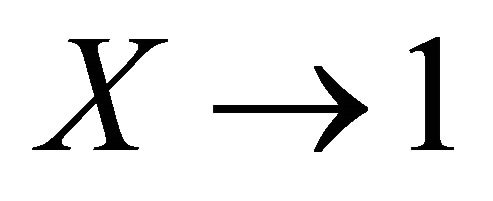 or
or , contrary to Lippmann’s approach (see Equation (3)).
, contrary to Lippmann’s approach (see Equation (3)).
More generally, for any kind of solid solution of the form 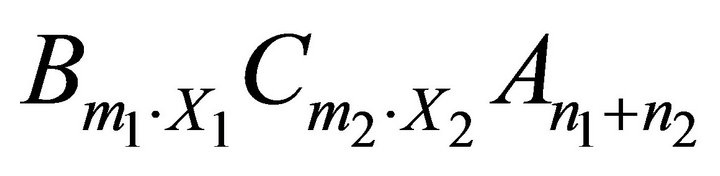 obtained from the endmembers
obtained from the endmembers 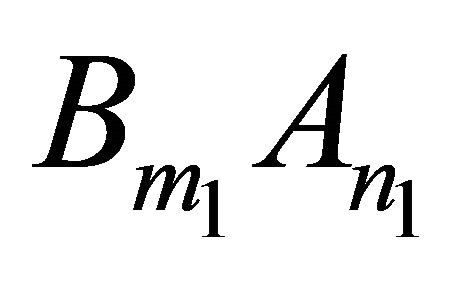 and
and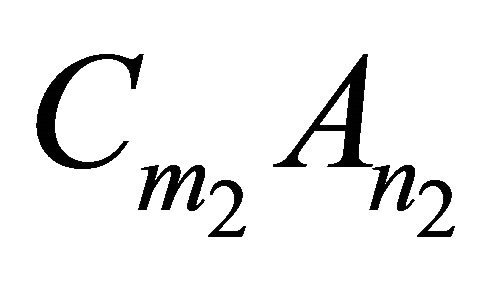 , equilibrium is defined by the following mass action equations:
, equilibrium is defined by the following mass action equations:
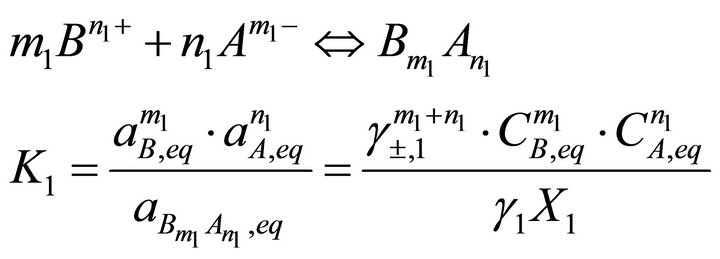 (18)
(18)
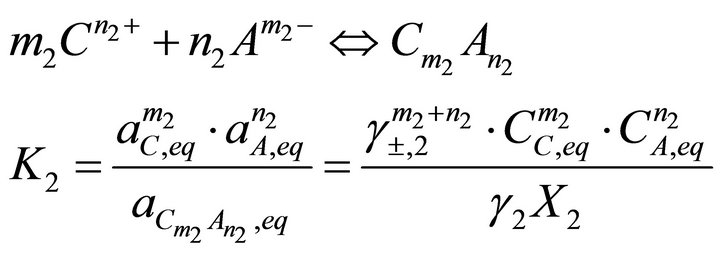 (19)
(19)
Using the new expression, the total solubility term and the supersaturation ratio are defined as follows:
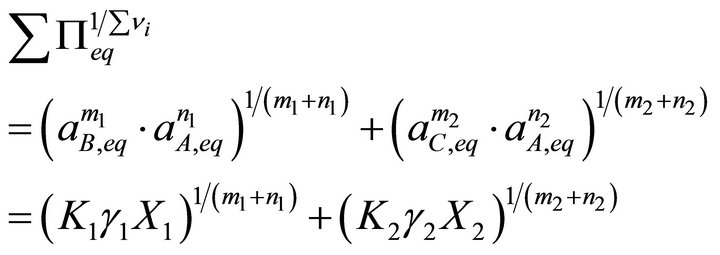 (20)
(20)
and
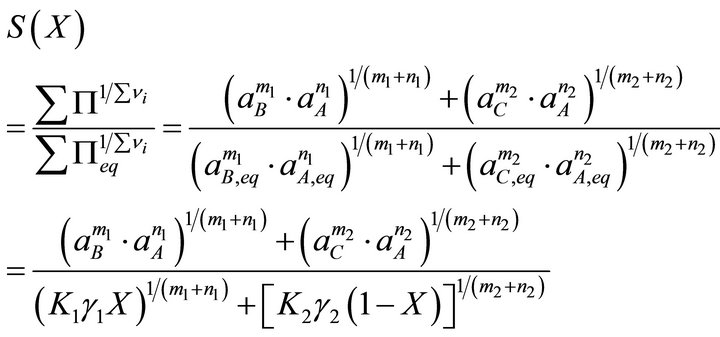 (21)
(21)
2.3. Other Expression of the Supersaturation
Applying the concept of the stoichiometric saturation to a solid solution [18] and the Lippmann approach [3], Pina et al. [7,9,19] derived the supersaturation ratio expression based simultaneously on equilibrium relations of Reactions (3) and (4) and on the formation of the solid solution according to the single reaction:
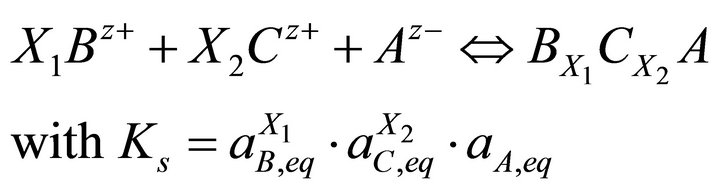 (22)
(22)
Using equilibrium Equations (3), (4) and (22), they propose the following expression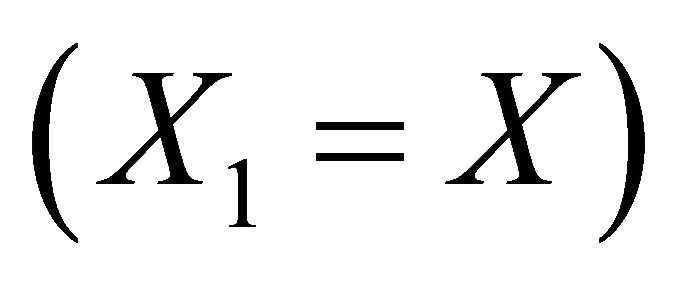 :
:
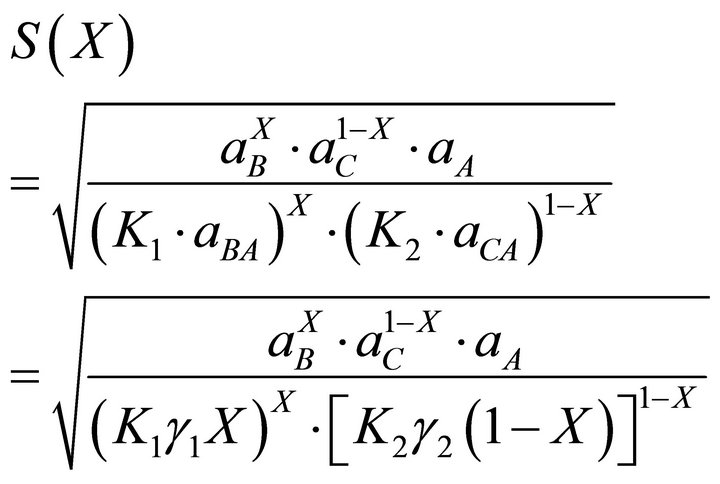 [19] (23)
[19] (23)
The weak point of the Putnis et al.’s formalism [20-25] is the dualism used to obtain the equilibrium expressions. Indeed the authors accept simultaneously the solid phase as composed of two endmembers BA and CA (Reactions (3) and (4)) and as composed of a single compound BX1CX2A (Reaction (22)). We have compared our formalism proposed in this study with the one proposed by Putnis et al. in the case of the coprecipitation of (Ba, Sr)SO4
where 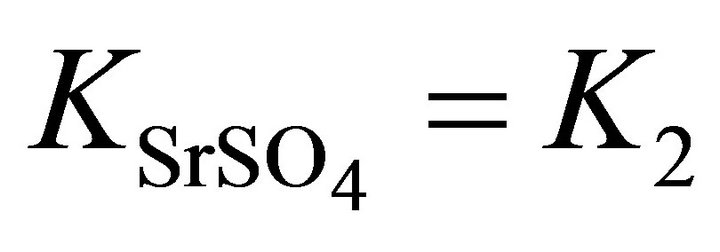 is three orders of magnitude higher than
is three orders of magnitude higher than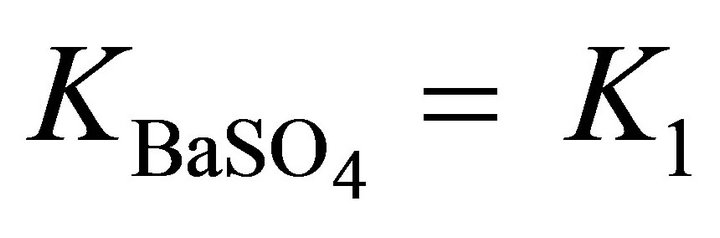 . The calculations of the supersaturation ratio for X1 values ranging from 0 to 1 (not shown here) give a maximum difference of 2.4 times higher for our expression than for the Putnis et al. expression. This difference is very sensible to the ratio
. The calculations of the supersaturation ratio for X1 values ranging from 0 to 1 (not shown here) give a maximum difference of 2.4 times higher for our expression than for the Putnis et al. expression. This difference is very sensible to the ratio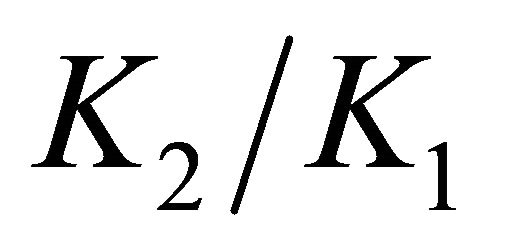 . When K1
. When K1
and K2 are of the same order of magnitude (which is the case in the nuclear industry), the values of supersaturation ratio obtained by the two approaches are almost the same [26]. Here, we can also note that the mathematical calculations based on the Putnis et al. formalism are much more complex than those corresponding to the formalism we propose. For all these reasons, in this article, only the new expression based on the analogy between liquid-vapour equilibrium and SS-AS equilibrium is used to calculate the supersaturation.
2.4. Determination of the Supersaturation Ratio Based Only on Liquid Phase Composition
As shown in Equations (16) and (17), the supersaturation is calculated as a function of the composition of the solid phase X. All authors in their studies have used the molar composition X to express the supersaturation ratio. However, during the precipitation reaction, the variation of the liquid phase composition is easily measured or known, while the composition of the solid phase can be known only at the end of precipitation process. For this reason, it is interesting to express the supersaturation based only on the composition of the liquid phase. Let us illustrate it using first the simple case expressed by Equations (4) and (5) for which the supersaturation ratio is given by Equation (17).
Considering a solid solution defined by Equations (4) and (5), the mole fractions of endmembers BA and CA in the solid solution are given by:
 (24)
(24)
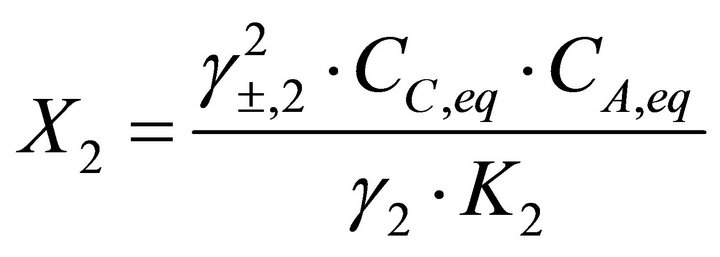 (25)
(25)
Knowing that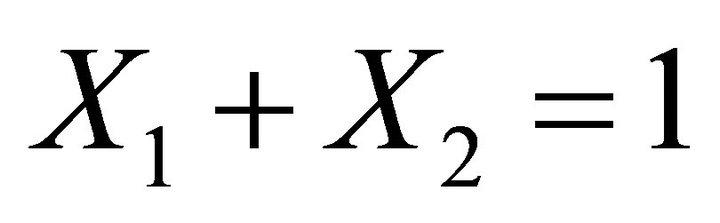 , the concentration of the reactant A can be deduced from Equations (24) and (25):
, the concentration of the reactant A can be deduced from Equations (24) and (25):
 (26)
(26)
The total solubility term expressed as a function of the liquid composition is given by Equation (15).
Substituting Equation (26) in Equation (15) and dividing the numerator and the denominator by 
lead to the relationship between the mole fraction of the solid phase X1 and the mole fraction in the liquid phase x1:
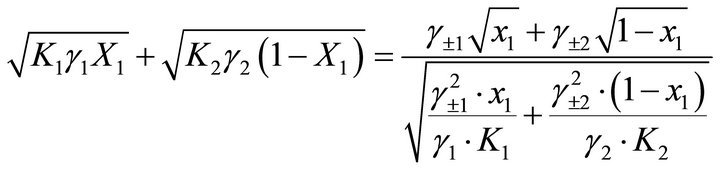 (27)
(27)
where x1 and x2 are the mole fractions of the endmembers in the liquid phase at equilibrium.
According to the Lippmann phase diagram, the aqueous solution at equilibrium has the same aqueous activity fraction as the supersaturated solution [3,8,11]. Consequently, x1 and x2 are defined as:
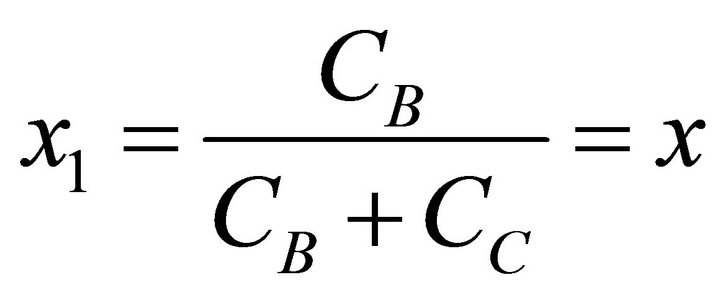 (28)
(28)
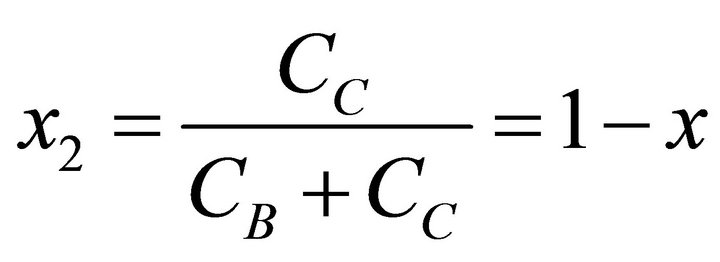 (29)
(29)
Equation (27) is very important since it links the relation liquid and solid phase compositions at any time of precipitation reaction. Finally, from Equation (27), the analytical solution of the relative supersaturation is obtained as a function of the composition of the aqueous solution only:
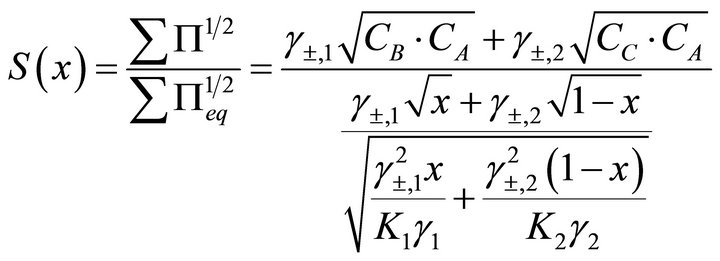 (30)
(30)
Let us use the same methodology to find the supersaturation ratio expression in our more complex case. A series of solid solutions can be synthesized by mixing an acid solution of uranium(IV) and neodymium(III) nitrate with an oxalic acid solution [22-27]. The solid solutions are formed by the following isostructural endmembers:
Endmember 1:
![]() (31)
(31)
Endmember 2:
![]() (32)
(32)
The mixed oxalates can be obtained only under specific experimental conditions used in the nuclear industry [2,23]. Three series of mixed lanthanide(III) and actinide(IV) were studied by Chapelet-Arab et al.: the hexagonal, the triclinic and the quadratic series. The originality of these structures is the existence of a mixed crystallographic site for tetravalent actinide and for trivalent lanthanide or actinide. The charge balance depending on the
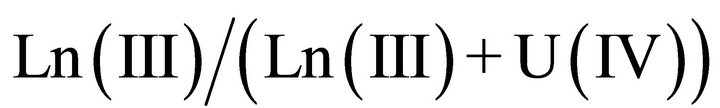 mole ratio is ensured by the adjustment of single charged ions within the structure
mole ratio is ensured by the adjustment of single charged ions within the structure
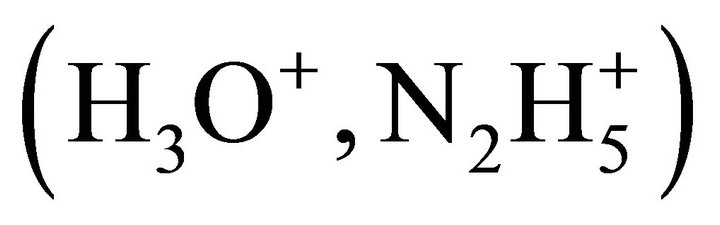 .
.
The solubility products of the endmembers 1 and 2 were experimentally determined by Costenoble under experimental conditions encountered in nuclear industry given in Table 1 [23-28].
The precipitation reactions of the endmembers are:

Table 1. Experimental conditions for obtaining the solid solutions of endmembers 1 and 2.
 (33)
(33)
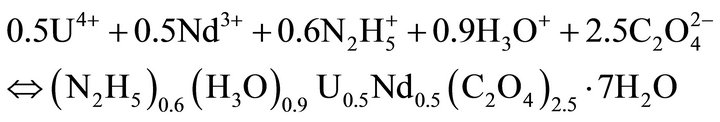 (34)
(34)
and their solubility products can be expressed as follows:
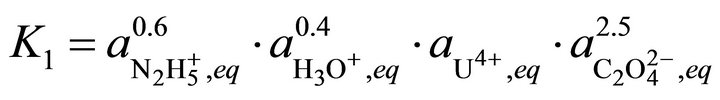 (35)
(35)
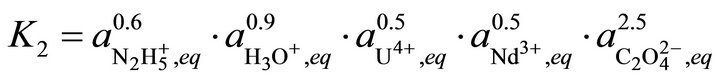 (36)
(36)
In the case of a solid solution formed by the copre cipitation of the above endmembers, the equilibrium relations are:
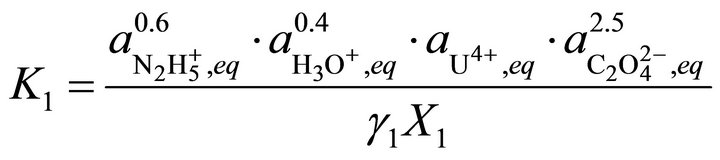 (37)
(37)
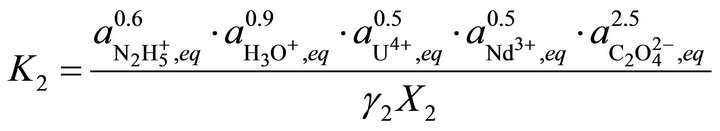 (38)
(38)
As discussed before (Equation (20)), the total solubility term can be written as:
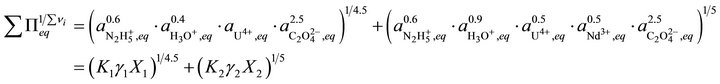 (39)
(39)
or:
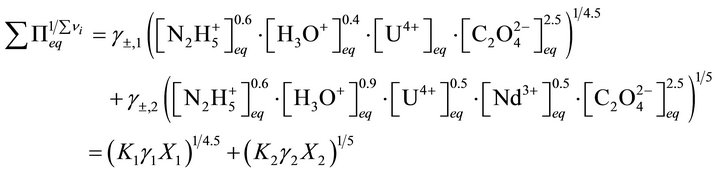 (40)
(40)
Based on these Equation (41), the supersaturation ratio during the coprecipitation is:
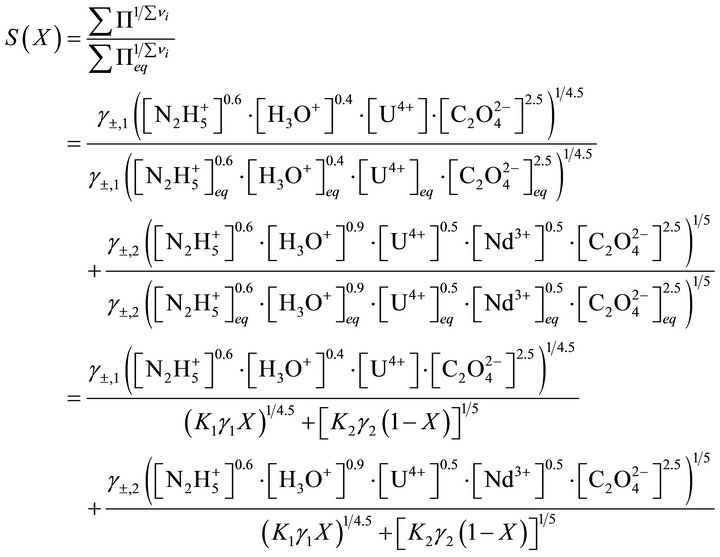 (41)
(41)
In Equation (41), the concentrations of all compounds in the liquid phase are known, while the solid phase composition X is not directly known, but must be determined by indirect complex calculations. As noted before, the supersaturation must be expressed only as a function of the liquid phase composition, since only this one isknown at any time of coprecipitation process. The compositions (molar fractions of endmembers) of the liquid and solid phases are defined as follows:
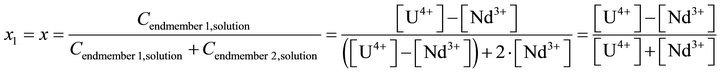 (42)
(42)
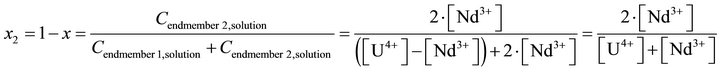 (43)
(43)
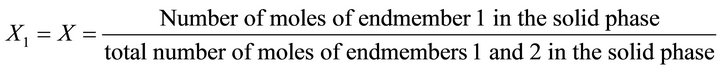 (44)
(44)
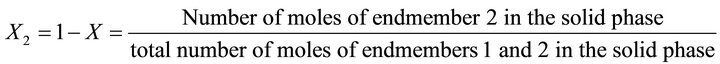 (45)
(45)
From Equations (6), (37) and (38) we can obtain:
 (46)
(46)
Substituting Equation (46) in Equation (40) yields:
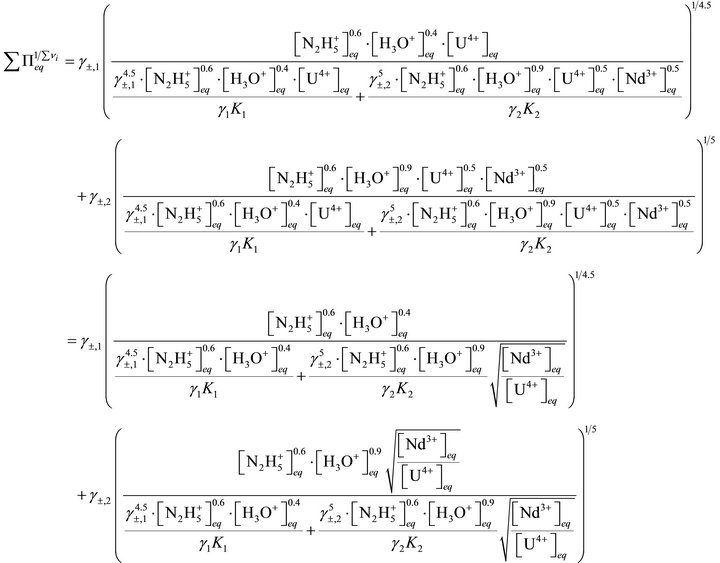 (47)
(47)
From the definition (42):
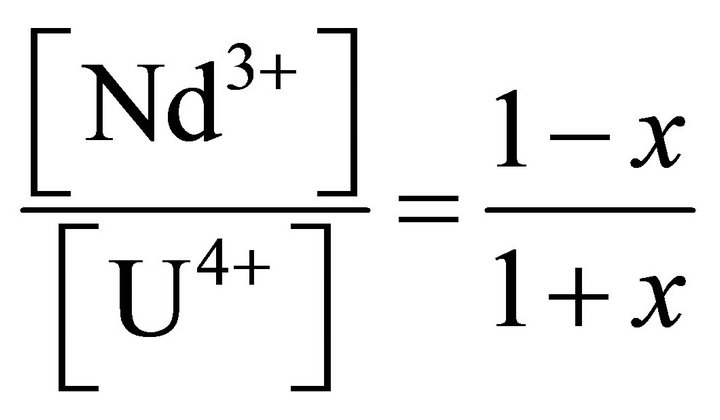 (48)
(48)
We can obtain:
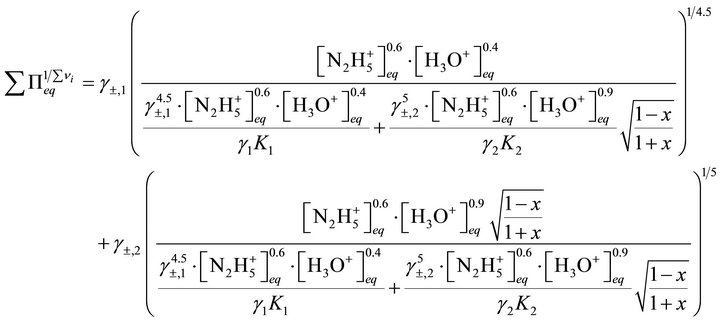 (49)
(49)
and the supersaturation ratio as a function of the liquid phase composition only:
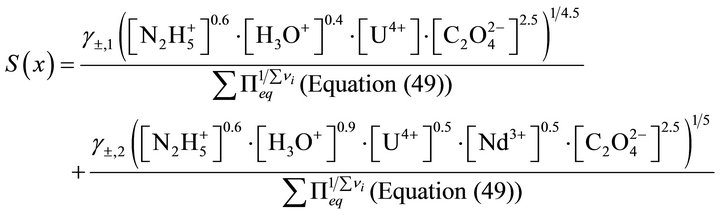 (50)
(50)
In addition, we can notice that the equalization of Equation (50) with the right term of Equation (40) gives the cumbersome implicit equation for the determination of the solid phase composition at equilibrium with the liquid phase composition (X versus x).
3. Experimental
The nucleation kinetics is studied using a stopped flow apparatus patented by the CEA/AREVA shown in Figure 1 [29].
This apparatus is equipped with a Hartridge-Roughton confined opposing jets mixing device. It is characterised by very high micromixing performances as micromixing

Figure 1. Patented apparatus for the nucleation kinetic. Patented apparatus for nucleation kinetic study [29].
times of the order of one millisecond can be achieved [30].
The apparatus, made of stainless steel material, is particularly appropriate to hostile environment, due to the simplicity and the experimental set up compactness. It requires a small solution volume and no unintentional release is possible. With all these safe use properties, this apparatus is well adapted to the radioactive material handling in glove boxes [31].
The block diagram of the stopped flow apparatus is represented in Figure 2. The thermostated tanks are supplied with reagents, 5 mL of each: uranium and neodymium nitrate solution and oxalic acid solution. The contact of the reagents is performed by two pistons, based on a crossbow mechanism. The pistons ensure a rapid and
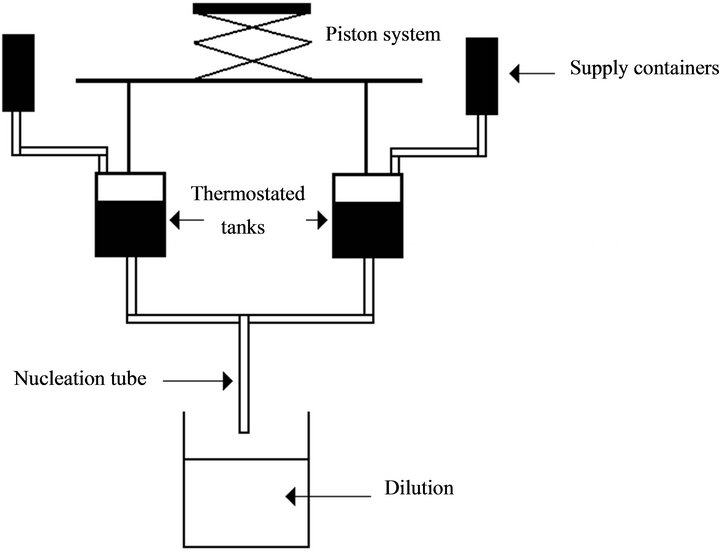
Figure 2. Principle of the experimental setup for the nucleation kinetic study.
simultaneous injection of the reagents in the nucleation tube. The nucleation occurs in the nucleation tube with a length of 10 cm and a diameter of 2 mm. The residence time is about 10 ms. Two optical detectors linked to an electronic system allows the nucleation process time in the tube to be measured.
The duration of the nucleation process is about 0.4 s. A dilution is performed at the tube outlet in a 500 mL vessel initially filled with nitric acid, oxalic acid and hydrazine solution. The role of this quench is to stop the nucleation process with a quick drop of the supersaturation. The dilution vessel is stirred by a 4-blade Rushton turbine at 1500 rpm with 4 baffles. As recommended by Nielsen [32], gelatine is introduced in a concentration of 2 g·L−1 in order to limit the agglomeration phenomena. The tube is placed in the discharging jet of the turbine to guarantee a quasi-instantaneous dilution. The solid particles formed can grow during 15 min to reach a detectable size range and the suspension is analysed by laser diffraction granulometry using a Coulter Counter apparatus. A preliminary study on the induction time [26] confirms that only nucleation takes place in the tube, as the residence time in the nucleation tube (10 ms) is lower than the induction period for all supersaturation values. The nuclei number retained corresponds to an average between 3 analysed samples. The nucleation rate is then determined using the total number of nuclei formed and the nucleation period measured with precision in each experiment. The method is well described in [31]. The crystals are observed by Scanning Electron Microscopy (SEM) and analysed by X-Ray diffractometry in order to be certain that the desired solid solution is formed.
A tetravalent uranium nitrate solution is purified on ion exchange resins in order to separate uranium(IV) from uranium(VI). In this way, pure solution containing 99% uranium(IV) is obtained and then characterized by UV-visible spectrophotometer (Shimadzu UV 2550). Uranium(IV) ions can be oxidized by nitrous acid (HNO2) which is presented in small quantities in nitric acid media. For this reason, hydrazinium nitrate is added in order to stabilize the tetravalent uranium nitrate solution for several months. Neodymium nitrate hexahydrate (99.9%, Alfa Aesar) is dissolved in the uranium nitrate solution with a determined 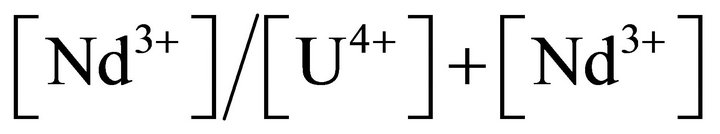 ratio. Oxalic acid solution with a concentration of 0.7 mol·L−1 is prepared from oxalic acid dihydrate (Normapur, >99.5%, VWR Prolabo). Deionised water is used in all experiments. The experiments are performed at room temperature under experimental conditions shown in Tables 1 and 2.
ratio. Oxalic acid solution with a concentration of 0.7 mol·L−1 is prepared from oxalic acid dihydrate (Normapur, >99.5%, VWR Prolabo). Deionised water is used in all experiments. The experiments are performed at room temperature under experimental conditions shown in Tables 1 and 2.
4. Results and Discussion
4.1. Analysis of Mixed Oxalate Crystals
The SEM photographs validate the formation of mixed oxalates and the absence of agglomeration (see Figure 3).
The particles are hexagonal rods which are the characteristic morphology of the solid solutions formed by the precipitation Reaction (1) [23].
In addition, careful X-Ray diffractometric analyses are performed. As it is shown in Figure 4, the X-Ray spectrum confirms the formation of pure mixed oxalate as it is consistent with the PDF card 04-11-8368 [22].
The composition of the solid phase is also analysed on different individual particles. The results lead to a homogeneous composition of individual particles.
4.2. Endmembers Solubility
The solubility products of endmembers are experimentally determined under the experimental conditions re-
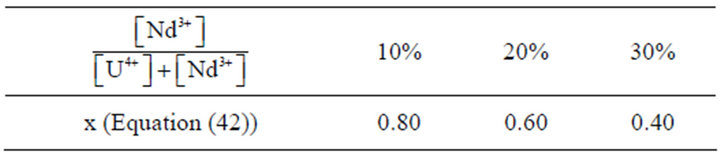
Table 2. Liquid phase compositions.


Figure 3. SEM photographs of uranium and neodymium mixed oxalates.
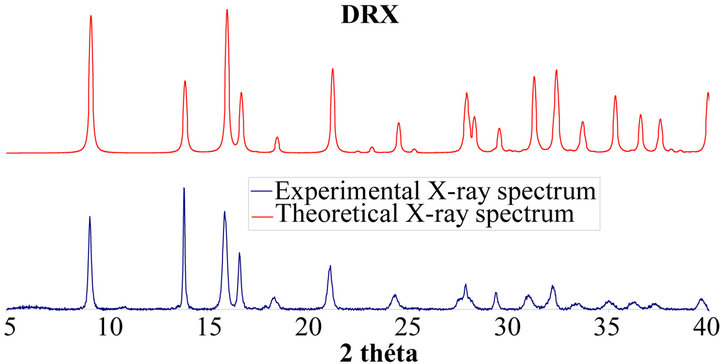
Figure 4. X-ray spectrum of uranium-neodymium oxalates.
ported in Table 1. The first step was to synthesize the two endmembers. Then solubility measurements are performed at room temperature in different vessels to study the dissolution of the co-precipitates as a function of time. When equilibrium is reached, the uranium(IV) and neodymium(III) concentrations are analysed by spectrophotometry and ICP-AES [28]. In his thesis, Costenoble remarked that the solid solutions of uranium-neodymium oxalates are the most probably ideal solid solutions due to their structural similarity, so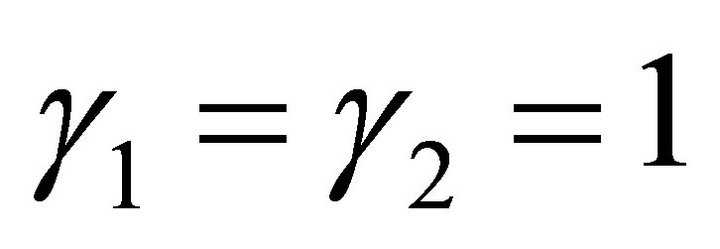 . On the contrary, the activity coefficients in solution were impossible to be determined, as no data are available. For instance, the individual contributions of hydrazinium and oxalic ions are not known for the calculation of activity coefficients according to the Bromley method. From Equations (35) and (36), it can be written:
. On the contrary, the activity coefficients in solution were impossible to be determined, as no data are available. For instance, the individual contributions of hydrazinium and oxalic ions are not known for the calculation of activity coefficients according to the Bromley method. From Equations (35) and (36), it can be written:
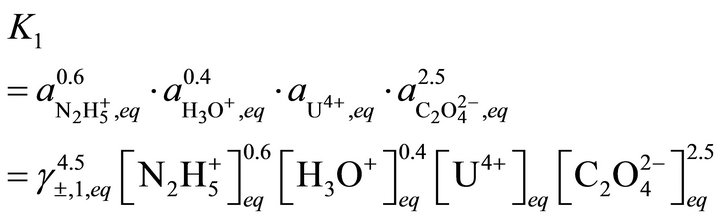 (51)
(51)
 (52)
(52)
Measuring the concentrations of all compounds in solution, Costenoble [24] has determined the values of the solubility apparent constants:
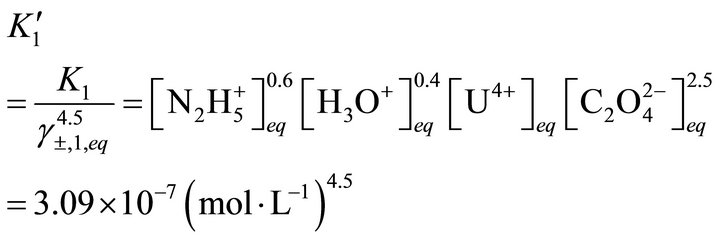 (53)
(53)
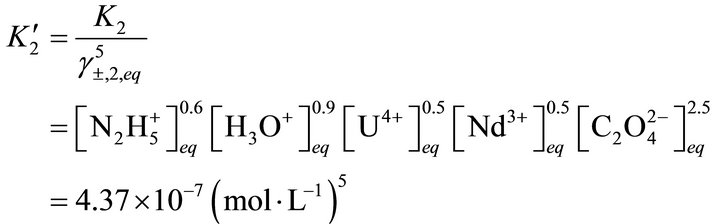 (54)
(54)
where 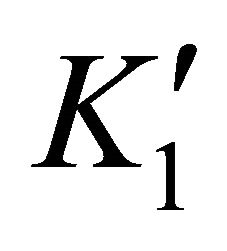 and
and 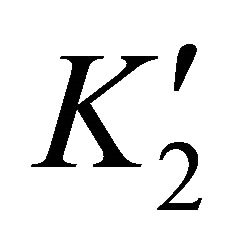 are the solubility apparent constants.
are the solubility apparent constants.
The supersaturation ratio is calculated by Equation
(50) using 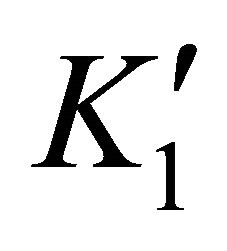 and
and 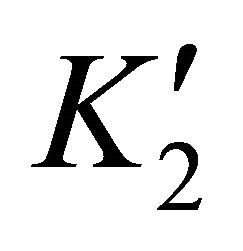 values. In addition, the coprecipitation is performed in concentrated solutions of ions
values. In addition, the coprecipitation is performed in concentrated solutions of ions
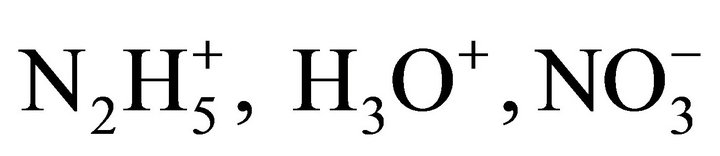 and
and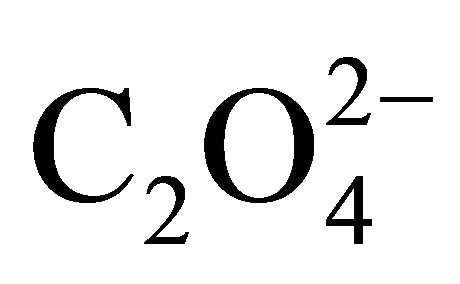 , so the ionic strength remains constant and then the activity coefficients in solution vary slightly during the precipitation process. For this reason, the supersaturation ratio can be calculated assuming
, so the ionic strength remains constant and then the activity coefficients in solution vary slightly during the precipitation process. For this reason, the supersaturation ratio can be calculated assuming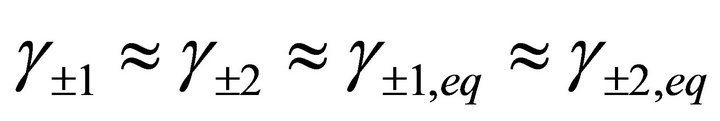 . So the activity coefficients can be simplified in Equation (50).
. So the activity coefficients can be simplified in Equation (50).
4.3. Determination of the Nucleation Kinetics
The primary nucleation kinetics of uranium and neodymium mixed oxalates is studied for different fixed
 ratio in solution (see Table 2) by varying their concentrations, so by varying the supersaturation ratio. In all published papers on this subject, the authors considered the primary nucleation kinetic law of solid solutions using the similar formula as for a single compound [33]:
ratio in solution (see Table 2) by varying their concentrations, so by varying the supersaturation ratio. In all published papers on this subject, the authors considered the primary nucleation kinetic law of solid solutions using the similar formula as for a single compound [33]:
 [33] (55)
[33] (55)
All our experiments proved the validity of this equation. For illustration, the experimental data and Equation
(55) are shown in Figure 5 for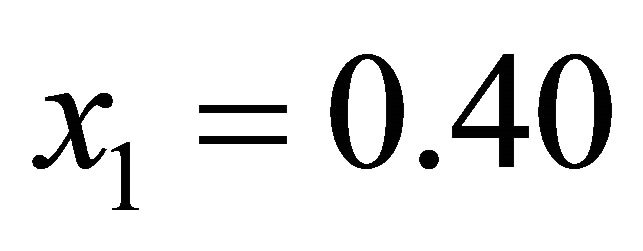 .
.
Using a non-linear regression technique on 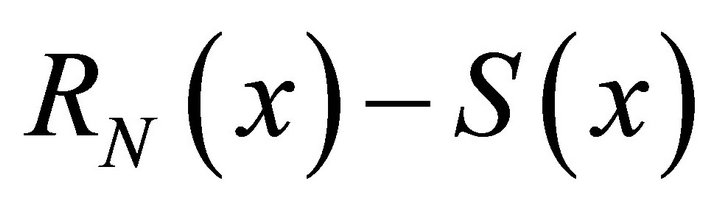 experimental data, it is found:
experimental data, it is found:
—primary homogeneous nucleation kinetics
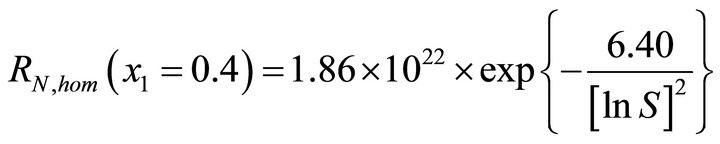 (56)
(56)
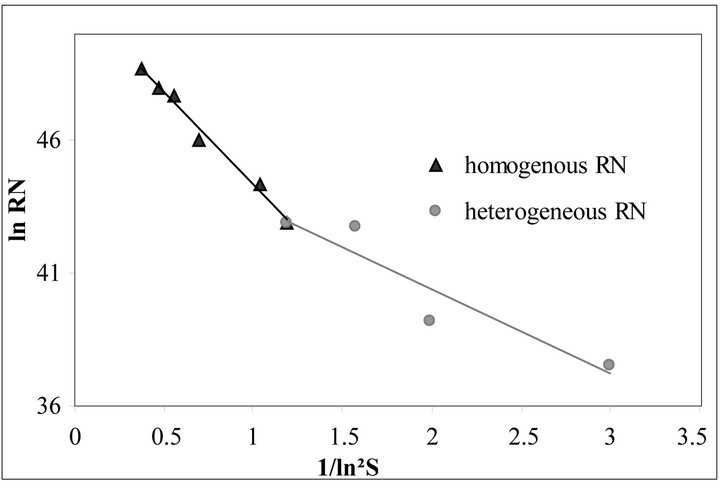
Figure 5. Primary nucleation kinetics for the 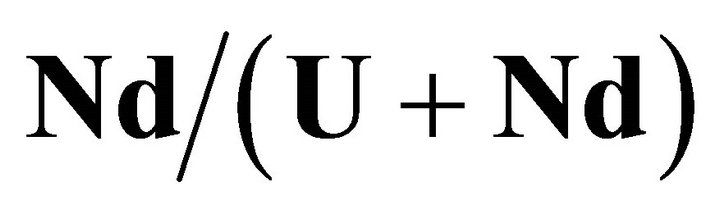 ratio equals to 30%
ratio equals to 30%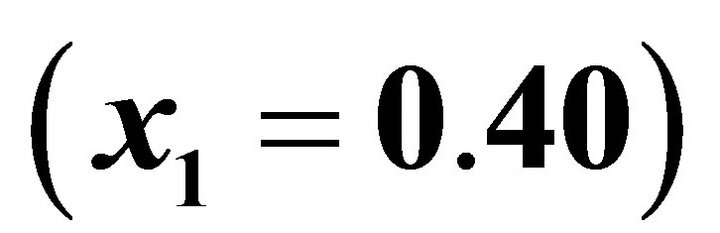 .
.
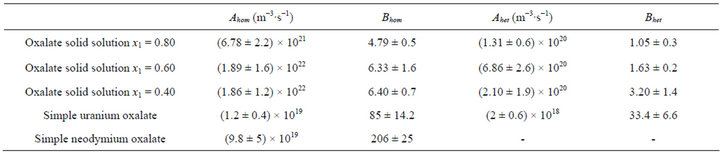
Table 3. Nucleation kinetic parameters for the oxalate solid solutions and the simple oxalates.
—primary heterogeneous nucleation kinetics
 (57)
(57)
The method accuracy is estimated from five identical experimental runs performed under the same operating conditions. According to the Student distribution with a 95% confident level, the measure uncertainty is equal to about 30%, which is acceptable for the nucleation rate measurements. The same methodology is used for the other x1 values and the results are gathered in Table 3.
4.4. Comparison with Simple Oxalates
The results obtained in this study can be compared with the results obtained for the nucleation rates of simple uranium oxalate and of simple neodymium oxalate [31]. The primary heterogeneous nucleation kinetic expression for neodymium oxalate was not determined. The data shown in Table 3 prove that the corresponding pre-exponential factors A are higher, while the exponential coefficients B are lower for solid solutions compared with simple uranium and neodymium oxalates.
Particularly interesting is the fact that the energetic barrier (proportional to B) of solid solutions is much lower than the energetic barrier of simple oxalates. All these data point out that the oxalate solid solutions are kinetically favoured compared with simple oxalates. Generally, it also proves the easiness to obtain the oxalate solid solutions in nuclear industry when oxalic ions are added to a mixture of lanthanide and actinide ions in nitric acid media.
5. Conclusion
This paper describes how to obtain new expressions for the determination of equilibrium relation and supersaturation ratio for any solid solution-aqueous solution (SSAS) system. An adequate nucleation rate expression is proposed in order to study the co-precipitation processes in nuclear industry. This approach is successfully applied to the uranium-neodymium oxalates co-precipitation. The experimental method developed to study the primary nucleation of solid solutions leads to satisfactory results although the expression of supersaturation ratio is complex. The experimental set up is simple and it is easy to carry out experiments, especially in the presence of dangerous and/or expensive elements. From all experimental results, the homogeneous and heterogeneous primary nucleation kinetic laws of solid solutions of uranium(IV)- neodymium(III) oxalate are obtained for different
 ratio
ratio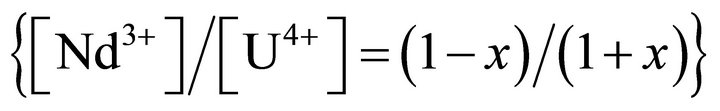 .
.
The values of the kinetic parameters point out that in an aqueous mixture of Nd3+ and U4+, the oxalate solid solutions are kinetically extremely favoured compared with their simple oxalates, which is a very interesting phenomenological result concerning the formation of oxalate solid solutions of lanthanides and actinides during the co-precipitation process. These kinetic results can be combined with a hydrodynamic model in the same way as it is done for the oxalic precipitation of uranium oxalate [34].
6. Acknowledgements
The authors gratefully acknowledge AREVA for its financial support. The authors are also thankful to the Metallographic and Chemical Analysis Laboratory from CEA for the SEM photos and the DRX spectrum.
REFERENCES
- S. Grandjean, A. Beres, J. Rousselle and C. Maillard, Patent No. FR/04510058, 2004.
- B. Arab-Chapelet, S. Grandjean, G. Nowogrocki and F. Abraham, “Synthesis of New Mixed Actinides Oxalates as Precursors of Actinides Oxide Solid Solutions,” Journal of Alloys and Compounds, Vol. 444-445, 2007, pp. 387-390. doi:10.1016/j.jallcom.2007.01.033
- F. Lippmann, “Phase Diagrams Depicting Aqueous Solubility of Binary Mineral Systems,” Neues Jahrbuch für Mineralogie Abhandlungen, Vol. 139, No. 1, 1980, pp. 1-25.
- P. D. Glynn and E. J. Reardon, “Solid-Solution Aqueous-Solution Equilibria—Thermodynamic Theory and Representation,” American Journal of Science, Vol. 290, No. 2, 1990, pp. 164-201. doi:10.2475/ajs.290.2.164
- M. Prieto, A. Putnis and L. Fernandez Diaz, “Crystallization of Solid-Solutions from Aqueous-Solutions in a Porous-Medium—Zoning in (Ba,Sr)SO4,” Geological Magazine, Vol. 130, No. 3, 1993, pp. 289-299.
- H. Gamsjager, E. Konigsberger and W. Preis, “Lippmann Diagrams: Theory and Application to Carbonate Systems,” Aquatic Geochemistry, Vol. 6, No. 2, 2000, pp. 119-132. doi:10.1023/A:1009690502299
- C. M. Pina, M. Enders and A. Putnis, “The Composition of Solid Solutions Crystallising from Aqueous Solutions: The Influence of Supersaturation and Growth Mechanisms,” Chemical Geology, Vol. 168, No. 3, 2000, pp 195-210.
- J. M. Astilleros, C. M. Pina, L. Fernandez Diaz and A. Putnis, “Supersaturation Functions in Binary Solid Solution-Aqueous Solution Systems,” Geochimica et Cosmochimica Acta, Vol. 67, No. 9, 2003, pp. 1601-1608. doi:10.1016/S0016-7037(02)01166-3
- C. M. Pina, A. Putnis and J. M. Astilleros, “The Growth Mechanisms of Solid Solutions Crystallising from Aqueous Solutions,” Chemical Geology, Vol. 204, No. 1-2, 2004, pp. 145-161. doi:10.1016/j.chemgeo.2003.12.002
- A. J. Andara, D. M. Heasman, A. Fernandez Gonzales and M. Prieto, “Characterization and Crystallization of Ba(SO4,SeO4) Solid Solution,” Crystal Growth & Design, Vol. 5, No. 4, 2005, pp. 1371-1378. doi:10.1021/cg0497290
- A. G. Shtukenberg, Y. O. Punin and P. Azimov, “Crystallization Kinetics in Binary Solid Solution-Aqueous Solution Systems,” American Journal of Science, Vol. 306, No. 7, 2006, pp. 553-574. doi:10.2475/07.2006.03
- J. M. Astilleros, C. M. Pina, L. Fernandez Diaz, M. Prieto and A. Putnis, “Nanoscale Phenomena during the Growth of Solid Solutions on Calcite {101-4} Surfaces,” Chemical Geology, Vol. 225, No. 3-4, 2006, pp. 322-335. doi:10.1016/j.chemgeo.2005.08.025
- C. A. YuHang, Asenjo, N. Sanchez Pastor, L. Fernandez Diaz, J. Gomez and C. M. Pina, “Growth of BaxSr1-xSO4 Nano-Steps on Barite (0 0 1) Face,” Surface Science, Vol. 601, No. 2, 2007, pp. 381-389.
- M. A. Prieto, F. Gonzalez, A. Putnis and L. F. Diaz, “Nucleation, Growth, and Zoning Phenomena in Crystallizing (Ba, Sr)CO3, Ba(SO4, CrO4), (Ba, Sr)SO4, and (Cd, Ca)CO3 Solid Solutions from Aqueous Solutions,” Geochimica Cosmochimica Acta, Vol. 61, No. 16, 1997, pp. 3383-3397. doi:10.1016/S0016-7037(97)00160-9
- C. Noguera, B. Fritz, A. Clement and Y. Amal, “Simulation of the Nucleation and Growth of Binary Solid Solutions in Aqueous Solutions,” Chemical Geology, Vol. 269, No. 1-2, 2010, pp. 89-99. doi:10.1016/j.chemgeo.2009.05.025
- A. G. Shtukenberg, Y. O. Punin and P. Azimov, “Reply to Comment: Supersaturation in Binary Solid Solution— Aqueous Solution Systems by M. Prieto, J. M. Astilleros, C. M. Pina, L. Fernandez-Diaz and A. Putnis,” American Journal of Science, Vol. 307, No. 7, 2007, pp. 1046-1050. doi:10.2475/07.2007.05
- M. Prieto, J. M. Astilleros, C. M. Pina, L. Fernandez Diaz and A. Putnis, “Comment: Supersaturation in Binary Solid Solution-Aqueous Solution Systems,” American Journal of Science, Vol. 307, No. 7, 2007, pp. 1034-1045. doi:10.2475/07.2007.04
- D. C. Thorstenson and L. N. Plummer, “Equilibrium Criteria for 2-Component Solids Reacting with Fixed Composition in an Aqueous Phase Example—Magnesian Calcites,” American Journal of Science, Vol. 277, No. 9, 1977, pp.1203-1223. doi:10.2475/ajs.277.9.1203
- C. M. Pina and A. Putnis, “The Kinetics of Nucleation of Solid Solutions from Aqueous Solutions: A New Model for Calculating Non-Equilibrium Distribution Coefficients,” Geochimica and Cosmochimica Acta, Vol. 66, No. 2, 2002, pp. 185-192. doi:10.1016/S0016-7037(01)00770-0
- A. Putnis, C. M. Pina, J. M. Astilleros, L. Fernandez Diaz and M. Prieto, “Nucleation of Solid Solutions Crystallizing from Aqueous Solutions,” Philosophical Transactions of the Royal Society of London Series A—Mathematical Physical and Engineering Sciences, Vol. 361, No. 1804, 2003, pp 615-631.
- V. Pacary, Y. Barre and E. Plasari, “Modeling and Comparison of Continuous and Semicontinuous Process for Simulating Decontamination of Liquid Nuclear Wastes by Coprecipitation of Strontium Ions with Barium Sulphate,” International Journal of Chemical Reactor Engineering, Vol. 6, No. A32, 2008.
- B. Chapelet-Arab, G. Nowogrocki, F. Abraham and S. Grandjean, “U(IV)/Ln(III) Unexpected Mixed Site in Polymetallic Oxalato Complexes. Part I. Substitution of Ln(III) for U(IV) from the New Oxalate (NH4)2U2(C2O4)5·0.7H2O,” Journal of Solid State Chemistry, Vol. 178, No. 10, 2005, pp. 3046-3054. doi:10.1016/j.jssc.2005.06.031
- B. Arab-Chapelet, S. Grandjean, G. Nowogrocki and F. Abraham, “Synthesis and Characterization of Mixed An(IV) An(III) Oxalates (An(IV) = Th, Np, U or Pu and An(III) = Pu or Am),” Journal of Nuclear Materials, Vol. 373, No. 1-3, 2008, pp. 259-268. doi:10.1016/j.jnucmat.2007.06.004
- S. Costenoble, “Modélisation de la Coprécipitation d’Oxalates Mixtes d’Uranium et de Plutonium Dans le Cadre du Recyclage du Combustible Nucléaire: Solubilité des Solutions Solides Oxalate,” Ph.D. Thesis, Lille Sciences and Technologies University, Lille, 2009.
- A. Putnis, M. Prieto and L. Fernandez Diaz, “Fluid Supersaturation and Crystallization in Porous-Media,” Geological Magazine, Vol. 132, No. 1, 1995, pp. 1-13. doi:10.1017/S0016756800011389
- D. Parmentier, M. Bertrand and E. Plasari, “Discussion sur l’Expression de la Sursaturation au Cours de la Coprécipitation d’Oxalates d’Actinides,” Proceedings of Cristal 6, Marseille, 2010.
- B. Chapelet-Arab, G. Nowogrocki, F. Abraham and S. Grandjean, “U(IV)/LN(III) Unexpected Mixed Site in Polymetallic Oxalato Complexes. Part II. Substitution of U(IV) for Ln(III) in the New Oxalates (N2H5)Ln(C2O4)2·nH2O (Ln = Nd, Gd),” Journal of Solid State Chemistry, Vol. 178, No. 10, 2005, pp. 3055-3065. doi:10.1016/j.jssc.2005.06.032
- S. Costenoble, S. Grandjean, P. Pochin, S. Picart and F. Abraham, “Determination and Modelling of the Solubility of Mixed Actinide(IV)-actinide(III) oxalates (An(IV) = U, Np, Pu and An(III) = Pu, Am),” Proceedings of Thermodynamics, London, 23-25 September 2009.
- M. Bertrand, P. Baron, E. Plasari and R. Lorrain, Patent No. EN 04/50637, 2004
- M. Bertrand, E. Plasari and P. Baron, “Methods for Characterization and Comparison of Mixing Efficiency of Different Confined Opposing Jet Mixing Devices,” Proceedings of the 12th European Conference on Mixing, Bologne, 2006.
- M. Bertrand-Andrieu, E. Plasari and P. Baron, “Determination of Nucleation and Crystal Growth Kinetics in Hostile Environment—Application to the Tetravalent Uranium Oxalate U(C2O4)2·6H2O,” Canadian Journal of Chemical Engineering, Vol. 82, No.5, 2004, pp. 930-938. doi:10.1002/cjce.5450820508
- A. E Nielsen, “Nucleation and Growth of Crystals at High Supersaturation,” Kristall und Technik, Vol. 4, No. 1, 1969, pp. 17-38. doi:10.1002/crat.19690040105
- M. Volmer and A. Weber, “Keimbildung in Tibersätting Gebilden,” Zeitschrift für physikalisch Chemie, Vol. 119, 1926, pp. 277-301.
- M. Bertrand, E. Plasari, O. Lebaigue, P. Baron, N. Lamarque and F. Ducros, “Hybrid LES-Multizonal Modelling of the Uranium Oxalate Precipitation,” Chemical Engineering Science, Vol. 77, 2012, pp 75-104. doi:10.1016/j.ces.2012.03.019
Nomenclature
ai: activity of ions in the aqueous solution, mol·m−3
aBA: activity of BA in the solid solution A: pre-exponential kinetic parameter, m−3·s−1
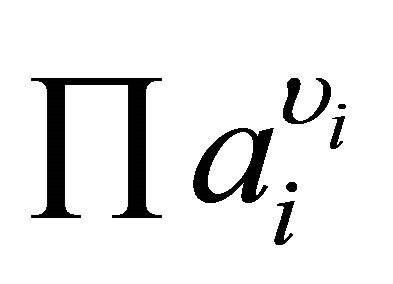 : product of the ionic activity, mol·m−3
: product of the ionic activity, mol·m−3
B: kinetic parameter Ci: [i] concentration of ions i, mol·m−3
KBA: solubility product of BA Ks: solubility product for simple salts
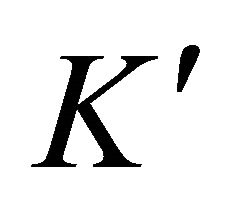 : solubility apparent constant
: solubility apparent constant
 : total solubility product
: total solubility product
 : total solubility term ?
: total solubility term ?
Pi: partial vapour pressure, Pa Peq: total vapour pressure of the liquid mixture, Pa RN: nucleation rate, m−3·s−1
s: absolute supersaturation ?
S: supersaturation ratio x: mole fraction in the liquid phase X: mole fraction in the solid phase
Greek letters
γ±: mean activity coefficient in the liquid phase
γ: solid phase activity coefficients
υi: stoechiometric number of ion i
Subscripts
1: endmember BA
2: endmember CA
eq: at equilibrium
het: heterogenous
hom: homogeneous

