ABSTRACT

In copper sulfide concentrates smelting, the off-gases from the Pierce Smith converter (PSC) furnace must be treated to prevent environmental impacts as they are highly corrosive and toxic. The purpose of this research project is to present a methodology for the simulation of a capture and cooling system of the smelting off-gases from a Pierce Smith copper converter, using computational fluid dynamics. Through this methodology, it is possible to obtain a simulation model of the smelting off-gases behavior with an average error of 9.88%. Basically, it demonstrates that the simulated tendencies of the metallurgical off-gases on the cooling hood and chamber can be reliable to predict the thermo-fluid dynamic behavior of the off-gases inside the studied off-gases handling system.

Keywords:

Capture Hood, Radiant Cooling System, Copper Sulfide Smelting Off-Gases, Computational Fluid Dynamics (CFD) Simulation

1. Introduction

Copper should be 99.99% pure to be commercialized. However, the copper percentage (grade) present on mines is usually around 1% and thus, the mineral must be treated in multistage processes, in order to reach the required purity to be placed on the market [1] . Regarding copper sulfide ores, once the rock is extracted from the mine, it is transported to a concentration plant, where it undergoes grinding and crushing. Subsequently, it is concentrated by flotation. Concentrate from the plant contains about 30% - 35% copper. Later, the concentrate is screened and sent to smelting to continue the process.

During smelting, the concentrate is melted and converted in a Teniente converter, in this case, and later, in a Pierce Smith converter [2] . This equipment operates at high temperatures to melt the concentrate and a great amount of gases is emanated during this process.

Some of the main chemical reactions occurring during copper sulfide conversion are described in equations (1) and (2). These equations also show the composition of the smelting off-gases emanated from the converters. [1] :

(1)

(2)

The main component of the off-gas emanated in the conversion of copper concentrates is SO₂. Additionally, during the industrial process, this off-gas is composed of variable parts of acid mist, H₂O, arsenic, selenium, among others, which are captured and sent to the off-gases handling system. In this step, the off-gas is conditioned and sent to the gas cleaning plant (GCP) to remove dust, acid mist and other impurities. The result is a gas containing high levels of SO₂, which is converted to SO₃. Finally, this compound reacts with water to produce H₂SO₄ [3] .

The off-gases handling process line is composed by many machines, where gases pass before reaching the gas cleaning plant. These machines carry out critical functions, e.g., capture, cooling and primary cleaning of suspended particulate matter in the gas. Each function must satisfy specific conditions to allow a correct operation of the off-gases handling system and the following processes in the off-gas handling line, mainly in the gas cleaning plant.

This project develops a new simulation methodology using computational fluid dynamics of heat transfer phenomena associated to the fluid-dynamics of the off-gas capture hood and radiant cooling system. Other studies have not performed simulations of an off-gas treatment comparable to the case analyzed in this research, so the simulation is original, both in its development and in the compilation of records for validation. This enables a better understanding of the phenomena involved in this process and their interactions.

2. Methodology

This project focuses on computational modeling and simulation from a thermo-fluid dynamics point of view. Both processes include heat transfer phenomena in two of the main components of the off-gases handling system on the PSC line in the Caletones Smelter in Chile. The off-gases capture hood [4] and the radiant cooler [5] , which are the first section of the system, are the equipment analyzed.

The studied off-gases handling system begins with the capture of the off-gases emanated from the PSC to the off-gas hood situated over this converter. The hood catches and cools the off-gases that enter it, due to pressure differences originated by induced draft fans located downstream from the system [5] . The first cooling step [6] occurs in the off-gas hood owing to, mainly, gas dilution in air at ambient temperature (average of 25˚C) and its combination with gas from the smelting process in the converter, where a temperature drop from 1200˚C to 600˚C, approximately, is estimated.

After the off-gas is caught and diluted, it goes through the radiant cooling chamber. In this type of chamber, the infiltrated off-gases flow enters, circulates and creates a heat transfer phenomenon by radiation and convection, inside and outside the chamber. The off-gas flow transfers heat to the chamber steel walls and there, the heat flow is transferred by conduction. Finally, another transfer takes place between the chamber walls and the environment by radiation and convection. In this case, the off-gases temperature descends as they go through four radiant tubes. A summary of this is shown in Figure 1.

Reaching a temperature near 350˚C is an important operating parameter, as it is the required temperature for operation in the next step, which consists in off-gas cleaning with an electrostatic precipitator.

This project develops a computational modeling and simulation of the off-gases path through this equipment with an ANSYS CFX program.

The model is based on key assumptions listed below:

Equipment discretization is achieved considering the smelter structural plans.

The model will be done considering species, based on metallurgical off-gas generation.

Gases behave as ideal gases.

Flow is in stable state.

The environmental conditions considered will be: 81,060 Pascal at 25˚C (temperature around smelting vessels).

The steps to achieve the simulation can be summarized as follows:

1) Creation of the three-dimensional geometry of the capture hood and the radiant cooling system;

2) Geometry meshing;

3) Boundary conditions definition;

4) Simulation;

5) Results validation.

Computational fluid dynamics is a tool for the solution of transport equations in each control volume for a volumetric discretization of the domain [5] .

The number of transport equations that must be solved depends on the quantity of models required to describe the fluid dynamics of the problem [7] .

A species or multi-component modeling [8] is chosen to model the off-gas mixture behavior in the converter mouth as it is orientated to gases that have molecular interaction. All of the calculated variables are weighed by the mass fraction of each component.

It is acceptable to assume that the species transport modeling does not allow chemical reactions as the SO₂ percentage transformed to SO₃ is less than 3%, in this case.

The turbulence model used in this project is called “Shear Stress Model” (SST). This model mixes k-omega strength and precision effectively, near the walls with the k-epsilon model, which is the appropriate model in spaces away from the wall [5] .

2.1. Radiant cooling System Modeling

The off-gases captured by the hood are sent to a cooling system which consists of four radiant tubes, where the heat loss results in cooling by radiation and convection between these four tubes.

The off-gases continue their way through these u-shaped tubes which are 1.5 meters in diameter and 20 meters long. Here, an important amount of heat has been already lost.

In these areas, a temperature of 390˚C to 350˚C is expected as well as an infiltration of 5% (depending on the model).

A 3D modeling of the real geometry of the equipment was made to effectuate the analysis, as shown in Figure 2. This geometry was obtained from existing plans in the smelting facility.

The SO₂ dilution grade can be measured with the simulation. The dilution occurs due to ambient air that enters through the radial space between the converter and the hood. This air is simulated with a control volume represented by a “box”, which dimensions are chosen minding an insignificant pressure gradient in the box walls.

A boundary condition will be the entering data to solve the proposed mathematical model. Some data were measured directly in the gas cooling system and others were measured in previous studies [9] .

The geometrical model in 3D of the gas cooling system incorporated in CFX 14.5 [8] is shown in Figure 3. It also stands out with colors the different zones where boundary conditions were established.

The established boundary conditions in the model are explained in detail below:

2.2. Inlet

The metallurgical off-gas starting point will be in the centre of the converter. Thus, it can be assumed that smelted copper fills just half of the converter. This condition explains why just the upper part of the converter is included in the modeling.

The composition of the metallurgical off-gases from the Pierce Smith converter is shown in Table 1.

This off-gas exits the converter at 1250˚C with a mass flow of 22.9 kg/s. Chemical reactions are not considered in the modeling and the gases are considered as species.

2.2.1. Environment

Environment will be the space around the converter and part of the cooling hood. The main objective of an ambient air modeling is to obtain infiltration air from that environment. The boundary condition type used in this case is “opening”, at 25˚C and with a relative pressure of 101,325 [Pa] (reference pressure is identical to the at

mospheric pressure).

Mass fractions for environmental conditions are shown in Table 2.

An opening type condition is allocated to this boundary condition and “artificial walls” are created in the boundaries, allowing the fluid to get in and out of the box without restrictions.

It is worth mentioning that data in input and environmental boundary conditions were measured in the smelter.

2.2.2. Cooling system walls

Wall condition will be the side of the steel plates that are in contact with the fluid. This includes pre-chamber, radiant tubes, chamber and outlet. Zones are shown in Table 2 and a boundary conditions summary is shown in Table 3.

Temperatures in Table 3 were obtained from thermographies [10] [11] Figure 4, and an energy balance was effectuated in the walls, as shown in equation (3)

(3)

h_ev: Heat transfer coefficient [W/m²×K]

k: Fluid Thermal conductivity [W/m×K]

ε: Emissivity

σ: Stefan-Boltzmann constant [W/m²×K⁴]

A: Heat transfer surface [m²]

T₁: Wall temperature in contact with the off-gases [K]

T₂: Wall temperature in contact with the environment [K]

T_amb: Environment temperature [K]

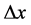: Wall thickness [m]

Condition 1 is the wall in contact with the gases and condition 2 is the wall in contact with the environment.

2.2.3. Outlet

Outlet will be at a pressure of −360 [Pa]. This pressure is an average number for a normal day of the cooling system operation.

A mesh sensibility analysis was done out to define the mesh. This analysis consisted in various simulations with identical configurations and different meshes. Each simulation used a thinner mesh until no difference was found in the results.

The mesh used for the computational fluid dynamics simulation is shown in Figure 5. The mesh was refined at the walls, in order that the maximum distance from the node to the wall would be about 1 mm. The final mesh has 1,293,987 nodes and 4,074,285 elements.

One of the main modeling parameters to be considered is related to the quality of the mesh used in the simulation [12] [13] . In this project, orthogonal quality and skewness are considered as criteria. The results are shown in Table 4.

Reference standard quality criteria for the orthogonal parameter are 0.2 minimum for a good quality meshing and 1 for an excellent quality meshing.

As for skewness quality, 0.5 is a minimum for good quality and 0 for excellent quality.

The simulation was carried out considering a stable modeling. Convergence criteria for continuity equations, momentum quantity and energy correspond to residual stabilization, with results under 1.0 × 10⁻³. This number is reached above 10,000 time steps.

3. Results

The simulation results from the PCS metallurgical off-gas cooling system is shown below. Important operational characteristics can be graphically observed, for example, velocity streamlines (Figure 6), temperature contours (Figure 7) and identification of zones in the environment, where a greater amount of heat is lost. In addition to the simulations, measurements were made in the area using equipment situated in the system. Isokinetic measurements were also carried out, which will be used later to validate the modeling.

Converter off-gas velocity streamlines are shown in Figure 6. These gases enter the cooling system, which allows the identification of the flow orientations. Here, it is possible to observe the behavior of the interior flow

and to distinguish flow recirculation zones and the characteristics of the off-gases flow. These characteristics include velocity distributions, which registered a maximum velocity of 37 m/s and a minimum of around 4 m/s.

The vorticity of the flow can be observed as it moves forward through the cooling system, creating preferential flow zones, which are located in the central tubes. These vorticity zones are located in the cooler chambers, specifically in the cooler outlet chamber. This phenomenon is exactly what was expected and it is attributed, mainly, to the convergence effect that off-gases have due to the cooler outlet tube geometry.

The temperature drop and its contours generated in the PSC cooling system are shown in Figure 7(a). Basically, it shows a cross section for the whole control volume studied along with the temperatures behavior.

Heat flux contours and the zone with greater heat exchange can be observed in Figure 7(b). This data is organized in Table 5 and it shows the different zones and their heat exchange with the environment.

The temperature profile that the gases have as they exit the cooling system is shown in Figure 7(c). This profile presents a temperature between 340˚C to 348˚C, approximately.

In Figure 7(d), an interesting phenomenon can be observed. The central tubes not only present higher flow velocities, but also higher temperatures, which can reach around 60˚C. This temperature is higher in central tubes in comparison with lateral tubes.

Data were obtained using measurement equipment with an empirical focus, during three days of operation with a one-minute interval: February 12, 13, and 14, 2013.

Three temperature sensors were used in this project. The first one is called PT-56605A, and it is located in the tubes inlet. The other two are called PT-56609A and PT-56609B. They operate in parallel in the cooler outlet as shown in Figure 7 and Figure 8 [14] . The PT-56605A sensor in the pre-chamber is shown in Figure 8.

The pressure under normal operating conditions is 6 [Pa], as it was the higher frequency of static pressure as shown in Figure 9(b)).

Additionally, two pressure sensors called PT-56609A and PT-56609B were used. These sensors are located in the cooling chamber, as shown in Figure 10.

As done with the pre-chamber sensor, the operation of the equipment under normal conditions was registered during three days, as shown in Figure 11.

It can be inferred from the chart that the 56-PIT-56609A sensor has more observations around −105 [Pa], whereas the 56-PIT-56609B sensor has more, mainly, in −107 [Pa].

The isokinetic measuring allowed to register the percentage of ambient air infiltration in the infiltration hood. This percentage is about 113%, approximately.

It is difficult to use equipment to validate the CFD modeling for the smelting off-gases cooler due to high

temperatures, accretions and high levels of corrosion inside the system. Therefore, a limited number of instruments can measure the conditions.

Another strategy to validate this equipment consists in isokinetic samples obtained with methodology N˚8 of the EPA [15] . This information allows the comparison of measured infiltrations with infiltrations calculated in the simulation.

According to the PT-56605A sensor, the highest frequency is 6 [Pa], whereas the simulation results obtained at the instrumental measuring point is 6.56 [Pa], approximately. Considering the tendency obtained from the measuring sensor, the simulation average error is 10%, in this point.

The points which represent each sensor were monitored with the simulation. The 56-PIT-56609A sensor presented −91.8322 [Pa] and the 56-PIT-56609B sensor, −114.644 [Pa], compared to measurements corresponding to −105 [Pa] and −107 [Pa], respectively. The percentage of error estimated for the 56-PIT-56609A sensor is 12.5% and 8% for the 56-PIT-56609B sensor.

The isokinetic measuring report determined an infiltration percentage of 113%, in the area. Approximately, 102% of infiltration was obtained with the simulation. If the number obtained in the measuring is considered as the real one, the error when determining the infiltration percentage is around 9%.

4. Discussion and Conclusions

It is possible to deduce from the simulation that turbulent phenomena happen where the sensors are located. Additionally, they operate under discontinuous rules. However, it is possible to consider the sensor measurements as a good approximation, guaranteed by smelting operational results. Considering the equipment measurements as correct, the simulation methodology represents the process correctly, with an average error of 9.88.

The simulation shows that a 51% of heat dissipation is in the off-gases capture hood zones. This percentage is the highest in the process, due to a great amount of ambient air infiltrated in that zone. The air is mixed with metallurgical off-gases from the Pierce Smith converter.

The temperature range in the outlet tube is between 340˚C and 348˚C. These temperatures adjust to the operational temperature of the next equipment in the process line, which is an electrostatic precipitator. It is interesting to observe that the temperature loss is mainly due to infiltration gases, which are not controlled by the cooling equipment itself, but by the flow that the network is capable of absorb from the environment.

The amount of heat emitted by radiation is 2.28 MW in the radiant tubes. This means 65% of the heat is transferred by the cooler due to radiation, mainly because there is a bigger area of heat transfer.

This large amount of dissipated energy suggests the possible implementation of energy cogeneration systems, from the dissipated heat.

As conclusions computational fluid dynamics allows the generation of representative modeling and simulation of the off-gases cooling and capturing process in the Pierce Smith copper converter. It is possible to observe flow velocities, electricity lines, vortex formation zones, pressure, temperature and heat fluxes.

Differences of, approximately, 9.88% of error are obtained when comparing the outcome obtained from the simulations with the data registered by the different sensors and also, with the infiltration characterized in the isokinetic measurements. This percentage is acceptable for this type of simulations.

Mainly, this means that the simulated tendencies of the metallurgical off-gases behavior on the radiant cooling hood and chamber are reliable to predict the thermo-fluid dynamic behavior of off-gases. Additionally, the tendencies can be used to improve the equipment and the processes.

Acknowledgements

This project was conducted with support from Universidad de Santiago de Chile, Facultad de Ingeniería; Codelco Chile, División El Teniente, Fundición Caletones; Conicyt Chile, Programa formación de capital humano avanzado, Becas de Doctorados Nacionales, Departamento de Ingeniería en Minas from Universidad de Santiago de Chile; Departamento de Ingeniería en Minas from Universidad de Santiago de Chile.

Cite this paper

Yerko Aguilera-Carvajal,Sebastián Pérez-Cortés,Juan Hurtado-Cruz,Erick Morales-Quezada, (2014) Computational Thermo-Fluid Dynamic Simulation of a Radiant Off-Gases Cooling System for Copper Smelting in a Pierce Smith Converter. International Journal of Modern Nonlinear Theory and Application,03,236-247. doi: 10.4236/ijmnta.2014.35026

References