International Journal of Modern Nonlinear Theory and Application
Vol.3 No.3(2014), Article ID:47872,11 pages
DOI:10.4236/ijmnta.2014.33013
Improvement of Power System Stability by Static Var Compensator and Tuning Employing Genetic Algorithm
Salma Keskes, Wissem Bahloul, Mohamed Ben Ali Kammoun
Commande des Machines Electriques et Reseaux de Puissance (CMERP), National Engineering School of Sfax, Sfax, Tunisia
Email: salmakeskes@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 May 2014; revised 26 June 2014; accepted 10 July 2014
ABSTRACT
The use of power systems as close to their operating limits can cause instability if a disturbance is occurred. The damping of the system’s oscillations can be obtained by conventional means such as voltage and speed regulation but also by Flexible AC Transmission System devices (FACTS). These devices are increasingly used in power systems. This paper presents a systematic procedure for modelling and simulation of a single-machine infinite-bus power system installed with a Static VAR Compensator (SVC). So the impact of the SVC on power system stability can be reasonably evaluated. Genetic algorithm (GA) optimization technique is applied to design robust power system stabilizer and SVC-controllers for single-machine infinite-bus (SMIB) and is employed to search for optimal controller parameters.
Keywords:Genetic Algorithm, MATLAB/SIMULINK, Power System Stabilizer, SVC-Controller, SMIB, Transient Stability

1. Introduction
Over the past two decades, power system is being operated nearer to their stability limits due to the economic and environmental reasons.
The small signal stability of power systems, especially the damping of inter-area oscillations, has become, therefore a priority [1] .
One of the main techniques employed to improve transient stability, and voltage regulation of generators consists of using power system stabilizer (PSS) that provides a maximum damping of electromechanical local modes.
Recently, there has been a surge of interest in the development and use of FACTS controllers in power transmission systems [2] [6] [11] .
These controllers utilize power electronics devices to provide more flexibility to AC power systems. The most popular type of FACTS devices in terms of application is the SVC [4] . This device is well known to improve power system properties such as steady state stability limits, voltage regulation, and damp power system oscillations [3] . The SVC is an electronic generator that dynamically controls the flow of power through a variable reactive admittance to the transmission network.
In this paper, a systematic procedure for modeling, simulation and optimal tuning of PSS and SVC-controller in a SMIB power system was presented where the MATLAB/SIMULINK based model was developed and genetic algorithm (GA) was employed to design the PSS and SVC-based controller.
The design problem of PSS and SVC based controller to improve power system stability is transformed into an optimization problem. The design objective is to improve the stability of a SMIB power system by SVC and provide efficient damping of low frequency oscillations, subjected to a disturbance.
The merits of this study are summarized as follows:
In Section 2, the modeling of power system under study, which is a SMIB power system with a PSS and Static Var Compensator (SVC), is presented. The proposed controller structure is described in this section.
In Section 3, problem formulation and a short overview of GA are presented. In Section 4, we simulate the power system to illustrate the effectiveness of the proposed approach and the role of SVC to improve transient stability. Also, we compare the results with those obtained when the stability is ensured only with PSS summarizes the results. Section 5 draws the conclusion.
2. System Modelling
2.1. Generator Model
The power system is represented by a single-machine-infinite-bus (SMIB) shown in Figure 1.
The complete dynamic model of alternator is 7th order.
As this model is complicated, a validated third order dynamic generator model is adopted [3] .
The power system can be modeled by a set of nonlinear differential equations are as follows:
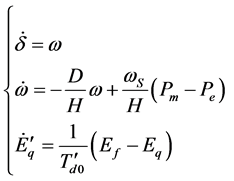 , (1)
, (1)
 (2)
(2)
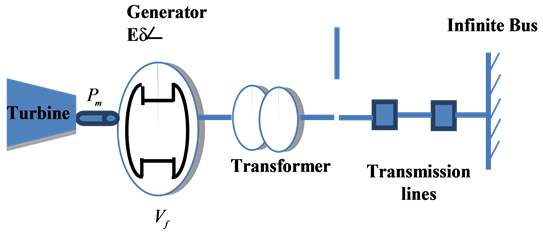
Figure 1. Single machine infinite bus.
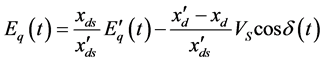 (3)
(3)
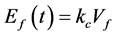 (4)
(4)
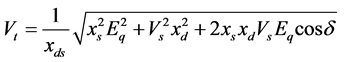 (5)
(5)
where
 (6)
(6)
The generator is equipped with PSS (Power System Stabilizer) which are used in conjunction with Automatic Voltage Regulators (AVR) to damp out the oscillations.
2.2. Structure of Power System Stabilizer
The operating function of a PSS is to produce a proper torque on the rotor of the
machine involved in such a way that the phase lag between the exciter input and
the machine electrical torque is compensated. The supplementary stabilizing signal
considered is one proportional to speed. The structure consists of a gain block
with gain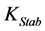 , a signal washout block and stage phase compensation
block as shown in Figure 2.
, a signal washout block and stage phase compensation
block as shown in Figure 2.
The input signal of the proposed controller is the speed deviation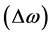 , and the output is the stabilizing signal
, and the output is the stabilizing signal
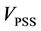 which is added to the reference excitation system voltage. The signal washout block
serves as a high-pass filter, with the time constant
which is added to the reference excitation system voltage. The signal washout block
serves as a high-pass filter, with the time constant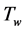 , high enough to allow signals associated with
oscillations in input signal to pass unchanged. From the viewpoint of the washout
function, the value of
, high enough to allow signals associated with
oscillations in input signal to pass unchanged. From the viewpoint of the washout
function, the value of
 is not critical and may be in the range of 1 to 20 seconds. The phase compensation
block (time constants
is not critical and may be in the range of 1 to 20 seconds. The phase compensation
block (time constants ,
,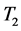 ) provides the appropriate phase-lead characteristics
to compensate for the phase lag between input and the output signals.
) provides the appropriate phase-lead characteristics
to compensate for the phase lag between input and the output signals.
The block diagram of the PSS with excitation system is shown in this figure.
2.3. SVC Modeling and Damping Controller Design
The SVC is a shunt FACTS and an important reactive compensation device. It is placed at the middle of the transmission line as shown in Figure 3.
SVC regulates the voltage at its terminals by controlling the amount of reactive power injected into, or absorbed from the power system.
When the system voltage is low, SVC generates reactive power (capacitive mode) and when the voltage is high, it absorbs reactive power (inductive mode).

Figure 2. Bloc diagramm of PSS.

Figure 3. Structure of the SVC.
Thus, the main benefit of the SVC for transient stability enhancement is direct and rapid bus voltage control.
The idea is to have an adjustable device impedance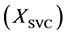 , it consists of Thyristor Switched Capacitor (TSC)
and Thyristor Controlled Reactors (TCR) as shown in Figure
4 [5] -[9]
. The SVC can be defined than, as a controlled susceptance (inverse of the impedance)
called
, it consists of Thyristor Switched Capacitor (TSC)
and Thyristor Controlled Reactors (TCR) as shown in Figure
4 [5] -[9]
. The SVC can be defined than, as a controlled susceptance (inverse of the impedance)
called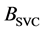 .
.
Where
 bus bar voltage,
bus bar voltage,
 is the fundamental-frequency reactance of the reactor,
is the fundamental-frequency reactance of the reactor,
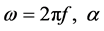 is the gating delay angle and
is the gating delay angle and
 is the conduction angle:
is the conduction angle: .
.
The fundamental component of the instantaneous current
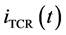 is given by is found by Fourier analysis:
is given by is found by Fourier analysis:
 (7)
(7)
The relationship between the firing angle
 and the steady state value of
and the steady state value of
 is given as follows:
is given as follows:
 (8)
(8)
The equivalent susceptance of the SVC,
 , is given by
, is given by
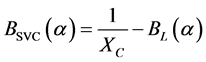 (9)
(9)
The major role of static VAC compensator is adjusting the voltage at its terminals. SVS is usually modeled by the block diagram shown in Figure 5.
The main controller of the tension can be proportional, integral or a combination of both actions.
The SVC dynamic regulator can be written as follows:
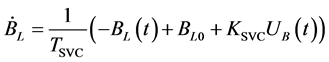 (10)
(10)
where
 is the susceptance of the inductor in SVC;
is the susceptance of the inductor in SVC;
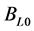 is the initial susceptance of the TCR;
is the initial susceptance of the TCR;
 the time constant of the SVC regulator,
the time constant of the SVC regulator,
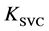 the gain of the SVC regulator and
the gain of the SVC regulator and
 is the input of the SVC regulator.
is the input of the SVC regulator.
The mathematical model of SMIB system with SVC on the transmission line may be presented by the classic third order model as given by Equation (1) and the SVC model represented by the fourth one [10] :
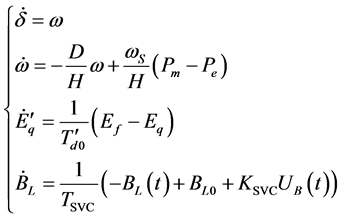 (11)
(11)
The electric equations for the equation the SMIB-SVC are:
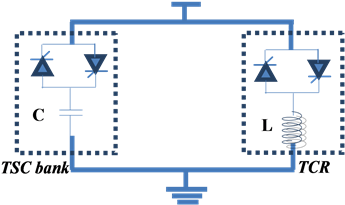
Figure 4. Single machine system with SVC.

Figure 5. Block diagram of the SVC controller.
 (12)
(12)
3. Problem Formulation
In the present study, a washout time constant of
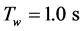 is used.
is used.
The stabilizer gains
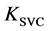 and
and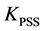 , and time constants
, and time constants ,
,
 and
and
 are remained to be determined.
are remained to be determined.
The parameters of the PSS and SVC are optimized using integral of time multiplied absolute value of the error (ITAE) as objective function:
 (13)
(13)
where
 denotes the speed deviation of SMIB system generator tsim is the time
range of the simulation.
denotes the speed deviation of SMIB system generator tsim is the time
range of the simulation.
Based on the objective function J optimization problem can be stated as:
Minimize J
subjected to:
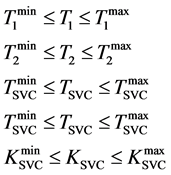
3.1. Overview of Genetic Algorithm (GA)
The genetic algorithm (GA) has been used to solve difficult engineering problems that are complex and difficult to solve by conventional optimization methods. GA maintains and manipulates a population of solutions and implements a survival of the fittest strategy in their search for better solutions. The fittest individuals of any population tend to reproduce and survive to the next generation thus improving successive generations. The inferior individuals can also survive and reproduce.
Implementation of GA requires the determination of six fundamental issues: chromosome representation, selection function, the genetic operators, initialization, termination and evaluation function [7] [8] . The computational flowchart of the GA optimization process employed in the present study is given in Figure 6.
3.2. Application of Genetic Algorithm (GA)
Table 1 shows the optimal values of PSS and SVC-controller parameters obtained by the GA for SMIB system.
4. Simulation and Results
This section illustrates the simulation of the mathematical model containing a simple transmission system containing single generator equipped with an excitation system and power system stabilizer (PSS) and connected to an infinite bus. The utility of placing the Static VAR Compensator (SVC) at transmission line of SMIB system is to improve transient stability and power oscillation damping of the system.
The transient stability improvement for the single-machine infinite-bus power system was thoroughly estimated from two types of defects.
To show the effectiveness of the proposed control scheme, we compare the performance of the power system under the proposed approach and the conventional PSS whose parameters are shown in Appendix.
4.1. Increase of the Mechanical Input Power
An alternator behavior simulation following a step change in the value of the mechanical power input is given. The simulation steps are organized as:
Step 1: The system is in pre-faulted steady state;
Step 2: A range of 0.2 p.u. pulse increase in the input mechanical power at t0 = 4 s;
Step 3: The system is in a post fault state.
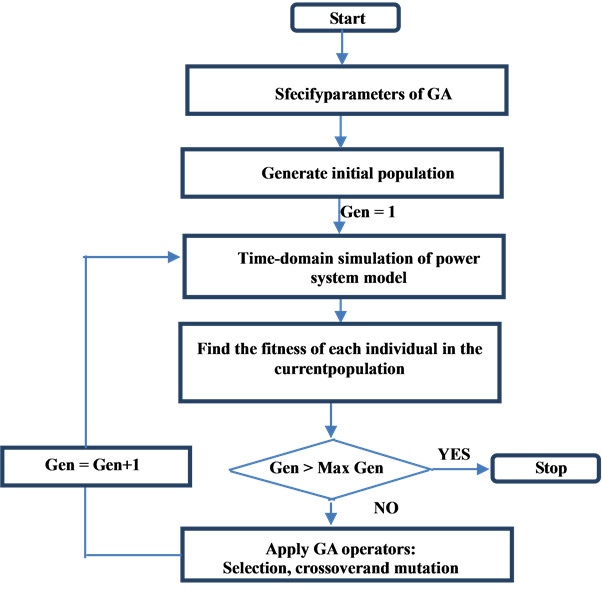
Figure 6. Flowchart of genetic algorithm.
Table 1. Optimized PSS and SVC-controller parametres for SMIB system.
Appendix
All data are in p.u. unless specified otherwise.
The parameters of the system are:
Generator parameters:

Initial condition:
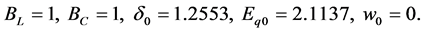
Parameters used for the excitation system:

PSS parameters:

Network parameters:



