ABSTRACT

We consider small vortices, such as tornadoes, dust devils, waterspouts, small hurricanes at low latitudes, and whirlpools, for which the Coriolis force can be neglected, and hence within which the flow is cyclostrophic. Such vortices are (at least approximately) cylindrically symmetrical about a vertical axis through the center of a calm central region or eye of radius $r_{\text{eye}}$ . In the region $r_{\text{eye}}\le r\le r_{max}$ fluid (gas or liquid) circulates about the eye with speed $v\propto r^n$ ( $n<0$ ). We take $r_{max}$ to be the outer periphery of the vortex, where the fluid speed is reduced to that of the surrounding wind field (in the cases of tornadoes, dust devils, waterspouts, and small hurricanes at low latitudes) or deemed negligible (in the case of whirlpools). If $n=-1$ , angular momentum is conserved within the fluid itself; if $n\ne -1$ , angular momentum must be exchanged with the surroundings to ensure conservation of total angular momentum. We derive the steepness and upper limit of the pressure gradients in vortices. We then discuss the power and energy of vortices. We compare the kinetic energy of atmospheric vortices and the power required to maintain them against frictional dissipation with the same quantities for Earth’s atmosphere as a whole. We explain why the kinetic energy of atmospheric vortices must be replaced on much shorter timescales than is the case for Earth’s atmosphere as a whole. Comparisons of cyclostrophic flow with geostrophic and friction-balanced flows are then provided. We then consider an analogy that might be drawn, at least to some extent, with gravitational systems, considering mainly spherically-symmetrical and cylindrically-symmetrical ones. Generation of kinetic energy at the expense of potential energy in fluid vortices, in geostrophic and friction-balanced flows, and in gravitational systems is then discussed. We explain the variations of pressure and gravitational gradients corresponding to generation of kinetic energy equaling, exceeding, and falling short of frictional dissipation. In the Appendix, we describe a simple method for maximizing power extraction from environmental fluid (water or air) flows, which is also applicable to artificial (e.g., internal combustion) engines. In summary, we provide an overview of features and energetics of Earth’s environmental fluid flows (focusing largely on vortices) and of gravitational analogies thereto that, even though mainly semiquantitative, hopefully may be helpful.

Keywords:

Vortex, Cyclostrophic Flow, Angular Momentum, Pressure Gradient, Geostrophic Flow, Friction-Balanced Flow, Power, Energy, Bernoulli’s Equation, Gravity

1. Introduction

There are various definitions of the term “vortex”. Sometimes any rotating system, or at least any rotating fluid (gas or liquid) system, is construed to be a vortex. For our purposes let us construe a vortex to be any rotating fluid (gas or liquid) system wherein the speed v of fluid motion increases monotonically inwards from the outer periphery $r_{max}$ towards decreasing radial distance r from the axis of rotation, i.e., v increasing monotonically with decreasing r, attaining a maximum value $v_{max}$ at the circumference of a calm area or eye of radius $r_{\text{eye}}$ about the axis of rotation. (This monotonic increase of v with decreasing r in numerous instances of real vortices is interrupted by local fluctuations, but in such instances it is the secular trend that we focus on.) Thus we construe tornadoes, dust devils, waterspouts, hurricanes, and whirlpools to be vortices, but not rotating fluid systems that lack an eye such as at least the vast majority of extratropical cyclones if not all of them, and all anticyclones. In short, we construe a vortex to be a cyclone with an eye. Our main interest concerning fluid (gas or liquid) systems will be in those meeting our construed definition of “vortex”, but we will also consider in some measure fluid systems not meeting this definition.

We consider small vortices, such as tornadoes, dust devils, waterspouts, small hurricanes at low latitudes, and whirlpools, for which the Coriolis force can be neglected, and hence within which the flow is cyclostrophic [1] [2]. Because waterspouts are intermediate in size, intensity, and lifetime between dust devils and tornadoes, their properties can be interpolated between those of dust devils and tornadoes, so we provide only limited consideration of them.

Even small hurricanes are much larger than even the largest tornadoes, let alone than waterspouts and dust devils, but they are still small enough that, especially at low latitudes, the Coriolis force can be neglected, at least in their maintenance. We do not consider their initial formative stages, in which the Coriolis force, even though small at low latitudes, is nevertheless important. The centripetal (sometimes construed as centrifugal) force is much smaller than the Coriolis force in the initial formative stages of hurricanes, even of small ones at low latitudes. But in fully-formed hurricanes, especially small ones at low latitudes, the reverse is true (referring to the first four paragraphs of Section 2 may be helpful). We employ the term “hurricanes” to encompass all tropical cyclones of this type, e.g., including Pacific typhoons, although we will occasionally refer to Pacific typhoons specifically.

In such vortices, the balance of forces on any parcel of moving fluid (gas or liquid: in the cases considered, air or water, respectively) can be considered cyclostrophic [1] [2] with negligible error [1] [2]. Such vortices are (at least approximately) cylindrically symmetrical about a vertical axis through the center of a calm central region or eye of radius $r_{\text{eye}}$ . In the region $r_{\text{eye}}\le r\le r_{\max }$ fluid circulates about the eye with speed $v\propto r^n$ ( $n<0$ ); within the eye, at $0\le r<r_{\text{eye}}$ , $v\approx 0\Rightarrow n\approx 0$ . We take $r_{max}$ to be the outer periphery of the vortex, where the fluid speed is reduced to that of the surrounding wind field (in the cases of tornadoes, dust devils, waterspouts, and small hurricanes at low latitudes) or deemed negligible (in the case of whirlpools). [If, not within our construed definition of “vortex”, $n\ge 0$ (of course if $n>0$ , v can increase only to a finite value with increasing r) then $r_{max}$ must be arbitrarily chosen.]

If $n=-1$ , angular momentum is conserved within the fluid itself; if $n\ne -1$ , angular momentum must be exchanged with the surroundings to ensure conservation of total angular momentum. Frictional losses typically result in $-1<n<0$ . In rare cases generation of angular momentum and kinetic energy in vortices can exceed frictional losses, resulting in $n<-1$ [A simple (nonvortex, noncyclonic) example for which $n<-1$ : Let the speed v of rotation of a rigid hoop of radius r about an axis through its center be increased. In this case, v increases while r remains fixed; thus $n=-\infty$ .] Note that (not within our construed definition of “vortex”) $n=0$ corresponds to constant v (v independent of r), and that $n=+1$ corresponds to solid-body (wheel-like) rotation.

As we construe vortices to be cyclones with eyes, minimum pressure obtains in the eye, with pressure increasing monotonically with increasing r, i.e., $\partial P/\partial r>0$ , in the region $r_{\text{eye}}\le r\le r_{max}$ . Let the sea-level or ground-level pressure at the outer periphery of a vortex be $P\left(r_{max}\right)$ and that in the eye be $P_{\text{eye}}$ . Of course $P_{\text{eye}}<P\left(r_{\max }\right)$ . The pressure difference between $r_{\text{max}}$ and the eye is $\Delta P_{\text{eye}}\equiv P\left(r_{\text{max}}\right)-P_{\text{eye}}>0$ . For atmospheric vortices such as tornadoes, dust devils, waterspouts, and hurricanes, unless otherwise noted we take the fluid density $\rho$ to be that of air at sea level or low-elevation ground level (≈1 kg/m³); for whirlpools we take $\rho$ to be the density of water (≈10³ kg/m³). We assume that horizontal (constant-altitude) changes in fluid density $\rho$ are small enough to neglect, i.e., that, corresponding to,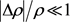. This is an excellent approximation for water in whirlpools, a very good approximation for air in dust devils and waterspouts, and a fairly good approximation for air in even the strongest hurricanes and strongest tornadoes. Indeed for whirlpools also neglecting vertical variations in water density 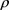is an excellent approximation (All pressures and densities are at sea level or low-elevation ground level unless otherwise noted.)

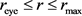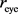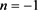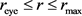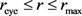If, as in the cases of most interest to us as per our construed definition of “vortex”, in the region, fluid speed has its greatest value, at, i.e., at the eye wall. In a Rankine-vortex model is assumed at [3] [4] ^FTNT0; in a modified-Rankine-vortex model, usually but not necessarily restricted to within the range, is assumed at [3] [4].^FTNT0 A calm eye and hence at probably is more commonplace than solid-body (wheel-like) rotation within the eye and hence at as per Rankine-vortex [3] [4] and modified-Rankine-vortex models [3] [4] of atmospheric vortices (tornadoes, dust devils, waterspouts, and hurricanes)^FTNTS0,1. More often than not there is little or no wind throughout the eye (not merely at the center of the eye) of atmospheric vortices, i.e., 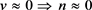from to very nearly, with v increasing from to within a very short radial distance just barely within. Indeed, in the case of whirlpools, there is not even any water within the eye at all, so must strictly obtain within the entire range! But, be that as it may, our main interest is in the region.

In Section 2, we discuss cyclostrophic flow, and derive the steepness and upper limit of the pressure gradient in vortices. In Section 3, we discuss the power and energy of vortices. We compare the kinetic energy of atmospheric vortices and the power required to maintain them against frictional dissipation with the same quantities for Earth’s atmosphere as a whole. We explain why the kinetic energy of atmospheric vortices must be replaced on much shorter timescales than is the case for Earth’s atmosphere as a whole. The effects on Earth’s atmosphere as a whole of a cutoff of insolation, and of its partial cutoff in the winter hemisphere, are discussed. Comparisons of cyclostrophic flow with geostrophic and friction-balanced flows are provided in Section 4. In Section 5 we consider an analogy that might be drawn, at least to some extent, with gravitational systems. We consider mainly spherically-symmetrical and cylindrically-symmetrical gravitational systems. Generation of kinetic energy at the expense of potential energy in cyclostrophic flow of fluid vortices, in geostrophic and friction-balanced flows, and in gravitational systems is discussed in Section 6. We explain the variations of pressure and gravitational gradients corresponding to generation of kinetic energy equaling, exceeding, and falling short of frictional dissipation. Concluding remarks are provided in Section 7. In the Appendix, we describe a simple method for maximizing power extraction from environmental fluid (water or air) flows. We also briefly explain the application of this method to artificial (e.g., internal combustion) engines. In summary, we provide an overview of features and energetics of Earth’s environmental fluid flows (focusing largely on vortices) and of gravitational analogies thereto that, even though mainly semiquantitative, hopefully may be helpful.

2. Cyclostrophic Flow, and Steepness and Upper Limit of the Pressure Gradient in Vortices

Consider a small fluid parcel of mass m, volume V, density, cross-sectional area A, and length L. Hence. Let the pressure be on one side of the small fluid parcel and P on the other side at a distance L away. [Without loss of generality, we can take. Since our fluid parcel is assumed small,.] Thus the pressure gradient across our small fluid parcel is. The net pressure-gradient force acting on our small fluid parcel is

. (1)

If our small fluid parcel is moving on a circular path about the center of an eye, at radial distance r from the center of the eye, at speed v, then the centripetal force required to keep it on this circular path is

. (2)

(Sometimes is alternatively construed as the centrifugal force that the fluid parcel experiences and that balances the pressure-gradient force.) In cyclostrophic balance [1] [2]

. (3)

Strictly, is attractive towards the center of a vortex and therefore negative, but we are concerned mainly with its magnitude, so we omit the minus sign.

Now let

(4)

at. Applying Equation (4) to the last line of Equation (3) yields, at,

, (5)

where is the average of in the range at the

altitudes where v and G are measured, most typically 10 m above the surface and at sea level or ground level, respectively. (Enclosure within angular brackets denotes the average of the enclosed quantity.) Since decreases radially inwards, the functional dependency of on r, considered alone, results in G decreasing with decreasing r. The approximation in the last term of Equation (5), which neglects this functional dependency, is justified because, in accordance with the third-to-last paragraph of Section 1, corresponding to

, is even at worst a fairly good approximation

for even the strongest hurricanes and strongest tornadoes, a very good approximation for dust devils and waterspouts, and an excellent approximation for whirlpools. Thus in cases wherein is typically at least a close approximation—tornadoes, dust devils, waterspouts, and whirlpools—G increases very rapidly inwards, i.e., , in the region [5]. (Reference [5] cites an excellent late 19^th-centry work^FINTIA for in-depth explanations.) In typical hurricanes, , with the most typical value perhaps. Corresponding to,; corresponding to,; and corresponding to,.

Let us briefly consider the range that is not within our construed definition of “vortex”, assuming the approximation in the last term of Equation (5). Note that, i.e., v independent of r, corresponds to; that corresponds to, i.e., to G independent of r; and that, i.e., solid-body (wheel-like) rotation, corresponds to. Thus for solid-body (wheel-like) rotation—and only for solid-body (wheel-like) rotation—do both v and G vary identically with r (both directly proportional to r), (Of course if, v can increase only to a finite value with increasing r.)

Perhaps at this point, we should note that irrespective of the existence of eyes, all cyclones (including whirlpools) and all anticyclones must have calm areas at their centers, because their centers are minima and maxima, respectively, of pressure, so the pressure gradient G must vanish at their centers.^FTNT1B But an

eye implies centripetal force per unit mass of

that is no longer sufficient to impose further inflow to within (sometimes alternatively construed as centrifugal force per unit mass at that prevents further inflow). Eyes exist only in vortices as per our construed definition in the first paragraph of Section 1: in the region is a necessary (but not sufficient) condition for the existence of an eye. All eyes are calm areas at the centers of cyclones, but not vice versa. At the very least most, and perhaps all, extratropical cyclones lack eyes. All anticyclones lack eyes.

If, as in the cases of most interest to us as per our construed definition of “vortex”, in the region, then the maximum fluid speed occurs at the eye wall, i.e., at, as does the maximum pressure gradient. By Bernoulli’s equation of energy conservation for fluid flow [6] [7] ^FTNT2, if (corresponding to) frictional losses can be neglected, then [6] [7]

, (6)

where is the dip of the isobaric surface that is at sea level or ground level in the eye from its altitude in the undisturbed atmosphere far from the vortex [6] [7] ^FTNT2. Thus is equal to the free-fall speed from altitude [6] [7] ^FTNT2. Applying the last line of Equation (3) and Equation (6) yields

. (7)

In the last term of Equation (7), is the average density of a vertical atmospheric column far from the vortex with base at sea level or ground level and top at.

Letting, by Bernoulli’s equation of energy conservation for fluid flow [6] [7] ^FTNT2, if (corresponding to) frictional losses can be neglected, at all in the region, Equations (6) and (7) are obviously modified to

(8)

and

, (9)

respectively, where is the dip of the isobaric surface that is at sea level or ground level at from its altitude in the undisturbed atmosphere far from the vortex [6] [7] ^FTNT2. Thus is equal to the free-fall speed from altitude [6] [7] ^FTNT2. In Equations (8) and (9), is the average of in the range at the altitudes where v and G are measured, most typically 10 m above the surface and at sea level or ground level, respectively. In the last term of Equation (9), is the average density of a vertical atmospheric column far from the vortex with base at sea level or ground level and top at. [The approximations in Equations (6)-(9) are consistent with that in the last term of Equation (5). If the inequality in applies, the approximations in Equations (8) and (9) are better than those in Equations (6) and (7).]

Again, Equations (6)-(9) represent theoretical upper limits, neglecting frictional losses, and hence corresponding to angular momentum being conserved within the fluid itself; i.e., to. Owing to frictional losses, in actual vortices n is typically at least very slightly larger than −1, and hence attainable values of v and G are typically at least very slightly smaller than those given in Equations (6)-(9). (In rare cases vortices may generate angular momentum and kinetic energy fast enough to more than offset frictional losses; hence in these rare cases.)

3. Power and Energy of Vortices

3.1. Very Small Atmospheric Vortices: Tornadoes, Dust Devils, and Waterspouts

The solar constant at Earth is ≈1400 W/m². Over day and night, over all four seasons, and over clear and cloudy weather, the average solar power flux density absorbed (and thence reradiated) by Earth’s surface is ≈200 W/m². Of this ≈200 W/m², ≈1% or ≈2 W/m² is converted into wind power flux density. The power required to maintain wind speed v against friction is, at least approximately,. A fair estimate of the root-mean-cube average surface wind speed on Earth (at the official anemometer elevation of 10 m above Earth’s surface assuming no obstructions) is ≈5 m/s. Thus a fair estimate of the power flux density required to maintain surface wind speed of v m/s is

. (10)

A wind at sea-level air density of delivers to a windmill. It was proven by Betz [8] [9] [10] ^FTNT3 that a maximum fraction of the wind’s energy can in principle be extracted by a windmill [8] [9] [10] ^FTNT3. [The dot-equal sign () means “very nearly equal to”]. Well-designed and well-built windmills can extract ≈45% of the wind’s energy, i.e., ≈3/4 of the Betz limit [8] [9] [10] ^FTNT3. [There is some questioning of the Betz limit concerning vertical-axis windmills [9] [10]. A simple method for maximization of power extraction from environmental fluid (water or air) flows is discussed in the Appendix.] Assuming extraction of, ≈14 m² of Earth’s surface are required to supply each 1 m² of windmill at the official anemometer elevation of 10 m above Earth’s surface assuming no obstructions. Considering a windmill at a higher elevation, say ≈200 m above Earth’s surface, where, say, , , and hence ≈58 m² of Earth’s surface are required to supply each 1 m² of such a windmill. Considering a flying windmill or kite windmill operating in the upper troposphere, at say 10⁴ m above Earth’s surface in middle latitudes, where and, say, , , and hence ≈750 m² of Earth’s surface are required to supply each 1 m² of such a windmill.

Consider first very small atmospheric vortices (tornadoes and dust devils). (Since waterspouts are intermediate in size, intensity, and lifetime between dust devils and tornadoes, we do not consider them explicitly, but interpolation between our results for dust devils and tornadoes can provide estimates.) The majority of the kinetic energy of these vortices is typically within the lower ≈1 km of Earth’s atmosphere. (Often their fastest winds are considerably closer to Earth’s surface than to ≈1 km above it.) Since we seek only approximate results we can take to be representative. We take the outer radius of a tornado or dust devil to be that at which the surface wind (at the official anemometer elevation of 10 m above Earth’s surface assuming no obstructions) is. Thus we take. Let

(11)

be the surface area of Earth in the region within a tornado or dust devil. Thus by Equations (10) and (11) the total power required to maintain a tornado’s or dust devil’s wind against friction, and hence also the frictional dissipation, is

, (12)

where is the root-mean-cube average wind speed at 10 m within. (Note: Don’t confuse these three symbols: P = pressure, = power flux density, = power.) Hence the total energy required to maintain a tornado or dust devil for the duration of its lifetime, and ultimately frictionally dissipated, is

. (13)

Since a tornado or dust devil is typically at least largely confined to the lower ≈1 km of Earth’s atmosphere, whose mass is » 1000kg per m² of Earth’s surface, its kinetic energy is

, (14)

where is the root-mean-square average wind speed at within the tornado or dust devil. Thus the kinetic energy of a tornado’s or dust devil’s winds must be replaced on a timescale

. (15)

Hence during its lifetime the kinetic energy of a tornado’s or dust devil’s winds must be regenerated N times to replace frictional losses, where

. (16)

In the third steps of Equations (15) and (16) we applied the approximation, where is the average wind speed in the region within a tornado or dust devil. Thus is approximately the e-folding time for if the free-energy input that generates a tornado’s or dust devil’s winds and maintains its winds against friction is cut off. For a typical, say, EF3^FTNT4, tornado, fair estimates are

and; hence and.

For a typical dust devil fair estimates are and; hence and ^FTNT4A.

Hence the kinetic energy of a typical tornado’s winds must be regenerated times during its lifetime to replace frictional dissipation. By contrast, a

typical dust devil’s winds must, essentially, be generated only once, the first time, because it does not live long enough for friction to dissipate a majority of the initially-generated kinetic energy of its winds. Of course, for exceptionally strong and/or long-lived tornadoes and dust devils, our estimates of N would be larger and for exceptionally weak and/or short-lived ones they would be smaller.^FTNTS4,4A Note that and N are independent of, because and, respectively, are independent of.

Waterspouts are intermediate in size, intensity, and lifetime between dust devils and tornadoes, and hence values of corresponding quantities are also intermediate for waterspouts.

3.2. Larger (But Still Small) Atmospheric Vortices: Small Hurricanes at Low Latitudes

Now consider small hurricanes at low latitudes. Even the smallest hurricanes are much larger than even the largest tornadoes, let alone than even the largest waterspouts or largest dust devils, but they are still small enough that, especially at low latitudes, the Coriolis force can be neglected, at least in their maintenance. We do not consider their initial formative stages, in which the Coriolis force, even though small at low latitudes, is important. The centripetal (sometimes construed as centrifugal) force is much smaller than the Coriolis force in the initial formative stages of hurricanes, even of small ones at low latitudes. But in fully-formed hurricanes, especially small ones at low latitudes, the reverse is true. (Referring to the first four paragraphs of Section 2 may be helpful.)

So we limit our considerations to fully-formed small hurricanes at low latitudes, for which the Coriolis force can be neglected, and hence for which the balance of forces on any parcel of moving air can be considered cyclostrophic [1] [2] with negligible error [1] [2]. We employ the term “hurricanes” to encompass all tropical cyclones of this type, e.g., including Pacific typhoons, although we will occasionally refer to Pacific typhoons specifically.

The majority of the kinetic energy of hurricane circulations is typically within the lower half of Earth’s troposphere. A fair estimate of the root-mean-cube average wind speed within the lower half of the low-latitude (tropical) troposphere is. Recalling the first two paragraphs of Section 3.1, the power flux density required to maintain wind speed v within the lower half of the low-latitude troposphere is

. (17)

The power flux density of »2 W/m² maintaining Earth’s winds against friction (recall the first two paragraphs of Section 3.1) sustains because the average friction over the entire lower half of the low-latitude troposphere is less than that at the official anemometer elevation for surface winds (10 m above Earth’s surface in the absence of obstructions). (The average wind speed is somewhat higher in the mid-latitude troposphere than the low-latitude troposphere owing to greater horizontal temperature contrasts in the former.)

We take the outer radius of a small low-latitude hurricane to be that at which the surface wind speed (at the official anemometer elevation of 10 m above Earth’s surface in the absence of obstructions) is. Thus we take. Let

(18)

be the surface area of Earth in the region within a small low-latitude hurricane. Thus the total power required to maintain the hurricane’s wind against friction, and hence also the frictional dissipation, is

, (19)

where is the root-mean-cube average wind speed at 10 m within. Hence the total energy required to maintain a small low-latitude hurricane for the duration of its lifetime, and ultimately frictionally dissipated, is

. (20)

Since the majority of the kinetic energy of the circulation of a small low-latitude hurricane is typically within the lower half of the troposphere, whose mass is »5 × 10³ kg per m² of Earth’s surface, its kinetic energy is

, (21)

where is the root-mean-square average wind speed in the region within the hurricane. Thus the kinetic energy of a hurricane’s winds must be replaced on a timescale

. (22)

Hence during its lifetime a hurricane’s winds must be regenerated N times to replace frictional losses, where

. (23)

In the third steps of Equations (22) and (23) we applied the approximation, where is the average wind speed in the region within a hurricane. Thus is approximately the e-folding time for if the free-energy input that generates a hurricane’s winds and maintains its winds against friction is cut off. For a typical, say, Category 3^FTNT5, small low-latitude hurricane fair estimates are and; hence and. Hence the kinetic energy of a typical small low-latitude hurricane’s winds must be regenerated »40 times during its lifetime to replace frictional dissipation. Note that, for hurricanes as for tornadoes, dust devils, and waterspouts, and N are independent of, because and, respectively, are independent of.

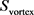
Thus the estimate of a typical hurricane’s energy as being about equal to that yielded by 2.2 megatons of TNT^FTNTS6,7 or to that of a magnitude-7 earthquake^FTNT7 (on the Richter scale) is a vast underestimate. Even a typical hurricane (,) generates, and ultimately frictionally dissipates during its lifetime, its kinetic energy times. And this figure is exceeded if and/or, as for exceptionally intense and/or long-lived hurricanes, and even more so for exceptionally intense and/or long-lived western Pacific typhoons. [Of course, even at moderately low latitudes, the Coriolis force may not be very small compared to the centripetal (sometimes construed as centrifugal) force in the outer regions of exceptionally large hurricanes and even more so of exceptionally large western Pacific typhoons.] We note that even the most active earthquake faults are doing well to manage one magnitude-7 (or larger) earthquake every few decades [11], and one magnitude-7 (or larger) earthquake per century or longer is more typical [11].

3.3. Comparison of Earth’s Atmospheric Vortices with Earth’s Atmosphere as a Whole

For Earth’s atmosphere as a whole, the root-mean-cube average wind speed is. The power flux density of »2 W/m² maintaining Earth’s winds against friction (recall the first two paragraphs of Section 3.1 and the third and fourth paragraphs of Section 3.2) sustains

because the fastest

winds contributing to are in the upper troposphere, where there is much less friction than at the official anemometer elevation for surface winds (10 m above Earth’s surface assuming no obstructions), with intermediate friction averaging over the lower half of the troposphere. The mass of Earth’s atmosphere per m² of Earth’s surface is »10⁴ kg. (Most of this atmospheric mass is, of course, within the troposphere.)

Neglecting the difference between the root-mean-cube and root-mean-square average wind speeds, the total kinetic energy of wind per m² of Earth’s surface is

. (24)

Thus the replacement timescale for the kinetic energy of Earth’s winds is^FTNT7A

. (25)

Hence ^FTNT7A for Earth’s troposphere as a whole is much longer than for tornadoes, for dust devils, and even for hurricanes. In tornadoes, is very short because very high wind speeds occur near the surface, where friction is greatest. In dust devils, maximum winds also occur near the surface but they are slower than in tornadoes, so is longer for dust devils than for tornadoes. (Waterspouts are intermediate between dust devils and tornadoes.) In hurricanes wind speeds are high, much closer to those in tornadoes than to those in dust devils, but hurricanes are much deeper vertically than dust devils or even tornadoes, so there is much more kinetic energy to be frictionally dissipated per m² of Earth’s surface, and also less friction per unit mass of air averaging over their entire depth, thus accounting for the longer for hurricanes. But for Earth’s atmosphere as a whole the vertical depth is maximized at the entire depth of the atmosphere (with sufficient accuracy at the entire depth of the troposphere), and maximum wind speeds are confined to the highest altitudes of the troposphere where friction is least. Hence for Earth’s atmosphere as a whole is much longer than even the longest of the other three given values (for hurricanes).

Thus if the supply of free energy to Earth’s atmosphere was cut off, Earth’s winds would cease with an e-folding time for of approximately one week.^FTNT7A (Of course.) But if the Sun was turned off, the supply of free energy to Earth’s atmosphere would not be immediately cut off: Earth’s winds would not cease with an e-folding time for of approximately one week, because the very large amount of thermal energy stored in Earth’s oceans would then become much more strongly thermodynamically available, i.e., much more completely upgraded to free energy. With insolation cut off, the continents would cool much faster (initially say at) than the oceans (initially say at), so a very large temperature difference would be generated between the surface temperature of the very cold continents and the surface temperature of the much less cold oceans. Thus a greatly increased fraction of the thermal energy stored in Earth’s oceans would be up-graded to free energy:

. (26)

The quantity is, of course, the Carnot efficiency.^FTNT8 It is free energy that generates Earth’s winds and maintains them in the face of frictional losses. If the Sun was turned off, would decrease only very slowly, but would initially increase very rapidly, so the free energy available to Earth’s atmosphere would initially be greatly increased. Hence wind speeds would initially increase: a period of strong winds would ensue, especially along and near the coasts of the continents, where the temperature gradient between the continents and the oceans would be steepest. As the oceans froze over, and thus, and hence Earth’s winds, would gradually diminish. Yet even through a layer of ice say ~1 m thick enough heat would flow from the liquid ocean below to keep (now the surface temperature of the oceanic ice layer) considerably warmer than. Only after the oceans had frozen over to a sufficient depth, which would probably require a timescale of months, would and thus finally vanish, and hence Earth’s winds finally cease.

Of course, a partial cutoff of insolation befalls the winter hemisphere of Earth. But as per Equation (26), atmospheric thermodynamic efficiency is on the whole higher in winter than in summer, because temperature differences between oceans and continents at any given latitude, and between low latitudes and high latitudes (substitute subscripts: ocean → lowlat and cont → highlat), are greater in winter than in summer. Increased atmospheric thermodynamic efficiency more than compensates for decreased insolation (decreased E), so (excepting convective weather systems, e.g., thunderstorms and hurricanes) on the whole is greater and hence atmospheric circulation is more vigorous in winter than in summer.

3.4. Whirlpools

A whirlpool in a sink is powered at the expense of the gravitational potential energy of the water. The maximum water speed, at the bottom of the eye wall at the drain, is (if frictional losses are negligible)

, (27)

where is the density of water, g is the acceleration due to gravity, H is the height of the water surface (above the floor of the sink) far from the whirlpool [6] [7], and is the free-fall speed from H (similarly as is the case with atmospheric vortices [6] [7] )^FTNT2. Let be the total mass of water in the sink. If, the surface area of the sink, is large compared to the area where the water level is significantly depressed by the whirlpool, the center of mass of the water in the sink is at elevation above the floor of the sink. Then, and the total gravitational potential energy of the water relative to the floor of the sink is

. (28)

Thus the power available to a whirlpool is

. (29)

Hence if the water is not replaced the e-folding time of a whirlpool is

(30)

The averages values in the denominators of Equation (30) obtain, approximately, when and therefore also have been reduced to 1/2 of their initial values, or, equivalently, when and therefore also have been reduced to of their initial values. The last approximation in Equation (30) becomes an equality if remains unaltered as the water level in the sink drops.

4. Geostrophic and Friction-Balanced Flows

Although our main concern in this paper is with cyclostrophic flow, comparisons with geostrophic flow (straight isobars)^FTNTS9,10, and with friction-balanced flows, may be edifying.

For geostrophic flow, Equation (1) remains applicable as it stands. Equations (2) and (3) are modified because the balance is now between the pressure-gradient force and the Coriolis force as per

, (31)

where is Earth’s angular sidereal rotational speed and is the latitude. Let be the total pressure difference between maximum and minimum surface barometric pressure in geostrophic flow. Then by Bernoulli’s equation of energy conservation for fluid flow [6] [7] ^FTNT2, if frictional losses can be neglected,

, (32)

where is the dip of the isobaric surface that is at sea level or ground level at the locations of minimum surface barometric pressure from its altitude at the locations of maximum surface barometric pressure [6] [7], and is the average of over the range of pressures at the altitudes where v and G are measured, most typically 10 m above the surface and at sea level or ground level, respectively^FTNT2. Thus is equal to the free-fall speed from altitude [6] [7] ^FTNT2. Applying the last line of Equation (31) and Equation (32) yields

. (33)

In the last two terms of Equation (33), is the average density of a vertical atmospheric column where the surface pressure is with base at sea level or ground level and top at.

If, letting, by Bernoulli’s equation of energy conservation for fluid flow [6] [7] ^FTNT2, if frictional losses can be neglected, Equations (32) and (33) are obviously modified to

(34)

and

, (35)

respectively. In Equations (34) and (35), is the average of over the range of pressures at the altitudes where v and G are measured, most typically 10m above the surface and at sea level or ground level, respectively, and is the dip of the isobaric surface that is at sea level or ground level at the locations of surface barometric pressure from its altitude at the locations of surface barometric pressure [6] [7] ^FTNT2. Thus v is equal to the free-fall speed from altitude [6] [7] ^FTNT2. In the last two terms of Equation (35), is the average density of a vertical atmospheric column where the surface pressure is with base at sea level or ground level and top at.

Corresponding to and hence even more so corresponding to if, is even at worst a fairly good approximation for all geostrophic (or quasi-geostrophic) flows in Earth’s atmosphere, and always an excellent approximation for all geostrophic (or quasi-geostrophic) flows in Earth’s oceans. Thus the approximations in Equations (32)-(35) are consistent with those in the last term of Equation (5) and in Equations (6)-(9). [If, the approximations in Equations (34) and (35) are better than those in Equations (32) and (33).] Again, Equations (32)-(35) represent theoretical upper limits, neglecting frictional losses.

Geostrophic (or quasi-geostrophic) flow is quite common from latitude polewards, both in Earth’s atmosphere and in its oceans. Of course, in Earth’s lower atmosphere, , whereas in its oceans,.

Let us also consider friction-balanced flows, wherein the pressure-gradient force per unit mass (or a component thereof) balances the frictional force per unit mass. Friction-balanced atmospheric and oceanic flows often occur at low latitudes, say, especially within a few degrees of or at the equator, where the Coriolis force is small (zero at the equator). Geostrophic and balanced^FTNT1B anticyclonic flows become increasingly difficult to maintain as decreases below ≈20˚, and are impossible to maintain at the equator. Thus in approaching the equator from latitude, these flows become progressively more friction-balanced, until at the equator they must be purely friction-balanced. Friction-balanced flow can also occur even at higher latitudes in, for example, the damming of cold waves by mountain ranges.^FTNT11 In such damming of cold waves, is balanced by the force exerted on the cold air by a mountain range, and typically only a component of the pressure-gradient force balances ^FTNT11: thus should in such cases be construed as the component of the pressure-gradient force that balances.^FTNT11 At all typical wind and ocean-current speeds, is, at least approximately, proportional to, i.e., , where C is a factor whose dimensions are (length)⁻¹, which accounts for, say, surface roughness. Applying Equation (1) and setting yields

. (36)

Another example of friction-balanced flow is river flow^FTNT12. The force driving the flow of a river, per unit mass of flowing water, is, where g is the acceleration due to gravity and is the slope. Most often for river flows. The frictional force retarding the motion of water in a river flowing at speed v, per unit mass of flowing water, within the entire range of river-flow speeds, is, at least approximately, proportional to. Because most of the friction retarding the flow of a river occurs via interaction with its river bed, this retarding frictional force, per unit mass of flowing water, is also, at least approximately, proportional to, where is a dimensionless factor accounting for, say, the roughness of the river bed, is the river bed’s wetted perimeter, and is the river’s cross-sectional area. Thus. Similarly to Equation (36), setting yields

. (37)

Most typically, decreases downstream, but increases slightly faster downstream, so v increases slightly downstream. (As previously noted, most often for river flows.)

Yet another example of friction-balanced flow is the flow of groundwater. The force driving the flow of groundwater, per unit mass, is, where g is the acceleration due to gravity and θ is the hydraulic gradient, i.e., the slope of the water table. Most often for groundwater flows (as for river flows) . The frictional force retarding the motion of groundwater flowing at speed v, per unit mass, within the entire range of groundwater-flow speeds, is, at least approximately, proportional to v. It is also proportional to a factor whose dimensions are (time)⁻¹, which accounts for, say, the porosity and other properties of the materials comprising the water table that determine the ease or difficulty of groundwater flow. Thus. Setting yields Darcy’s Law [12] [13] ^FTNT13:

. (38)

Note that Darcy’s Law^FTNT13 in hydrology [12] [13] is essentially equivalent to Ohm’s law^FTNT14 in electrical circuits [13].

Groundwater flows occur at much smaller Reynolds numbers than river-water flows, atmospheric winds, and most oceanic flows. At small Reynolds numbers (as for groundwater flows, with rare exceptions^FTNT13) viscous drag is predominant so, at least approximately,: viscous shear forces are, at least to a first approximation, proportional to v [14] [15]. At large Reynolds numbers (as for atmospheric winds, river-water flows, and most oceanic flows), inertial drag is predominant, so, at least to a first approximation,: both (i) the mass of fluid and (ii) the velocity change and hence momentum change imparted per unit mass of fluid moving past a given location are, at least to a first approximation, proportional to v; two factors of v amount to [14] [15].

5. Gravity

5.1. Is There an Analogy?

There is, at least superficially, similarity between the spiral rainbands of hurricanes and the spiral arms of a galaxy such as our own Milky Way. Air orbits about the eye in a hurricane. Stars, including the Sun, as well as gas, dust, etc., orbit about the center of the Milky Way, and of course orbital motion can occur about any gravitating body. Thus can a galaxy such as our own Milky Way, or any gravitating system in general, be in any way construed as cyclonic? (Clearly a galaxy such as our own Milky Way, or any gravitating system in general, cannot be construed as anticyclonic, because gravity is an attractive force, and the pressure-gradient force is attractive in cyclones but repulsive in anticyclones.)

Can an analogy be drawn? A cute little book [16], even though scientifically inaccurate, at any rate suggested this at least superficial similarity, and hence the possibility of an analogy, to the author of this present paper. Such an analogy may also seem suggestive based on more recent, scientifically accurate, books [17] [18] [19]. The similarity between not only the spiral rainbands of hurricanes and the spiral arms of a galaxy such as our own Milky Way, but also between both and other structures (albeit not with respect to either the Milky Way or these other structures being construed as cyclonic) has been noted by authors of other more recent, scientifically accurate, books [20] as well^FTNT15.

Perhaps an analogy can be drawn, at least to some extent. Recall that in a cyclone, minimum pressure occurs at the center (in the eye if the cyclone has one and hence is a vortex as per our construed definition in the first paragraph of Section 1), and pressure increases monotonically with increasing r (in the region if the cyclone has an eye, and perhaps somewhat beyond). But the pressure in the intergalactic space surrounding the Milky Way, and indeed in the space surrounding any gravitating body, is for all practical purposes zero. Thus if the Milky Way, and indeed any gravitating body, is to be construed as cyclonic, then the pressure within its domain must be construed as negative, decreasing radially inwards, and most strongly negative at its center. Hence gravity must be construed as generating a negative pressure or tension.

If gravity generates tension, then space must be capable of supporting tension. If space is construed as a medium rather than as mere nothingness, then perhaps this tension could be construed as warping or curving space. Perhaps this might provide a physical interpretation for the statement: “Spacetime tells matter how to move, matter tells spacetime how to curve [21] ” . [Whereas the entirety of spacetime tells matter how to move and matter tells the entirety of spacetime how to curve [21], pressures (including tensions) and pressure gradients (including tension gradients) are purely spatial^FTNT15A, although of course they can evolve with time^FTNT15A. In this Section 5, we consider only unchanging gravitators, and hence only unchanging pressures (specifically tensions) and only unchanging pressure gradients (specifically tension gradients)^FTNT15A.] For, how can nothingness tell matter how to move, and how can matter tell nothingness how to curve? Does the phrase “curvature of nothingness” even have any meaning? Perhaps the classical vacuum might be construed as nothingness, but the quantum-mechanical vacuum certainly cannot [22] [23] [24]. Moreover, since a medium capable of supporting tension is required for the transmission of transverse waves [by contrast, longitudinal waves, e.g., sound, can travel through any (material, i.e., nonvacuum) medium], and since electromagnetic radiation is comprised of transverse waves, can space be construed as a latter-20th-century and 21st-century interpretation of the ether [sometimes spelled aether (the a is silent)] postulated in 19th-century physics [25] [26] ^FTNT15B? Concerning the latter point, the conventional viewpoint is, of course, that electromagnetic waves serve as their own medium—their own ether—via the continual handoff of energy from transverse electric field to transverse magnetic field to transverse electric field… [27].

5.2. Spherically-Symmetrical Gravity

For an isolated nonrotating spherically-symmetrical gravitator of radius and mass M for which Newtonian theory is sufficiently accurate for calculation of orbital velocity, escape velocity, and gravitational potential and hence of magnitude ^FTNT16, i.e., for which General Relativity need not be employed for these purposes, applying Equations (4) and (5), at

. (39)

[The universal gravitational constant should not be confused with the pressure gradient (in this case tension gradient) G.]

At about an isolated nonrotating spherically-symmetrical gravitator, so either or can be used.^FTNT16 In Equations (39)-(43) and the associated discussions we choose for closer analogy with the maximum speed attainable consistent with conservation of energy^FTNT16 as per Bernoulli’s equation for fluid flow [6] [7] ^FTNT2: recall Equations (6)-(9) and the associated discussions. But we note that, applying Equation (2) and that the gravitational force between particles of masses M and m is, for circular orbits of a test particle of mass and size can be derived similarly to Equation (3):

. (40)

Strictly, is attractive towards the center of a gravitating body and therefore negative, but we are concerned mainly with its magnitude, so we omit the minus sign.

Radial spatial intervals of unity () in the absence of gravity [in the case of an isolated nonrotating spherically-symmetrical gravitator in the] are stretched in the weak-gravitational-field limit () to [28] ^{FTNTS17−17B}

. (41)

For weak spherically-symmetrical gravitational fields at [28] ^{FTNTS17−17B}

. (42)

Qualitatively, we should expect that if tension, i.e., negative pressure, is effected by an isolated nonrotating spherically-symmetrical gravitator, then such tension would radially stretch space, but leave unaltered space perpendicular to the radial, i.e., leave unaltered the Euclidean ruler-distance measure 2πr of any circumference and the Euclidean (ruler-distance)² measure 4πr² of any spherical shell about the center of the gravitator^{FTNTS15A,17–17B}. [Also of course time is dilated radially inwards^{FTNTS15A,17–17B}, in the weak-field limit as per the plus (+) signs in Equations (41) and (42) being replaced by minus (−) signs^{FTNTS15A,17–17B}, but we focus on the spatial, specifically spatial radial, gravitational modifications of spacetime^{FTNTS15A,17–17B}.] Qualitatively, this radial stretching of space seems consistent with any circumference and any spherical shell about the center of an isolated nonrotating spherically-symmetrical gravitator whose respective Euclidean ruler-distance and (ruler-distance)² measures are 2πr and 4πr² possessing a radius whose ruler-distance measure exceeds the Euclidean value r [in the weak-field limit by approximately the ratio given by Equations (41) and (42)]^{FTNTS15A,17–17B}. Quantitatively, we may be on less certain ground if we try to relate to the degree of radial stretching of space^{FTNTS15A,17–17B}, but let us try anyway.

Can we draw the following analogy at, as per Equations (6) and (8), with the help of Equations (39) and (42), letting be the average density within r?

(spherical symmetry,)?

(more general geometry,)? (43)

The question marks in Equation (43) emphasize its speculative nature, and that it likely has at best only qualitative validity: For example: (a) In Equation (43) is it more correct to employ as per Equation (39) or as per Equation (40)? If as per Equation (40) had been employed, then in the first two lines of Equation (43), hence halving the terms immediately following the equal (=) signs in the last two lines thereof. (b) In strong gravitational fields wherein and even is a significant fraction of c and is a significant fraction of, the Newtonian approximations as per Equations (39)-(43) and the associated discussions must be modified^FTNT18.

Yet, at least prima facie, our result of Equation (43) seems to be qualitatively reasonable: that for a given, the less massive the gravitator, the larger must be for a given. At least prima facie, it seems qualitatively reasonable that, for a given, a more spatially compact and denser gravitator—a larger—should correspond to a larger.

For the region of the Milky Way in the vicinity of the Sun, for most purposes Newtonian theory is sufficiently accurate. But this region is not in the space surrounding an isolated nonrotating spherically-symmetrical gravitator: the Milky Way rotates, is not perfectly spherically-symmetrical, and most importantly its mass is not entirely within the radius of the Sun’s orbit about the center of the Milky Way but extends well beyond the Sun’s orbit^FTNTS19-21. In the region of Milky Way in the vicinity of the Sun’s orbit, , i.e., ~ independent of r^FTNTS19−21. [By Equations (39) and (40) and the associated discussions this implies that in the vicinity of the Sun’s orbit ~ independent of r ~ independent of r.] Hence applying Equations (4) and (5):

. (44)

Thus perhaps our analogy can be drawn, at least to some extent. But we cannot expect more than qualitative validity from our simplified, or even oversimplified, analyses. Yet it should be noted that an elastic-strain theory of gravity has been considered on a much more rigorous level [29] ^FTNT22.

5.3. Cylindrically-Symmetrical Gravity

For comparison, let us consider (in the Newtonian approximation) the gravitational field of an isolated nonrotating long cylindrical mass M of radius and finite length, at radial distance r from its central axis and at the center of its length (from both ends), with.

The gravitational force on a test particle of mass and size in this cylindrical case can be derived from that in the more usual spherical case (a simple example of Gauss’ Law^FTNT23):

. (45)

In Equation (45) is the surface area of a Gaussian surface everywhere perpendicular to the lines of force [for spherical symmetry and for cylindrical symmetry (neglecting the ends of a cylinder)] and is the linear mass density of a cylinder. Setting for orbital motion in this cylindrical case, and applying Equation (2), yields [in similarity with Equations (3) and (40)]:

. (46)

Thus in this cylindrical case is independent of r, i.e.,. Hence applying Equations (4) and (5):

. (47)

Note the similarity of the results of Equations (44) and (47). Of course in this cylindrical case the test mass m is the only orbiting mass, whereas in the Milky Way in the vicinity of the Sun’s orbit there are numerous other orbiting masses, and these extend well beyond the Sun’s orbit. Thus note the similarity of the relation between the variation of G and the variation of v in these two cases, despite the difference in the physics between these two cases.

Calculation of for the cylindrically-symmetrical case is not as straightforward as for the spherically-symmetrical case. In the region:

. (48)

For an infinitely long () cylindrical gravitator, for any finite, however small, diverges (albeit only logarithmically) with increasing r. Therefore if we cannot set in the limit. Thus not even the most powerful rocket, indeed not even light, can escape from an infinitely long sewing thread! Thus if there is no Newtonian (weak-field) limit for a cylindrically-symmetrical gravitational field, not even for that of a sewing thread. For finite l (as stipulated in the first sentence of this Section 5.3) in the weak-field limit gradually changes from that given by Equation (45) if to that for a spherically-symmetrical gravitational field as per Equation (40) if; and from that given by Equation (48) to that for a spherically-symmetrical gravitational field as per Equations (39)-(43).

Thus, again, perhaps our analogy can be drawn, at least to some extent. But, again, we cannot expect more than qualitative validity from our simplified, or even oversimplified, analyses. Yet, we again note that an elastic-strain theory of gravity has been considered on a much more rigorous level [29] ^FTNT22.

6. Generation of Kinetic Energy in the Cyclostrophic, Geostrophic, Friction-Balance, and Gravitational Cases

In order to generate kinetic energy in cyclostrophic fluid flow, the fluid must be able to spiral inwards down a hill, or rather down into a pit, of pressure, crossing isobars towards lower pressure, so that the potential energy represented by high pressure can be traded for kinetic energy at lower pressure, in accordance with Bernoulli’s equation of energy conservation for fluid flow [6] [7] ^FTNT2, as per Equations (6) and (8). But in order to spiral inwards down a hill, or rather down into a pit, of pressure, there must be friction. In the absence of friction the fluid would simply orbit at fixed r always instantaneously parallel to the isobars and consequently with fixed v, and hence would never be able to spiral inwards down a hill, or rather down into a pit, of pressure. If in cyclostrophic flow G increases with decreasing r as, generation of kinetic energy matches frictional loss so v is constant, independent of r. If in cyclostrophic flow G increases with decreasing r faster than as, generation of kinetic energy exceeds frictional loss so v increases with decreasing r. If in cyclostrophic flow G increases with decreasing r more slowly than as, generation of kinetic energy falls short of matching frictional loss so v decreases with decreasing r. [This presumes the approximation in the last term of Equation (5). Refer to Sections 1 and 2 as necessary.]

Although our main concern in this paper is with cyclostrophic flow, comparisons with generation of kinetic energy in geostrophic flow (straight isobars)^FTNTS9,10, in friction-balanced flows, and also in gravitational cases, may be edifying (Refer to Sections 4 and 5 as necessary.)

In order to generate kinetic energy in geostrophic fluid flow, the fluid must be able to move down a hill of pressure, crossing isobars towards lower pressure, so that the potential energy represented by high pressure can be traded for kinetic energy at lower pressure, in accordance with Bernoulli’s equation of energy conservation for fluid flow [6] [7] ^FTNT2, as per Equations (32) and (34). But in order to move down a hill of pressure, there must be friction. In the absence of friction the fluid would simply move at fixed pressure always parallel to the isobars and consequently with fixed v, and hence would never be able to move down a hill of pressure. If in geostrophic flow is constant (independent of pressure), generation of kinetic energy matches frictional loss so v is also constant (independent of pressure). If in geostrophic flow increases in the direction of decreasing pressure, generation of kinetic energy exceeds frictional loss so v also increases in the direction of decreasing pressure. If in geostrophic flow decreases in the direction of decreasing pressure, generation of kinetic energy falls short of matching frictional loss so v also decreases in the direction of decreasing pressure.

In friction-balanced fluid flows, the fluid is always able to move down a hill of pressure or of elevation, crossing isobars towards lower pressure or contours towards lower elevation, so that the potential energy represented by high pressure or high elevation can always be traded for kinetic energy at lower pressure or lower elevation. If in friction-balanced atmospheric or oceanic flow is constant (independent of pressure), generation of kinetic energy matches frictional loss so v is also constant (independent of pressure). If in friction-balanced atmospheric or oceanic flow increases in the direction of decreasing pressure, generation of kinetic energy exceeds frictional loss so v also increases in the direction of decreasing pressure. If in friction-balanced atmospheric or oceanic flow decreases in the direction of decreasing pressure, generation of kinetic energy falls short of matching frictional loss so v also decreases in the direction of decreasing pressure.

All river and groundwater flows are friction-balanced flows: thus in these flows the water is always able to move downhill, so that the potential energy represented by high elevation can always be traded for kinetic energy at lower elevation. If in river flow is constant, generation of kinetic energy matches frictional loss so v is also constant (independent of elevation). If in river flow increases downstream, generation of kinetic energy exceeds frictional loss so v also increases downstream. If in river flow decreases downstream, generation of kinetic energy falls short of matching frictional loss so v also decreases downstream. [As noted in the paragraph immediately following Equation (37), in most rivers, and hence also v, increases slightly downstream.] If in groundwater flow is constant, generation of kinetic energy matches frictional loss so v is also constant (independent of elevation). If in groundwater flow increases downhill, generation of kinetic energy exceeds frictional loss so v also increases downhill. If in groundwater flow decreases downhill, generation of kinetic energy falls short of matching frictional loss so v also decreases downhill. (As noted in the fifth-to-last through second-to-last paragraphs of Section 4, most often for both river-water flows and groundwater flows.)

In cyclones with eyes—vortices as per our construed definition in the first paragraph of Section 1 (tornadoes, dust devils, waterspouts, hurricanes, and whirlpools)—maximum fluid speeds typically attain a large fraction of the maxima allowed by Bernoulli’s equation of energy conservation for fluid flow [6] [7] as per Equations (6) and (8)^FTNT2. By contrast, in extratropical synoptic-scale weather systems (extratropical cyclones and anticyclones, and geostrophic flow) maximum wind speeds typically attain only a small fraction of the maxima thereby allowed, e.g., as per Equations (32) and (34) for geostrophic flow. This is in accordance with what is observed on typical weather maps. The pressure gradient typically steepens towards lower pressure much more closely to corresponding to conservation of angular momentum within the fluid itself (recall the fifth paragraph of Section 1 and the fourth paragraph of Section 2) [5] than to the minimum (only marginally exceeding in cyclostrophic flow) required for v to increase with decreasing r—assuming at least some friction to allow the wind to move down hills, or rather down into pits, of pressure—in cyclones with eyes. By contrast, in extratropical cyclones the pressure gradient typically steepens little, if at all, towards lower pressure. Thus maximum winds in extratropical cyclones are usually considerably slower than those in hurricanes, and typically occur at intermediate distances between the center and the outer periphery, rather than near (but not at) the center (at the eye wall) as in cyclones with eyes in general and hurricanes in particular. Maximum winds in anticyclones are usually slower yet, and typically occur close to the periphery. At the very least most, and perhaps all, extratropical cyclones lack eyes. All anticyclones lack eyes. (Of course, all cyclones are pits of pressure and all anticyclones are hills of pressure.)

In friction-balanced flow, most commonly, at least approximately, generation of kinetic energy matches frictional loss, so v remains at least approximately constant (in river flow v most typically increases downstream but only slightly). Hence in friction-balanced flow v usually does not attain a significant fraction of the maximum value allowed by energy conservation in accordance with Bernoulli’s equation of energy conservation for fluid flow [6] [7] as per Equations (6), (8), (32), and (34)^FTNT2.

The first paragraph of this Section 6 applies, as per Section 5, in gravitational cases too. The pits in these cases are gravitational potential wells, but so too are, ultimately, the pits of pressure represented by cyclones and the bottoms of the hills of pressure represented by anticyclones and by geostrophic flows. In the absence of friction, a satellite orbits at fixed r and hence with fixed v. With friction it will spiral inwards and hence lose potential energy, which can be traded for a gain of kinetic energy and for frictional dissipation. Since, as per Equations (39) and (40) and the associated discussions, in the case of spherically-symmetrical gravitation (since this is faster than) generation of kinetic energy exceeds frictional loss so v increases as a satellite spirals inwards towards decreasing r. By contrast, in the vicinity of the Sun’s orbit in the Milky Way, or in the case of cylindrically-symmetrical gravitation, , hence generation of kinetic energy matches frictional loss sov remains constant as a satellite spirals inwards towards decreasing r. If with as, for example, typically obtains close to the centers of galaxies^FTNT24, generation of kinetic energy falls short of matching frictional loss so v decreases as a satellite spirals inwards towards decreasing r.

7. Concluding Remarks

Introductory discussions were provided in Section 1. In Section 2 we discussed cyclostrophic flow, and derived the steepness and upper limit of the pressure gradient in vortices. In Section 3 we discussed the energy and power of vortices, including, in the case of atmospheric vortices, estimates of the number of times that the kinetic energy of a vortex must be regenerated during its lifetime to replace frictional dissipation. We explained why the kinetic energy of atmospheric vortices must be replaced on much shorter timescales than is the case for Earth’s atmosphere as a whole. The effects on Earth’s atmosphere as a whole of a cutoff of insolation, and of its partial cutoff in the winter hemisphere, were discussed. We considered only small atmospheric vortices, namely tornadoes, dust devils, waterspouts, and small hurricanes at low latitudes, so that we could assume that the Coriolis force can be neglected, and hence that the balance of forces on any parcel of moving air can be considered cyclostrophic [1] [2] with negligible error [1] [2]. [Waterspouts were given only limited consideration, because they are intermediate in size, intensity, and lifetime between dust devils and tornadoes, and hence their properties can be interpolated between those of dust devils and tornadoes. Even small hurricanes are much larger than even the largest tornadoes, let alone than even the largest waterspouts or dust devils, but they are still small enough that, especially at low latitudes, the Coriolis force can be neglected (except in their initial formative stages, which we did not consider).] We also considered whirlpools, which are even smaller and hence for which the cyclostrophic approximation [1] [2] is even more accurate [1] [2]. We neglected horizontal (constant-altitude) variations in fluid density. This is an excellent approximation for water in whirlpools, a very good approximation for air in dust devils and waterspouts, and a fairly good approximation for air in even the strongest hurricanes and strongest tornadoes. Indeed for whirlpools also neglecting vertical variations in water density is an excellent approximation. Comparisons with geostrophic and friction-balanced flows were provided in Section 4, again where feasible neglecting variations in fluid density. In Section 5 we considered an analogy that might be drawn, at least to some extent, with gravitational systems. We considered mainly spherically-symmetrical and cylindrically-symmetrical gravitational systems. In Section 6 we discussed generation of kinetic energy at the expense of potential energy in fluid vortices, in geostrophic and friction-balanced flows, and in gravitational systems. We explained the variations of pressure gradients and gravitational gradients corresponding to generation of kinetic energy equaling, exceeding, and falling short of frictional dissipation. Expanding on the second paragraph of Section 3.1 where windmills were briefly discussed, the Appendix describes a simple method for maximizing power extraction from environmental fluid (water or air) flows. It also briefly explains the application of this method to artificial (e.g., internal combustion) engines. Our overview of features and energetics of Earth’s environmental fluid flows (focusing largely on vortices), even though mainly semiquantitative, hopefully may be helpful. Our attempt to draw analogies with respect to gravitational systems, even though of at most qualitative validity, hopefully may also be helpful. Despite the limitations of our analyses being mostly semiquantitative, hopefully they are helpful.

Acknowledgements

I am very grateful to Dr. Donald H. Kobe, Dr. Kurt W. Hess, and Dr. Stan Czamanski for very perceptive scientific discussions concerning fluid dynamics, especially those with Dr. Donald H. Kobe concerning fluid friction, those with Dr. Kurt W. Hess concerning tropical cyclones, windmills, and ocean currents, and those with Dr. Stan Czamanski pertinent to the Appendix. I thank Dr. Donald H. Kobe, Dr. Stan Czamanski, and Dr. S. Mort Zimmermanfor very insightful general scientific discussions over many years. I also thank Dr. Kurt W. Hess, Dan Zimmerman, and Robert H. Shelton for very insightful general scientific discussions at times. Additionally, I thank Robert H. Shelton for very helpful advice concerning diction.

Footnotes

Footnote 0: See also: (a) Ref. [1], pp. 357-358; (b) the references cited in Endnotes 3-6 of Ref. [3]; and (c) Mueller, K.J., DeMaria, M., Knaff, J., Kossin, J.P., and Vonder Haar, T.H. (2006) Objective Estimation of Tropical CycloneWind Structure from Infrared Satellite Data. Weather and Forecasting, 21, 990-1005 (especially Section 3).

Footnote 1: See Ref. [1], Exercise 8.6.

Footnote 1A: Reference [5] cites: Ferrel, W. (1893). A Popular Treatise on the Winds. 2nd Edition, John Wiley & Sons, New York, 347-449 (Chapter VII). This book [reissued: (1964) Chapman & Hall, Limited, London] is accessible online at https://archive.org/details/cu31924002972606.

Footnote 1B: There is an additional restriction on wind speed in anticyclones, which requires not only calms at their centers but upper limits on wind speed in general, if the flow is balanced. See Ref. 1, Section 7.2 (especially Subsection 7.2.6) and Ref. 2, Sections 1.1-1.3 and 3.2 (especially Subsection 3.2.5). If the flow is not balanced then this additional restriction with respect to upper limits on wind speed does not apply.

Footnote 2: In slightly generalized form Bernoulli’s equation of energy conservation for fluid flow can account for compressibility and frictional energy dissipation. See Refs. [6] [7], especially Ref. [7]. While the material cited in Ref. [5] and in Footnote 1A focuses on vortices (especially tornadoes), the equality of pressure-gradient-driven and free-fall-driven wind speeds discussed therein is valid in general.

Footnote 3: See also: “Betz’s law” (most recently revised in 2019) at https://www.wikipedia.org, references cited therein, and other Wikipedia articles cited therein. Note: All Wikipedia articles have Talk pages, wherein strengths and weaknesses of the articles, along with suggestions for their improvement, are discussed.

Footnote 4: See: “Enhanced F Scale for Tornado Damage” (Update implemented on 1 February 2007) at https://www.spc.noaa.gov/faq/tornado/ef-scale.html. The distribution of lifetimes, sizes, and maximum wind speeds of tornadoes is very unsymmetrical: it is strongly positively skewed (see Weisstein, E.W. “Skewness.” From MathWorld— A Wolfram Web Resource. http://mathworld.wolfram.com/Skewness.html), with long tails extending towards high values well above the average. See for example: Ernest, A. and Childs, S. (2014) Adjustments in Tornado Counts, F-Scale Intensity, and Path Width for Assessing Significant Tornado Destruction. Journal of Applied Meteorology and Climatology, 53, 1494-1505; and Merritt, L. (2015) Tornado Frequency and Intensity in Oklahoma at http://apollo.ea.gatech.edu/EAS4480/2015/LaurenM Data Final Project.pptx.

Footnote 4A: The distribution of lifetimes, sizes, and maximum wind speeds of dust devils is very unsymmetrical: it is strongly positively skewed (see Weisstein, E.W. “Skewness” cited in Footnote 4) with long tails extending towards high values well above the average. This asymmetry is probably even more pronounced in the case of dust devils than in the case of tornadoes. Also in the case of dust devils there tends to be underestimation more than in the case of tornadoes, because the circulation of dust devils can extend beyond the range of visible dust. See for example: Sinclair, P.C. (1967) General Characteristics of Dust Devils. Journal of Applied Meteorology, 8, 32-45; and Cooley, J.R. (1971) Dust Devil Meteorology (NOAA Technical Memorandum NWSCR-42) at https://repository.library.noaa.gov/view/noaa/14125noaa_14125_DS1.pdf? (the short form of this website, noaa_14125_DS1.pdf, probably suffices for access).

Footnote 5: See: “Saffir-Simpson Hurricane Wind Scale” (Updated 2 January 2019 to include central North Pacific examples: left-click on “About the Saffir-Simpson Hurricane Wind Scale (PDF)” ) at https://www.nhc.noaa.gov/aboutsshws.php.

Footnote 6: See Ref. [3], p. 152.

Footnote 7: See Ref. [4], pp. 137-138.

Footnote 7A: Our estimate of ≈1 week is comparable to that of ≈100 hours given in Subsection VI.11 “Energy Changes in Atmospheric Wind Systems” (see especially p. 471) of Stewart, H. J., Section VI “Kinematics and Dynamics of Fluid Flow”. In Berry, F.A., Jr., Bollay, E., and Beers, N.R., eds., Handbook of Meteorology, McGraw-Hill, New York, 1945.

Footnote 8: See Ref. [6], Chaps. 18 and 20.

Footnote 9: See Ref. [1], Section 7.2, especially Subsections 7.2.4-7.2.5.

Footnote 10: See Ref. [2], Sections 2.4.1 and 3.2.2.

Footnote 11: See Ref. [1], Section 8.2.3.

Footnote 12: See Ref. [11], pp. 310-312.

Footnote 13: See also: “Darcy’s law” (most recently revised in 2019) at https://www.wikipedia.org, references cited therein, and other Wikipedia articles cited therein.

Footnote 14: See also Ref. [6], Section 26-4.

Footnote 15: See Ref. [4], p. 4.

Footnote 15A: See Ref. [22], Section 21.4.

Footnote 15B: See also Ref. [27], pp. 495-496.

Footnote 16: See Ref. [6], Chap. 13.

Footnote 17: Ruler distance is discussed, and distinguished from other distance measures in relativity, in Ref. [25], Chap. 11 (especially Sections 11.1-11.5 and most especially Section 11.5), Exercise 11.12, and pp. 384-385. Circumferences and spherical shells about the center of an isolated nonrotating spherically-symmetrical gravitator retain their respective Euclidean (ruler-distance) and (ruler-distance)² measures 2πr and 4πr² even in the case of black holes: (i) for the Schwarzschild horizon with respect to black-hole dynamics (see Ref. [22], Box 33.4 and Section 33.8), (ii) for the Schwarzschild horizon with respect to Hawking radiation [see Ref. [25], Section 12.6 and Exercise 12.13), and (iii) even for collapsing spherical shells within the Schwarzschild horizon (see Ref. [25], Sections 12.1D and 12.1E). Concerning (iii), even though r becomes a timelike coordinate within the Schwarzschild horizon of a (nonrotating, uncharged) black hole, it nonetheless also still retains its spatial geometrical significance.

Footnote 17A: The excess (extra-Euclidean) radial ruler distance (in the weak-field limit) of from the center to the surface of a nonrotating sphere of mass M and uniform density discussed in Ref. [28] is a special case of the more general result discussed in Section 11.5 of Ref. [25].

Footnote 17B: See Ref. [25], Section 1.16 and Chapters 8-15 (especially Chaps. 8-11 and Sections 14.1-14.2, 15.1, and 15.5) concerning gravity in general. {As an aside, as per the third-to-last and second-to-last paragraphs and Figure 9.2 of Section 9.2 and as per Sections 9.6 and 9.7 of Ref. [25], we note that an observer on a rotating disk construes a centrifugal = gravitational field, ruler-distance circumference 2πr, and ruler-distance radius >r). By contrast, an external observer construes no field, ruler-distance radius r, and Lorentz-contracted ruler-distance circumference < 2πr. Both observe the same ratio [(ruler-distance radius) ÷ (ruler-distance circumference)] > 1/2π.}

Footnote 18: See Ref. [25], Chapters 11-12, especially Section 12.2.

Footnote 19: See Ref. [17], Section 14.1.6.

Footnote 20: See Ref. [18], Section 24.3 (especially pp. 914-919), and pp. 951-956.

Footnote 21: See Ref. [19], Section 10.3 (especially pp. 406-411), and pp. 443-448.

Footnote 22: See Ref. [22], pp. 426-428 and 1206-1208.

Footnote 23: See Ref. [6], Chap. 23.

Footnote 24: See Ref. [17], pp. 490-491 (especially Figure 14.8 on p. 490).

Footnote 25: See also: “Unconventional wind turbines” (most recently revised in 2019) at https://www.wikipedia.org, references cited therein, and other Wikipedia articles cited therein.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

Cite this paper

Denur, J. (2018) Pressure Gradient, Power, and Energy of Vortices. Open Journal of Fluid Dynamics, 8, 216-249. https://doi.org/10.4236/ojfd.2018.82015

References

Appendix: A Simple Method for Maximizing Power Extraction from Environmental Fluid Flows

In the second paragraph of Section 3.1, windmills were briefly discussed. In this Appendix, we expand on the second paragraph of Section 3.1, and describe a simple method for maximizing power extraction from environmental fluid (water or air) flows; e.g., power extraction from the flow of a river by a waterwheel, from the wind by a windmill, etc. If for example a waterwheel or windmill is spinning freely with no load imposed on it, so that it is not required to supply any torque nor any power, it will spin at its maximum possible angular velocity in a given environmental fluid flow. (For a freely-spinning undershot waterwheel of radius in a river flowing at linear velocity v,.) As the load imposed on a waterwheel or windmill is increased and it is required to supply increasing torque, its angular velocity will decrease monotonically. At maximum possible load, with it being required to supply maximum possible torque, its angular velocity will have decreased to zero, so again it will supply zero power. Thus the power

(A1)

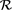
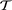
extracted from an environmental fluid flow will be maximized at intermediate values of and.

Let be plotted as a function of on a graph whose origin is (,), with increasing linearly upwards on the vertical axis and increasing linearly to the right on the horizontal axis. Now to maximize:

(A2)

Thus is maximized at the point on the versus plot where the

positive slope from the origin () to that point is equal to the magnitude of the negative slope of the tangent at that point. Hence this is

the optimum point () on the versus plot, corresponding to maximum power extracted from an environmental fluid flow.

Thus a waterwheel or a windmill will achieve its maximum possible power output and hence its maximum possible efficiency if operating at this optimum point () on its versus plot, in accordance with Equation (A2). For a windmill the upper bound on this maximum possible efficiency is generally construed to be the Betz limit [8] [9] [10].^FTNT3 The Betz limit has been questioned for vertical-axis wind turbines [9] [10], but vertical-axis wind turbines generally have lower efficiencies than horizontal-axis ones [9] [10]. (But since they do not have to swivel into the wind, vertical-axis wind turbines have fewer moving parts than horizontal-axis ones; also, they have balanced weight distributions about their centers and occupy less space than horizontal-axis wind turbines [9] [10].) An equivalent of the Betz limit for vertical-axis wind turbines might yet be derived [9] [10]. But whether or not the Betz limit is always an upper bound, a windmill will achieve its maximum possible power output and hence its maximum possible efficiency if operating at this optimum point() on its versus plot, in accordance with Equation (A2).

It should be noted that novel systems for extracting energy from the wind are being developed. These include: (a) improved designs for vertical-axis wind turbines [30], (b) flying windmills [31], and (c) wind-harvesting systems with no moving parts [32] [33] [34].^FTN24 The latter share with vertical-axis wind turbines balanced weight distributions about their centers and occupying less space than horizontal-axis wind turbines—in addition to having no moving parts at all rather than merely fewer moving parts than horizontal-axis wind turbines. Perhaps Equations (A1) and (A2) could apply for nonrotary [32] [33] [34] wind-energy systems^FTNT25 and nonrotary water-energy systems if appropriate analogs of and were employed, and perhaps an equivalent of the Betz limit might (or might not) exist for nonrotary wind-energy and nonrotary water-energy systems.^FTNT25

In extraction of power by rotary devices (e.g., waterwheels, horizontal-axis windmills, vertical-axis windmills, and flying windmills [30] [31] ) from environmental fluid flows, always decreases monotonically with increasing, because environmental fluid flows cannot increase with increasing of the power-extracting device. By contrast, for artificial engines (e.g., internal combustion engines), this need not be the case, because fuel flow to an artificial engine can increase with increasing ω of the engine: hence can increase with increasing [35]. Nonetheless, fuel flow to an artificial (e.g., internal combustion) engine cannot increase with increasing indefinitely, and hence cannot increase with increasing indefinitely [35]. Thus also for artificial (e.g., internal combustion) engines, (brake) power output is maximized as per the first three paragraphs of this Appendix [35]. (Note: In Figure 63 on p. 130 of Ref. [35], the origins and of the and axes do not coincide. But this can be compensated for when employing Figure 63 on p. 130 of Ref. [35].)