ABSTRACT

This paper describes a new method of calculation of one-dimensional steady compressible gas flows in channels with possible heat and mass exchange through perforated sidewalls. The channel is divided into small elements of a finite size for which mass, energy and momentum conservation laws are written in the integral form, assuming linear distribution of the parameters along the length. As a result, the calculation is reduced to finding the roots of a quadratic algebraic equation, thus providing an alternative to numerical methods based on differential equations. The advantage of this method is its high tolerance to coarse discretization of the calculation area as well as its good applicability for transonic flow calculations.

Keywords:

Method of Calculation, Steady Compressible Flow, Channel with Perforated Sidewalls, Heat and Mass Exchange, Finite Size Elements, One-Dimensional Approach

1. Method’s Description

Let us consider a compressible gas flow along a channel with a variable cross- section area and perforated sidewalls through which heat and mass exchange is possible.

Let us divide this channel into many small elements of finite length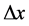. Cross-section 1 is the element’s entry and cross-section 2 is its exit (see Figure 1).

The mass, energy and momentum conservation laws for this element can be written in the following one-dimensional integral form:

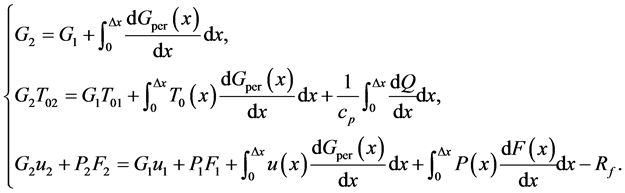(1)

Here:

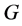―gas mass flow,

―total temperature,

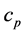―specific heat at constant pressure,

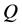―heat flow between the gas and the sidewalls,

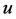―gas velocity,

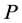―pressure,

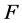―cross-section area,

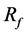―walls’ friction force.

Indices 1, 2, and “per” designate cross-sections 1 and 2 and perforation.

As the element’s length 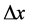is small, we may assume that the cross-section area and all the flow parameters are linearly distributed along the element’s length. Let us also assume that the longitudinal velocity of the cross-perforation flow is equal to the average longitudinal velocity of the main flow between cross- sections 1 and 2. This can happen if the pressure difference at the perforation holes is high enough to suck the gas from the core of the flow rather than from its boundary layer.

As such, the third equation of the system (1) can be re-written as follows:

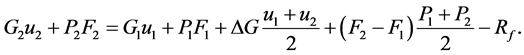(2)

Here: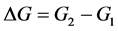―total mass flow through the perforation holes.

The walls’ friction force 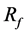can be described by the hydraulic relationship:

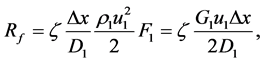
where―hydraulic friction coefficient depending on the walls’ roughness and Reynolds number,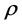―gas density,―hydraulic diameter of the element.

Let us transform the Equation (2) by dividing both its parts by and taking into account that:

After grouping the terms we shall have:

Now we should note that:

and, besides:

where:

―gas constant,

―static and total temperature,

―specific heat ratio,

―characteristic Mach number (the ratio of the local gas speed to the speed of sound under the sonic conditions).

After some transformations we shall obtain a quadratic algebraic equation for the characteristic Mach number at the element’s exit:

where:

(3)

(4)

(5)

The total temperature at the element’s exit included in the coefficient can be found from the second equation of the system (1), which describes the energy conservation law. The following variants are possible:

1) The additional gas is injected into the element through the perforation holes, and the total temperature of this gas is known. Then:

(6)

Here:

―total heat flow between the gas and the element’s walls.

2) The gas is partly sucked away from the element through the perforation holes. Then:

(7)

3) There is no mass exchange. Then:

(8)

4) There is no mass- and heat exchange. Then:

(9)

Thus, the characteristic Mach number at the element’s exit can be calculated by a simple algebraic formula:

(10)

where the coefficients, , and should be calculated by formulas (3)-(5) taking into account the relationships (6)-(9). “Plus” and “minus” signs before the root correspond to supersonic and subsonic solutions.

In case of a constant cross-section area and the absence of external influences (i.e. when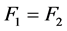,) this formula gives two trivial solutions:

The second solution describes a normal shock wave and therefore may physically exist just for.

Then all other gas parameters at the cross-section 2 can be easily found:

(11)

(12)

(13)

In such a manner, by dividing the channel into small discrete elements and sequentially calculating the flow parameters in each element with the help of relationships (10)-(13) we may calculate the gas flow along the whole channel. To complete this system of equations three additional conditions have to be taken into account:

・ The total pressure losses in the channel should be equal to the external pressure difference between the channel’s inlet and outlet. For subsonic flows this requirement can be met by iterative adjustment of the flow velocity at the channel’s entry. For supersonic flows this requirement can be met by iterative adjustment of the shock wave’s position inside the channel (i.e. finding the element in which the sign before the root in the Equation (10) should be changed from “+” to “−”).

・ The mass flow through the perforation holes should be calculated based on the pressure difference at the perforation holes and the size of these holes, taking into account the total pressure losses caused by the gas cross- perforation flow.

・ The heat flow should be calculated based on the temperature difference between the gas and the sidewalls.

2. Examples of Application

Figure 2 shows an example of the use of the considered method for the calculation of the static pressure recovery factor:

along the length (, where―length,―entry diameter) of a subsonic conical diffuser upon its division into n = 1, 2, 4 and 8 elements. Also shown is the experimental data from the work [1] . It can be seen that the considered method works even with very rough discretization of the calculation area. With an increase of the number of elements the calculation error quickly decreases.

One more advantage of this method is its good applicability for transonic flow calculations. Unlike numerical methods based on the known differential equation:

(14)

this method makes it possible to calculate flows at numbers very close to 1. The denominator in the Equation (14) turns into zero at, while in the considered method it is just radicand in the numerator in the Equation (10) that turns into zero.

Due to this feature, this method can be used for calculations of transonic gas flows in channels. Figure 3 shows an example of calculation of Mach number distribution along the length (, where―length,―entry width & height) of a perforated test section of a transonic wind tunnel. Also shown are the experimental results, obtained by the author in one of TsAGI’s wind tunnels.

As can be seen from Figure 3, the considered method makes it possible to successfully simulate such experimental effects as “suction nozzle” and “suction diffuser” (caused by the gas forced by suction through the perforation holes), as well as a system of shock waves in the end of the test section, which is simulated by one normal shock wave.

3. Conclusions

1) An algebraic method of calculation of one-dimensional steady compressible gas flows in channels is presented, which is an alternative to finite-difference methods.

2) The advantage of this method is its high tolerance to coarse discretization of the calculation area as well as its good applicability for transonic flow calculations.

Cite this paper

Tolmachev, A. (2017) Algebraic Calculation Method of One-Dimensional Steady Compressible Gas Flow. Open Journal of Fluid Dynamics, 7, 83-88. https://doi.org/10.4236/ojfd.2017.71006

References