Open Journal of Fluid Dynamics
Vol.06 No.04(2016), Article ID:72618,11 pages
10.4236/ojfd.2016.64025
Experimental and Numerical Investigation of the Solar Chimney Power Plant’s Turbine
Magdy Bassily Hanna1, Tarek Abdel-Malak Mekhail2, Omar Mohamed Dahab3, Mohamed Fathy Cidek Esmail2, Ahmed Rekaby Abdel-Rahman1*
1Faculty of Engineering, Mechanical Power and Energy Department, Minia University, Minia, Egypt
2Faculty of Energy Engineering, Mechanical Power Department, Aswan University, Aswan, Egypt
3Faculty of Engineering, Mechanical Power Department, Aswan University, Aswan, Egypt

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: October 5, 2016; Accepted: December 5, 2016; Published: December 8, 2016
ABSTRACT
The solar chimney power plant is a relatively new electricity generation concept, based on renewable energy, combining the greenhouse effect with the chimney suction. The solar chimney powerplant consists of three parts, the solar collector, the chimney and the turbine generator unit, of which the study was focused on the later part. To evaluate the turbine performance inside the solar chimney powerplant, experimental system was constructed in Aswan, Egypt that has a metrological site (23˚58'N and 32˚47'E) occurs. The system was constructed to evaluate the performance of the solar chimney turbine and power generation characteristic in the hottest site where Aswan is located at the nearest of the Tropic of Cancer at the summer season. Velocity, electric power generation and the turbine efficiency are studying in this work. The numerical analyses were performed by using a commercial code CFX, ANSYS 16.1 to simulate the flow through the turbine and overall system. The study shows that the range of power generated (1.2 W - 4.4 W). It can be estimated, according to the results, the variation trend in pressure drops with the turbine rotation speed increase with small differences when the turbine rotation speed surpasses 1800 rpm with average efficiency of 57%. It is concluded that the theoretical model is basically valid for the system under study, and the CFD simulation can be used conveniently to predict the performance of the system, the comparison between them and experimental result shows a good agreement.
Keywords:
Solar Chimney, Natural Convection, Turbine Modeling, CFD

1. Introduction
Current electricity production from fossil fuels like natural gas, oil or coal is damaging to the environment and stresses the limitation that it relies upon nonrenewable energy sources.
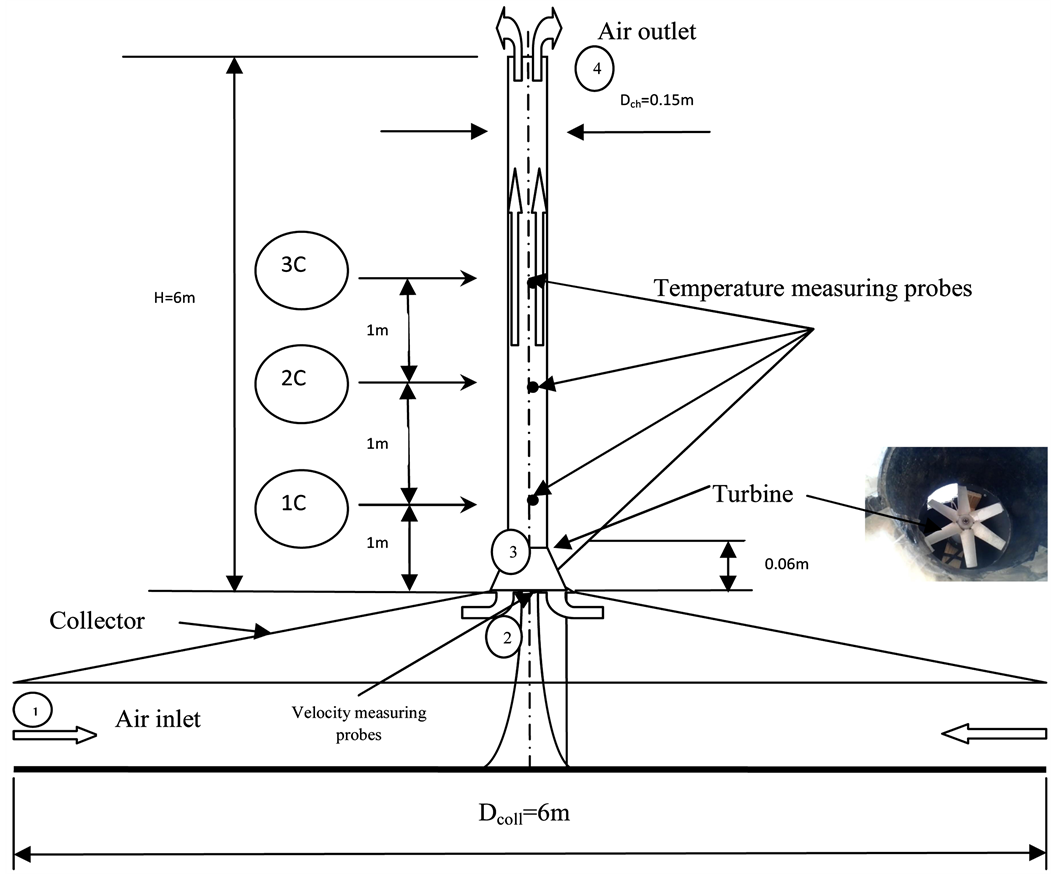
Solar chimney is simple and modern energy source also classified as efficient solar power technology. The solar chimney power plant system represents a possibility for the use of solar energy as a clean energy. It mainly consists of three components, namely, a solar collector, a chimney and turbine that work on the vertical axis. The layout of solar chimney power plant and its turbine are shown in Figure 1.
The collector consists of a circular transparent roof and the ground under the collector floor surface. Solar radiation heats the ground, which in turn heats the air under the collector roof like in a greenhouse. The hot air rises and escapes through the chimney.
Figure 1. Schematic diagram of a solar chimney power plant and its turbine.
The resulting airflow is used to generate electricity via one vertical turbine. Von Backström et al., vertical turbine has characteristics between those of wind turbines and gas turbines [1] it has more blades than the typical 2 or 3 of wind turbines, but not as much as gas turbines; the rotor blades are adjustable, like those of wind turbines, but, as in gas turbines, the flow is enclosed.
A single vertical axis turbine is used by Schlaich [2] , configurations with multiple vertical axis turbines or multiple horizontal axis turbines have also been proposed by Schlaich [2] .
More analytical models to predict the performance of solar chimney power plants have been proposed since the early 1980s. Haaf et al. [3] present a simple model, which they used for the design of the pilot plant in Manzanares. Pasumarthi and Sherif [4] show a more detailed model, which they verify against their own experimental results and results of the Manzanares pilot plant (Pasumarthi and Sherif) [5] . Gannon and Von Backström [6] adapted the standard gas turbine cycle to define a standard solar chimney cycle. Recent comprehensive models have been developed by Bernardes et al. [7] and Pretorius and Kröger [8] .
There are many studies carried out with small-sized physical models constructed on-site. Krisst (1983) [9] built a solar tower setup of 10 W in Connecticut, U.S.A., with its collector of 6 m diameter and 10 m height. Kulunk (1985) [10] demonstrated a plant with 9 m2 collector and 2 m high tower of 3.5 cm radius with power output of 0.14 W in Izmit, Turkey. Pasumarthi and Sherif (1998) [4] developed an approximate mathematical model for a solar tower plant and followed with a subsequent article (Pasumarthi and Sherif, 1998) [5] validating the model against experimental results from small- scale plant models in the University of Florida. In particular, the influence of various geometrical configurations on the performance and efficiency is investigated. Zhou et al. (2007) [11] built a pilot experimental setup in China with 10 m roof diameter and 8 m tower height and 0.3 m diameter, with a rated power of 50 W.
In the present study, the main aim of the study is to investigation the performance of a solar chimney power plant’s turbine with a single vertical axis by using CFX, ANSYS16.1 and performance measurements. Several days tested in Aswan city which has the metrological site nearest the Equator at summer season (23˚58'N and 32˚47'E). The test rig used; which is designed particularly for this experimental study was constructed to evaluate the overall performance of the turbine under different operating conditions.
2. System Description
The experimental test rig used in the present work to evaluate the solar chimney powerplant is shown in Figure 1. The test rig consists of solar collector, chimney, turbine and measuring instruments. The air stream flows from the ambient inlet to the solar collector that it can be warm up and flows through the chimney across turbine and it discharge into ambient through natural draft effect from chimney exist. In this work, the design, modeling and performance of the solar chimney turbine are studied. Main features of the plant are the collector diameter of 6 m, the chimney constructed from PVC pipe with a diameter of 0.15 m and height of 6, the collector is constructed using iron beams with wooden wired network use to support a clear plastic cover. The collector surface is designed with inclination with collector height from the ground of 0.25 m at the outer rim and 0.5 m at the inner core, the inner core and the outer rim of the solar collector are have 0.5 m and 3 m in diameter respectively. A single turbine with vertical axis with 0.02 m diameter at the hub and 0.144 m at tip.
The air speed was measured using PASCO’s data acquisition software which has uncertainty of ±0.1 m/s. The solar radiation is measured using Protective Glass Dome and Solar Shield (pyranometer) with uncertainty of ±0.1 W/m2. The revolution of the turbine rotor is measured using Extech 461895 Combination Contact/Photo Tachometer that has accuracy: 0.05% rdg +1 digit. Electric power can be measured using the device has the model no DT9025A can measure DC/AC voltage DC/AC current, resistance and capacitance. It also can be used for diode and continuity test.
3. The Modeling of the Turbine
The turbine with six blades can be modeled on the CFD simulation according, the geometry of the flow passage and the turbine is defined according to the geometry and dimensions of the test rig under this study (Table 1). The working fluid is assumed to be ideal gas. The speed of the rotor would be chosen according to the aero dynamic for the aerofoil selected for this turbine which it has a suitable characteristic for the low pressure turbine. The initial parameters can be evaluated by the axial components of
Table 1. Dimension of the turbine and the whole system.
the chimney inlet and the turbine exit flow velocities are optimized for turbine performance, the simulation can be achieved after about 8000 iterations in which the convergence occurs.
The commercial CFD code “CFX” (ANSYS, 16.1) has been a reliable tool to simulate the flow in solar chimney [12] . Consequently, the numerical model had been built using CFX in this work. The numerical mesh consists of 1,400,164 volume cells, 729,242 faces and 190156 nodes, the standard k-ε with wall functions was used. In this model, the eddy viscosity 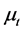 is evaluated from the turbulent kinetic energy k and the dissipation of the turbulent kinetic energy ε:
is evaluated from the turbulent kinetic energy k and the dissipation of the turbulent kinetic energy ε:
k and ε equations [13] :
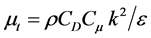 (1)
(1)
The grid independence was performed an investigation of grid independence was carried out to find the proper mesh. The test shows that the system with (1,400,164 elements) has logical results (Table 2).
4. Mathematical Model
The air inside a system is less dense than the atmospheric air outside. The air moves in and out of the solar chimney system continuously, driven by the pressure difference between the inside and outside. This pressure difference will be called the available driving pressure and symbolized as dptot. Neglecting friction losses [12] , dptot can be subdivided into a turbine extraction component representing the pressure extracted at the turbine, and a dynamic component describing the kinetic energy of the airflow [14] :
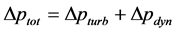 (2)
(2)
where subscript tot and dyn were referred to the differences in total and dynamic pressures around the turbine respectively
Let us define the ratio pturb/ptot as x, so that
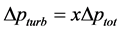 (3)
(3)
The optimal pressure ratio is defined as the following relation [14] ;
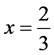 (4)
(4)
Table 2. Boundary conditions of the system model.
The available turbine power is computed using the following expression [14] ;
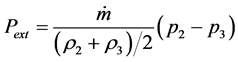 (5)
(5)
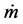 is the mass flow rate,
is the mass flow rate, 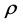 is the density of the air and
is the density of the air and  is the pressures of the air. Point 2 and 3 were referred to the positions before and after the turbine respectively.
is the pressures of the air. Point 2 and 3 were referred to the positions before and after the turbine respectively.
The efficiency of the turbine generator units can be defined as electrical power generated from turbine generator units with respect to the power extracted from the flow by the turbine.
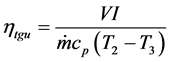 (6)
(6)
where V is the volt and I is the ampere.
The overall efficiency of the system can be defined as the ratio of the useful energy required to drive the turbine which it located at the base of the turbine to generates electricity to the total energy added to the solar chimney power plant, then the efficiency of the system is equal the result from multiplying the efficiencies of the solar collector which it was reasonable to adding heat to the working fluid of the plant, turbine-gene- rator, and the chimney that it is reasonable for up drafting the air to passes through the vertical turbine.
The role of the plant chimney is to convert the thermal flow brought into the solar collector 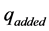 by the sun into the turbine specific work pext and kinetic energy at the exit. As indicated by Figure 1 chimney efficiency equals [15] [16] :
by the sun into the turbine specific work pext and kinetic energy at the exit. As indicated by Figure 1 chimney efficiency equals [15] [16] :
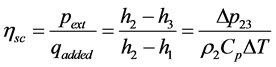 (7)
(7)
h is the enthalpy of the air Kj/kg, 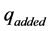 is the heat added to the air from the solar collector,
is the heat added to the air from the solar collector, 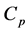 is a specific heat Kj/kg C. The main task of the turbine assembly is the efficient power transformation of a portion of the available working potential. The most important turbine loss in the solar chimney power plant (besides the internal fluid friction power loss) is the availability of the exit kinetic energy. In the case under consideration, the appropriate turbine efficiency
is a specific heat Kj/kg C. The main task of the turbine assembly is the efficient power transformation of a portion of the available working potential. The most important turbine loss in the solar chimney power plant (besides the internal fluid friction power loss) is the availability of the exit kinetic energy. In the case under consideration, the appropriate turbine efficiency 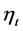 is defined as follows [16] :
is defined as follows [16] :

Which 
The overall plant efficiency 

5. Results and Discussion
In this section, The experimental results were discussed and finally the comparisons between the numerical results and the experimental results were discussed. The results in general are focusing on the days that they have the maximum recording values of the solar radiations (1200, 1150, 1100 W/m2) and the lower value of the solar radiations (1050 W/m2).
Figure 2 illustrates the output power from the turbine-generator unit that represents the electric power through all run days. It may be observed that the curves presenting all run days nearly has the same trend that the electrical power recorded from the beginning of the test day at 6:00 AM until 6:00 PM, the maximum value was recorded at 2:00 PM and then decreases until 6:00 PM. On the other hand; higher values of electrical power recorded at days 2nd, 4th, 6th June and 6th May. The output power generation from this system would be in range (1.2 W to 4.49W).
Figure 3 shows the effect of the average air outlet temperature from the solar collector on the turbine rotational speeds and the velocity at the chimney entrance. The fig shows that the rotational speed of the turbine increase with velocity of the chimney inlet significantly so with the increase in the average air outlet temperature. The reason is that, when all the other parameters such as the environment parameters and the solar radiation are constant, large amount of heat added to the flow in the solar collector increase the energy of the flow, that it was dissipated a part of this energy on the shape of kinetic energy at the chimney entrance. This kinetic energy was overcome the resistant force of the turbine rotor that is causing the turbine to run.
Figure 4 shows that the pressure drop (electrical power) across the turbine increases remarkably with the increase in the turbine rotation speed. The increase in pressure drop across the turbine means that an increasing part of driving force of the solar chimney power plant systems is used to drive the turbine. The variation trend in pressure drop with the turbine rotation speed increase with small differences when the turbine
Figure 2. Variation of the output power from the turbine-generator unit with time of days.
Figure 3. Effect of the average air temperature (Tao) on the turbine rotational speed and the velocity (Vch).
Figure 4. The effect of the turbine rotational speed on the output power.
rotation speed surpasses 1650 rpm, which means that the utilization of pressure drop of the system reaches up to its limitation, and it is not necessary to increase the turbine rotation speed any more.
The efficiency of the overall system (see Equation (9)) that is shown in Figure 5 the overall efficiency would be depend on the solar radiation, that is the increasing in solar radiation would be caused increasing in the overall efficiency of the plant that was recorded, the maximum average efficiency recorded in day 6th June that it has the maximum values of the solar radiation (2.3%). in general days (6th, 4th, 2nd June and 6th May) are have the following average efficiency of the overall system 2.37%, 2.0%, 1.5% and 1.1%. in spite of this value of the overall solar chimney power plant was low, the maximum efficiency of the solar chimney power plant in this study is specify as the high
Figure 5. Variation of the overall efficiency of the whole system with time of days.
value than Nizetic et al. [17] , for the reason of this fact, the chimney efficiency is very low, which causes substantial reduction in overall efficiency of SCPP. Chimney height which is directly proportional to its efficiency has a major impact on its efficiency.
Figure 6 shows the velocity vectors in detail in the turbine region, it can be easily seen from this figure that the velocity changes greatly around the turbine blades and especially at the tip of the blade, air velocity might be a few times larger than the main flow in the chimney.
Figure 7 shows that the numerical and the theoretical and experimental results of the overall system efficiency, the numerical result is higher than the experimental result by 8.4% and the theoretical result is higher than the experimental by 5.4%, Figure 6 shows that the simulation result for the available power for the turbine is higher than experimental results by 7.3%.
6. Conclusions
On the basis of the experimental, theoretical and numerical simulation results obtained for ten run days for solar chimney power plant with a 6-blade turbine manufactured and tested in Aswan, Egypt, the following conclusions can be drawn:
The ambient temperature, however, plays an important role in affecting power generation for the solar power plant. Most importantly, the performance of solar chimney was proportional to the outlet air temperature from the solar collector especially in the interval from 1:00 PM to 3:00 PM. It can be estimated, according to the results, that the operation rotational speed of the turbine might be selected as 1650 rpm with turbine average efficiency of 57%. It is concluded that the numerical model is basically valid for the solar chimney thermal power generating system, and the simulation with the model can be used conveniently to predict the performance of any system for solar chimney power generation, the comparison between them and experimental result shows a good agreement. Finally the maximum efficiency of the solar chimney power plant in this
Figure 6. Velocity vectors in the turbine region.
Figure 7. Comparison between available power input to the turbine experimental, mathematical model and numerical.
study is specified as the high value than it is in previous work according to the site that the study was performing in Aswan, Egypt.
Cite this paper
Hanna, M.B., Mekhail, T.A.-M., Dahab, O.M., Esmail, M.F.C. and Abdel-Rahman, A.R. (2016) Experimental and Numerical Investigation of the Solar Chimney Power Plant’s Turbine. Open Journal of Fluid Dynamics, 6, 332-342. http://dx.doi.org/10.4236/ojfd.2016.64025
References
- 1. Von Backström, T.W. and Gannon, A.J. (2004) Solar Chimney Turbine Characteristics. Solar Energy, 76, 235-241.
- 2. Schlaich, J. (1995) The Solar Chimney—Electricity from the Sun. Axel Menges.
- 3. Haaf, W., Friedrich, K., Mayr, G. and Schlaich, J. (1983) Solar Chimneys; Part I: Principle and Construction of the Pilot Plant in Manzanares. International Journal of Solar Energy, 2, 3-20.
http://dx.doi.org/10.1080/01425918308909911 - 4. Pasumarthi, N. and Sherif, S.A. (1998) Experimental and Theoretical Performance of a Demonstration Solar Chimney Model—Part I: Mathematical Model Development. International Journal of Energy Research, 22, 277-288.
http://dx.doi.org/10.1002/(SICI)1099-114X(19980310)22:3<277::AID-ER380>3.0.CO;2-R - 5. Pasumarthi, N. and Sherif, S.A. (1998) Experimental and Theoretical Performance of a Demonstration Solar Chimney Model—Part II: Experimental and Theoretical Results and Economic Analysis. International Journal of Energy Research, 22, 443-461.
http://dx.doi.org/10.1002/(SICI)1099-114X(199804)22:5<443::AID-ER381>3.0.CO;2-V - 6. Gannon, A.J. and Von Backström, T.W. (2000) Solar Chimney Cycle Analysis with System Loss and Solar Collector Performance. Journal of Solar Energy Engineering, 122, 133-137.
http://dx.doi.org/10.1115/1.1314379 - 7. Bernardes, M.A. dos S., Voβ, A. and Weinrebe, G. (2003) Thermal and Technical Analyses of Solar Chimneys. Solar Energy, 75, 511-524. http://dx.doi.org/10.1016/j.solener.2003.09.012
- 8. Pretorius, J.P. and Kröger, D.G. (2006) Solar Chimney Power Plant Performance. Journal of Solar Energy Engineering, 128, 302–311.
http://dx.doi.org/10.1115/1.2210491 - 9. Krisst, R.J.K. (1983) Energy Transfer System. Alternative Sources of Energy, 63, 8-11.
- 10. Kulunk, H. (1985) A Prototype Solar Convection Chimney Operated under Izmit Conditions. In: Veiroglu, T.N., Ed., Proceedings of the 7th Miami International Conference on Alternative Energy Sources, Vol. 162.
- 11. Zhou, X., Yang, J., Xiao, B. and Hou, G. (2007) Simulation of a Pilot Solar Chimney Thermal Power Generating Equipment. Renewable Energy, 32, 1637-1644.
http://dx.doi.org/10.1016/j.renene.2006.07.008 - 12. ANSYS. INC 2016.
- 13. Pastohr, H., Kornadt, O. and Gurlebeck, K. (2004) Numerical and Analytical Calculations of the Temperature and Flow Field in the Upwind Power Plant. International Journal of Energy Research, 28, 495-510. http://dx.doi.org/10.1002/er.978
- 14. Koonsrisuk, A. and Chitsomboon, T. (2009) A Single Dimensionless Variable for Solar Tower Plant Modeling. Solar Energy, 83, 2136-2143.
http://dx.doi.org/10.1016/j.solener.2009.07.015 - 15. Mullett, L.B. (1987) The Solar Chimney—Overall Efficiency, Design and Performance. International Journal of Ambient Energy, 8, 35-40.
http://dx.doi.org/10.1080/01430750.1987.9675512 - 16. Koonsrisuk, A., Lorente, S. and Bejan, A. (2010) Constructal Solar Chimney Configuration. International Journal of Heat and Mass Transfer, 53, 327-333.
http://dx.doi.org/10.1016/j.ijheatmasstransfer.2009.09.026 - 17. Nizetic, S., Ninic, N. and Klarin, B. (2008) Analysis and Feasibility of Implementing Solar Chimney Power Plants in the Mediterranean Region. Energy, 33, 1680-1690.
http://dx.doi.org/10.1016/j.energy.2008.05.012