Open Journal of Fluid Dynamics
Vol.04 No.03(2014), Article ID:49915,12 pages
10.4236/ojfd.2014.43024
Large Eddy Simulation of Pseudo-Shock Waves Using Wall Model
Sangwook Lee, Yousuke Ogino, Keisuke Sawada
Department of Aerospace Engineering, Tohoku University, Sendai, Japan
Email: lee@cfd.mech.tohoku.ac.jp, yogi@cfd.mech.tohoku.ac.jp, sawada@cfd.mech.tohoku.ac.jp
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 July 2014; revised 22 August 2014; accepted 12 September 2014
ABSTRACT
A supersonic turbulent flowfield involving the pseudo-shock waves in an isolator of a supersonic combustion ramjet is computed using two different LES codes which are a high-order upwind finite volume scheme, and a sixth order compact differencing scheme utilizing the localized artificial diffusivity method for stabilizing shock waves and employing a wall model to enable the use of coarse mesh. In the validation study where a supersonic turbulent boundary layer flow over a flat plate is examined, both LES codes are well validated using velocity profile in the boundary layer given by the hot-wire anemometry and normal stress given by the laser Doppler anemometry. In particular, the sixth order compact differencing scheme gives closer agreements with these experimental data. Then, the validated LES codes are applied to solve the Mach number 2.5 supersonic turbulent flowfield involving the pseudo-shock waves. It is shown that typical features of unsteady flowfield of the pseudo-shock waves are well obtained by both schemes. Again, it is indicated that the sixth order compact differencing scheme gives closer agreements with the existing velocity data obtained by particle image velocimetry and pressure fluctuation data on the wall surface. Besides, the computational cost of the compact differencing scheme is found to be 1/7 of that for the upwind finite volume scheme, even though a wall model is solved at each grid point on the wall surface. Therefore, the obtained results in the present study allow recommending the sixth order compact differencing scheme with a wall model for simulating supersonic turbulent flowfield in an isolator involving the pseudo-shock waves.
Keywords:
Large Eddy Simulation, Wall Model, Pseudo-Shock Wave

1. Introduction
For future high-speed propulsion system of aerospace vehicles, dual-mode ramjet engines have been investigated extensively in various institutions. However, according to the recent research reviews [1] [2] , there yet remain a lot of technical issues that must be resolved before putting them into practical use. One of such remaining issues is the proper control of pseudo-shock waves, known as pre-combustion shock waves that appear in the isolator of the engine. The pseudo-shock waves are a noteworthy interaction phenomenon between shock waves and boundary layer, which can alter the combustion mode from supersonic combustion to subsonic one. In most cases, the pseudo-shock waves composed of a series of oblique shock waves, X or lambda shaped shock waves, depend on the Mach number of the freestream and the boundary layer thickness. They include several shock waves, expansion fans, separation of boundary layer and slip lines. The pseudo-shock waves are known to help mix the injected fuel with oxidizer air flow, and to improve combustion efficiency. However, if the pseudo-shock waves go into the inlet due to higher back pressure caused by too much heat release in combustor, most of air cannot enter into the inlet, and the inlet then falls into an unstart condition. The aim of setting an isolator between the inlet and combustor is to contain and stabilize the pseudo-shock waves. A longer isolator can certainly contain the pseudo-shock waves stably, but it causes to increasing engine mass, frictional loss, and cooling requirement. In order to properly determine the isolator length, it is extremely important to have a capability of accurately predicting the possible length of the pseudo-shock waves at various inlet conditions.
Experiments [3] -[5] are very important to obtain the structure of the pseudo-shock waves, but it is sometimes difficult to collect detailed information about the flowfield of the pseudo-shcok waves because they emerge in supersonic flow in a duct. This shock wave is intrinsically an unsteady phenomenon and needs precise adjustment of the back pressure in the isolator. Furthermore, experimental studies are expensive because large scale facilities capable of operating over a wide range of Mach number are needed. An attempt to measure the pseudo-shock waves in flight experiment will be extremely high-cost. On the other hand, Computational Fluid Dynamics (CFD) can provide all the information of flowfield involving the pseudo-shock waves at a reasonable cost. The flowfield of the pseudo-shock waves was numerically studied using the Reynolds Averaged Navier-Stokes (RANS) equations [6] [7] . Because the RANS simulation cannot reproduce temporal evolution of turbulent structures, numerical studies have been rapidly shifted to utilize Large Eddy Simulation (LES). Although LES requires much higher computational cost than that for RANS simulation, LES is expected to provide both qualitative and quantitative information about complicated flowfield inside of an engine, particularly in the isolator where significant unsteady interaction of turbulent boundary layer and shock wave occurs.
LES calculation of the pseudo-shock waves in an isolator is not entirely new. For example, John et al. [8] carried out one such simulation. In their study, simulations of pseudo-shock waves were accomplished by utilizing a hybrid LES and RANS code. However, their computed results were not thoroughly validated through experimental data. Before utilizing LES for practical sizing of an isolator, it is indeed necessary to validate LES code using experimental data. In this study, we will first focus on the comparison of the computed mean streamwise velocity profiles and normal stress profiles with existing experimental data for a supersonic turbulent boundary layer on a flat plate. In addition, we will also attempt to justify the use of wall model in LES simulation combined with a sixth order compact differencing scheme with the localized artificial diffusivity model [9] in order to reduce computing time substantially. The computed results given by the higher-order upwind finite volume scheme employed in the previous study [10] are also compared with the experimental data. It is interesting to see the possible influence of numerical viscosity inherently involved in the computed results using an upwind scheme. Then, the pseudo-shock waves in an isolator are computed using these LES codes. Detailed comparisons are made with the existing experimental data to show that one of the present LES codes can reproduce turbulent flowfield involving the pseudo-shock waves fairly well.
In the following, we will first describe the numerical methods with the computed results of validation study in section 2, and then show the computational setup in section 3. The detailed comparisons of the computed results and experimental data are shown, and the related discussions are given in section 4. Finally, in section 5, we will give the conclusions obtained in this study.
2. Numerical Methods
2.1 Governing Equation and Subgrid-Scale Model
The governing equations are the spatially filtered mass, momentum, and energy conservation equations and the perfect gas equation of state [10] given below
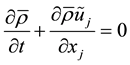 (1)
(1)
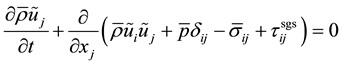 (2)
(2)
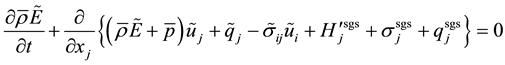 (3)
(3)
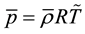 (4)
(4)
where the tilde ~ denotes the Favre filtering defined as , in which the overbar − represents the spatial filtering. The Favre filtered form of the total energy per unit mass is defined by
, in which the overbar − represents the spatial filtering. The Favre filtered form of the total energy per unit mass is defined by
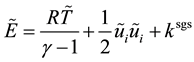 (5)
(5)
In above equations, 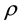 is the density,
is the density, 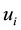 (i = 1, 2, and 3) are the velocity vector components in Cartesian coordinates
(i = 1, 2, and 3) are the velocity vector components in Cartesian coordinates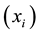 ,
, 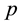 is the static pressure, T is the static temperature, and
is the static pressure, T is the static temperature, and 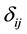 is the Kronecker’s delta, R (= 287 J/Kg×K) is the gas constant of air,
is the Kronecker’s delta, R (= 287 J/Kg×K) is the gas constant of air, 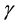 (= 1.4) is the ratio of the constant specific heats. These
(= 1.4) is the ratio of the constant specific heats. These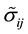 ,
, 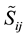 , and
, and 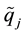 are given by
are given by
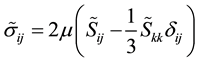 (6)
(6)


where 

The SGS (Subgrid-Scale) terms, denoted with the superscript sgs in the governing equations, need to be modeled in order to close the system of equations. The SGS stress tensor 

The selective mixed-scale model [11] is used to evaluate the SGS eddy viscosity. This model is categorized as a dynamic eddy viscosity model and was validated in supersonic channel flow [11] and subsonic crossflow jet [12] . The eddy viscosity is given by

where 






The SGS total enthalpy flux vector 

in which the filtered total enthalpy is defined by

and the turbulent Prandtl number of
2.2. Numerical Schemes
In this study, two different schemes described below are assessed for conducting LES of the pseudo-shock waves in an isolator.
1) Scheme A
It is a high order MUSCL TVD upwind finite volume scheme in which a third order interpolation is employed to evaluate the dependent variables at the interface of computational cells [13] . Because of the third order interpolation, the formal spatial accuracy of the scheme becomes fourth order for 1D problems but remains second order for multidimensional problems due to lower spatial accuracy in flux integration of finite volume formulation. This scheme has been successfully applied to yield highly resolved solutions for various problems including the previous study of LES for compressible flows [10] . The numerical convective flux at the cell interface is evaluated by the Simple Low-dissipation AUSM [14] (SLAU) scheme, which is a member of AUSM type upwind scheme, while the viscous terms are evaluated by the second order central differencing scheme. The time advancement is performed by using the classical third order Runge-Kutta scheme. The non-dimensional time step, defined as


2) Scheme B
The Navier-Stokes equations are solved using a sixth order accurate compact differencing scheme coupled with an eighth order lowpass spatial filter [15] . In order to capture shock waves stably, the localized artificial diffusivity method (LAD) [9] is employed. The fourth order Runge-Kutta method is adopted for time integration. The non-dimensional time step of 


where the eddy viscosity 

in which 




2.3. Validation of LES Schemes
A supersonic turbulent boundary layer on a flat plate is one of the fundamental compressible flowfields suitable for validation of LES codes. The simulated flow conditions are summarized in Table 1. The turbulent inflow is given by the rescaling method which will be mentioned in section 3. The computed results given by scheme A and scheme B are compared with the existing experimental data such as the velocity profile given by the hot- wire anemometry (HWA) and the normal stress given by the laser Doppler anemometry (LDA) appeared in [17] . The existing LES result of Sagaut et al. [17] is also compared with the present LES results.
Three different computational grids referred to as coarse (113 × 91 × 45), medium (159 × 121 × 61), and fine (225 × 170 × 89) are employed for scheme A in the present validation study, while another mesh summarized in Table 2 is employed for scheme B. The minimum mesh interval at the wall surface for scheme A computation is less than 


Figure 1 shows the computed 



In Figure 2, the computed normal stress profiles are compared with LDA experimental data and the LES result of Sagaut et al. [17] , where 


Table 1. Simulated flow conditions.
Table 2. Grid parameters for scheme B.
Figure 1. Comparison of 
Figure 2. Comparison of normal stress profiles.
those given by LDA data and also LES result of Sagaut et al. In addition, the normal stress profiles show a plateau in between 0.25δ and 0.75δ. On the other hand, the normal stress between 0.1δ and 0.25δ given by scheme B agrees well with LDA data, though a plateau also appears in between 0.25δ and 0.75δ. Similar tendency was also observed in the LES result of Sagaut et al. in between 0.1δ and 0.5δ.
It should be noted that scheme A does not attain a grid converged solution using the fine mesh. Among several possible reasons, this can be attributed most likely to the use of TVD limiter and use of upwind numerical flux in scheme A. The LES code attempts to resolve vortices of grid size, but the TVD limiter will inevitably limit the velocity peak of small vortices to yield velocity jump of order of grid size at the cell interface. This jump then results in to introduce numerical viscosity through the use of an upwind scheme. The larger 
The use of wall model in scheme B certainly enables us to employ a larger time step due to use of coarse mesh in near wall region. For the present supersonic turbulent flow over a flat plate, the computational cost to carry out LES using scheme A with the medium mesh is found seven times higher than that using scheme B.
3. Computational Setup
In the works of Choi et al. [18] and Hoshino et al. [19] , the pseudo-shock waves were measured in a duct having a square cross section whose height H was 30 mm and the length of the duct was 290 mm (9.67 H). The Mach number Ma was 2.5, the total pressure p0 was 100 kPa, and the total temperature T0 was 290 K at the inlet of the duct. The Reynolds number based on the duct height was 3 × 105. As shown in Figure 3, the computational meshes (Mesh A and Mesh B) discretize the entire duct region. Table 3 shows the parameters of these computational meshes. Mesh A is employed for scheme A, and mesh B for scheme B. The minimum mesh interval of mesh A satisfies both 

The turbulent inflow condition at the inlet is given by the multiwall rescaling method proposed by Boles et al. [20] which is an extension of the rescaling method introduced by Sagaut et al. [17] . The multiwall rescaling method is conducted in the domain enclosed by the dotted lines in Figure 3. As shown in the next section, the inflow exhibits large scale turbulent bulges and low speed streaks which are typical features of turbulent boundary layer flows. The validity of the given turbulent inflow is examined in terms of the boundary layer thickness and velocity profiles at the rescaling point chosen at 12δ form the inlet boundary.
4. Results and Discussions
In Figure 4, the instantaneous distribution of the streamwise velocity component computed by scheme B are plotted on the center plane, the exit plane and the horizontal plane which is slightly lifted from the bottom wall. One can find turbulent bulges and low speed streaks in between the inlet and the first shock wave. In addition, the x-shaped first shock wave on the center plane can be clearly seen. In the downstream of the first shock wave, there appear the second and third shock waves. Those shock waves are the characteristic feature of the pseudo-shock waves. The interaction of these shock waves with the unsteady turbulent boundary layer forms complicated flow structures involving separated flow regions that appear on the wall surface as well as at the corner region.
Figure 5 shows a comparison of the schlieren image taken at an arbitrary instant in the experiment [19] (top) with the computed images by scheme A (middle) using the medium mesh and that by scheme B (bottom). One can say that these schlieren images resemble each other. In particular, the intervals of the shock waves look quite similar. It seems, however, that the turbulent boundary layers in front of the foot of the first shock wave computed by both scheme A and scheme B become slightly thicker than that in the experiment. A detailed comparison of the computed schlieren images indicates that the first shock wave in near wall region given by scheme B is more clearly visible than that given by scheme A. Therefore, it can be said that the present compact scheme utilizing the local artificial diffusivity model (scheme B) can capture shock waves quite well in the complicated turbulent flowfield.
Figure 6 compares the mean streamwise velocity component plotted on several 

Table 3. Grid parameters.
Figure 3. Schematic illustration of computational domain.
Figure 4. Instantaneous distribution of the streamwise velocity component.
Figure 5. Comparison of schlieren images in the centerplane. Experiment (Top), scheme A (middle), and scheme B (bottom).
Figure 6. Comparison of streamwise mean velocity distributions plotted in 

of 


Figure 7 shows the velocity fluctuation intensities in the cross sections at 

Figure 7. The distributions of velocity fluctuation intensity for x, y, and z components in 

scheme A and the third row the scheme B, while those in the first column are the intensity of velocity fluctuation of x component, the second column the y component and the third column the z component. One can find that the computed velocity fluctuation intensities in the core region become weaker than the surrounding region. This tendency agrees well with the experimental data. The high intensities in x component of velocity fluctuation at four corners of the square cross section at 

The wall pressure distributions obtained in the experiment [19] , that computed by scheme A and by scheme B are shown in Figure 8. The computed pressures are averaged over 10 ms. The onset location of pressure rise on the wall surface was determined 
In Figure 9, the wall pressure fluctuations at





Figure 8. Comparison of wall pressure profiles.
Figure 9. Comparison of wall pressure fluctuations in the center plane at
Figure 10. Comparison of power spectrum density of pressure fluctuations at
(≈300 Hz) do appear as observed in Figure 9. In addition, high frequency components remain only in the computed pressure fluctuations. At
Finally, the root mean square (RMS) of pressure fluctuations along the centerline of the bottom wall is shown in Figure 11. One can find that these RMS rapidly increase at the foot of the first shock wave due to significant unsteady shock motions. Although the RMS of the computed pressure fluctuations upstream of the first shock wave becomes twice larger than that of the experimental data due to thicker turbulent boundary layer in
Figure 11. RMS profiles of pressure fluctuations.
the computed result as indicated in Figure 5, the obtained RMS by scheme B reasonably agrees with the experimental data behind the first shock wave, while that given by scheme A obviously overestimates the fluctuation level.
The computed results indicate that both scheme A and scheme B can obtain typical features of the pseudo- shock waves quite well. In particular, scheme B gives the computed results that are close to experimental data of velocity and pressure fluctuations, in addition to the overall unsteady flowfield where significant interaction of shock waves and turbulent boundary layer occurs. Because the computational cost of scheme B is substantially lower than that of scheme A, LES simulation of the pseudo-shock waves in an isolator now seems feasible. Future works will aim to enhance mixing of fuel and oxidizer air flow in combustion chamber utilizing the pseudo- shock waves in an isolator, and these will be presented elsewhere.
5. Conclusions
In the present study, a supersonic turbulent flowfield in an isolator involving the pseudo-shock waves is computed using two different LES codes. Scheme A is a high-order upwind finite volume scheme. Scheme B is a sixth order compact differencing scheme utilizing localized artificial diffusivity method to capture shock waves stably and employing a wall model to enable the use of coarse mesh at the wall surface. Followings are obtained in the course of the present study:
1) A supersonic turbulent boundary layer flow over a flat plate is computed by two LES codes (scheme A and scheme B). By comparing with the existing experimental data and the LES results, these two codes are successfully validated. In particular, closer agreements with the experimental data and also the LES results are shown when scheme B is employed in LES.
2) The validated LES codes are applied to solve the pseudo-shock waves in an isolator. Typical features of unsteady flowfield of the pseudo-shock waves are well obtained by both scheme A and scheme B. Again, it is shown that scheme B gives closer agreements with the existing experimental data of the pseudo-shock waves.
3) The computational cost of scheme B is found to be 1/7 of that of scheme A, even though the wall model is solved at each grid point on the wall surface.
4) Through comparisons, the obtained results in the present study allow recommending the compact differencing scheme with a wall model (scheme B) for simulating supersonic turbulent flowfield in an isolator involving the pseudo-shock waves.
Acknowledgements
The first author gratefully thank to Dr. Byuong-il Choi and Prof. Goro Masuya for providing experimental data and also for stimulating discussions. All the computations are conducted by SX-9 supercomputer at the Cyberscience Center, Tohoku University.
References
- Ronald, S.F. (2004) A Century of Ramjet Propulsion Technology Evolution. Journal of Propulsion and Power, 20, 27- 58. http://dx.doi.org/10.2514/1.9178
- Bouchez, M., Perillat, V., Avrashkov, V. and Kopchenov, V. (2011) Numerical and Experimental Scientific Investigation of Combustion in a Translating Cowl Dual-Mode Ramjet. 17th AIAA international Space Planes and Hypersonic Systems and Technologies Conference, San Francisco, 11-14 April 2011, 2011-2313
- Tamaki, T., Tomita, Y. and Yamane, R. (1970) A Study of Pseudo-Shock: 1st Report, λ-Type Pseudo-Shock. Japan Society of Mechanical Engineers, 13, 51-58. http://dx.doi.org/10.1299/jsme1958.13.51
- Waltrup, P.J. and Billig, F.S. (1973) Structure of Shock Wave in Cylindrical Duct. AIAA Journal, 11, 1404-1408. http://dx.doi.org/10.2514/3.50600
- Sullins. G. and McLafferty, G. (1992) Experimental Results of Shock Trains in Rectangular Ducts. AIAA 4th International Aerospace Planes Conference, Orlando, 1-4 December 1992, 92-5103.
- Sun, L.Q., Sugiyama, H., Mizobata, K. and Fukuda, K. (2003) Numerical and Experimental Investigations on the Mach 2 Pseudo-Shock Wave in a Square Duct. Journal of Visualization, 6, 363-370. http://dx.doi.org/10.1007/BF03181743
- Kawatsu, K., Koike, S., Kumasaka, T., Masuya, G. and Takita, K. (2005) Pseudo-Shock Wave Produced by Backpressure in Straight and Diverging Rectangular Ducts. AIAA/CIRA 13th International Space Planes and Hypersonic Systems and Technologies, Capua, 16-20 May 2005, 2005-3285.
- John, A.B., Hagenmaier, M.A. and Hsuet, K.Y. (2011) Analysis of Hybrid LES/RANS Simulations of a Back Pressured Supersonic Isolator. 47th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibition, San Diego, 31 July-3 August 2011, 2011-5825.
- Kawai, S. and Lele, S.K. (2008) Localized Artificial Diffusivity Scheme for Discontinuity Capturing on Curvilinear meshes. Journal of Computational Physics, 227, 9498-9526. http://dx.doi.org/10.1016/j.jcp.2008.06.034
- Watanabe, J., Kouchi, T., Takita, K. and Masuya, G. (2011) Numerical Study on Turbulent Structure of Transverse Jet into Supersonic Flow. AIAA Journal, 49, 2057-2067. http://dx.doi.org/10.2514/1.J051067
- Lenormand, E., Sagaut, P. and Ta Phuoc, L. (2000) Large Eddy Simulation of Subsonic and Supersonic Channel Flow at Moderate Reynolds Number. International Journal for Numerical Methods in Fluids, 32, 369-406. http://dx.doi.org/10.1002/(SICI)1097-0363(20000229)32:4<369::AID-FLD943>3.0.CO;2-6
- Dandois, J., Garnier, E. and Sagaut, P. (2006) Unsteady Simulation of a Synthetic Jet in a Crossflow. AIAA Journal, 44, 225-238. http://dx.doi.org/10.2514/1.13462
- Yamamoto, S. and Daiguji, H. (1993) Higher-Order―Accurate Upwind Schemes for Solving the Compressible Euler and Navier-Stokes Equations. Computers & Fluids, 22, 259-270. http://dx.doi.org/10.1016/0045-7930(93)90058-H
- Shima, E. and Kitamura, K. (2009) On New Simple Low-Dissipation Scheme of AUSM-Family for All Speeds. 47th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, 5-8 January 2009, 2009-136.
- Lele, S.K. (1992) Compact Finite Difference Schemes with Spectral-Like Resolution. Journal of Computational Physics, 103, 16-42. http://dx.doi.org/10.1016/0021-9991(92)90324-R
- Kawai, S. and Larsson, J. (2012) Wall-Modeling in Large Eddy Simulation: Length scales, Grid Resolution, and Accuracy. Physics of Fluids, 24, 015105. http://dx.doi.org/10.1063/1.3678331
- Sagaut, P., Garnier, E., Tromeur, E., Larcheveque, L. and Labourasse, E. (2004) Turbulent Inflow Conditions for Large-Eddy Simulation of Compressible Wall-Bounded Flows. AIAA Journal, 42, 469-477. http://dx.doi.org/10.2514/1.3461
- Choi, B., Takae, T., Kouchi, T. and Masuya, G. (2012) Mean and Turbullent Velocity Field for Jet Injected into Supersonic Flow with Pseudo-Shock Wave. Journal of Propulsion and Power, 28, 971-981. http://dx.doi.org/10.2514/1.B34371
- Hoshino, T., Kouchi, T. and Masuya, G. (2010) Stability of Pseudo-Shock Waves in a Straight Rectangular Duct installing Corner-Bumps. Proceedings of the 54th Space Sciences and Technology Conference, Shizuoka, 17-19 November 2010, JSASS Paper, 2010-4146. (in Japanese)
- Boles, J.A., Choi, J.I., Edwards, J.R. and Baurle, R.A. (2010) Multi-Wall Recycling/Rescaling Method for Inflow Turbulence Generation. 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, 4-7 January 2010, 2010-1699.
Nomenclature
E : Total energy
f : Frequency
G : Power spectrum
H : Duct height
H' : Total enthalpy
Ma : Mach number
p : Pressure
q : Heat flux
Re : Reynolds number
T : Temperature
t : Time
u : x component of velocity vector
v : y component of velocity vector
x : Streamwise coordinate
y : Vertical coordinate
z : Spanwise coordinate
μ : Molecular viscosity
δ : Boundary layer thickness
ρ : Density
κ : Thermal conductivity
τ : Shear stress
σ : Viscous stress
Subscripts
ave : Average value
match : Matching location
rms : Root mean square
w : Wall value
∞ : Free stream
Superscripts
sgs : Sub grid scale
+ : Wall unit quantity
’ : Fluctuation













