Received 30 April 2015; accepted 31 May 2015; published 3 June 2015

ABSTRACT

Mixing generated by gravitational acceleration and the role of local turbulence measured through multifractal methods is examined in numerical experiments of Rayleigh-Taylor and Richtmyer- Meshkov driven front occurring at density interfaces. The global advance of the fronts is compared with laboratory experiments and Nusselt and Sherwood numbers are calculated in both large eddy simulation (LES) and kinematic simulation KS models. In this experimental method, the mixing processes are generated by the evolution of a discrete set of forced turbulent plumes. We describe the corresponding qualitative results and the quantitative conclusions based on measures of the density field and of the height of the fluid layers. We present an experimental analysis to characterize the partial mixing process. The conclusions of this analysis are related to the mixing efficiency and the height of the final mixed layer as functions of the Atwood number, which ranges from 9.8 × 10⁻³ to 1.34 × 10⁻¹.

Keywords:

Rayleigh-Taylor Instability, Richtmyer-Meshkov Instability, Mixing Efficiency, Front Evolution, Fractal Dimension

1. Introduction

Numerical results on the advance of a mixing or non-mixing front occurring at a density interface due to gravitational or forced acceleration are analyzed considering the fractal structure of the front; the numerical simulations are compared with experiments both when the gravitational acceleration is responsible for the mixing and when a suddent acceleration (shock) forces the mixing. The first case constitutes a Rayleigh-Taylor (RT) instability driven mixing front, and the second case forces Richtmyer-Meshkov (RM) instability that produces further mixing coupled with heat and mass transport. The instability produced, RT in its simplest forms, occurs when a layer of dense fluid is placed on top of a less dense layer in a gravitational field. On the other hand, if a stable two fluid layer configuration accelerating (e.g. falling in a gravitational field) is suddenly decelerated, then RM develops during the short time that the upward acceleration dominates gravitational acceleration, g.

In almost all practical circumstances, at high Reynolds number, the instabilities form a turbulent front between the two layers, which in principle should become independent of the initial conditions as turbulence develops. The advance of this front is described in [1] [2] when forced by RT and in [3] driven by RM.

The Rayleigh-Taylor front thickness evolves in time as δ = 2cgΑτ² where δ is the width of the growing region of instability, g is the gravitational acceleration and A is the Atwood number defined as

(1)

where ρ₁ is the density of the upper layer and ρ₂ is the density of the lower layer.

A large eddy simulation numerical model using FLUENT as well as a dedicated code was used to predict some of the features of the experiments. Different models on the interaction of the bubble generated buoyancy flux and on the boundary conditions are compared with the experiments. The aspect ratios of the bubble induced convective cells are seen to depend on the boundary conditions applied to the enclosure.

In the context of determining the influence of structure on mixing ability, multifractal analysis is used to determine the regions of the front which contribute most to molecular mixing. Both the global and local Nusselt and Sherwood numbers are calculated.

2. Front Evolution

The stability of an interface between two superposed fluids of different density was studied by Taylor [4] for the case when the dense fluid is accelerated towards the less dense fluid, the linear theory can be found in [5] . For inviscid fluids, the interface is always unstable, with the growth rate of the unstable modes increasing as their wavelengths decrease. The instability of the short waves can be reduced by dissipative mechanisms such as surface tension or viscosity, and then linear theory predicts the maximum growth rate to occur at a finite wavelength. For the viscous two-layer case, where the upper layer (density ρ₁) is denser than the lower layer (density ρ₂), the wavelength λ_m of maximum growth rate is

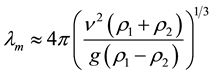(2)

where ν is the mean kinematic viscosity of the two layers and g is the acceleration of gravity. The corresponding maximum growth rate is

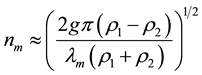(3)

While the linear theory for two infinite layers is well established, the development of the instability to finite amplitude is not amenable to analytic treatment. There have been a number of semi-analytical and numerical studies in recent years, but they all involve simplifying assumptions which raise serious doubts about their validity particularly when applications to mixing are sought. The RT front may be characterized by the development of the instability through three stages before breaking up into chaotic turbulent mixing. First, a perturbation of wavelength λ_m grows exponentially with growth rate n_m. Second, when this perturbation reaches a height of approximately 1/2 λ_m, the growth rate decreases and larger structures appear. And third, the scale of dominant structures continues to increase and memory of the initial conditions is supposedly lost; viscosity does not affect the latter growth of the large structures. This result concerning the independence of the large amplitude structures on the initial conditions has led to consider that the width of the mixing region depends only on ρ₁, ρ₂, g and time, t. Then dimensional analysis gives

(4)

where c is considered to be a (universal) constant. The value of the constant c, has been investigated experimentally and its value for experiments at different values of the Atwood number, A, do not show large variations, with a limit clearly seen for the larger A experiments performed. Values of c previously obtained experimentally have been in the range (0.03, 0.035) in experiments with three dimensional effects and large density differences between the two fluids, A ≥ 1.5 [6] [7] . Ref. [1] measured c for values of A in the range 1 × 10⁻⁴ to 5.0 × 10⁻² and found values of c = 0.035 ± 0.005. Numerical calculations in two dimensions gave values of c in the range (0.02, 0.025). The smaller values are explained in terms of two dimensional effects inhibiting the growth of the large scale.

In a similar way as in the experiments a Rayleigh-Taylor mixing front has been simulated using FLUENT in the large eddy simulation small scale parameterization mode. See Figure 1 for sequences of the advance of the mixing front, using the non-dimensional time described above. The global aspects of the mixing front are seen to depend strongly on the random initial perturbation as found by [2] .

The structure of the RM instability has a very different evolution as Figure 2 shows. The growth of the mixing zone is linear in time, and is proportional to the velocity resulting from the integral of the suddent acceleration during the shock time. A similarity solution may be also described linearly dependent on time.

Nusselt and Sherwood Numbers

The global mass and heat flow may be evaluated if the two different miscible layers have different solute concentrations and different temperatures. In the model as well as in the experiments the density difference may be caused by both salt and heat. The Prandtl number for water is Pr = 6.8 and the Schmidt number for brine is Sc = 812 at 22˚C. The Sherwood number defined as Sh = h_mL/D and the Nusselt Number Nu = hL/k_f were calculated as averages over the center region of the interfacial region leaving D/4 to the sides of the numerical domain (or

experimental box sides) to avoid lateral influences from the walls. Concerning the fractal analysis, it is usually used to identify different dynamic processes that might influence the flow.

The box-counting algorithm, able to detect the self-similar characteristics for different image intensity levels, This technique is used in the Numerical simulations for velocity, vorticity and volume fraction images reflecting a physical aspect that is advected by the RT or RM flows, we can thereby define the fractal dimension D(i) as a function of the intensity i of the relevant variable. This dimension is calculated using the box counting method (see Figure 3). A convoluted line, which is embedded in a plane (that is why it is usually referred to as D2, or fractal dimension within an Euclidean plane of dimension 2). If it is a single Euclidean line, its (non-fractal) dimension will be one. If it fills the plane its dimension will be two. The box-counting algorithm divides the embedding Euclidean plane in smaller and smaller boxes (e.g., by dividing the initial length L₀ by n, which is the recurrence level of the iteration). For each box of size L₀/n it is then decided if the convoluted line, which is analysed, is intersecting that box. The number N(i) is the number of boxes which were intersected by the convoluted line (at intensity level i). For example, Table 1 shows that different regions of the flow have different maximum fractal dimensions D(i).

3. Results and Discussion

Figure 4 shows the evolution of the multifractal dimension (calculated performing the box-counting algorithm) for each level of velocity modulus (a) and volume fraction (b). Much more relevant information can be extracted from these evolutions than from the maximum value presented by [2] , furthermore it is of great interest to study independently the fractal properties of velocity, volume fraction and vorticity fields. The fact that the RT front is

accelerating is reflected in Figure 4 (left) that shows how initially there is a small range of velocities and the regions of higher velocity take some time to develop a fractal structure. It seems that precisely these “fast vortical spots” that lie at the sides of the bubbles and spikes are responsible for most of the transport. More work is still needed in order to fully interpret the results of the fractal analysis, but it is interesting to compare changes in the fractal dimension with other experimental set ups. Information about the mixing can be extracted from the thickening of the edges due to the phenolphthalein color change in [2] , or in the numerical simulations, and this thickness can be now analyzed with a digitizer system. For lower density runs with phenolphthalein, it was apparent that the vorticity originated by the plate increased mixing at the center of the vortices produced by it. This effect can be avoided using intermediate density differences. Both in the experiments and in the numerical simulations the fractal evolution that indicates a transition to a turbulent flow is apparent as shown in [2] by the increase in the maximum fractal dimension of the interface center (50/50 mixing ratio) between D_max = 1 and 1.4. The spectra and fractal aspects of the numerical simulations are compared with the experiments, for example inFigure 4 (right) scatter-plot of the multi-fractal dimension at two times of the different volume fractions of the front indicates its non-uniform curdling.

4. Conclusions

The regions of higher local fractal dimension increase, both in number and with higher values as time evolves for both the RT and the RM experiments until a non-dimensional time of 3 - 4. After that time, the decrease of the RM front is faster than that of the RT. On the other hand, the RM fronts achieve faster a self similar fully turbulent level that corresponds to a fractal dimension of 1.4 - 1.5 for a wide range of velocities and volume fractions. Both the Sherwood and Nusselt numbers depend on the maximum fractal dimensions. The results may be also interpreted using a kinematic simulation model to investigate the role of different espectral cascade pro- cesses at the smallest scales down to the Batchelor scales [8] . The generalized Richardson’s law consists on supposing that the relative dispersion D² of two particles in a turbulent flow varies in time as D² ~ t^a, and then finds out the relationship between p (the order of the structure function) and the potential dispersion in time, a. Ref. [9] found out, by dimensional analysis, supposing that the relative dispersion D² is only function of the energy spectra E(D) ~ D^β at the considered scale and time t, that

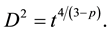(5)

But as argued and shown by [8] , for β > 3, the experimental results do not match with this theoretical formula but rather stabilize towards a constant 4 - 8 depending on whether the total energy is maintained constant or just the energy of the integral scales is maintained constant. It is interesting to relate D(i) to the frequency spectrum or to the spatial spectra obtained from the Fourier transform of the time or spatial correlation functions, usual in studies of turbulence. The reason is that from such frequency spectra the corresponding fractal dimension may be derived, if the tracer scalar is passively advected by a turbulent flow. Then the fractal dimension might be related to the energy of the turbulence with a certain spatial or temporal dependence, which is usually termed as intermittency, then the frequency spectrum exponent, provided an inertial sub-range exists, is also a function of the box-counting fractal dimension as demonstrated by [10] .

Acknowledgements

Support from European Union through ISTC-1481 and INTAS-projects, and from MCT-FTN2001-2220 and DURSI XT2000-0052 local projects are acknowledged. Thanks are also due to the Pluri Disciplinary Institute of the Complutense University of Madrid.

References