Open Journal of Fluid Dynamics
Vol.2 No.3(2012), Article ID:22532,10 pages DOI:10.4236/ojfd.2012.23010
Lattice Boltzmann Simulations in the Slip and Transition Flow Regime with the Peano Framework
Faculty of Informatics, TU München, Munich, Germany
Email: neumanph@in.tum.de
Received May 15, 2012; revised June 22, 2012; accepted July 15, 2012
Keywords: Lattice Boltzmann; Microflows; Knudsen Number; Channel Flow; Transition Flow; Slip Flow
ABSTRACT
We present simulation results of flows in the finite Knudsen range, which is in the slip and transition flow regime. Our implementations are based on the Lattice Boltzmann method and are accomplished within the Peano framework. We validate our code by solving twoand three-dimensional channel flow problems and compare our results with respective experiments from other research groups. We further apply our Lattice Boltzmann solver to the geometrical setup of a microreactor consisting of differently sized channels and a reactor chamber. Here, we apply static adaptive grids to further reduce computational costs. We further investigate the influence of using a simple BGK collision kernel in coarse grid regions which are further away from the slip boundaries. Our results are in good agreement with theory and non-adaptive simulations, demonstrating the validity and the capabilities of our adaptive simulation software for flow problems at finite Knudsen numbers.
1. Introduction
The investigation of microflows and rarefied gases is a crucial step in the development of many micro-electromechanical systems. The respective devices—micro-actuators, -jets, -sensors or -pumps—find application in a multitude of different fields ranging from medicine and biotechnology to safety technology and home electronics. As improvements in manufacturing technology yield a further miniaturisation of these objects, simulation methods need to be provided to allow for flow studies on the microscale. Simulations on the molecular level are still too expensive for setups which are relevant for realworld applications, so that macroor mesoscopic methods are required. It has been shown by several groups that standard continuum descriptions such as the incompressible Navier-Stokes equations are not valid anymore in several microflow scenarios (see amongst others [1]), due to the molecular length scales reaching the same size as the characteristic length scale of the underlying flow problem. This effect implies a non-vanishing, but finite Knudsen number Kn which is defined as
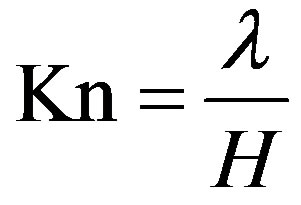 (1)
(1)
and relates the molecular mean free path λ to the characteristic length scale H of the flow problem. Table 1 lists the different flow regimes, depending on the Knudsen number. Different methods have been proposed over the last years to extend existing continuum approaches to the finite Knudsen regime, i.e. to the slip and transition flow regime [2-8]. In this context, the Lattice Boltzmann method (LBM) has attracted particular attention, due to its kinetic origin and implementational simplicity. However, only few publications address the application of the LB approach to practical problems [9], such as [10].
In the present contribution, we present the extension of our existing adaptive LBM implementation within the Peano framework [11] to the slip and transition flow regime. The methods are based on the models proposed in [2] and [6], respectively.
We shortly review the methodology of the LBM and its extensions and give a short overview of the existing LBM application within the Peano framework in Section 2. We validate our implementation for twoand threedimensional channel flow scenarios in Section 3, comparing our results with those of other research groups. Within the same section, we present numerical results for

Table 1. Different flow regimes can be characterised via the Knudsen number [12].
flow simulations in a microreactor, given by a complex network of differently sized ducts and a reaction chamber. We use static adaptive grids to allow for a fine resolution of the small ducts and a coarser representation of the reactor chamber. We point out the advantage of using adaptive grids for the respective scenario types with respect to both accuracy and computational efficiency. Finally, we draw a short conclusion and give an outlook to future work in Section 4.
2. Theory
2.1. The Lattice Boltzmann Method
The Lattice Boltzmann method (LBM) is derived from the Boltzmann equation by breaking down the velocity space to a finite set of lattice velocities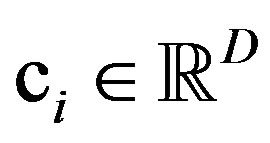 ,
,  , where D denotes the dimension of space. Populations of molecules
, where D denotes the dimension of space. Populations of molecules 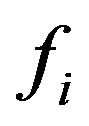 that are associated with each lattice velocity collide in each cell
that are associated with each lattice velocity collide in each cell 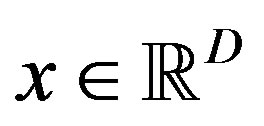 at time
at time 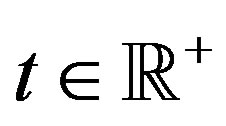 and are propagated to the respective neighbour cells following the update rule:
and are propagated to the respective neighbour cells following the update rule:
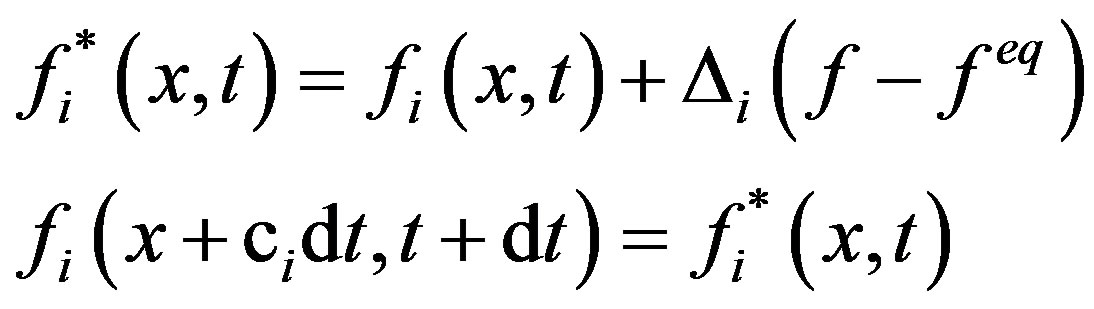 (2)
(2)
where 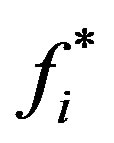 denotes the post-collision state of the distributions,
denotes the post-collision state of the distributions, 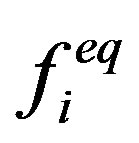 the equilibrium state [14] and dt the time step. The molecular interaction is described by the collision operator
the equilibrium state [14] and dt the time step. The molecular interaction is described by the collision operator 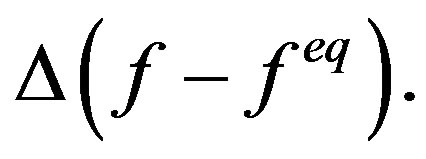 Different models for
Different models for 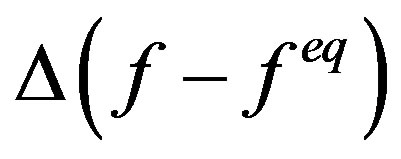 have been previously proposed; in the following, we will consider the single-relaxation-time (BGK) model [15] and the multiple-relaxation-time (MRT) scheme [16-18]. The BGK collision operator is given by
have been previously proposed; in the following, we will consider the single-relaxation-time (BGK) model [15] and the multiple-relaxation-time (MRT) scheme [16-18]. The BGK collision operator is given by
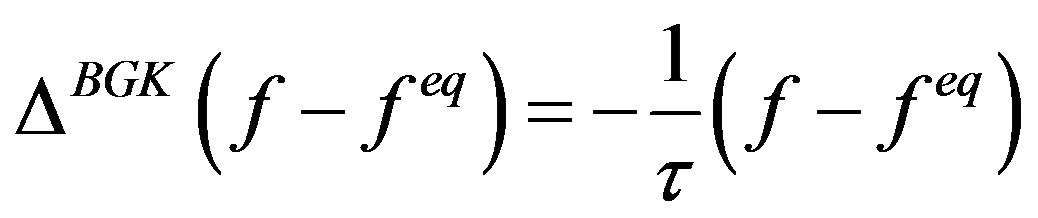 (3)
(3)
where 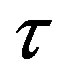 is the relaxation time of the fluid; the relaxation time is uniquely defined by the kinematic viscosity
is the relaxation time of the fluid; the relaxation time is uniquely defined by the kinematic viscosity 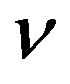 of the fluid,
of the fluid, 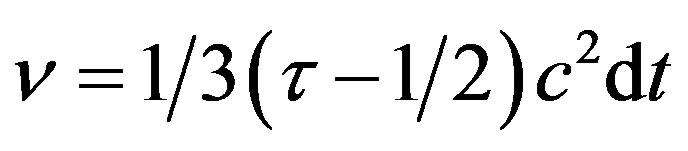 with
with 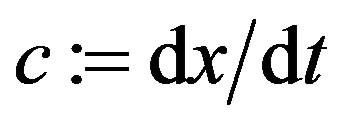 and lattice spacing
and lattice spacing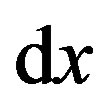 . Due to its simplicity and its low computational costs, the BGK approximation is most commonly used for macroscopic flow considerations. The multiple-relaxation-time scheme carries out the relaxation of the moments instead of relaxing the non-equilibrium parts
. Due to its simplicity and its low computational costs, the BGK approximation is most commonly used for macroscopic flow considerations. The multiple-relaxation-time scheme carries out the relaxation of the moments instead of relaxing the non-equilibrium parts 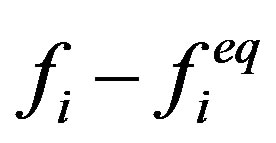 directly. It is described by
directly. It is described by
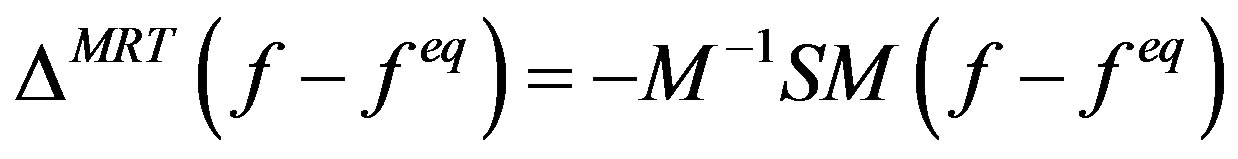 . (4)
. (4)
The matrix  refers to the transformation matrix from the velocity to the moment space, and
refers to the transformation matrix from the velocity to the moment space, and 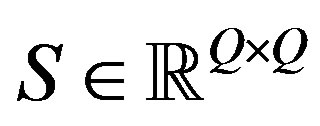 is a diagonal matrix containing the relaxation parameters for the single moments. It has been shown [16] that the MRT collision operator is approximate 15% computationally more expensive than BGK methods and has better stability properties [18].
is a diagonal matrix containing the relaxation parameters for the single moments. It has been shown [16] that the MRT collision operator is approximate 15% computationally more expensive than BGK methods and has better stability properties [18].
2.2. Extension to Finite Knudsen Numbers
Based on kinetic theory, the LBM provides a natural access to microscale modeling, and different extensions have been proposed over the last years to extend the method to the range of finite Knudsen numbers.
Niu et al. [19] extended the entropic model from Ansumali and Karlin to the finite Knudsen range, introducing a relation between the Knudsen number and the relaxation time 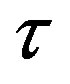 and adopting the respective diffuse boundary condition to include velocity slip. Works into similar directions have been published at about the same time by Tang et al. [3]. Sbragaglia and Succi presented a new formulation of kinetic boundary conditions for flows at finite Knudsen numbers in [20]; therefore, they proposed models based on slip, reflection and accomodation coefficients. Toschi and Succi proposed a stochastic handling of finite Knudsen number flows within the context of Lattice Boltzmann simulations in [4]. Virtual wall collisions of the Lattice Boltzmann particles are incorporated into the Lattice Boltzmann model, yielding satisfactory results for flow regimes up to Knudsen numbers ~30. Zhang et al. report a successful qualitative Knudsen minimum prediction in [21]. Their results show good agreement for Knudsen numbers up to ~0.4 and only differ for higher numbers, due to numerical errors induced by the increasing value of the BGK-relaxationtime
and adopting the respective diffuse boundary condition to include velocity slip. Works into similar directions have been published at about the same time by Tang et al. [3]. Sbragaglia and Succi presented a new formulation of kinetic boundary conditions for flows at finite Knudsen numbers in [20]; therefore, they proposed models based on slip, reflection and accomodation coefficients. Toschi and Succi proposed a stochastic handling of finite Knudsen number flows within the context of Lattice Boltzmann simulations in [4]. Virtual wall collisions of the Lattice Boltzmann particles are incorporated into the Lattice Boltzmann model, yielding satisfactory results for flow regimes up to Knudsen numbers ~30. Zhang et al. report a successful qualitative Knudsen minimum prediction in [21]. Their results show good agreement for Knudsen numbers up to ~0.4 and only differ for higher numbers, due to numerical errors induced by the increasing value of the BGK-relaxationtime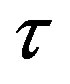 . In order to suppress artificial slip effects near walls, Verhaeghe et al. [6] propose a MRT-based model, including a particular tuning of the relaxation parameters. Their results show excellent agreement in the slip flow regime, however, they point out deficiencies of the slip flow model for higher Knudsen numbers. A respective extension to the transition flow regime has been developed recently by Li et al. [2]. Another approach to rarefied gas modeling using Lattice Boltzmann methods is reported in [22,23] where—based on the Hermite projection method—higher-order Lattice Boltzmann models are constructed and yield promising results for both slip and transition flow regime.
. In order to suppress artificial slip effects near walls, Verhaeghe et al. [6] propose a MRT-based model, including a particular tuning of the relaxation parameters. Their results show excellent agreement in the slip flow regime, however, they point out deficiencies of the slip flow model for higher Knudsen numbers. A respective extension to the transition flow regime has been developed recently by Li et al. [2]. Another approach to rarefied gas modeling using Lattice Boltzmann methods is reported in [22,23] where—based on the Hermite projection method—higher-order Lattice Boltzmann models are constructed and yield promising results for both slip and transition flow regime.
Though a variety of models has been published over the last years, only few models have been extended to practical use cases, such as simulations in complex geometries [24] or three-dimensional scenarios [25].
In the following, we shortly describe the models that our implementations are based on; see [2,6,26] for detailed discussions. We subsequently describe a simple bounce-back based extension for geometrical setups of branched duct structures; all our discussions apply analogously to twoand three-dimensional scenarios.
Stepping towards the finite Knudsen number regime, the dynamic viscosity 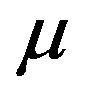 of the fluid cannot be considered constant anymore, due to the strong impact of the
of the fluid cannot be considered constant anymore, due to the strong impact of the
 (a)
(a)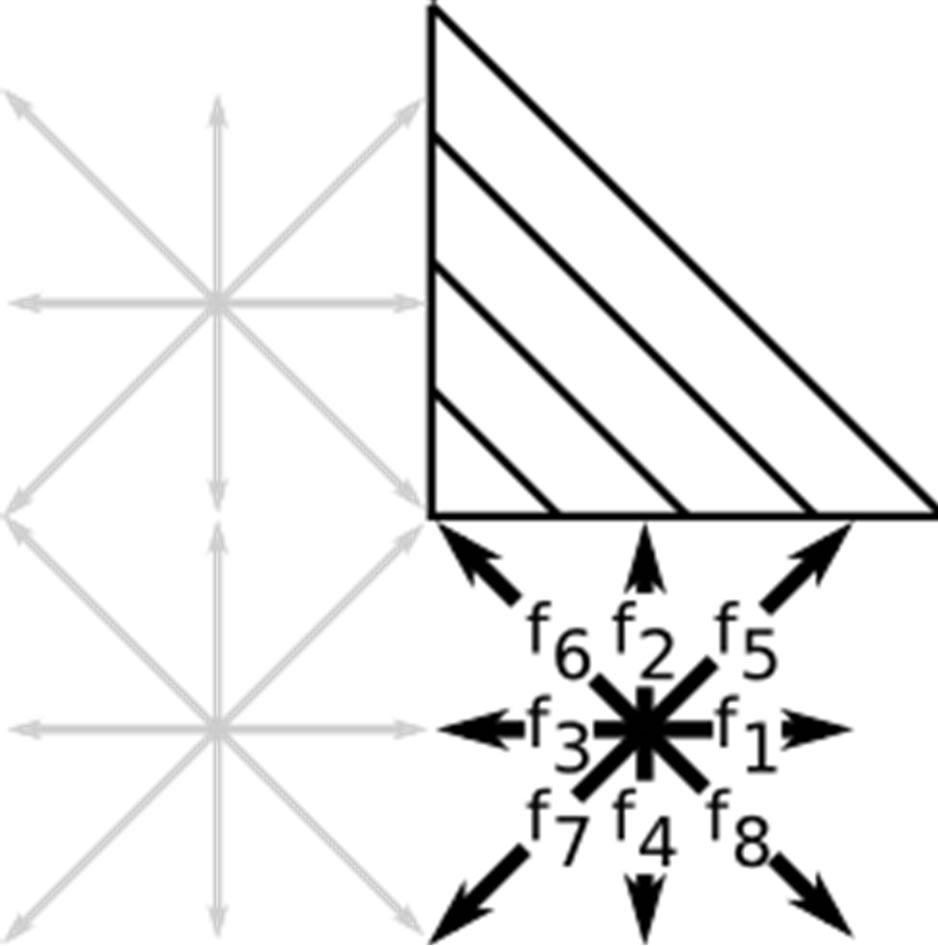 (b)
(b)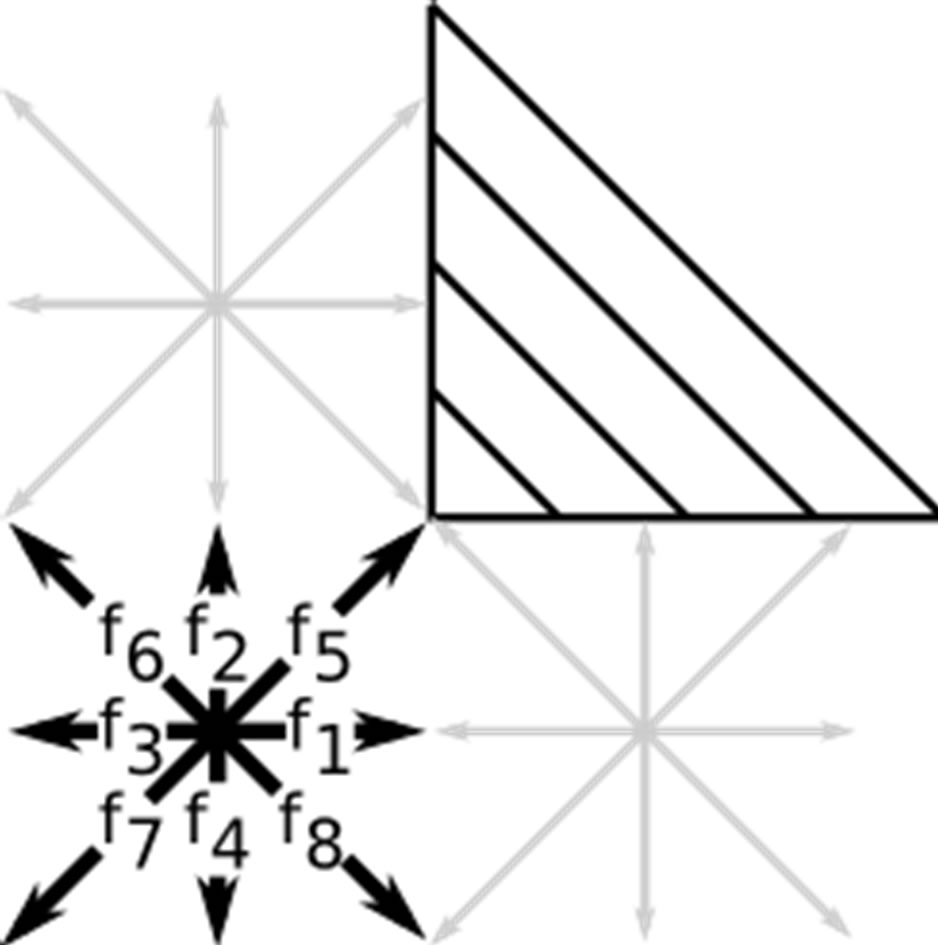 (c)
(c)
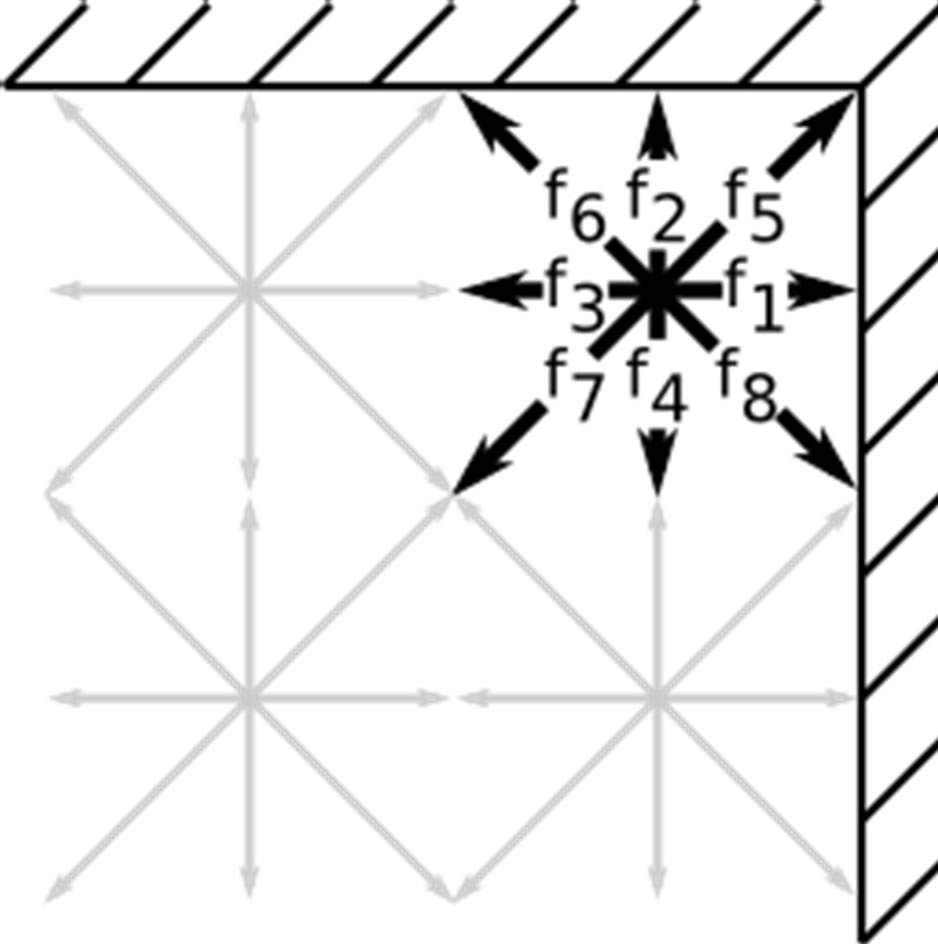
Figure 1. Corner cells (a), cells adjacent (b) or diagonally adjacent (c) to wall corners demand special treatment when using combined bounce-back specular reflection boundary conditions.
walls on the micro-scale simulation. Near walls, the molecular mean free path is significantly shortened as molecules may collide with the walls. This yields a reduction of the dynamic viscosity. Several methods have been proposed to account for this reduction, see amongst others [8,26-29]. We apply the viscosity adjustment presented in [26] where a Bosanquet-type of expression is proposed for the effective viscosity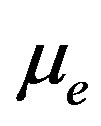 :
:
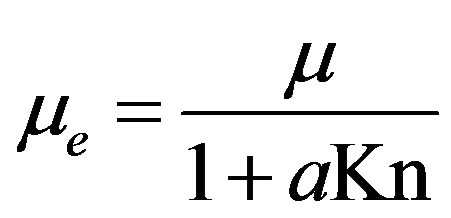 (5)
(5)
where 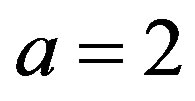 produces a good approximation over a wide range of Knudsen numbers [30]. The Knudsen number Kn is given by the expression proposed by [2]:
produces a good approximation over a wide range of Knudsen numbers [30]. The Knudsen number Kn is given by the expression proposed by [2]:
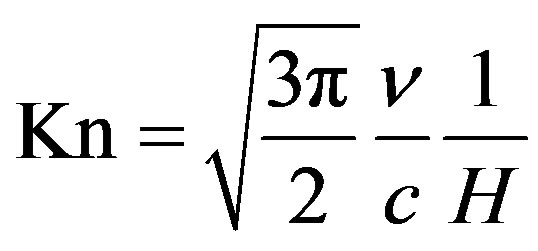 (6)
(6)
where  is the characteristic length scale of the problem.
is the characteristic length scale of the problem.
Besides, the no-slip condition which is used to model walls in most macro-scale flow simulations, is not valid anymore in the micro-regime. Additional slip occurs and needs to be incorporated into the boundary conditions, respectively. For simulations in the slip flow regime, we apply a combination of the standard bounce-back and diffusive reflective (BBDR) boundary condition [6]:
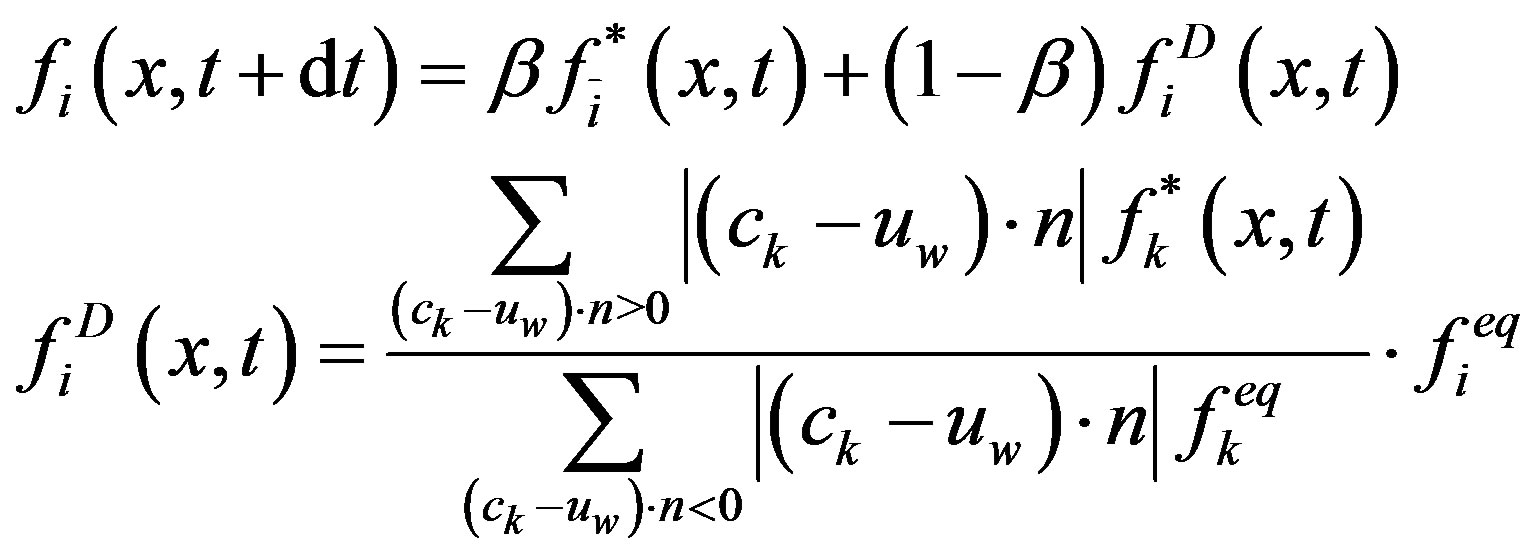 (7)
(7)
where 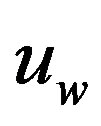 denotes the velocity at the wall, n the outward-pointing normal of the boundary and
denotes the velocity at the wall, n the outward-pointing normal of the boundary and 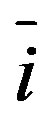 the direction opposite to direction
the direction opposite to direction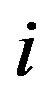 . The parameter
. The parameter 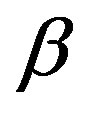 is chosen according to [6] as
is chosen according to [6] as
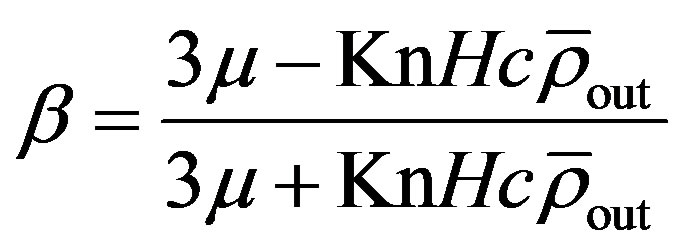 (8)
(8)
such that the first-order slip boundary condition from [31] is fulfilled:
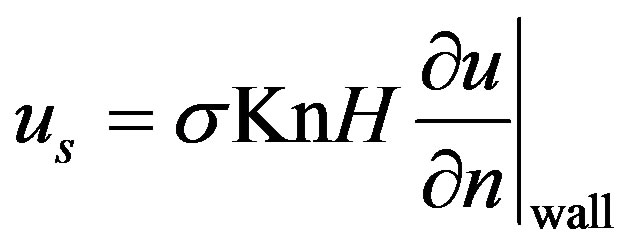 (9)
(9)
In Equation (8), 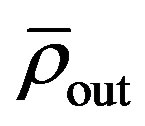 denotes the average density at the outlet of a channel-like scenario and
denotes the average density at the outlet of a channel-like scenario and 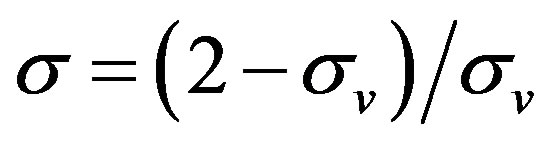 with tangential momentum accommodation coefficient
with tangential momentum accommodation coefficient 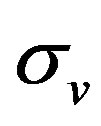 which is considered to be unity in the following. Boundary conditions for transition flows are implemented by an analogous linear combination between bounce-back and specular reflection (BBSR) conditions [2], resembling second-order boundary conditions:
which is considered to be unity in the following. Boundary conditions for transition flows are implemented by an analogous linear combination between bounce-back and specular reflection (BBSR) conditions [2], resembling second-order boundary conditions:
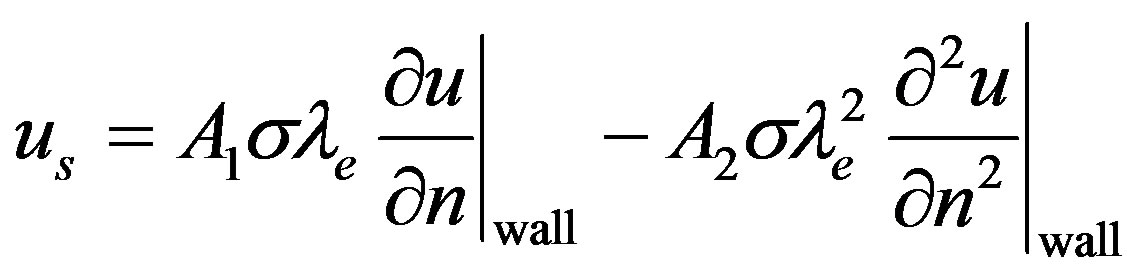 (10)
(10)
where 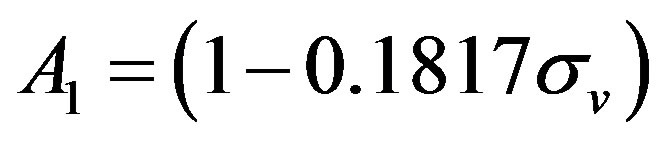 and
and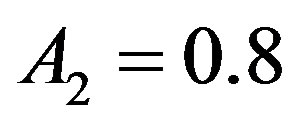 ; the parameter
; the parameter 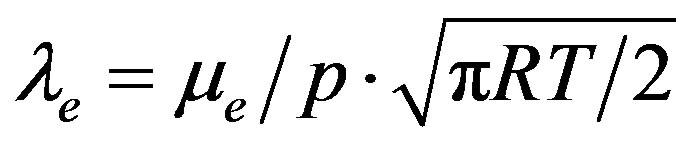 denotes the effective mean free path. The respective weighting factor
denotes the effective mean free path. The respective weighting factor 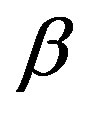 evolves in this case to be
evolves in this case to be
 . (11)
. (11)
The model extensions described above have been validated in [2] and [6] for two-dimensional channel scenarios with planar boundaries. For detailed discussions on microscopic slip effects, see [12], as well as [13] for a review on slip models for gas microflows.
Considering systems which consist of several channellike structures, a special treatment of the distributions 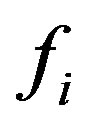 is required near corners and edges of the flow domain. Figure 1 sketches the problematic geometries in the case of the BBDR conditions for a two-dimensional setup. Corner cells have distributions which collide with more than one wall, as
is required near corners and edges of the flow domain. Figure 1 sketches the problematic geometries in the case of the BBDR conditions for a two-dimensional setup. Corner cells have distributions which collide with more than one wall, as 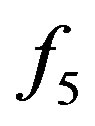 does in Figure 1(a). Even though
does in Figure 1(a). Even though 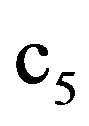 represents a discretisation of the velocity space and thus combines velocities evenly distributed around
represents a discretisation of the velocity space and thus combines velocities evenly distributed around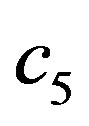 , one cannot simply split the distribution functions equally up among the adjacent walls and perform a normal BBDR; this would even not maintain a zero velocity equilibrium state. In order to overcome this deficiency and to be mass conservative, a bounce-back scheme will be applied for those distributions which collide with multiple walls. If a cell is adjacent to a wall corner, the problem arises how to deal with distributions which can be propagated to diagonally adjacent cells and be part of a wall collision at the same time, see
, one cannot simply split the distribution functions equally up among the adjacent walls and perform a normal BBDR; this would even not maintain a zero velocity equilibrium state. In order to overcome this deficiency and to be mass conservative, a bounce-back scheme will be applied for those distributions which collide with multiple walls. If a cell is adjacent to a wall corner, the problem arises how to deal with distributions which can be propagated to diagonally adjacent cells and be part of a wall collision at the same time, see 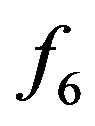 in Figure 1(b). Applying both mechanisms would not be mass conservative and splitting distributions up into a streaming and a collision part would again destroy a zero velocity equilibrium state. Therefore, those distributions are only propagated to their adjacent destinations and excluded from any subsequent boundary collision process. Distributions which collide with a wall corner directly, as it is the case for
in Figure 1(b). Applying both mechanisms would not be mass conservative and splitting distributions up into a streaming and a collision part would again destroy a zero velocity equilibrium state. Therefore, those distributions are only propagated to their adjacent destinations and excluded from any subsequent boundary collision process. Distributions which collide with a wall corner directly, as it is the case for 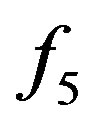 in Figure 1(c), are bounced back from the wall. Similar issues can be encountered when using the BBSR boundary condition. In these cases, we also apply the standard bounce-back scheme to the relevant distribution functions. The bounce-back method typically models no-slip walls and does not capture the additional microfluidic slip. However, with the number of corner nodes in a simulation being of O(1) and considering the fact that our channel-like scenarios are dominated by planar boundary structures, we consider the influence of these nodes to be of less importance.
in Figure 1(c), are bounced back from the wall. Similar issues can be encountered when using the BBSR boundary condition. In these cases, we also apply the standard bounce-back scheme to the relevant distribution functions. The bounce-back method typically models no-slip walls and does not capture the additional microfluidic slip. However, with the number of corner nodes in a simulation being of O(1) and considering the fact that our channel-like scenarios are dominated by planar boundary structures, we consider the influence of these nodes to be of less importance.
Besides the combined boundary techniques and the viscosity adjustment, the application of the MRT collision scheme with particular sets of relaxation parameters is required to suppress artificial slip effects near the walls. The BGK model induces numerical slip which—in contrast to the tuned MRT models—may yield unphysical results as discussed in [6]; a tuning of the BGK operator to remove these artifacts may not be possible. For a derivation of the tuned relaxation parameter sets for the MRT collision operator, see [2] and [6].
2.3. The Peano Framework
The Lattice Boltzmann model and the respective slip and transition flow extensions are implemented within the Lattice Boltzmann application [11,32] of the Peano framework [33]. This framework provides adaptive Cartesian grid structures that are traversed along the iterates of the space-filling Peano curve. A block-structured approach to LBM-based simulations within Peano has recently been presented and validated; for details, see [11]. The respective implementation allows for twoand three-dimensional Lattice Boltzmann simulations on adaptive static or dynamic Cartesian grids. It enables coarse-graining and refining of both the spatial resolution of the simulation and the properties of the fluid. The latter can for example be established by using different collision models on different grid levels which can significantly reduce computational costs as pointed out in [11].
3. Numerical Results
3.1. Validation: Channel Flows (2D)
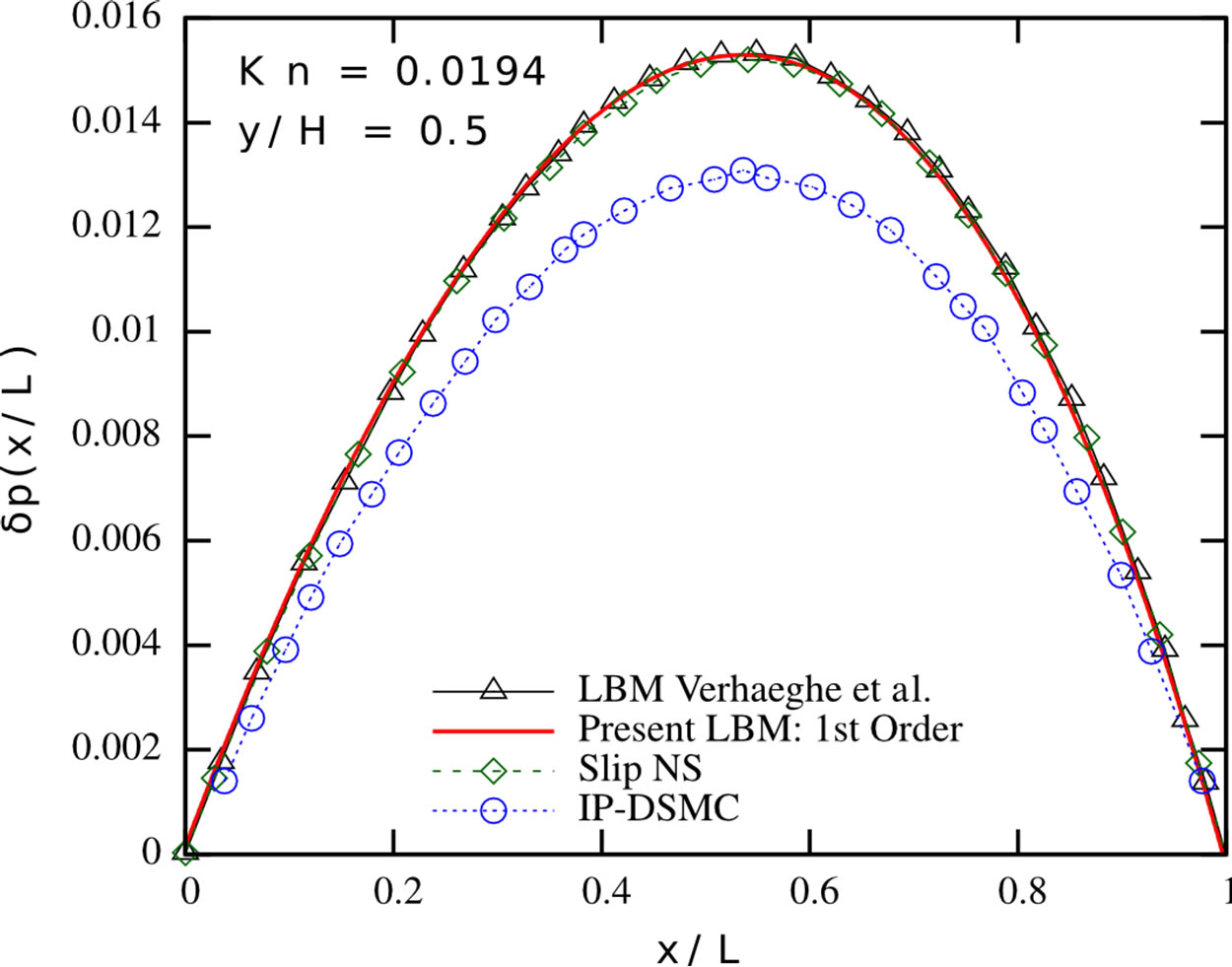
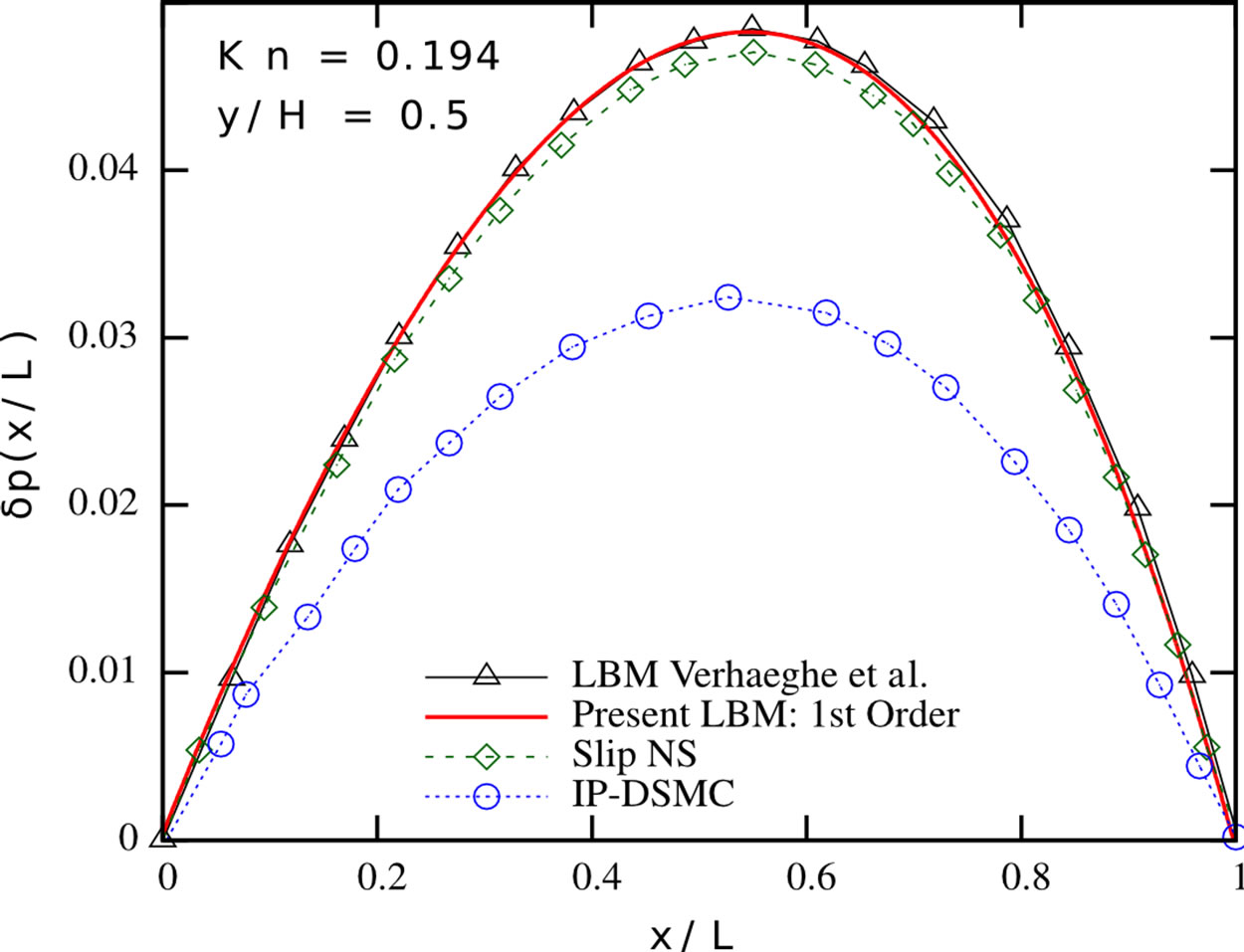
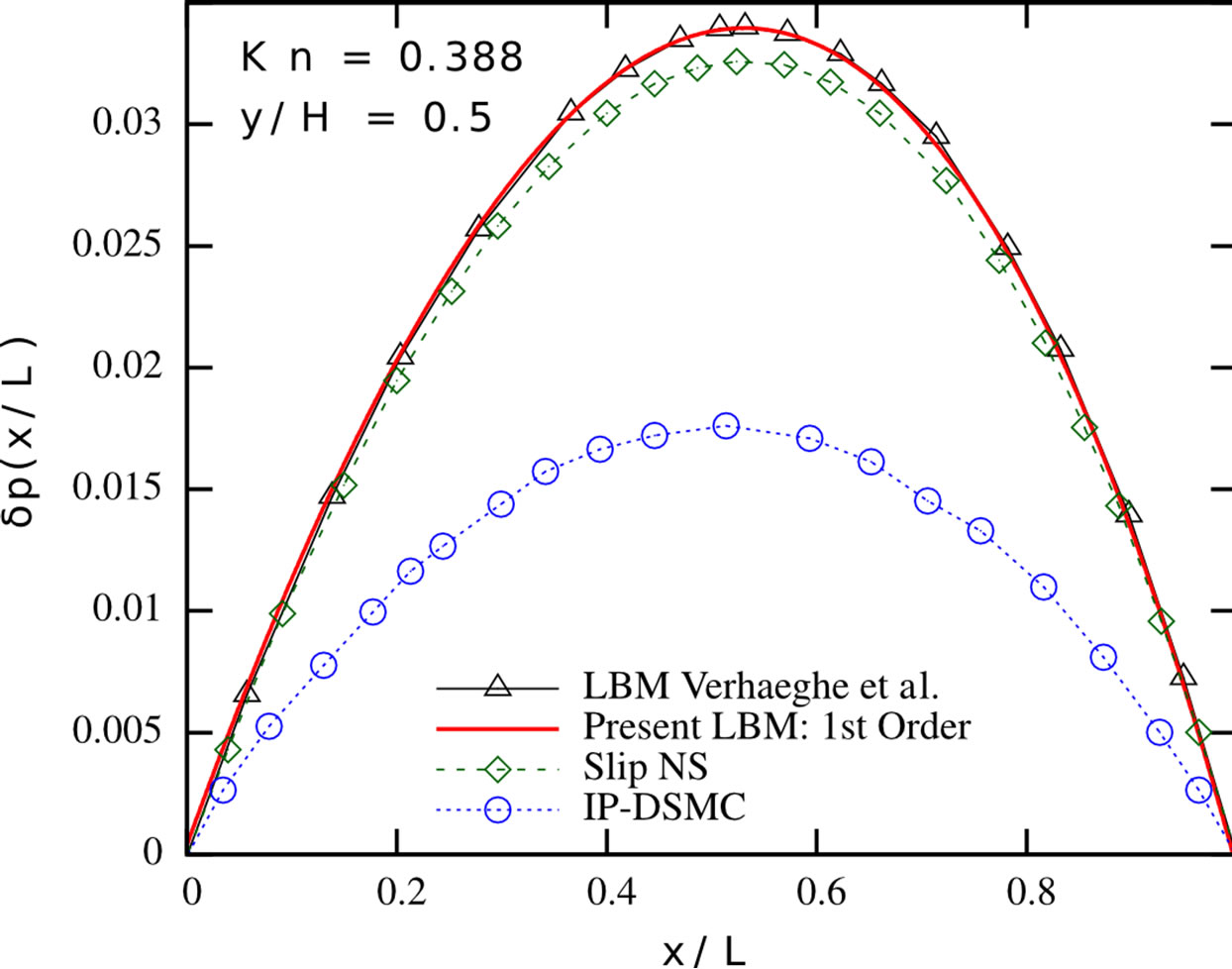
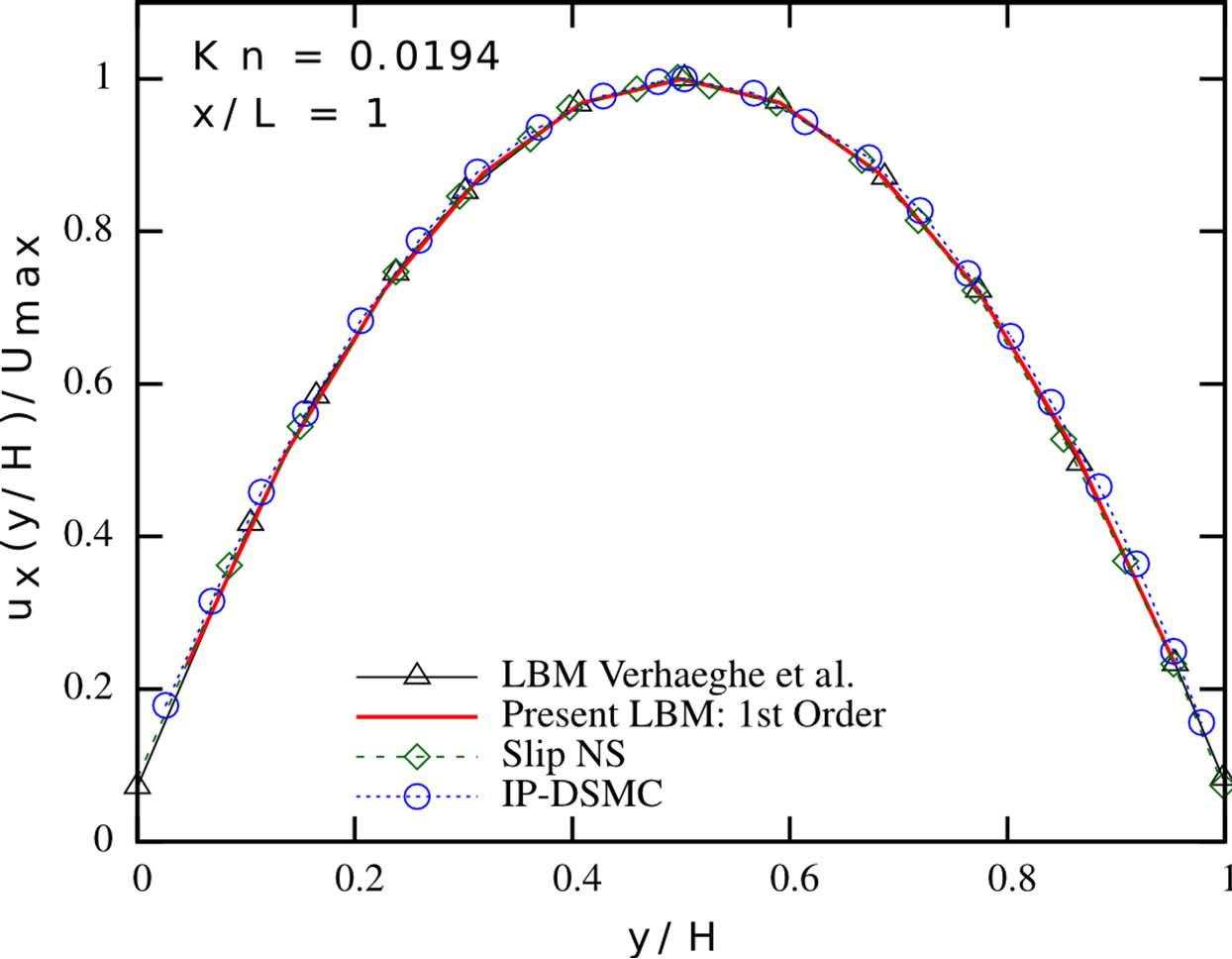
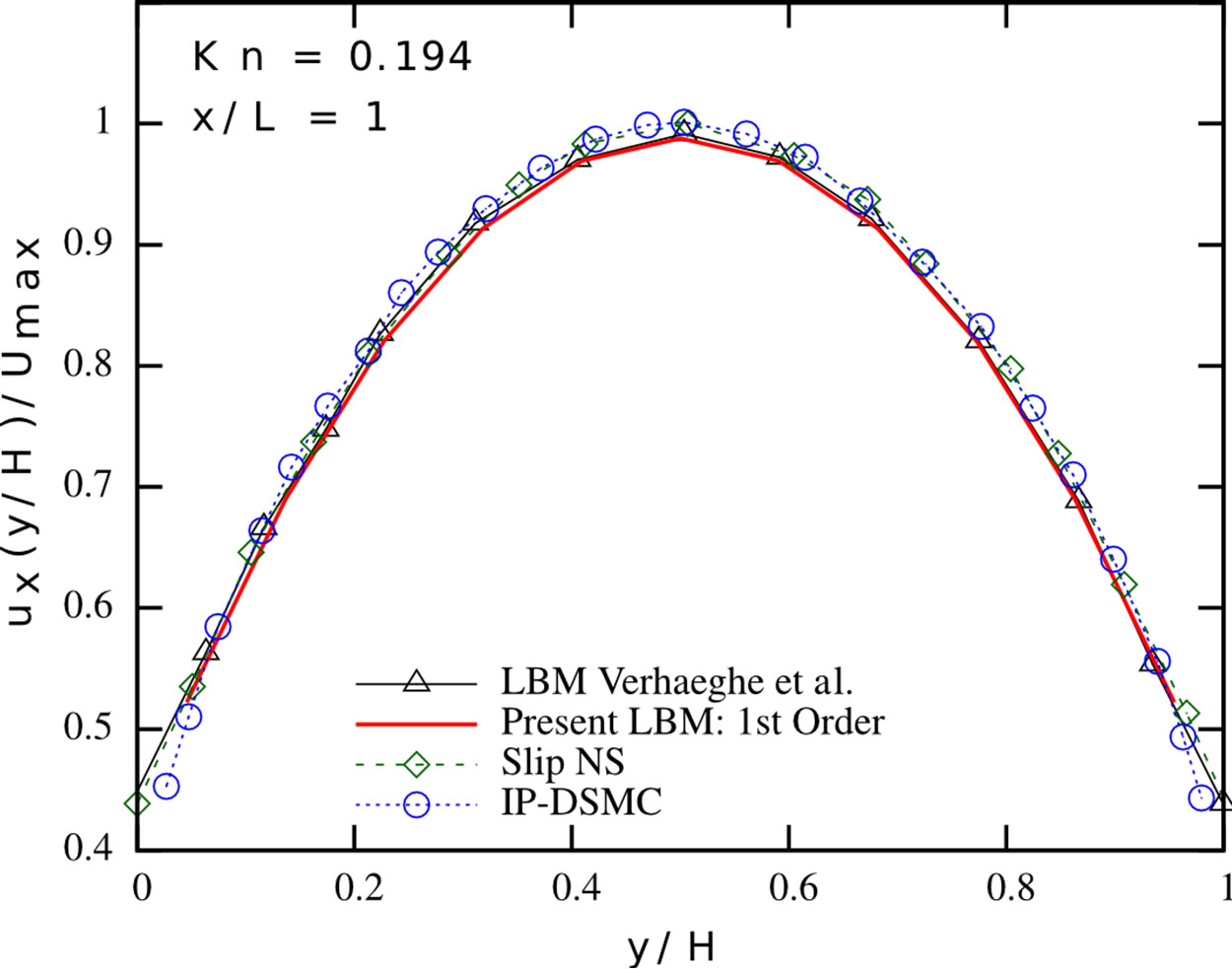
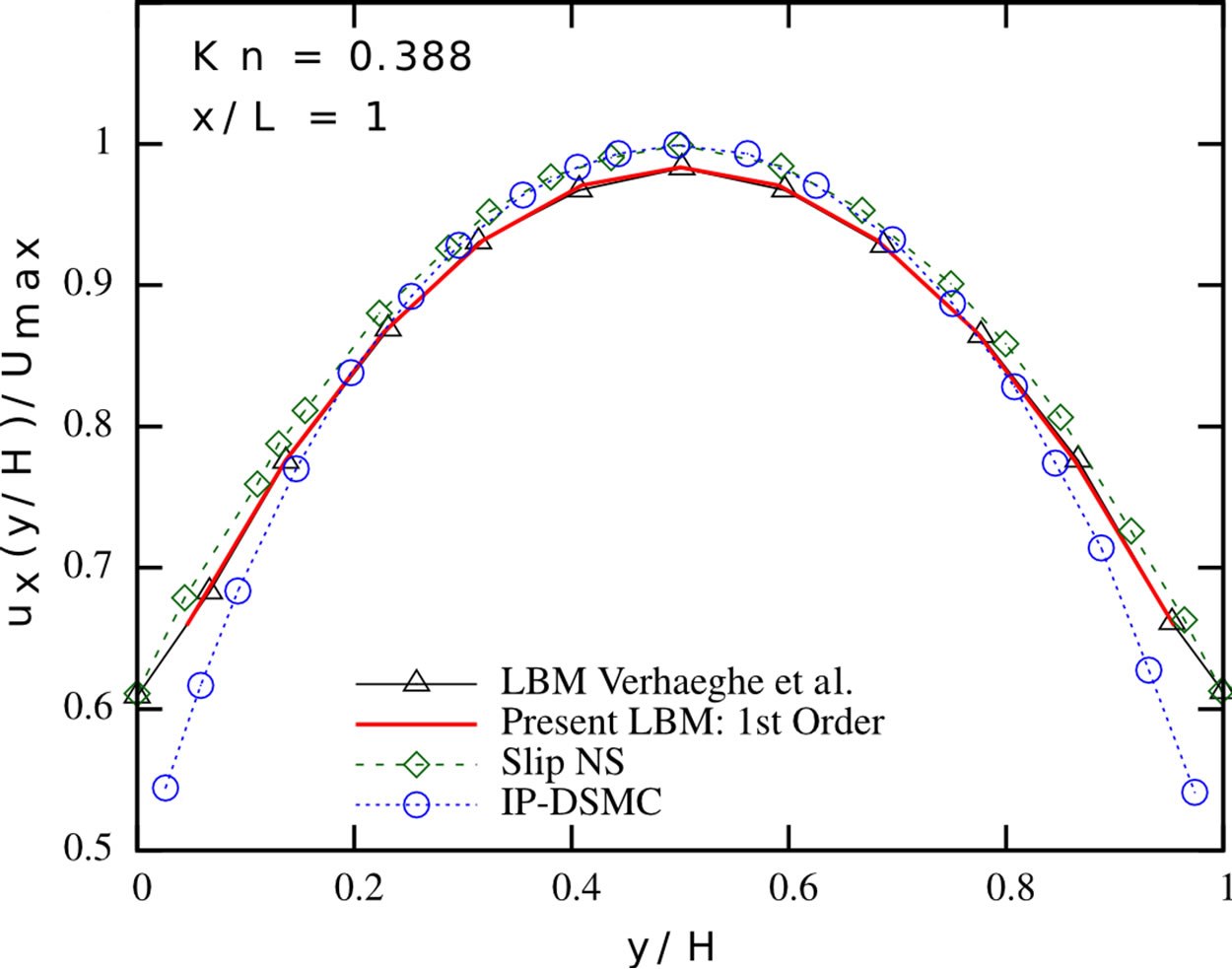
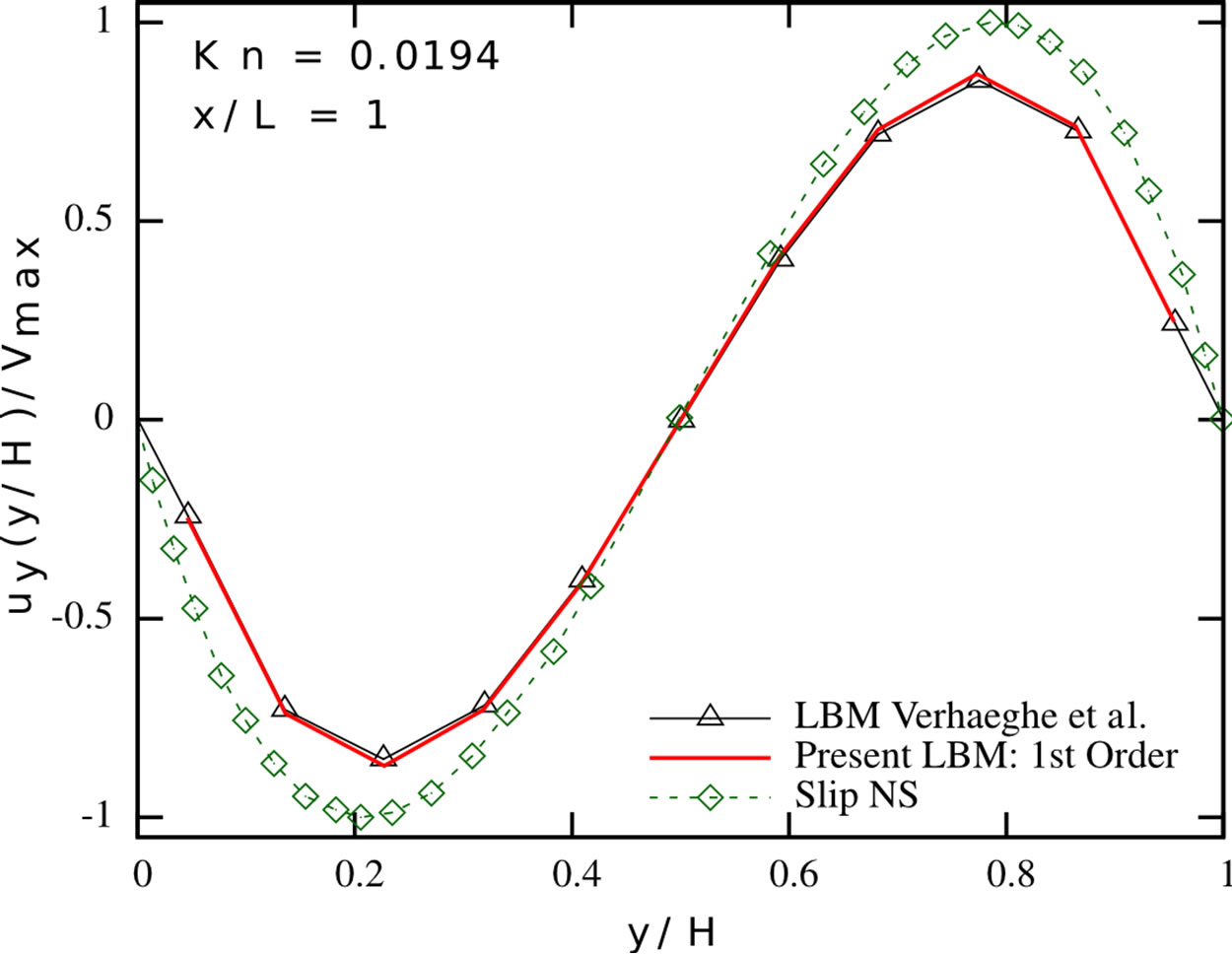
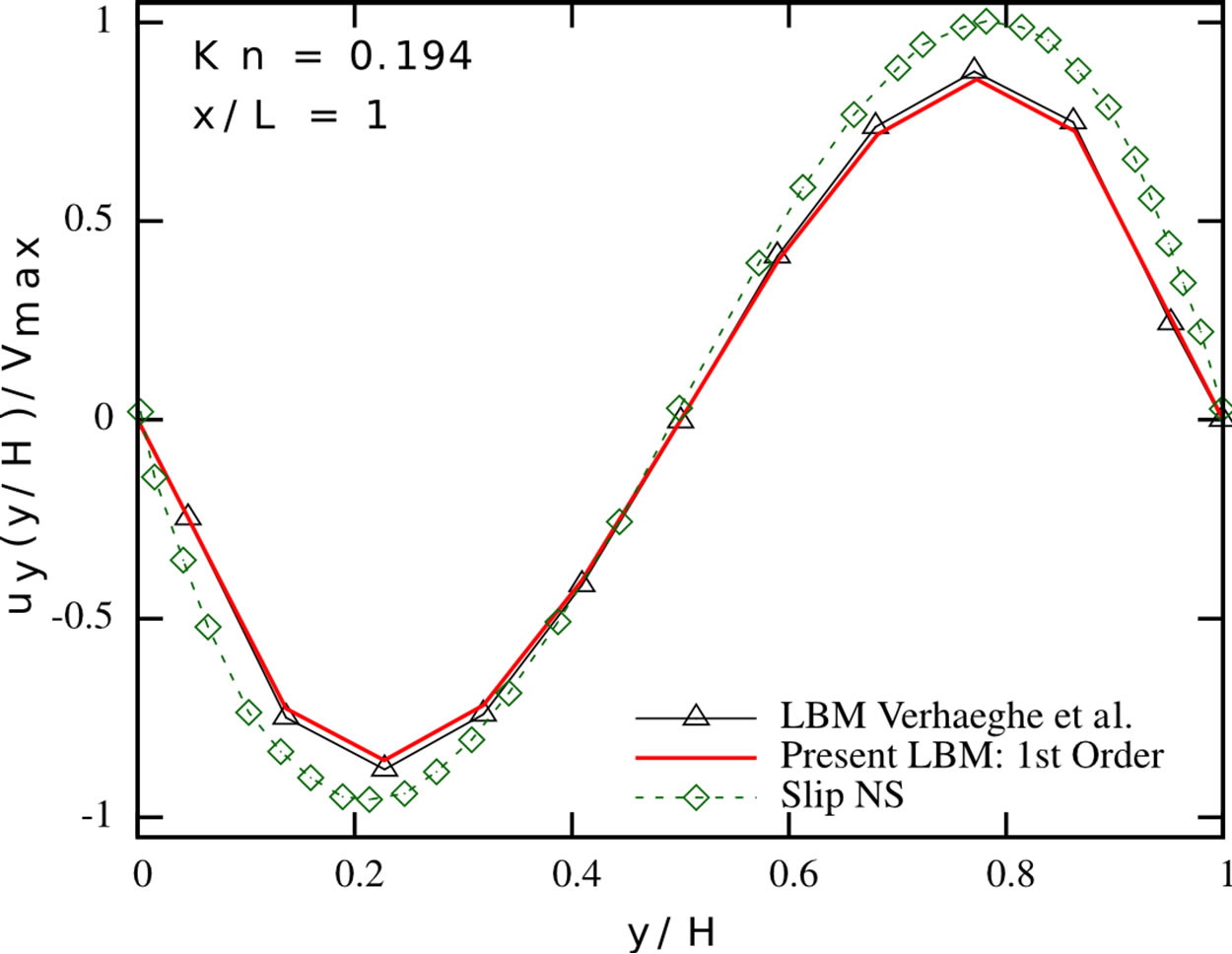
We validate our implementations and therefore consider different channel flow scenarios. We compare our simulations to the results from [2] and [6]. In a first series, we carry out simulations in the slip flow regime, considering pressure-driven Poiseuille flow in a 2D channel. We apply the tuned MRT collision operator and the firstorder boundary conditions from the previous section and study the flow for different Knudsen numbers, using a 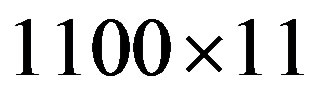 grid. The results are depicted in Figure 2. Our numerical results match the results reported in [6], indicating the correctness of our implementations. The limitations of this approach with respect to higher Knudsen number flows also become apparent from Figure 2: the first-order Navier-Stokes slip solution provides a good estimate of the streamwise velocity profile for Kn = 0.0194 and Kn = 0.0194, but strongly overestimates the slip occurring at the wall for higher Knudsen number flows. The presented first-order Lattice Boltzmann scheme shows a similar behaviour—it is valid in the slip flow regime, but needs further modifications when entering the transition flow regime. Both the first-order NavierStokes and first-order Lattice Boltzmann scheme show a significantly stronger pressure deviation from the linear pressure distribution, which is typically encountered in macro-scale channels, than the Direct Simulation Monte-Carlo method. In order to extend the usability range of our method, we checked the results for periodic channel flows according to the setups presented in [2].
grid. The results are depicted in Figure 2. Our numerical results match the results reported in [6], indicating the correctness of our implementations. The limitations of this approach with respect to higher Knudsen number flows also become apparent from Figure 2: the first-order Navier-Stokes slip solution provides a good estimate of the streamwise velocity profile for Kn = 0.0194 and Kn = 0.0194, but strongly overestimates the slip occurring at the wall for higher Knudsen number flows. The presented first-order Lattice Boltzmann scheme shows a similar behaviour—it is valid in the slip flow regime, but needs further modifications when entering the transition flow regime. Both the first-order NavierStokes and first-order Lattice Boltzmann scheme show a significantly stronger pressure deviation from the linear pressure distribution, which is typically encountered in macro-scale channels, than the Direct Simulation Monte-Carlo method. In order to extend the usability range of our method, we checked the results for periodic channel flows according to the setups presented in [2].
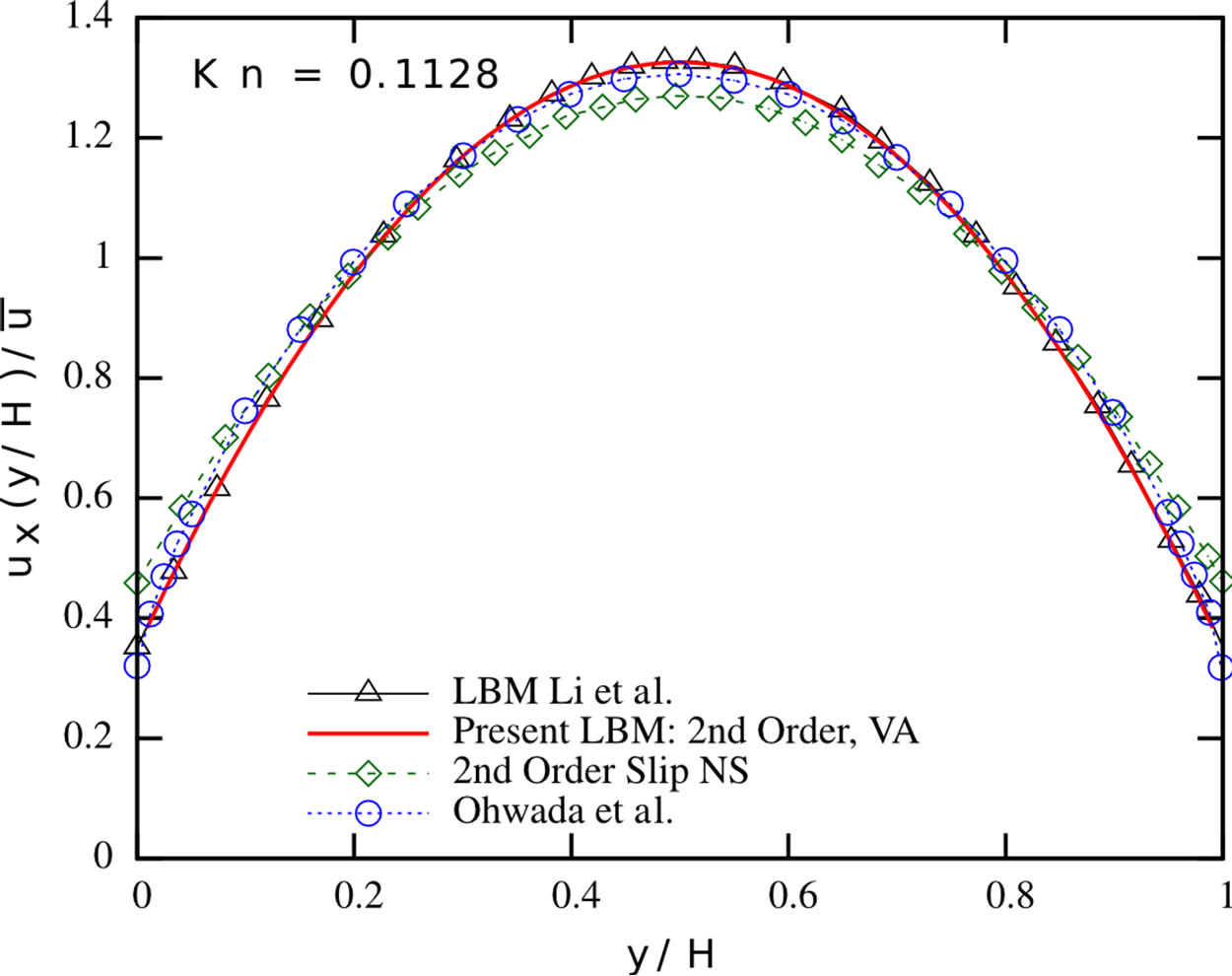
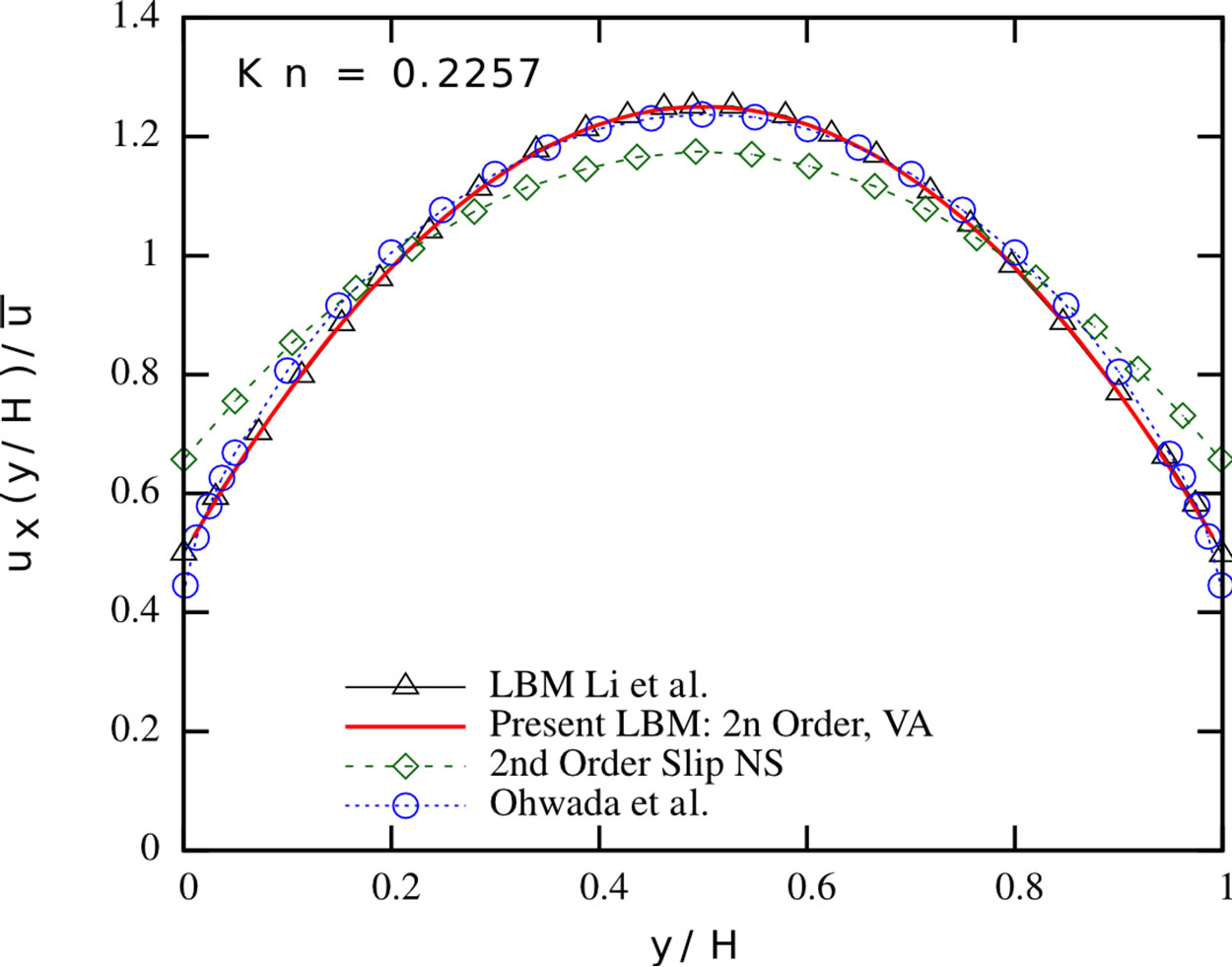
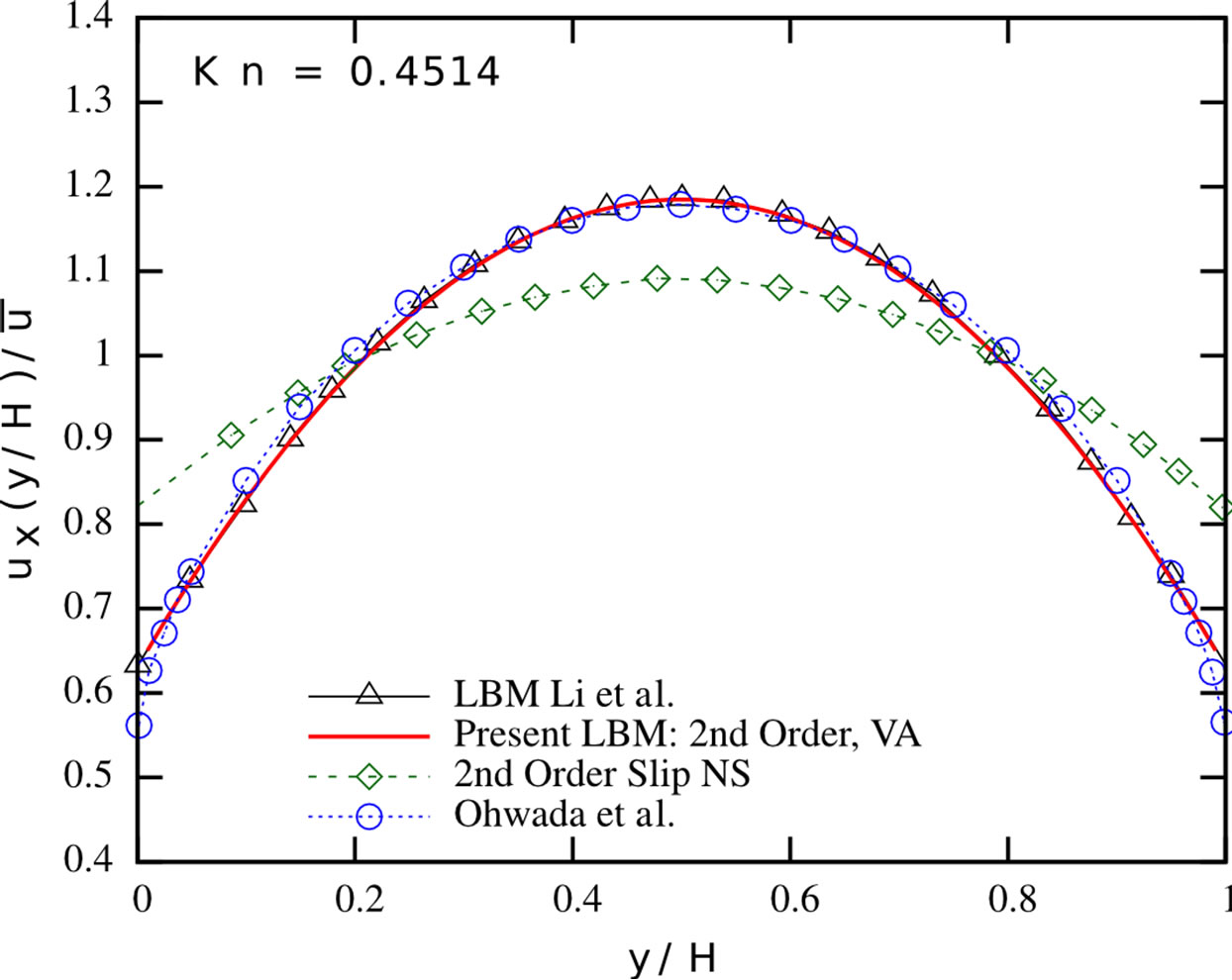
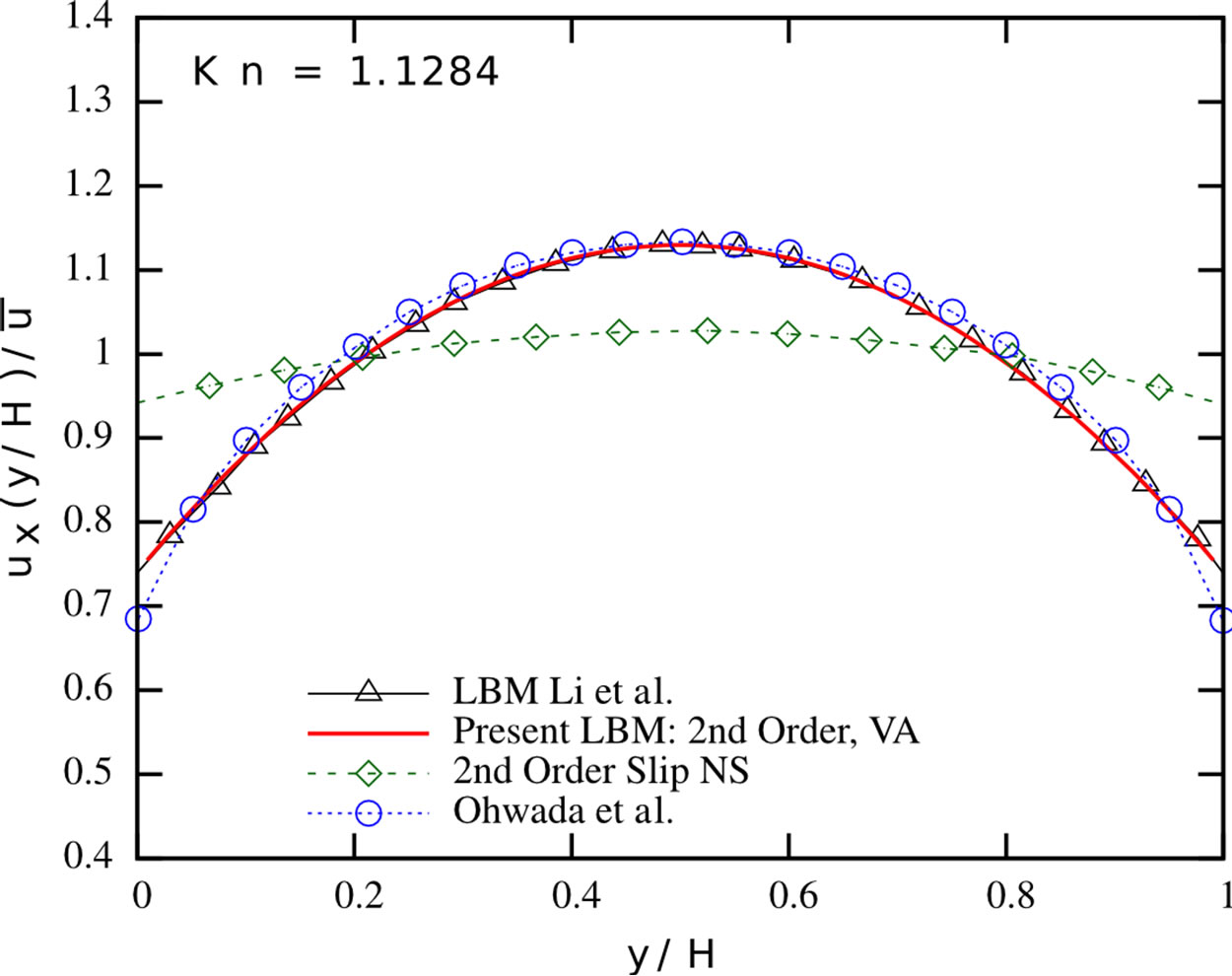
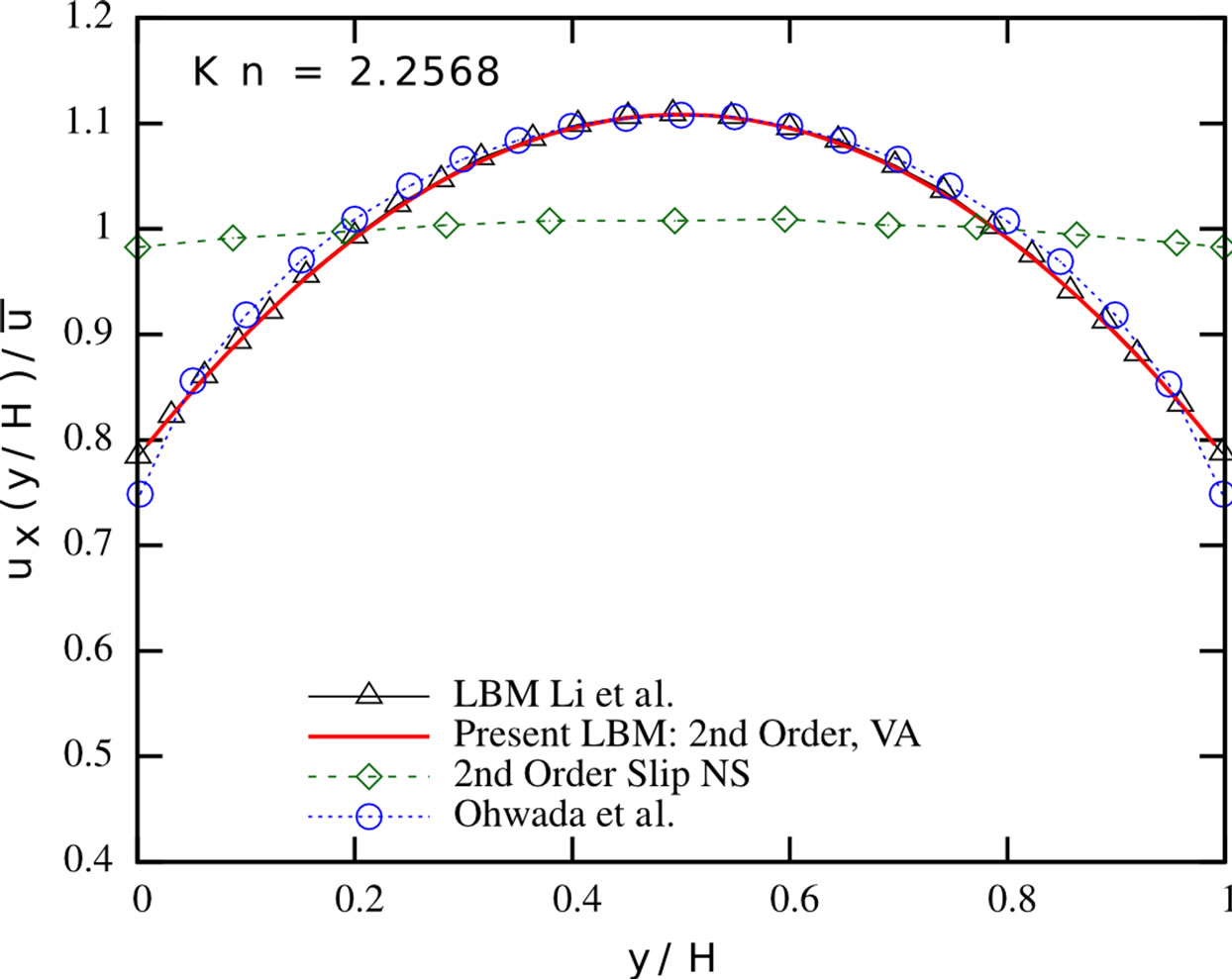
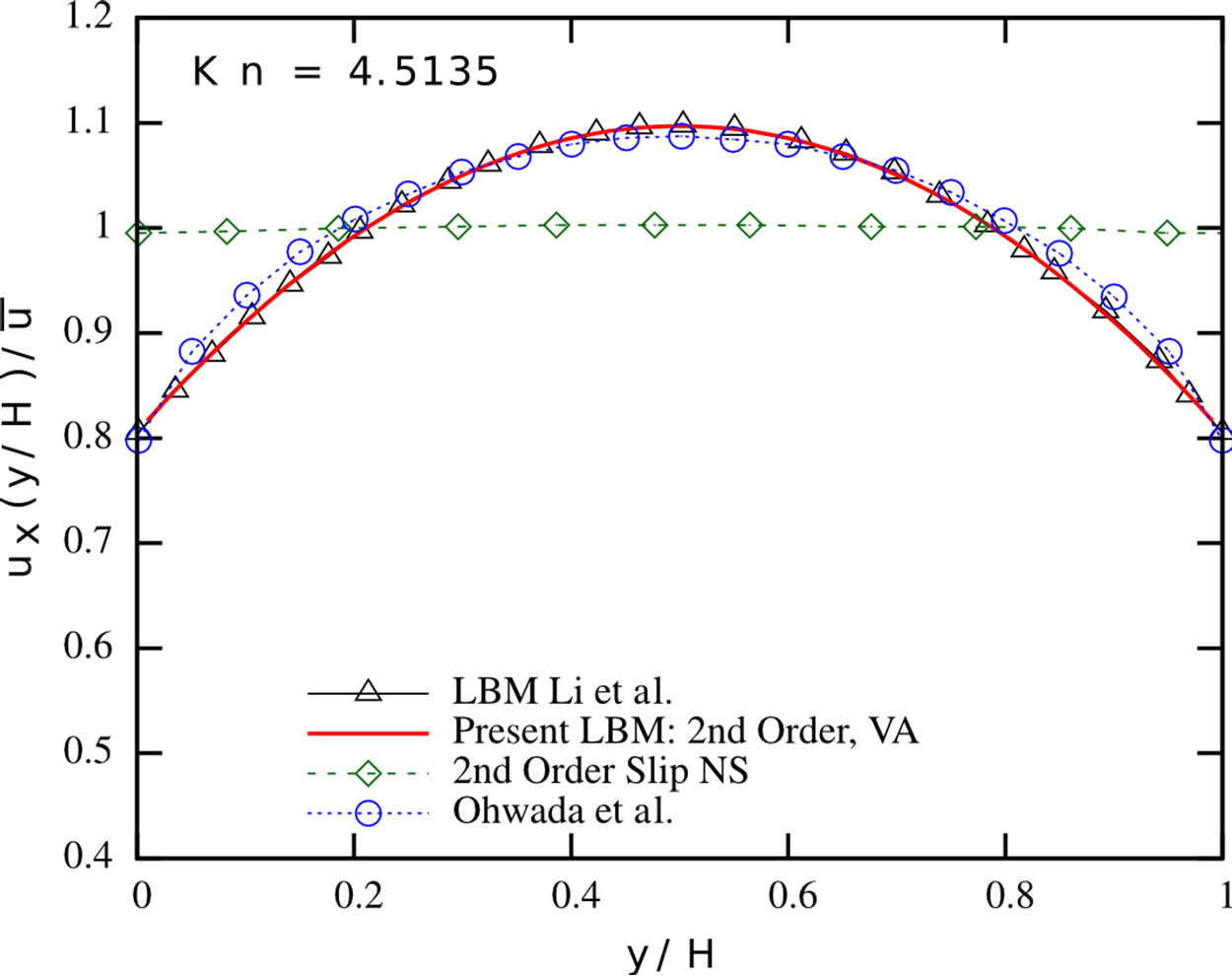
Figure 3 presents the evolving streamwise velocity profile for Knudsen numbers in the range of [0.1128; 4.5135]. Our results perfectly fit the ones reported by Li et al.
3.2. Validation: Channel Flows (3D)
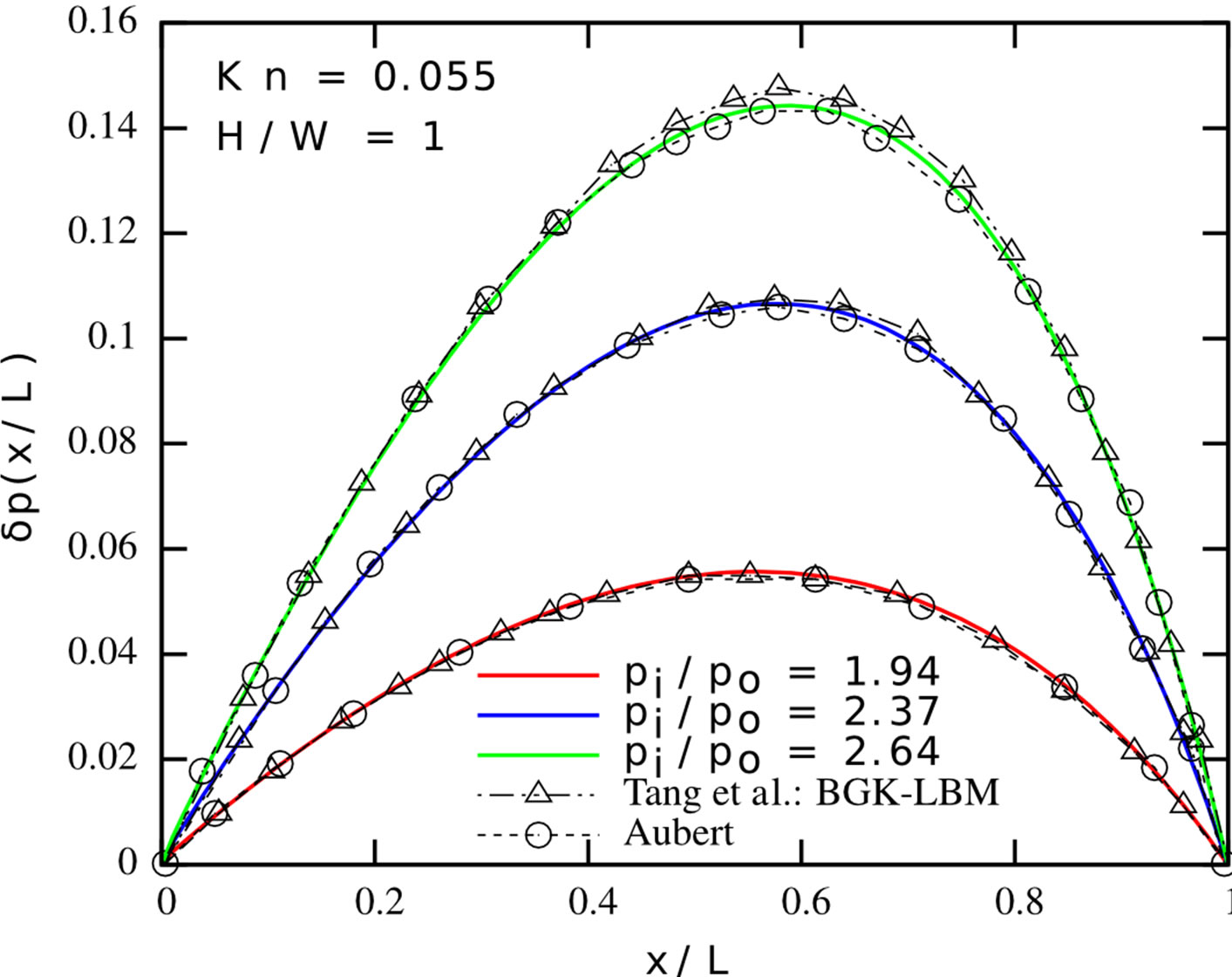
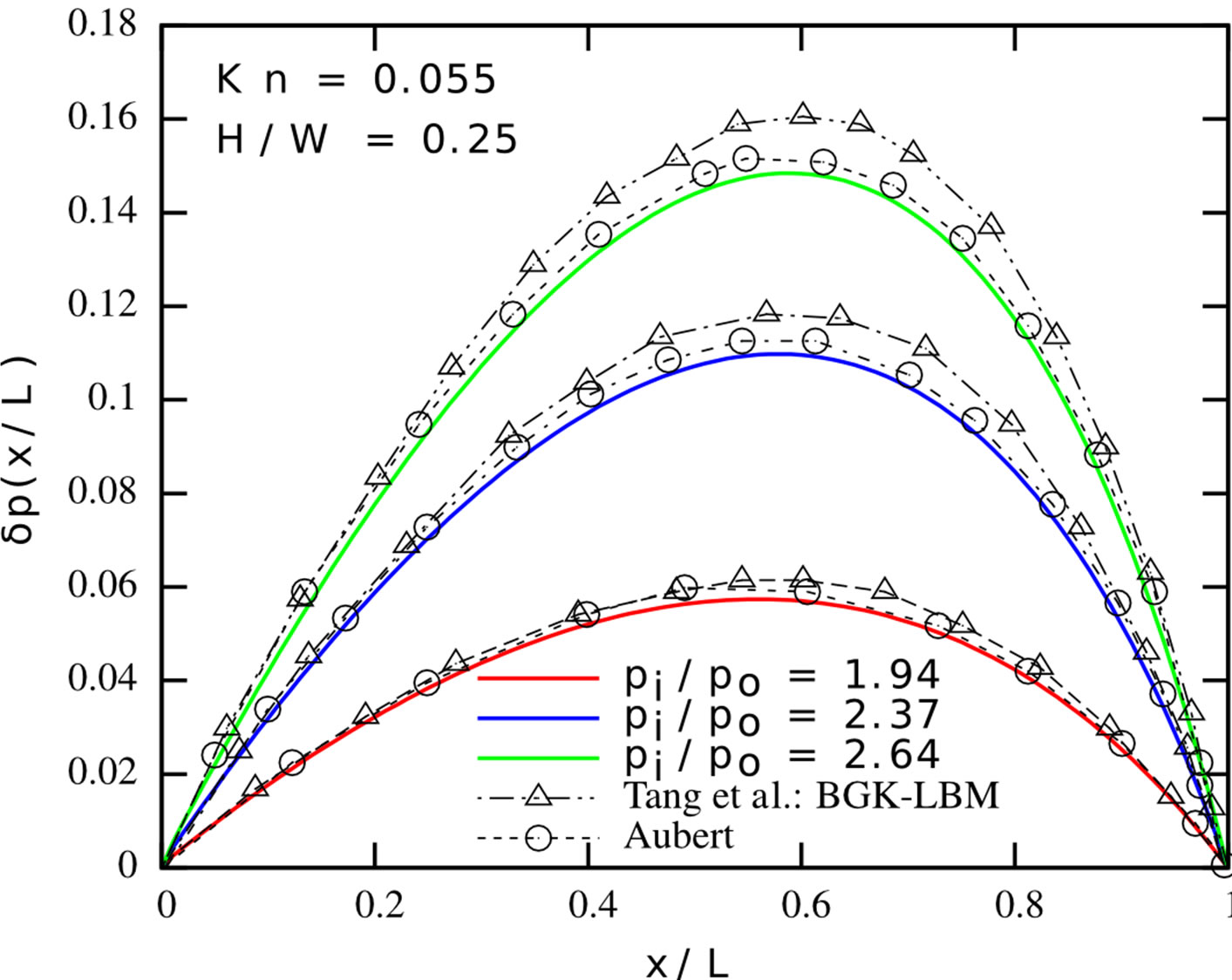
The three-dimensional implementation is validated by comparing the pressure deviation from the linear distribution along the centerline of a Poiseuille flow with the results of other researchers: Tang et al. [25] employed the LBM with the BGK collision operator and special boundary conditions to accommodate for the occurring slip in order to solve the problem numerically. Aubert and Colin [34] proposed an analytical model for gaseous flows which they used to obtain analytical data. The three-dimensional channel is simulated for the height-towidth ratios of 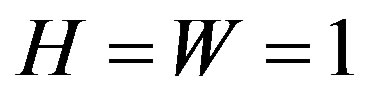 and 0.25 with grid sizes of
and 0.25 with grid sizes of 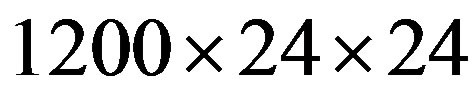 nodes and
nodes and 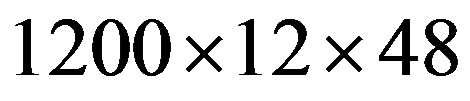 nodes, respectively. The Knudsen number is set to
nodes, respectively. The Knudsen number is set to 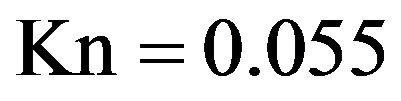 and
and
|
|
|
|
|
|
|
|
|
|
|
|
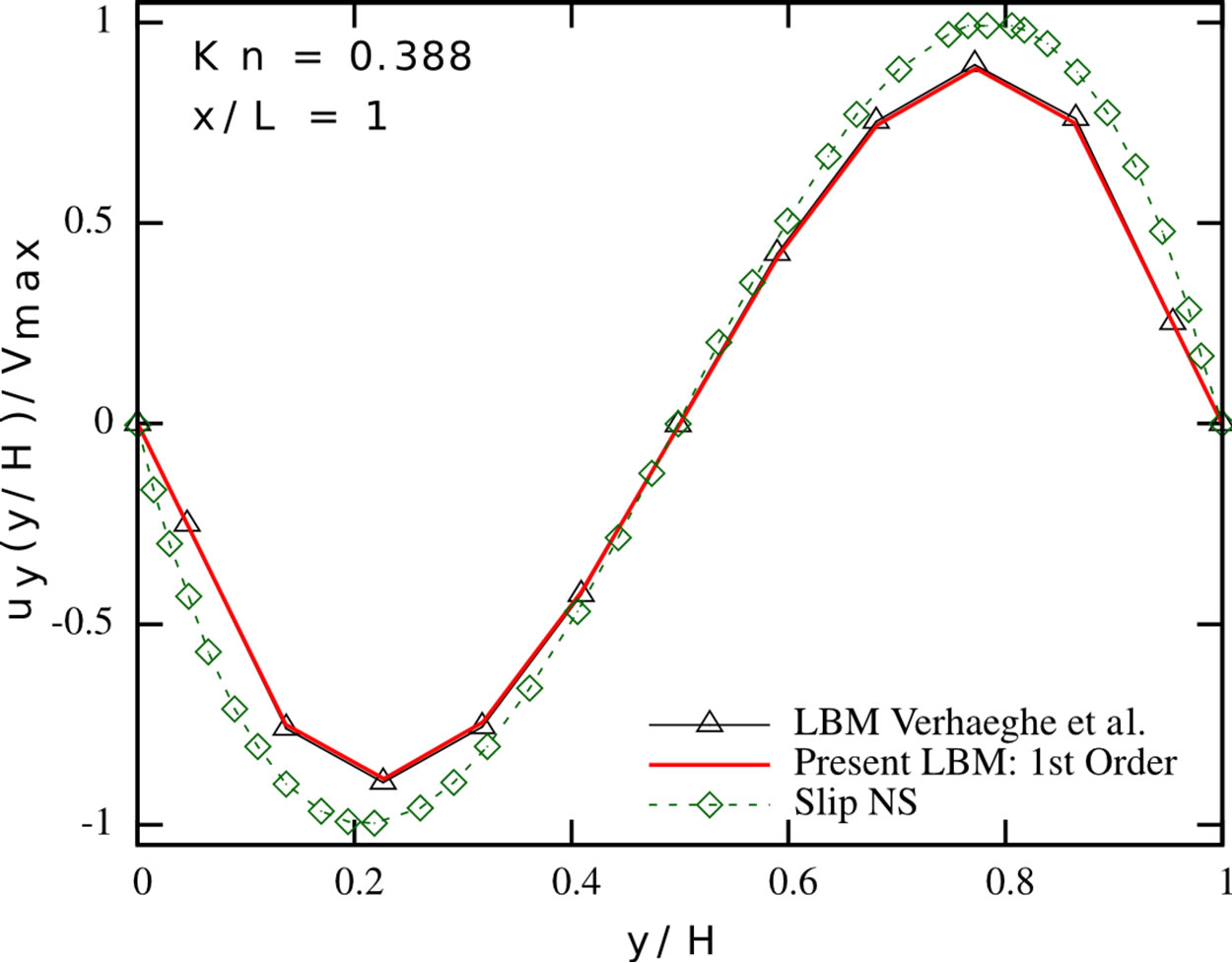
Figure 2. Pressure deviation from the linear distribution along the centerline (top row), normalised streamwise velocity profile (mid row) and normalised spanwise velocity profile (bottom row) in a pressure-driven Poiseuille flow at different Knudsen numbers. Present LBM (solid red line), LBM proposed by Verhaeghe et al. [6] (black triangles), first-order slip NavierStokes solution [6] (green diamonds) and IP-DSMC proposed by Shen et al. [35] (blue circles). Left: Kn = 0.0194; Center: Kn = 0.194; Right: Kn = 0.388.
the results are calculated for the pressure ratios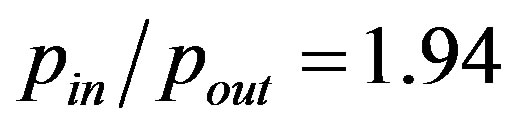 , 2.37 and 2.64. The obtained data provided in Figure 4 are in good agreement with the results of Tang et al. and Aubert and Colin.
, 2.37 and 2.64. The obtained data provided in Figure 4 are in good agreement with the results of Tang et al. and Aubert and Colin.
3.3. Microreactor Simulations
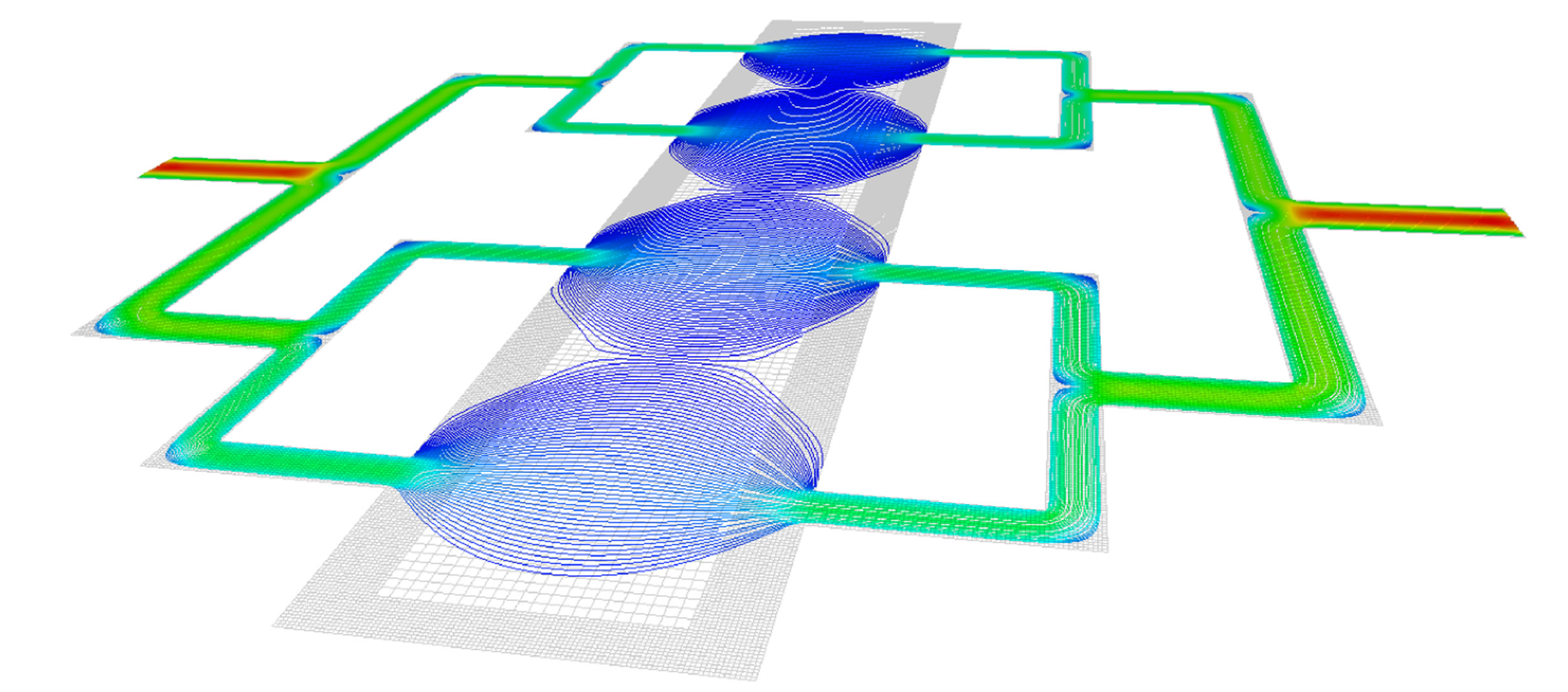
In the following, we apply the method to a microreactor duct-system as it can be found in typical microflow engineering setups [36]. Figure 5 shows the twoand three-dimensional representations of the respective geometry. The system consists of branch-like structures transporting polluted fluid into the reactor chamber. In this chamber, reaction processes-such as the oxidation of pollutants [36]—take place before the clean fluid leaves the system again via another channel system. We conducted different experiments starting with a two-dimensional setup. In our implementations [11], we use static adaptive grids together with a volumetric adaptivity approach for the LBM [37], [38] to speed up the computations. The inner part of the reactor chamber is resolved by a coarse grid whereas the small-sized ducts and the regions near the walls of the chamber are discretized using a fine grid, with a cell size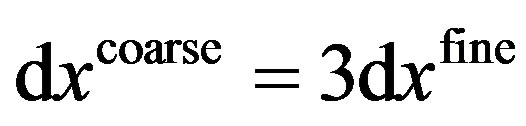 ; see [11] for details on the discretisation process. The second-order slip boundary conditions consistent with the MRT collision operator including viscosity adjustment are applied at all walls of the system. The Knudsen number used in our simulation lies between 0.11 and 0.21, depending on the size of the respective ducts. We compared the flow properties at different cross sections, see Figure 6. To validate our boundary treatment near geometric corners, we first compared the mass flux before and after the branching. We therefore evaluated the respective integral expressions for the mass flux over the cross
; see [11] for details on the discretisation process. The second-order slip boundary conditions consistent with the MRT collision operator including viscosity adjustment are applied at all walls of the system. The Knudsen number used in our simulation lies between 0.11 and 0.21, depending on the size of the respective ducts. We compared the flow properties at different cross sections, see Figure 6. To validate our boundary treatment near geometric corners, we first compared the mass flux before and after the branching. We therefore evaluated the respective integral expressions for the mass flux over the cross
|
|
|
|
|
|
|
|
Figure 3. Normalised streamwise velocity profiles: Present LBM with second-order boundary conditions and viscosity adjustment (solid red line), LBM proposed by Li et al. [2] (black triangles), second-order slip velocity Navier-Stokes solution by Hadjiconstantinou [39] (green diamonds) and the solution of the linearised Boltzmann equation by Ohwada et al. [40] (blue circles) of Poiseuille flows at different Knudsen numbers.
|
|
|
Figure 4. Pressure deviation along the centerline of differently sized channels for a pressure driven Poiseuille flow: Left: H/W = 1; Right: H/W = 0.25. Present LBM with first-order boundary conditions and viscosity adjustment (solid lines), LBM proposed by Tang et al. [25] (black triangles), analytical solution by Aubert and Colin [34] (black circles).
|
|
|
Figure 5. Microreactor duct-system. Left: Two-dimensional setup with visualisation of the underlying adaptive grid and the velocity field via streamlines. Right: Three-dimensional setup with density visualisation in the inlet duct system.
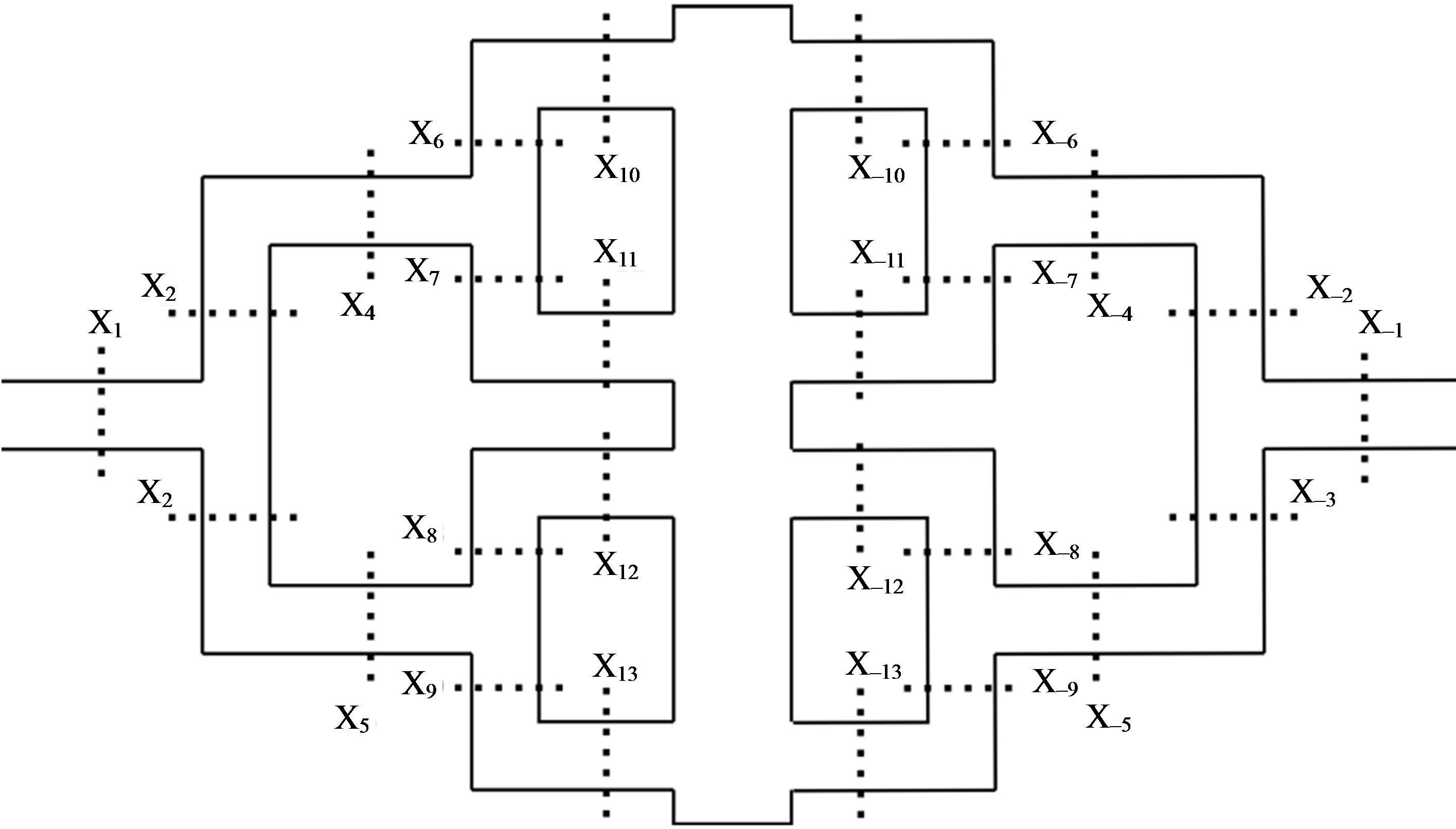
Figure 6. Cross sections at different positions within the reactor.
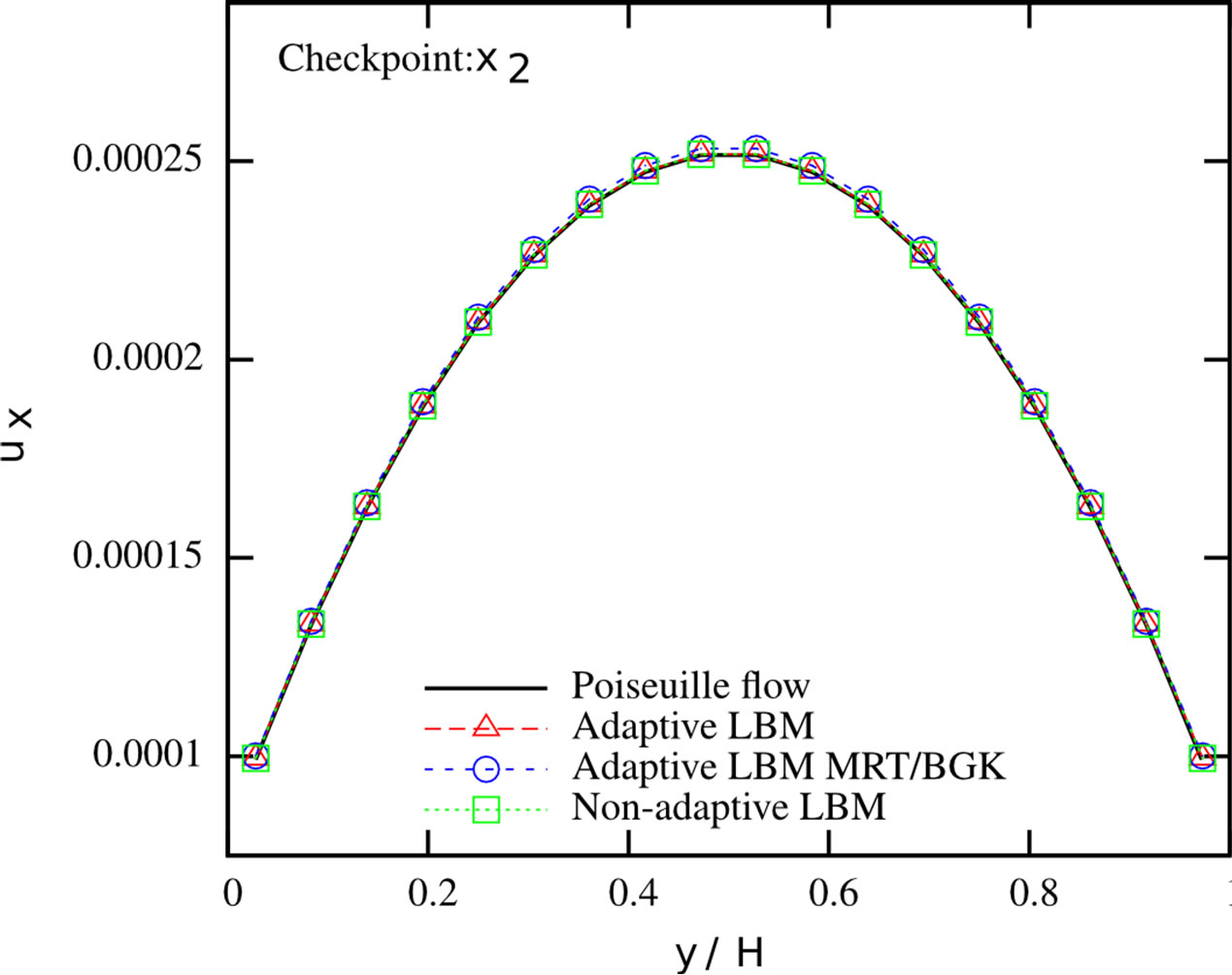
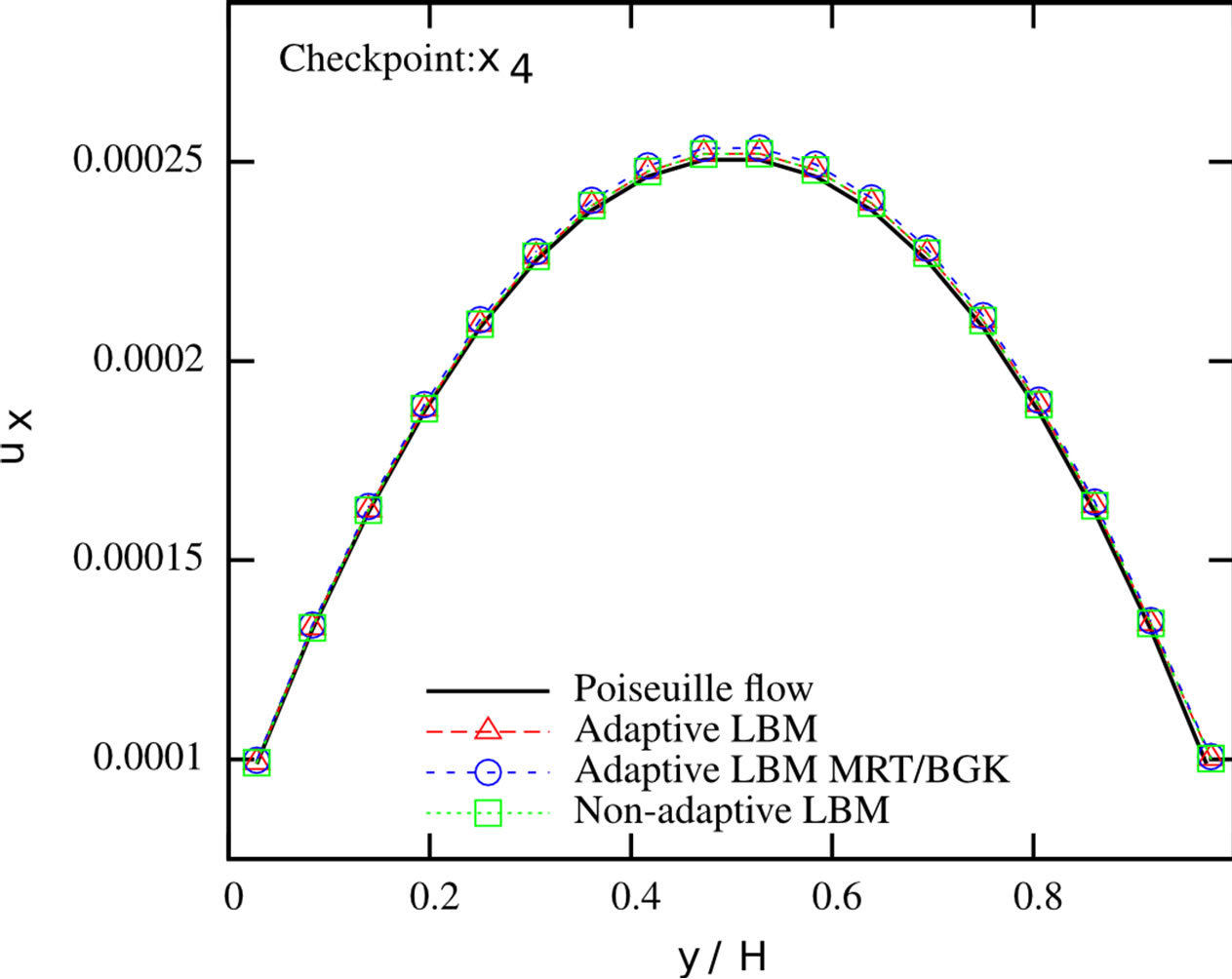
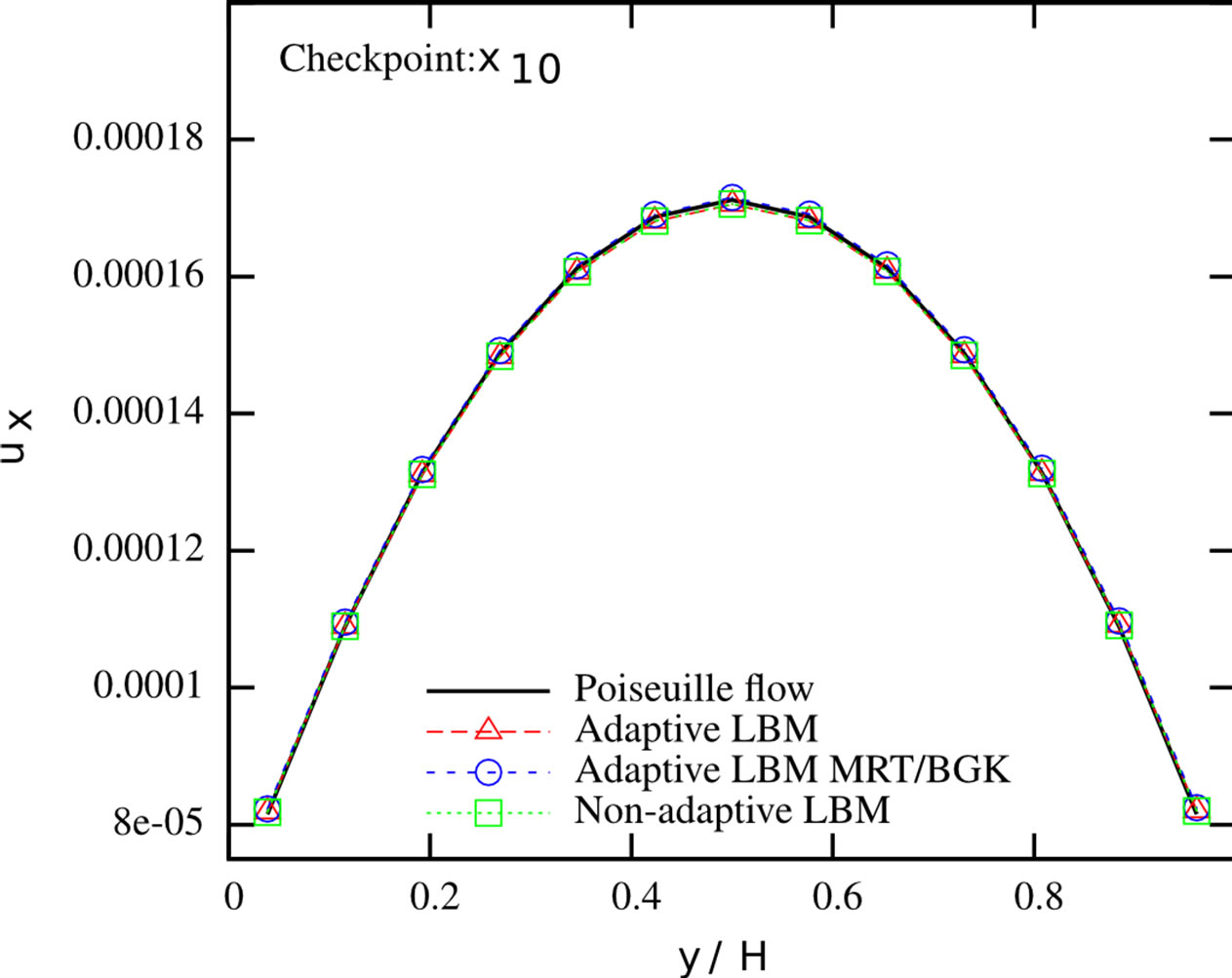
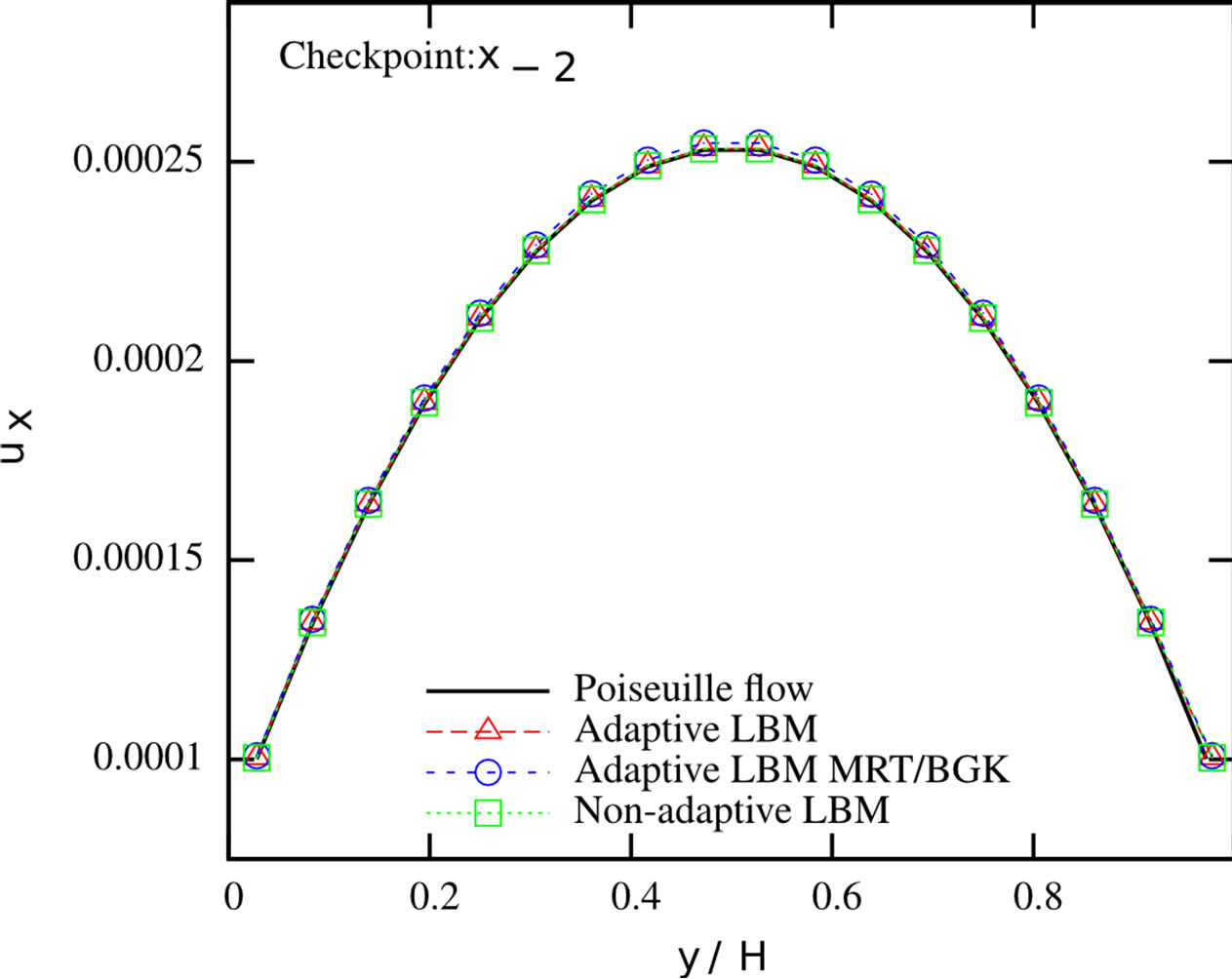
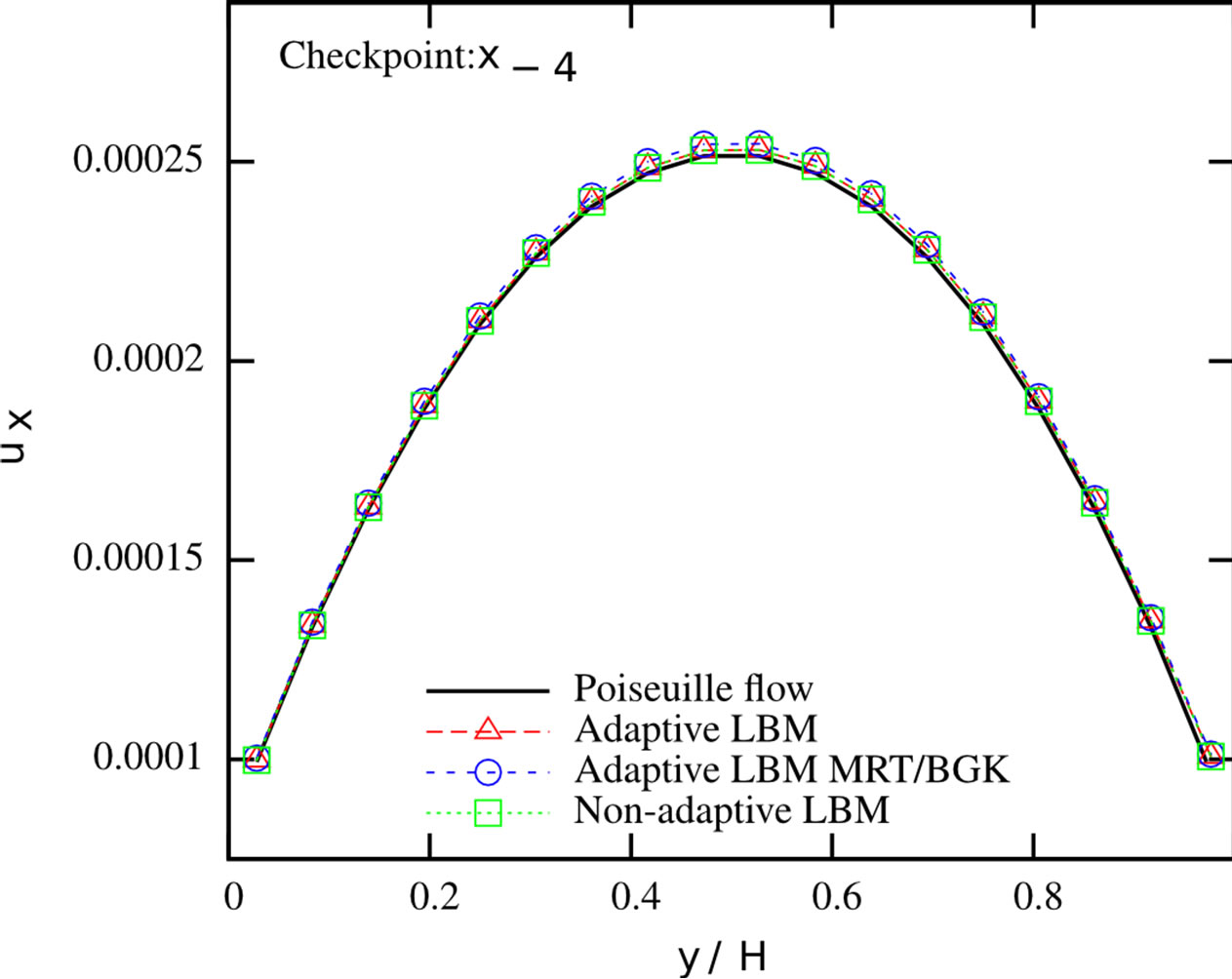
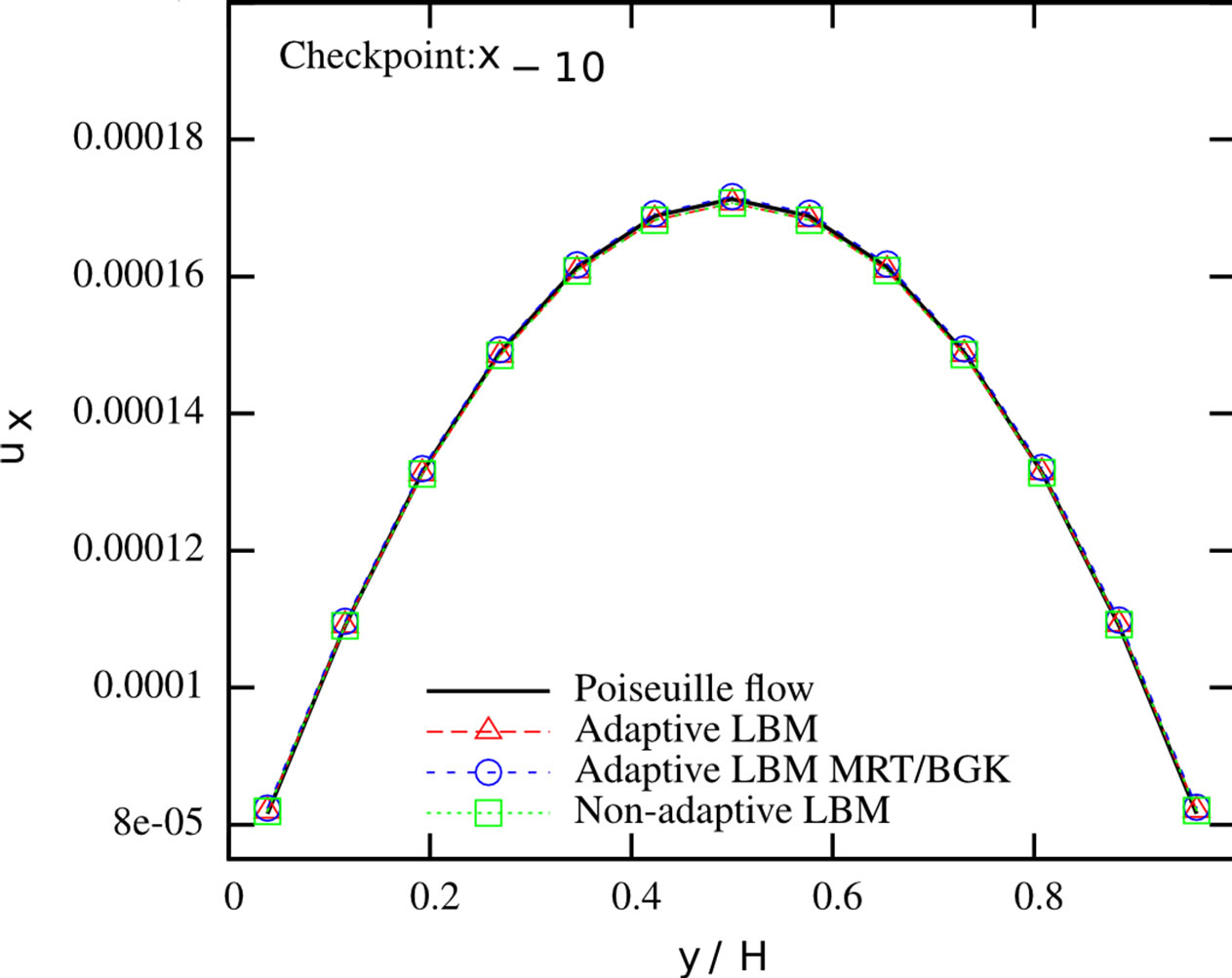
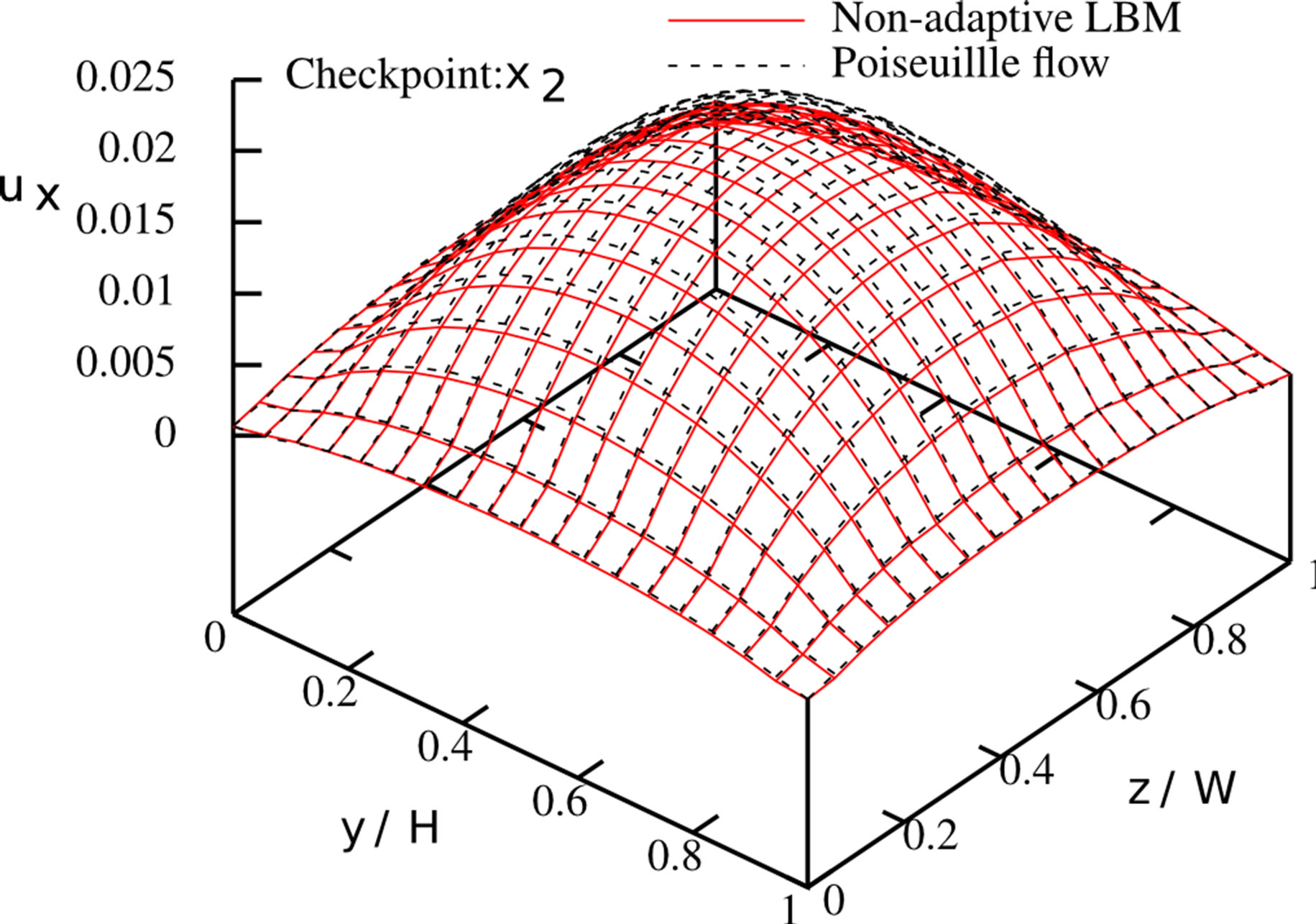
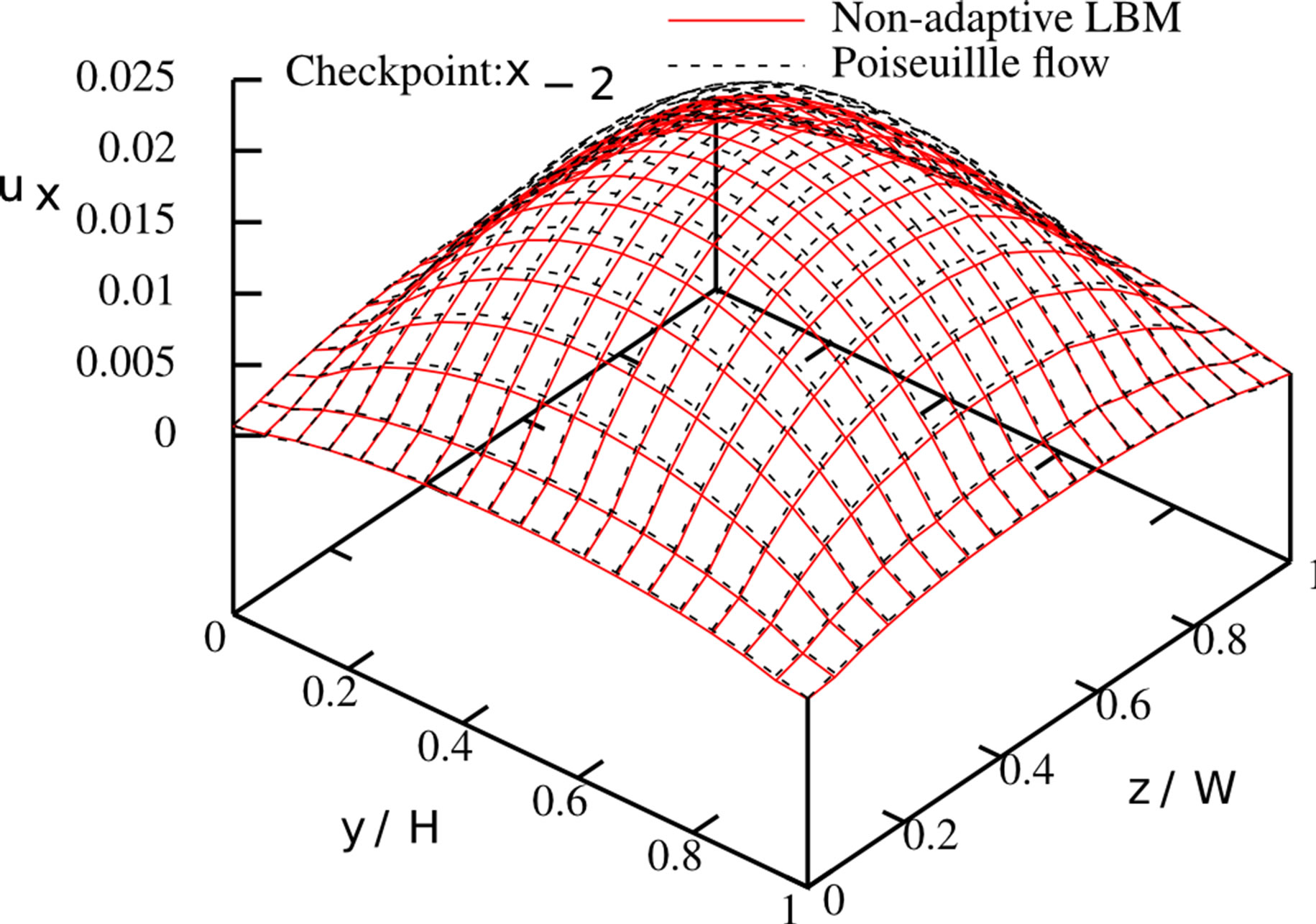
sections from Figure 6. We found that the mass flux deviations are less than 0.4% in each of the branches. We further checked the velocity profiles at the cross sections. We compared them to the results from a non-adaptive simulation of a Poiseuille flow where the fine grid and the respective MRT collision rule are applied in the whole domain. The profiles are given in Figure 7. It can be seen that the streamwise velocity profiles at the different checkpoints agree very well with the solution of the Poiseuille flows. The largest pointwise deviation between the Poiseuille flow and the different solutions can be found in Table 2. Both adaptive and completely resolved simulations show nearly identical deviations, indicating the validity of our adaptive simulation setup. A speedup of 1.154 could be observed, going from the regular to the static adaptive simulation.
In order to further reduce computational time besides the application of adaptive grids, we investigated the influence of applying the BGK collision operator-instead of the tuned MRT model-on the coarse grid level in the inner part of the reaction chamber. No wall interactions are encountered for the coarse cells in this region. As a consequence, the motivation for the choice of the MRT scheme from Section 2.2 does not play a crucial role in this part of the domain. The largest pointwise error and the velocity profiles are also depicted in Table 2 and Figure 7. The adaptive grid solution using both the MRT and BGK collision operator is similar to the other solutions, with maximum deviations of less than 0.6% from the adaptive pure MRT solution. Reducing the computational load on the coarse grid by the simplified collision process yields a further reduction of 1.5% in the computational time, compared to the computational time of the adaptive grid with MRT collision rules on both grid levels. The effect of the refined collision model strongly depends on the ratio of coarse grid to fine grid nodes, which amounts in our case to 0.07. In total, the adaptive grid using a resolution dependent collision model decreases the computational time by 14.6% in comparison to the regular simulation.
In the next step, we simulated a three-dimensional setup. We used a non-adaptive grid consisting of 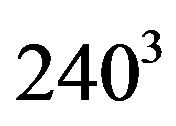 cells. The first-order slip boundary condition and the MRT with viscosity adjustment were employed for the whole domain. The size of the duct system and the reaction chamber were chosen such that the Knudsen numbers within the channels and inside the chamber are
cells. The first-order slip boundary condition and the MRT with viscosity adjustment were employed for the whole domain. The size of the duct system and the reaction chamber were chosen such that the Knudsen numbers within the channels and inside the chamber are 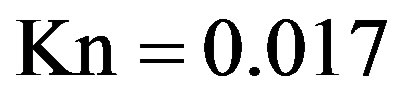 and
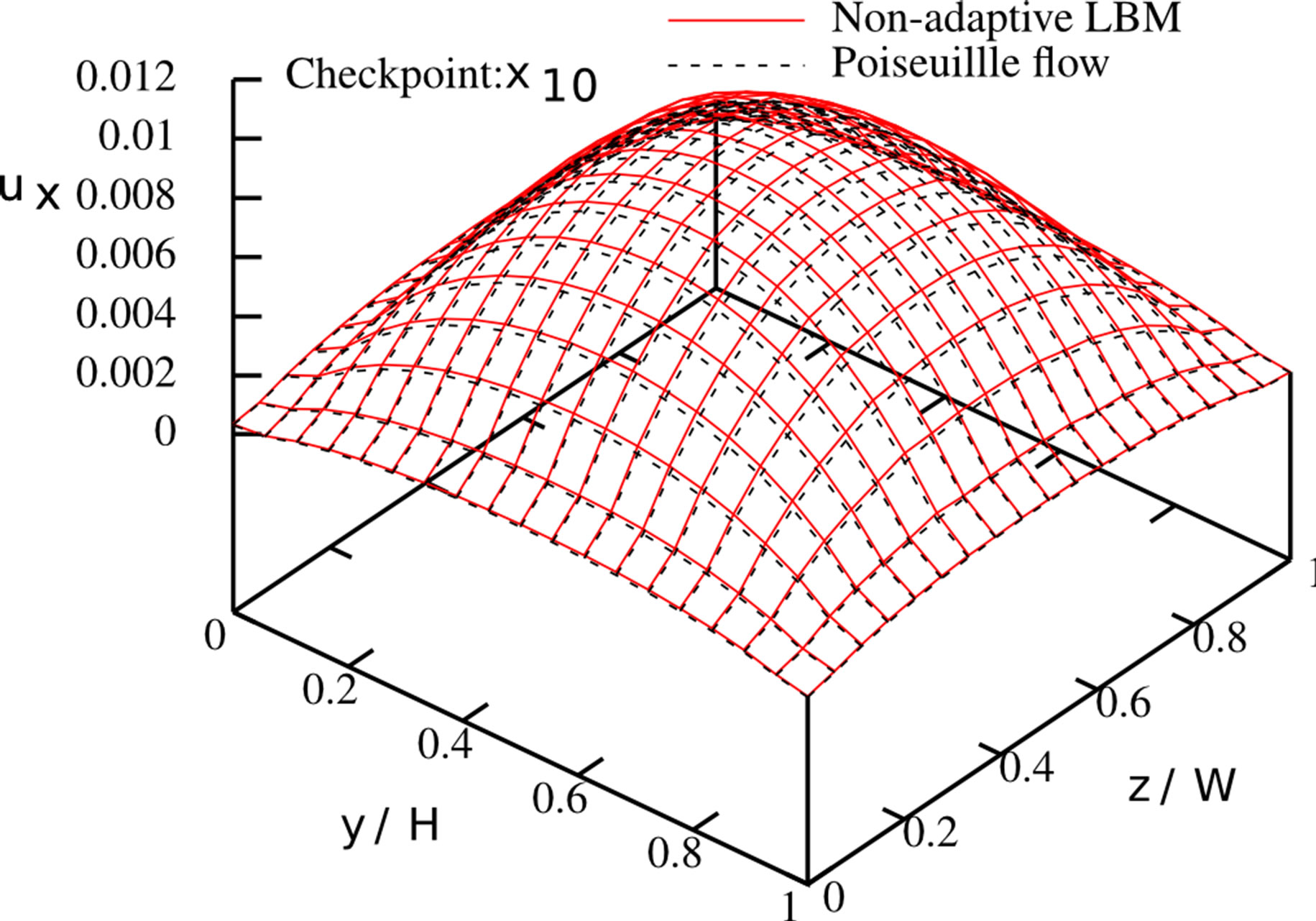
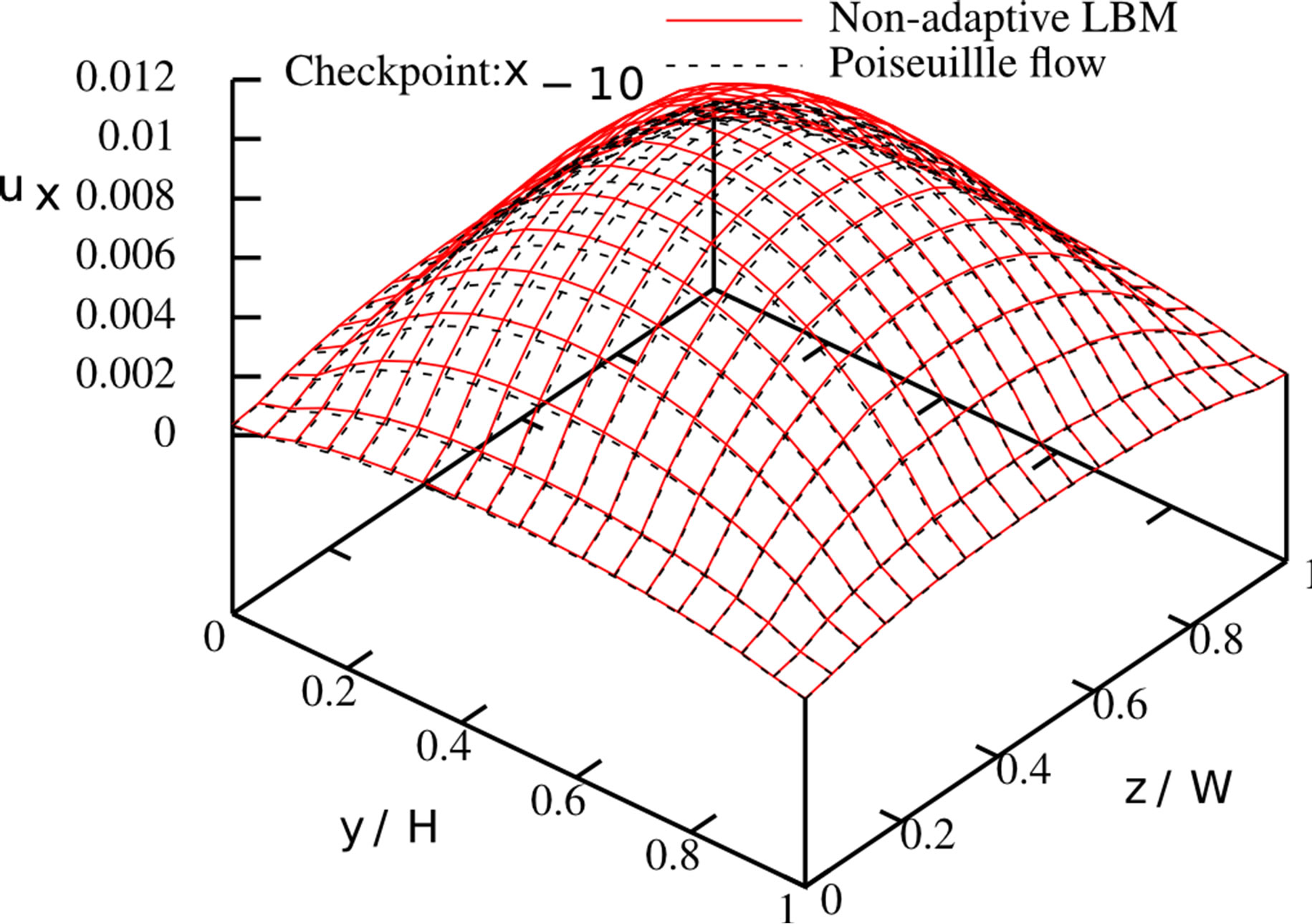
and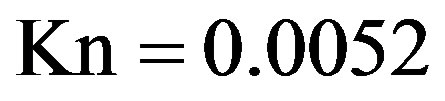 , respectively. In order to validate the results, we compared the streamwise velocity profiles to Poiseuille flows with similar conditions, see Figure 8; they are in good accordance. We further investigated the mass flux at junctions to evaluate the influence of the special boundary treatment on three-dimensional geometries. The relative mass flux error does not exceed 0.4%.
, respectively. In order to validate the results, we compared the streamwise velocity profiles to Poiseuille flows with similar conditions, see Figure 8; they are in good accordance. We further investigated the mass flux at junctions to evaluate the influence of the special boundary treatment on three-dimensional geometries. The relative mass flux error does not exceed 0.4%.
4. Conclusion and Outlook
We presented the extension of our adaptive Lattice Boltzmann implementation to the slip and transition flow regime. The code was validated in pressure-driven and periodic channel flow scenarios. The results show excellent agreement with the results of other research groups. We extended our code to allow for the simulation of complex duct systems using the half-way bounce-back scheme at corner nodes. Our results from the microreactor simulations agree very well with the predictions of the pure channel results, as well as with non-adaptive simulations of the same underlying setup.
Applying the concept of spatial adaptivity reduced the computational time by 13.1 percent in case of the micro-
|
|
|
|
|
|
|
|
Figure 7. Streamwise velocity profiles at different cross sections of the duct system. Adaptive LBM with MRT scheme applied on all levels (red), adaptive LBM with MRT/BGK combination (blue), non-adaptive LBM (green) and respective Poiseuille flow profile (black).
|
|
|
|
|
|
Figure 8. Streamwise velocity profiles at different cross sections of the three-dimensional duct system. Non-adaptive LBM (red) and respective Poiseuille flow profile (black).
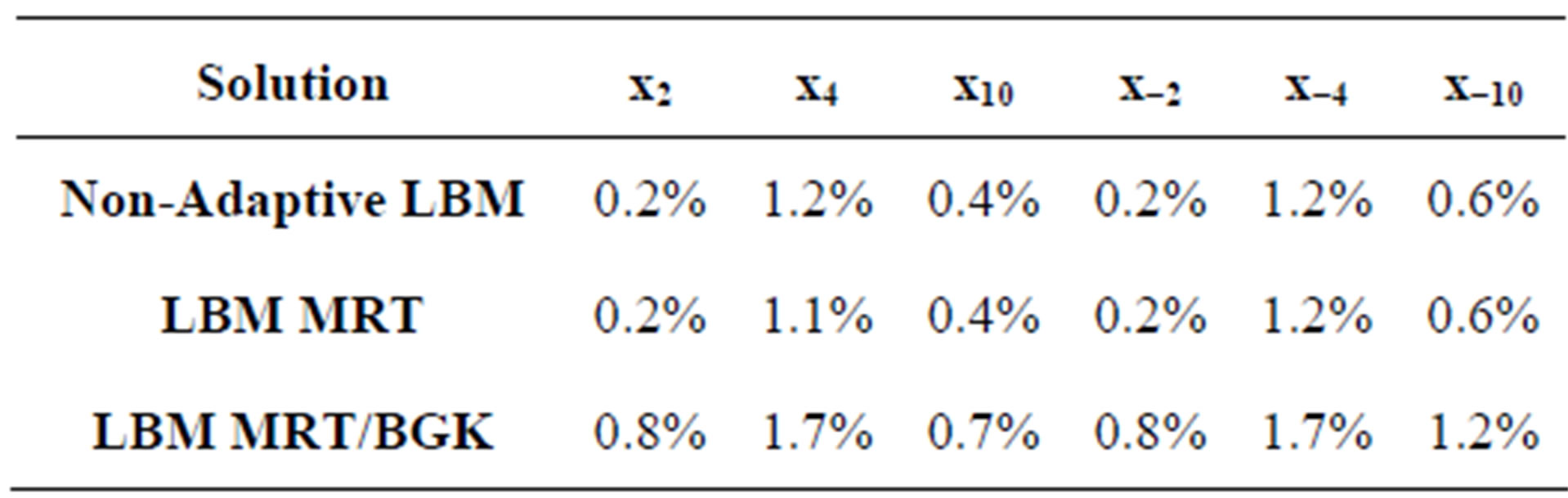
Table 2. Largest pointwise deviation of the streamwise velocity between different solutions and the Poiseuille flow results.
reactor simulation. The slip corrections, that are required near the boundaries and in the small-sized ducts, were found to be negligible in the inner part of the big-sized reactor chamber. Besides the spatial adaptivity concept, a simplification of the collision step could be applied in this area. This approach led to a slight increase in performance while still yielding acceptable results.
In our future work, we plan to approach the molecular regime. More focus is to be put on spatial adaptivity: higher gains in performance than in the present microreactor simulation are expected, for example in the case of bigger reactor chambers where the rigorous coarsening of the discretisation within the chamber significantly pays off. Besides, as the presented LBM scheme is only valid in the slip and transition flow regime, multiscale approaches (see amongst others [41,42]) may account for a further reduction in length and time scales; however, massively parallel simulation software may be required for the simulation of realistic three-dimensional setups. A first step towards the latter challenge has already been taken in the context of coupled Lattice Boltzmann-Molecular Dynamics simulations [43].
5. Acknowledgements
The authors gratefully acknowledge the support of the TUM’s Faculty Graduate Center CeDoSIA at Technische Universität München. They further thank the Munich Centre of Advanced Computing and the King Abdullah University of Science and Technology (KAUST, Award No. UK-c0020) for providing computational resources. Till Rohrmann particularly thanks Li-Shi Luo for his immediate and extensive advice during the development of the MRT-based slip flow scheme.
REFERENCES
- Y. Zheng, A. L. Garcia and B. J. Alder, “Comparison of Kinetic Theory and Hydrodynamics for Poiseuille Flow,” Journal of Statistical Physics, Vol. 109, No. 314, 2002, pp. 495-505. doi:10.1023/A:1020498111819
- T. Q. Li, Y. He, G. Tang and W. Tao, “Lattice Boltzmann Modeling of Microchannel Flows in the Transition Flow Regime,” Microfluidics and Nanofluidics, Vol. 10, No. 3, 2011, pp. 607-618. doi:10.1007/s10404-010-0693-1
- G. H. Tang, W. Q. Tao and Y. L. He, “Lattice Boltzmann Method for Gaseous Microflows Using Kinetic Theory Boundary Conditions,” Physics of Fluids, Vol. 17, No. 5, 2005, Article ID: 058101. doi:10.1063/1.1897010
- F. Toschi and S. Succi, “Lattice Boltzmann Method at Finite Knudsen Numbers,” Europhysics Letters, Vol. 69, No. 4, 2005, pp. 549-555. doi:10.1209/epl/i2004-10393-0
- F. J. Uribe and A. L. Garcia, “Burnett Description for Plane Poiseuille Flow,” Physical Review E, Vol. 60, No. 4, 1999, pp. 4063-4078. doi:10.1103/PhysRevE.60.4063
- F. Verhaeghe, L.-S. Luo and B. Blanpain, “Lattice Boltzmann Modeling of Microchannel Flow in the Slip Flow Regime,” Journal of Computational Physics, Vol. 228, No. 1, 2009, pp. 147-157. doi:10.1016/j.jcp.2008.09.004
- K. Xu, “Super-Burnett Solutions for Poiseuille Flow,” Physics of Fluids, Vol. 15, No. 7, 2003, pp. 2077-2080. doi:10.1063/1.1577564
- Y.-H. Zhang, X.-J. Gu, R. W. Barber and D. R. Emerson, “Capturing Knudsen Layer Phenomena Using a Lattice Boltzmann Model”, Physical Review E, Vol. 74, 2006, Article ID: 046704.
- X. Shan, “Lattice Boltzmann in Microand Nano-Flow Simulations,” IMA Journal of Applied Mathematics, Vol. 76, No. 5, 2011, pp. 650-660. doi:10.1093/imamat/hxr009
- C. E. Colosqui, D. M. Karabacak, K. L. Ekinci and V. Yakhot, “Lattice Boltzmann Simulation of Electromechanical Resonators in Gaseous Media,” The Journal of Fluid Mechanics, Vol. 652, 2010, pp. 241-257. doi:10.1017/S0022112010000042
- P. Neumann and T. Neckel, “A Dynamic Mesh Refinement Technique for Lattice Boltzmann Simulations on Octree-Like Grids,” Computational Mechanics, 2012. doi:10.1007/s00466-012-0721-y
- G. Karniadakis, A. Beskok and N. Aluru, “Microflows and Nanoflows: Fundamentals and Simulation,” Springer, New York, 2005.
- W.-M. Zhang, G. Meng and X. Wei, “A Review on Slip Models for Gas Microflows,” Microfluidics and Nanofluidics, 2012. doi:10.1007/s10404-012-1012-9
- S. Succi, “The Lattice Boltzmann Equation for Fluid Dynamics and Beyond,” Oxford University Press, Oxford, 2001.
- P. L. Bhatnagar, E. P. Gross and M. Krook, “A Model for Collision Processes in Gases. I. Small Amplitude Processes in Charged and Neutral One-Component Systems,” Physical Review, Vol. 94, 1954, pp. 511-525. doi:10.1103/PhysRev.94.511
- D. D’Humières, “Generalized lattice Boltzmann Equations, Rarefied Gas Dynamics: Theory and Simulations,” Progress in Astronautics and Aeronautics, Vol. 159, 1992, pp. 450-458.
- D. D’Humières, I. Ginzburg, M. Krafczyk, P. Lallemand and L.-S. Luo, “Multiple-Relaxation-Time Lattice Boltzmann Models in Three Dimensions,” Philosophical Transactions of the Royal Society A, Vol. 360, No. 1792, 2002, pp. 437-451. doi:10.1098/rsta.2001.0955
- P. Lallemand and L.-S. Luo, “Theory of the Lattice Boltzmann Method: Dispersion, Dissipation, Isotropy, Galilean Invariance, and Stability,” Physical Review E, Vol. 61, No. 6, 2000, pp. 6546-6562. doi:10.1103/PhysRevE.61.6546
- X. D. Niu, C. Shu and Y. T. Chew, “A Lattice Boltzmann BGK Model for Simulation of Micro Flows,” Europhysics Letters, Vol. 67, No. 4, 2004, pp. 600-606. doi:10.1209/epl/i2003-10307-8
- M. Sbragaglia and S. Succi, “Analytical Calculation of Slip Flow in Lattice Boltzmann Models with Kinetic Boundary Conditions,” Physics of Fluids, Vol. 17, No. 9, 2005, Article ID: 093602. doi:10.1063/1.2044829
- Y. Zhang, R. Qin and D. R. Emerson, “Lattice Boltzmann Simulation of Rarefied Gas Flows in Microchannels,” Physical Review E, Vol. 71, 2005, Article ID: 047702.
- L. d. Izarra, J.-L. Rouet and B. Izrar, “High-Order Lattice Boltzmann Models for Gas Flow for a Wide Range of Knudsen Numbers,” Physical Review E, Vol. 84, 2011, Article ID: 066705.
- J. Meng and Y. Zhang, “Gauss-Hermite Quadratures and Accuracy of Lattice Boltzmann Models for Nonequilibrium Gas Flows,” Physical Review E, Vol. 83, 2011, Article ID: 036704.
- G. H. Tang, W. Q. Tao and Y. L. He, “Gas Slippage Effect on Microscale Porous Flow Using the Lattice Boltzmann Method,” Physical Review E, Vol. 72, 2005, Article ID: 056301.
- G. H. Tang, W. Q. Tao and Y. L. He, “Three-Dimensional Lattice Boltzmann Model for Gaseous Flow in Rectangular Microducts and Microscale Porous Media,” Journal of Applied Physics, Vol. 97, 2005, Article ID: 104918.
- A. Beskok and G.E. Karniadakis, “A Model for Flows in Channels, Pipes, and Ducts at Micro and Nano Scales,” Microscale Thermophysical Engineering, Vol. 3, 1999, pp. 43-77.
- D. W. Stops, “The Mean Free Path of Gas Molecules in the Transition Regime,” Journal of Physics D: Applied Physics, Vol. 3, No. 5, 1970, pp. 685-696. doi:10.1088/0022-3727/3/5/307
- G. H. Tang, Y. H. Zhang, X. J. Gu and D. R. Emerson, “Lattice Boltzmann Modelling Knudsen Layer Effect in Non-Equilibrium Flows,” Europhysics Letters, Vol. 83, 2008.
- M. Nourmohammadzadeh, M. Rahnama, S. Jafari and A. R. Akhgar, “Microchannel Flow Simulation in Transition Regime Using Lattice Boltzmann Method,” Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, Vol. 226, No. 2, 2012, pp. 552-562. doi:10.1177/0954406211413959
- V. Michalis, A. Kalarakis, E. Skouras and V. Burganos, “Rarefaction Effects on Gas Viscosity in the Knudsen Transition Regime,” Microfluidics and Nanofluidics, Vol. 9, No. 4-5, 2010, pp. 847-853. doi:10.1007/s10404-010-0606-3
- A. Beskok, G. E. Karniadakis and W. Trimmer, “Rarefaction and Compressibility Effects in Gas Microflows,” Transactions of the ASME, Vol. 118, 1996, pp. 448-456.
- M. Mehl, T. Neckel and P. Neumann, “Navier-Stokes and Lattice-Boltzmann on Octree-Like Grids in the Peano Framework,” International Journal for Numerical Methods in Fluids, Vol. 65, No. 1, 2010, pp. 67-86. doi:10.1002/fld.2469
- H.-J. Bungartz, M. Mehl, T. Neckel and T. Weinzierl, “The PDE Framework Peano Applied to Fluid Dynamics: An Efficient Implementation of a Parallel Multiscale Fluid Dynamics Solver on Octree-Like Adaptive Cartesian Grids,” Computational Mechanics, Vol. 46, No. 1, 2010, pp. 103-114. doi:10.1007/s00466-009-0436-x
- C. Colin and S. Aubert, “High-Order Boundary Conditions for Gaseous Flows in Rectangular Microducts,” Microscale Thermophysical Engineering, Vol. 5, No. 1, 2001, pp. 41-54. doi:10.1080/108939501300005367
- C. Shen, D. B. Tian, C. Xie and J. Fan, “Examination of the LBM in Simulation of Microchannel Flow in Transitional Regime,” Microscale Thermophysical Engineering, Vol. 8, No. 4, 2004, pp. 423-432. doi:10.1080/10893950490516983
- L. Lei, N. Wang, X. M. Zhang, Q. Tai, D. P. Tsai and H. L. W. Chan, “Optofluidic Planar Reactors for Photocatalytic Water Treatment Using Solar Energy,” Biomicrofluidics, Vol. 4, No. 4, 2010.
- H. Chen, “Volumetric Formulation of the Lattice Boltzmann Method for Fluid Dynamics: Basic Concept,” Physical Review E, Vol. 58, No. 3, 1998, pp. 3955-3963. doi:10.1103/PhysRevE.58.3955
- M. Rohde, D. Kandhai, J. J. Derksen and H. E. A. van den Akker, “A Generic, Mass Conservative Local Grid Refinement Technique for Lattice-Boltzmann Schemes,” International Journal for Numerical Methods in Fluids, Vol. 51, No. 4, 2006, pp. 439-468. doi:10.1002/fld.1140
- N. G. Hadjiconstantinou, “Comment on Cercignani’s Second-Order Slip Coefficient,” Physics of Fluids, Vol. 15, No. 6, 2003, pp. 2352-2354. doi:10.1063/1.1587155
- T. Ohwada, Y. Sone and K. Aoki, “Numerical Analysis of the Shear and Thermal Creep Flows of a Rarefied Gas over a Plane Wall on the Basis of the Linearized Boltzmann Equation for Hard-Sphere Molecules,” Physics of Fluids, Vol. 1, No. 9, 1989, pp. 1588-1599. doi:10.1063/1.857304
- J. Meng, Y. Zhang and X. Shan, “Multiscale Lattice Boltzmann Approach to Modeling Gas Flows,” Physical Review E, Vol. 83, 2011, Article ID: 046701.
- A. Dupuis, E. M. Kotsalis and P. Koumoutsakos, “Coupling Lattice Boltzmann and Molecular Dynamics Models for Dense Fluids,” Physical Review E, Vol. 75, 2007, Article ID: 046704.
- P. Neumann and N. Tchipev, “A Coupling Tool for Parallel Molecular Dynamics-Continuum Simulations,” Proceedings of the International Symposium on Parallel and Distributed Computing, 2012 Accepted.