Open Journal of Applied Sciences
Vol.05 No.05(2015), Article ID:56552,7 pages
10.4236/ojapps.2015.55023
Design of Underground Pipelines under Arbitrary Seismic Loading
Diyorbek Bekmirzaev
Institute of Seismic Stability of Structures, Academy of Sciences of the Republic of Uzbekistan, Tashkent, Republic of Uzbekistan
Email: diyorbek_84@mail.ru
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 April 2015; accepted 18 May 2015; published 22 May 2015
ABSTRACT
On the basis of Hamilton-Ostrogradskiy variation principle a system of equations of linear pipeline vibrations interacting with surrounding soil is derived with appropriate boundary and initial conditions under arbitrary direction of seismic effect. Dynamic problem of underground pipeline is solved by finite difference method of the second order of accuracy with different combinations of boundary conditions under the effect of seismic load on a given law with arbitrary direction. Numerical implementation of the problem is realized.
Keywords:
Underground Pipeline, Seismo-Dynamics, Boundary Conditions, Seismic Effect, “Pipeline-Soil” System Interaction, Finite Difference Method

1. Introduction
Current state of computing resources allows considering more closely numerous factors and determining more reliably the actual stress-strain state of underground pipeline.
In this regard, republican and foreign works have been analyzed, in particular, proceedings of XIV (Beijing, 2008) and XV (Lisbon, 2012) World Conferences on Earthquake Engineering and International Conference on Design in Geotechnical Engineering (Tokyo, 2009), associated with the study of seismic systems of pipelines, such as underground gas-, water- and oil-pipelines, to improve developed theory by new data, to evaluate its effectiveness and to establish the level of this work [1] - [3] .
At present, industrial enterprises and life support systems play a crucial role in human life and in economic development of the country: for this reason, their structural safety under extreme conditions, such as strong earthquakes, should be provided, especially when a large number of toxic and combustible materials are transported by these facilities. After the earthquake event, accident rate in pipelines is often increasing. In underground structures, the failure of one part affects the performance of the whole system, while in ground structures it is local. Therefore, diversified study of seismic vulnerability assessment was carried out for a number of industrial facilities and life support systems, such as pipelines, underground storage tanks and reservoirs.
Modern cities are growing not only in breadth, in height, but also in depth, using underground space. Pipelines of hot and cold water supply, sewage system, electric, telephone cable lines, along with subway lines, garages, etc. all create a new environment, which differs from the traditional soil medium. All located under modern megalopolis is likely to be regarded as a soil medium with disturbed structure. The key problem is, on one hand, design feature of the structures, and on the other, evaluation of interaction nature in “structure-soil” system [4] .
Fundamental analysis of the effects of earthquakes on underground pipes has been conducted; main types of damage have been stated; the effect of impact depth, soil conditions, geometrical sizes, types of joining and the quality of construction on seismic stability of underground pipelines for various purposes has been revealed [5] - [7] .
Practical significance of the problem consists in the following. Many large metropolitan areas are located in seismically active areas. Therefore, the design of underground structures becomes more difficult. Analysis of many earthquakes all over the world shows that the majority of destructions of underground pipelines occur on the border and close to it [8] . In this paper the solution of the problem of underground pipeline is studied under seismic load of arbitrary direction with different boundary conditions.
2. Statement of the Problem
To study combined longitudinal, transverse vibrations of underground structures such as pipelines under arbitrary direction of seismic load we will consider applied theory of bar oscillations. This paper investigates a seismo-dynamics of underground pipelines based on the theory of seismo-dynamics of underground structures, with mathematical model of bar theory discussed by Bekmirzaev D.A. and Rashidov T.R. for the case of bar points displacements under combined action of longitudinal and transversal forces [9] .
Based on the assumptions given in [9] , the pipeline is modeled in the form of a bar (Figure 1), α―is an angle of incidence of seismic wave, and displacements are selected as follows:
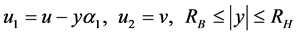 (1)
(1)
where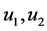 ―are displacements of the points of a pipeline, u―longitudinal displacements, v―transversal displacements,
―are displacements of the points of a pipeline, u―longitudinal displacements, v―transversal displacements,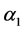 ―an angle of rotation of pipe section.
―an angle of rotation of pipe section.
When δ―is a thickness, DH―external diameter, and l―a length of cylinder shell, then at relative dimensions, expressed through order values,
 (2)
(2)
the discussed structure may be referred to a category of long cylinder shells. Such shells, independent on form and geometrical sizes of the profile, may be called thin-walled bars [10] . The pipeline under discussion always meets the condition (2).
Figure 1. Scheme of underground pipeline under arbitrary directed seismic effect on horizontal plane.
Assume that pipeline is strained elastically; so Hooke’s law is considered for pipe material:
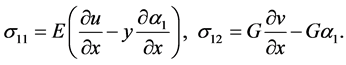 (3)
(3)
To derive differential equations with boundary and initial conditions we will use Hamilton-Ostrogradskiy variation principle:
 (4)
(4)
where Т―is kinetic, П―potential energy, А―work of external forces, t―time. On the basis of Hamilton-Ostro- gradskiy variation principle (4), considering relationships (1) and (3) the following system of differential equations is derived:
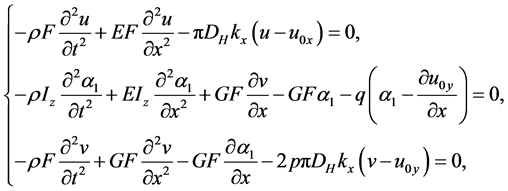 (5)
(5)
natural boundary conditions
 (6)
(6)
and initial conditions
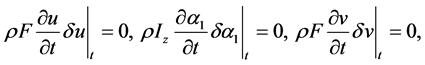 (7)
(7)
where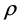 ―is a density of pipeline material, F―an area of its cross section, E―modulus of elasticity of pipeline material, G―modulus of elasticity under shear,
―is a density of pipeline material, F―an area of its cross section, E―modulus of elasticity of pipeline material, G―modulus of elasticity under shear,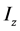 ―inertia moment of cross-section,
―inertia moment of cross-section, ―pipeline coordinates
―pipeline coordinates 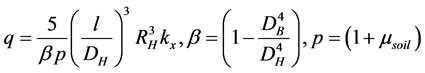 [6] .
[6] .
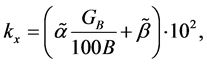 (8)
(8)
where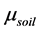 ―is Poisson ratio of soil,
―is Poisson ratio of soil,







Intensity of normal and tangential stresses


except intensity of tangential stresses

From natural boundary conditions (6) we may obtain their different combinations. The system of Equations (5) with boundary (6) and initial conditions (7) is solved by finite difference method of the second order of accuracy. Based on computer algorithm, a program for problem-oriented Borland Delphi 7 language was developed and numerical results were obtained.
3. Analysis of the Results of Numerical Studies
The algorithm and design program for underground pipelines in case of incidence of seismic wave at an angle to the pipe axis have been worked out; this corresponds to arbitrary seismic loading in the form of accelerograms or seismograms. As an example we will consider the following problems:
Problem. Consider a steel underground pipeline. Stated problem is solved on the basis of computer implementation of the algorithm. The mechanical and geometrical parameters of underground pipeline and soil are selected as follows:
Modulus of elasticity












ratio of soil

From the nature of an earthquake it is known that it has a complex character and effects on the structure and underground pipelines in arbitrary direction. Such effects of seismic loads on underground pipes complicate an assessment of stress-strain state of underground structures.
In this problem underground pipeline under seismic load works on tension, compression and bending. In the process of vibration of underground pipeline phases of displacements and stresses are changing. Results of problem solution are given in the form of graphs.
Vibration time is chosen in such a way that under all three boundary conditions the pipeline is either in tensile state Figure 2(a) or in compressed one―Figure 2(b) at α = 0, and normal stress at a given time along the length of a pipeline is changing as in Figure 2(c) in tensile state and Figure 2(d)―in compressed one at α = 0.


Figure 2. Changes of longitudinal displacement and normal stress along the axis of the pipeline at given time: 1) both ends of the pipeline are jammed, 2) the left end of the pipeline is jammed, the right one is free, 3) both ends are elastically fixed.
The effect of seismic load along the axis of underground pipeline under different boundary conditions and different times of changes of longitudinal displacement and normal stress along pipeline axis are shown in Figure 2 (α = 0). Time is chosen so that the pipeline is in tensile or compressed state.
Three boundary conditions are examined:
1. Both ends of the pipeline are jammed,
2. The left end is jammed, the right one is free,
3. Both ends of the pipeline are elastically fixed,
where


Analysis of results in Figure 2 shows that maximum values of longitudinal displacement at boundary conditions 1 and 3 are within the span of the pipeline, and boundary conditions 2―at free end of the pipeline. Longitudinal stress has its maximum value at jammed ends or elastically fixed ends of the pipeline. It should be noted that the value of normal stress at jammed end of the pipeline is greater than the one at elastically fixed end of the pipeline (see Figure 2).
The changes of transversal displacement and tangential stress under seismic loads transversal to the axis of the pipeline at different boundary conditions and at different times are shown in Figure 3.


Figure 3. Changes of transversal displacement and tangential stress along the axis of the pipeline at given time: 1) both ends of the pipeline are jammed, 2) the left end of the pipeline is jammed, the right one is free, 3) both ends are elastically fixed.
Here, as in Figure 2, transverse displacement reaches its maximum value at boundary conditions 1 and 3 in pipeline range, and at boundary conditions 2-at the free end of the pipeline (Figure 3). Shear stress has its maximum values at jammed and elastically fixed ends of the pipeline (Figure 3). This corresponds to a change in the value of normal stress (Figure 2).
At each boundary condition the time is chosen so that transverse displacement has either positive value Figure 3(a) or negative one―Figure 3(b) at α = 90, and tangential stress at a given time along the length of the pipeline is changing as in Figure 3(c) in tensile state and Figure 3(d)―in compressed one at α = 90.
The law of soil motion is considered in the form



boundary conditions and at the change of incidence angle of seismic load on pipeline axis is solved with these data.
Figure 4 shows the changes of maximum values of longitudinal and transversal displacements, and normal and tangential stresses when the direction of the effect of seismic loads is changing. If consider the figures with increasing angle of seismic load effect, maximum values of transversal displacements and tangential stresses are also increasing (Figure 4(b) and Figure 4(d)). When an angle of the effect of seismic load is increasing, the values of maximal longitudinal displacement and normal stress are decreasing (Figure 4(a) and Figure 4(c)).
To determine strength characteristics of the pipeline it is necessary to determine the intensity of normal and tangential stresses. This operation is performed by formulas (9) and (10).
The results are shown in Figure 5. Here it should be noted that, in general with increasing angle of incidence of seismic load, intensity values of normal and tangential stresses are also increasing (Figure 5). It should be also noted that elastically fixed pipelines (relative to other boundary conditions (1, 2)) have lower intensity values of normal and tangential stresses (Figure 5).
4. Conclusions
An algorithm for solution of obtained equations and the design program are worked out. The solution is built on the


Figure 4. Change of longitudinal and transversal displacements and normal and tangential stresses at alteration of incidence angle of seismic loads: 1) both ends of the pipeline are jammed, 2) the left end of the pipeline is jammed, the right one is free, 3) both ends are elastically fixed.

Figure 5. Changes of intensity of normal and tangential stresses at alteration of incidence angle of seismic load: 1) both ends of the pipeline are jammed, 2) the left end of the pipeline is jammed, the right one is free, 3) both ends are elastically fixed.
basis of finite difference method; that allows simultaneously specifying the initial and boundary conditions, soil response and the decision itself. The results are obtained under different boundary conditions. From analysis of the results, it is evident that stress-strain state of the pipeline with elastically fixed ends is lower than with other combination of boundary conditions. It can be concluded that in design of underground pipeline, joining parts must be close to elastically fixed conditions. Thus stress-strain state of the pipeline decreases by 20% - 40% relative to the rigidly fixed boundary conditions. Maximal normal stresses occur under longitudinal seismic loading, and tangential stress reaches its maximum value at transversal seismic loading of the pipeline.
Results of the intensity of normal and tangential stresses of the pipeline are given. This makes it possible to evaluate strength characteristics of underground pipelines during strong earthquakes in seismically active areas. Presented methods and software tools provide a comprehensive analysis of the strength of underground pipeline under seismic actions and implement a systematic approach to determining the effects of the earthquake on stress-strain state of the pipeline and to planning engineering measures to ensure safe and reliable operation of underground pipeline in zones of high seismic risk. Developed algorithms and design programs allow us to consider pipeline vibrations under different types of loading, types of ends fixing and soil parameters. All these procedures allow us to determine actual loading and displacements occurring in sections of the pipeline under different seismic loadings. This makes it possible to improve regulatory documents on earthquake-resistant engineering of underground networks of supply pipelines [11] and to develop universal applied programs of design and construction.
Cite this paper
Diyorbek Bekmirzaev, (2015) Design of Underground Pipelines under Arbitrary Seismic Loading. Open Journal of Applied Sciences,05,226-232. doi: 10.4236/ojapps.2015.55023
References
- 1. The 14th World Conference on Earthquake Engineering, Beijing (2008).
- 2. The 15th World Conference on Earthquake Engineering, Lisbon (2012).
- 3. Proceeding of International Conference on Performance-Based Design in Earthquake Geotechnical Engineering, Tokyo (2009).
- 4. Rashidov, T.R. and An, E.V. (2013) Seismo-Dynamics of Structures, Interacting with Soil. Uzbek Journal “Problems of Mechanics”, 3-4, 40-45.
- 5. Rashidov, T.R. (1973) Dynamic Theory of Seismic Stability of Complex Systems of Underground Structures. FAN, Tashkent, 180 p.
- 6. Rashidov, T.R. and Khojmetov, G.Kh. (1985) Seismic Stability of Underground Pipelines. FAN, Tashkent, 153 p.
- 7. Tashkent Earthquake on 26th of April, 1966 (1971) FAN, Tashkent, 672 p.
- 8. Ghekhman, A.S. and Zainetdinov, Kh. (1988) Design, Construction and Operation of Pipelines in Seismic Regions. Stroyizdat, Moscow, 184 p.
- 9. Bekmirzaev, D.A. and Rashidov, T.R. (2014) Solution of the Problem of Seismo-Dynamics of Underground Pipelines under Loading of Arbitrary Direction. Uzbek Journal “Problems of Mechanics”, 3-4, 8-13.
- 10. Vlasov, V.Z. (1963) Selected Works. Volume II. USSR Academy of Sciences, Moscow, 508 p.
- 11. Building Code (1996) Engineering in Seismic Regions. КМК 2.01.03-96, Tashkent, 88 p.
- 12. Aleksandrov, А.V. and Potapov, V.D. (1990) Bases of the Theory of Elasticity and Plasticity: Text-Book for Engineering Colleges. High School, Moscow, 400 p.








