Open Journal of Applied Sciences
Vol.05 No.04(2015), Article ID:55959,12 pages
10.4236/ojapps.2015.54017
Optical Characterization of (TMA)2ZnCl4 Single Crystals in the Normal Phase
A. Abu El-Fadl*, M. Almokhtar, A. M. Nashaat
Physics Department, Faculty of Science, Assiut University, Assiut, Egypt
Email: *abulfadla@yahoo.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 April 2015; accepted 23 April 2015; published 24 April 2015
ABSTRACT
The transmittance (T) and the reflectance (R) were measured for (TMA)2ZnCl4 single crystals and hence the absorption coefficient (α), extinction coefficient (Kex.), refractive index (n), real and imaginary dielectric constants (e¢, e²) of (TMA)2ZnCl4 crystals were calculated as a function of photon energy. The analysis of the spectra behavior of the absorption coefficient in the absorption region revealed indirect transition. The dispersion of the refractive index is discussed in terms of the single oscillator Wemple-DiDomenico model. The single oscillator energy (E0), the dispersion energy (Ed), the lattice dielectric constant (εL) and the ratio of free charge carrier concentration to the effective mass (N/m*) were estimated. The FTIR spectra were recorded to study the functional groups of the as grown and annealed samples.
Keywords:
(TMA)2ZnCl4 Single Crystals, Optical Band Gap, Refractive Index, Dispersion Parameters, FTIR Spectroscopy

1. Introduction
The A2BX4 type crystals (with A = K, NH4, Rb; B = Zn, Co; X = Cl, Br) have been interested because of their incommensurately modulated structures and the successive phase transitions [1] . In the recent past, the study of incommensurate phases in matter has grown explosively with the discovery of over a hundred materials exhibiting incommensurate properties. Many of these materials belong to the ferroelectric A2BX4 family [1] , which exhibit in addition to the well-known normal-commensurate phase transitions one or several intermediate incommensurate phases. In these phases a local atomic property (like spontaneous polarization in ferroelectrics) is modulated with a period which is incommensurate with the underlying lattice periodicity [2] .
The compounds belonging to TMA family have attracted much interest because of exhibiting some peculiar characteristics associated with the phase transition. Among them [N(CH3)4]2ZnC14 (hereafter (TMA)2ZnCl4) with b-K2SeO4 type structure as the normal (or prototype) phase at the high temperature region. (TMA)2ZnCl4 exhibits a sequence of structural phase transitions. It turns incommensurate when cooled through a first-order phase transition occurring at TINC = 296 K, becomes ferroelectric by lock-in of the incommensurate modulation at TC-F = 279 K, and at TC2 = 276.3 K another first-order ferroelectric phase transition takes place at 181 K is monoclinic, phase V between 181 K and 163 K is monoclinic or triclinic, and phase VI, which is stable below 163 K, is orthorhombic. The highest temperature phase, Phase I, has Pmcn symmetry. In this phase one unit cell contains four formula units consisting of two inequivalent types of tetramethylammonium ions [3] .
Many investigations have been performed on (TMA)2ZnCl4 crystals including studies of the effect of electric field and mechanical stress (uniaxial or shear stress) on dielectric permittivity and spontaneous polarization by Styrkowiec and Czapla [4] . They concluded that, the electric field shifts the transition point Tc1, (IC) to higher temperature and the transition point Tc2 (ferroelectric ferroelastic) lower. It is found that the dielectric constant and the shift of the transition point are dependent on the uniaxial stresses and this stress can also induce a change of the crystal symmetry. Linear birefringence (LB) behavior of [N(CH3)4]2ZnC14 and [N(CH3)4]2CuC14 was studied in the critical region on normal-incommensurate phase transition by Kim et al. [5] . The temperature dependences of birefingence and dielectric permittivity of [N(CH3)4]2ZnC14 and [N(CH3)4]2CoC14 are measured by Sveleba et al. [6] . The long-periodic commensurate phases appear within the incommensurate phase under the influence of external electric fields (E) and mechanical stresses. In the other hand Sveleba et al. [7] investigated the optical birefringence, optical indicatrix rotation, and residual intensity of [N(CH3)4]2ZnCl4 crystals doped with Ni2+ in the parent and incommensurate phases. Their temperature dependences obtained are nonlinear in a wide temperature range. It is shown that the nature of this nonlinearity is related to the presence of local spatial regions of the correlated motion of tetrahedral groups. Studies on the behaviour of the modulation wave vector in [(CH3)4)N]2ZnC14−xBrx compounds as a function of composition (x) and temperature were performed by Vogels et al. [8] . Time evolution of dielectric permittivity in [N(CH3)4]2ZnC14 crystals was measured at the fixed temperature by Styrkowiec [2] . In both incommensurate (II) and Ferroelectric (III) phases, a long- term relaxation of permittivity has been confirmed.
Little attention has been paid to the study of optical properties near the absorption edge of (TMA)2ZnCl4 crystal. This contribution reports the results of investigation of some optical properties of [N(CH3)4]2ZnC14 crystals in the normal phase. Another goal of the present work is to get some information about the vibration bands by Fourier transform infrared (FTIR) spectroscopic studies.
2. Experimental
(TMA)2ZnCl4 single crystals were grown using the solution growth technique from saturated solutions by slow cooling from 45˚C to 35˚C instead of isothermal evaporation. The raw material used for growth was obtained by mixing aqueous solutions of tetramethylammonium chloride (C4H12NCl) and Zinc chloride (ZnCl2) in stoichiometric amounts. Typically the growth runs lasted from 30 - 50 days. During this period the average cooling and growth rates were 0.2˚C/day and 0.3 mm/day, respectively. After an initial capping period, the crystal grew clear to heights ranging from 10 to 15 mm each. From the as grown crystals specimens were formed into b-plates with size of about 0.8 mm in thickness and 36 mm2 in area using a wet thread saw. The specimens used for optical measurements were clear, transparent and free from any noticeable defects. More details about the grown crys- tals are shown elsewhere [9] .
The optical transmittance was recorded at room temperature using Shimadzu UV-VIS dual beam scanning spectrophotometer in the energy range 2.1 - 6.4 eV. The incident unpolarized light was nearly perpendicular to (010) plane. The surrounding medium was air. The relative specular reflectance was measured at an incident angle of 5˚, while the sample was placed horizontally facing downward and was illuminated from the bottom.
The FTIR spectra were recorded in the range 400 - 4000 cm−1 employing a NICOLET FTIR 6700 spectrometer by the KBr pellet method to study the functional groups of the samples.
3. Results and Discussions
3.1. Optical Transmittance
Transmission spectrum is very important for any nonlinear optical (NLO) material, because a nonlinear optical material can be of practical use only if it has wide transparency window. Figure 1 shows the variation of the optical transmission (T) and reflectance (R) spectrum as a function of wavelength for (TMA)2ZnCl4 single crystal recorded in the range 190 to 900 nm at room temperature. From Figure 1, the lower cut off wavelength is obtained and listed in Table 1. UV-Vis-NIR spectrum, reveal that, (TMA)2ZnCl4 crystal is conveniently transparent from 300 to 900 nm with about 60% of transmittance and there is almost a steady transmittance in the visible region. The high transmission or low absorption in the region 300 - 900 nm makes the material to obtain low reflectance and refractive index which is a suitable property for antireflection coating solar thermal devices and nonlinear optical applications.
Electronic transitions between the valence band and the conduction band in crystals starts at the absorption edge that corresponds to the energy difference between the lowest minimum of the conduction band and the highest maximum of the valence band. The value of the energy gap depends in a rather subtle way on the structure and the actual values of the pseudopotential in the crystal. The optical behavior of a material is generally utilized to determine its optical constants for example the absorption coefficient a. The absorption coefficient (a) was calculated by means of the ratio recording technique in order to eliminate the reflection losses. This was achieved by placing a thin crystal in the way of reference beam, and another thicker one in the way of the sam- ple beam. Assuming that the change in reflection with thickness is negligible, the ratio of the transmittance of two samples of different thicknesses is given by [10] :
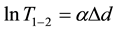 (1)
(1)
Figure 1. Spectral variation of transmission and reflectance of (TMA)2ZnCl4 single crystal.
Table 1. Optical constants for (TMA)2ZnCl4 crystal in the normal phase.
where T is the transmittance and d is the crystal thickness.
Figure 2(a) shows the spectral response of the total absorption coefficient (α) for (TMA)2ZnCl4 crystal. The α-hν dependence exhibits a long tail at the low energy part. It can be seen that the absorption increases slowly with increasing photon energy in the range below 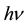 = 6.1 eV. At photon energies
= 6.1 eV. At photon energies  > 6.1 eV, the spectra showed a steeper increase of the absorption coefficient. It can be assumed that this increase in α(hν) is due to the onset of interband transitions at the fundamental edge.
> 6.1 eV, the spectra showed a steeper increase of the absorption coefficient. It can be assumed that this increase in α(hν) is due to the onset of interband transitions at the fundamental edge.
The relationship between absorption coefficient α and photon energy 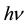 can be expressed as [11] :
can be expressed as [11] :
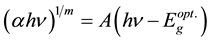 (2)
(2)
where A is a constant nearly independent of photon energy and 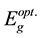 is the optical energy gap. Here m repre- sents an index that can take any of the values: 2, 3/2, 1/2 or 3 depending on the type of transition responsible for the absorption. For allowed direct transition m = 1/2 while m = 3/2 for forbidden direct transition. For allowed
is the optical energy gap. Here m repre- sents an index that can take any of the values: 2, 3/2, 1/2 or 3 depending on the type of transition responsible for the absorption. For allowed direct transition m = 1/2 while m = 3/2 for forbidden direct transition. For allowed


Figure 2. (a) The photon energy dependence of α and (b) The photon energy dependence of (αhν)1/2 (inset shows the linear fit and the value of optical energy gap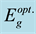 ) for (TMA)2ZnCl4 single crystal.
) for (TMA)2ZnCl4 single crystal.
indirect transition m = 2 and for forbidden indirect transition m = 3. The range within which this equation is valid is very small and hence it becomes too difficult to determine exactly the value of the exponent m [12] .
In a small energy range, the dependence of 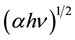 on
on 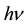 for (TMA)2ZnCl4 samples is shown in Figure 2(b). The dependence of
for (TMA)2ZnCl4 samples is shown in Figure 2(b). The dependence of 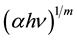 on photon energy hν for onset gaps was plotted for different values of m and the best fit was obtained for m = 2. This indicates that the optical absorption obeys Equation (2) with m = 2 which means that (TMA)2ZnCl4 crystal is an indirect material and the fundamental edge is due to allowed indirect transitions. By extrapolating the straight lines to the value, where
on photon energy hν for onset gaps was plotted for different values of m and the best fit was obtained for m = 2. This indicates that the optical absorption obeys Equation (2) with m = 2 which means that (TMA)2ZnCl4 crystal is an indirect material and the fundamental edge is due to allowed indirect transitions. By extrapolating the straight lines to the value, where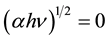 , value of
, value of 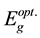 was determined. The obtained value is 5.903 eV. This value has good agreement with those calculated by El-Korashy [13] which reported direct band gap energy value of 5.89 eV at 300 K (the normal paraelectric phase) for this crystal.
was determined. The obtained value is 5.903 eV. This value has good agreement with those calculated by El-Korashy [13] which reported direct band gap energy value of 5.89 eV at 300 K (the normal paraelectric phase) for this crystal.
3.2. Optical Constants
The reflectance of the surface (R) is written in terms of refractive index (n) [14] as:

The optical constants (n, Kex.) were determined from the transmission (T) and reflection (R) spectrum. The absorption coefficient α is related to extinction coefficient Kex. by:

Figure 3 shows the plot of extinction coefficient (Kex.) as a function of photon energy (hν). From the graph, it is clear that extinction coefficient (Kex.) value increases with increase in the photon energy. The dependence of refractive index (n) on the energy is also shown in Figure 3 and it is seen that the refractive index decreases as the photon energy increases. Thus, the extinction coefficient (Kex.) and refractive index (n) depend on the photon energy. It is understood that the higher value of photon energy will enhance the optical efficiency of the material. Hence, by tailoring the photon energy, one can achieve the desired material for optical device fabrication.
The complex dielectric constant(


where 

Figure 3. Extinction coefficient (Kex.) and refractive index (n) versus photon energy for (TMA)2ZnCl4 single crystal.
The variation of the imaginary 

The optical conductivity is a measure of the frequency response of the material when irradiated with light is given by the relation [15] :

where c is the velocity of light. The electrical conductivity is related to the optical conductivity by the relation:

The energy dependence of the optical and electrical conductivities is illustrated in Figure 5. The obtained re- sults for extinction coefficient and optical conductivity are in fair agreement with those obtained by Girisun et al.
Figure 4. The dependence of the real 

Figure 5. The dependence of the optical σopt. and electrical σele. conductivities on the photon energy for (TMA)2ZnCl4 single crystal.
[15] for tristhiourea zinc sulphate (ZTS) and by Raj et al. [16] for L-Alaninium Malate (LAM) single crystals. The high magnitude of optical conductivity (1.45 ´ 1010 s‒1) and the low extinction coefficient (10‒5) confirms the presence of very high photo response nature of the material. This makes the material more prominent for device applications in information processing and computing.
For further analysis of the experimental results, the electric susceptibility χc can be calculated according to the relation [17] :


where ɛ0 is the dielectric constant in the absence of any contribution from free carriers. The energy dependence of the electric susceptibility is similar to that of the imaginary 
Lattice dielectric constant εL and contribution of charge carriers (N) can be calculated by the fitting of the linear part of the relation [18] ;

where e is electronic charge, c is the velocity of light and 
The molar polarizability αp of (TMA)2ZnCl4 single crystals can be deduced according to the Clausius-Mos- sotti local-field polarizability model [20] from the relation:

where L is the Avogadro’s number, ρ is the density of material and M molecular weight. The photon energy dependence of 
Figure 6. The dependence of the electrical susceptibility χc on the photon energy for (TMA)2ZnCl4 single crystal.
Figure 7. Variation of n2 versus λ2 (inset shows the linear fit of the linear part of the curve near the optical energy gap) for (TMA)2ZnCl4 single crystal.
Figure 8. Plot of 


3.3. Dispersion Characterizations
The dispersion of refractive index of (TMA)2ZnCl4 has been fitted to Wemple and DiDomenico (WDD) model which is based on single oscillator formula [21] [22] .

where E0 is single oscillator energy or average energy gap and Ed is dispersion energy and 




The moments of optical dispersion spectra 



The zero-frequency refractive index (static refractive index) is obtained using Equation (13), by putting

Furthermore the values of static refractive index zero-frequency refractive index n0 are also calculated and recorded in Table 2.
Figure 9. Plot of 
Table 2. Normal dispersion of (TMA)2ZnCl4 single crystals.
The values of dispersion parameters and the optical moments gathered in Table 2, are strongly agree with Wemple [21] and DiDomenico [22] .
The refractive index n can also be analyzed to determine the oscillator strength S0 for (TMA)2ZnCl4 crystals. The refractive index is represented by a single Sellmeier oscillator at low energies [25] :

where λ0 is the oscillator wavelength. If we put

S0 is the average oscillator strength. The plotting of 

in Figure 10. The intersection with 


and λ0 were determined and listed in Table 2.
3.4. Fourier Transform Infrared Spectroscopy
FTIR spectra carried out in the range 400 - 4000 cm−1 of as grown (TMA)2ZnCl4 crystals and crystals annealed for 1 and 2 hours in the paraelectric phase at 150˚C have been assigned in Table 3 and the functional groups have been identified (Figure 11). The band observed at 950 cm−1 is assigned to C-N stretching mode of vibration. The rocking of CH3 is assigned to the bands observed at 1071 and 1280 cm−1. The band at 1415 cm−1 is assigned to the in-plane bending mode of CH3 and the out-of-plane bending is assigned to the band at 1487 cm−1. Symmetric and asymmetric stretching of CH3 is observed at 2952 and 3022 cm−1 respectively. The band observed around 3435 cm−1 and 1635 cm−1 are assigned to the O-H stretching and bending vibration of water molecule present in the KBr compound. The values assigned were in close agreement with the assignments made by Ganguly et al. [26] , as shown in Table 3.
The FTIR spectra for specimens annealed at different temperatures in the normal phase (Figure 11), shows the same peaks assigned for the as grown crystal have been observed (Table 3). There is a slight shift in the peak positions because of the hydrogen bonding. There is no significant variation in the vibration frequencies with thermal annealing. With increasing annealing duration, the absorption peaks centered at 949.78, 1287.27,
Figure 10. Plot of 
Table 3. Characteristic frequencies of various functional groups of (TMA)2ZnCl4 crystal.
Figure 11. FTIR spectrum of as grown and annealed (TMA)2ZnCl4 single crystal.
1415.52 and 3023.88 cm−1 decreases in intensity, while the peaks at 1597 and 1636 cm−1 increase in intensity. Another significant spectral feature observed is the transformation of sharp peaks as at 457.05, 1287.27 and near 3470 cm−1 to a broad hump with increasing the annealing duration. Also there is a complete removal of some peaks such as the peaks centered at 2366 cm−1 and 2758 cm−1 which decrease in intensity and then vanish completely.
Sveleba et al. [6] showed that, the temperature dependences of the birefringence δ(Δnc) for [N(CH3)4]2ZnC14 crystal specimen annealed at 370 K for 1.5 h brought about a reduction of the rate of nonlinear variation of δ(Δnc) with the temperature. Also deviations from linear temperature dependences are observed in the dielectric permittivity temperature dependence measurements. They attribute this behavior to fluctuation processes and/or the appearance of a new phase state of the crystal.
4. Conclusions
1. Optical transmission studies showed that (TMA)2ZnCl4 crystal was optically transparent in the entire visible region with a lower cut-off below 256 nm. From the data the absorption coefficient (α) and the optical band gap 
2. The refractive index (n) was calculated as a function of photon energy. Values of the optical and electrical conductivities (sopt. & sele.) and the lattice dielectric constant (εL) and the ratio of free charge carrier concentration to the effective mass (N/m*) were estimated at room temperature for samples of (TMA)2ZnCl4 and listed in Table 1.
3. The refractive index values have been fitted to the single oscillator Wemple-DiDomenico (WDD) model. The single oscillator energy (E0), the dispersion energy (Ed), Static refractive index n0, Moments of the optical dispersion spectra M‒1 and M‒3, Static refractive index n0 and the Oscillator strength S0 are calculated and presented in Table 2.
4. FTIR spectra was measured for the as grown and annealed crystals as shown graphically in Figure 11. CH3, C-N and C-N-C groups are identified (Table 3) by the frequency assignments. For annealed samples, some absorption peaks decrease or increase in intensities. There is a transformation of some sharp peaks to broad humps.
References
- Axe, J.D., Lizumi, M. and Shirane, G. (1986) In: Blinc, R. and Levanyuk, A.P., Eds., Incommensurate Phases in Dielec- trics, Vol. 2, North-Holland, Amsterdam.
- Styrkowiec, R. (1998) Time Relaxation of Dielectric Permittivity in [N(CH3)4]2ZnCl4 Crystals. Ferroelectrics Letters, 24, 25-32. http://dx.doi.org/10.1080/07315179808204452
- Lim, A.R., Park, D.K., Chang, J.-H. and Jeong, S.-Y. (2001) Ferroelastic Domain Switching Behaviour of [N(CH3)4]2CuC14 and [N(CH3)4]2ZnC14 Single Crystals Studied by External Stress. Journal of the Physical Society of Japan, 70, 1937- 1941. http://dx.doi.org/10.1143/JPSJ.70.1937
- Styrkowiec, R. and Czapla, Z. (1997) Dielectric Properties of [N(CH3)4]2ZnCl4 Crystal under Influence of Electric Field and Uniaxial Stresses. Phase Transitions, 60, 155-172. http://dx.doi.org/10.1080/01411599708207994
- Kim, D.-Y., Kwun, S.-I. and Yoon, J.-G. (1998) Linear Birefringence Behavior of (NH4)2ZnC14 and [N(CH)4]2CuC14 near the Normal-Incommensurate Phase Transition. Journal of the Korean Physical Society, 32, 898-901.
- Sveleba, S., Zhmurko, V., Kapustianik, V., Polovinko, I. and Trybula, Z. (1993) Influence of Electric Field and Mechanical Stresses on the Properties of Incommensurate Phases in (N(CH3)4)2ZnCl4 and (N(CH3)4)2CoCl4 Crystals. Physica Status Solidi (a), 140, 573-585. http://dx.doi.org/10.1002/pssa.2211400229
- Sveleba, S.A., Katerinchuk, I.M. and Semotyuk, O.V. (2010) Temperature Dependence of the Crystal-Optics Characteristics of [N(CH3)4]2ZnCl4:Ni2+ Crystals with Correlated Motion of Tetrahedral Groups. Crystallography Reports, 55, 253-257. http://dx.doi.org/10.1134/S1063774510020161
- Vogels, L.J.P., Meekes, H. and de Boer, J.L. (1994) An X-Ray Diffraction Study on the Temperature and Chemical Com- position Dependence of the Modulation Wave Vector in ((CH3)4N)2ZnCl4−xBrx Compounds. Journal of Physics: Condensed Matter, 6, 8205-8218. http://dx.doi.org/10.1088/0953-8984/6/40/012
- Abu El-Fadl, A. and Nashaat, A.M. (BSP-TOOPTSJ-2015-25) Temperature Dependence of the Optical Band Gap and Optical Parameters of Tetramethyl Ammonium Tetrachlorozincate (TMA)2ZnCl4 Single Crystals around the Normal and Incommensurate Phase Transitions. Paper Submitted for Publications in Journal of Modern Optics.
- Bassani, F. and Parravicini, G.P. (1975) Electronic States and Optical Transitions in Solids. Pergamon, New York.
- Hasegawa, H., Yazaki, S. and Shimizu, T. (1978) Effects of Annealing on Gap States in Amorphous Si Films. Solid State Communications, 26, 407-410. http://dx.doi.org/10.1016/0038-1098(78)90515-X
- Cohen, M.H., Fritzsche, H. and Ovshinsky, S.R. (1969) Simple Band Model for Amorphous Semiconducting Alloys. Physical Review Letters, 22, 1065-1067. http://dx.doi.org/10.1103/PhysRevLett.22.1065
- El-Korashy, A. (2000) Optical Band Gap Studies of [N(CH3)4]2ZnCl4 Single Crystals on the Paraelectric Phase. Journal of Materials Science Letters, 19, 29-31. http://dx.doi.org/10.1023/A:1006791429248
- Abu El-Fadl, A., Gaffar, M.A. and Omar, M.H. (1999) Absorption Spectra and Optical Parameters of Lithium-Potassium Sulphate Single Crystals. Physica B, 269, 403-408. http://dx.doi.org/10.1016/S0921-4526(99)00117-9
- Sabari Girisun, T.C. and Dhanuskodi, S. (2009) Linear and Nonlinear Optical Properties of Tristhiourea Zinc Sulphate Single Crystals. Crystal Research and Technology, 44, 1297-1302. http://dx.doi.org/10.1002/crat.200900351
- Victor Antony Raj, M., Prem Anand, D. and Madhavan, J. (2013) Linear and Non Linear Optical Properties of L-Alaninium Malate (LAM) Single Crystal an Efficient Organic NLO Material. Sciencia Acta Xaveriana, 4, 41-50.
- Aziz, M.S. and El-Mallah, H.M. (2009) Electrical and Optical Properties of Azo Dye. Indian Journal of Pure and Applied Physics, 47, 530-534.
- Dahshan, A., Amer, H.H. and Aly, K.A. (2008) Compositional Dependence of the Optical Constants of Amorphous GexAs20Se80−x Thin Films. Journal of Physics D: Applied Physics, 41, Article ID: 215401. http://dx.doi.org/10.1088/0022-3727/41/21/215401
- Abdel-Aziz, M.M., El-Metwally, E.G., Fadel, M., Labib, H.H. and Afifi, M.A. (2001) Optical Properties of Amorphous Ge Se9?x Tlx System Films. Thin Solid Films, 386, 99-104. http://dx.doi.org/10.1016/S0040-6090(01)00765-9
- Zeng, J.S.Q., Greif, R., Stevens, P., Ayers, M. and Hunt, A. (1996) Effective Optical Constants n and κ and Extinction Coefficient of Silica Aerogel. Journal of Materials Research, 11, 687-693. http://dx.doi.org/10.1557/JMR.1996.0083
- Wemple, S.H. and DiDomenico Jr., M. (1971) Behavior of the Electronic Dielectric Constant in Covalent and Ionic Materials. Physical Review B, 3, 1338-1351. http://dx.doi.org/10.1103/PhysRevB.3.1338
- Wemple, S.H. and DiDomenico, M. (1969) Optical Dispersion and the Structure of Solids. Physical Review Letters, 23, 1156-1160. http://dx.doi.org/10.1103/PhysRevLett.23.1156
- Fadel, M., Fayek, S.A., Abou-Helal, M.O., Ibrahim, M.M. and Shakra, A.M. (2009) Structural and Optical Properties of SeGe and SeGeX (X = In, Sb and Bi) Amorphous Films. Journal of Alloys and Compounds, 485, 604-609. http://dx.doi.org/10.1016/j.jallcom.2009.06.057
- Gupta, V. and Mansingh, A. (1996) Influence of Post Deposition Annealing on the Structural and Optical Properties of Sputtered Zinc Oxide Film. Journal of Applied Physics, 80, 1063-1073. http://dx.doi.org/10.1063/1.362842
- Tanaka, K. (1980) Optical Properties and Photoinduced Changes in Amorphous AsxS100−x Films. Thin Solid Films, 66, 271-279. http://dx.doi.org/10.1016/0040-6090(80)90381-8
- Ganguly, S., Rao, K.J. and Rao, C.N.R. (1985) An Infrared Spectroscopic Study of the Incommensurate Transitions and Related Phase Changes in K2Pb[Cu(NO2)6] and [N(CH3)4]2MX4 (M = Mn, Co, Cu or Zn and X = Cl or Br). Spectrochimica Acta Part A, 41, 307-314. http://dx.doi.org/10.1016/0584-8539(85)80109-4
NOTES
*Corresponding author.













