Advances in Linear Algebra & Matrix Theory
Vol.06 No.04(2016), Article ID:73050,11 pages
10.4236/alamt.2016.64015
L-Fuzzy Vector Subspaces and Its Fuzzy Dimension
Chun’e Huang1*, Yan Song2, Xiruo Wang2
1College of Biochemical Engineering, Beijing Union University, Beijing, China
2Mudanjiang Normal University, Mudanjiang, China

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: November 8, 2016; Accepted: December 25, 2016; Published: December 28, 2016
ABSTRACT
In this paper, we introduce the definition of L-fuzzy vector subspace, define its dimension by an L-fuzzy natural number. For a finite-dimensional L-fuzzy vector subspace, we prove that the equality 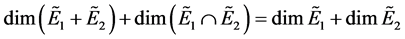 holds without any restricted conditions. At the same time, we deduce that the formula
holds without any restricted conditions. At the same time, we deduce that the formula 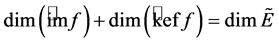 holds.
holds.
Keywords:
L-Fuzzy Sets, L-Fuzzy Vector Subspace, L-Fuzzy Dimension

1. Introduction
Firstly, fuzzy vector subspace was introduced by Katsaras and Liu [1] . Then its pro- perties and characters were investigated (see [2] [3] [4] [5] , etc). The dimension of a fuzzy vector space was defined as a n-tuple by Lowen [6] . Subsequently, it was defined as a non-negative real number or infinity by Lubczonok [5] , and proved that the for- mula
 (1)
(1)
is valid under certain conditions, where  and
and 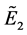 are fuzzy vector spaces. Recently, basis and dimension of a fuzzy vector space were redefined as a fuzzy set and a fuzzy natural number by Shi and Huang [7] , respectively. Under the definitions, more pro- perties of (crisp) vector spaces were correct in fuzzy vector spaces.
are fuzzy vector spaces. Recently, basis and dimension of a fuzzy vector space were redefined as a fuzzy set and a fuzzy natural number by Shi and Huang [7] , respectively. Under the definitions, more pro- perties of (crisp) vector spaces were correct in fuzzy vector spaces.
In this paper, we generalize the results in [7] to L lattice, and prove that some for- mulas still hold in the lattice L. In particular, we present the definition of L-fuzzy vector subspace and its -fuzzy dimension. The L-fuzzy dimension of a finite dimensional fuzzy vector subspace is a fuzzy natural number. We prove that (1) holds without any re- stricted conditions and  holds.
holds.
2. Preliminaries
Given a set 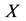 and a completely distributive lattice L, we denote the power set of
and a completely distributive lattice L, we denote the power set of  and the set of all L-fuzzy sets on
and the set of all L-fuzzy sets on  (or L-sets for short) by
(or L-sets for short) by 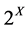 and
and , respec- tively . For any
, respec- tively . For any , we denote the cardinality of
, we denote the cardinality of 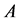 by
by .
.
An element 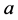 in L is called a prime element if
in L is called a prime element if 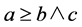 implies
implies 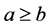 or
or .
. 





The binary relation 


















In [10] , Wang thought that 



Throughout this paper, 




If 

Some properties of these cut sets can be found in [11] - [16] .
In [17] Shi introduced the concept of L-fuzzy natural numbers(denoted by



(1)
(2)
(3) For any 

3. L-Fuzzy Vector Subspaces
Definition 3.1. L-fuzzy vector subspace is a pair 





In this definition, when

Let 


We can obtain some properties of 
Theorem 3.2. Let 

(1)
(2) For any
The prove is trivial and omitted.
Remark: Since 



Example 3.3. Let 
Let 


We can easily check 





Theorem 3.4. Let 


(1) 
(2) (a)
(b)
(3) For any 


The prove is trivial and omitted.
In the following paper, the vector spaces we discuss are finite-dimensional. For their L-fuzzy vector subspaces, the following observation will be useful.
Remark: Let 





In the fact, let 















Theorem 3.5. Let 


(1) 
(2) For all

(3) For all

(4) For all

(5) For all

(6) For all

Proof. We prove 







Since 












Therefore 
















Therefore 
Theorem 3.6. Let 



(1) 
(2) For all

Proof. 
















Therefore 
We can define the operations between two L-fuzzy vector subspaces analogous to fuzzy vector subspaces.
Definition 3.7. Let 








Definition 3.8. Let 






Theorem 3.9. Let 


(1) 


(2) 


The proof of the theorem is trivial and it is omitted.
Theorem 3.10. Let 


(1) For all
(2) For all
(3) For any
(4) For any
Proof. The proofs of (1) and (2) are easy by the definition of 
(3) For any
(4) By the definition of the sum of L-fuzzy vector subspaces, for any 
Theorem 3.11. Let 




(1)
(2)
The prove is trivial and omitted.
4. Fuzzy Dimension of L-Fuzzy Vector Subspaces
Definition 4.1. Let 

is called the L-fuzzy dimensional function of the L-fuzzy vector subspace



Theorem 4.2. For each 

Proof. For any





exists 



This completes the proof.
Theorem 4.3. Let the pair 

If 

In particular, 

Proof. In order to prove










In order to prove for any



Therefore
Theorem 4.4. Let 

In particular, 
Proof. 
Let













Therefore for any


Theorem 4.5. Let 

Proof. We denote the sum of 



Therefore
Definition 4.6. Suppose that 

(1) 

(2) For all
Theorem 4.7. Suppose that 




The prove is trivial and omitted.
Theorem 4.8. Suppose that 

Proof. Suppose that 



Since 

Therefore
5. Conclusion
In this paper, L-fuzzy vector subspace is defined and showed that its dimension is an L-fuzzy natural number. Based on the definitions, some good properties of crisp vector spaces are hold in a finite-dimensional L-fuzzy vector subspace. In particular, the
equality 

Acknowledgements
The authors would like to thank the reviewers for their valuable comments and sug- gestions.
Fund
The project is by the Science & Technology Program of Beijing Municipal Commission of Education (KM201611417007), the NNSF of China (11371002), the academic youth backbone project of Heilongjiang Education Department (1251G3036), the foundation of Heilongjiang Province (A201209).
Cite this paper
Huang, C.E, Song, Y. and Wang, X.R. (2016) L-Fuzzy Vector Subspaces and Its Fuzzy Dimension. Advances in Linear Algebra & Matrix Theory, 6, 158-168. http://dx.doi.org/10.4236/alamt.2016.64015
References
- 1. Katsaras, A.K. and Liu, D.B. (1977) Fuzzy Vector Spaces and Fuzzy Topological Vector Spaces. Journal of Mathematical Analysis and Applications, 58, 135-146.
https://doi.org/10.1016/0022-247X(77)90233-5 - 2. Lubczonok, G. and Murali, V. (2002) On Flags and Fuzzy Subspaces of Vector Spaces. Fuzzy Sets and Systems, 125, 201-207.
https://doi.org/10.1016/S0165-0114(00)00129-9 - 3. Abdukhalikov, K.S., Tulenbaev, M.S. and Umirbarv, U.U. (1994) On Fuzzy Bases of Vector Spaces. Fuzzy Sets and Systems, 63, 201-206.
https://doi.org/10.1016/0165-0114(94)90350-6 - 4. Abdukhalikov, K.S. (1996) The Dual of a Fuzzy Subspace. Fuzzy Sets and Systems, 82, 375-381.
https://doi.org/10.1016/0165-0114(96)84977-3 - 5. Lubczonok, P. (1990) Fuzzy Vector Spaces. Fuzzy Sets and Systems, 38, 329-343.
https://doi.org/10.1016/0165-0114(90)90206-L - 6. Lowen, R. (1980) Convex Fuzzy Sets. Fuzzy Sets and Systems, 3, 291-310.
https://doi.org/10.1016/0165-0114(80)90025-1 - 7. Shi, F.G. and Huang, C.E. (2010) Fuzzy Bases and the Fuzzy Dimension of Fuzzy Vector Spaces. Mathematical Communications, 15, 303-310.
- 8. Gierz, G., et al. (2003) Continuous Lattices and Domains. Encyclopedia of Mathematics and its Applications, Cambridge University Press, Cambridge.
https://doi.org/10.1017/CBO9780511542725 - 9. Dwinger, P. (1982) Characterizations of the Complete Homomorphic Images of a Completely Distributive Complete Lattice I. Indagationes Mathematicae (Proceedings), 85, 403-414.
https://doi.org/10.1016/1385-7258(82)90034-8 - 10. Wang, G.-J. (1992) Theory of Topological Molecular Lattices. Fuzzy Sets and Systems, 47, 351-376.
https://doi.org/10.1016/0165-0114(92)90301-J - 11. Huang, H.-L. and Shi, F.-G. (2008) L-Fuzzy Numbers and Their Properties. Information Sciences, 178, 1141-1151.
https://doi.org/10.1016/j.ins.2007.10.001 - 12. Shi, F.-G. (2000) L-Fuzzy Relation and L-Fuzzy Subgroup. Journal of Fuzzy Mathematics, 8, 491-499.
- 13. Negoita, C.V. and Ralescu, D.A. (1975) Applications of Fuzzy Sets to Systems Analysis, Interdisciplinary Systems Research Series 11, Birkhaeuser, Basel.
https://doi.org/10.1007/978-3-0348-5921-9 - 14. Shi, F.-G. (1995) Theory of Lβ-Nested Sets and Lα-Nested Sets and Its Applications. Fuzzy Systems and Mathematics, 4, 65-72. (In Chinese)
- 15. Shi, F.-G. (1996) L-Fuzzy Sets and Prime Element Nested Sets. Journal of Mathematical Research and Exposition, 16, 398-402. (In Chinese)
- 16. Shi, F.-G. (1996) Theory of Molecular Nested Sets and Its Applications. Journal of Yantai Teachers University, 1, 33-36. (In Chinese)
- 17. Shi, F.-G. (2009) A New Approach to the Fuzzification of Matroids. Fuzzy Sets and Systems, 160, 696-705.
https://doi.org/10.1016/j.fss.2008.05.007





















































