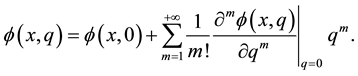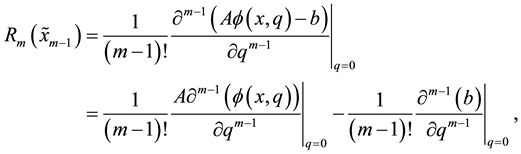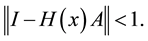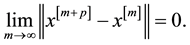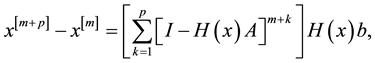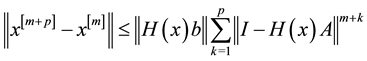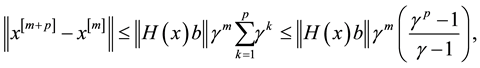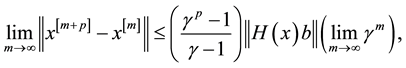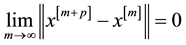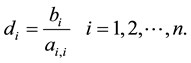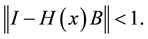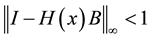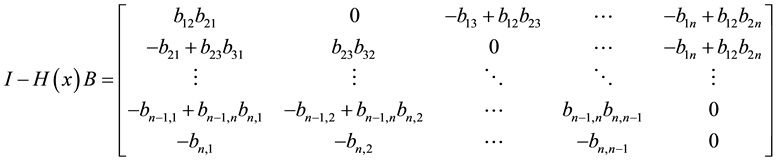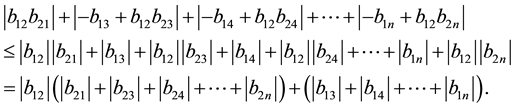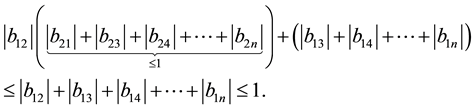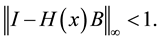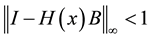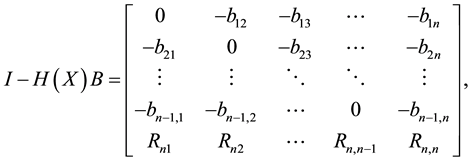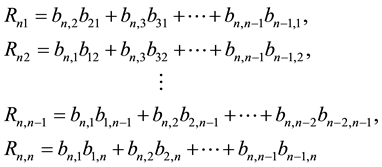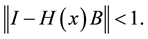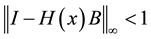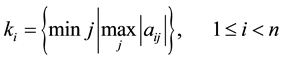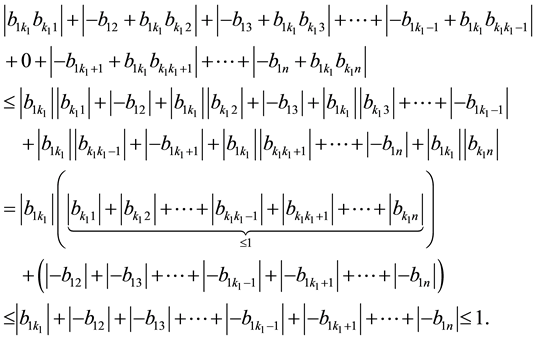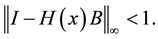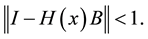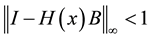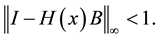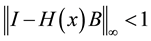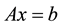Advances in Linear Algebra & Matrix Theory
Vol.05 No.03(2015), Article ID:59739,8 pages
10.4236/alamt.2015.53012
Application of Different H(x) in Homotopy Analysis Methods for Solving Systems of Linear Equations
Mohammad Hasan Khani1, Jalil Rashidinia2, Sajjad Zia Borujeni1,2*
1Department of Mathematics, Islamic Azad University, Shahin Shahr Branch, Isfahan, Iran
2Department of Mathematics, Islamic Azad University, Central Tehran Branch, Tehran, Iran
Email: *Azaliyazia@yahoo.com, *Saj.ziaBorujeni.sci@iauctb.ac.ir
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 6 August 2015; accepted 18 September 2015; published 21 September 2015
ABSTRACT
In this paper, we present homotopy analysis method (HAM) for solving system of linear equations and use of different H(x) in this method. The numerical results indicate that this method performs better than the homotopy perturbation method (HPM) for solving linear systems.
Keywords:
HAM, HPM, Linear System

1. Introduction
Approximating the solutions of the system of linear and nonlinear equations has widespread applications in applied mathematics [1] -[11] . Many techniques including homotopy perturbation method (HPM) [12] and iterative methods [13] were suggested to search for the solution of linear systems. In 2009 Keramati [2] and in 2011 Liu [3] in their articles applied HPM to the solution of the system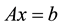 . In this article we used homotopy analysis method [14] [15] with different H(x) to solve linear system
. In this article we used homotopy analysis method [14] [15] with different H(x) to solve linear system
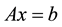 and showed that our results were better than the HPM results; then convergence of the method was considered.
and showed that our results were better than the HPM results; then convergence of the method was considered.
Consider a linear system
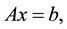 (1)
(1)
where
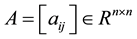 is nonsingular and
is nonsingular and
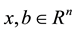 is a vector.
is a vector.
First of all, the basic ideas of the homotopy analysis method are being discussed.
Let
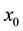 be an initial guess of x, and
be an initial guess of x, and
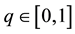 be called the embedding parameter. The homotopy analysis method is based on a kind of continuous mapping
be called the embedding parameter. The homotopy analysis method is based on a kind of continuous mapping
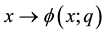 such that, as the embedding parameter q increases from 0 to 1,
such that, as the embedding parameter q increases from 0 to 1,
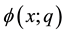 varies from the initial guess
varies from the initial guess
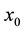 to the exact solution x. To ensure this, choose such an auxiliary linear operator as
to the exact solution x. To ensure this, choose such an auxiliary linear operator as
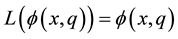 (2)
(2)
and we define the operator
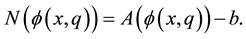 (3)
(3)
Let
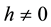 and
and
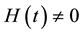 denote the so-called auxiliary parameter and auxiliary matrix, respectively. Using the embedding parameter
denote the so-called auxiliary parameter and auxiliary matrix, respectively. Using the embedding parameter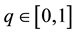 , we construct a family of equations
, we construct a family of equations
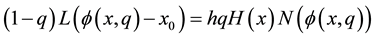
from (2) and (3) we have
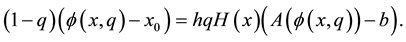
Obviously, at q = 0 and q = 1, one has

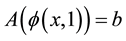
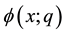
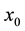
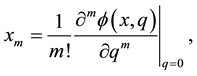
where
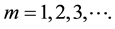
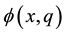

By using (5) we have
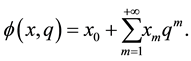
If the series (6) is convergent at q = 1, then using the relationship
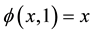
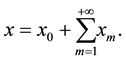
Now we have the so-called mth-order deformation equation
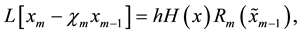
where
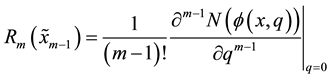
and

By using (2) we obtain

Also by using (3) and (9) we have
and then
Finally by using (11) we obtain
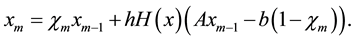
Now with the initial guess
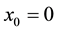

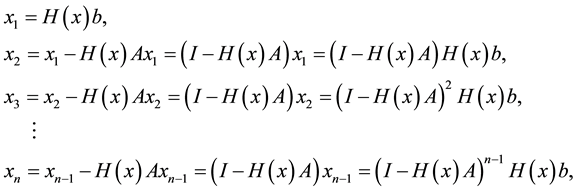
hence, by substituting (13) in (7) we obtain
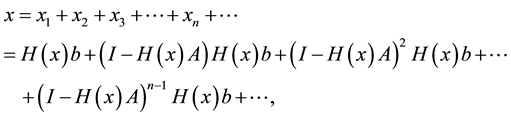
and by factor of

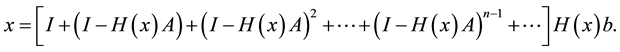
Now we have to prove the convergence of (15).
Theorem 1. The sequence
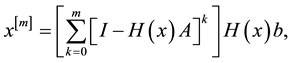
Proof: Following ([2] , Theorem 1) we have to show that
Now considering
then
let
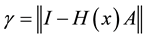
so we have
since
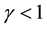
which completes the proof.
2. Main Results
In this section For solving the linear system (1) we apply different H(x) and the convergence of the method is checked. At first assume that A is a nonsingular diagonally dominate matrix and
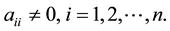

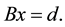
where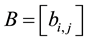
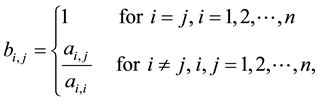
and
Now we apply different H(x) and the convergence of the method is tested.
1) we propose

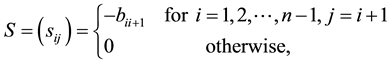
and show that
Theorem 2. If A is diagonally dominated and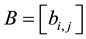
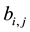
Proof: By direct calculation we have
and first row is satisfied:
Since A is diagonally dominated, B is diagonally dominated and we have
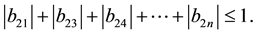
Now by using (19) we obtain
This relation satisfis for other rows also and
2) We propose
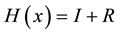
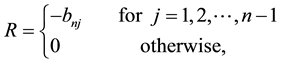
and show that
Theorem 3. If A is diagonally dominated and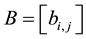

Proof: Following Theorem (2)
such that
and last row is satisfied:
This relation satisfis for other rows also
3) We propose

Theorem 4. If A is diagonally dominated and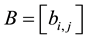
Proof: Similar to proof of Theorems (2) and (3).
4) We propose

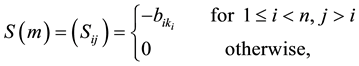
and show that
Theorem 5. If A is diagonally dominated and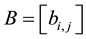
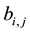
Proof: Following Theorem (2) after expanding
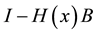
This relation satisfis for other rows also
5) We propose

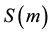
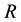
Theorem 6. If A is diagonally dominated and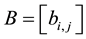
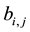
Proof: Similar to proof of Theorems (3) and (5).
6) We propose

Theorem 7. If A is diagonally dominated and
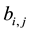
Proof: Following Theorem (2) after expanding
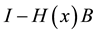
This relation satisfis for other rows also
7) We propose

Theorem 8. If A is diagonally dominated and
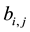
Proof: Similar to proof of Theorems (3) and (7).
Now in the next section we apply
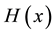
3. Numerical Results
In this section, we present some numerical examples to apply HAM and HPM methods for solving linear system. We used of Matlab 2013 for numerical results.
Example 1. Consider the linear system
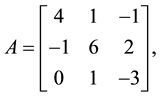


Table 1 shows the iteration number,error,spectral radius of iteration matrix and computation time.
According to Table 1 we obtain the desirable result for solving this system by seven iterations with HAM and

In this example the matrices S and
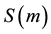
Example 2. In this example we apply HAM method for solving the linear system
where A is a
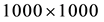
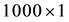
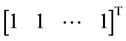
Table 1. Camparision between HPM and HAM for 3 ´ 3 system.
Table 2. Camparision between HPM and HAM for 1000 ´ 1000 system.
4. Conclusion
From the numerical results, we have seen that the HAM method with different
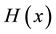
Acknowledgements
We thank Islamic Azad University for support researcher plan entitled: “Combination of Iterative methods and semi analytic methods for solving linear systems” and the Editor and the referee for their comments.
Cite this paper
Mohammad HasanKhani,JalilRashidinia,Sajjad ZiaBorujeni, (2015) Application of Different H(x) in Homotopy Analysis Methods for Solving Systems of Linear Equations. Advances in Linear Algebra & Matrix Theory,05,129-137. doi: 10.4236/alamt.2015.53012
References
- 1. Nazari, A.M. and Zia Borujeni, S. (2012) A Modified Precondition in the Gauss-Seidel Method. Advances in Linear Algebra & Matrix Theory, 1, 31-37.
http://dx.doi.org/10.4236/alamt.2012.23005 - 2. Keramati, B. (2009) An Approach to the Solution of Linear System of Equations by He’s Homotopy Perturbation Method. Chaos, Solitons and Fractals, 41, 152-156.
http://dx.doi.org/10.1016/j.chaos.2007.11.020 - 3. Liu, H.K. (2011) Application of Homotopy Perturbation Methods for Solving Systems of Linear Equations. Applied Mathematics and Computation, 217, 5259-5264.
http://dx.doi.org/10.1016/j.amc.2010.11.024 - 4. Liao, S.J. (1992) The Proposed Homotopy Analysis Technique for the Solution of Nonlinear Problems. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai.
- 5. Morimoto, M., Harada, K., Sakakihara, M. and Sawami, H. (2004) The Gauss-Seidel Iterative Method with the Preconditioning Matrix.(I+S+Sm). Japan Journal of Industrial and Applied Mathematics, 21, 25-34.
http://dx.doi.org/10.1007/BF03167430 - 6. Niki, H., Kohno, T. and Morimoto, M. (2008) The Preconditioned Gauss-Seidel Method Faster than the SOR Method. Journal of Computational and Applied Mathematics, 218, 59-71.
http://dx.doi.org/10.1016/j.cam.2007.07.002 - 7. Niki, H., Kohno, T. and Abe, K. (2009) An Extended GS Method for Dense Linear System. Journal of Computational and Applied Mathematics, 231, 177-186.
http://dx.doi.org/10.1016/j.cam.2009.02.005 - 8. Yusefoglu, E. (2009) An Improvement to Homotopy Perturbation Method for Solving System of Linear Equations. Computers & Mathematics with Applications, 58, 2231-2235.
http://dx.doi.org/10.1016/j.camwa.2009.03.010 - 9. Yuan, J.Y. and Zontini, D.D. (2012) Comparison Theorems of Preconditioned Gauss-Seidel Methods for M-Matrices. Applied Mathematics and Computation, 219, 1947-1957.
http://dx.doi.org/10.1016/j.amc.2012.08.037 - 10. Gunawardena, A.D., Jain, S.K. and Snyder, L. (1991) Modified Iterative Method for Consistent Linear Systems. Linear Algebra and Its Applications, 154-156, 123-143.
http://dx.doi.org/10.1016/0024-3795(91)90376-8 - 11. Kohno, T. and Niki, H. (2009) A Note on the Preconditioner Pm=(I+Sm). Journal of Computational and Applied Mathematics, 225, 316-319.
http://dx.doi.org/10.1016/j.cam.2008.07.042 - 12. He, J.H. (2003) Homotopy Perturbation Method: A New Non-Linear Analytical Technique. Applied Mathematics and Computation, 135, 73-79.
http://dx.doi.org/10.1016/S0096-3003(01)00312-5 - 13. Saad, Y. (2003) Iterative Methods for Sparse Linear Systems. SIAM Press, PHiladelphia.
http://dx.doi.org/10.1137/1.9780898718003 - 14. Liao, S.J. (2003) Beyond Perturbation: Introduction to the Homotopy Analysis Method. Chapman & Hall/CRC Press, Boca Raton.
http://dx.doi.org/10.1201/9780203491164 - 15. Liao, S.J. (2009) Notes on the Homotopy Analysis Method: Some Definitions and Theorems. Communications in Nonlinear Science and Numerical Simulation, 14, 983-997.
http://dx.doi.org/10.1016/j.cnsns.2008.04.013 - 16. Sen, S. (1983) Topology and Geometry for Physicists. Academic Press, Waltham.
NOTES
*Corresponding author.