American Journal of Analytical Chemistry
Vol.06 No.13(2015), Article ID:62008,8 pages
10.4236/ajac.2015.613098
Atomic epn(ep) Spin Models and Spectral Lines
Daekyoum Kim1, Baik-Hyon Ha2
1Kwongmyoung-Si, Kyoungki-Do, South Korea
2Emeritus, Chemical Engineering Department, Hanyang University, Seoul, South Korea

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 September 2015; accepted 15 December 2015; published 18 December 2015
ABSTRACT
We confirmed that how many kinds of epn spins the atoms have by calculating heat capacity of metals according to energy levels in the previous reference. To know more the spin models of epn of hydrogen and helium are imagined and their line spectra are counted. And the explanation of interference is discussed. Gas atoms make line spectra by optical interference. Solid atoms make them by exciting the lowest epns of their cluster first. They all make s, p energy orbit. One axis is composed of two epns. 1s or 2s of atoms except for lithium generally makes the symmetric axis. When each energy level is filled up by epns, these are symmetrically paired first. The atoms which fit the number of line spectra correctly by optical interference are hydrogen and helium. By counting the number of alignments of epns spins within the cluster, the atoms which fit the number of line spectra correctly are lithium, beryllium and phosphorus. The number of line spectra of the rest atoms which we have counted approaches the experimented numbers approximately, not correctly.
Keywords:
Atomic Model, Atomic Cluster, Spectral Lines, Resonance

1. Introduction
Humphreys [1] -[3] says that we can explain the line spectra through interferometric measurement on some gas atoms. The line spectra of atoms come out much more than their atomic number. Until now one electronic atomic model is solved through Schrödinger’s equation, and then its energy levels are used on interpreting the line spectra.
Hence 4 kinds of spin energy level for each epn (one electron + one proton + one neutron) with one additional energy level in the previous reference [4] are assumed and used on explaining the heat capacity of metals according to energy levels without any problems. The arrangement of spins of each epn (or ep) is that the proton (+neutron) is situated in the inside of a sphere consistently and its electron in the outside of the sphere. An ep is an epn of a hydrogen atom. Hydrogen atoms have also 4 kinds of ep spin models as showed in Figure 1 which seem to be useful on movement and for stability.
The discharge of hydrogen or helium is not the pure interference like coherent wave. Since hydrogen and helium are gases, they make line spectra through discharge in the quartz cylinder. To make the line spectra the mixing among the discharges of atoms may occur. The optical interference is composed of 1, or 2, or 3 kinds of epns (eps). It may not be possible in the present diffraction grating equipment that more epns than 3 gather and discharge. A characteristic of optical interference is that its intensity is obtained by productions (collisions), not by smooth vector additions. The optical interference of one kind of epn means that one proton, its neutron and its electron are composed to make a line spectrum in collision. In the optical interference of one epn, 3 points (one electron, its proton, its neutron) make one face. The points have different electricity one another as we see in Figure 2 which is showed in Ref. [4] . Each point attracts one another by consuming its mass as Einstein said. Finally they make one point face and then have the largest intensity. The optical interference of 2 epns means that 2 faces make 90˚ - 180˚. According to the proceedings of discharge of each epn, their intensities are obtained by the production of the intensities of two epns, and their combination angle decreases the intensity. The optical interference of 3 epns is described in the same manner.
Figure 1. Atomic epn spin models of hydrogen.
Figure 2. Three resonances (photons) in an interference of an epn.
2. Atomic Models and Line Spectra
In order to find the evidence which the atoms have 4 kinds of the orbital spins, we looked over the line spectra from hydrogen to the atoms which we can figure out. It is recorded that the gas, hydrogen (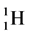 ) whose atomic spin models are shown in Figure 1 has 8 line spectra which are recorded in Ref. [5] . Even if it is hard to handle its original reference and its precise contents about the line spectra, we could guess some plausible physical concepts. We get the number from four solo epn optical interference line spectra of
) whose atomic spin models are shown in Figure 1 has 8 line spectra which are recorded in Ref. [5] . Even if it is hard to handle its original reference and its precise contents about the line spectra, we could guess some plausible physical concepts. We get the number from four solo epn optical interference line spectra of 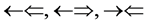 and
and , three two epns optical interference line spectra of
, three two epns optical interference line spectra of 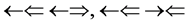 and
and , one three epns interference line spectrum of
, one three epns interference line spectrum of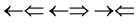 . Here X-ray spin (
. Here X-ray spin (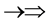 ) does make the two epn and three epn line spectra with the other spins, but they are not measured. In the above the double arrow means a proton and the single arrow its electron.
) does make the two epn and three epn line spectra with the other spins, but they are not measured. In the above the double arrow means a proton and the single arrow its electron.
The basic epn spin alignments of 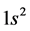 of the gas,
of the gas, 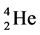 whose atomic spin models are shown in Figure 3 are
whose atomic spin models are shown in Figure 3 are ,
, 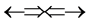 ,
,  and
and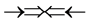 . In the above the double arrow means a proton (+neutron) and the single arrow its electron. It is believed that the epns in the atom are seen to be perfect symmetric but not to be symmetric in making line spectra because each epn in the axes makes its own solo optical interference line spectrum. Here Pauli’s exclusion principle is applied. As we see in Figure 4 and Figure 5 the bonding and non-bonding between two orbital neutrons in the core of helium atom are the attraction between the different
. In the above the double arrow means a proton (+neutron) and the single arrow its electron. It is believed that the epns in the atom are seen to be perfect symmetric but not to be symmetric in making line spectra because each epn in the axes makes its own solo optical interference line spectrum. Here Pauli’s exclusion principle is applied. As we see in Figure 4 and Figure 5 the bonding and non-bonding between two orbital neutrons in the core of helium atom are the attraction between the different
Figure 3. Atomic epn spin models of helium.
Figure 4. Bondings between a proton and a neutron in a helium atom.
charges on the neutrons and the sliding by the same direction, basing on the stability of the atom. Hence for 33 line spectra of helium atom [5] we can get exactly the number 33 from 8 solo epn optical interference line spectra (







For 48 line spectra [5] of 














Figure 5. Nonbondings between a proton and a neutron in a helium atom.
Figure 6. Atomic epn spin models of lithium atoms.
Table 1. epn spin alignments of lithium cluster.
Total number of different epn spins of 




One cluster of lithium metal has 32 atoms of different epn spins [6] . Then the number of epn spins for each energy level is 24. Finally for 48 line spectra of one cluster lithium metal we can get the number exactly from 24 × 2 of which 2 means two energy levels (
For 72 line spectra [5] of 

























For 25 line spectra of 










The electronic configuration of 















the lowest energy level epns spin (

Figure 7. An atomic epn spin resonance model of a free neutron in beryllium
Figure 8. An atomic epn spin model of boron.
Figure 9. An atomic epn spin model of carbon.
abbreviated, we get 61 from 64. The existence of the molecule of 













The electronic configuration of 











Hence for 74 line spectra [5] of nitrogen as a gas we get the number 76 from 20 solo epn optical inter- ference line spectra with the excitation of 





The electronic configuration of 









They all make 20 solo epn optical interference line spectra by taking 









For 24 line spectra [5] of 

3. Conclusions
The non-metal atoms like gases H, He, N, and O make one, two and three epns optical interference line spectra. Their











1) The epns of metal atoms like Li, Be and Na do not make the interference line spectra. They make line spectra by forming the different spin alignments. The guess comes by counting the line spectra of 

2) Hund’s rule is not applied. The epns of all atoms here have a tendency to be paired first. A free neutron is situated in the cores of the atoms seen from the resonance of
Cite this paper
DaekyoumKim,Baik-HyonHa, (2015) Atomic epn(ep) Spin Models and Spectral Lines. American Journal of Analytical Chemistry,06,1030-1037. doi: 10.4236/ajac.2015.613098
References
- 1. Humphreys, C.J. and Kostkowski, H.J. (1952) Infrared Spectra of Noble Gases (12000 to 19000 A). Journal of Research of the National Bureau of Standards—Physics and Chemistry, 49, 73-84.
http://dx.doi.org/10.6028/jres.049.010 - 2. Martin, W.C. (1960) Energy Levels and Spectrum of Neutral Helium (4HeI). Journal of Research of the National Bureau of Standards—Physics and Chemistry, 64, 19-28.
http://dx.doi.org/10.6028/jres.064A.003 - 3. Litzen, U. (1970) Improved Experimental Values for Some Hydrogen-Like Levels of He I. Physica Scripta, 2, 103-105.
http://dx.doi.org/10.1088/0031-8949/2/3/006 - 4. Kim, D., et al. (2010) New Physics: Sae Mulli (The Korean Physical Society), 60, 729-740.
- 5. Lide, D.R. and Frederikse, H.P.R. (1997) CRE Handbook of Chemistry and Physics. 78th Edition, CRE Press, 10-52.
- 6. Hecht, E. (2000) Optics. 2nd Edition, Korean Translators, Jangsu and Cho Jae-Heeng et al., 466.
- 7. Levine, I.N. (1978) Physical Chemistry. McGraw-Hill Co., 587.
- 8. Ishigaki, Y. and Yasuhara, H. (2002) Journal of the Korean Physical Society, 40, 1056-1059.












