American Journal of Analytical Chemistry
Vol.05 No.13(2014), Article ID:50016,17 pages
10.4236/ajac.2014.513095
Formulation of Titration Curves for Some Redox Systems
Anna M. Michałowska-Kaczmarczyk1, Maciej Rymanowski2, Agustin G. Asuero3, Marcin Toporek4, Tadeusz Michałowski4*
1Department of Oncology, The University Hospital in Cracow, Cracow, Poland
2Regional Subcarpathian Forensic Laboratory of Police, Rzeszów, Poland
3Department of Analytical Chemistry, The University of Seville, Seville, Spain
4Department of Analytical Chemistry, Technical University of Cracow, Cracow, Poland
Email: *michalot@o2.pl
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 24 July 2014; revised 7 September 2014; accepted 24 September 2014
ABSTRACT
The formalism realised according to the Generalised Approach to Electrolytic Systems (GATES) is presented and applied to typical redox systems known from the laboratory practice. In any redox system, the Generalized Electron Balance (GEB), perceived as the law of the matter conservation, is derivable from linear combination 2・f(O) − f(H) of elemental balances: f(O) for oxygen and f(H) for hydrogen. It is an equation linearly independent from other (charge and concentration) balances referred to an electrolytic redox system (aqueous media) of any degree of complexity, and named as the primary form of GEB and then denoted as pr-GEB. A compact equation for GEB is obtained from linear combination of 2・f(O) − f(H) with other (charge and concentration) balances. For a non-redox electrolytic system, of any degree of complexity, the balance 2・f(O) − f(H) is not an independent equation. In the derivation of GEB, all known components (species) of the system tested, taken in their real (i.e., hydrated) form, are involved in the balances, and none simplifying assumptions are needed. The redox systems are simulated with use of an iterative computer program.
Keywords:
Solution Thermodynamics, Generalized Approach to Electrolytic Systems, Generalized Electron Balance, Redox Titration

1. Introduction
Redox systems are considered as the most important and the most complex electrolytic systems. The possibility
of correct mathematical formulation of redox systems of any degree of complexity was possible only after for- mulation of the Generalized Electron Balance (GEB) that is fully compatible with charge and concentration ba- lances.
As were stated in [1] - [6] , the linear combination 2・f(O) − f(H) of elemental balances: f(H) for H and f(O) for O, when referred to any redox (static or dynamic) system, is an equation independent on charge and concentra- tion balances; the related formulation, termed later as the Approach II to GEB, is equivalent to one obtained according to the Approach I, based on the principle of common pool of electrons introduced by electron-active elements named―in convention of “card game”―as “players”. The electron-non-active elements are named as “fans”, and electrons are considered as “money”, transferred between “players”; the “fans” accounts are intact, in this convention. The Approach I to GEB, named also as the “short” version of GEB, needs a knowledge of oxidation degrees for all elements in the species participating the system considered. The great advantage of the Approach II, called also as the “long” version of GEB, is that none prior knowledge on oxidation degrees of all elements in complex species of definite composition and charge is needed. Both approaches are valid for aqueous and mixed-solvent media, with amphiprotic co-solvents involved.
Both Approaches (I, II) were discovered (1992, 2007) by Michałowski, and presented also in [7] - [16] . When referred to a non-redox system, 2・f(O) − f(H) is a linear combination of other (charge and concentration) balances related to this system, i.e., it is not an independent balance. Concentration balances are referred to other elements X (≠H, O) or groups of elements named as cores. Assuming k as a number of concentration balances, we have k+2 independent balances for a redox system, and k+1 balances for a non-redox system. It also clearly explains why the concentration balances are formulated in non-redox systems only for elements different from H and O. Some species in the balances are involved in expressions for the related equilibrium constants. The complete set of independent equilibrium constants is required for this purpose. The equilibrium constants for redox systems are: standard potentials (E0i), dissociation constants, stability constants of complexes, etc. This way, any redox (or non-redox) system can be formulated, provided that the related equilibrium constants for the complex species involved in the balances are known beforehand. However, GEB and―consequently―other balances, can be formulated on different levels of prior/pre-assumed knowledge of the system considered. The basic re- quirement put in these balances is their consistency (non-contradiction) that enables to carry out the calculations, made according to iterative computer programs.
From the very beginning, GEB was perceived as the missing balance needed for quantitative description of redox systems. GEB is fully compatible with other (charge and concentration) balances related to the system in question. This viewpoint was expressed also in the titles of successive papers: “Formulation of Generalized Equations for Redox Titration Curves” [9] and “A Unified Quantitative Approach to Electrolytic Systems” [10] . The term “Generalized Approach to Electrolytic Systems”, designated by acronym GATES, was used explicitly in [15] [16] and later. The GATES is perceived as the holistic, thermodynamic approach to redox and non-redox, mono- and polyphase, equilibrium metastable and non-equilibrium electrolytic systems of any degree of complexity [2] . The acronym GATES/GEB means GATES referred to redox systems. The fundamental advantage of the Approach II to GEB is that none prior knowledge on oxidation degree of elements in complex species of definite elemental composition and external charge is needed. The GEB is perceived as the general law of conservation, as a law of Nature, related to electrolytic redox systems in aqueous, non-aqueous and mixed solvent media, with amphiprotic (co)solvents involved.
The present article provides typical examples of formulation of the balances according to both Approaches (I, II) for dynamic redox systems, realized within GATES in titrimetric methods of analysis [5] [6] . For this purpose, we consider V0 mL of FeSO4 (C0) + H2SO4 (C01) solution as titrand (D) titrated with V mL of KMnO4 (C) (in the System A) or Ce(SO4)2 (C) + H2SO4 (C1) (in the System B); the admixtures of CO2 in D and the titrant (T) were also included. The species in the related systems are considered in their natural forms, i.e., as hydrates in
aqueous media [5] [6] . For the species of i-th kind,  , we apply the notation
, we apply the notation
 (1)
(1)
where ni ≥ 0, Ni is a number of these entities. For example, N19 ions 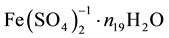 contain 2N19n19 atoms
contain 2N19n19 atoms
of H, N19(8 + n19) atoms of O, N19 atoms of Fe, and 2N19 atoms of S.
In this paper, all concentrations are expressed in mol/L, and all volumes in mL.
2. The Principle of Formulation of the Approach I to GEB
The Approach I can be considered on the card game principle, with electrons as money (cash), electron-active elements as players, and electron-non-active elements as fans.
2.1. System A
Let us consider V0 mL of D composed of N10 molecules of FeSO4∙7H2O (melanterite), N20 molecules of CO2, N30 molecules of H2SO4 and N40 molecules of H2O titrated with V mL of T composed of KMnO4 (N50), CO2 (N60), H2O (N70). In the D+T mixture, the following species are formed:
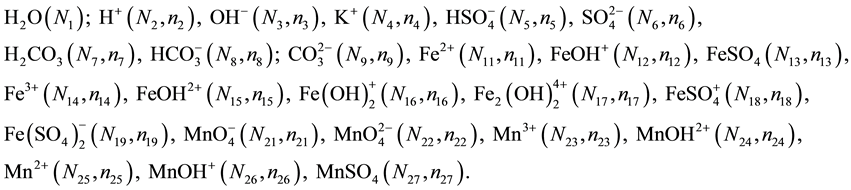 (2)
(2)
In this system, Mn and Fe are considered as players, and other elements (K, S, O, H) as fans. The transmission of electrons occurs between different species formed in the system by Fe and Mn, whereas such transmission does not occur between fans (the fans’ accounts are intact). Player and fans can be involved in the same
species; e.g., 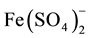 involves Fe (player) and S and O (fans).
involves Fe (player) and S and O (fans).
Let V mL be a total volume of T added from the start up to a given point of the titration. A common pool of electrons introduced by players is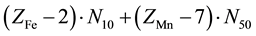 , where ZFe = 26 and ZMn = 25 are the atomic numbers for Fe and Mn, resp. These electrons are dissipated between different species formed in the mixture, namely:
, where ZFe = 26 and ZMn = 25 are the atomic numbers for Fe and Mn, resp. These electrons are dissipated between different species formed in the mixture, namely: 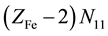 electrons in Fe2+・n11H2O,
electrons in Fe2+・n11H2O, 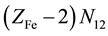 electrons in FeOH+・n12H2O, ・・・,
electrons in FeOH+・n12H2O, ・・・, 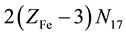
electrons in , ・・・,
, ・・・, 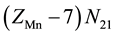 electrons in
electrons in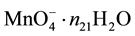 , ・・・,
, ・・・,  electrons in MnSO4・n27H2O. Then the electron balance is as follows:
electrons in MnSO4・n27H2O. Then the electron balance is as follows:
 (3)
(3)
The number Ni of the species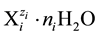 in V0 + V [mL] of the dynamic D+T system, is involved with its molar concentration
in V0 + V [mL] of the dynamic D+T system, is involved with its molar concentration
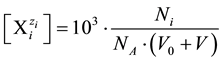 (4)
(4)
Moreover, we have:

where NA − Avogadro’s number; concentrations are expressed in mol/L, and volumes in mL. Applying (4) and (5) in (3), we obtain the equation for GEB written in terms of concentrations

2.2. System B
Let us consider V0 mL of D composed of N10 molecules of FeSO4∙7H2O (melanterite), N20 molecules of CO2, N30 molecules of H2SO4 and N40 molecules of H2O, titrated with V mL of T composed of Ce(SO4)2 (N50), H2SO4 (N60), H2O (N70) and CO2 (N80). In the D+T mixture, the following species are formed:

A common pool of electrons, introduced by Fe and Ce as the players, is


Ce4+, ・・・, 




Applying (4) and (5) in (8), we obtain the equation for GEB written in terms of concentrations

3. The Principle of Formulation of the Approach II to GEB
3.1. System A
Let us refer to the system presented in section 2.1. The species in the closed system are involved in the following elemental balances:
・ f(H):

・ f(O):

・ f(Fe):

・ f(C):

・ f(S):

・ f(K):

・ f(Mn):

・ charge balance:

Then from (2) and (3) we get pr-GEB = 2f(O) − f(H)

Combination of (18) with (17), 4・f(C) (13), 6・f(S) (14), and f(K) (15) gives:

Subtraction of (19) from ZFe・f(Fe) + ZMn・f(Mn) gives Equation (3) and then Equation (6). The equivalency of Approaches I and II in this system is thus proved.
Combination of (19), 3・f(Fe) (12) and 2・f(Mn) (16) gives

Applying (4) and (5) in (20) we get

It is the simplest form of GEB for this system.
3.2. System B
Let us refer to the system presented in section 2.2. The species in the closed system are involved in the following, elemental balances:
・ f(H):

・ f(O):

・ f(Fe)―as Equation (12)
・ f(C)―as Equation (13)
・ f(S):

・ f(Ce):

・ charge balance:

Then from (22) and (23) we get pr-GEB = 2・f(O) − f(H)

From combination of (26), (27), 4・f(C) (13), 6・f(S) (24) we have:

Subtraction of (28) from ZFe・f(Fe) + ZMn・f(Ce) gives Equation (8) and then Equation (9). The equivalency of Approaches I and II in this system is thus proved. Combination of (28), 3・f(Fe) (12) and 2・f(Ce) (25) gives

Applying (4) and (5) in (29) we get

It is the simplest form of GEB for this system.
4. Completing the Balances
The GEB are completed by concentration and charge balances. All the balances should be specified in the molar concentration unit, because the molar concentrations are present in the expressions for the corresponding equilibrium constants.
4.1. System A
The concentration balances are defined on the basis of equations (12) - (14), (16) and relations (4), (5):




where:

The relation [K+] = CV/(V0+V) resulting from (15) is not considered as a balance, in principle; it enters as a number (at a particular V value) the related charge balance

4.2. System B
The concentration balances are defined on the basis of equations (12a), (13a), (24a) - (26a), see relations (4), (5).



5. Equilibrium Constants
The equilibrium constants related to both Systems (A and B) [17] [18] are collected in Table 1 (stability constants of complexes) and Table 2 (standard potentials).
Table 1. Values of logKi of stability constants Ki for indicated complex species applied in the simulations of the redox titrations.
Table 2. Standard potentials applied in the simulations of the redox titrations.
The equilibrium constants for non-redox reactions are defined immediately on the basis of mass action law. In the case of redox systems, where standard potentials, E0 [V], are the equilibrium constants specified in the related tables of equilibrium data, a two-step procedure is applied [11] .
The species of the same element with different oxidation degrees are interrelated in expressions, defined on the basis of the reaction notation. In particular, the redox potential E [V] for the reaction

is defined by equation

Denoting:


we get

At T = 298.15 K, 



Generalizing, we refer to redox reaction, written correctly according to the scheme

where zi > 0. Then we get:



The standard potentials: E0 in (33) and E0i in (40) are referred to standard hydrogen electrode (SHE); [e−] denote molar concentration of electrons in the solution. The choice of SHE is arbitrary, however, and it is natural to look for an absolute standard such as the vacuum level, commonly used in other branches of physics and che-
mistry. Applying the identity 

Comparing the related terms in (42) and (41a), we get:


where E0 is the correction involved with absolute electrode potential. The value E0 = 4.44 ± 0.02 V at 298.15 K
is recommended by IUPAC [19] ), and then 

(see Equation (41)) there is always the difference E − E0i, i.e., the ratio of concentrations of any oxidized and reduced forms of an element does not depend on the E-scale applied.
6. Graphical Presentation of the Data
It is advised to present the graphs on the planes, with the fraction titrated Φ [22] [23]

on the abscissa. Putting F instead of V on the abscissa provides a kind of normalization on the related plots obtained on the stage of graphical presentation of the results obtained from iterative calculations [6] . It should also be noted that F plays a key role in formulation of the Generalized Equivalence Mass (GEM) concept [24] [25] .
6.1. System A
The speciation curves for Fe and Mn species during titration of V0 = 100 mL of FeSO4 (C0 = 0.01 mol/L) + H2SO4 (C01 = 1.0 mol/L) with V mL of KMnO4 (C = 0.02 mol/L) are presented in Figure 1(a) & Figure 1(b); C02 = C2 = 0. The E vs. F relationship is presented in Figure 2 and, in more a detailed manner, in Figure 3(a) & Figure 3(b). The E vs. F relationship is presented in Figure 4. It should be noted, among others, that concentrations of sulfate complexes of ferric ions exceed significantly the concentration of Fe3+ ions. Concentrations of
Mn3+ and MnOH2+ exceed the concentration of
High buffer capacity of the titrand, resulting from presence of H2SO4 (C01) in it, causes rather small growth in
pH value of the system considered (Figure 4); the pH changes result from acid-base properties of 
that act like “octopus” [26] in reaction with H+ ions (Equation (32)).
6.2. System B
The speciation curves for Fe and Ce species during titration of V0 = 100 mL of FeSO4 (C0 = 0.01 mol/L) + H2SO4 (C01 = 1.0 mol/L) with V mL of Ce(SO4)2 (C = 0.1 mol/L) + H2SO4 (C1 = 0.5 mol/L); C02 = C2 = 0, are presented in Figure 5. The E vs. F relationship is presented in Figure 6 and, in more a detailed manner, in Figure 7(a) & Figure 7(b). The E vs. F relationship is presented in Figure 8.
The changes in slope of the curves presented in Figure 8 resulted mainly from differences between C01 and C1 values; the solution of Ce(SO4)2 is prepared by dissolution of this salt in H2SO4. Note that the plot obtained at C01 = C1 = 0.5 is not exactly parallel to Φ axis; small changes in pH value result there from other effects involved with this titration.
7. Discussion
Two equivalent approaches (Approach I and Approach II) to Generalized Electron balance (GEB) in electrolytic redox systems are presented. The Approach I is based on the principle of common pool of electrons, whereas the Approach II originates from the linear combination 2・f(O) − f(H) of elemental balances f(O) and f(H) for O and H, formulated for a redox system. For non-redox systems, 2・f(O) − f(H) is a linear combination of other (charge and concentration) balances, i.e., it is not an independent equation. In all instances, the balances are ultimately expressed in terms of molar concentrations [mol/L] of compounds and species, Equations (4) and (5).

Figure 1. Speciation curves for (1a) Fe-species and (1b) Mn-species in the System A, where V0 = 100 mL of FeSO4 (C0 = 0.01 mol/L) + H2SO4 (C01 = 1.0 mol/L) is titrated with V mL of KMnO4 (C = 0.02 mol/L); Φ (Equation (46)).
Figure 2. The E = E (Φ) curves plotted for the System A, at V0 = 100, C0 = 0.01, C = 0.02, and different C01 values, indicated in Figure 3.

Figure 3. Enlarged fragments of the curves in Figure 2: a) before, b) after the equivalence point; the numbers at the lines indicate C01 values.
Figure 4. The pH = pH (F) relationship for the System A at V0 = 100, C0 = 0.01, C = 0.02, and C01 values indicated at the corresponding lines.

Figure 5. Speciation curves for (a) Fe-species and (b) Ce-species in the System B, where V0 = 100 mL of FeSO4 (C0 = 0.01 mol/L) + H2SO4 (C01 mol/L) is titrated with V mL of Ce(SO4)2 (C = 0.1 mol/L) + H2SO4 (C1 = 0.5 mol/L); Φ (Equation (46)).
Figure 6. The E = E(Φ) curves plotted for the System B, at V0 = 100, C0 = 0.01, C = 0.1, and different C01 values, indicated in Figure 7.

Figure 7. Enlarged fragments: (7a) before and (7b) after the equivalence point of the curves in Figure 6; the numbers at the lines indicate C01 values.
Figure 8. The pH = pH (Φ) relationship for the System B at V0 = 100, C0 = 0.01, C = 0.1, C1 = 0.5 and C01 values indicated at the corresponding lines.
The generalised approach to electrolytic systems (GATES) involving GEB concept is based on firm, mathematical (algebraic) foundations, not on an extremely ‘fragile’ chemical notation principle, that is only a faint imitation of a true, algebraic notation. It is a new proposal against ones known hitherto, particularly represented by Pourbaix diagrams [27] , appearing graphically only the predominant species on (pH, E) two-dimensional (2-D) plane. The Pourbaix diagram becomes completely destroyed (and then useless) if a new component, e.g. strong complexing agent, be introduced. Applying this diagram, the E value must be previously measured. According to GATES/GEB approach, the E value is calculated; it is a great difference. According to GATES, it is possible to resolve any system of entrance substances and to obtain any relationships in graphical (2-D or 3-D) presentation.
The Approach I can be applied for the systems where the oxidation numbers of all elements can easily be determined. From the Approach II viewpoint, the term “oxidation number” is not ascribed to any element of the species in the system considered; known (or pre-assumed) composition of a species, expressed by its formula together with external charge of this species, provides an information sufficient to formulate the related balances. This fact is of capital importance, when redox equilibria are involved e.g., with ions and radicals/ion-radicals and other complex organic species [6] . Among others, GEB was formulated [2] for batch systems with Fenton reagent involved [28] , where radicals play a key role [29] - [34] . Approach II offers also special advantages when referred to redox systems, where organic species of great complexity, e.g. plant pigments participating redox reactions [35] -[40] , are considered.
Another kind of batch system are the systems where oscillating chemical reactions of Belousov-Zhabotinsky (BZ) or Briggs-Rauscher (BR) type occur. For these systems, the principles of a kinetic model were proposed [6] [10] . The related model consists of the set of balances and their time derivatives, considered as holonomic constraints in the systems. In the redox system similar to one of the BR type, the kinetic effects involved with malonic acid iodination were lately tested in dynamic (titration) system [23] .
The species in the redox systems are thus involved in charge, GEB and elemental balances. Moreover, the terms: “oxidant” and “reducer” are not ascribed there to particular species. All attainable physicochemical knowledge can be involved in the algorithms formulated within GATES/GEB, and none simplifying assumptions are needed.
Some qualitative knowledge on the system tested is also valuable; it is particularly desired in the case of metastable systems [5] . In nearly all more complex systems, one can indicate the species (or a group of species)
that are in a metastable state, relative to the solvent (e.g., 
the system (e.g., H2SO4 versus H2S).
The Approaches I and II to redox systems are based on general rules of conservation, namely (1˚) the rule of charge conservation, (2˚) the rule of a matter conservation, and (3˚) the chemical rule of mass action. The law of matter conservation is perceived from the viewpoint of conservation of particular elements in a closed system. This way, the problems involved with isotopic effects/neutrons and abundances of particular elements in the system are thus omitted. Although the paper refers to systems with stable isotopes, an extension on the systems where (α, β−, β+ or electron capture) radioactive decay occur, is also possible. This approach is justified by the fact that the physicochemical knowledge on electrolytic (in general) and redox (in particular) chemical systems is related primarily to the matter with natural isotopic composition. Moreover, the isotopic effects manifest themselves only slightly (or are rather neglected within the limits of experimental error) with respect to elements X of higher atomic numbers ZX.
The solving of redox systems within the GATES/GEB, established in 1992 [2] , is fundamentally innovative when compared with earlier approaches to the subject in question [41] - [53] , denoted later as EA, for brevity.
A comprehensive knowledge of the redox systems in terms of their mathematical formalism was practically non-existent before 1992. EA were based essentially on the stoichiometric reaction equations and included only two pairs {(Oxi, Redi) çi=1,2} of components involved in these equations, e.g. [Fe2+] + [Fe3+] = C0V0/(V0 + V) and [Ce4+] + [Ce3+] = CV/(V0 + V) for the System B―compare with (12a) and (25a). Concentration balances for the accompanying (e.g., sulfate) species were not formulated, compare with (14a), (24a). Even relatively simple redox systems, as ones presented in this paper, involve far greater number of components, see (2) and (7). Other species are involved, among others, in charge balance. It is obvious that a redox reaction notation does not include all “players”. What is more, the species involved in redox reactions presented by EA are, generally, the constituents of lesser concentration. For example, the Systems A and B were represented by reactions: (32) and

respectively [54] [55] , although [FeSO4] exceeds 

also at equivalence point, see Figure 1(a), Figure 5(a) Figure 5(b). Omission of the sulphate complexes is a falsification of reality, when referred to the systems considered, where H2SO4 acts, simultaneously, as buffering and
complexing agent. The notation
nating species, stated on the basis of speciation curves presented in Figure 5(a) Figure 5(b), gives better approximation of the process occurred in the System B than the reaction (47). Similar remark can be referred to the System
A; e.g., [Mn3+] and [MnOH2+] exceed 
ation [Fe2+] − [Ce4+] = (C0V0 − CV)/(V0 + V) obtained on the basis of Equation (47), was applied in EA, e.g. in [56] , to the titration made in the System B; this equation should be compared with exact Equation (30). Similarly,
the equation 
pared with exact Equation (21). Concluding, the “electron balances” formulated up to 1992 were slavishly related to the stoichiometric reaction notations. Incomplete form of those balances needs incomplete forms of the remaining balances, otherwise the contradictory system of equations is not resolvable.
The correct resolution of the problem within GATES/GEB is based on a solution of a system of algebraic equations, not on a (pre-assumed) chemical reaction notation, as were done in EA. The formulation of reaction notations on the basis of the related speciation plots (Figure 1(a), Figure 1(b) and Figure 4(a), Figure 4(b)) is a next, facultative (not obligatory) step made after calculations made according to GATES/GEB and graphical presentation of the results thus obtained. This way, one can compare effectivities of competitive reactions. This viewpoint is a complete reversal to EA.
For example, it were stated [5] [8] , on the basis of GATES/GEB, that the efficiency of reaction (i)



ca. 104 times smaller than for the reaction (iv)
(i) and (iii) are cited in all handbooks referred to the problem in question; both pairs of reactions appear the same stoichiometry, 3:6 = 1:2.
Within GATES, one can use all the available quantitative knowledge provided by tables of equilibrium constants. According to earlier approaches, only two “formal” potentials (as substitutes of standard potentials) were considered and used for determination of the equilibrium constant for total (summary) reaction. Within GATES, every complex species is involved in the balances, together with the related equilibrium constant value. Within GATES, also a qualitative knowledge is applied, mainly in the context of the metastable systems; this way, different reaction paths can be studied [5] [6] .
In EA, the charge balance has not been involved in calculations, although this concept was known before. To avoid a formulation of contradictory equations, pH = const during the titration was assumed in EA. However, such an assumption is not acceptable, for example, in (1) Br2 with NaOH; (2) I2 with NaOH in presence of (2a) KI, (2b) H2CO3, (2c) CCl4 (liquid-liquid extraction system), (2d) KI + H2CO3 + CCl4; an interesting case where (3) MgSO4 is added into I2 + KI + NaOH was also considered. In all these systems, described in [7] , the disproportionation reactions were accompanied by other effects.
The assumption pH = const is only approximately valid in buffered systems, such as System A and System B considered in this paper, where an excess of strong acid is added into D or/and T. However, in these cases, the changes in pH are distinct/noticeable, see Figure 4, Figure 8.
The results obtained from simulated titrations can always be considered as a reference to real behaviour of the system tested, frequently corrupted by kinetic phenomena. It enables also to demonstrate limitations of some analytical methods, e.g. ones concerning accuracy and precision of the pH-static titration [57] .
The simulating procedure applied for resolution of redox systems of different degree of complexity enables to choose the best conditions of analysis (optimisation a priori). Another advantage is the possibility to follow some details invisible in an experiment; it particularly refers to dynamic speciation analysis, realised only in simulated titrations.
Resolution of equilibria in redox dynamic (titration) systems is justly considered among the most difficult topics of interest, but the reasons of these difficulties were not put rightly. The main difficulties in the right description of redox systems arise on the line of junction between thermodynamics and kinetics; this line is not precisely defined in many metastable systems. This remark refers also to some kinetic systems, e.g. the titration of ferricyanide with ascorbic acid [58] [59] .
In EA, titration curves were discussed in piecemeal fashion: one approximate description for the part before the equivalence point, a different approximation for the part beyond this point and, finally, yet another formula for the equivalence (eq) point [53] . As refers to the System B, the equality [Ce3+] = [Fe3+] was applied at the eq
point. This equality is invalid, however, owing to the fact that

pressed by the related GEB, is obligatory. On this basis, one can find the points (Φ, E) also in close vicinity of the equivalence point, see Table 3.
The value Eeq = (0.771 + 1.70)/2 = 1.236 V, calculated according to EA, is different from 1.034 V (see Table 2 and Table 3). Analogous tables referred to other, also more complex redox systems presented in [5] [6] [10] [11] , give similar discrepancies; it particularly refers to more complex formulae for Eeq, presented in [41] [43] [44] [53] . For comparison, the GATES/GEB applied to redox systems enables to calculate the coordinates referred to any point (Φ, E), considered as the end (e) point (Φe, Ee), not only for equivalence (eq) point(s).
Table 3. The (Φ, E) values related to the System A (C0 = 0.01; C01 = 1.0, C = 0.02); E calculated vs. NHE.
8. Conclusion
The GATES/GEB based on physical (charge conservation), physico-chemical (elements conservation) and che- mical (mass action) laws, expressed―as a whole―in the system of algebraic (not chemical) equations, is the great step towards reductionism of sciences. Despite the fact that chemistry, as a whole, cannot be considered in terms of physical sciences [60] , the discovery of GEB enabled to avoid a reasoning based on a chemical reaction notation principle, that provided only a superficial/deceptive and descriptive knowledge on the systems considered. This way, GATES confirms the Kant opinion, expressed in his Critique of Pure Reason (1781), that the real knowledge inherent in every branch of natural science is involved in mathematics contained therein.
Cite this paper
Anna M.Michałowska-Kaczmarczyk,MaciejRymanowski,Agustin G.Asuero,MarcinToporek,TadeuszMichałowski, (2014) Formulation of Titration Curves for Some Redox Systems. American Journal of Analytical Chemistry,05,861-878. doi: 10.4236/ajac.2014.513095
References
- 1. Michalowski, T., Toporek, M., Michalowska-Kaczmarczyk, A.M. and Asuero, A.G. (2013) New Trends in Studies on Electrolytic Redox Systems. Electrochimica Acta, 109, 519-531.
http://dx.doi.org/10.1016/j.electacta.2013.07.125 - 2. Michalowski, T., Michalowska-Kaczmarczyk, A.M. and Toporek, M. (2013) Formulation of General Criterion Distinguishing between Non-Redox and Redox Systems. Electrochimica Acta, 112, 199-211.
http://dx.doi.org/10.1016/j.electacta.2013.08.153 - 3. Michalowska-Kaczmarczyk, A.M. and Michalowski, T. (2013) Comparative Balancing of Non-Redox and Redox Electrolytic Systems and Its Consequences. American Journal of Analytical Chemistry, 4, 46-53.
http://dx.doi.org/10.4236/ajac.2013.410A1006 - 4. Michalowska-Kaczmarczyk, A.M. and Michalowski, T. (2014) Compact Formulation of Redox Systems According to GATES/GEB Principles, Journal of Analytical Sciences. Methods and Instrumentation, 4, 39-45.
- 5. Michalowski, T. (2010) The Generalized Approach to Electrolytic Systems: I. Physicochemical and Analytical Implications. Critical Reviews in Analytical Chemistry, 40, 2-16.
http://dx.doi.org/10.1080/10408340903001292 - 6. Michalowski, T. (2011) Application of GATES and MATLAB for Resolution of Equilibrium, Metastable and Non-Equilibrium Electrolytic Systems. In: Michalowski, T., Ed., Applications of MATLAB in Science and Engineering, Chapter 1, InTech—Open Access Publisher in the Fields of Science, Technology and Medicine, Rijeka, Croatia.
http://www.intechopen.com/books/show/title/applications-of-matlab-in-science-and-engineering . - 7. Michalowski, T. (1994) Calculation of pH and Potential E for Bromine Aqueous Solutions. Journal of Chemical Education, 71, 560-562.
http://dx.doi.org/10.1021/ed071p560 - 8. Michalowski, T. and Lesiak, A. (1994) Acid-Base Titration Curves in Disproportionating Redox Systems. Journal of Chemical Education, 71, 632-636.
http://dx.doi.org/10.1021/ed071p632 - 9. Michalowski, T. and Lesiak, A. (1994) Formulation of Generalized Equations for Redox Titration Curves. Chemia Analityczna (Analytical Chemistry) (Warsaw), 39, 623-637.
- 10. Michalowski, T., Wajda, N. and Janecki, D. (1996) A Unified Quantitative Approach to Electrolytic Systems. Chemia Analityczna (Analytical Chemistry) (Warsaw), 41, 667-685.
- 11. Michalowski, T. (2001) Calculations in Analytical Chemistry with Elements of Computer Programming (in Polish). PK, Cracow.
- 12. Michalowski, T. (2007) Complementarity of Physical and Chemical Laws in the Context of Electrolytic Systems. In: Maciejowska, I., Ruszak, M. and Witkowski, S., Eds, Use of Information Technology in Academic Teaching of Chemistry, Jagiellonian University, Cracow, 155-161.
http://www.chemia.uj.edu.pl/~ictchem/book.html - 13. Michalowski, T., Baterowicz, A., Madej, A. and Kochana, J. (2001) Extended Gran Method and Its Applicability for Simultaneous Determination of Fe(II) and Fe(III). Analytica Chimica Acta, 442, 287-293.
http://dx.doi.org/10.1016/S0003-2670(01)01172-2 - 14. Michalowski, T., Toporek, M. and Rymanowski, M. (2005) Overview on the Gran and Other Linearization Methods Applied in Titrimetric Analyses. Talanta, 65, 1241-1253.
http://dx.doi.org/10.1016/j.talanta.2004.08.053 - 15. Michalowski, T., Kupiec, K. and Rymanowski, M. (2008) Numerical Analysis of the Gran Methods A Comparative Study. Analytica Chimica Acta, 606, 172-183.
http://dx.doi.org/10.1016/j.aca.2007.11.020 - 16. Ponikvar, M., Michalowski, T., Kupiec, K., Wybraniec, S. and Rymanowski, M. (2008) Experimental Verification of the Modified Gran Methods Applicable to Redox Systems. Analytica Chimica Acta, 628, 181-189.
http://dx.doi.org/10.1016/j.aca.2008.09.012 - 17. Inczedy, J. (1976) Analytical Applications of Complex Equilibia. E. Horwood, Chichester.
- 18. Lurie, Yu. (1971) Handbook of Analytical Chemistry (in Russian). Izd. Khimia, Moscow.
- 19. Trasatti, S. (1986) The Absolute Electrode Potential: An Explanatory Note (Recommendations 1986). International Union of Pure and Applied Chemistry, Pure and Applied Chemistry, 58, 955-966.
http://dx.doi.org/10.1351/pac198658070955 - 20. Tsiplakides, D. and Vayenas, C.G. (2002) The Absolute Potential Scale in Solid State Electrochemistry. Solid State Ionics, 152-153, 625-639.
http://dx.doi.org/10.1016/S0167-2738(02)00396-X - 21. Tsiplakides, D. and Vayenas, C.G. (2011) Electrode Work Function and Absolute Potential Scale in Solid State Electrochemistry. In: Comninellis, C., Doyle, M. and Winnick, J., Eds., Energy and Electrochemical Processes for a Cleaner Environment, Electrochemical Society Proceedings, Inc., 206.
http://www.iupac.org/publications/pac/1986/pdf/5807x0955.pdf - 22. Asuero, A.G. and Michalowski, T. (2011) Comprehensive Formulation of Titration Curves for Complex Acid-Base Systems and Its Analytical Implications. Critical Reviews in Analytical Chemistry, 41, 151-187.
http://dx.doi.org/10.1080/10408347.2011.559440 - 23. Michalowski, T., Ponikvar-Svet, M., Asuero, A.G. and Kupiec, K. (2012) Thermodynamic and Kinetic Effects Involved with pH Titration of As(III) with Iodine in a Buffered Malonate System. Journal of Solution Chemistry, 41, 436-446.
http://dx.doi.org/10.1007/s10953-012-9815-6 - 24. Michalowski, T., Pietrzyk, A., Ponikvar-Svet, M. and Rymanowski, M. (2010) The Generalized Approach to Electrolytic Systems: II. The Generalized Equivalent Mass (GEM) Concept. Critical Reviews in Analytical Chemistry, 40, 17-29.
http://dx.doi.org/10.1080/10408340903001342 - 25. Michalowski, T., Asuero, A.G., Ponikvar-Svet, M., Toporek, M., Pietrzyk, A. and Rymanowski, M. (2012) Liebig-Deniges Method of Cyanide Determination: A Comparative Study of Two Approaches. Journal of Solution Chemistry, 41, 1224-1239.
http://dx.doi.org/10.1007/s10953-012-9864-x - 26. Michalowski, T., Rymanowski, M. and Pietrzyk, A. (2005) Nontypical Bronsted Acids and Bases. Journal of Chemical Education, 82, 470-472.
http://dx.doi.org/10.1021/ed082p470 - 27. Pourbaix, M. (1963) Atlas of Electrochemical Equilibria. Gauthier-Villars, Paris.
- 28. Walling, C. (1975) Fenton’s Reagent Revisited. Accounts of Chemical Research, 8, 125-131.
http://dx.doi.org/10.1021/ar50088a003 - 29. Luehrs, D.C. and Roher, A.E. (2007) Demonstration of the Fenton Reaction. Journal of Chemical Education, 84, 1290. http://dx.doi.org/10.1021/ed084p1290
- 30. Wink, D.A., Wink, C.B., Nims, R.W. and Ford, P.C. (1994) Oxidizing Intermediates Generated in the Fenton Reagent: Kinetic Arguments against the Intermediacy of the Hydroxyl Radical. Environmental Health Perspectives, 102, 11-15.
http://dx.doi.org/10.1289/ehp.94102s311 - 31. De Heredia, J.B., Torregrosa, J., Dominguez, J.R. and Perez, J.A. (2001) Kinetic Model for Phenolic Compound Oxidation by Fenton’s Reagent. Chemosphere, 45, 85-90.
http://dx.doi.org/10.1016/S0045-6535(01)00056-X - 32. Panzella, L., Manini, P., Napolitano, A. and d’Ischia, M. (2004) Free Radical Oxidation of (E)-Retinoic Acid by the Fenton Reagent: Competing Epoxidation and Oxidative Breakdown Pathways and Novel Products of 5,6-Epoxyretinoic Acid Transformation. Chemical Research in Toxicology, 17, 1716-1724.
http://dx.doi.org/10.1021/tx049794b - 33. Lin, Y.H. and Wang, T.H. (2001) Weibull Modeling of the Fenton’s Oxidation Process. Journal of Environmental Science and Health. Part A, Toxic/Hazardous Substances & Environmental Engineering, 36, 17-23.
http://dx.doi.org/10.1081/ESE-100000468 - 34. Goldstein, S., Meyerstein, D. and Czapski, G. (1993) The Fenton Reagents. Free Radical Biology and Medicine, 15, 435-445.
http://dx.doi.org/10.1016/0891-5849(93)90043-T - 35. Pietrzkowski, Z., Nemzer, B., Spórna, A., Stalica, P., Treser, W., Keller, R., Jimenez, R., Michalowski, T. and Wybraniec, S. (2010) Influence of Betalain-Rich Extract on Reduction of Discomfort Associated with Osteoarthritis. New Medicine, 1, 12-17.
- 36. Nemzer, B., Pietrzkowski, Z., Spórna, A., Stalica, P., Thresher, W., Michalowski, T. and Wybraniec, S. (2011) Betalainic and Nutritional Profiles of Pigment-Enriched Red Beet Root (Beta vulgaris L.) Dried Extracts. Food Chemistry, 127, 42-53.
http://dx.doi.org/10.1016/j.foodchem.2010.12.081 - 37. Wybraniec, S. and Michalowski, T. (2011) New Pathways of Betanidin and Betanin Enzymatic Oxidation. Journal of Agricultural and Food Chemistry, 59, 9612-9622.
http://dx.doi.org/10.1021/jf2020107 - 38. Wybraniec, S., Stalica, P., Spórna, A., Nemzer, B., Pietrzkowski, Z. and Michalowski, T. (2011) Antioxidant Activity of Betanidin: Electrochemical Study in Aqueous Media. Journal of Agricultural and Food Chemistry, 59, 12163-12170.
http://dx.doi.org/10.1021/jf2024769 - 39. Wybraniec, S., Starzak, K., Skopińska, A., Szaleniec, M., Slupski, J., Mitka, K., Kowalski, P. and Michalowski, T. (2013) Effects of Metal Cations on Betanin Stability in Aqueous-Organic Solutions. Food Science and Biotechnology, 22, 353-363.
http://dx.doi.org/10.1007/s10068-013-0088-7 - 40. Wybraniec, S., Starzak, K., Skopińska, A., Nemzer, B., Pietrzkowski, Z. and Michalowski, T. (2013) Studies on Non-Enzymatic Oxidation Mechanism in Neobetanin, Betanin and Decarboxylated Betanins. Journal of Agricultural and Food Chemistry, 61, 6465-6476.
http://dx.doi.org/10.1021/jf400818s - 41. Bard, A.J. and Simonsen, S.H. (1960) The General Equation for the Equivalence Point Potential in Oxidation-Reduction Titrations. Journal of Chemical Education, 37, 364-366.
http://dx.doi.org/10.1021/ed037p364 - 42. Bishop, E. (1962) Some Theoretical Considerations in Analytical Chemistry: Part VI. The Precise Calculation of Data for Redox Titration Curves. Analytica Chimica Acta, 26, 397-405.
http://dx.doi.org/10.1016/S0003-2670(00)88405-6 - 43. Goldman, J.A. (1965) The Equivalence Point Potential in Redox Titrations. Analytica Chimica Acta, 33, 217-218.
http://dx.doi.org/10.1016/S0003-2670(01)84877-7 - 44. Goldman, J.A. (1966) Further Considerations on Redox Titration Equations. Journal of Electroanalytical Chemistry, 11, 416-424.
http://dx.doi.org/10.1016/0022-0728(66)80010-4 - 45. Goldman, J.A. (1966) A General Equation for the Description of Redox Titration Curves. Journal of Electroanalytical Chemistry, 11, 255-261.
http://dx.doi.org/10.1016/0022-0728(66)80090-6 - 46. Goldman, J.A. (1967) The Locations of Inflection Points on Titration Curves for Symmetrical Redox Reactions. Journal of Electroanalytical Chemistry and Interfacial Electrochemistry, 14, 373-383.
http://dx.doi.org/10.1016/0022-0728(67)80018-4 - 47. Goldman, J.A. (1968) Redox Equilibria, Part IV. Titration Curve Equations for Homogeneous and Symmetrical Redox Reactions. Journal of Electroanalytical Chemistry and Interfacial Electrochemistry, 16, 47-59.
http://dx.doi.org/10.1016/S0022-0728(68)80276-1 - 48. Goldman, J.A. (1968) Redox Equilibria: V. The Locations of Inflection Points on Titration Curves for Homogeneous Reactions. Journal of Electroanalytical Chemistry and Interfacial Electrochemistry, 18, 41-45.
http://dx.doi.org/10.1016/S0022-0728(68)80158-5 - 49. Goldman, J.A. (1968) Redox Equilibria: Part VI. A Completely General Titration Curve Equation for Homogeneous and Symmetrical Redox Reactions. Journal of Electroanalytical Chemistry and Interfacial Electrochemistry, 19, 205-214.
http://dx.doi.org/10.1016/S0022-0728(68)80119-6 - 50. Sriramam, K. (1976) A Study on the Theory of Action of Reversible Redox Indicators. Talanta, 23, 864-866.
http://dx.doi.org/10.1016/0039-9140(76)80107-5 - 51. Meretoja, A., Lukkari, O. and Hakoila, E. (1978) Redox Titrations-II. Location of Inflection Points on Titration Curves for Homogeneous Redox Reactions. Talanta, 25, 557-562.
http://dx.doi.org/10.1016/0039-9140(78)80146-5 - 52. Stur, J., Bos, M. and van der Linden, W.E. (1984) A Generalized Approach for the Calculation and Automation of Potentiometric Titrations Part 2. Redox Titrations. Analytica Chimica Acta, 158, 125-129.
http://dx.doi.org/10.1016/S0003-2670(00)84819-9 - 53. de Levie, R. (1992) A Simple Expression for the Redox Titration Curve. Journal of Electroanalytical Chemistry, 323, 347-355.
http://dx.doi.org/10.1016/0022-0728(92)80022-V - 54. Rieger, P.H. (1994) Electrochemistry. 2nd Edition, Chapman & Hall, Inc., New York.
http://dx.doi.org/10.1007/978-94-011-0691-7 - 55. Raj, G. (2009) Advanced Physical Chemistry. 35th Edition, GOEL Publication House, Meerut.
- 56. da Conceicao Silva Barreto, M., de Lucena Medeiros, L. and César de Holanda Furtado, P. (2001) Indirect Potentiometric Titration of Fe(III) with Ce(IV) by Gran’s Method. Journal of Chemical Education, 78, 91.
http://dx.doi.org/10.1021/ed078p91 - 57. Michalowski, T., Toporek, M. and Rymanowski, M. (2007) pH-Static Titration: A Quasistatic Approach. Journal of Chemical Education, 84, 142-150.
http://dx.doi.org/10.1021/ed084p142 - 58. Nóbrega, J.A. and Rocha, F.R.P. (1997) Ionic Strength Effect on the Rate of Reduction of Hexacyanoferrate(III) by Ascorbic Acid: A Flow Injection Kinetic Experiment. Journal of Chemical Education, 74, 560-562.
http://dx.doi.org/10.1021/ed074p560 - 59. Huang, T.H., Salter, G., Kahn, S.L. and Gindt, Y.M. (2007) Redox Titration of Ferricyanide to Ferrocyanide with Ascorbic Acid: Illustrating the Nernst Equation and Beer-Lambert Law. Journal of Chemical Education, 84, 1461-1463.
http://dx.doi.org/10.1021/ed084p1461 - 60. Labarca, M. and Lombardi, O. (2008) The End of the Dream of Unity. Current Science, 94, 438-439.
NOTES
*Corresponding author.







