American Journal of Analytical Chemistry
Vol.3 No.12A(2012), Article ID:26143,6 pages DOI:10.4236/ajac.2012.312A119
The Analysis of the Equilibrium Cluster Structure in Supercritical Carbon Dioxide
Computer and Information Systems Department, Russian New University (ROSNOU), Moscow, Russia
Email: Sedunov.b@gmail.com
Received October 15, 2012; revised November 18, 2012; accepted November 28, 2012
Keywords: Real Gas; Supercritical Fluid; Cluster; Bond Energy; Carbon Dioxide
ABSTRACT
The monomer fraction density based analysis of precise thermophysical data for pure fluids is developed to study the molecular structures in supercritical fluids in general and in CO2 in particular. The series expansion by powers of the monomer fraction density of the potential energy density is used to discover the cluster structure in supercritical fluids and the clusters’ bond energies in CO2. The method of clusters separation between classes of loose and dense clusters in the CO2 supercritical fluid is developed. The method of the energetically averaged number of dense clusters is developed to study the mechanism of the soft structural transition between the gas-like and liquid-like fluids in the supercritical CO2.
1. Introduction
Supercritical fluids (SCF) are widely used in modern chemical technologies due to the remarkable mixture of solvent power, characteristic to liquids, and transport properties, specific for gases. This mixture of properties is especially favorable for the Supercritical fluid extraction (SFE) [1,2] that needs both in the high solubility and in the high mobility of the components to be extracted.
For SFE the most commonly used SCF is Carbon Dioxide, due to its critical temperature Tc staying close to room temperatures (Tc = 304.1282 K) and low enough critical pressure Pc that does not require too expensive technological equipment (Pc = 73.773 bar) [3]. The next advantage of CO2 is its low cost and non-toxicity. Some properties of the supercritical CO2 are the subjects of this research.
The mixture of properties specific for liquids and gases in supercritical fluids is due to their high heterogeneity resulting from the plurality of large clusters in the gas-like zone of the fluid and large pores in the liquidlike zone.
Dr. Keiko Nishikawa et al. have first reported the high density fluctuations in a number of supercritical fluids, including CO2, studied by the X-ray diffraction and Raman spectroscopy [4-6]. In these works the peak line of density fluctuations on the (T, P) diagram was discovered and named as the ridge.
A similar sort of the ridge line Pr (T) may be seen on the diagrams of many thermophysical properties, such as heat capacities, compressibility factors, etc. [7]. While the pressure P grows at a constant supercritical temperature T, the fluid passes through the structural transition [7-9] from the gas-like structure to the liquid-like one. At the ICCT 2010 the author wrongly referred it to the phase transition [8], but the supercritical fluid is a heterogeneous multiphase system that can change only its structure at changing pressure or temperature.
The gas-like structure near the ridge is filled with clusters of different dimensions and the liquid-like structure contains different pores in such a way that the average densities of both structures become equal at the ridge and stay not too far from the critical density Dc. The ridge line Pr (T) is the extension of the saturation line Psat (T) to the supercritical zone, but depends on the nature of the property selected to build this line [7-9].
So, we have a plurality of the extension lines, forming together the zone of the soft structural transition [7]. This zone widens with a growth of the T-Tc difference. This zone is the zone of large but controllable changes in thermophysical properties and can be recommended as the zone favorable for technological processes. For further perfection of technologies based on supercritical fluids it is important to understand the complex mechanisms of clusters and pores formation in these media.
This paper has a goal to develop the methods of the analytical study of precise experimental data concerning the thermophysical properties of pure supercritical fluids, such as CO2. Now the thermophysical data for many pure fluids are accumulated in precise databases, such as the NIST database [3]. The computer aided analysis of data from these databases provides an improvement of both physical and mathematical models and may give the vision of the fluid’s structure.
2. The Method and Preliminary Results of the Analysis
The developed here method of the computer aided analysis of thermophysical data for pure supercritical fluids is based on the monomer fraction density [10] as the main variable for series expansions of the equilibrium thermophysical values. The widely used in science and practice virial equations are useful tools to generalize the experimental data. But they do not provide a clear physical interpretation of the virial coefficients. Their arguments, pressure P or density D, are the mixtures of partial quantities Pn, Dn related to n-particle cluster fractions. It does not permit to apply the Mass action law to cluster fractions in pure fluids.
2.1. The Monomer Fraction Density as the Argument for Series Expansions
To provide the extraction of the molecular interaction parameters [11] of the fluid under investigation from the thermophysical data, the chemical thermodynamics principles, applied to a pure fluid, require basing on the variable related to the monomer fraction, such as the monomer fraction density. The monomer fraction density is the analogue of the fugacity in the density measurement and can be found from the Equation (1) [10]:
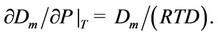 (1)
(1)
This Equation is valid for any pressure, but its integration requires small values both for the initial pressure and for the digital processing step [10,11]. A typical result of the Dm computation is shown on the Figure 1.
The Figure 1 shows a great difference between the total density D and the partial monomer fraction density, Dm, at near critical and supercritical pressures. Therefore,

Figure 1. The monomer fraction density Dm (thin line) as compared to the total density D (thick line) and the ideal gas density Dp = P/RT (dashed line) for CO2 at the supercritical temperature T = 310 K.
the results of series expansions of thermophysical values by powers of D and Dm are quite different.
2.2. The Ridge at the Transition between the Gas-Like and Liquid-Like Structures
In this investigation the supercritical fluid is studied in the zone between the critical Pc and the ridge pressure Pr. But to come to this zone we should also carefully study the real gas in the zone from zero to critical pressure. The computation of the clusters’ bond parameters is performed step-by-step from small to larger clusters. This process stops near the ridge pressure Pr. Over the ridge pressure quite other mechanisms govern the properties of the liquid-like fluid that is better to name as the foamlike fluid.
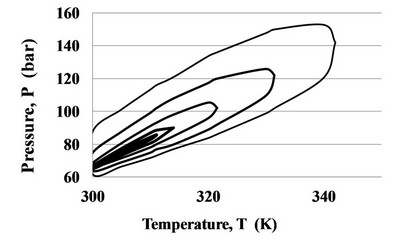
The top line of the ridge pressure Pr (T) grows with temperature in coordinates T-P and is the extension of the saturation curve Psat (T), while on the plane T-D the top line of the ridge density Dr (T) in CO2 is close to Dc = 10.6249 mol/l (Figure 2).
The structure of the supercritical fluid at pressures lower the ridge pressure consists of different size clusters flying in vacuum, but over the ridge pressure the picture is quite contrary: the structure is foam-like and contains pores of different sizes spread in the continuous liquid media [7], Figure 3. At the ridge pressure the average densities of both structures become equal and there coexist large regions with the gas-like structure and large
 (a)
(a) (b)
(b)
Figure 2. The ridge in CO2 in coordinates T-P (a) and T-D (b), built by lines of constant Cp equal to: 900, 500, 300, 200, 150 J/mol K.
regions with the foam-like structure. It gives rise to the giant fluctuations of density, directly measured in works of Dr. K. Nishikawa and her group [4-6].
2.3. The Method to Find the Molecular Interaction Parameters
To estimate the molecular interaction parameters, the author recommends using the density UD of the potential energy U. In our phenomenological approach the potential energy U of the fluid can be defined as the difference between the internal energies E at the existing pressure P and zero pressure: U = E(T, P) – E(T, 0). Figure 4 shows a typical pressure dependence of the U (P) in CO2 at T = 310 K.
To understand the physical sense of the potential energy density UD it is useful to compare it with the material density ρ, measured in kg/l, for a mixture of gases with molecular weights Mi and molar densities Di:

The potential energy density UD in pure real gases and gas-like supercritical fluids is given by a similar formula:

Here Dn are the molar densities of n-particle cluster fractions and En—the bond energies of the n-particle

Figure 3. The supercritical fluid structures at pressures lower the ridge pressure (left) and over the ridge pressure (right).
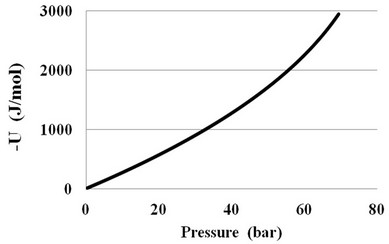
Figure 4. The pressure dependence of the potential energy in CO2 at supercritical T = 310 K.
clusters. The En values may change with temperature due to the changing of the predominant isomer configurations in cluster fractions [11]. The partial potential energies of the n-particle clusters in a unit volume are:
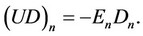
The (UD)n values are the n-power terms of the potential energy density UD series expansion by the monomer fraction density Dm. The series expansion of UD starts from the second power, because the monomers do not contribute in the potential energy density.
The bond energies En of clusters in real gases and supercritical fluids are the averaged energies of the clusters decomposition on monomers. Unlike molecules with a wide separation of quantum levels, the clusters possess densely spaced levels of bound states [11] and their energy of bonding fluctuates both in time and in a plurality of clusters with the same number of particles. Therefore, our analysis can provide only the averaged values for bond energies of n-particle cluster fractions.
To find the En values we use the series expansion coefficients  and plot the logarithm of the Kun (T) versus the reverse temperature. In the zone of temperatures, where the graph is linear, the slope of the line gives the cluster bond energy in K (Figure 5).
and plot the logarithm of the Kun (T) versus the reverse temperature. In the zone of temperatures, where the graph is linear, the slope of the line gives the cluster bond energy in K (Figure 5).
The found so pair interaction energy in CO2 slightly grows to lower temperatures and reaches the value of E2 = 352 K near the triple point. It tells about some hindering of the molecular rotation in CO2 dimers at low temperatures.
It is useful to note that the found estimations for the pair bond energy in the CO2 gas give values exceeding the critical temperature value by 10% - 15%. But in the typical wan der Waals gases, such as noble gases or Nitrogen, the pair bond energies measured in K are much lower than their critical temperatures [11]. So, the Carbon Dioxide gas in this respect stays between the wan der Waals gases and the polar gases. For example, in the polar gas, Water vapor, the pair bond energy is two-three times larger than the critical temperature [11]. It tells about a noticeable influence of the atomic charges in CO2
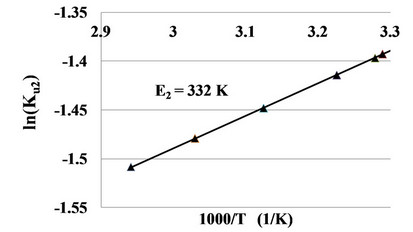
Figure 5. Estimation of the bond energy, measured in K, (E2 = 332 K) at supercritical temperatures 304 - 340 K for dimers in the carbon dioxide real gas.
on the molecular interaction, in spite of the zero polar moment in the symmetric molecule of CO2.
3. Two Classes of Clusters in the Supercritical Carbon Dioxide
To find the expansion coefficients Kun at a fixed temperature T we expand by powers of Dm the function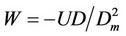 . In this function all clusters are taken into account together with dimers.
. In this function all clusters are taken into account together with dimers.
3.1. The Approach to the Reverse Mathematical Problem via the Reverse Function
The extraction of the molecular interaction parameters from experimental data is the reverse mathematical problem suffering from errors in initial data and in algorithms of the data processing. The thermophysical data from the NIST database [3] are very precise and mutually correlated. In this research special measures have been taken to diminish the influence of the initial and digital processing errors on the final results.
First, we find the limit of the function W at zero density, Ku2. The constant Ku2 is the second series expansion coefficient of the potential energy density. Then, we divide Ku2 by W and notice that in CO2 the received so graph possesses a long linear part at Dm < 1 mol/l and supercritical temperatures, Figure 6.
The reverse W−1 (Dm) function makes easier the analysis of the cluster structure near the ridge. Instead of extra large and nonlinear dependence of the W (Dm) in the supercritical region (Figure 7) we have a simple, almost linear graph (Figure 6) with deviations from linearity having a clear physical sense.
The soft structural transition is reflected on this diagram by the transition of the graph line to lower values of its tangent of slope. The growth of tangents of slope near Dm = 2 mol/l at T = 310 K means a large contribution of tightly bound, densely packed, clusters in the potential energy. The further is the temperature from the critical one, the smoother is the transition and the lower is the influence of the attraction forces between molecules. At
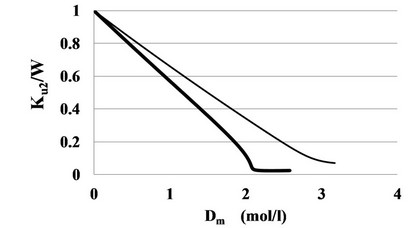
Figure 6. The close to linear dependence of the reverse W−1 function at Dm < 1 mol/l in CO2 and at supercritical temperatures: 310 K (thick line); 340 K (thin line).

Figure 7. The pressure dependence of the W function (thick line) and its components: Wl (thin line) and Wd (dashed line) at supercritical temperature T = 305 K.
T = 340 K the deviation to larger tangents almost vanishes that tells about the domination of the repulsion forces between molecules over attraction forces near Dm = 3 mol/l.
The linear dependence of the W−1 at Dm < 1 mol/l has a form Ku2/W = (1 – V3Dm), where V3 (T) is the three-particle interaction effective volume. This dependence, if extrapolated to larger values of Dm, creates the linear function Ku2/Wl for all range of possible Dm values: Ku2/Wl = (1 – V3 Dm). The function Wl (Dm) describes the contribution in the potential energy of slightly bound clusters that may be named as the loose clusters.
3.2. The Loose and Dense Cluster Fractions in Supercritical CO2
The linearization of the 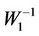 function permits us to use the geometric progression to find the series expansion coefficients for all class of n-particle loose clusters. They possess a universal interaction law for every new molecule with the (n – 1)-particle cluster. This universal interaction starts from the 3-particle cluster having not more than two bonds of the third molecule to a dimer.
function permits us to use the geometric progression to find the series expansion coefficients for all class of n-particle loose clusters. They possess a universal interaction law for every new molecule with the (n – 1)-particle cluster. This universal interaction starts from the 3-particle cluster having not more than two bonds of the third molecule to a dimer.
Therefore, all n-particle loose clusters in their class are formed by binding of a monomer molecule to the existing (n – 1)-particle cluster by not more than two bonds. This structure of clusters does not use all possible bonds between molecules and is really loose. Their contribution to the W (Dm) function, Wl (Dm), is shown by the thin line on the Figure 7. At this stage of investigation it is not possible to suggest a clear configuration of the loose clusters. For that it is needed to study the bond parameters for loose clusters in a row of gases just to understand the basic principles of their aggregation.
The difference between W and Wl corresponds to the contribution in the potential energy of the tightly bound clusters with a dense structure. This part of the W (Dm) is named here as Wd (Dm). The class of dense clusters becomes significant only at pressures approaching the ridge value.
The analysis of the Wd (Dm) function reflecting the contribution of dense clusters in the total potential energy of the CO2 supercritical fluid gives the expansion coefficients Kund for dense cluster fractions. Unlike the class of loose clusters with all numbers of particles in clusters, the class of dense clusters has a jumping row of numbers. For example, at T = 305 K a noticeable contribution in the potential energy seems to be provided by the dense clusters with numbers of particles: 7, 12, 24, 56, 143, 372, 1086. So, the supercritical CO2 near the critical point contain nanosized densely packed clusters with a wide distribution of their dimensions. The bond structure of dense clusters also should be studied later.
3.3. The Estimation of the Average Numbers of Molecules in Dense Clusters
The energetically averaged number of particles in the class of dense clusters at this temperature and at the ridge pressure estimated by the method, described later, is 283. Their share in the potential energy of the supercritical CO2 is as large as 70% at T = 305 K and P =Pr.
A very steep growth of the Wd (Dm) function near the ridge complicates the computation of the dense clusters’ parameters. But there is the way to find the averaged characteristics of clusters in the dense class.
For that we analyze the interdependence between logarithms of Dm and Wd. The differentiation of ln (Wd) by ln (Dm) provides a satisfactory estimation of the energetically averaged number of particles in the class of dense clusters Nav at every density (Figure 8).
The Figure 8 shows that quite near the critical point there is a steep growth of the averaged number of particles in the class of dense clusters when the density approaches its critical value. At T < Tc the maximal value of this number is limited because the saturation density becomes significantly smaller than Dc.
At T = 310 K the maximal value of the averaged number is also smaller than at T = 305 K, but in this case because of the growing role of intermolecular repulsions. At the density over the critical density the Nav (D) de-
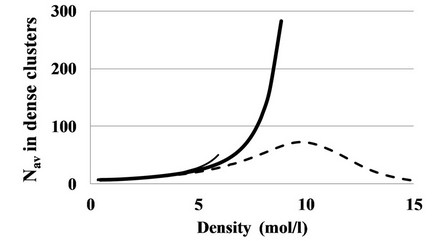
Figure 8. The density dependence of the energetically averaged numbers of particles Nav in the class of dense clusters in CO2 at temperatures: 300 K (thin line), 305 K (thick line) and 310 K (dashed line).
pendence looks like the clusters become smaller. It is not so: in this case not clusters, but the pores, become smaller in the foam-like structure. So, there is a hope to penetrate through the ridge to the liquid-like structure with our analysis. But it requires the further development and verification of the monomer fraction based series expansion method for this range of densities.
4. Conclusions
• The monomer fraction density based analysis of precise thermophysical data for pure fluids provides the physically clear picture of complex molecular structures in supercritical fluids in general and in Carbon Dioxide in particular.
• The potential energy density, if expanded in series by powers of the monomer fraction density, may provide information about the cluster fractions’ populations in real gases and supercritical fluids and the clusters’ bond energies.
• The comparison of the pair molecular interaction bond energy in CO2, expressed in K, with the value of critical temperature shows that CO2 stays between typical wan der Waals and polar gases.
• The separation of clusters in the CO2 real gas and supercritical fluid between classes of loose and dense clusters provides a vision of the cluster structures for both classes.
• In the supercritical CO2 near the ridge the energetically averaged number of particles in clusters of the dense class quickly grows due to attraction forces in the gas-like supercritical fluid, but over the ridge density this number falls due to growing role of repulsion forces between molecules in the liquid-like supercritical fluid.
REFERENCES
- M. A. McHugh and V. J. Krukonis, “Supercritical Fluid Extraction: Principles and Practice,” Butterworth Publishers, Stoneham, 1986.
- L. T. Taylor, “Supercritical Fluid Extraction,” John Wiley & Sons Ltd., New York, 1996.
- NIST, “Thermophysical Properties of Fluid Systems,” 2012. http://webbook.nist.gov/chemistry/fluid
- K. Nishikawa and T. Morita, “Inhomogeneity of Molecular Distribution in Supercritical Fluids,” Chemical Physics Letters, Vol. 316, No. 3, 2000, pp. 238-242. doi:10.1016/S0009-2614(99)01241-5
- K. Nishikawa, et al., “Raman Spectral Changes of Neat CO2 across the Ridge of Density Fluctuation in Supercritical Region,” Chemical Physics Letters, Vol. 320, No. 3-4, 2000, pp. 323-327. doi:10.1016/S0009-2614(00)00249-9
- K. Nishikawa, et al., “Local Density Enhancement in Neat Supercritical Fluid Due to Attractive Intermolecular Interactions,” Chemical Physics Letters, Vol. 368, No. 1-2, 2003, pp. 209-214. doi:10.1016/S0009-2614(02)01851-1
- B. Sedunov, “Structural Transition in Supercritical Fluids,” Journal of Thermodynamics, Vol. 2011, 2011, Article ID: 194353, 5 p.
- B. Sedunov, “Soft Phase Transition in Supercritical Fluids,” The 21st IUPAC International Conference on Chemical Thermodynamics, Tsukuba, 2010, p. 104.
- B. Sedunov, “Soft Structural Transitions in Fluids,” The 22nd International Conference on Chemical Thermodynamics (ICCT) and the 67th Calorimetry Conference (CALCON), Buzios, 2012.
- B. Sedunov, “Monomer Fraction in Real Gases,” International Journal of Thermodynamics, Vol. 11, No. 1, 2008, pp. 1-9.
- B. Sedunov, “Equilibrium Molecular Interactions in Pure Gases,” Journal of Thermodynamics, Vol. 2012, 2012, Article ID: 859047, 13 p.

