ABSTRACT

This is the first paper in a two part series on black holes. In this work, we concern ourselves with the event horizon. A second follow-up paper will deal with its internal structure. We hypothesize that black holes are 4-dimensional spatial, steady state, self-contained spheres filled with black-body radiation. As such, the event horizon marks the boundary between two adjacent spaces, 4-D and 3-D, and there, we consider the radiative transfers involving black-body photons. We generalize the Stefan-Boltzmann law assuming that photons can transition between different dimensional spaces, and we can show how for a 3-D/4-D interface, one can only have zero, or net positive, transfer of radiative energy into the black hole. We find that we can predict the temperature just inside the event horizon, on the 4-D side, given the mass, or radius, of the black hole. For an isolated black hole with no radiative heat inflow, we will assume that the temperature, on the outside, is the CMB temperature, $T_2=2.725\text{K}$ . We take into account the full complement of radiative energy, which for a black body will consist of internal energy density, radiative pressure, and entropy density. It is specifically the entropy density which is responsible for the heat flowing in. We also generalize the Young-Laplace equation for a 4-D/3-D interface. We derive an expression for the surface tension, and prove that it is necessarily positive, and finite, for a 4-D/3-D membrane. This is important as it will lead to an inherently positively curved object, which a black hole is. With this surface tension, we can determine the work needed to expand the black hole. We give two formulations, one involving the surface tension directly, and the other involving the coefficient of surface tension. Because two surfaces are expanding, the 4-D and the 3-D surfaces, there are two radiative contributions to the work done, one positive, which assists expansion. The other is negative, which will resist an increase in volume. The 4-D side promotes expansion whereas the 3-D side hinders it. At the surface itself, we also have gravity, which is the major contribution to the finite surface tension in almost all situations, which we calculate in the second paper. The surface tension depends not only on the size, or mass, of the black hole, but also on the outside surface temperature, quantities which are accessible observationally. Outside surface temperature will also determine inflow. Finally, we develop a “waterfall model” for a black hole, based on what happens at the event horizon. There we find a sharp discontinuity in temperature upon entering the event horizon, from the 3-D side. This is due to the increased surface area in 4-D space, $A_R^{\left(4\right)}=2{\text{π}}^2{R}^3$ , versus the 3-D surface area, $A_R^{\left(3\right)}=4\text{π}{R}^2$ . This leads to much reduced radiative pressures, internal energy densities, and total energy densities just inside the event horizon. All quantities are explicitly calculated in terms of the outside surface temperature, and size of a black hole. Any net radiative heat inflow into the black hole, if it is non-zero, is restricted by the condition that, $0<1/c\text{d}Q/\text{d}t<4F_R^{\left(3\right)}$ , where, $F_R^{\left(3\right)}$ , is the 3-D radiative force applied to the event horizon, pushing it in. We argue throughout this paper that a 3-D/3-D interface would not have the same desirable characteristics as a 4-D/3-D interface. This includes allowing for only zero or net positive heat inflow into the black hole, an inherently positive finite radiative surface tension, much reduced temperatures just inside the event horizon, and limits on inflow.

Keywords:

Black Holes, 4-D Spatial Balls, Black Body Radiation, Stefan-Boltzmann Law, Young-Laplace Relation

1. Introduction

Black holes are mysterious objects about which we still know very little. They have long intrigued physicists and fascinated the general public ever since they were first proposed [1]. Now, however, there is compelling and mounting evidence that they do, in fact, exist [2] [3] [4]. Catalogues of observed black hole candidates have been constructed, are readily available [5], and are typically ranked according to their mass and distance from the earth. However, we still know very little about what they consist of, how they are structured internally, and what holds them together. Gravity, of course, plays a central role and the strong gravity which they produce, being very compact and massive objects, prevents photons from escaping once the event horizon has been reached. The photons, upon reaching the event horizon, simply do not have the requisite escape velocity being constrained to move at the speed of light. And so, there is no radiative heat outflow, or very little if we believe in black hole evaporative processes. The interior temperature of a black hole must also be quite low for otherwise they would not appear black, and yet they pack a considerable amount of mass/energy within a relatively small volume. What happens to the photons, and in-falling matter, once they enter the black hole? Is all information and identity lost, often referred to as information loss paradox? Is there a singularity at the center of a black hole, as many suspect? Can this lead to worm holes, and white holes? These are all questions, which remain to be answered.

The event horizon, in particular, is a complete mystery. This interface must have certain characteristics, which allow for net radiative heat inflow but zero (or very little) heat outflow. It must be a relatively stable structure because it can withstand tremendous gravitational forces. And yet, it can, and does expand upon massive and massless particle inflow. It seems to function as a sort of membrane, almost bubble like in character. There must be internal forces pushing out, which prevent complete collapse due to gravity. With or without inflow, there is a tremendous mass packed within a very small volume. How is that mass distributed, and what prevents complete implosion? Is there really a rip or tear in the space-time continuum at the center of a black hole, as is commonly thought?

A third central question is why do black holes have a much reduced temperature within their interiors? As such, would they not continuously swallow up the surrounding CMB radiation? There is also dark matter and dark energy. All are in direct contact with the event horizon, and all have been in direct contact since black holes were formed. Why does a black hole not feed upon this continuous and plentiful source of matter/energy? One would think that due to the ambient mass/energy, a black hole would expand continuously. And, that expansion would have been much more pronounced in earlier cosmological epochs, when the CMB temperature was much, much higher, and the universe was much more compact. The standard argument is that this inflow would lead to very small effects, numerically, and therefore does not contribute significantly to expansion. Also, the rip or tear at the center of a black hole would prevent temperature from building up within its interior. We will argue, however, that there is no rip or tear at the center of a black hole. Instead, there must be a barrier of sorts which prevents permanent inflow of CMB photons and other pervasive forms of mass/energy surrounding the black hole. Having very low temperatures on the inside, the standard 3-D Stefan-Boltzmann law would not prevent black holes from permanently absorbing CMB photons, and bringing the black hole temperature up to CMB temperatures.

We can take this a step further. If the CMB temperature is the lowest possible temperature since formation of the universe, and if black holes are in constant thermal contact with the cosmic background, then how could they form, and evolve, at a lower temperature? We believe this is a valid argument against the permanent inflow model, which we will sometimes refer to as the PIM model. The permanent inflow model cannot be disproven, or proven, observationally, because, as stated, the effects are numerically small, at least in the present epoch. Expansion would not be measurable. Logically, however, we think that the PIM model makes little sense. Unless there is a mechanism, which would force the temperature out of the black hole, we believe in a natural barrier to entry. Our thinking is that, black holes, being 4-D spatial objects, have an inherently lower temperature on the inside, at least close to its surface, which is near the event horizon. We also believe that true isolated, static black holes, can exist. In fact this is the basic assumption behind our two papers. From this, we can show that, then, we have either no net radiative heat inflow, $\text{d}Q/\text{d}t=0$ , or, positive net radiative heat inflow, $\text{d}Q/\text{d}t>0$ , but now between 3-D/4-D space. Radiative heat flowing out of the black hole is not possible other than through evaporative processes such as Hawking radiation. In this regard, it can be noted that, observationally, orbiting stars around black hole candidates seem to have stable orbits. Isolated, static black holes would certainly conform to this picture.

We will make two central assumptions in both papers, other than a black hole being a 4-D object. The first is that isolated, static black holes are not only possible, but likely. In fact, we will assume they must exist. And the second assumption will be that the CMB temperature can be used to find the temperature just inside the event horizon, on the 4-D side. This holds true today, as well as in earlier cosmological times. It is interesting to note that positive, net radiative heat outflow out of a black hole will not be possible given our assumptions above. It is something we can show within our model. The fact that black holes are black, observationally, demands a theoretical explanation.

To answer the questions posed above, we will make a leap of faith. We propose that black holes are 4-D spatial objects, spherically symmetric and packed with blackbody radiation, embedded in 3-D space. Their radiative mass distribution is distributed in such a way as to make them appear black. A three dimensional analogy would be liquid droplets in a gas, but here we are dealing with a 4-D droplet, and, furthermore, as it will turn out, not of uniform density. We can imagine black holes to be droplets of 4-D radiation, to be precise, within a greater 3-D universe. The event horizon is the interface between 4-D space and 3-D space. This is where the rip or tear in the space-time continuum occurs, and not at the center of the black hole, as commonly thought. Indeed, as we shall see in the follow up paper, the black hole is well-behaved within its interior and has no singularity at its center. While at first sight, this interpretation may seem fanciful and even far-fetched, we will soon see that certain characteristics emerge within this picture, which seem to make sense. It is the goal of this paper, and the follow-up paper, to show that this hypothesis may have some validity.

We will build our model with two papers. The first work, this paper, deals with the event horizon itself. The second paper, which follows this, will deal almost exclusively with the internal structure of a black hole. Both papers are lengthy and involve a considerable amount of formulae. However we believe this to be necessary in order to make a convincing case, which will support this novel hypothesis.

Interestingly, as we develop our model, we will also show that a black hole cannot be a 3-D ball packed with black-body radiation, or for that matter, a 2-D construct. There are several reasons for this, the most important of which are the following. We list these in bullet form.

1) 2-D and 3-D balls of blackbody radiation cannot pack the requisite amount of radiative mass in such a small volume. The temperatures would have to be incredibly large, even at the surface of a black hole.

2) 3-D objects will not allow for a natural discontinuity at the interface, which is needed to define a radiative surface tension. A finite, positive surface tension is required to define a curved object in space, which a black hole inherently is.

3) A 3-D object cannot guarantee that there is no net heat outflow whereas a 4-D object can.

4) 3-D/3-D radiative transfers of energy cannot allow for substantially lower surface temperatures within the black hole event horizon, which is just underneath the surface.

5) 3-D/3-D transfers of radiative energy will not allow for much reduced radiation pressures, internal energy densities, entropy densities, and total energy (radiative mass) densities, etc. just inside the event horizon. These quantities, incidentally, will all increase dramatically within the black hole itself, as one approaches, $r\to 0$ , in order to pack in the required radiative mass.

6) 3-D/3-D interfaces will not prevent CMB photons, and other pervasive forms of matter/energy surrounding a black hole, from being continuously pulled in. With our 4-D/3-D model we can provide a barrier, or lip, which prevents permanent inflow and expansion of a black hole. In fact, the outside 3-D surface temperature, $T_2=2.725\text{K}$ , will serve as an input in order to define an equilibrium temperature for a black hole, on its inside surface, when there is no inflow. This is what we will call an isolated, static black hole. For temperatures, $T_2>2.725\text{K}$ , we will have radiative heat inflow, i.e., $\text{d}Q/\text{d}t>0$ , the amount of which will depend on the value of $T_2$ . We reserve temperature, $T_1$ , for the temperature just inside the event horizon, on the 4-D side. This will always be substantially lower than the temperature just outside the event horizon, with or without radiative inflow.

There are other reasons for settling on a 4-D/3-D interface, but these will be among the most important.

It has not gone unnoticed that black holes appear, and act very much like balls of blackbody radiation [6] [7]. Moreover, it is also known that blackbody radiation was the primordial substance in the early universe [8] [9] [10] [11]. It filled essentially all of space, and it has been conjectured that the particles in the standard model “froze-out”, each at a particular temperature, as the universe cooled [12] [13] [14]. For energies above, 1 TeV, corresponding to a background temperature in excess of 10¹⁶ K, all particles in the standard model are relativistic, i.e., in the form of radiation. Thirdly, the concept of ball lightning (Kugelblitz in German) has been applied to blackbody radiation and, in particular, to the formation of black holes. The idea is that the black body radiation is so concentrated in intensity that it curves that space-time itself around it, and forms a black hole [15] [16] [17]. A black hole is thus a ball of radiation which gives it its radiant mass. John Wheeler [16], himself, already in 1955, even explored the notion of creating elementary particles in this way. We will also allude to this as a possible mechanism for producing “elementary particles”. So the basic ideas presented in this paper have been thought of before. What is new here is the hypothesis that the black hole is, in reality, a 4-D spatial object, filled with blackbody radiation, and possibly other radiations. As such, the temperature does not have to exceed the Planck temperature. Far from it, as we shall see. We will also show in our second, follow-up work how to pack that radiation. This is also novel. We will introduce a probability distribution function to pack the required radiative mass, and still keep the inside surface temperature, just inside the event horizon on the 4-D side, very low. The black hole will therefore not emit radiation, other than through mechanisms such as Hawking radiation.

There have been 2-D models proposed for black holes, so-called holographic models [18] [19] [20]. This ties in to the work done by Bekenstein [21] [22], and others relating to black hole entropy. The entropy is calculated in terms of the 3-D black hole surface area, as multiples of Planck area, so-called Plankions. Such models predict enormous amounts of entropy associated with a black hole; in fact, using such calculations, most of the entropy in the universe is in the form of black hole entropy [23] [24] [25] [26]. Supermassive black holes contribute, by far, the most entropy. We do not believe entropy to be an intrinsic variable, dependent on surface area. Rather, we think that entropy is an extrinsic variable, dependent on volume. Moreover, it is a 4-D volume we should be considering, and integrating over. In the follow up paper, we calculate the total entropy associated with a black hole. For a black hole having the mass of the sun, the entropy in our model is calculated to be only 1.63 × 10³⁷ J/K. This is only about 2 orders of magnitude greater than the entropy of the sun itself, which is approximately, 10³⁵ J/K. The Bekenstein model gives the entropy as, $S_{\text{Bekenstein}}=\left(1/4\right)c^3{k}_B/\left(G\hslash \right)\left(4\text{π}{R}^2\right)$ , which for a black hole of one solar mass gives, 1.50 × 10⁵⁴ J/K. His entropy is much greater than that of the sun by almost nineteen orders of magnitude! Moreover, the Bekenstein entropy scales as, $S_{\text{Bekenstein}}~R^2$ . Our entropy also scales appreciably, comparable to, $R^2$ , but not according to a clear power law. If our model is correct, a black hole is thus a highly-ordered state, contrary to what current consensus claims. The calculation will be presented in the follow-up paper for several black holes, each with a different mass.

In this paper, and the next, we will ignore/discount Hawking radiation [27] [28] [29] [30]. While it may exist, we proceed as if it does not. Other evaporative or leakage processes such as quantum mechanical tunneling [31] [32] [33] through the event horizon will also be ignored. Should they exist, they will be 2^nd order corrections, at best, to the results presented here. The temperatures just inside the event horizon within our model will be shown to be considerably higher than the Hawking temperature, which is given by the formula, $T_H=\hslash c^3/\left(8\text{π}GM{k}_B\right)$ . Nevertheless, the inside surface temperatures will still be much less than they are on the outside. Moreover, within the black hole itself, those same 4-D temperatures will increase dramatically as one approaches the interior of the 4-D black hole. At the very center of the black hole, at, $r=0$ , we theorize that we will have a maximum but finite radiative energy density for a finite volume.

The outline of the paper is as follows. In Section 2, we consider the 4-D/3-D interface, and generalize the Stefan-Boltzmann law to account for radiative energy transfers between different spaces. We show that radiative heat energy density is not the only component, which transfers. When transferring between spatial dimensions, other forms of radiative energy flow, such as internal energy density and radiative pressure. It is an all or nothing proposition. To maintain the blackbody identity of the photons at a particular temperature, all components, or none, carry over. In this section, we will prove that there can only be positive radiative energy inflow into the black hole once the event horizon is reached, or none. In Section 3, we consider the expansion of a black hole upon net inflow of radiation. We define the surface tension and model the event horizon as an infinitely thin membrane, a bubble of sorts. We derive key relations for the work done, in terms of surface tension and coefficient of surface tension. Because there are two surfaces expanding, the four-dimensional and the three-dimensional, we must take both into account for radiation. Then there is also gravity, which will also want to prevent the 4-D surface from expanding in size. This is included although the specific details will be worked out in the subsequent paper. In this section we generalize the Young-Laplace equations for an interface separating two different spaces, one 3-D and the other 4-D.

In Section 4, we build upon the ideas developed in sections II and III. We show that there is a sharp discontinuity in temperature when crossing the 3-D/4-D threshold. This discontinuity is due to the discontinuity in space itself, because in going from the 3-D world to the 4-D space, the surface area increases abruptly and dramatically, from, $A_R^{\left(3\right)}=4\text{π}{R}^2$ , to $A_R^{\left(4\right)}=2{\text{π}}^2{R}^3$ , for the same radius, R. This discontinuity in surface area leads to a precipitous drop in temperature just inside the event horizon. Moreover, this will translate into decreased internal energy densities, reduced radiative pressures, and much smaller entropy densities just inside the black hole. All these quantities will depend on the outside radiative temperature and the size, or mass, of the black hole. In this section, we present our so-called “waterfall model” for the event horizon of a black hole. The summary and conclusions are highlighted in Section 5, our final section. Finally we have an appendix (Appendix A), where we consider non-spherical symmetry, and the emission of quadrupole gravitational radiation. We show that our model can be extended to this situation, and we work out a few numerical examples.

2. Generalization of the Stefan-Boltzmann Law

We start with the radiative flux emitted in N-dimensional space. As is known [34], a blackbody at temperature, T, emits a radiative flux, sometimes called radiancy, ${\Phi }^{\left(N\right)}\left(T\right)$ , given by

${\Phi }^{\left(N\right)}\left(T\right)=\text{d}Q/\text{d}t1/A^{\left(N\right)}={\sigma }^{\left(N\right)}{T}^{N+1}$ (2-1)

In this equation, dQ stands for the amount of radiative heat emitted in time, dt, and the superscript, (N), refers to the number of spatial dimensions. The surface area in N-dimensional space, $A^{\left(N\right)}$ , is that area through which radiative energy can escape, and ${\sigma }^{\left(N\right)}$ is the Stefan-Boltzmann constant, generalized to N-spatial dimensions. The hyper-surface, $A^{\left(N\right)}$ , in Equation (2-1), can be calculated using the formula [35] [36],

$A^{\left(N\right)}=A^{\left(N\right)}\left(R\right)=2{\text{π}}^{N/2}{R}^{N-1}/\Gamma \left(N/2\right)$ (2-2)

In Equation, (2-2), R is the radius in N-space, and $\Gamma \left(x\right)$ is the gamma function. We assume spherical symmetry for this self-contained ball of blackbody radiation. The generalized Stefan-Boltzmann constant, ${\sigma }^{\left(N\right)}$ , in Equation (2-1), is determined by the following formula [34],

${\sigma }^{\left(N\right)}={\left(2/c\right)}^{N-1}{\left(\sqrt{\text{π}}\right)}^{N-2}\left(k_B^{N+1}/h^N\right)N\left(N-1\right)\Gamma \left(\frac{N}{2}\right)\zeta \left(N+1\right)$ (2-3)

In this equation, $k_B$ is Boltzmann’s constant, c equals the speed of light, h is Planck’s constant, $\zeta \left(x\right)$ is the zeta function, and $\Gamma \left(x\right)$ is, again, the gamma function.

In 4-D space, Equation (2-2) gives, $A_R^{\left(4\right)}=2{\text{π}}^2{R}^3$ , whereas in 3-D space, we obtain the familiar $A_R^{\left(3\right)}=4\text{π}{R}^2$ . We can also determine the values for the Stefan-Boltzmann constants, in 4-dimensional, 3-dimensional and 2-dimensional space. Using Equation, (2-3), we obtain numerically

${\sigma }^{\left(4\right)}=3.021\times {10}^{-5}\text{Watts}/\left({\text{m}}^3\cdot {\text{K}}^5\right)$ (2-4a)

${\sigma }^{\left(3\right)}=5.670\times {10}^{-8}\text{Watts}/\left({\text{m}}^2\cdot {\text{K}}^4\right)$ (2-4b)

${\sigma }^{\left(2\right)}=9.614\times {10}^{-11}\text{Watts}/\left(\text{m}\cdot {\text{K}}^3\right)$ (2-4c)

We will be using MKS units throughout this paper, even when not explicitly written out. The radiative flux, ${\Phi }^{\left(N\right)}$ , is measured in Watts/m^N in Equation, (2-1). The emissivity factor will always be taken as unity as we are assuming a perfect blackbody. All superscripts in parenthesis, next to a quantity, will refer to the number of spatial dimensions over which the quantity is defined.

We use Equation (2-1), as our basic starting point, to find the radiative transfer of heat energy between adjoining spatial dimensions. For a 3-D to 4-D spatial transfer of radiative energy, we may claim that, using this equation,

$\text{d}Q/\text{d}t=\text{d}{Q}^{\left(3\right)}/\text{d}t-\text{d}{Q}^{\left(4\right)}/\text{d}t=A^{\left(3\right)}{\sigma }^{\left(3\right)}{T}_2^4-A^{\left(4\right)}{\sigma }^{\left(4\right)}{T}_1^5$ (2-5)

In this expression, $\text{d}{Q}^{\left(3\right)}/\text{d}t$ , is the radiative heat power exiting the 3-D space and entering the 4-D space. The quantity, $\text{d}{Q}^{\left(4\right)}/\text{d}t$ , on the other hand, is the radiative heat power exiting the 4-D space and entering the 3-D space. The temperature, $T_2$ , is the temperature just outside the black hole, in 3-D space. We define the temperature, $T_1$ , as the temperature just inside the event horizon, in 4-D space. The respective surface areas are found using Equation, (2-2). Equation, (2-5), is a direct extension of Equation, (2-1), and we call this the first generalized version of the Stefan-Boltzmann equation for radiative transfers between adjoining spatial dimensions. We note that even though surface areas, $A^{\left(3\right)}$ , and, $A^{\left(4\right)}$ , have differing units, Equation, (2-5), is dimensionally consistent. We will assume that the event horizon is infinitesimally thin, and as such, the temperatures, $T_1$ , and, $T_2$ , are defined at effectively the same radius, just on different sides of radius, R.

It is obvious from relation, (2-5), that $\text{d}Q/\text{d}t$ will be positive if the first term on the right hand side exceeds the second. If $\text{d}Q/\text{d}t>0$ , then we will have net inflow. For a black hole, we can prove that this is the only possibility, other than $\text{d}Q/\text{d}t=0$ . We will, however, have to assume a 4-D/3-D interface. We will designate a black hole with no net inflow as an isolated, static black hole (ISBH). If there is net inflow, we call that a dynamic black hole (DBH). We called the temperature just outside the event horizon, on the 3-D side, $T_2$ . For $T_2$ , we will assume a temperature of 2.725 K if the black hole is an ISBH. In other cosmological epochs, this temperature would have to be modified. For a DBH, the temperature on the outside will be larger than the CMB temperature. In Equation, (2-5), $T_1$ , is the temperature just inside the event horizon, within the black hole on the 4-D side. As will be seen shortly, this temperature is determined by the radius of the black hole, or what is equivalent, by its mass. Because of the Schwarzschild condition, $R=2GM/c^2$ , the two quantities are proportional. We will often make use of the Schwarzschild relation throughout this paper without explaining it. In practice, $T_2$ , can be quite large. Due to friction and superheating of massive and massless inflows, the temperatures can reach X-ray temperatures, 1.16 × 10⁶ K to 1.16 × 10⁹ K for soft and hard X-rays, and higher. These X-ray emissions would correspond to photon energies from a few MeV to a few GeV. Emissions of this type are readily discernable, observationally, if not too far away. Black hole masses, and thus radii, can also be estimated in many instances. This will give us enough information to calculate the specific amount of inflow using Equation, (2-5). For the temperature, $T_1$ , we assume an equilibrium temperature, calculated as if the black hole had no inflow. This quantity is based strictly on the size, or mass, of the black hole, which at the moment of inflow has a unique value.

Focusing further on Equation, (2-5), we specialize to the case where there is no inflow. In this instance, $\text{d}Q/\text{d}t=0$ , and Equation, (2-5), reduces to

$A^{\left(4\right)}{\sigma }^{\left(4\right)}{T}_1^5=A^{\left(3\right)}{\sigma }^{\left(3\right)}{T}_2^4$

$2{\text{π}}^2{R}^3{\sigma }^{\left(4\right)}{T}_1^5=4\text{π}{R}^2{\sigma }^{\left(3\right)}{2.725}^4$

Solving for $T_1$ gives

$T_1=0.581R^{-1/5}$ (2-6)

We have used Equations, (2-4a), and, (2-4b), to obtain this simplified result. This we call the equilibrium temperature, just inside the event horizon. It is determined strictly in terms of radius, or equivalently, mass, for a specified black hole. The black hole can and will expand upon inflow. And inflow will be determined using a different and higher value for $T_2$ by means of Equation, (2-5), and this $T_1$ value. However, until such time that the black hole has expanded, the temperature to be used at the event horizon on the inside is $T_1$ , as determined by this Equation, (2-6). From Equation, (2-6), it is clear that a black hole having greater mass will have a lessor temperature just inside the event horizon.

If we consider a black hole having the mass of the sun (not realistic), then the Hawking temperature would give an inside temperature of about 62 nK. Equation, (2-6), gives a much higher inside surface temperature of 0.117 K, at the event horizon. Clearly Hawking radiation and evaporative processes are second order effects. For black holes having masses of 10 times and 10⁶ times solar mass, we obtain using Equation, (2-6), 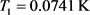, and, , respectively. These are more realistic values as black holes are required to have masses many times that of the sun.

Coming back to Equation, (2-5), in time dt, the amount of radiant heat entering the black hole is

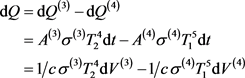(2-7)

In the third line of this equation, we made use of, 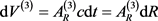, and a corresponding equation in 4-D,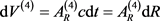. The infinitesimal volume element, , is the volume of heat leaving 3-D space, and entering the black hole, a 4-D object, in time dt. By contrast, 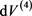, is the infinitesimal volume exiting 4-D space, the black hole, and entering 3-D space in time, dt. Because heat enters and exits at the speed of light, we set,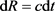. Even though we have a constant exchange of photons, back and forth, it will be seen that only zero or net positive inflow is allowed, due to the different dimensionality of adjoining spaces.

In N-dimensional space, a hyper-volume can be defined for a N-dimensional ball. The expression [35] [36] is

(2-8)

The superscript “N” in parenthesis on a physical quantity will always refer to the spatial dimension over which the quantity is defined. 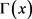is, again, the gamma function, and N equals the number of spatial dimensions. From Equation, (2-8), it follows that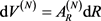, where, 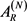, is specified by Equation, (2-2). This was utilized in Equation, (2-7). In 4-D space, Equation, (2-8), gives a volume equal to,.

The expression, Equation, (2-3), and the relations, Equations, (2-4), through to, (2-7), are not quite correct. The 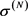coefficients are very close to being perfect, but have to be adjusted slightly. This is due to the fact that when blackbody photons transfer between spatial dimensions, it is not just internal energy density or radiative heat density, separately, which transfer. When blackbody photons transfer, the associated internal energy density, plus the radiative pressure, plus the heat density all transfer as one unit. It is an all, or nothing, proposition such that the black body identity of the photons can be maintained in both spaces. All of these quantities depend on temperature, and if temperature changes, which it does, so do all of the above at the same time. This was shown in a previous work [37], where we considered a 1^st order phase transition at a particular temperature and pressure. The situation here is totally different because, as we shall soon see, there will be an abrupt change in temperature at the event horizon. In the previous work, the temperature remained fixed when the transition occurred. Nevertheless, even though the situation is very different because we are talking about radiative transfer, versus a discontinuous phase transition, maintaining the identity of the photons in their respective spatial dimension requires that all forms of blackbody energy transfer.

To see this more clearly, let equal the total radiative energy transferred in time, dt, into the black hole from 3-D space. As argued in a previous work, it will consist of various components,

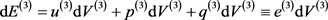(2-9)

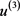In Equation (2-9), , is the total radiative energy “density”, defined loosely in terms of the internal energy density, , the radiative pressure, , and the heat energy density, , as follows,

(2-10)

Equation (2-10), really only makes sense when multiplied by a corresponding volume. We are mixing pressure, having units of N/m², with energy density, measured in J/m³, on the right hand side of Equation, (2-10), which is really only valid if we form a product with a volume. When forming a product with volume, we obtain energy and stored work, which are both measured in Joules, even though the pressure and energy density have different units. So, when we write an “equation” such as relation, (2-10), this is what is inferred.

In 4-D space we have a similar definition. Let equal the total radiative energy transferred in time, dt, from the black hole into 3-D space. It also consists of various components

(2-11)

Moreover, by definition, the total radiative energy “density” is found by using

(2-12)

In these equation, , is the 4-D internal energy density, , the 4-D radiative pressure, and, the 4-D heat density, all defined over 4-D space. Being 4-D quantities, the densities and pressures have different units than those of their 3-D counterparts. Again, Equation, (2-12), is only valid if multiplied by a corresponding volume, and this is to be tacitly assumed for an Equation, such as (2-12), to make sense.

We next note that and are related. And, so too, are, and. As is known [38] [39] [40] [41], the internal energy density in N-dimensional space is given by the following function, which depends only on temperature and the dimensionality of space, N:

(2-13)

In this equation, is Boltzmann’s constant, c equals the speed of light, h is Planck’s constant, is the zeta function, and is the gamma function. Moreover, the radiative pressure, heat density, and the entropy density, , are related to via the equations,

(2-14)

These relations depend only on the dimensionality of space, N, and the temperature, T, because is, in itself, a function of temperature and dimension. Thus, we can construct the quantity, , and define it by

(2-15)

However, by Equations, (2-14), can be written a variety of ways,

(2-16)

This implies that can be re-expressed as

(2-17)

In Equations, (2-17), is the internal energy transferred in time dt, and is the corresponding radiative heat transferred within the same time, dt. We notice that will always equal, irrespective of the number of spatial dimensions! This allows us to write

(2-18)

Using Equations, (2-16), it follows that in 3-D space,

(2-19)

In 4-D space, we find, however, that

(2-20)

Notice the different factors in both sets of equations, as they will be important. Moreover, Equations, (2-17), show us that, if,

(2-21)

If, however, the number of spatial dimensions equals, , then we find

(2-22)

We emphasize, once more, that Equations (2-10), (2-12), (2-16), (2-19) and (2-20) really only make sense when multiplied by a corresponding volume because we are mixing pressure and energy density within the same expression. Technically, these equations are only correct if we form a product with a volume, which is how we use these equations.

Coming back to Equation, (2-18), we can write this equation for the radiative heat transfer a variety of ways. We utilize Equations, (2-21), and, (2-22), and find

(2-23)

Furthermore, we keep in mind that, , and, , are the internal energy and heat energy exiting the 3-D world in time dt, and entering the black hole. The quantities, , and, , on the other hand, are the internal energy and heat energy exiting the 4-D world, and entering the 3-D world in time, dt. As such, we can write

(2-24a)

(2-24b)

(2-25a)

(2-25b)

In Equations, (2-24), and (2-25), the 3-D surface area equals, , and the 4-D surface area equals,. We next substitute the last equalities of Equations, (2-24), and, (2-25), into Equations, (2-23). We then re-arrange terms to obtain,

(2-26)

In the last line, we have defined the radiative forces at radius, R, in three and four spatial dimensions as

, (2-27a,b)

We keep in mind that, , , and are all defined in terms of a temperature just outside the event horizon,. Hence, we have the subscript “2” on. The quantities, , , and, on the other hand, are all defined in terms of, which is the temperature just inside the event horizon, within the black hole. This is reflected in the subscript “1” on. See Equations, (2-13), and, (2-14).

Next, we revisit Equations, (2-13), and, (2-3). We notice that can be rewritten in terms of,. In fact, we can prove that the radiative internal energy densities, , , and, can be reformulated as

(2-28a)

(2-28b)

(2-28c)

In Equations (2-28a)-(2-28c), the coefficients, , and are defined by what follows in their respective line. They hold in 4-dimensional, 3-dimensional and 2-dimensional space, respectively, for blackbody radiation. We include the 2-dimensional relations here for completeness, and as a matter of reference.

We substitute Equations, (2-28a), and, (2-28b), into the second line of Equation, (2-26). We thereby obtain, after multiplying through by the velocity of light, c,

(2-29)

The coefficients, and are specified by Equations, (2-4b), and, (2-4a), respectively. In Equation, (2-29), the appropriate temperatures have been denoted. Just outside the black hole, in 3-D space, we have temperature,. Within the black hole, just inside the event horizon, in 4-D space, we have temperature,. The surface areas, , and, , are those appropriate for three and four spatial dimensions.

We now compare Equation, (2-29), to Equation, (2-5). We notice right away that we have a discrepancy. Equation, (2-29), has an extra factor of (16/3) in front of the term. There is also an additional factor of (15π/8) sitting out in front of the term. We believe that Equation, (2-29), is correct. And that Equation, (2-5), needs to be modified. Equation, (2-29), takes all forms of radiative energy, as well as spatial dimension into account, whereas Equation, (2-5), only takes internal energy and no change in spatial dimension into account. We first explain the factor of (16/3). Because we are in 3-D space, the total energy density is 8/3 the internal energy density. See Equation, (2-19). Also, in 3-D, by Equation, (2-28b),. Combining the two factors gives us (32/3c) in front of the term. We divide by 2 to obtain 16/3 since the heat energy is always one-half the total energy density. In 4-D space, the total energy density is 10/4 times the internal energy density, as seen by Equation, (2-20). Also in 4-D,. See Equation, (2-28a). Multiplying both factors gives 30π/8c. We take half of that for heat transfer to obtain the factor, (15π/8). We call Equation, (2-29), the second generalized Stefan-Boltzmann equation for radiative transfers between adjoining spatial dimensions. In our view, it is the correct expression.

With this in mind, let us rewrite Equation, (2-29), as

(2-30)

where, by definition, the primed variables have been recast in terms of the original unprimed variables, as follows,

and (2-31a,b)

The unprimed sigma values were given by Equations ((2-4a), (2-4b)). We will be working with this version of the generalized Stefan-Boltzmann law, Equation (2-30), which we call the 2^nd generalized version of the Stefan-Boltzmann law. It is our contention that this is correct. This Equation (2-30), is equivalent to Equations, (2-26).

With the new Stefan-Boltzmann constants, defined in Equations ((2-31a), (2-31b)), we can recalculate the equilibrium inside surface temperature of a black hole. By setting, , Equation (2-30), reduces to

(2-32)

Solving for gives

(2-33a)

or, what is equivalent,

(2-33b)

Upon comparison with Equation, (2-6), we note that, numerically, there is virtually no difference between the two results. As far as this result is concerned, the 2^nd generalized Stefan-Boltzmann law gives an almost identical calculation for the equilibrium temperature just inside the event horizon, as our 1^st version, Equation, (2-5). Nevertheless, let us calculate the inside surface temperature for three black holes. We focus on three black holes; one having the mass of the sun, another having a mass 10 times the mass of the sun, and for the third black hole, we assume a mass, 10⁶ times the mass of the sun. For these three massive black holes, we calculate the radii using the Schwarzschild relation, and substitute these radii into Equation, (2-33). We thereby obtain,

(2-34)

As stated, these values for are very close to the values obtained previously. We also note that these temperatures, just inside the event horizon in 4-D space, are very much higher in value when compared to the Hawking temperature.

There are many ways of writing our 2^nd generalized version of the Stefan-Boltzmann law. Equation (2-30), is one way to express it. Other ways are by means of Equations (2-26). If we use the second line of Equation (2-26), and insert the values for and using Equations (2-28b) and (2-28a), we can reformulate the law very explicitly in terms of radius and temperatures. The result is

(2-35)

Again, , is defined in terms of temperature, , whereas, , is defined in terms of temperature,. This is made explicit in the second line of Equation, (2-35). Knowing the temperature just outside the black hole, , and the mass, or size, of the black hole, we can determine using this equation. For the temperature, , we use the condition, (2-33b). That condition assumed that the temperature just outside the event horizon is, , which is an assumed input. The last line in Equation (2-35) is an alternative, but equivalent formulation. It is obtained by realizing that Equation (2-33), is a consequence of (2-32), or, what is equivalent, setting the second line in Equation (2-26), equal to zero. This allows us to represent the 4-D quantities in terms of the 3-D quantities, i.e., the second term on the right hand side of Equation (2-26), can be expressed in terms of the first term on the right hand side. This bypasses the need to figure out first. The last line in Equation (2-35), is particularly useful in that now, all quantities are defined in three-dimensional space, and are accessible observationally.

The lip, or barrier to entry, is also readily apparent. Utilizing the last line of Equation, (2-35), we see that there can be no net outflow. For that to happen, the external outside temperature would have to be less than the cosmic microwave background, which cannot happen! The cosmic microwave background is what we used to eliminate the 4-D term, the term, in Equation, (2-26). The second term on the right hand side of the last line in Equation, (2-35), is a disguised version of. This term is what creates the lip, or barrier, for potentially instreaming CMB photons. To make a long story short, we can only have net inflow, or, no net inflow, i.e.,. The quantity, , can never be negative, which means that there can be no outflow out of the black hole. This is a direct consequence of the 4-D/3-D interface. We would not have this condition if the black hole were defined as a three dimensional entity.

We close this section by establishing a limit for the amount of inflow. We focus on the last line of Equation, (2-26). If, , then we have an isolated, static, black hole (ISBH), and

(ISBH) (2-36)

If, on the other hand, , then we have a dynamic black hole (DBH), which leads us to conclude that,

(DBH) (2-37)

It is clear that, in general,. We further note that, , because the temperature and radius are always positive. See the second term on the right hand side of Equation (2-35), where is explicitly written out. We rewrite the last line of Equation, (2-26), as

However, the left hand side of this equation is positive definite. Thus, the right hand side must also be. This, in turn, leads to the condition,

(2-38)

This shows that the amount of radiative heat inflow is restricted to be less than, , where, , is the 3-D radiative force acting from the outside in. This places limits on the intake of radiative heat into a black hole. This is a specific, and interesting, prediction of our model.

We emphasize that this limit placed on radiative heat inflow is a direct consequence of having a 4-D/3-D interface for the event horizon. Equation, (2-38), follow from Equations (2-36), and (2-37). These, in turn, depend on the last line of Equation (2-26). The factors of 4 and 5 in Equation (2-26), are due to the dimensionality of space itself. See, for example, Equations (2-19) and (2-20). More specifically, refer to the last equalities in each. Radiative inflow would not be restricted if the black hole were a 3-D object, because those factors sitting out in front of and would essentially be the same. In other words, we would not be able to distinguish between, , and,.

Also, for a 3-D/3-D boundary, the Stefan-Boltzmann law would not allow us to have a lessor temperature just inside the event horizon. A 4-D/3-D is a requirement for that. The different surface areas between the 3-D and the 4-D space, is what causes the sudden drop in temperature, as will be demonstrated in section IV. See, also, the second line of Equation, (2-35), and specialize to the particular situation where we have no net heat inflow. This will relate the temperature on the inside of the event horizon, , defined over 4-D space, to that on the outside of the event horizon, , defined over 3-D space.

We can evaluate the quantity, , using the first term on the right hand side of Equation (2-35). We obtain

(2-39)

If the outside surface temperature is, , this reduces to

(2-40)

For outside surface temperatures in excess of, 2.725 K, the value for can be much higher as seen by Equation (2-39). For example, hard photonic X-ray emissions just outside a black hole would indicate temperatures in excess of, 10⁹ K. Because of the factor in Equation (2-39), we can expect much higher limits placed for radiative heat inflow under these conditions, 10³⁶ times higher than what is indicated by Equation (2-40). The inequality (2-38), may also help explain the circulating nature of radiative heat inflow before entering the event horizon of a black hole.

3. Generalization of the Young-Laplace Equations for Surface Tension at the Event Horizon

The surface tension will play a key role in our analysis of the black hole event horizon. We first recognize that expanding a black hole event horizon requires work, or input energy. That work can be expressed very simply as

(3-1)

here, is the surface tension, and dR is the increase in radius. The surface tension acts on the 4-D/3-D membrane, identified as the event horizon, and will pull the surface in.

Another formulation for the positive work done in expanding the event horizon is in terms of pressure. Ordinarily, the pressure just inside the membrane has to be larger than the pressure just outside in order to guarantee a positive curvature for the object. However, in the case of a 4-D/3-D membrane, this will not hold true. The surface area changes in this case, and as a consequence, the radiative pressure on the inside will actually be less than that on the outside. Remember that we are going from a surface area of, , to, , upon entering the black hole. But we first consider the conventional 3-D case where surface area does not change upon crossing the membrane.

For conventional 3-D objects such as liquid droplets or bubble films, it is known that gives the outward force, where is the inner pressure, is the outside pressure, and A is the surface area. For hydrostatic equilibrium, the two forces, the surface tension, and the outward force due to pressure difference, must balance. Thus,

(3-2)

For a 3-D sphere, the Young-Laplace equation reads

(3-3)

The coefficient of surface tension, , is measured in units of Newtons/meter, and are the curvatures in the x, y direction. Because of spherical symmetry, we set,. Similarly, for a 4-D sphere, we extrapolate and claim that,

(3-4)

The 4-D coefficient of surface tension, , is measured in Newtons/meter², and are the curvatures in the x, y, z sense. Again, we set , because we want spherical symmetry. The cause of surface tension in the case of liquid droplets, gas bubbles, soap bubbles, etc. are intermolecular forces. For the case of a black hole, the surface tension is caused by the difference in radiative force at the interface, and, more importantly, gravity, as we shall see shortly.

To expand a surface in 3-D space, we use Equation, (3-1), and write

(3-5)

where dV is the increase in volume. In 4-D we use the same formula, Equation, (3-1), but now,

(3-6)

here, has units of Newtons/meters³ and dV is measured in (meters)⁴. We see that, , in both 3-D and 4-D space. Therefore, using Equations, (3-3), and, (3-4), we can write,

(3-7a)

(3-7b)

Substituting Equation, (3-7a), into Equation, (3-5), gives

(3-8)

This holds true because,. Similarly, substituting Equation, (3-7b), into Equation, (3-6), renders

(3-9)

here,. Equations, (3-8), and, (3-9), give the work done in terms of, , and, , which in turn, are defined by Equations, (3-3), and, (3-4), respectively. The quantities, , and, , are called the coefficients of surface tension.

For a black hole to expand, two surfaces have to expand, the 3-D surface and the 4-D surface. For our 4-D blackbody black hole radiation model, we set

(3-10)

In this equation, , is the 3-D radiative pressure force pushing the event horizon in, and is the 4-D radiative pressure force pushing the event horizon out. We also have the absolute value of the gravitational force, , which acts on the event horizon, and which wants to pull it in. We only count this once, and because it is derived within the black hole, which is a 4-D construct, the gravitational force, itself, is 4-D. The total contribution to actual work done is given by Equation, (3-10), which will be positive for an increase in R, from R to R + dR. As mentioned, R, characterizes the event horizon. From Equation, (3-10), we see that the total work will consist of three separate components, and each goes into defining the surface tension, on the left hand side of this equation.

As we have seen in the last section the radiative force, , is always larger than its 4-D counterpart,. Refer to Equations, (2-36), and, (2-37). In fact, using these two conditions, and Equation, (2-26), we see that

(3-11)

Therefore, by Equations, (3-10), and, (3-11), another way to write the 4-D/3-D radiative surface tension is

(3-12)

For an isolated static black hole (ISBH), , and, , which is definitely greater than zero. For a dynamic black hole (DBH), where, , we obtain an even larger radiative surface tension by Equation, (3-12). In fact, knowing the outer surface temperature allows us to calculate the amount of heat inflow as shown in the last section. We also have a larger value for because the outside temperature is now larger. It is interesting to remark that, even without gravity, a ball of radiation is positively curved, if that ball of blackbody radiation has 4 spatial dimensions. This, we believe, is a very significant result, as it may relate to elementary particles, and the formation of black holes.

The full surface tension has to include the gravitational force acting on the event horizon. By Equations, (3-10), and, (3-11), we can write,

(3-13)

We can thus calculate the associated surface tension using Equation, (3-13), if we know the value of the 4-D gravitational force at the event horizon, and. In the next paper, we will calculate an expression for,. It will turn out to be immense. In fact, the radiative forces are insignificant in comparison, except in the most extreme of circumstances. In expanding the black hole, we will see that the work done is essentially against gravity. Moreover, with, or without, gravity, the surface tension is positive definite, making the black hole a positively curved object in space.

An alternative formulation to Equations, (3-10), and, (3-13), is

(3-14)

This is the infinitesimal positive work done by inflowing matter/radiation in expanding the black hole event horizon in both 3-D and 4-D space. The term, , will fight expansion, whereas the product, , will assist in expanding the membrane, and hence we have the difference in sign in Equation, (3-14). We also have gravity, which fights expansion of the event horizon. In other words, it will hinder an increase in event horizon surface area. The last term on the right hand side of Equation, (3-14), represents this contribution to the infinitesimal work done. Its associated coefficient of surface tension is,. We will give actual expressions for, and, in the next section, where it will be seen that both are radius and temperature dependent. The coefficient, , can only be specified in the follow up paper, once we derive an expression for gravitational force,. The gravitational force at the surface will turn out to be model dependent.

Equations, (3-1), and, (3-10), led us to conclude that the radiative portion of surface tension is the difference in radiative forces,. We also saw, by Equation, (3-12), that this surface tension is positive and finite. We wish to write the surface tension in another form. By invoking Equations, (2-37a,b), (2-14), and, (2-28a,b), we can demonstrate that

(3-15a)

(3-15b)

Hence, a new way to write this part of the surface tension is

(3-16)

In the second line of Equation, (3-16), we have used the identity,

(3-17)

This is a disguised version of Equation, (2-33). We previously saw that is a function of, R, and,. See Equation, (3-12), and the discussion that followed. The Equation, (3-16), is an alternative formulation. It is more direct than calculating first, and then inserting this value into Equation, (3-12). Moreover, with this new formulation, we once again see that the radiative surface tension can never be zero. The lowest temperature allowed in Equation, (3-16), is, and for that value, we obtain, as before.

We next give some numerical values. We first consider an isolated, static, black hole, where,. In this instance, by Equations (3-12) and (3-15a),

(ISBH) (3-18)

In the last equality, we have set the temperature, , and used the numerical value of, specified in Equation, (2-28b). Equation, (3-18), just re-produces results obtained earlier, in Equations, (2-39), and, (2-40). Equation, (3-18), tells us, that for an isolated black hole, the radiative surface tension increases as the radius squared.

For the three black hole masses considered in Equations, (2-34), we use Equation (3-18), to calculate the associated radiative surface tensions. Mass first gets converted to radius using the Schwarzschild relation,. The results of this calculation are:

(3-19)

All forces are measured in Newtons. We notice that both small and large black holes have hardly any radiative surface tension, given their significant size. The values indicated in Equations, (3-19), are really quite small. We will see, however, that what holds the black hole together isn’t just radiative surface tension. It is gravity! And gravity acts within the black hole, as well as on its surface, as will be shown in the follow up paper. The values indicated in Equation, (3-19), hold for an isolated, static black hole (ISBH), where there is zero inflow.

We should also mention that other forces will invariably come into play beside blackbody radiation and gravity, in stabilizing the event horizon. These will also prevent the black hole from expanding outwards. There is dark energy, and dark matter, and ordinary matter. These components are not taken into account in Equations, (3-10), nor in, (3-14), which is equivalent. CMB photons contribute very little, in the present epoch, to the total energy density of the universe, only about 10⁻⁵ of the total amount. Also, in those regions of space where matter is prevalent, and where black holes are to be found, CMB photons contribute an even smaller percentage. Equations, (3-19), only considers blackbody photons. Nonetheless, they do indicate that an inherently positive, finite value exists for the radiative surface tension, even if the black hole is pure photonic radiation. This was the case in the very early universe.

We next consider a dynamic black hole, where. In this instance, both terms on the right hand side in the second line of Equations, (3-12), contribute. Using Equation, (2-35), and specifically, the last line, we can calculate. This then gets substituted into the second line of Equation, (3-12), to find. For determining the value of, we can use the second equality in Equation, (3-18), namely,. For an evaluation of, , it is therefore necessary to specify the temperature just outside the event horizon, , as well as the radius, R, of the black hole. A more direct method to determine would simply be to use the last line in Equation, (3-16). Needless to say, the radiative surface tension will be much higher for a dynamic black hole than for an isolated static, black hole even if the radius is the same. Both terms, , and, , will increase in the situation where we have a dynamic black hole.

We emphasize that a positive surface tension is needed in order to define a positively curved object such as a black hole. Our surface tension is inherently positive definite as seen by Equations, (3-12), or (3-16); it can never be less than. And this is just the radiative component. Again, this is a consequence of a 4-D/3-D interface. Upon retracing our steps, the disparity is due to the factor of 5 versus 4 for a 4-D versus 3-D space. See, for example, Equations, (2-36), and, (2-37). These factors are a direct consequence of the dimensionality of space! See also the last equalities in Equations, (2-19), and (2-20). If the black hole were defined as a 3-D blackbody ball of radiation, there would be no such inherent radiative surface tension. This, obviously, is another compelling argument for considering the black hole as a 4-D object, embedded in a 3-D space.

We close this section by mentioning that in the Appendix A, we consider non-spherical symmetry. Surface tension leads to work done, and we consider radiative black body inflow under the assumption that the black hole has the shape of an oblate spheroid. Rotating black holes assume this shape, and if there is net inflow, we can demonstrate that gravitational quadrupole radiation will be emitted. We calculate a few such examples to show the robustness of the model.

4. Radiative Waterfall Model for the Event Horizon of a Black Hole

We now have the required tools to discuss what happens at the event horizon, given our 4-D radiation model for a black hole. The results will only hold at the 4-D/3-D interface. In a follow-up paper we will discuss the internal structure of a black hole.

For now, however, we will indicate that hydrostatic equilibrium has to be maintained layer by layer within the black hole. We therefore set

(4-1)

here, , is the radiative force pushing the layer out, at radius, r, which acts on a segment of thickness, dr, between radii, r, and, r + dr. The quantity, , is the radiative force pushing the layer in, at radius, r + dr. On the right hand side we have, , which is the gravitational force pulling the layer in. The layer is at radius, r and of thickness, dr. In a follow-up paper, we will give a specific temperature gradient within the black hole. Because it will depend on radius, r, we will write,. It will turn out that, , which will make the left hand side of Equation, (4-1), positive. The gravitational force is, of course, directed radially inwards, and has magnitude given by the right hand side of Equation, (4-1). We will derive explicit expressions for, , and for with in the subsequent paper. Because, , the internal energy density, the radiative pressure, and the radiative heat density, will all decrease as one increases the radius, starting from the center of the black hole. As was seen in section II, the quantities depend on temperature and temperature only. See Equations, (2-28a), and, (2-20). One can also claim that these quantities are radius dependent because the temperature inside the black hole is radius dependent. Outside of the black hole we do not have any such layering because the temperature is, by and large, uniform. Also, the blackbody photons there on the outside are “unbounded”, i.e., not trapped within a confining volume except that of the entire universe, itself.

We now come back to the event horizon. At the event horizon, we will assume that the 4-D space abruptly changes into 3-D space, at radius,. In other words, the event horizon has no thickness. Moreover the radiative force, which pushes the event horizon out, is,. On the other hand, the radiative force, which pushes the event horizon in, from the 3-D side, is,. See Equations, (2-27a,b). We also have the gravitational force, , pulling the event horizon in. It seeks to prevent any 4-D surface area increase. The quantity, , will refer to the magnitude. If there is no inflow, then we know that,. With inflow,. The quantity, , is defined in terms of, as can be seen by Equation, (2-28b). From the second equality in Equations, (2-19), we recognize that (when multiplied by an appropriate volume element). The 4-D radiative pressure, , acting from within the black hole and pushing the event horizon out, is at a different temperature,. The event horizon is assumed to be infinitely thin, i.e., it has no thickness. Gravity will make an abrupt jump in value when entering the black hole, as will be shown in the 2^nd paper. The gravitational coupling constant, which is Newton’s constant in 3-dimensions, will increase abruptly upon entry into the 4-D space. The gravitational potential, however, can be chosen to have the same value at, , in both three and four dimensional space, by choosing the constant of integration appropriately. We will show that where, , is the gravitational potential in N-dimensional space at,. The difference in radiative force is, of course, the radiative surface tension. The actual expression for surface tension is given by the first line in Equations, (3-13), and this net force pushes the event horizon in.

We first calculate the relevant densities and radiative pressure, just outside the event horizon, on the 3-D side. We assume, for the time being, that we are dealing with an isolated, static black hole. Using our CMB temperature of, 2.725 K, we find using Equations, (2-28b), and, (2-19),

, (ISBH) (4-2a,b)

, (ISBH) (4-2c,d)

Just inside the event horizon, on the 4-D side, we use a different set of equations. We use the temperature, specified by Equation, (2-33). We also employ relations, (2-28a), and, (2-20). The results are now black hole radius dependent,

in J/m⁴ (ISBH) (4-3a)

in N/m³ (ISBH) (4-3b)

in J/m⁴ (ISBH) (4-3c)

in J/(m⁴∙K) (ISBH) (4-3d)

For the second equality of Equation, (4-3a), we have substituted Equation, (2-33). We notice that the size, or mass, of a black hole will have a direct impact on the various densities and radiative pressure, just inside the surface. In fact, as the radius increases, the densities and pressure will decrease according to Equations, (4-3a,b,c,d). Also note the different units between Equations, (4.2a,b,c,d), and, (4-3a,b,c,d). This makes a difference determination impossible. However, we can set up ratios to see how the 4-D quantities relate to the corresponding 3-D quantities.

For an isolated, static black hole, we know that Equation, (2-36), holds. Therefore, by Equations, (2-27a,b), we must have

(ISBH) (4-4)

We use this to construct the ratio,. We substitute our expressions for 3-D and 4-D surface areas, and simplify. We thereby obtain

(ISBH) (4-5)

Moreover, due to the identities in Equations, (2-19), and (2-20), we can further prove that

(ISBH) (4-6)

(ISBH) (4-7)

(ISBH) (4-8)

In the last equation, we have made use of

(ISBH) (4-9)

See Equation, (2-33). What is important to note in Equations, (4-5), through to, (4-9), is the fact that, due to the presence of R, we have a discontinuous jump in value in all these quantities as one enters the black hole. The decreasing jump in value, or gap, depends on the size (or mass) of a black hole. The 4-D densities, will decrease abruptly from the corresponding 3-D quantities as one breaks through the event horizon envelope. This holds for the radiative pressure and temperature, as well, as seen in Equation, (4-5), and, (4-9). This break in value is what we refer to as our “waterfall model”. Many quantities will drop precipitously as one makes their way into the black hole. Again, this is a direct consequence of the change in dimensionality of space. No such drop in value would occur if the black hole were a 3-D construct.

We have seen that the temperature changes abruptly upon entering the 4-D space through Equation, (2-9). Another way of expressing it is to make use of the second line in relation, (2-35). If, then this allows us to write

(ISBH) (4-10)

We solve this equation for. The result is

(ISBH) (4-11)

Equation, (4-11), is another way to express the discontinuity in temperature, because of the presence of R on the right hand side. The mass, or size, of the black hole will determine the discontinuous jump in temperature. If we substitute into Equation, (4-11), and solve for, then we would obtain (2-33). There has to be a break in temperature at the event horizon. As far as we know, this abrupt change in temperature upon entering the black hole proper has never been theoretically modeled before. It has been stated more as an accepted observational fact, given that black holes appear black. Here we provide an unequivocal theoretical reason for why this is so. A change in spatial dimension gives a natural explanation for not only this decrease in temperature, but also for the other quantities decreasing abruptly and discontinuously, upon entering a black hole.

Equations, (4-5), through to, (4-9), are also intriguing from another perspective, namely elementary particles. Attempts have been made in the past, to identify elementary particles as mini-black holes. As with black holes, outward characteristics such as charge, spin and mass are what is observed. The interior seems to defy an explanation. We notice that if the radius is made very, very small, in Equations, (4-5), through to, (4-9), we obtain incredibly large values for 4-D radiative pressures, internal energy densities, heat densities, entropy densities, etc.. This may turn out to be an intriguing way to model elementary particles. These mini-black holes have the opposite behavior than their macroscopic counterparts, in that their temperatures, radiative pressures, internal energy densities, etc. would increase (sky-rocket) within their immediate interior. For macroscopic black holes, we have seen that those values for density and pressure decrease in value. Another compelling argument for this identification with elementary particles is the fact that no gravity is assumed. We would obtain a natural curvature in space due to radiative surface tension, and radiative surface tension only. This, of course, would take us too far afield in this work. But we definitely find this to be an intriguing line of research. The second paper will show us how to go into the specifics about modeling this very possibility.

Our waterfall model also extends to the radiative force, , changing abruptly at the event horizon to a new value, , where is the radiative force just inside the 4-D space. See Equations, (2-36), and, (2-37). We have a step-function decrease due to the discontinuity of space, and the different surface areas involved. This is literally what causes the radiative surface tension, defined as, , to be greater than zero. The inequality holds for net inflow of radiative heat (and energy), whereas the equality is valid for an isolated, static black hole with no net inflow. In the second paper which follows, we will also see that the gravitational force changes abruptly at the event horizon. Upon crossing the 3-D/4-D threshold, it will suddenly increase in value over its 3-D counterpart. All these facts will support our waterfall hypothesis. We believe that the 3-D photons literally drop out of view upon reaching the event horizon due to the abrupt change in spatial dimension.

It is important to realize that, within this model, what causes the photons to disappear is not that the escape velocity exceeds that of light. This is one way of looking at it, and it assumes that there are no other photons pushing back at the event horizon. We would have a situation where the black hole just grows and grows. We do believe that 4-D internal photons do push back at the event horizon. The 4-D photons hold back the floodgates, so to speak. But because they are 4-D, they cannot push back with the same force as the 3-D photons pushing in. Our interpretation is that, as a consequence, the 3-D photons are pulled in and fall into a gravitational hole once they enter this new 4-D space. Those photons have to exceed a certain threshold temperature on the outside, which we chose to equal, 2.725 K. In a sense the photons fall off a cliff upon entering the event horizon, and are never seen again. We can also think of the event horizon as a kind of simple machine. The sudden increase in surface area when entering the 3-D/4-D threshold causes a step-like decrease in radiative pressure, and radiative force. This is a trap from which photons cannot escape. What makes this unique is that it is the change in spatial dimension which causes this increase in surface area, and ultimately, this photon trap.

For a dynamic black hole, we must have the condition, , and the outside surface temperature, , plays an important role. For a black hole of a given size (or mass), the temperature, , will determine the amount of radiative heat inflow via Equation, (2-35). Obviously, needs to be larger than 2.725 K for there to be inflow. An alternative formulation is through Equation, (2-26). From the last line, for there to be inflow, we must have,. We will use this inequality to establish other inequalities, which are pertinent to this situation. Using Equations, (2-27a,b), this inequality can be written as

(DBH) (4-12)

Substituting, and, , and simplifying gives

(DBH) (4-13)

Upon comparison with Equation, (4-5), we see that this makes sense because the denominator on the left hand side is greater than that in Equation, (4-5). In Equation, (4-5), we assumed an outside temperature of 2.725 K, whereas here,. From the inequality, (4-12), it also follows that

(DBH) (4-14)

Using our formulae for surface areas in 3-dimensional and 4-dimensional space, and rearranging, we find that

(DBH) (4-15)

Comparing with Equation, (4-6), we notice that the inequality is again due to the higher outside temperature,. An isolated, static black hole assumes that,. Continuing in this vein, we can further demonstrate that

(DBH) (4-16)

(DBH) (4-17)

and,

(DBH) (4-18)

For the inequality in relation, (4-17), we note that in terms of proportionality,. The temperature, , is fixed by the relation, (2-33). However, the temperature, , increases for a dynamic black hole over that of an isolated, static black hole. As a consequence, we obtain the inequality shown in relation, (4-17).

We next consider net heat inflow. From section III, we know that positive work has to be done by an external agent in order to cause the black hole to expand its volume. That external agent can only be in-falling matter/energy. One way to describe the work done is through Equations, (3-1), and, (3-10). Another formulation is through Equation, (3-14). We focus, on Equation, (3-10). The radiative surface tension is given by the expression, (3-16). Using this expression, we calculate the work done against radiation in increasing the black hole from an initial radius, to a final radius,. We obtain,

(4-19)

In the 3^rd line, we assumed that the outside surface temperature is held constant during the expansion process. For the 4^th line we used Equations, (2-19), and, (2-28b). We also defined, , as the 3-D radiative pressure at a temperature of 2.725 K. The result from Equation, (4-19), tells us that the total work done, against radiative forces, is simply proportional to the increase in 3-D volume,. The outside temperature also plays a role because it will determine a value for. It is to be noticed that a volume increase is necessary in order for work to be done.

Another way to find the work done is through Equation, (3-14), which makes use of the coefficients of surface tension. This will give us the same result as Equation, (4-19), and so we will not reproduce it. Instead we will focus of the coefficients themselves, which will round off the discussion. Knowing the surface areas in 3-D and 4-D space, we can easily demonstrate that, , and. These, we substitute into Equation, (3-13), to obtain,

(4-20)

Upon comparison with Equation, (3-1), it is clear that

(4-21)

Moreover, since, , it is found upon comparing with Equation, (4-21), that

, (4-22a,b)

The radiative forces at the event horizon can thus be related to the radiative coefficients of surface tension. Taking a final step, we use Equations, (2-27a,b), and substitute these into Equations, (4-22a,b), to eliminate, and. Upon simplification, the results are even more direct,

, (4-23a,b)

These just reproduce Equations, (3-3), and, (3-4), which were put forward previously, more as a claim, than as a fact. The coefficients, , and, , are just constants which indicate how easy, or how difficult, it is to stretch the event horizon membrane. Larger values indicate more work is necessary. From these equations, we see what these coefficients depend on the size, and the temperatures, inside and outside, of a black hole. The radiative pressure, , depends on the outside surface temperature, , whereas, the radiative pressure, , depends on the inside surface temperature,.

We can rewrite Equations, (4-23a,b), to show this more explicitly. From Equations, (2-19), and (2-20), we know that, and,. It is also possible to express and directly in terms of temperature, using Equations, (2-28b), and, (2-28a). Substituting these relations into Equations, (4-23a,b), gives us

(4-24a)

(4-24b)

We see clearly that and are temperature and radius dependent. The former depends on the outside surface temperature, whereas the latter depends on the inner surface temperature. Both coefficients are proportional to radius.

To see just how easy it is to stretch the membrane, the event horizon, against radiative forces, we consider a numerical example. We consider a black hole having a mass, ten times the mass of the sun. We will assume an increase in radius by a factor of 1.1, or, 10%. Thus, the radius will increase from an initial value, , to a final value, , where we have used the Schwarzschild relation to find the radius, given a specific mass. Finally let us assume an outside surface temperature of, , which is held constant during the expansion process. The 3-D volume increase is, correspondingly,

(4-27)

The 3-D radiative pressure at, , is,

(4-28)

We use the expression, (4-19), to find the work done against radiative forces. At a temperature, , the second term within the square brackets in Equation, (4-19), is truly insignificant, compared to the value calculated in Equation, (4-28). Thus, we can ignore it, and the total work done against radiative forces is simply,

(4-29)

This is the work done against radiative, and radiative forces only. Gravity will also have to be considered, which will be the case in a follow up paper. The radiative work done in Equation, (4-29), may seem considerable, but it will be next to nothing when compared to the work done against gravity, for the same situation. We will see that in the next paper, where we will give an expression for the 4-D gravitational force. However a crude order of magnitude estimate shows us that an increase of mass by 10% for the black hole of 10 solar masses, amounts to a mass difference of one solar mass, (1.99 × 10³⁰ kg). If we multiply this by, , the corresponding increase in energy is, The value indicated in Equation, (4-29), is insignificant when compared to this. Larger surrounding temperatures will be considered in our follow-up paper.

We close this section by emphasizing, once more, that the waterfall model presented here is a direct consequence of the assumed change in spatial dimension at the event horizon. A 3-D/3-D interface would not allow for a precipitous drop in temperature when crossing the boundary. We would not have much reduced internal energy densities, entropy densities, and radiative pressures, when entering the black hole. Nor would the radiative force due to blackbody photons drop abruptly upon entry into the black hole. Finally, a 3-D/3-D event horizon will not allow for gravity to increase dramatically upon entry into the black hole, as will be shown in a follow-up paper. But then again, a 3-D/3-D interface would also not allow for a rip in the space-time fabric, as there would be no a-priori discontinuity in space at the event horizon.

5. Summary and Conclusions

In this work, we presented a model for a black hole based on a 4-D spatial sphere filled with blackbody radiation. We focused on the event horizon and argued for an interface, which separates 4-D space, the black hole, from 3-D space, the surroundings. For a static black hole with no inflow, , and the ambient temperature is taken to equal 2.725 K, the CMB temperature. If there is net inflow into the black hole, , and the surrounding 3-D temperature, , must be higher. See Equation (2-35), where in the last line, this is made very explicit. Because the outside temperature, , can never be lower than 2.725 K, we can never have net outflow out of the black hole. And thus, we have established the condition that,. We have distinguished between the temperature just inside the event horizon, , which is on the 4-D side, and the temperature, , just outside the event horizon, which is on the 3-D side. Because the event horizon is assumed infinitely thin, both temperatures are effectively at the same radius, R. The event horizon is a membrane separating the 4-D space from our 3-D world, and we argue that there is a sharp discontinuity at the event horizon. As such we established, in this paper, conditions and equations, which must apply if such a scenario is realized in nature. We focused exclusively on blackbody photonic radiation, although this scheme can be generalized later to include other types of radiation including fermionic components.

In Section 2, we first generalized the Stefan-Boltzmann law for radiative transfers between three dimensional and four dimensional spaces. The result is Equation (2-26), or Equation (2-35), if we bring the right hand side in terms of 3-D quantities. All superscripts refer to the dimensionality of space over which the physical quantity is defined. In Equation, (2-26), , is the rate of radiative heat emitted from 3-D space and this enters the 4-D black hole. The quantity, , by contrast, is the heat given off per unit time by the 4-D black hole, and this enters the 3-D space. In other words, there is a constant exchange of photonic energy back and forth, just like in the ordinary Stefan-Boltzmann law in 3-D space, when they are at the same temperature. Here, however, we have different temperatures on either side of the event horizon for no net inflow/outflow due to the different dimensionality of space. It will turn out that the temperature within the event horizon is always less than that on the outside, even if there is no net radiative flow. We also find that for there to be net outflow from the black hole, the temperature on the outside would have to be less than the CMB temperature, which is not possible. See the last line of Equation (2-35), where this is clearly stated. This equation enforces the condition that,. The right hand side of Equation (2-35), is either positive for a dynamic black hole with inflow, or zero for an isolated, static black hole with no net heat inflow. We have discounted/ignored Hawking radiation and other forms of evaporative leakages emanating from the black hole, as these will turn out to be second order corrections at best. In Equations (2-26) and (2-35), , and, are the 3-D and 4-D surface areas through which heat (photons) can escape.

We argued that the first version of the Stefan-Boltzmann generalization for radiative transfers between spatial dimensions, given by Equations (2-5) and (2-7), is incorrect. These equations do not take into account all forms of blackbody energy, which consists of internal energy density, radiation pressure, and radiative heat energy. These quantities are all defined at a specific temperature, and if the temperature changes, as, for example, upon entering the event horizon, then these quantities must also change collectively as one unit. It is an all or nothing proposition. Moreover, we have to concern ourselves with the different dimensionality of space, when moving from one dimension to the next. Hence, Equations (2-5) and (2-7), have to be modified. The correct expressions for the generalized Stefan-Boltzmann law are Equations (2-26) and (2-35). There, the factors are correct, and we call these relations, the 2^nd generalized versions of the Stefan-Boltzmann law. They take the dimensionality of space into account, as well as all forms of radiative energy transfer. See the discussion following Equation (2-29), and Equations, (2-28a,b). Numerically, the differences between the two versions are slight. Nevertheless the distinction is important.

With our generalized Stefan-Boltzmann equations, we can predict the amount of radiative heat inflow, given the temperature just outside the event horizon, and the mass, or radius, of a black hole. These are quantities, which are accessible observationally. If the temperature just outside the event horizon, , equals 2.275 K, then we have by Equation (2-35), an isolated, static black hole, where. In this situation, the temperature just inside the event horizon can be determined from Equation (2-33). We find that. Equation, (4-25), is another version of the same equation. If the temperature just outside the event horizon, , is greater than 2.275 K, then we have a dynamic black hole with inflow, where. This will lead to expansion, but until such time that the event horizon has actually expanded, we still use Equation (2-33), or (4-25), to determine inside surface temperature,. Some inside surface temperatures for various black holes are evaluated numerically in Equations (3-34). We also have an interesting restriction on radiative heat inflow, specified by relation, (2-38). This restriction is important if outside surface temperatures are close to, 2.725 K; at higher outside temperatures, this lip, or barrier, is inconsequential. This restriction is a by-product of the 4-D/3-D interface.

In Section 3, we focused on the surface tension. The black hole has positive curvature, and therefore, there must be a positive surface tension associated with the event horizon. The radiative surface tension is the difference in radiative forces between the outside, and the inside, of the event horizon. The formal relation is Equation, (3-10), or, (3-12), where it is seen that. We define as the radiative force acting from the outside in, and is the radiative force acting from the inside out, at radius, R. The radiative pressure, , is defined exclusively in terms of temperature, , just outside the event horizon, whereas the radiative pressure, , is defined exclusively in terms of temperature, , which is the equilibrium temperature just inside the event horizon. The total expression for surface tension was derived by considering the amount of work done in expanding the black hole. It also includes gravity, which in Equation, (3-10), is given by the last term on the right hand side. In Equation, (3-14), we have, correspondingly, the last term on the right hand side. We will derive an expression for the 4-D gravitational force in our follow up paper. For now, we will just indicate that this is, by far, the major component which will contribute to the total work done upon expanding the black hole, except in the most extreme of situations. It is also to be noticed that radiative heat inflow can be expressed in terms of, , and. See the last line of Equation, (2-26). An interesting version of radiative surface tension is Equation, (3-12), where we have expressed the surface tension due to radiation directly in terms of heat inflow. Both terms on the right hand side increase upon net heat inflow, and therefore, the radiative surface tension can increase dramatically in such situations.

With or without heat inflow, there is a jump or gap in radiative force upon entering the black hole. The radiative surface tension can never equal zero. In fact, Equation, (3-12), shows that at a very minimum, for, the radiative surface tension equals. In this situation, Equation, (3-18), applies, and we notice that the radiative surface tension is strictly proportional to. For a dynamic black hole with inflow, Equation, (3-16), must be used, where we see first-hand that temperature, , also comes into play. In Equations, (3-19), we have calculated some specific radiative surface tensions for an isolated, static black hole. Gravitational surface tension will have to be added to this.

In this section, section III, we have calculated the radiative work done in expanding a black hole upon net radiative inflow. The work done is given by expressions, (3-11), or, equivalently, (3-14). To expand the black hole, both the 3-D and the 4-D surface areas have to expand. We have generalized the Young-Laplace relations in Equations, (3-3), and (3-4). Both contribute to the expansion process as shown in Equation, (3-14), where one term assists, and the other term hinders, the expansion process. See Equations, (3-7a,b), for the connection between radiative surface tension and radiative coefficients of surface tension. Both formulations give the same results for the amount of work required if we expand from an initial volume to a final volume, as they must.

In Section 4, we brought the ideas developed in sections II and III together. We proposed a so-called “waterfall model” to describe what happens at the event horizon. Due to the change in spatial dimension, we have a sharp discontinuity at the event horizon. The temperature, the radiative pressure, the internal energy density, the radiative heat density, and the entropy density, all drop precipitously in value at the 3-D/4-D interface upon entering the black hole. We have conditions, (4-5), (4-6), (4-7), (4-8), and (4-9), which hold for an isolated, static, black hole (ISBH). All physical quantities on the inside depend strictly on their counterparts in 3-D space, as well as, on size, or mass, of the black hole. For a dynamic black hole (DBH), we have the inequalities, relations, (4-12), through to, (4-18). To find the values for the inside variables, we resort to relations, (4-12), through to, (4-18). We see that we need not only the size, or mass, of the black hole, but also a specific outside temperature,. This outside temperature would have to be specified in order to evaluate the specific entries.

If we have an isolated, static black hole, then, , by Equation, (2-26). For a dynamic black hole, , and can be evaluated most simply, by using Equation, (2-35). In both instances, we have a drop in value for radiative force, because,. This is precisely what led to a non-zero value for the radiative surface tension, , which, in turn, guaranteed a positive curvature for a black hole, even in the absence of gravity. Refer to Equations, (3-12), and, (3-16). This surface tension, or discontinuity in radiative force, is precisely due to the change in spatial dimension.

Our waterfall model explains why we have a discontinuity at the event horizon. We cannot see the black hole, because once photons enter, they disappear from view due to the much reduced temperatures, radiative pressures, internal and other energy densities on the 4-D side. But more importantly, the radiative forces are such that, once entered, there is no escape. Due to the sudden drop in radiative force, they have entered a radiative trap. They have reached the point of no return, because of the inherent drop in radiative force. It is as if we have a waterfall which drops abruptly, and enters a region which opens up into a much wider valley (space). The water cannot jump back up into the original space. All radiative quantities take a sharp drop in value, and the ultimate flow depends on the size, or mass, of the black hole, as well as on the outside surface temperature.

Some numerical values for an isolated, static black hole (ISBH) are indicated by Equations, (4-2a,b,c,d), and (4-3a,b,c,d). Equations (4-2a,b,c,d) hold just outside the event horizon, while Equations, (4-3a,b,c,d), hold just inside the event horizon. Just inside the event horizon, the values are quite low as can be appreciated by comparing values relative to the outside. The Young-Laplace coefficients associated with radiative surface tension are given by Equations, (4-24a), and (4-26). We see that and are both radius and temperature dependent. The coefficient, , is dependent on the temperature on the outside, whereas, , is evaluated using the temperature just inside the event horizon. Both are proportional to radius, R. The total radiative work done in expanding from an initial radius, , to a final value, , can be found using Equation, (4-19). This result assumes that the temperature on the outside surface remains constant. We see by this expression that we can determine the work done by analyzing what happens in 3-D space.

We have emphasized throughout this paper why a black hole cannot be identified with a 3-D blackbody ball of radiation. First, no intrinsic, finite positive radiative surface tension can be defined for such a situation. The positive-definite radiative surface tension is due precisely to the change in spatial dimension. Second, our waterfall model goes a long way towards explaining why photons are pulled into the black hole once the event horizon is reached. We have a sudden drop in key thermodynamic variables at the interface, including temperature. All quantities drop abruptly because of the change in spatial dimension. Third, if black holes were three dimensional, the Stefan-Boltzmann law would not prevent continuous inflow of CMB photons. The cosmic microwave background has been in thermal contact with the event horizon since cosmological time, and, as such, a black hole should have fed indiscriminately on such CMB photons, as well as on dark matter and dark energy. One would imagine that the same equilibrium temperature would be reached in short order, on both sides of the event horizon, due to the conventional Stefan-Boltzmann law. With a 4-D black hole, we have an internal mechanism to prevent indiscriminate expansion. We have a natural barrier, or lip, for entry. Fourth, for a 4-D black hole, radiative inflow is restricted by Equation, (2-38). This factors significantly if the outside surface temperature, , approaches 2.725 K. For a 3-D object, no such restriction would exist. Fifth, a 3-D/4-D interface allows for a substantial cooling of photons once they enter the black hole. A 3-D/3-D interface does not. Finally, as will be shown in a follow-up paper, a 3-D black hole filled with blackbody radiation simply does not have the capacity to store so much radiative energy within such a compact volume. In order for a 3-D black hole to do that, the surface temperature just inside the event horizon would be extreme. A 4-D black hole, on the other hand, can pack in the needed radiative mass, and distribute it appropriately within a relatively small, from our perspective 3-D volume. We can think of black holes as exotic 4-D spatial capacitors, but instead of storing charge, they store radiative mass. More will be said on this point in the follow up paper.

We have spent a considerable amount of time discussing the positive aspects of this model. However, much work needs to be done, as we have only scratched the surface. One task would be to catalogue black holes according to their mass and check if the relations for heat inflow, specified here, make sense, given the outside surface temperatures. Our generalized Stefan-Boltzmann equations give clear predictions for based on radius, R, and outside surface temperature,. Using Equation, (2-35), does the rate at which heat disappears into the black hole, conform to the ambient temperature and radius? We could check whether black holes expand according to Equation, (4-19). We can also investigate the limits, which the model predicts, such as are indicated by Equations, (2-38), (2-39), and, (2-40).

Another line of inquiry would be to consider other forms of radiation, including fermionic components. How would their incorporation affect the results presented here? What about expansion? Equations, (3-10), and, (3-14), could be modified to include other surface tension contributions, such as dark matter, ordinary matter, and dark energy. They may increase, or potentially even decrease (in the case of dark energy), the total work done when a black hole expands in volume. We can define surface tension coefficients for such additional contributions, and evaluate the work done upon expansion in these instances.

An additional area of research would be to consider the symmetries of the metric within our 4-dimensional black hole. Which symmetries are allowed, i.e., are exhibited, if we have a 4-D spatial black hole? At first sight, we can expect that the metric associated with this higher dimensional space will be invariant under specific general coordinate transformations, but this has to be investigated, and worked out in detail. A systematic and straightforward way to find symmetries of the metric in higher curved spaces is to use the Killing equation [42] [43]. By constructing all possible independent solutions of this differential equation, one can find all the symmetries associated with our 5-d metric,. In general, we expect that the number of symmetries of a curved space-time will be no larger than that of flat space, as is proved in reference [23]. For our 4-spatial dimensional, spherically symmetric, blackbody, we focus on the energy-momentum stress tensor, , where, , are the curved (world) space-time coordinates. We have a static situation, where, , is the only relevant component of the 5-d stress tensor. The components, , and, vanish in this 5-d space, because within our black hole there is no flux. Our black hole stores radiative mass but does not transfer it.

Upon entering the 4-D black hole, filled with black body radiation, the energy-momentum stress tensor defined for a black body [44] changes from, . The relativistic mass density in three dimensional space, , is given in terms of temperature, , whereas, in 4-D space, we have, , where, , is the new temperature, just inside the event horizon. This temperature change, with associated reduced pressures and densities, are direct consequences of the waterfall model. Since determines the metric, , in 3-D space, we can assume that will determine, , within the 4-D black hole. The question is to investigate the role of the Killing vectors in this higher dimensional space-time, and to discover the symmetries for our inherently non-vacuum solution. Our black holes are isotropic, but not homogeneous. Therefore, we cannot expect a maximally symmetric space. Is the isometry just due to the isotropy of the black body (rotations in 4-spatial dimensions), or are there other hidden symmetries? This is another avenue for further research.

We can also consider the formation of black holes as a function of cosmological time. The CMB temperature has evolved as a function of time. Thus, the black hole should also evolve. Does the distribution of black holes throughout the universe match the predictions of Equation, (2-35)? According to this equation, there should be reduced heat inflow at higher CMB temperatures for a specific outside temperature and radius. Did the black hole radius increase much less in the distant past for the same external conditions? Moreover, in regards to evolution, one might think in terms of formation. How do black holes form? For a water droplet to form, it takes nucleation, such a dust, about which the water molecules can coalesce. Does something similar happen here with black hole formation? What would be the conditions under which they would form, and could that be tied into the WMAP and Planck CMB temperature data? The most massive black holes are found at the centers of most galaxies. This might not be an accident as these are natural nucleation sites about which stars and other black holes could aggregate.

An even wilder conjecture might be to consider black holes from the perspective of spatial dimension of the universe as a whole, and fragmentation. Are black holes dinosaurs, left over from a bygone era, when space itself might have been 4-D? Perhaps they are the remnants of a time when the universe was four dimensional, and upon cooling, underwent a phase transition into three dimensions. See references, [37], and, [45], in this regard. The black holes, representing sufficiently dense pockets of trapped radiation, may have resisted conversion into three-dimensional space. These are all intriguing aspects, which could be studied.

We close by remarking that there is a follow-up paper, which builds upon the ideas presented here. In the follow-up paper, we develop a model to help explain the internal structure of a black hole. We focus on how the radiation is layered within the black hole, and calculate important quantities such as total mass, entropy, gravitational force, gravitational potential, etc. There, we will obtain some results, which are even more surprising. Without further elaboration, we encourage the reader to view this work as well.

Acknowledgements

With these two papers, the author would like to thank his children, Kira, Juergen, and Henry, for their love and support. They have been a constant source of encouragement, inspiration, joy and goodwill, throughout my entire life. They are, first and foremost, my proudest achievement, and will always remain so.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

Cite this paper

Pilot, C. (2019) Are Black Holes 4-D Spatial Balls Filled with Black Body Radiation? Generalization of the Stefan-Boltzmann Law and Young-Laplace Relation for Spatial Radiative Transfers. Journal of High Energy Physics, Gravitation and Cosmology, 5, 638-682. https://doi.org/10.4236/jhepgc.2019.53036

References

Appendix A: Non-Spherically Symmetric Black Hole and Gravitational Quadrupole Radiation

In this section, we consider our generalized Stefan-Boltzmann law in light of a non-spherically symmetric black hole. We show that this leads to gravitational quadrupole radiation.

Gravitational quadrupole radiation is given by the formula [A1]

(A-1)

where, , stands for the gravitational radiation given off in time, dt, and is the quadrupole moment, defined by,

(A-2)

The dot over a quantity denotes a derivative with respect to time. For gravitational quadrupole radiation we recognize that, 1) a non-spherically symmetric distribution of mass is needed, and 2) a time dependent quadrupole moment is necessary with non-vanishing.

A simple extension of spherical symmetry is to assume an oblate spheroid for the externally viewed 3-D black hole, where the equatorial axis is larger than the polar axis. A rotating body assumes this shape, and we will consider black body radiative inflow into this type of black hole. The surface is characterized by the equation,

(A-3)

where the polar radius, b, is less than the equatorial radius, a. The 3-D volume is, , and the 3-D surface area is specified by [A2],

(A-4)

In this equation, the eccentricity is defined as. We will also make use of the oblateness, or flattening parameter, f, defined as,. For this oblate spheroid, we focus on the moment, which is the relevant moment for this kind of geometry.

To keep the discussion simple, we will assume a mass distribution which has constant density. In actual fact, in our model, the radiative mass density, is a function of 4-D radius where within the black hole. This will lead to a value which will be different than the one which we are about to use. However, since we are interested in an order of magnitude estimate, and a proof of concept, we treat the easier case of a constant mass density. Our distribution is anyways, to begin with, very model dependent. We also state that, even though Equation, (A-4), is given in 3-D terms, it is valid for our model with a 3-D/4-D interface. If one sits outside the black hole, we can think of the black hole as a 3-D construct. It is only when one penetrates to within the black hole that we see its 4-D structure. From the outside, we can therefore treat the constant density as an effective density.

For a constant mass density, it can be shown that [A3],

(A-5)

In the last line, we notice that, , is the mass of the spherically deformed black hole. The above moment can also be rewritten as,

(A-6)

In this equation, we have used our definitions for eccentricity, , and oblateness, f, defined previously. For spherical symmetry, both, , and, f vanish. Either of these parameters determines the shape of the black hole.

We will assume that as the black hole expands, the shape stays constant. The black hole is pulling in black body radiation uniformly from all sides, and at an equal rate, surface area wise. Therefore, when we take the time derivative of Equation, (A-6), with respect to time, we obtain,

(A-7)

Taking further time derivatives allows us to write, after some simplification,

(A-8)

We are interested in a linear approximation. Therefore, we set, on the right hand side of Equation, (A-8). We consider here a rate of expansion which is assumed a-priori small, and the accelerating components will be ignored. For a burst of quadrupole gravitational radiation, the second and third terms on the right hand side will, undoubtedly, be important, and, in this situation, cannot be ignored.

We substitute our linearized version of Equation, (A-8), into Equation, (A-4), and obtain

(A-9)

Our goal is to provide an estimate for this expression. This will demonstrate that black body radiative inflow can, and will, generate gravitational waves if the black hole is, a-priori, non-spherically symmetric.

We first focus on the term. To be specific, let us assume that,. This implies that

(A-10)

With this assignment, we are assuming very little deviation from a perfect spherically symmetric black hole. Second, let us assume that the equatorial radius, a, assumes the value, meters. This would correspond to a Schwarzschild radius where the black hole has a mass equal to that of the sun. Our black hole will have a mass slightly less, due to our slightly reduced volume. For the eccentricity chosen,

(A-11)

This is close, but not equal to the mass of the sun,. For these values, Equation, (A-5), gives

(A-12)

Substituting this into Equation, (A-9), renders

(A-13)

The emitted gravitational radiation is measured in Watts since we are using MKS units throughout this paper for numerical evaluations.

We next focus on the term in Equation, (A-13). First, let us consider spherical symmetry. From section III, we know that the work needed to expand the black hole is given by

(A-14)

In this equation, stands for the total surface tension, which will consist of a radiative component, , and a gravitational component,. For most situations, is negligible when compared to,. The exception is when we are dealing with a fantastically massive black hole , where the surrounding black body surface temperature is also very high. For our very modest black hole, this is not the case, and therefore, we will ignore the radiative contribution,. Second, we can estimate/calculate for a black hole having the mass of the sun. This is nothing but the gravitational force acting at its surface. For a radius, , we find Newtons. See the second paper, which was submitted simultaneously with this one, where we perform the calculation in detail. This result is model dependent, i.e., we have assumed a particular mass distribution within the black hole. Since we are interested in an order of magnitude estimate, we will use this number. Third, the work needed to expand the black hole is 1/10 the total radiative energy inflow assuming this is the only influx (assumed here). This, in turn, is 1/5 the total radiative heat inflow. See section II in the text. Therefore,

(A-15)

This is the work required per unit time to expand the black hole assuming spherical symmetry.

Our generalized Stefan-Boltzmann law reads (see section II),

(A-16)

where, is the 3-D radiative force on the 3-D side, just outside the event horizon at temperature,. And the quantity, , is the 4-D radiative force just inside the event horizon, where the temperature is. The quantity, , stands for the net radiative heat inflow. Because of our 4-D/3-D model, we have as a direct consequence, into the black hole. We require a dynamical situation, and so, we will assume, a priori, that,. Another way to write the above equation is,

(A-17)

In this equation,. In Equation, (A-17), we have recast the 4-D quantities in terms of 3-D quantities, observed outside the black hole. See Equation, (2-35), in the text, where this equation is derived from Equation, (A-16). Equation, (A-17), assumes spherical symmetry.

We next relax this requirement. If the surface is not spherically symmetric, as in Equation, (A-4), which holds for an oblate spheroid, then we must substitute (A-4), in place of, in Equation, (A-17). Everything else stays the same. It is easy to imagine this kind of black hole receiving heat uniformly from its surroundings. We can evaluate Equation, (A-4), for an oblate spheroid having, and meters, which are the conditions considered previously. The result is,

(A-18)

This is to be compared to, , which holds for a perfect sphere. Our oblate spheroid has a lessor surface area due to its slightly deformed shape.

We also note that with our new shape, Equation, (A-10), should be rewritten as,

(A-19)

where, is the gravitational pull at the equator of the oblate spheroid. Another way to rewrite Equation, (A-19), is to utilize Equation, (A-17). This will allow us to write,

(A-20)

As mentioned, Newtons, for, a model specific estimate. The surface area is as indicated in Equation, (A-18). And for the temperature, , let us assume a specific value. We will take this temperature to equal, , a relatively large blackbody temperature, just outside the event horizon. We want substantial radiative heat inflow into our non-spherically symmetric black hole. Evaluating the expansion rate in the equatorial plane using Equation, (A-20), gives, under these conditions

(A-21)

This amounts to an increase of only 2.86 meters per year, if the outside blackbody temperature remains steady. Clearly electromagnetic radiation, on its own, will not cause dramatic increases in size.

Moreover, we can now evaluate the gravitational radiation thrown off by this slightly non-spherically symmetric black hole. Using Equation, (A-13), we find,

(A-22)

This is a very, very small amount of gravitational radiation, and yet, it is non-zero. We have thus shown that quadrupole gravitational radiation does exist within our model if we have a dynamic inflow situation, and the mass is not distributed in a perfectly spherically symmetric manner within the black hole.

If we carry out a similar analysis for a much more massive black hole, having mass, , with eccentricity, , we obtain a much larger value for the gravitational quadrupole radiation. Here, , and we still take the outside black body temperature to equal, , for the sake of argument. The relevant surface gravity at the equator has also been worked out, and equals, Newtons. Using these inputs, and following the same steps as before, we find

(A-23)

This is greater than what we obtained in Equation, (A-22), but still relatively unimpressive given the size of the object under consideration, the eccentricity, and the external temperature. This gravitational luminosity is approximately equal to 10,000 times the luminosity of the sun.

In our model, instreaming black body radiation will increase the radiative mass of the black hole if the outside black body temperature exceeds the CMB temperature. Even for substantial outside temperatures, we have seen that the rate of increase is not large. Under extreme conditions, such as coalescence, black hole mergers, in-fall of a star, etc., the black hole mass will increase much more dramatically. And as a consequence, the gravitational radiative bursts will be much more impressive. These are also dynamical and non-spherically symmetric situations, but ones where black body radiation will, almost certainly, play a secondary role. It is difficult to imagine how instreaming radiative inflows can compete with these other inflows, under such circumstances.

We close by remarking that almost all of the inflowing radiative black body radiation will increase the size of the black hole. In a spherically symmetric situation, it appears that all of it will be used up to increase the binding energy of the black hole. It is just that, if inflow is asymmetric, a tiny amount will be siphoned off as gravitational radiation. This will escape to the outside world. The asymmetry does not seem to allow for a perfect 100% utilization, i.e., a perfect 100% increase in radiative mass.

References