ABSTRACT

We start where we use an inflaton value due to use of a scale factor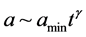. Also we use 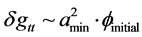as the variation of the time component of the metric tensor 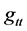in Pre-Planckian Space-time up to the Planckian spacetime initial values. In doing so, we come up with a polynomial expression for a minimum time step; we can call 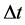which leads to a development of the arrow of time. We show an inter relationship between the formation of the Arrow of time, and Causal structure, assuming the setting of H = 0 in the Friedman equation This in turn leads to entropy production at the start of causal structure in the onset of inflation. This then leads to three and a quarter pages of 7 open questions we think have to be answered, subsequently. It is noted that high frequency gravitational waves as specified are due to the 1/delta t entry in Equation (45) of the document which comes out to about 44 Hertz, and certainly is high frequency gravitational waves for the initial cosmological conditions, so this is definitely about high frequency gravitational wave focused initial conditions.

Keywords:

Inflaton Physics, Causal Structure Entropy, HFGW

1. Examination of the Minimum Time Step, in Pre-Planckian Space-Time as a Root of a Polynomial Equation

We initiate our work, citing [1] to the effect that we have a polynomial equation for the formation of a root finding procedure for, namely if

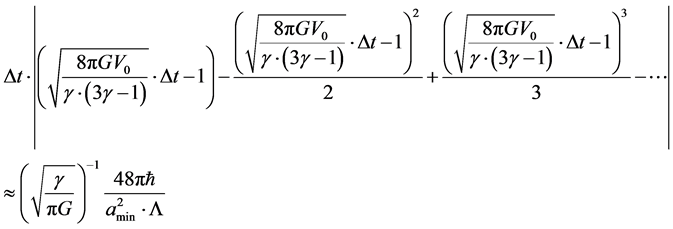(1)

From here, we then cited, in [1] , using [2] , a criteria as to formation of entropy, i.e. if 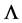is an invariant cosmological “constant” and if Equation (2) holds, we can use the existence of nonzero initial entropy as the formation point of an arrow of time.

(2)

In short, our view is that the formation of a minimum time step, if it satisfies Equation (2) which is a necessary and sufficient condition for the formation of an arrow of time, at the start of cosmological evolution, we have a necessary and sufficient condition for the initiation of an arrow of time. In other words, Equation (2) being non zero with a minimum time step, is necessary and sufficient for the formation of an arrow of time. The remainder of our article is focused upon the issues of a necessary and sufficient condition for causal structure being initiated, along the lines of Dowker, as in [3] .

2. Considerations as to the Start of Causal Structure of Space-Time

In [1] , we make our treatment of the existence of causal structure, as given by writing its emergence as contingent upon having

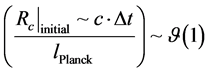(3)

We have assumed in writing this, that our initial starting point for which we can write a Friedman Equation with H = 0 is a finite, very small ball of space- time and that within this structure that the Friedman Equation follows the following conventions, namely

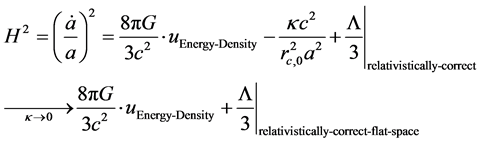(4)

The relativistically correct Friedman equation assumes, that within the confines of the regime for where H = 0 that we write equal to zero; i.e. there is no effective curvature within the confines of Pre-Planckian Space-time and that we make the following assumptions, namely that satisfying Equation (3) above is contingent upon [4] where we are assuming that the volume is normalized to =1, i.e. Planck length is set equal to one.

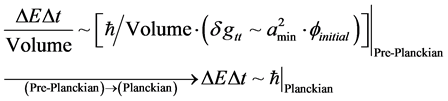(5)

i.e. the regime of where we have the initiation of causal structure, if allowed would be contingent upon the behavior of [5] [6] [7]

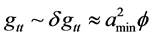(6)

i.e. the right hand side of Equation (6) is the square of the scale factor, which we assume is ~10^-110, due to [5] [6] , and an inflaton given by [8]

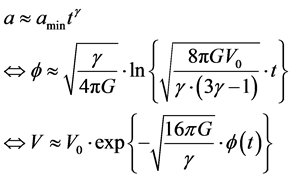(7)

These are the items which were enfolded into the derivation of Equation (1) of reference [1] i.e. our following claim is that Causal structure commences if we can say the following,

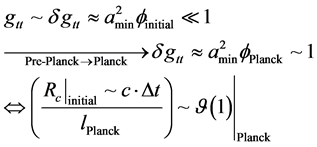(8)

3. So What Is the Root of Our Approximation for a Time Step?

Here for the satisfying of Equation (8) is contingent upon 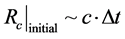as an initial event horizon, of our bubble of space-time being of the order of magnitude of Planck Length, for the satisfaction of forming a regime of space time which may have causal structure as given by Dowker [3] , i.e. at the boundary of a space-time initial bubble [5] [6] which may contravene the Penrose conjecture [9] as to initial singularities.

Furthermore, this is not incommensurate with what Penrose wrote himself in [10] , namely reviewing the Weyl Curvature hypothesis, as given in [10] , i.e. singularities as presumed in initial space-time are very different from singularities of black holes, and that modification of the Weyl curvature hypothesis, may be allowing for what Penrose referred to as gravitational clumping initially to boost the initial entropy, above a presumed initial value. i.e. this we believe is commensurate with Equation (2) above, and is crucially important.

We close this inquiry by noting that what we have done is also conditional upon [11] [12] to the effect that we can write the genesis of our time step formula, as given by Equation (1) above as crucially dependent upon, the following

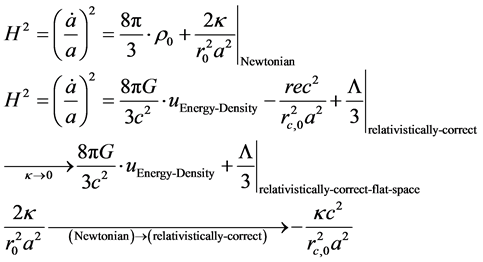(9)

In the third line of Equation (9) the essential substitution is to go from a in the Newtonian case where we have the universe as bounded if in a gravitational sense, or unbounded in a gravitational sense, if to the question of, in relativity of negative curvature, or positive curvature, with. Here what we do, in our own adaptation of Equation (9) is to realize that the Newtonian case involves the conservation of energy for an expanding universe, while we conflate the 2^nd and 3^rd relativistic case involves changing from a mass density, , by an energy Density, which is a generalized version of what we are attempting to analyze.

So, in the Pre Planckian regime of Space-time, our initial assumption is twofold, i.e. we assume that we cannot reference either or. The default choice we will pick is, in the Pre Planckian space-time to simplify our analysis, is to then set. And then we will re image the energy density which will then be in conjunction with a revitalized version of a modified early universe version of the Heisenberg Uncertainty principle.

4. Links to Entropy Production

We claim that what we are doing is contingent upon having, with a specified time step, and this at the boundary of H = 0, as a precursor for forming a causal structure i.e. this will enable us to make full sense out of Equation (9) provided, that within the pre Planckian space-time we have what appears to be paradoxical, i.e. a NEGATIVE energy density, but this consistent with having a negative energy density prior to the Causal barrier, of H = 0. The type of causal set was designated a Conformal causal set, by L. Crowell, [13] whom reviewed an earlier version of this document in the FQXI contest, sans the explicit reference to entropy. Also, we claim that our mixing of entropy and causal structures is an early universe take off of the following document which initially was for black holes, but which we claim is relevant for Pre Planckian structure [14] , but in doing so we make use of the following thought experiment as to forming entropy, gravitons and the like from the following use of H = 0

(10)

The key to this development is accessing the negative energy density in pre Planckian space-time , which if one crosses a causal barrier at H = 0, having this initial energy density, in Pre Causal space-time as negative, which once past the Causal barrier becomes positive, whereas the magnitude of the initial energy would be set at

(11)

In doing so, we have the mass if a graviton is specified as in [15] . And then the open question to be asked is, do we have in this case a situation where say the gravitons act as information carriers from a prior universe? Our intuition says yes, and we will follow up upon this with necessary and sufficient conditions for cyclic universe interpretations of this model, in a future publication.

In this case, the mass of a graviton, would be of the order of 10^−62 grams, which would specify, then a very small initial energy if we have that we are also using the Ng approximation for infinite quantum statistics of [16]

(12)

As well as an initial frequency of the “particles” given by

(13)

We also claim, that this procedure, is in its own way tandem with [17] which in turn has another “bubble” in the start of space-time.

We furthermore claim that additional development of this methodology will entail use of reconciling this work with page 428 of Baez, and Muniain, [18] , specifically as an alternative to the well-researched section on Canonical quantization, used in ADM relativity i.e. what we are doing is by default coming up with an alternative to what has been done in [18] and other places, as well as making a semi classical linkage to gravitons and entropy.

5. Seven Open Questions, Which Remain to Be Answered

To close this section, one of the remaining problems which have to be addressed in this methodology is to address what was brought up by Tolman, [19] , i.e. if we have a cyclical universe that from each cyclical “bounce”, from cycle to cycle, entropy will increase especially at the beginning.

Our Causal structure argument has to be tweaked in order to avoid this development, which will be a topic of a future publication i.e. we need to have exact referencing of a nonzero, but not incrementally increasing initial entropy, per start of a cosmological cycle.

The final set up of our problem will also entail the use of, also reconciling the H = 0 structure of the Causal structure boundary, with what is given for the initial expansion of the Universe as given by [20] , i.e.

(14)

Here, the term is for degrees of freedom of the universe, which is usually of the order of 100, [21] but the author got figures in the ballpark of about 1000, in [22] . Needless to state, with being an enormous value, and the mass scale being less than or equal to Planck’s mass, the question of what causes a perturbation from H = 0 to Equation (14) needs to be addressed i.e. do we have to say that was initially zero, and then obtained an enormous value?

Last but not least, is that we have in our pre causal Pre Planckian structure,

(15)

What values of the Cosmological constant are we assuming in the Pre Planckian to Planckian Universe transition?

Either it is of the sort where remains invariant, or else we have to say [23]

(16)

This has to be worked out, for the obvious reasons, as well as looking at, if we have an iterative process for the generation of along the lines of looking at an iterative dynamical systems mapping, i.e. a chaotic map driven increase in degrees of freedom from a low point to a high point with vacuum thermal energy initially tied to [22]

(17)

Not only this, we should also consider if we are looking at massive gravitons, an analytical bridge between Pre Planckian representations of Gravitons and the following Planckian, to post Planckian space-time physics as given by a regime of space-time where we go from close to zero, or initially zero Pre Planckian space-time temperatures, to the super-hot initial conditions of inflation, i.e. note that as given by Giovanni, the figure of 10⁸⁸ as due to gravitons can be seen to come from [5] , page 156 as

(18)

There are two questions which this raises: What would be the driving impetus to go from a low temperature pre space time temperature, then to Planck time entropy, then to the entropy of today as given in Equation (18)?

One way to look at it would be to suggest as done by H. Kadlecova [24] in the 12 Marcel Grossman meeting the typical energy stress tensor, using, instead, Gyratons, with an electro-magnetic energy density addition to effective Electromagnetic cosmological value as given by

(19)

i.e. that there be, due to effective E and M fields, a boost from an initially low vacuum energy to a higher ones, as given by Kadlecova [24] [25]

(20)

How would Equation (25) is used in Equation (11) to Equation (15) affect our Pre Planckian to Planckian physics results? This needs to be considered.

Last but not least, if we are considering massive gravitons, we should look at the following perturbative terms added to a metric tensor by massive gravitons. I.e. understand the values as influenced by massive gravitons. As read from Beckwith [26] we get excessive nonlinearity, and the equations of perturbation of the metric tensor are given by the following treatment by Hinterbichler [27] , if, and we look at a mass induced suppression factor put in of, with m perhaps the mass of a massive graviton, and M say Planck’s mass then

(21)

(22)

(23)

Here, we have that these are solutions to the following equation, as given by [27]

(24)

So the question remains how to be bridge Equation (23) and Equation (24) to the massive graviton conditions we are considering for Pre Planckian space- time? Clearly, Equation (23) and Equation (24) are for Planckian to Post Planckian space-time physics.

Here, we are assuming for Equation (23) and Equation (24)

(25)

And use the value of the radius of the universe, as given by , and rather than a super partner Gravitino, use the.

How do they get bridged to the Pre Planckian regime?

One possible benefit, if we get this matter of information theory and entropy settled i.e. does the following make sense?

In an earlier document the author submitted to FQXI, in 2012, the author tried to make the following linkage between presumed super partners (SUSY), in the electroweak regime of space-time, and the mass of non-super partner particles i.e. in 2012, the supposition was that

(26)

In an earlier document, the idea was to make a bridge between presumed total mass of Gravitinos, , in the electroweak era with their counterpart in

Gravitons, today, which we called,. In Equation (26), we also

had being the presumed radius of the universe in the electroweak era, with the radius of the universe “today”.

Equation (26) was a presumed “conservation law”.

The problem, in all this, is that there is still not definitive evidence of super partners in CERN! Nor may there ever be found either! Can we, then if we abandon the idea of super partners, come up with a bridge between Pre Planckian to Planckian physics, using gravitons, along the lines of Equation (26)? This requires a review, of the issues, brought up in [28] , and to see if they are necessary.

We should note in passing that [29] [30] [31] are important considerations, with [29] giving the details of gravitational wave detection, as noted by LIGO in 2016. [30] Confirms the essence of scalar tensor theories as a competitor to General Relativity which should be falsified, if possible, and [31] goes into more of massive body generation of gravitational waves which certainly is appropriate here in the early universe.

With that the questions are laid out for review and consideration.

Acknowledgements

This work is supported in part by National Nature Science Foundation of China Grant No. 11375279.

Cite this paper

Beckwith, A.W. (2017) How a Minimum Time Step Leads to a Causal Structure Used to Form Initial Entropy Production and High Frequency Gravitons, with 7 Subsequent Open Questions. Journal of High Energy Physics, Gravitation and Cosmology, 3, 493-502. https://doi.org/10.4236/jhepgc.2017.33038

References