Journal of High Energy Physics, Gravitation and Cosmology
Vol.03 No.02(2017), Article ID:74913,13 pages
10.4236/jhepgc.2017.32021
Methodology of Wavelets in Relativistic Heavy Ion Collisions in One Dimensional Phase Space ( -Space)
-Space)
Vyacheslav V. Lyashenko1, M. Ayaz Ahmad2, Zhanna V. Deineko3, Mir Hashim Rasool4
1Department of Informatics, Kharkiv National University of Radio Electronics, Kharkiv, Ukraine
2Physics Department, Faculty of Science, University of Tabuk, Tabuk, Saudi Arabia
3Department of Media Systems and Technology, Kharkiv National University of Radio Electronics, Kharkiv, Ukraine
4Department of Physics, Islamic University of Science and Technology, Awantipora, India
Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: February 9, 2017; Accepted: March 24, 2017; Published: March 27, 2017
ABSTRACT
An attempt has been made to apply the wavelet methodology for the study of the results of the chaotic behavior of multiparticle production in relativistic heavy ion collisions. We reviewed the data that describes the collisions of relativistic heavy ion for the case 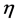 -space in 1-D phase space of variable. We compared the experimental data and UrQMD data using wavelet coherency. We discussed the results of the comparison.
-space in 1-D phase space of variable. We compared the experimental data and UrQMD data using wavelet coherency. We discussed the results of the comparison.
Keywords:
Wavelet Coherence, Morlet Wavelet, Heavy Ion Collisions, Reaction Dynamics, Phase Space, Normalized Factorial Moments

1. Introduction
Particle physics is the science of the fundamental structure of matter. One of the directions of particle physics is the study of high-energy nuclear matter. The interest in the study of high-energy nuclear matter has increased many folds due to the possibility of studying unstable states of nuclear matter under extreme condition of high energy density and high temperature. The study of non-statistical fluctuations in relativistic nuclear collisions has recently also attracted a great deal of attention due to the possibility of extracting important information about the mechanism of multiparticle production in such collisions [1] [2] . The multiplicity of charged particles in high energy nucleus-nucleus interactions is an important parameter which indicates how many particles are produced in that interaction. In the same time the multiplicity distributions of produced particles help in learning the interaction mechanism [3] [4] .
But it is appropriate to study the field in terms of theoretical and the experimental points of view. This will help understand the relationship between theory and experiment, understand the complicated moments which may arise. Theory predicts phenomenon, which can be verified by experiments, and experiments very often provide new insight through unexpected results, which in turn lead to the improvement in theoretical description. In the present paper, an attempt has been made to find the relationship between the stability of a theoretical model and experiment to study the collisions of relativistic heavy ion. This exercise has been made to perform the study of (E-by-E) spatial fluctuations of relativistic shower particles produced in the collisions of 28Si + Em at energy 14.6A GeV in 1-D phase space of  -variable (the case
-variable (the case 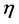 -space) [5] . The findings are compared with the predictions of Ultra-relativistic Quantum Molecular Dynamics (UrQMD) model [6] [7] .
-space) [5] . The findings are compared with the predictions of Ultra-relativistic Quantum Molecular Dynamics (UrQMD) model [6] [7] .
To solve this problem we use wavelets ideology [8] [9] . This is due to the fact that various processes and the phenomenon can have quite difficult structure, and contain local features of the various form and time extent. Wavelet-analysis transforms the original data to hierarchical structure by means of the wavelet transformations which results to the set of wavelet coefficients. If the signal is discontinuous, only those wavelets will have high amplitudes, where the maximum value will appear near the discontinuity point, which will allow detecting image contour. At the same time, discontinuity point is a sharp intermittent transition during some process. Quantitatively, it can be estimated by the value of the first derivative of such process, taking into consideration that the first derivative of intermittent transitions is very high. If the transition is in the form of discontinuity point, then the first derivative tends to infinity. The sharper the transition, the higher the derivative value is. Smooth transitions will have small derivative values. This allows us to determine the presence of special characteristics of the analyzed one, as well as the point where these characteristics may arise [10] [11] . Thus methodology of wavelet analysis allows taking into consideration the particular characteristics study by decomposing source data into a plurality of approximate and detailed coefficients. This allows conducting a detailed analysis of the original data.
2. Some Experimental Details
To obtain the data, FUJI nuclear emulsion pellicles were irradiated horizontally with a beam of 28Si nuclei at 14.6A GeV at Alternating Gradient Synchrophasotron (AGS) of Brookhaven National Laboratory (BNL), New York, USA have been used. The nuclear emulsion experiment is a versatile detector for the study of nuclear reactions in high energy heavy ion collisions. It has the ability to detect and identify the secondary charged particles in the outlet channel of nuclear reactions. The method of line scanning has been adopted to scan the stacks, which was carried out carefully using Japan made NIKON (LABOPHOT and Tc-BIOPHOT) high-resolution microscopes with 8 cm movable stage using 40× objectives and 10× eyepieces by two independent observers, so that the bias in the detection, counting and measurements can be minimized. The interactions due to beam tracks making an angle < 2˚ to the mean direction and lying in emulsion at depths > 35 mm from either surface of the pellicles were included in the final statistics [5] [12] .
3. Mathematical Formalism for Obtaining Data
In order to perform a meaningful analysis of chaoticity, normalized cumulative variable (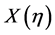 ) were used to reduce the effect of non-uniformity in single charged particle distributions. At the same time, we consider only one component in 1-D phase space of
) were used to reduce the effect of non-uniformity in single charged particle distributions. At the same time, we consider only one component in 1-D phase space of 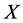 -variable (this is the case
-variable (this is the case 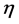 -space). The single charged particle density distribution is not flat in the analysis of the fluctuation in phase space variable. This non-uniformity of the particle spectra influences the scaling behaviour of scaled factorial moments. Bialas and Gazdzicki [13] proposed a method to construct a set of variables, which drastically reduces the distortion of intermittency due to the non-uniformity of single particle density distribution. According to them, the new scaled variable
-space). The single charged particle density distribution is not flat in the analysis of the fluctuation in phase space variable. This non-uniformity of the particle spectra influences the scaling behaviour of scaled factorial moments. Bialas and Gazdzicki [13] proposed a method to construct a set of variables, which drastically reduces the distortion of intermittency due to the non-uniformity of single particle density distribution. According to them, the new scaled variable 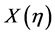 is related to the single particle density distribution
is related to the single particle density distribution 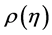 by the following relation:
by the following relation:
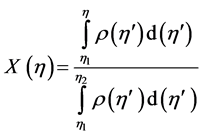 , (1)
, (1)
where, 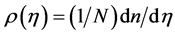 is the single particle pseudo rapidity density distribution of the shower particles and
is the single particle pseudo rapidity density distribution of the shower particles and  and
and 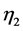 are the two extreme points in the distribution ρ(η) (or
are the two extreme points in the distribution ρ(η) (or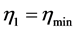 ,
,  ,). Should also be noted that, in terms of new scaled variable (
,). Should also be noted that, in terms of new scaled variable (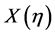 ) the single particle density distribution is always uniform in between X = 0 and 1.
) the single particle density distribution is always uniform in between X = 0 and 1.
Various experimental efforts have established the existence of the empirical phenomenon of “intermittency” in multiparticle production using normalized scaled factorial moments. On the basis of bin averaging the normalized scaled factorial moments of the order of q is defined in vertical form as [5] [12] [13] :
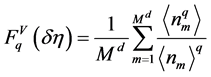 (2)
(2)
and its horizontal form is defined as [5] [12] [13] :
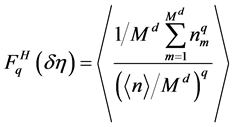 , (3)
, (3)
where, 




Recently, Cao and Hwa first introduced to measure the spatial pattern of particles in an event using normalized factorial moments associated with it. In contrast to the horizontally averaged vertical moments, 


where, M is the partition number in phase space, 

The event factorial moments, 




where, 


In order to quantify the degree of the fluctuations, a new normalized moment related to the chaotic nature of the system is defined as [14] [15] [16] :

where, p is any positive real number, it should not be negative, 
The other relevant details may be seen in works [5] [12] .
Thus, we examine the relationship between, 





We can see (see Figure 1), which is experimental data and UrQMD data can be varied in a certain range. Thus, we have a few of time series. These time series should be compared using the ideology of wavelets. For this we will use the wavelet coherency.
4. Methods of Wavelet Analysis as Tool to Study Time Series
The basis of formal generalization of continuous wavelet transformation on the time interval 


Figure 1. Variations of 


where 



In this case, feasibility of wavelet analysis in time series study is determined by the fact that the method of wavelet analysis allows to discover the local features of the studied time series due to the decomposition of the input data [18] [19] . That is, the wavelet transformation defines the hierarchical structure of the input of the studied time series. Underlying this statement is the fact that information flows, generated by fractal time series have properties detected by wavelet transform, making it even more informative [10] . Then wavelet transform allows adding input characteristics of time series that are investigated.
In addition, the empowerment of study time series using wavelet analysis methodology promotes the use of various procedures of wavelet transformation: even-scaled analysis, cross wavelet transformation, wavelet coherence. Then wavelet analysis methodology has been widely used in the disclosure of dynamics of time series that define various data [10] [11] .
One of the main wavelet transformation methods used for generalized cross-reference analysis between different time series is wavelet coherence. It allows calculating local correlation of two time series in a region of time-frequency. It uses the following formalized model: wavelet coherence as the squared absolute value of the smoothed cross wavelet spectra 



where 
We use Morlet wavelet that is a complex wavelet with a good time-frequency localization, as a parent one [20] - [26] . The squared wavelet coherency coefficient is in the range
5. Result and Discussion
We consider the wavelet coherency for each pair of time series of the natural log 

In Figures 2-6 you can check the results of wavelet coherence between selected time series. Each of the following figures indicated a sepa-rate group of time series that match each other. This comparison is displayed in the time-frequency plane. In this case the time scale is equal to the consistent change of values 


On the vertical axis are the weighted characteristics of the analyzed data series in frequency space. Along each of the figures importance scale is presented as separate columns for reflections. Maximum reflection is speaks about full coherence between the experimental data and UrQMD data. Defined lines are a manifestation of localization for individual irregularities within studied time series according to importance of irregularities. In general, each point of wavelet reflects shown in Figures 2-6 is their value in the time-frequency space, which is calculated through wavelet transformation.
The phase difference, indicated by arrows, gives us details about delays of oscillation of the two examined time series. Arrows pointing to the right (left) when the time series are in-phase (anti-phase) or are positively (negatively) correlated. Arrow pointing up means that the first time series leads the second one, arrow pointing down indicates that the second time series leads the first one. In our case, these data suggest discrepancy of the experimental data according to the model.
We see that with increasing values q of unbalance occurs between the experimental data and UrQMD data. This is observed for all values p. With increasing the values of p and when is increased the values q imbalance between the experimental data and UrQMD data increasing. Especially it is typical for q = 4. Such
Table 1. The correspondence between a sequence number and value of
Figure 2. Wavelet coherence between the experimental data and UrQMD data for p = 0.5. (a) q = 2; (b) q = 3; (c) q = 4.
Figure 3. Wavelet coherence between the experimental data and UrQMD data for p = 0.9. (a) q = 2; (b) q = 3; (c) q = 4.
Figure 4. Wavelet coherence between the experimental data and UrQMD data for p = 1.2. (a) q = 2; (b) q = 3; (c) q = 4.
Figure 5. Wavelet coherence between the experimental data and UrQMD data for p = 1.4. (a) q = 2; (b) q = 3; (c) q = 4.
Figure 6. Wavelet coherence between the experimental data and UrQMD data for p = 1.6. (a) q = 2; (b) q = 3; (c) q = 4.
an increase is observed for the mean values
6. Conclusions
The results of the study can determine the appropriate application of wavelet analysis methodology as disclosure of wavelet coherency between the studied data series as a tool for the study collisions of relativistic heavy ion. Some comparative results between the experimental data and UrQMD data have been obtained from the analysis of event-by-event fluctuations of produced charged particles in heavy ion collisions at 14.6A GeV. We showed overall consistency between the experimental data and UrQMD data. But we also note that coherence decreases with increasing values of q. This result was obtained for the case 
Acknowledgements
The authors would like to acknowledge the keen support for this work of the Department of Physics, Faculty of Science, University of Tabuk, Saudi Arabia and also the Department of Informatics, Kharkiv National University of Radio-Electronics, Kharkiv, Ukraine [22] - [32] .
Cite this paper
Lyashenko, V.V., Ahmad, M.A., Deineko, Z.V. and Rasool, M.H. (2017) Methodology of Wavelets in Relativistic Heavy Ion Collisions in One Dimensional Phase Space (
References
- 1. Ahmad, S. and Ahmad, M.A. (2006) A Comparative Study of Multifractal Moments in Relativistic Heavy-Ion Collisions. Journal of Physics G: Nuclear and Particle Physics, 32, 1279-1293.
https://doi.org/10.1088/0954-3899/32/9/006 - 2. El-Harby, A.A. and Behery, G.M. (2008) Automatic Neural Network System for Vorticity of Square Cylinders with Different Corner Radii. Journal of Applied Mathematics & Informatics, 26, 911-923.
- 3. El-Bakry, M.Y. and El-Metwally, K.A. (2003) Neural Network Model for Proton-Proton Collision at High Energy. Chaos, Solitons & Fractals, 16, 279-285.
- 4. Abou-Moussa, Z. (2002) Compound Multiplicity in the Collisions of 4.1 A GeV/c 22Ne Nuclei with Nuclear Emulsion. Canadian Journal of Physics, 80, 109-117.
https://doi.org/10.1139/p01-143 - 5. Ahmad, M.A., Rasool, M.H., Ahmad, S., Ahmad, N.A. and Madani, J.H. (2013) Chaotic Behaviour of Multiparticle Production in Relativistic Heavy ion Collisions. International Journal of Enhanced Research in Science Technology & Engineering, 2, 77-89.
- 6. Bass, S.A., et al. (1998) Microscopic Models for Ultrarelativistic Heavy Ion Collisions. Progress in Particle and Nuclear Physics, 41, 255-369.
- 7. Bleicher, M., et al. (1999) Relativistic Hadron-Hadron Collisions in the Ultra-Relativistic Quantum Molecular Dynamics Model. Journal of Physics G: Nuclear and Particle Physics, 25, 1859-1924.
https://doi.org/10.1088/0954-3899/25/9/308 - 8. Lyashenko, V., Kobylin, O. and Ahmad, M.A. (2014) General Methodology for Implementation of Image Normalization Procedure Using Its Wavelet Transform. International Journal of Science and Research, 3, 2870-2877.
- 9. Lyashenko, V.V., Ahmad, M.A. and Kobylin, O. (2016) Wavelet Analysis as a Learning Tool a Polymer Composites. American Journal of Engineering Research, 6, 1-6.
- 10. Lyashenko, V., Deineko, Z. and Ahmad, A. (2015) Properties of Wavelet Coefficients of Self-Similar Time Series. International Journal of Scientific and Engineering Research, 6, 1492-1499.
- 11. Lyashenko, V.V., Matarneh, R. and Deineko, Z.V. (2016) Using the Properties of Wavelet Coefficients of Time Series for Image Analysis and Processing. Journal of Computer Sciences and Applications, 4, 27-34.
- 12. Rasool, M.H., Ahmad, S. and Ahmad, M.A. (2015) Signal of Unusual Large Fluctuations in 32S-Em Interactions at SPS Energies. Journal of the Korean Physical Society, 67, 448-457.
https://doi.org/10.3938/jkps.67.448 - 13. Bialas, M. and Gradzicki, M. (1990) A New Variable to Study Intermittency. Physics Letters B, 252, 483-486.
- 14. Cao, Z. and Hwa, R.C. (2000) Erraticity Analysis of Multiparticle Production. Physical Review D, 61, Article ID: 074011.
https://doi.org/10.1103/PhysRevD.61.074011 - 15. Bialas, A. and Czyz, W. (2000) Event by Event Analysis and Entropy of Multiparticle Systems. Physical Review D, 61, Article ID: 074021.
https://doi.org/10.1103/PhysRevD.61.074021 - 16. Ghosh, D., Deb, A., Mondal, M. and Ghosh, J. (2003) Erraticity Analysis of Multipion Data in 32S-AgBr Interactions at 200A GeV. Physical Review C, 68, Article ID: 024908.
https://doi.org/10.1103/PhysRevC.68.024908 - 17. Kingsbury, N. (1999) Image Processing with Complex Wavelets. Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 357, 2543-2560.
https://doi.org/10.1098/rsta.1999.0447 - 18. Heil, C.E. and Walnut, D.F. (1989) Continuous and Discrete Wavelet Transforms. SIAM Review, 31, 628-666.
https://doi.org/10.1137/1031129 - 19. Delbeke, L. and Abry, P. (2000) Stochastic Integral Representation and Properties of the Wavelet Coefficients of Linear Fractional Stable Motion. Stochastic Processes and Their Applications, 86, 177-182.
- 20. Torrence, C. and Webster, P.J. (1999) Interdecadal Changes in the ENSO-Monsoon System. Journal of Climate, 12, 2679-2690.
https://doi.org/10.1175/1520-0442(1999)012<2679:ICITEM>2.0.CO;2 - 21. Grinsted, A., Moore, J.C. and Jevrejeva, S. (2004) Application of the Cross Wavelet Transform and Wavelet Coherence to Geophysical Time Series. Nonlinear Processes in Geophysics, 11, 561-566.
https://doi.org/10.5194/npg-11-561-2004 - 22. Ahmad S., Ahmad, M.A., Irfan, M. and Zafar, M. (2006) Study of Non-Statistical Fluctuations in Relativistic Nuclear Collisions. Journal of the Physical Society of Japan, 75, Article ID: 064604.
https://doi.org/10.1143/JPSJ.75.064604 - 23. Ahmad, S. and Ahmad, M.A. (2006) Some Observations Related to Intermittency and Multifractality in 28Si and 12C-Nucleus Collisiond at 4.5A GeV. Nuclear Physics A, 780, 206-221.
- 24. Ahmad, M.A. (2010) A Study of Intermittency and Multifractality in 28Si-Emulsion Collisions at 14.6A GeV. PhD Thesis, Aligarh Muslim University, Aligarh, India.
- 25. Rasool, M.H., Ahmad, M.A., Bhat, M.A. and Ahmad, S. (2015) Study of Compound Particle Production in 28Si and 32Semulsion Collisions at 14.6 and 200 AGeV. World Journal of Nuclear Science and Technology, 5, 208-220.
https://doi.org/10.4236/wjnst.2015.53021 - 26. Tariq, M., Ahmad, M.A., Ahmad, S. and Zafar, M. (2007) Analysis of High NS-Multiplicity Events Produced in Relativistic Heavy Ion Collisions at 4.5A GeV/c. Romanian Reports in Physics, 59, 773-790.
- 27. Rasool, M.H., Ahmad, M.A., Singh, O. and Ahmad, S. (2015) Some Important Features of Relativistic Charged Particles Produced in 32S-Emulsion Interactions at 200 AGeV/c. Journal of Modern Physics, 6, 1498-1509.
https://doi.org/10.4236/jmp.2015.611154 - 28. Ahmad, M.A., Rasool, M.H., Ahmad, S., Madani, J.H. and Ayad, R. (2013) Study of Deconfinement Phase Transition in Heavy Ion Collisions at BNL Energies. International Journal of Applied Physics and Mathematics, 3, 289-292.
https://doi.org/10.7763/ijapm.2013.v3.223 - 29. Ahmad, M.A., Rasool, M.H. and Ahmad, S. (2013) Scaling Nature of Target Fragments in the Interactions of 28Si-Emulsion at Energy 14.6A GeV. Ukrainian Journal of Physics, 58, 944-955.
https://doi.org/10.15407/ujpe58.10.0944 - 30. Ahmad, M.A. and Ahmad, S. (2012) Study of Angular Distribution and KNO Scaling in the Collisions of 28Si with Emulsion Nuclei at 14.6A GeV. Ukrainian Journal of Physics, 57, 1205-1213.
- 31. Rasool, M.H., Ahmad, M.A. and Ahmad, S. (2015) Multifractal Study and Multifractal Specific Heat of Singly Charged Particles Produced in 32SEm Interactions at 200 AGeV. Chaos Solitons & Fractal, 81, 197-202.
- 32. Rasool, M.H., Ahmad, M.A., Singh, O. and Ahmad, S. (2015) Multiplicities of Forward -Backward Relativistic Charged Particles Produced in 32S-Emulsion Interactions at 200 A GeV/c. Chinese Journal of Physics-Taipei, 53, 100302-100312.








