World Journal of Cardiovascular Diseases
Vol.06 No.07(2016), Article ID:69038,11 pages
10.4236/wjcd.2016.67026
Value of Topology Approach to Diagnose of CAD Based on Magnetocardiographic Current Distribution Maps in Difficult-to-Diagnose Patients
I. Chaikovsky1, L. Stadnyuk2, A. Verba3, Yu. Vasetskyi4, M. Budnyk1, G. Mjasnikov5, A. Kazmirchuk5, A. Lomakovskyi6
1Glushkov Institute of Cybernetics, National Academy of Science, Kiev, Ukraine
2Shupyk National Medical Academy of Post-Graduate Education, Kiev, Ukraine
3Department of Military Medicine, Ministry of Defense, Kiev, Ukraine
4Institute of Electrodynamics, National Academy of Science, Kyiv, Ukraine
5National Military Medical Center, Ministry of Defense, Kiev, Ukraine
6Strazhesko National Scientific Center of Cardiology, Kiev, Ukraine

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 June 2016; accepted 23 July 2016; published 26 July 2016
ABSTRACT
Objective: The purpose of this work is to examine the usefulness of the topological approach for analysis of current density maps during ST-T interval in detection of coronary artery disease (CAD) in patients with proved CAD but normal results of routine tests. Materials and Methods: The patient group included 123 patients. Coronary angiography was done due to chest pain. The control group consisted of 124 healthy volunteers. The MCG test was done by 4-channels MCG system installed at unshielded setting. An integral topological index Kideal, consisting of 4 parameters, has been counted. Results and Conclusions: It is shown that Kideal was higher in patient group compared to control one. Sensitivity was 87%, and specificity was 64%. The topological analysis of MCG current density maps is a valuable tool in noninvasive detection of CAD in difficult-to-diag- nose patients with uninformative results of routine tests.
Keywords:
Magnetocardiography, Coronary Artery Disease, Current Distribution, Difficult-to-Diagnose Patients, Topology Parameters

1. Introduction
The aim of the magnetocardiographic (MCG) investigation is to estimate electrical activity of the myocardium in terms of current density distribution (CDD) instead of the surface electrical potential in order to reveal heart abnormality at early stage. However, “raw” information contained in the magnetic signal is not appropriate for direct interpretation. A clear system of diagnostic criteria is required similar to the system that has evolved in electrocardiography (ECG).
The analysis of the MCG could be described at successive levels of computerized MCG signal processing [1] . The most advanced level of analysis is based on so-called inverse solution, i.e. modeling of electrical activity in the entire heart. Analysis of the distributed sources in a form of current density vectors is the most understandable for physicians. The current distribution maps obtained are easy to classify in terms of norm or pathology.
There are some approaches for visual sorting of these map which could be provided by physician-expert [2] - [4] . A visual classification is widely used in clinical practice but has some obvious disadvantages, associated with the subjectivity of such evaluation. An objective classification is more reliable in everyday clinical practice, especially in context of medical stuff training and reproducibility of the results.
The approach, proposed in this paper proceeds from the following considerations. The electrical generator of the heart may be represented as an extended current source located in the frontier area, separating excited and non-excited areas of heart muscle. This excitation wavefront, integrated in a medium with homogeneous conductivity, should be directed left-downwards, to the sector 10˚ - 80˚ (the normal direction for ventricular repolarisation creates two equal symmetrical current vortexes). Any pathological processes in the heart muscle will lead to decrease of electrical non-homogeneity, resulted in asymmetry of vortices and, further, additional excitation wavefronts appearance. These pathological wavefronts contribute to a non-dipole patter of the maps and in most cases the wavefronts do not have left-downward directions. Hence, the zones of larger current vectors with normal directions were appeared lesser.
Thus, topological approach takes into consideration a presence of wavefronts (directions and numbers of wavefronts) and generates current distribution structure (parameters of current vertexes). More widely, topological parameters are characteristic of number, geometric shape, location, relative intensity, form, ovality, connectivity, etc. of areas with high and low density currents.
Results of MCG examinations are especially valuable in that clinical cases which are “difficult-to-diagnose” based on routine diagnostic techniques, first of all in detection of coronary artery disease (CAD). The non-inva- sive diagnosis of CAD continues to be an actual clinical task. Resting ECG is often normal in these patients and the diagnostic accuracy of EchoCG and other functional tests such as nuclear imaging is often not good enough and can be related with risk. Thus MCG is hopeful as a novel fully-non-invasive diagnostic method for CAD detection [5] - [8] .
The purpose of this paper is a elaboration of novel method for objective computerized sorting of the current density vectors maps, and testing of this approach in patients with proved CAD but non-conclusive resting ECG and EchoCG.
2. Methods
2.1. Patient Groups (Formed during 2011-2014 Year)
Overall 123 patients (106 male, 17 female, age 60 ± 4.5 years) suffering from stable or unstable angina and angiographically verified CAD with stenosis of ³50% of at least one coronary vessel but with normal or unspecifically changed ECG at rest (absence of ST-segment depression or elevation, negative T-waves no more than in 2 leads), normal left ventricular function, absence of wall motion disturbances, without prior myocardial infarction were enrolled in this survey. 79 patients were underwent coronary angiography because of chest pain. 124 healthy subjects were included in control group (100 male, 24 female, age 51 ± 3.1 years). The patients were chosen successively from all patients admitted to Cardiology Clinics of National Military Medical Center during the years 2010-2013, with the indication for coronary angiography due to chest pain. The control group comprised of healthy volunteers with no history of any cardiovascular disease, normal ECG at rest and stress as well as a normal resting echocardiogram. In 7 volunteers, echocardiography under dobutamine stress was performed, with a negative result.
2.2. Data Acquisition
12 lead ECG and MCG were accomplished in all subjects. MCG investigations were done using 4-channel SQUID-gradientometer of the 2nd order in a stable or moveable unshielded setting. The sensitivity of apparatus was 25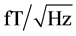 , recording bandwidth―from 0.1 Hz up to 120 Hz.
, recording bandwidth―from 0.1 Hz up to 120 Hz.
MCG recordings were taken at 36 pre-thoracic points (6 × 6 with a 4 cm pitch). Hence, the measurement grid constitutes 20 cm square over the pericardial area. The sensor was positioned as close to the thorax as possible, directly over the heart initially at the jugulum. The examination table with the patient resting in the same position was then moved in a systematic fashion to each of the 9 predetermined positions (each of them includes 4 measurement points) under the SQUID detector. Data were recorded at each position during 30 seconds with simultaneous registration of lead II of the surface ECG. All steps of data acquisition and analysis were performed by software MAGWIN [9] .
Coronary angiography and left heart catheterization were acquired in multiple projections using the Judkins technique according to standard clinical practice (Siemens Cathcor,
In MCG in each raw data set all beats were preprocessed and averaged at each position. For further analysis the reconstruction of current density vector (CDV) maps was applied. The CDV maps represent the 2 dimensional image of the cardiac de- and repolarization process on 100 positions, whereby every map is recalculated from data of all points of registration. In both groups CDV maps were generated every 10 ms within the ST-T interval starting with the J-point. As a result about 20 maps have been obtained for every recording.
2.3. Models of Current Distribution and Parameters for Maps Sorting
A concept of “ideal” current map is utilized to develop clinically useful classification systems for analysis of a structure of a current distribution in human heart. Based upon the existing understanding of the current initiation in the cardiac muscle, the 2-dimensional models are considered for current distributions in a healthy heart (ideal distribution) and upon pathological alterations, characterized by additional distributed sources (or fronts of the sources) as well as by the heterogeneous conductivity. Using qualitative analysis of the current map structure, the characteristics are derived, which are appropriate as a basis for classification parameters reflecting real processes in a cardiac muscle. Two classification systems of parameters and an algorithm for generation of the decision rules for every of the systems are considered.
2.4. Models of Current Distribution
The model of distribution current is based on approach that is widely used for solving of MCG problem [10] [11] . Electrical generator of the myocardium during repolarization can be represented as a system of current sources distributed along lines of small thickness―fronts of sources. As it is noticed in [12] , similar approximation of the current sources in macroscopic zones of myocardium is sufficiently accurate only at relatively large distance from the sources and, in particular, upon MCG measurements of the magnetic fields.
According to the model, the sources are not distributed throughout the volume, but only at the interface between excited and unexcited zones. In the interior of the sources charge movement occurs due to non-electrical (concentration) forces. Outside the sources, the current flows in a conductive medium with properties. In the present work 2D model is considered for distribution current, created by one or several expanded sources of small thickness.
Let us assume that in a medium with uniform conductivity s, current is generated by the sources distributed along the front of a length L (Figure 1(a)). Let us consider such a front as a double layer of the current sources with densities 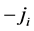 and
and 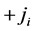 (Figure 1(b)). If the thickness of the source a is negligible compared to the longitudinal front dimension and distance r to the observation points Q, it is always possible to choose an element of the front length dl from the condition
(Figure 1(b)). If the thickness of the source a is negligible compared to the longitudinal front dimension and distance r to the observation points Q, it is always possible to choose an element of the front length dl from the condition . In that case, outside the front the field can be found as a superposition of the dipole sources. Inside thin extended source the density current and intensity of the electric field are uniform.
. In that case, outside the front the field can be found as a superposition of the dipole sources. Inside thin extended source the density current and intensity of the electric field are uniform.
With regard to the assumptions made, it is easy to show that the potential j and the current function y, created by the distributed sources, in an arbitrary point of the plane Q(x, y) can be expressed as follows [9] :

Figure 1. Wavefront propagation (a) and its structure as double current layer (b).
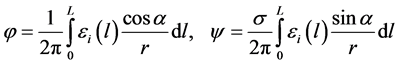 , (1)
, (1)
where 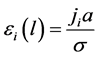 is an electromotive force of the source, distributed along the front.
is an electromotive force of the source, distributed along the front. 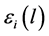 value determines
value determines
the surface density of the dipole moment of the double electric layer along the front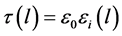 .
.
The intensity of the electric field E and the current density in a conductive medium j = sE are represented by
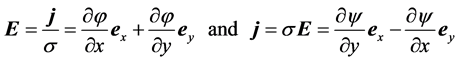 . (2)
. (2)
In ECG a potential distribution j is used more often [11] .
For investigation of the heart magnetic field, current function y is more suitable. In that case current lines are determined by the condition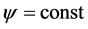 , at that the difference of two magnitudes y gives the total current between correspondent lines, which magnitude is independent from the choice of the cross-section s between the lines:
, at that the difference of two magnitudes y gives the total current between correspondent lines, which magnitude is independent from the choice of the cross-section s between the lines:
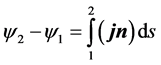 . (3)
. (3)
We consider several typical examples of the current distribution, obtained via modeling of the current distribution in a medium. In a 2D (plane) model assume that every separate front is characterized by a straight line of a finite length in relation to the fact that front of the sources usually presents a slightly curved surface. Moreover, assume that an electromotive force or surface density of the sources dipole moment are distributed along the front symmetrically regarding the central point and parabolically fall down to the periphery.
Under uniform conductivity, solitary front creates two symmetrical vortex currents. At the bottom of Figure 2(a) current distribution for the front with a resultant dipole moment directed to the bottom links is shown, which is a normal direction for the repolarization phase. Figure 2(a) at the top represent isolines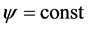 , at that the extra heavy line shows front of the distributed current source and arrows designate direction and magnitude of the current density. Figure at the bottom shows the resultant field of the CDV in a uniform medium. Current density has a maximum nearby the central zone of the front, the area is highlighted with gray.
, at that the extra heavy line shows front of the distributed current source and arrows designate direction and magnitude of the current density. Figure at the bottom shows the resultant field of the CDV in a uniform medium. Current density has a maximum nearby the central zone of the front, the area is highlighted with gray.
An example of calculations of the current distribution in the presence of the fronts from several sources is shown in Figure 2(b). We notice that parallel fronts, directed one towards another, create currents picture having more current vortexes. Intensity of every vortex depends on the relative intensity and mutual orientation of the source fronts.
At Figure 2 two areas with increased current density are highlighted, the currents are at that directed one towards another. The situation with a single source but non-uniform conductivity is illustrated by Figure 2(с). Current distribution is calculated for a sole front perpendicular to the medium border (s1/s2 = 5). Even in that simplest case current vortexes become deformed and asymmetrical.
Current maps when several source fronts possess preferred orientation is represented in Figure 2(d). A specific feature of this case is a “channel” for the preferred spreading of the current surrounded with a series of the low intensive current vortexes. The calculation was performed for a homogenous medium. Nevertheless, similar
Figure 2. Variants of CDV maps for different structure of medium.
picture is typical for inhomogeneous medium with an increased conductivity along the preferred current direction.
Of course, variants of the current distribution maps is by no means restricted to the cited examples that outline, nevertheless, in which direction current maps of the human heart are distorted upon definite deviation from the normal state.
Investigation of the character of the current spreading in the medium can make use of several aspects of the structure. Both distributions of the current function y and current density vector j can serve, as a background for analysis. Main peculiarities of the topology of the current distribution in the medium are obtained from the analysis of points with a zero current density (critical points) [13] :
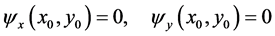 (4)
(4)
If at given point second derivatives 

here
As is well known, quadratic form in (5) determines behavior of the level lines 

The following three types of the critical points are possible.
1) Elliptical critical point (apex or trough). Discriminant 


main directions, at that the semi-axes ratio equals

follows from the circulation of the electric field intensity 
is equal to the total current of the source
2) Hyperbolic critical point (saddle). Discriminant
of the angle is defined by the following relationship
rate different sets of the current lines creating own current vortexes. Every vortex is characterized by current determined by the difference of the y function values taken in the central point and at the separatrixes


3) Parabolic critical point. Discriminant 
2.5. Parameters of Maps Sorting
On the background of the described approach, the system for the description of the CDV maps was elaborated. This system generates numerical indices for deviation of the maps from the normal ones, with values of the indices being normalized to the interval [0, 1], at that the higher the magnitude of the index the more deviation from the normal map.
As the starting point “ideal” for ventricular repolarisation map [13] were taken. From the physiologic point of view this map represents ideally homogeneity current distribution within uniform electroconductive medium, directed to the normal direction. The classification value of this ideal map, presented on the Figure 2(a), is 0. The methods for evaluation of distance between an “ideal” map and each current map are described below.
At the first stage, all elliptic and hyperbolic critical points are found, and for them characteristic values and main directions are determined. Nevertheless, for further analysis, as it was already referred, are used only critical points with ratio of the eigen-values of the quadratic form within the defined range:

where pm and ps are the boundary values for elliptic and hyperbolic points, respectively.
Development of a system of parameters is based on assumptions that the observed vortex current structure is stipulated by distributed sources in a form of the fronts of the sources. Second stage is, therefore, to search out the fronts of the sources. The inverse problem is not posed in the work, and finding of the front positions and their intensity is based on assumptions resulting from analysis of the current spreading in a conductive medium.
First assumption is associated with location and configuration of the fronts. It is believed that every front has at the boundary elliptical critical points with minimal and maximal function values, respectively. However, not every pair of such points can belong to the same front, but only that which has no the vortexes stipulated by the other fronts between the points. Therefore, front can exist providing the monotonous current structure between critical points, to avoid an assumption on alteration of the source current direction along the front. As the fronts are commonly only slightly curved [3] , it is acceptable to choose a midpoint between front ends and consider the front as passing through the point and being the equipotential line
The next assumption refers to the determination of the sources intensity. The intensity If of a front is believed to coincide with value of the current leaking between the ends of the front. The assumption is fulfilled for solitary fronts. Yet for simplicity sake, in the presence of several fronts we neglect the contribution of the currents from the neighbouring fronts into the current between the defined critical points.
Finally, the third step is defining quantitative characteristics of the current maps. To characterize deviation of the current maps from the ideal one the following parameters Pi are introduced:




Parameters of the dipole structure Pf and direction Pdir play a main role for classification, others, Pas and Pell, are subsidiary ones. P-parameters change from zero for ideal map, to the 1 in the opposite case. To the contrast, four Ri parameters that supplement Pi parameters to the unit, show contribution of the ideal map features.
Every of Ri parameters, with exception of Rf, is a function of its characteristics rij, relevant to every of the source fronts, with weight coefficients wj, determined by the intensity of correspondent fronts:

where N is a number of the significant front sources, i.e. sources with relative intensity 


Summarizing Rideal parameter to characterize the degree of ideality of the map includes four Ri parameters, describing separate features. In the formulation of the rule for construction of Rideal we proceed from the following prerequisites. Let us consider all Ri parameters to be independent. Summarizing parameter Rideal includes a main part from the parameters of the dipole structure Rf and parameter of the direction Rdir with a weight W and an auxiliary part from all four parameters with a weight 1-W, and in a simplest way can be expressed by the equation:

If only one of the main parameters is close to zero, hence the summarizing parameter Rideal is close to zero, whereas non-ideality of the auxiliary parameters nullifies only auxiliary part of (10).
Supplemented parameter 

2.6. Software Package for Map Classification
Suggested Topologic Map Classification subsystem [9] , integrated into software MAGWIN, make analysis and interpretation of the magnetocardiograms in clinical conditions. Two parts of subsystem, utilizing topological and vector methods for getting classification parameters, operate independently from another.
With topological method, the program generates predetermined number of the consecutive current maps displayed at the screen as level lines and vector field of the current density (Figure 3(b)). At the maps of the level lines (at the top links), calculated configuration of the source fronts are indicated, at that the length of the arrows corresponds to the relative current density at the front lines. For every map parameters Pi and summarized parameter of the map deviation from the ideal one Kideal are presented.
Such a representation enables one to control the results, suggested by classification system. In individual window the program generates generalized parameters Kideal of all maps in the chosen interval of the cardio cycle (Figure 3(a)). Mean values, calculated at the whole interval


Figure 3. Example of the representation of the current maps (a) and their parameters (b) in the topological method of analysis.
2.7. Statistical Analysis and Classification
Statistical analysis of quantitative indexes was carried out using Student’s criterion to validate deviations between the mean values in the groups studied. Sensitivity and specificity were calculated based on the values of the index 


Threshold value having the most discrimination power was determined using a receiver operating characteristic (ROC) curve as parametrical dependence between SE and 


Sensitivity was determined as a percentage ratio of CAD patients, classified by the test into the patient group, and specificity as the percentage ratio of the patients without CAD examined, classified by the test into the control group.
Sample size N is calculated according to [15] as

As seen from (13) above, we need 4 values: Zα, Z1-β, standard deviation SD and effect size Δ, reflecting the difference between groups. First and second parameters are pre-defined, but two last are estimated. Let us assume that p < 0.001 and 85% power are acceptable. From [15] , we get the following values: Zα = 3.2905 (two-tailed test) and Z1-β = 1.0364.
3. Results
Patient group (CAD) has parameter (11) 0.70 SD 0.17 and sensitivity SE = 0.87, and Control group has parameter 0.44 SD 0.18 and specificity SP = 0.64. Despite considerable data dispersion, the mean values are distinguishable with a high degree of significance, p < 0.001. Experimental ROC-curve at different thresholds 
The average SD = 0.175 and effect size Δ = 0.70 − 0.44 = 0.26. Thus, in accordance with (13) minimal sample size is equal to 17 persons in each group. The number of patients in patients groups examined as well as in control group is significantly higher than this number.
4. Discussion and Conclusion
The reason for obvious differences between healthy subjects and CAD patients is a more inhomogeneous repolarization process in CAD patients. The physiological cause of this fact could be the existence of myocardial ischemia at resting state. However, the complete absence of ischemia under resting conditions is conventional explanation for a normal resting ECG in CAD patients. Meaning that ischemia is a dynamical process with an time continuum beginning with modifications on molecular basis followed by some nonspecific alterations in the 12-leads routine ECG, resulting in wall motion disturbances and angina as a final step, it could be possible that MCG can reveal ischemic changes in a very early phase of such a process.
The causes of electrical inhomogeneity are manifold; firstly it is the alterations of repolarization caused by apoptosis [16] . Then, previous episodes of myocardial ischemia may result in appearance of lesser zones of cell necrosis, in turn resulting in impaired electrogenesis. The multiple shifts in ionic transfer also may take place. It is noted that proposed method is intended to detect regional inhomogeneity, and is less sensitive to other types of inhomogeneity (global, transmural, etc.).
It is shown that CAD patients with significant coronary stenosis but normal resting ECG and Echo could be diagnosed with the help of a fully noninvasive method. This fact is of great clinical interest.
The results of previous investigations with a multichannel magnetocardiographic system, installed inside a shielded rooms, were often limited by the high costs of the measurement system itself and by the shortage of patients e.g. c.q. clinician recognition. The present data show the results of a much less costly system installed in
Figure 4. ROC-curve for groups examined.
unshielded clinical setting. A further confirmation of these results in a greater population would be an important step towards the aim to restrict invasive procedures like coronary angiography to those patients in whom the diagnosis of CAD is confirmed prior to the procedure and in whom interventional therapy appears to be indicated.
Logic and clear approach of results interpretation is mandatory necessary condition of widespread clinical recognition of the magnetocardiography. MCG technology is relatively young and closely associated with computerized technologies of data preprocessing and interpretation. A plenty of approaches and indexes for medical interpretation are available in the present phase of MCG evolution and have to be evaluated concerning its clinical relevance [17] [18] .
Proposed in this paper technology for objective CDV map sorting is based on logic indicators of current distribution in the course of ventricular repolarisation: homogeneity of the excitation (presence/absence of additional excitation wavefronts, uniformity of conductivity) and direction of the large vectors. This technology permits to objectively classify each measurement in one of the two classes―norm or pathology.
Differences between “difficult-to-diagnose” CAD patients with normal ECG and EchoCG and healthy subjects without any complaints and history of heart diseases are obvious. The sensitivity and specificity obtained by proposed classification system are superior to those obtained by resting ECG and EchoCG and even stress- ECG and comparable with the results of stress-EchoCG and methods of nuclear cardiology.
It should be stressed that in our study sensitivity was clearly higher than specificity (87% vs. 64%). These facts could be explained in such a way: rather comprehensive algorhythm is able to detect very little abnormalities of the maps structure but at the same time less “immune” to fortuitous distortion, caused probably by external noise.
To set up MCG in a clinical routine, a few major requirements have to be fulfilled. One of the most important requirements is the way to present MCG data. The images, which are generated by software of magnetocardiographic system, are unwonted for clinicians. In other word, clinicians are incompetent to use the knowledge, contained in the magnetocardiographic images. Hence, it is extremely important to show the information in physiologically understandable form. Physiological terms for magnetocardiography, foremost analyzing homogeneity of electrical characteristics of the heart muscle may be the dispersion of conduction velocity in different zones of myocardium, first of all within ventricular repolarization.
It is logic to develop proper software permitting to present the magnetocardiographic data in a way clinicians are used to see e.g., for instant in a form of myocardial bull’s-eyes images, similar to nuclear cardiology tests. The automatic sorting system and method of information display are the steps toward this goal.
There are some limitations of this study. The most important of these limitations is the relatively few number of subjects examined. Then despite rather clear physical ideas behind the classification systems, there are some empirical coefficients to be defined more precisely.
Farther elaboration of magnetocardiographic measurement systems, installed in unshielded settings and, especially, enhancement in the data interpretation appear warranted in order to make full use of the doubtless capability of this novel method in the diagnostic of myocardial ischemia in coronary artery disease patients.
Acknowledgements
Authors truly thank for the financial support The Ministry of Education and Science of Ukraine and National Academy of Science of Ukraine. The authors declare that there is no conflict of interest regarding the publication of this paper.
Human Subjects/Informed Consent Statement
All procedures followed were in accordance with the ethical standards of the responsible committee on human experimentation (institutional and national) and with the Helsinki Declaration of 1975, as revised in 2000. Informed consent was obtained from all patients for being included in the study.
Cite this paper
I. Chaikovsky,L. Stadnyuk,A. Verba,Yu. Vasetskyi,M. Budnyk,G. Mjasnikov,A. Kazmirchuk,A. Lomakovskyi, (2016) Value of Topology Approach to Diagnose of CAD Based on Magnetocardiographic Current Distribution Maps in Difficult-to-Diagnose Patients. World Journal of Cardiovascular Diseases,06,235-245. doi: 10.4236/wjcd.2016.67026
References
- 1. Chaikovsky, I., Primin, M., Nedayvoda, I. and Budnyk, M. (2012) Magnetocardiography in Unshieled Setting: Heart Electrical Image Based on 2D and 3D Data in Comparison with Perfusion Image Based on PET Results. In: Chaikovsky, I. and Sydorova, N., Eds., Coronary Artery Disease, InTech, Rijeka, 43-58.
http://dx.doi.org/10.5772/30122 - 2. Hailer, B., Chaikovsky, I., van Leeuven, P., et al. (2005) The Value of MCG in PTS with and Without Relevant Stenoses of the Coronary Arteries Using an Unshielded System. PACE, 28, 8-16.
http://dx.doi.org/10.1111/j.1540-8159.2005.09318.x - 3. Sosnitsky, V., Voitovych, I., Boichak, M., et al. (2011) Magnetic Mapping of the Heart—New Information Technology of Noninvasive Electrophysiology. Reports of the National Academy of Sciences of Ukraine, 1, 166-171.
- 4. Tolstrup, K., Madsen, B.E., Ruiz, J.A., et al. (2006) Non-Invasive Resting Magnetocardiographic Imaging for the Rapid Detection of Ischemia in Subjects Presenting with Chest Pain. Cardiology, 106, 270-276.
http://dx.doi.org/10.1159/000093490 - 5. Steinberg, B., Roguin, A., Watkins, S., et al. (2005) Magnetocardiogram Recording in Non-Shielded Environment— Reproducibility and Ischemia Detection. ANE, 10, 152-160.
- 6. Chaikovsky, I., Hailer, B., Sosnytskyy, V., et al. (2014) Predictive Value of the Complex Magnetocardio-graphic Index in Patients with Intermediate Pretest Probability of the Chronic CAD: Results of a Two-Center Study. Coronary Artery Disease, 25, 474-484.
http://dx.doi.org/10.1097/MCA.0000000000000107 - 7. Chaikovsky, I., Stadnjuk, L., Mjasnikov, G., et al. (2014) 2D and 3D Analysis of Magnetocardiographic Data in the Evaluation of the Ventricular Repolari-zation Changes under Exercise Stress Test in Patients with CAD. World Journal of Cardiovascular Diseases, 4, 399-404.
http://dx.doi.org/10.4236/wjcd.2014.48050 - 8. Dovbysh, A., Martynenko, S., Kovalenko, A. and Budnyk, N. (2011) Information-Extreme Algorithm for Recognizing Current Distribution Maps in Magnetocardiography. Journal of Automation and Information Sciences, 43, 63-70.
http://dx.doi.org/10.1615/JAutomatInfScien.v43.i2.60 - 9. Fainzilberg, L. (2008) Information Technologies of Complex Signals Processing: Theory and Practice. Naukova Dumka, Kyiv.
- 10. Romanovich, S. (1997) Supercurrents: Forward & Inverse Problems. Proceedings of 6th International Conference on Superconductive Electronics, Berlin, 25-28 June 1997, 344-346.
- 11. Romanovich, S. (1997) Reconstruction of Three-Component Dipoles within Layer. Biomedizinische Technick, 42, 227-230.
- 12. Titomir, L. (1980) Electrical Generator of the Heart. Nauka, S-Peterburg.
- 13. Vasetskyi, Yu. and Chaikovsky, I. (2002) Model of Current Distribution Generated by Extended Electrical Sources and Its Usage for Current Maps Classification. Nowak, H., Haueisen, J., Giessler, F. and Huonker, R., Eds., BIOMAG2002: Proceedings of 13th International Conference on Biomagnetism, VDE Verlag Gmbh, Berlin-Offenbach, 10-14 August 2002, 846-848.
- 14. Metz, C.E. (2000) Fundamental ROC Analysis. Progress in Medical Physics and Psychophysics. In: Van Metter, R., Beutel, J. and Kundel, H., Eds., Handbook of Medical Imaging, SPIE Press, Bellingham, 754-769.
http://dx.doi.org/10.1117/3.832716.ch15 - 15. Kadam, P. and Bhalerao S. (2010) Sample Size Calculation. International Journal of Ayurveda Research, 1, 55-57.
http://dx.doi.org/10.4103/0974-7788.59946 - 16. Buja, L.M. and Entman, M.L. (1998) Modes of Myocardial Cell Injury and Cell Death in Ischemic Heart Disease. Circulation, 98, 355-1357.
http://dx.doi.org/10.1161/01.CIR.98.14.1355 - 17. Ebmeyer, S., Chaikovsky, I., Hailer, B., Erbel, R., Wojczik, H., Budnyk, M. and Simon, R. (2007) Predictive Value of the Magnetocardiogram for Location of Regional Ischemia or Infarction as Detected by Quantitative Analysis of the Coronary Arteriogram. New Frontiers in Biomagnetism. Proceedings of the 15th International Conference on Biomagnetism, Vancouver, 21-25 August 2006, 463-467.
http://dx.doi.org/10.1016/j.ics.2007.02.008 - 18. Udovychenko, Y., Popov, A. and Chaikovsky, I. (2014) Current Density Distribution Maps Threshold. 2014 IEEE 34th International Conference on Electronics and Nanotechnology (ELNANO), Kyiv, 15-18 April 2014, 313-315.
http://dx.doi.org/10.1109/ELNANO.2014.6873904



