Open Journal of Epidemiology
Vol.3 No.3(2013), Article ID:36297,10 pages DOI:10.4236/ojepi.2013.33021
Mathematical analysis of drug resistance in vertical transmission of HIV/AIDS
![]()
1Basic Sciences Programme, Natural Resources College of Malawi, Lilongwe, Malawi
2Department of Basic Sciences, Botswana College of Agriculture, Gaborone, Botswana
3Mathematics Department, University of Dar es Salaam, Dar es Salaam, Tanzania
Email: *estomihmassawe@yahoo.com
Copyright © 2013 Symon Chibaya et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received 2 July 2013; revised 31 July 2013; accepted 12 August 2013
Keywords: Dynamics of HIV/AIDS; Vertical Transmission; Drug Resistance
ABSTRACT
A nonlinear mathematical model of vertical transmission of HIV/AIDS is proposed to study the effects of drug resistance in the spread of the disease. The study assumes that treatment leads to the evolution of drug resistance in some pockets of the population. We use traditional methods to determine conditions for existence and stability of disease-free and endemic equilibrium points of the model. The study showed that the burden of the disease may be reduced if the reproduction number is reduced below unity and may persist if the reproduction number is raised above unity. Furthermore, evolution of drug resistance due to treatment may change the cause of the epidemic.
1. INTRODUCTION
Diseases can be transmitted in various ways, some of which can be classified as horizontal or vertical. In the case of HIV/AIDS, horizontal transmission can result from direct physical contact between an infected individual and a susceptible individual. In this case, HIV infection is from the infected blood, semen and vaginal fluids to the exposure individuals. This often occurs when having unprotected sex with a person who has HIV. The other risks of HIV infection comprise of sharing needles, syringes or other equipment, illicit drugs for injection or during injection drug use (when needles are shared) with an infected HIV person. Any HIV infected individual can transmit the disease irrespective of the stage or treatment status. However, high risks of infections are in the early stages of infection and during full blown AIDS stages. These stages are associated with high viral loads.
Vertical transmission, on the other hand, results from direct transfer of a disease from an infected mother to an unborn or newly born offspring. Some of the diseases that can be transmitted vertically include chagas, dengue fever and hepatitis B. Vertical transmission of HIV/ AIDS generally occurs during pregnancy, delivery or breastfeeding and may be influenced by many factors such as maternal viral load and the type of delivery [1,2]. This type of transmission is sometimes called motherto-child transmission or ethically parent-to-child transmission. Research has shown that, not all pregnancies in HIV-infected women result in vertical transmission.
Pediatric HIV is a major contributor to high mortality rates among infants and children in sub-Saharan Africa and it remains a leading cause of deaths in children under the age of 5 years. It is estimated that one third of HIV positive infants die before their first birthday, while 50% die by their second birthday. Consequences of vertical transmission include reduction of life expectancy of HIV positive individuals [3]. Worldwide, one percent of pregnant women are HIV-positive and 95% of these HIV positive women live in sub-Saharan Africa. In the absence of treatment, approximately 25% - 50% of HIVpositive mothers will transmit the virus to their newborns during pregnancy, childbirth, or breastfeeding [4]. In sub-Saharan Africa, over 1000 newborns are infected with HIV every day, despite available medical interventions. The high rates of vertical transmission in Africa are attributed to low rates accessibility of intervention programmes and lack of adherence to the necessary medications to prevent mother-to-child transmission.
Prevention of mother-to-child transmission of HIV (PMTCT) can dramatically reduce the risk of vertical transmission. Success stories have been reported in the United States and Europe and it remains a serious challenge to Africa [3]. Prevention of mother-to-child transmission involves the use of antiretroviral therapy (ART), caesarean section [5,6] and refraining from breastfeeding. Antiretroviral drugs are administered during pregnancy, at delivery and postnatally to the child and mothers. In resource-poor countries, short course regimens based on single dose nevirapine to the mother and infant are being used [7]. In summary, the burden of vertical transmission of HIV can be reduced by enrolling parentto-child prevention programs which involve testing the mothers and blocking of transmission through the use of antiretroviral drugs, elective caesarean section and use of replacement infant feeding [8].
Drug resistance refers to the ability of microorganisms to adapt, survive and multiply in the presence of drugs that would normally kill or weaken them. In the case of HIV, the virus adapts and multiplies in the presence of antiretroviral (ARV) drugs often making mistakes of copying its genetic blueprint RNA. Some of these mistakes, called mutations, can make HIV resistant to one or more ARV drugs. With regard to vertical transmission, we are concerned with the potential selection of drug– resistant virus following short course of ARV treatment to prevent parent-to-child transmission (PPCT). Reports show that up to 20% of women who receive a single dose of nevirapine in HIVNET regime developed resistance [9] and this leads to the development of strains of HIV resistant to multiple combinations of ARVs.
This study therefore extends mathematical models of vertical transmission with treatment by incorporating the effects of drug resistance. The main objective of the study is to investigate the effects of vertical transmission and evolution of drug resistance in the HIV disease dynamics. The paper is arranged as follows: Section 1 introduces the study, model formulation is presented in Section 2, Section 3 presents model analysis, Section 4 presents numerical simulations while Section 5 discusses the results and presents the conclusions of the study.
2. MODEL FORMULATION
A mathematical model of a disease transmitted both horizontally and vertically in which the treatment programme results in the evolution of drug resistance is proposed and analysed. The proposed model sub-divides the population of interest into seven compartments, depending on their disease status and type of pathogen (i.e. resistant or wild strain). The sub-populations are the Susceptibles S(t), drug resistant infectives IR, drug sensitive infectives Iw, treated drug sensitive infective Tw, treated drug resistant infective TR, AIDS drug sensitive Aw and AIDS drug resistant class AR. The total population at time t is given by
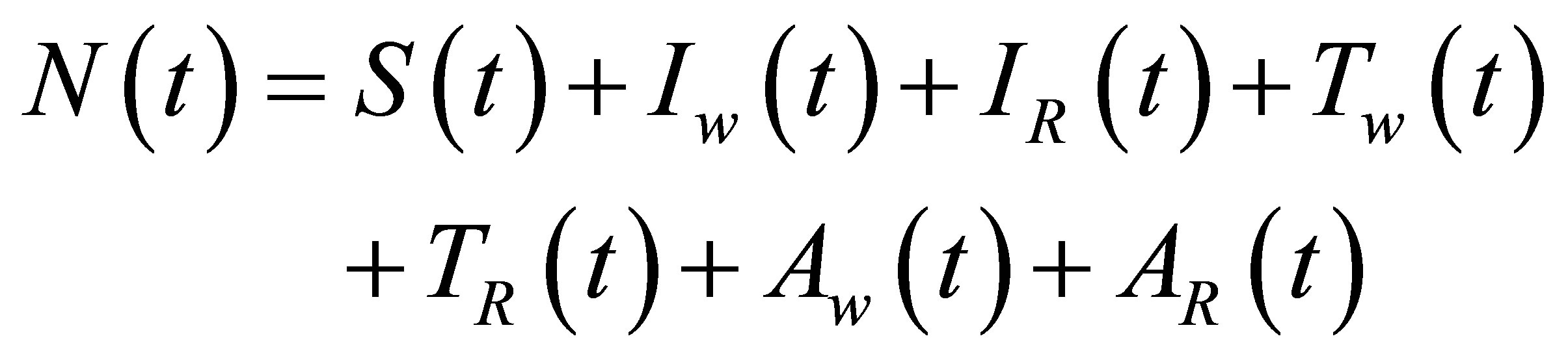 (1)
(1)
To reduce the size of the model we relaxed the distinction between the asymptomatic (no clinical signs) and symptomatic (clinical signs) stages of HIV (WHO staging of HIV). We assumed mass action type of force of infection as opposed to standard incidence to allow for mathematical tractability of the model. This assumption is an over simplification of reality particularly highly infectious diseases like HIV. We further assume that treatment only reduces the level of infectiousness. Table 1 below presents the definitions and descriptions of the parameters and state variables used in the model. It is worth stating that all model parameters non-negative and all have values in the open set (0, ∞) except ρ which picks values in the set [1, ∞).
The problem described above can be represented schematically by the flow diagram below (Figure 1):
The model description above leads to a system of nonlinear ordinary differential equations:
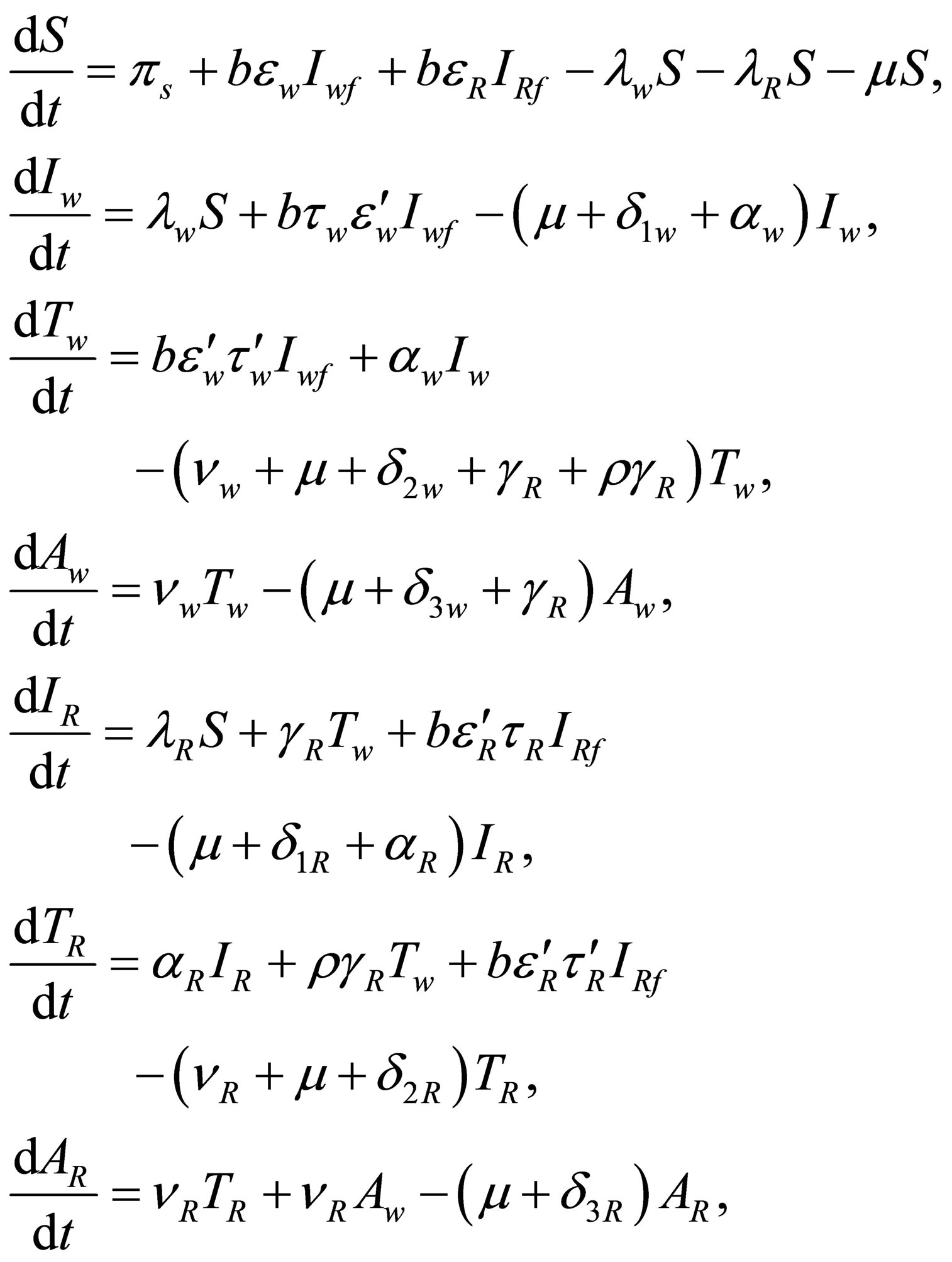 (2)
(2)
where
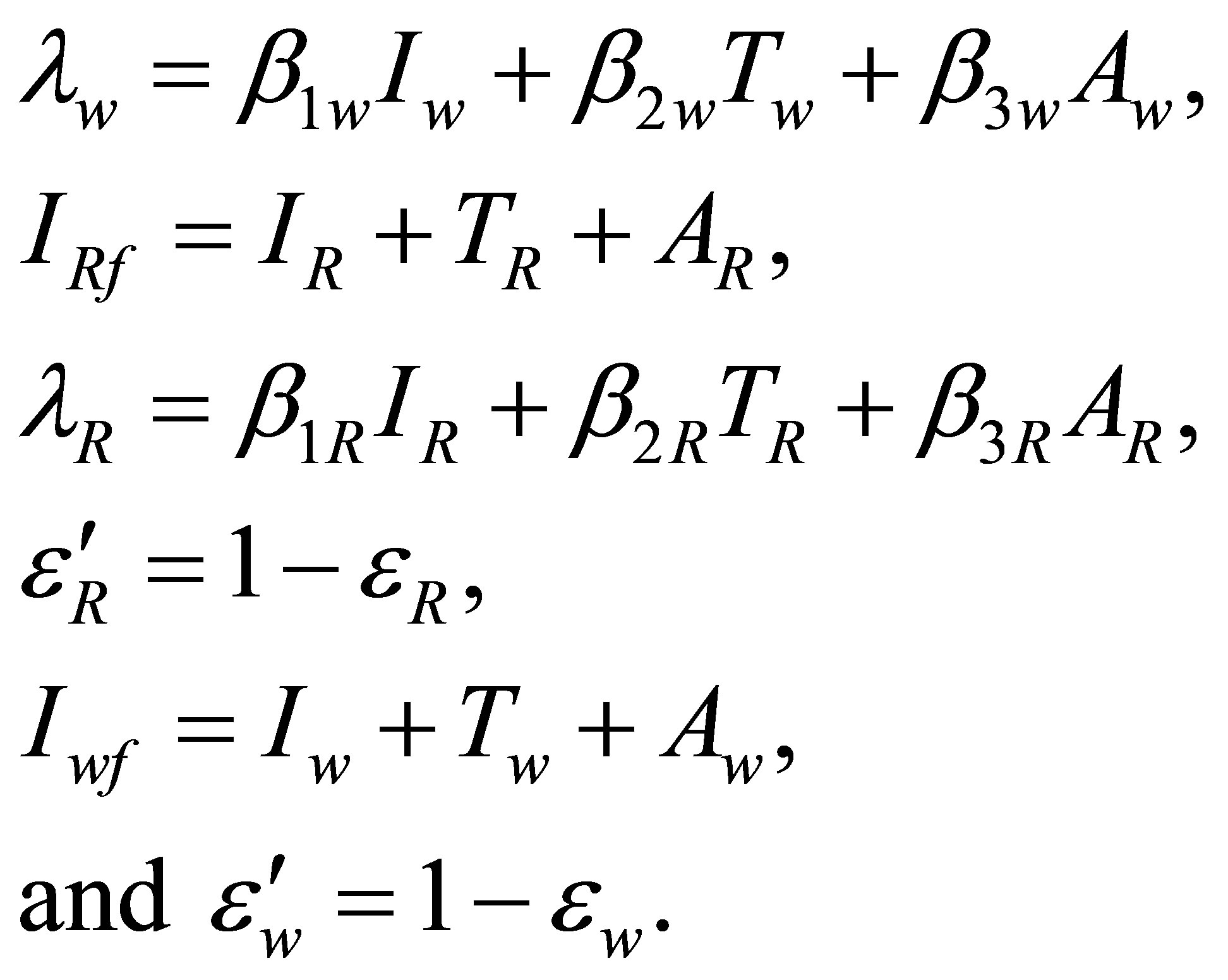
3. MODEL ANALYSIS
System (2) is analysed to find conditions for existence
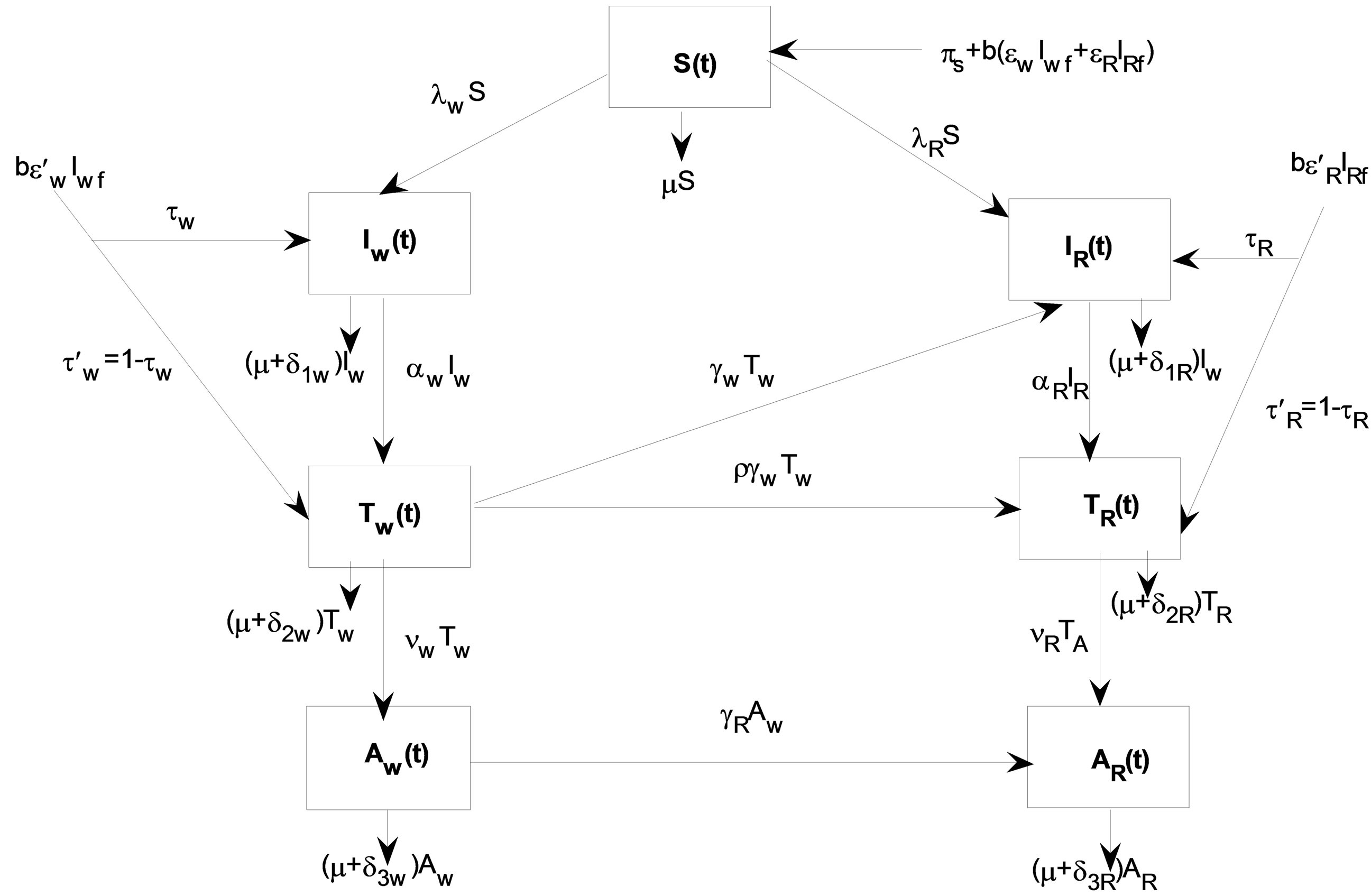
Figure 1. Vertical transmission model of HIV with drug resistance.

Table 1. Parameters and their descriptions.
and stability of disease free and endemic equilibrium points. This analysis of the model allows us to determine the impact of drug resistant virus in the treatment and vertical transmission on the transmission of HIV/AIDS infection in a population characterized in terms of the reproductive number R0.
3.1. Positivity of Solutions
Adding equations of system (2) we obtain an equation governing changes in the total population
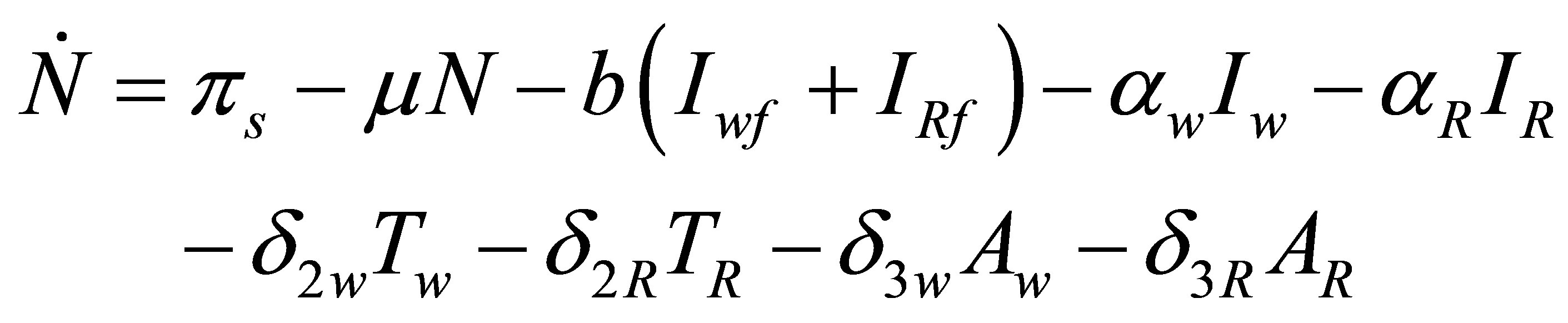
In the absence of HIV infection the total population converges to 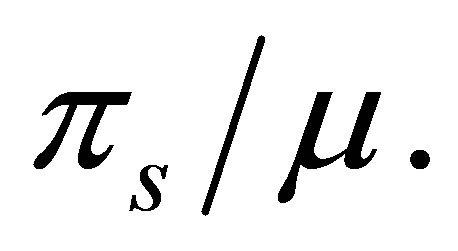 It follows that the
It follows that the
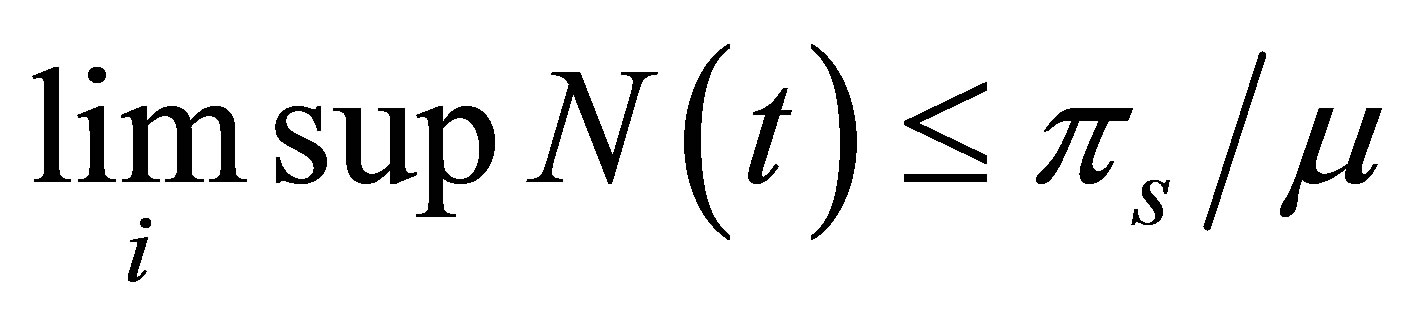 and it suffices to study system (2)
and it suffices to study system (2)
in an invariant set
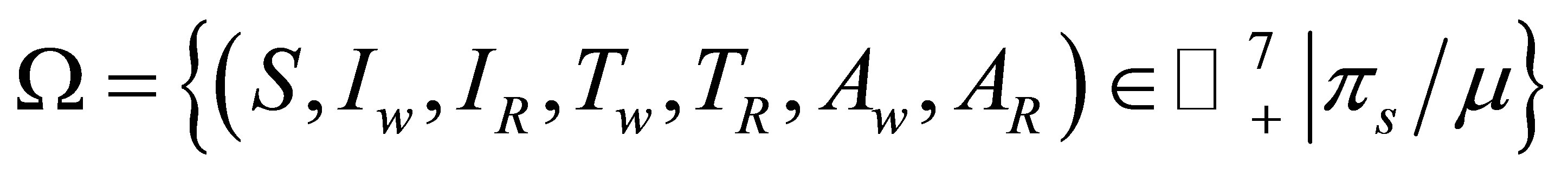
We now show that the initial data of (S, Iw, IR, Tw, TR, Aw, AR) which are non-negative lead to solutions that remain non-negative for all t ≥ 0.
Theorem 3.5 Let
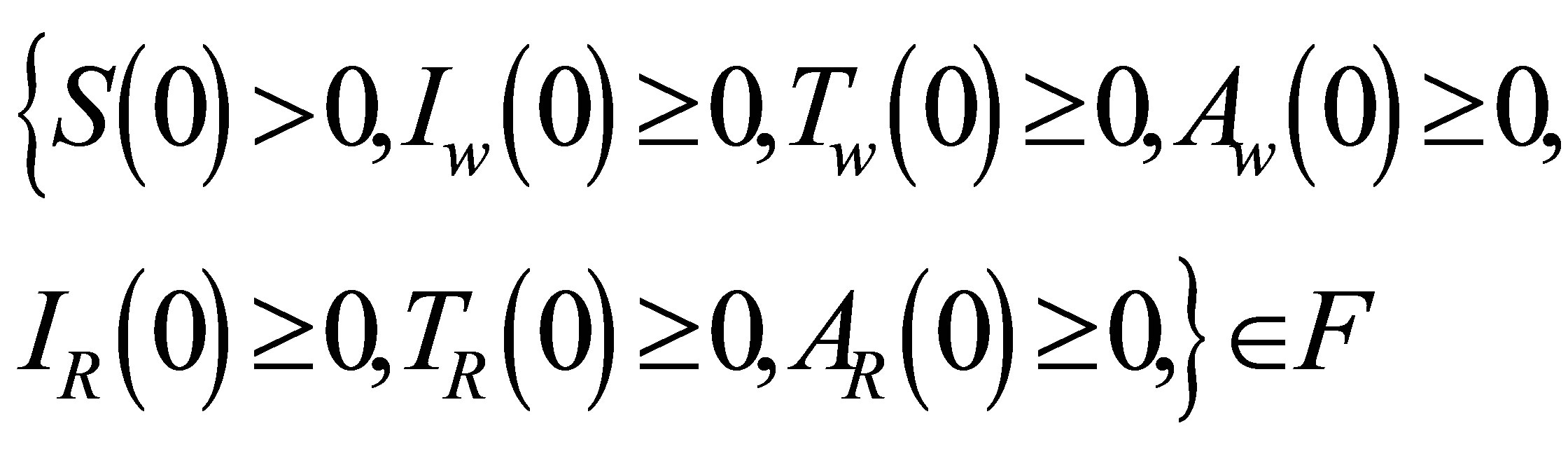
where 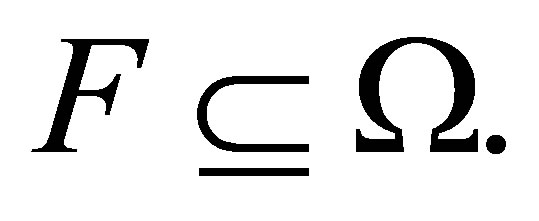 Then the solutions {S(t), Iw(t), Tw(t), Aw(t), IR(t), TR(t), AR(t)} of the model system of Equation (2) are positive
Then the solutions {S(t), Iw(t), Tw(t), Aw(t), IR(t), TR(t), AR(t)} of the model system of Equation (2) are positive .
.
Proof From the first equation of (2), we have

which gives

As  we obtain
we obtain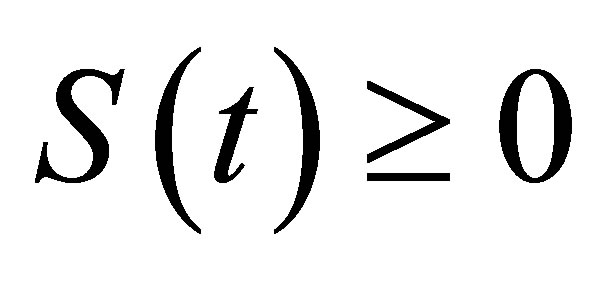 . Hence all feasible solution of system (2) enter the region
. Hence all feasible solution of system (2) enter the region
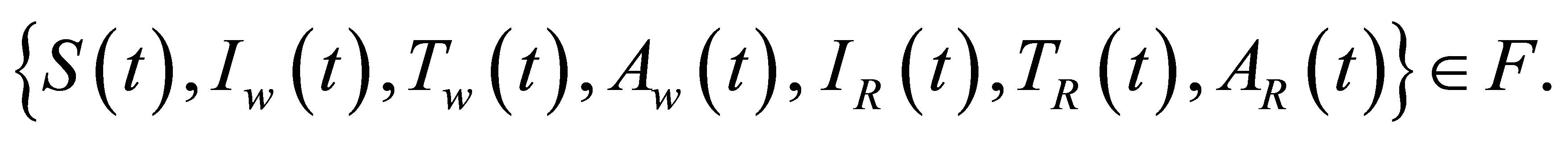
Similar proofs can be established for the positivity of Iw, Tw, Aw, IR, TR, AR.
Thus, the equations of system (2) are well posed.
3.2. Steady State Solutions
The equilibrium solutions of the model (2) are obtained by setting the right hand side of system (2) to zero, to solve the following system of non-linear equations:
 (3)
(3)
From the equation of  we have
we have 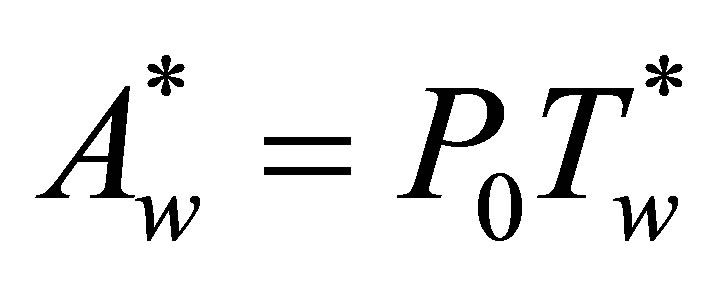 where
where
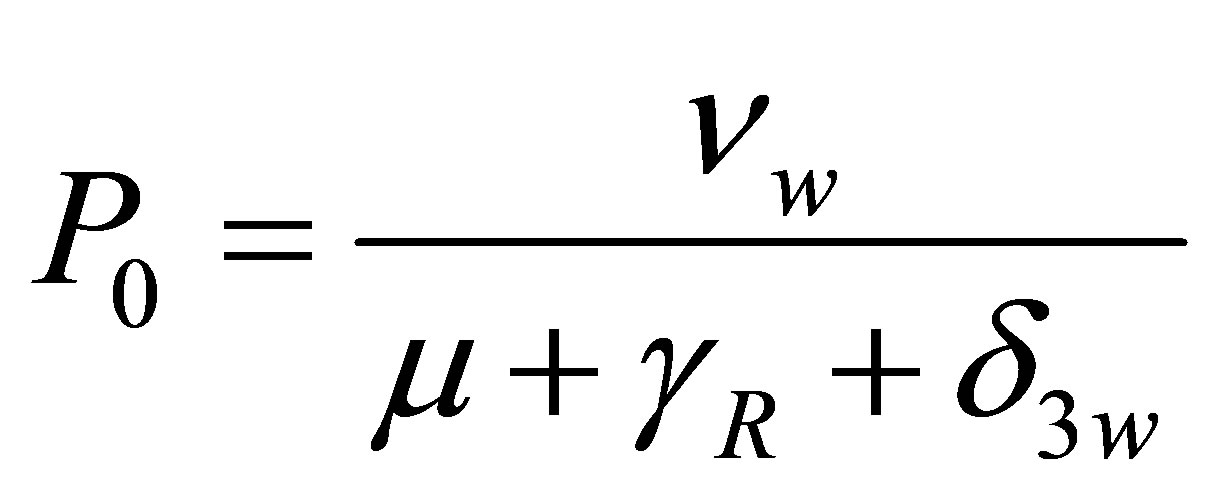
Substituting 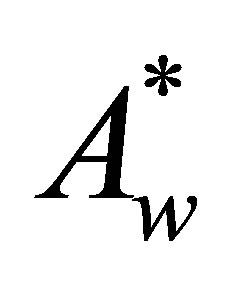 in the expressions for
in the expressions for  and
and 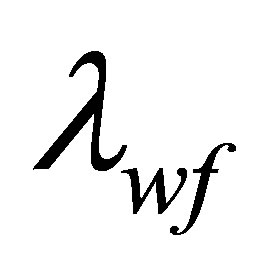 yields
yields
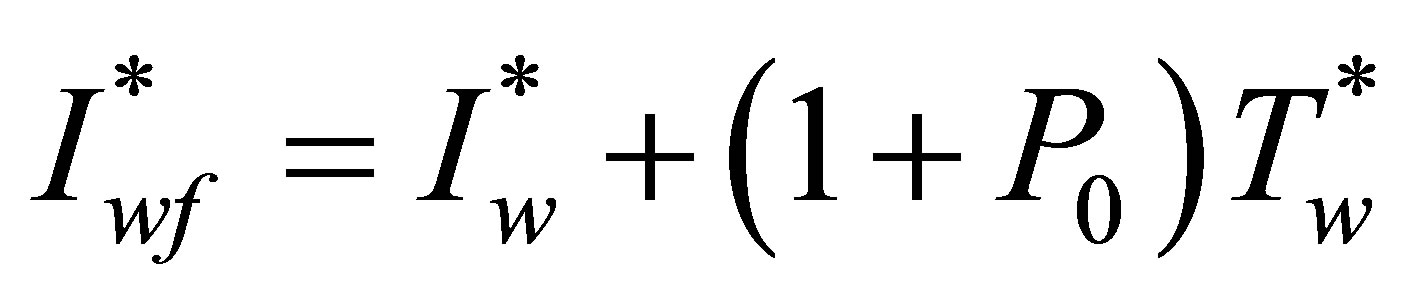
and
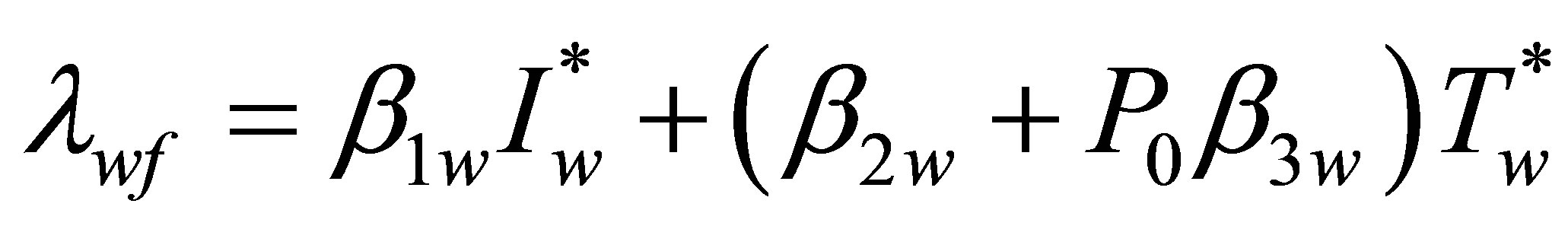
which upon substitution in the equations for 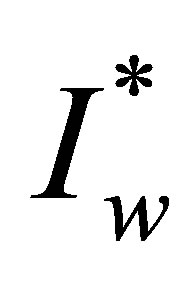 and
and 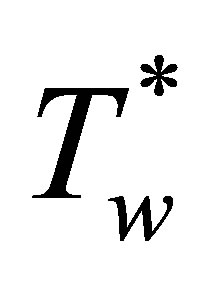 gives
gives  with
with 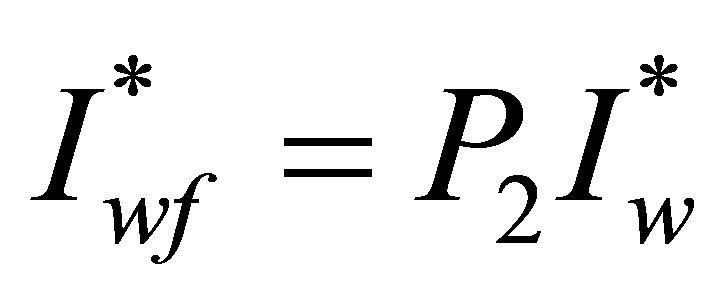 and
and 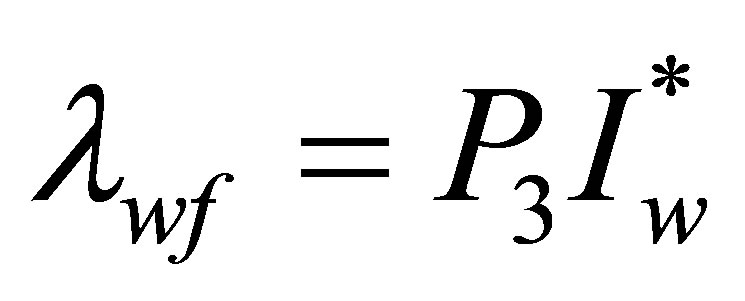 where
where

and
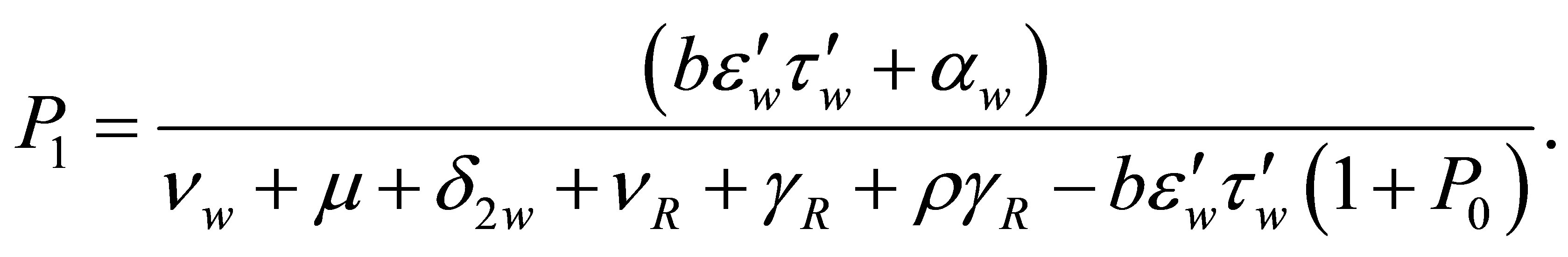
Defining

to be threshold parameter due to the wild strain, and then substituting for 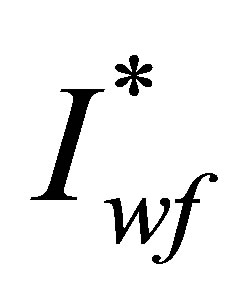 and
and  in the equation for
in the equation for  we obtain
we obtain 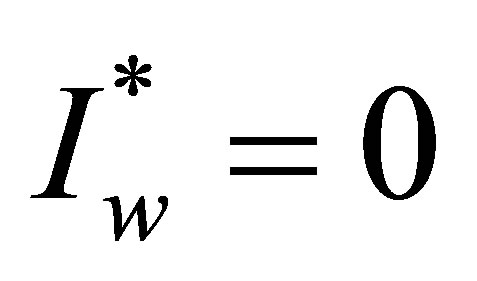 or
or

The solution 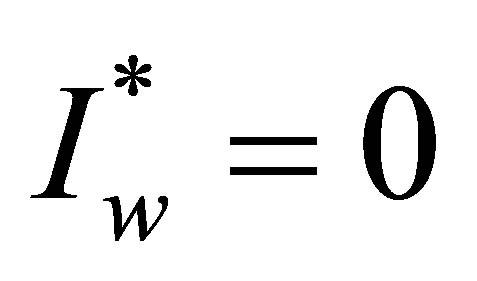 yields
yields  where
where
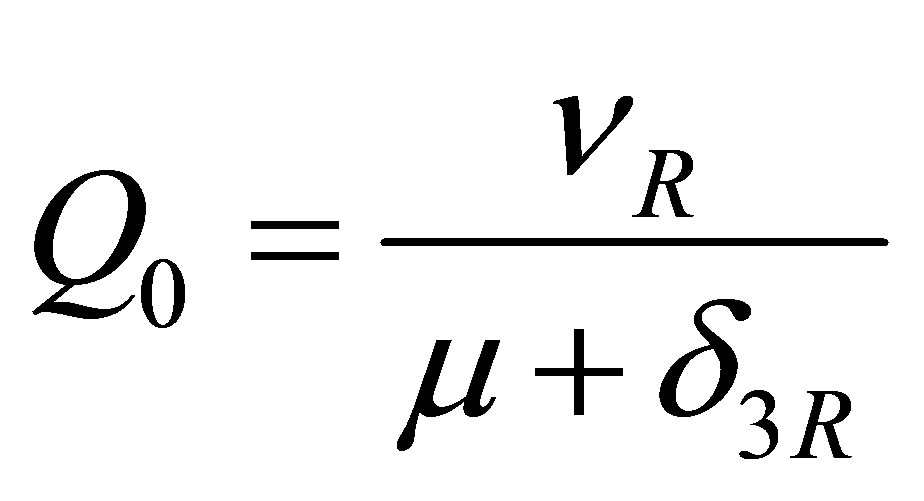
Substituting 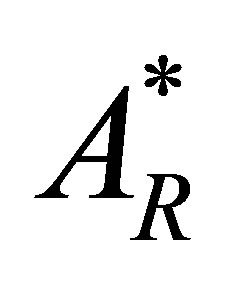 in the expressions for
in the expressions for 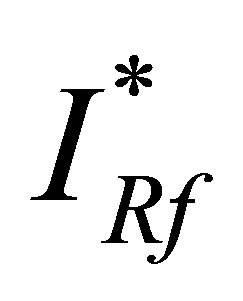 and
and 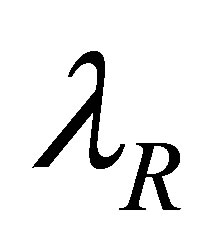 we get
we get

and
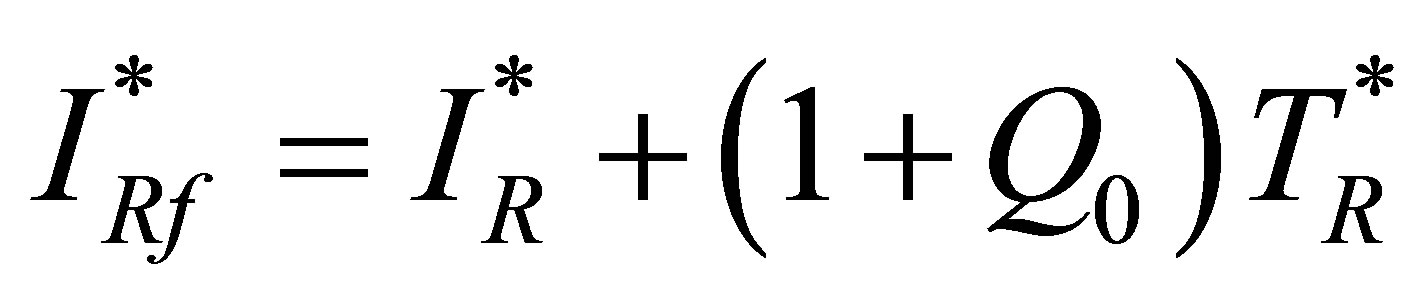 .
.
The expression for 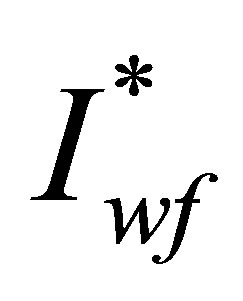 together with an equation for
together with an equation for 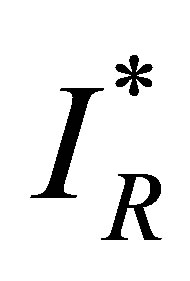 give
give 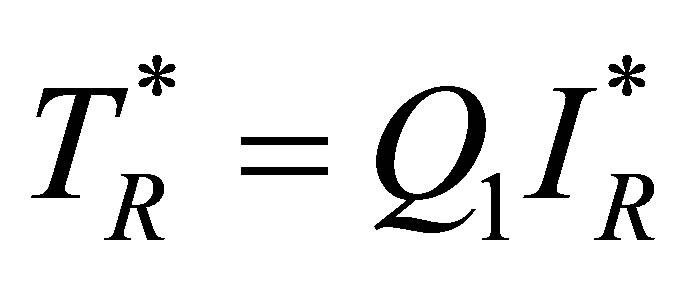 where
where
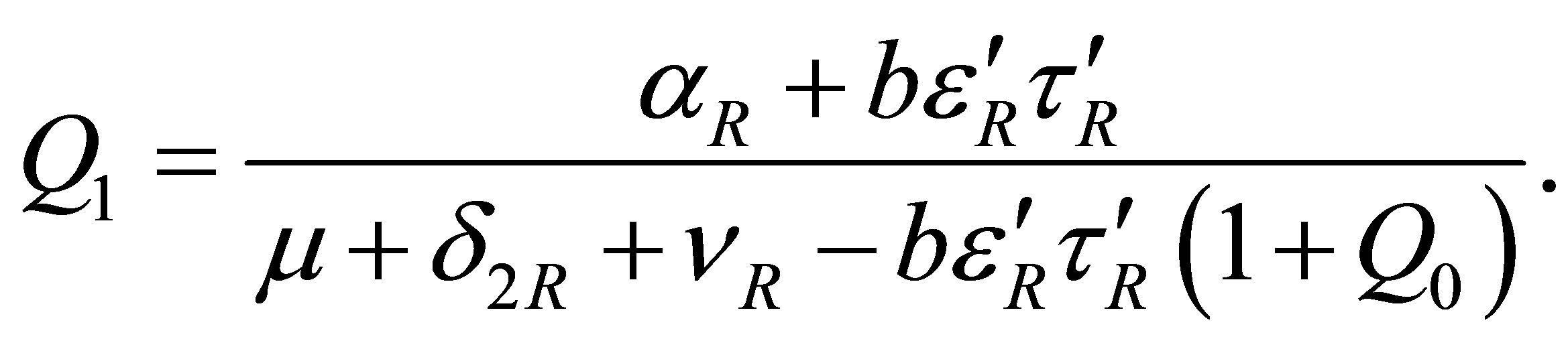
provided that
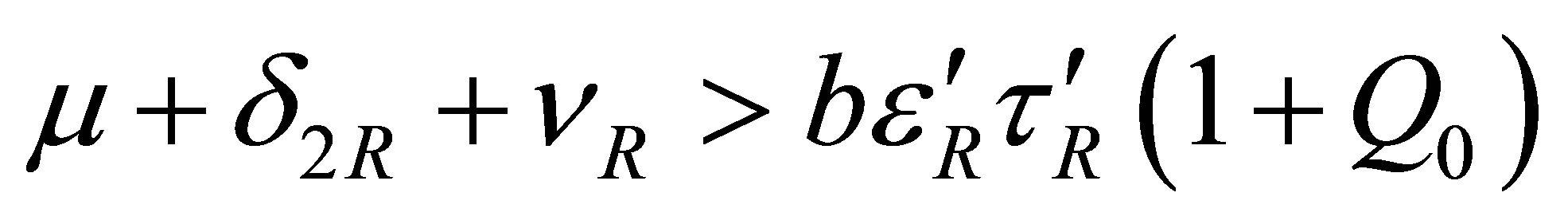 .
.
With this expression for 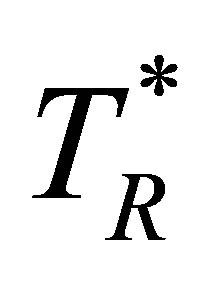 the expressions for
the expressions for 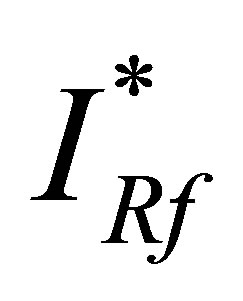 and
and 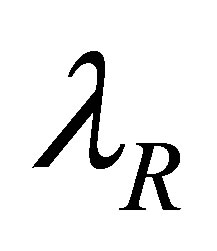 reduce to
reduce to 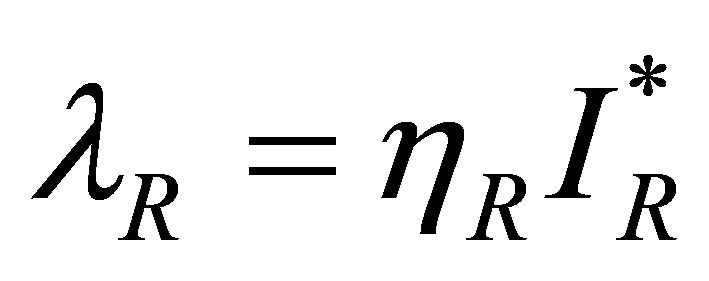 and
and 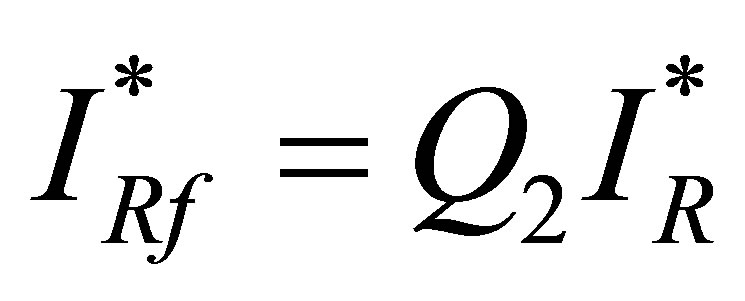 where
where

and
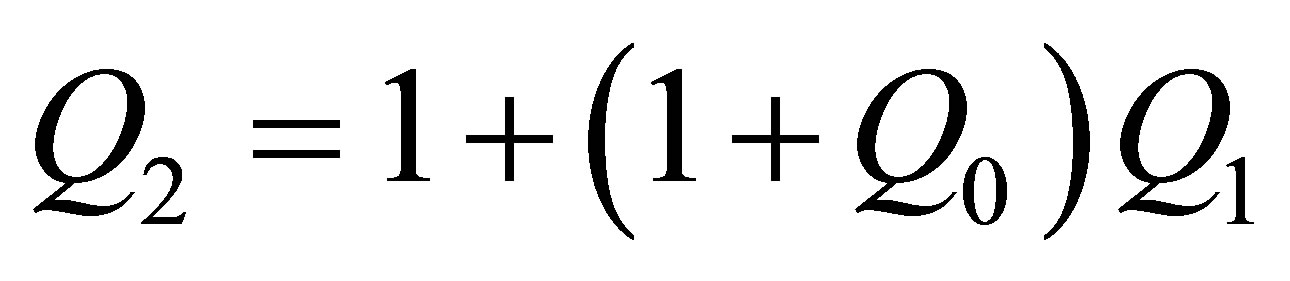
Substituting for  and
and 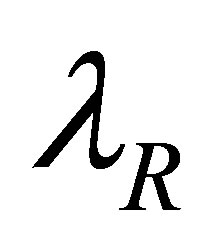 in the equation for
in the equation for 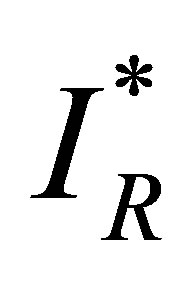 we obtaining
we obtaining 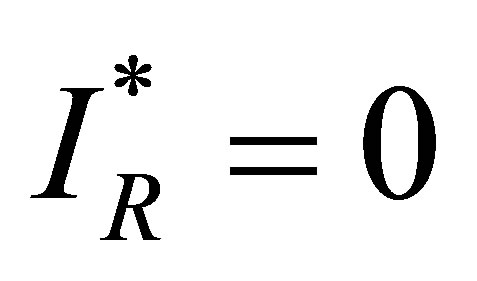
or
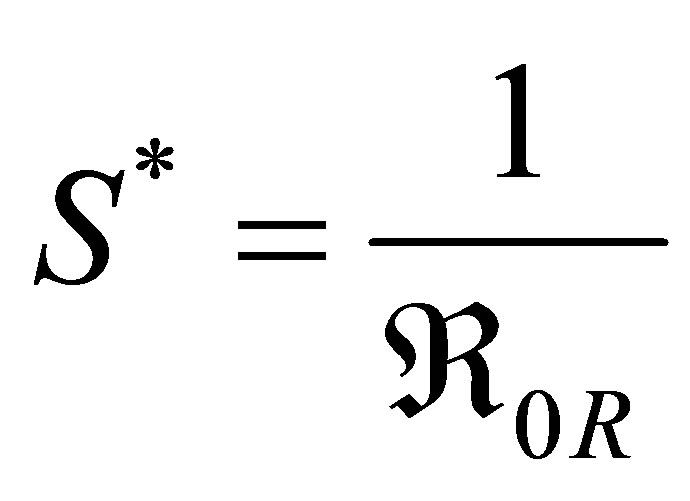 .
.
3.2.1. Disease-Free Equilibrium
The solution 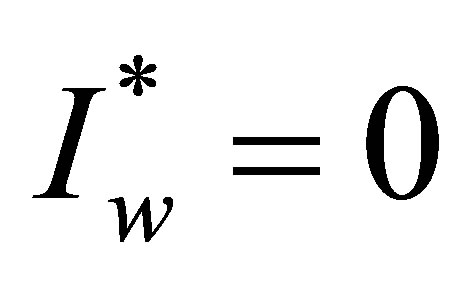 and
and 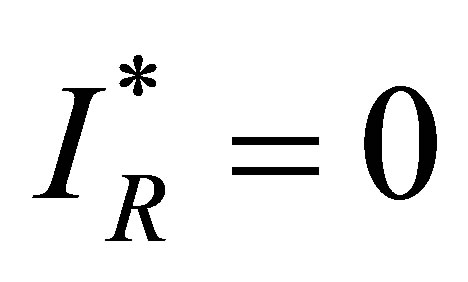 lead to the disease–free equilibrium point
lead to the disease–free equilibrium point
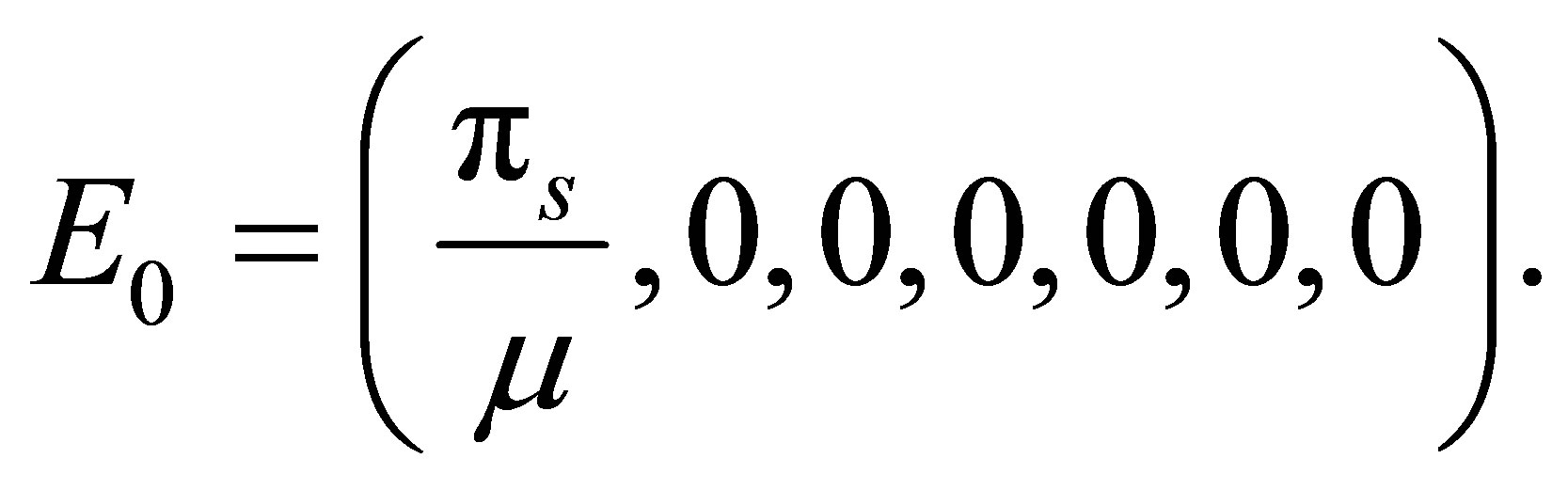
3.2.2. Wild Strain-Free Equilibrium
The solutions 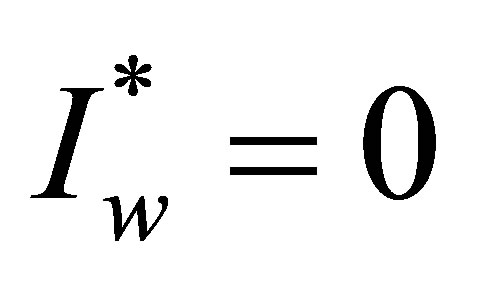
and
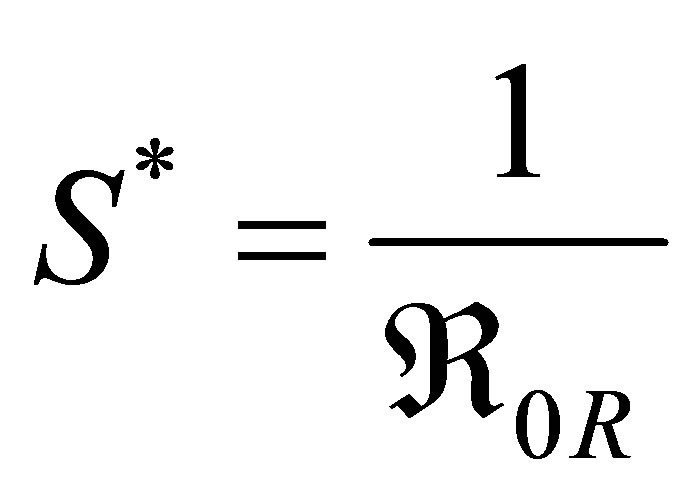
lead to an drug resistant strain endemic equilibrium given by 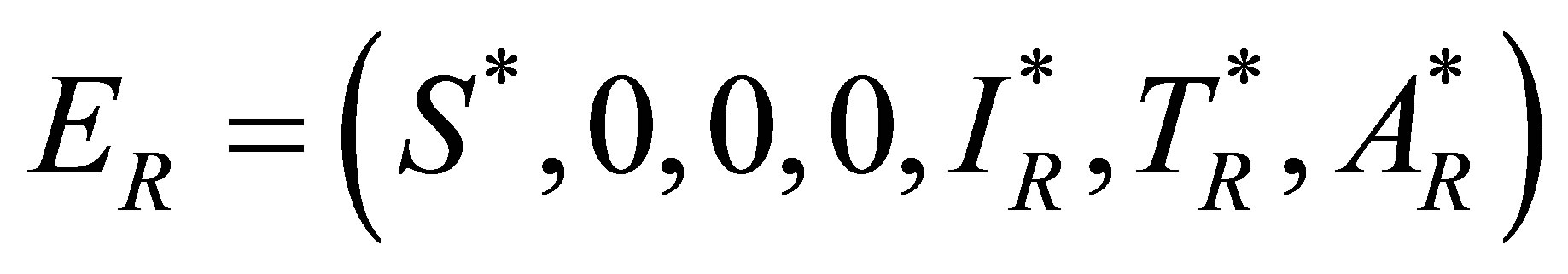 with coordinates
with coordinates
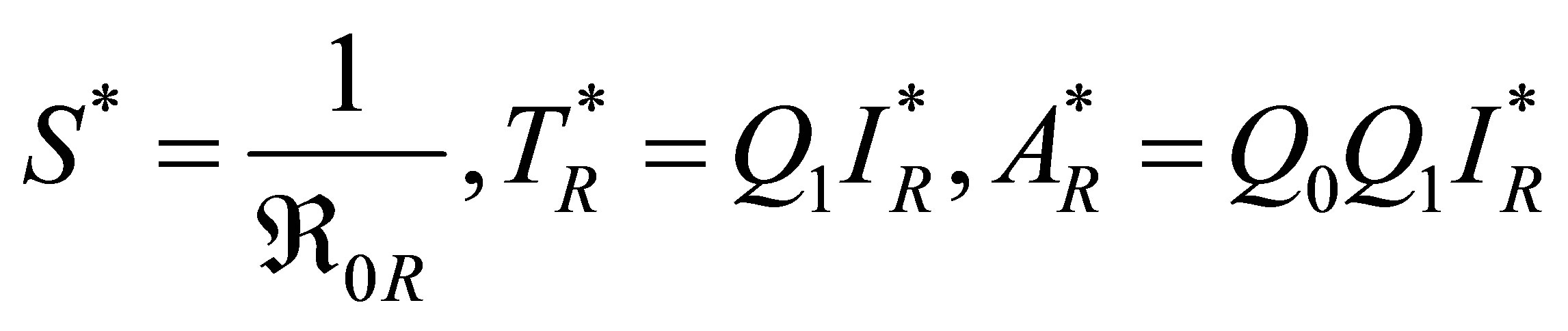 and
and
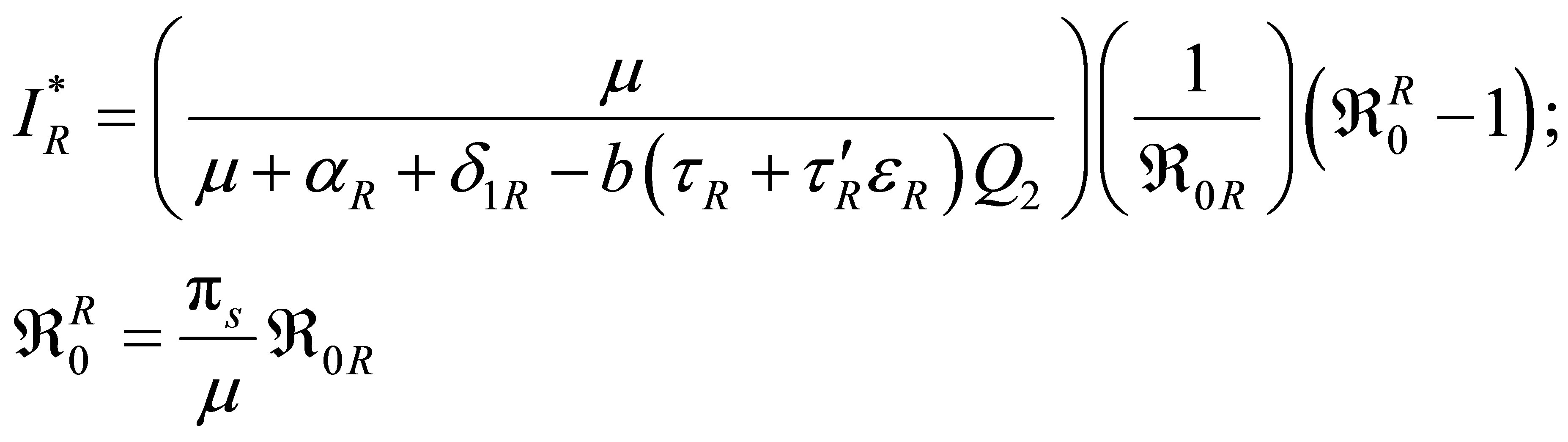 .
.
3.2.3. Drug Resistant Strain-Free Equilibrium
The solutions  and
and
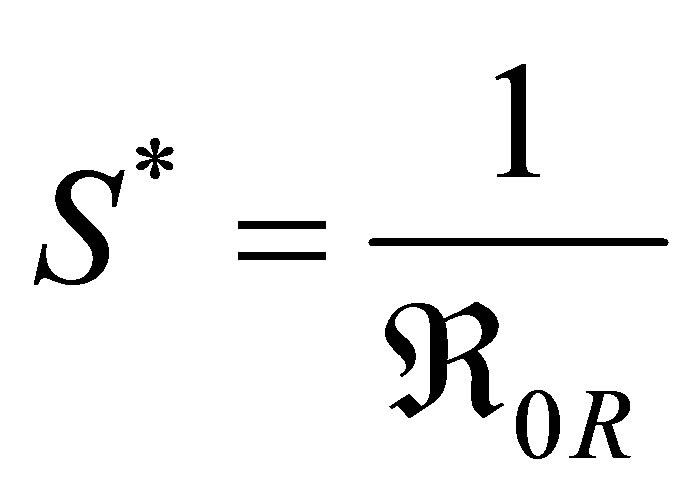
lead to an drug resistant strain endemic equilibrium given by
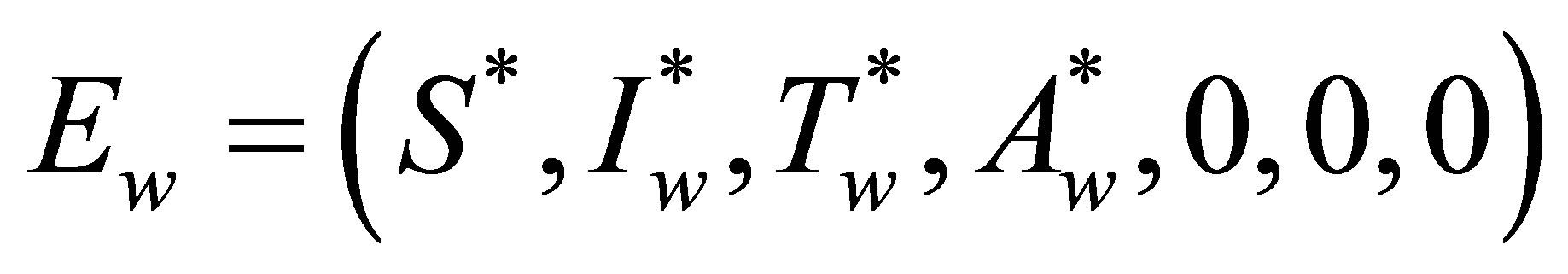
with coordinates
 and
and
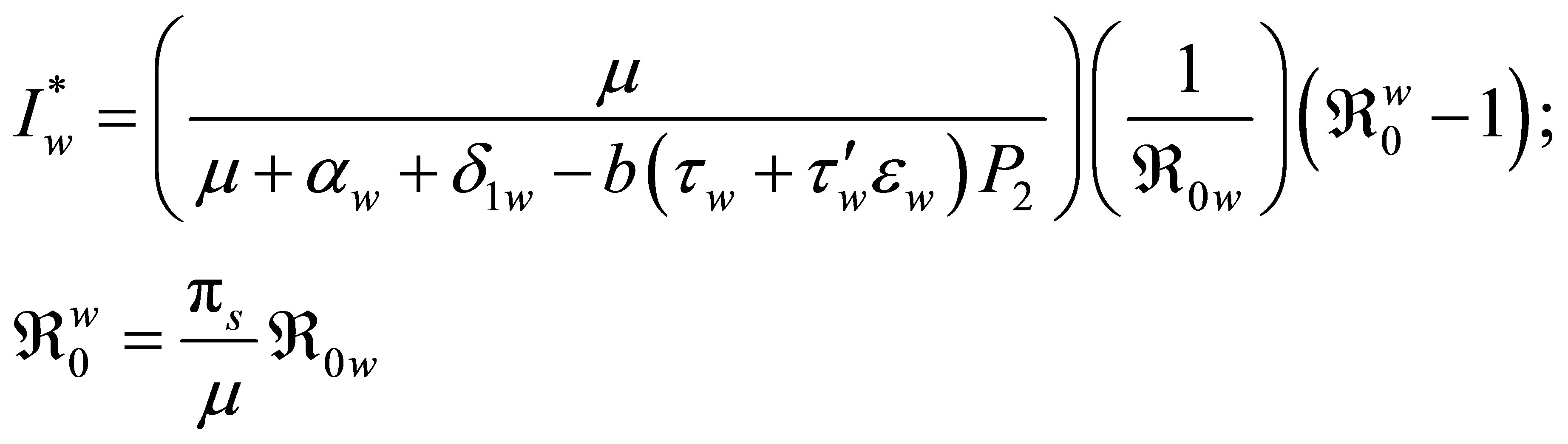 .
.
3.2.4. Coexistence of Wild and Resistant Strains
In this case, we consider 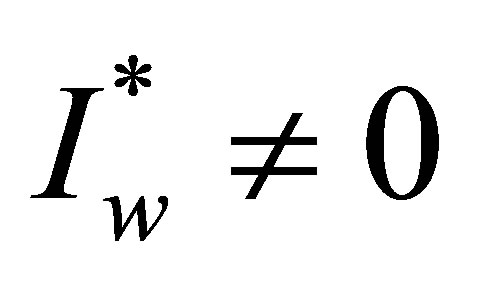 and
and
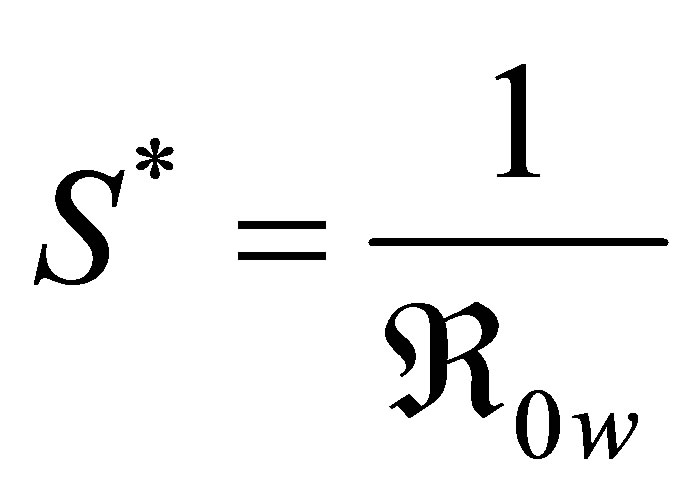 .
.
The equation for 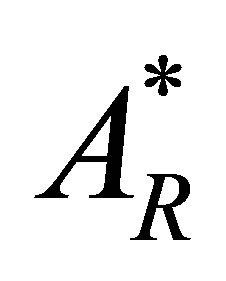 leads to
leads to

where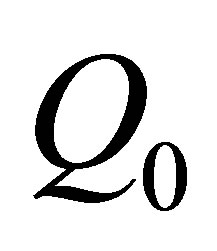 ,
, 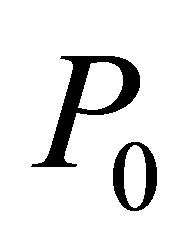 and
and 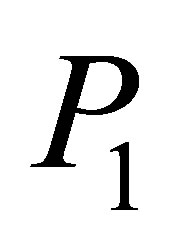 are as defined above. Substituting
are as defined above. Substituting 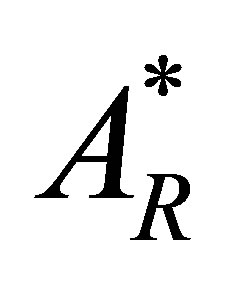 in the expressions for
in the expressions for  and
and 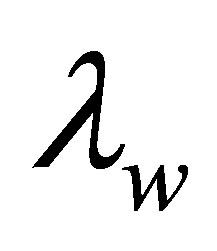 yields
yields
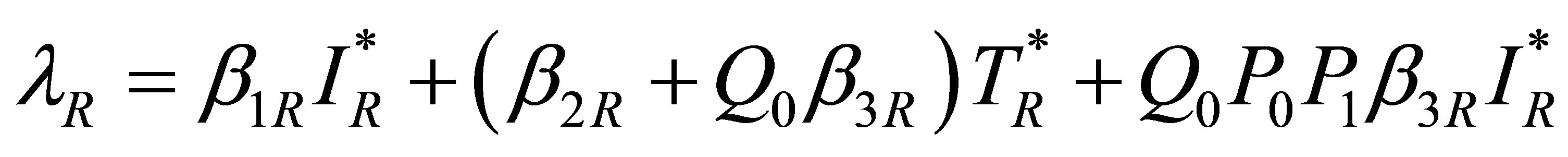
and
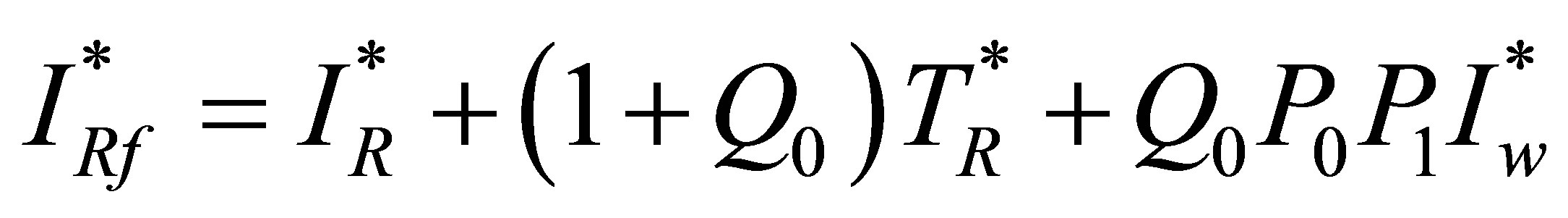
Substitution of 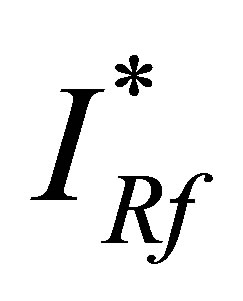 and
and 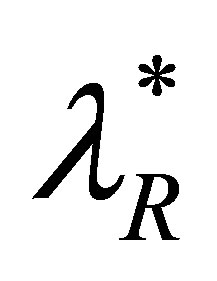 in the equation for
in the equation for 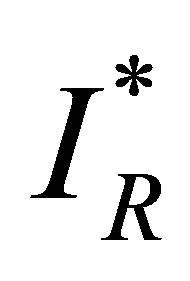 results in
results in
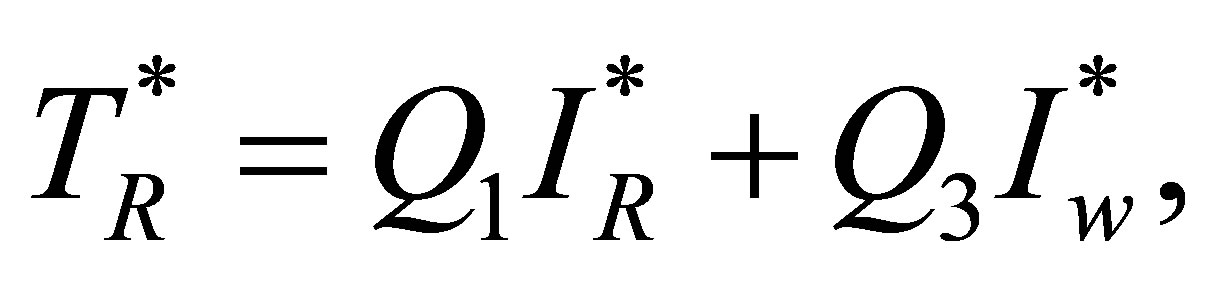
where
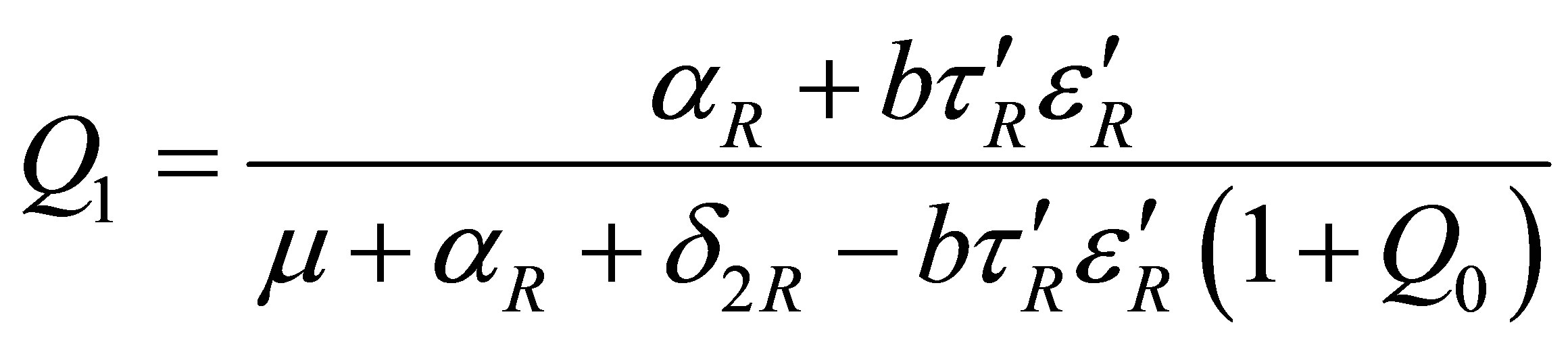
and
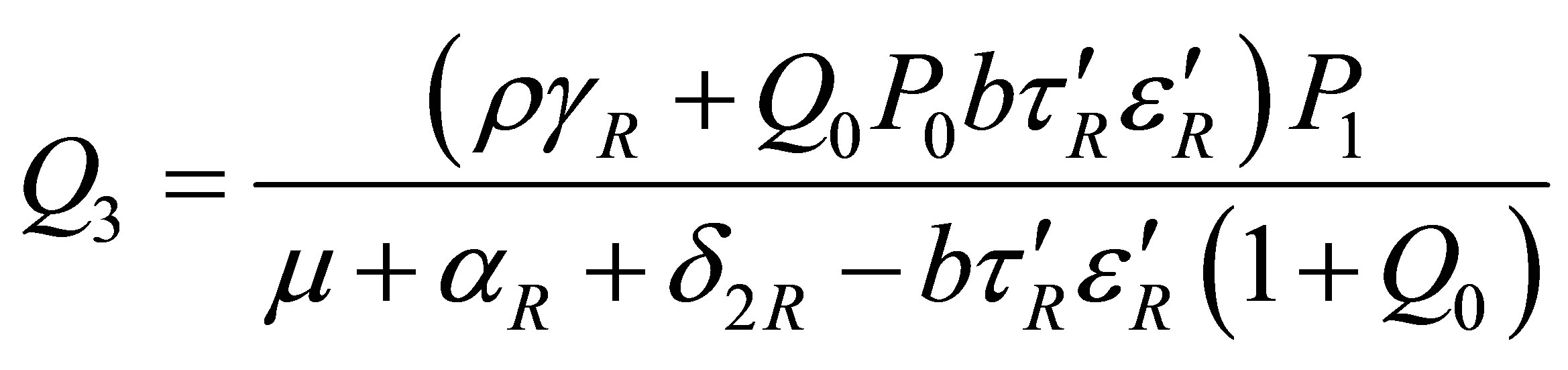
The expression for 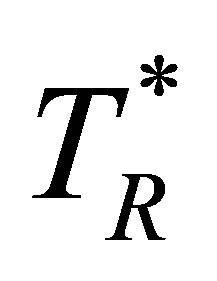 gives to
gives to  and
and

where
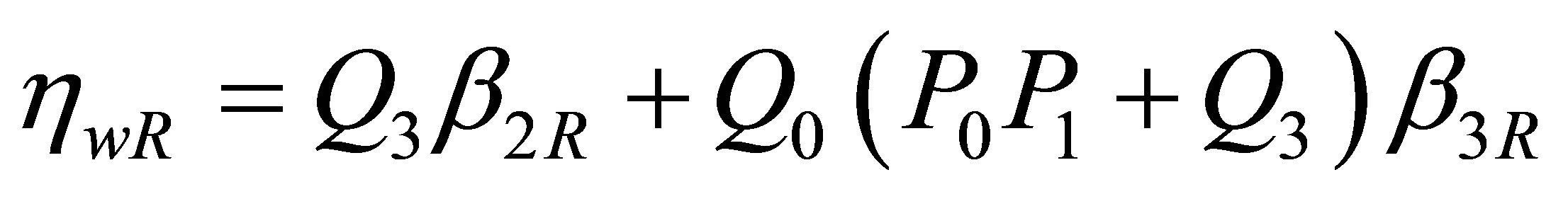
and

Let
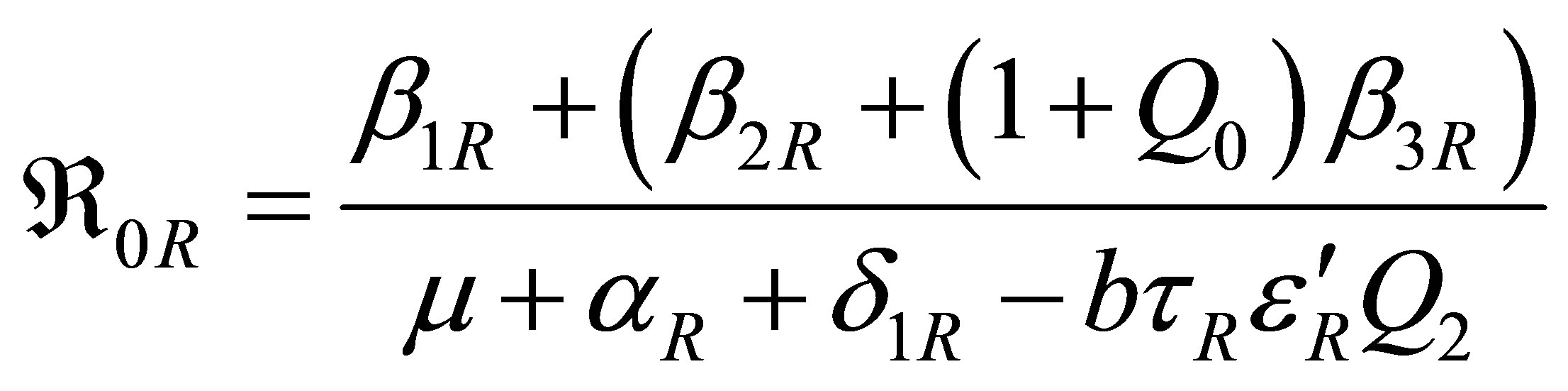
be the threshold parameter due to drug resistance and
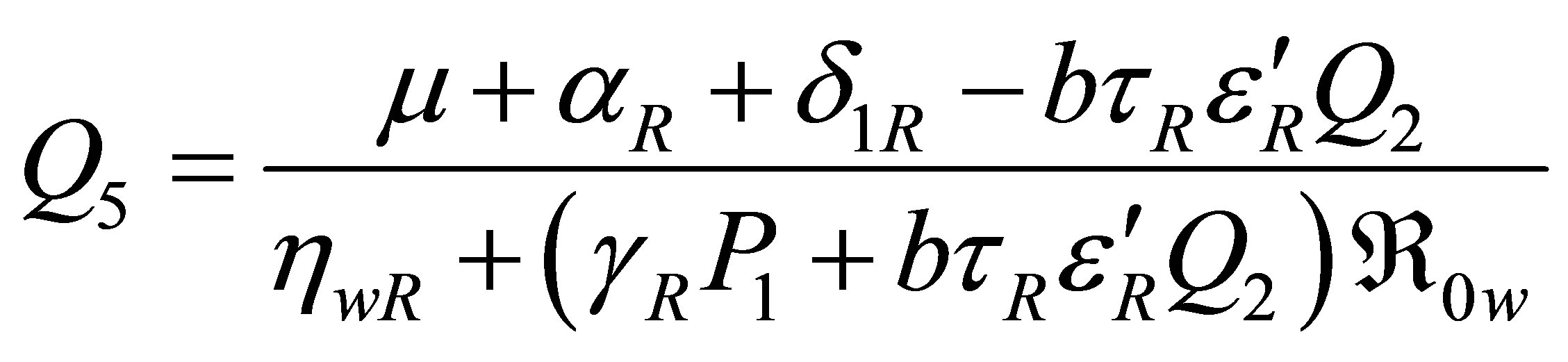
Then we establish a relationship between 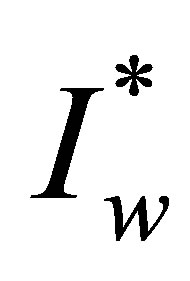 and
and 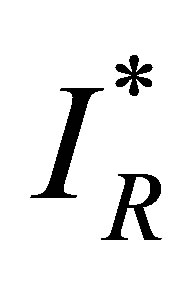 as
as
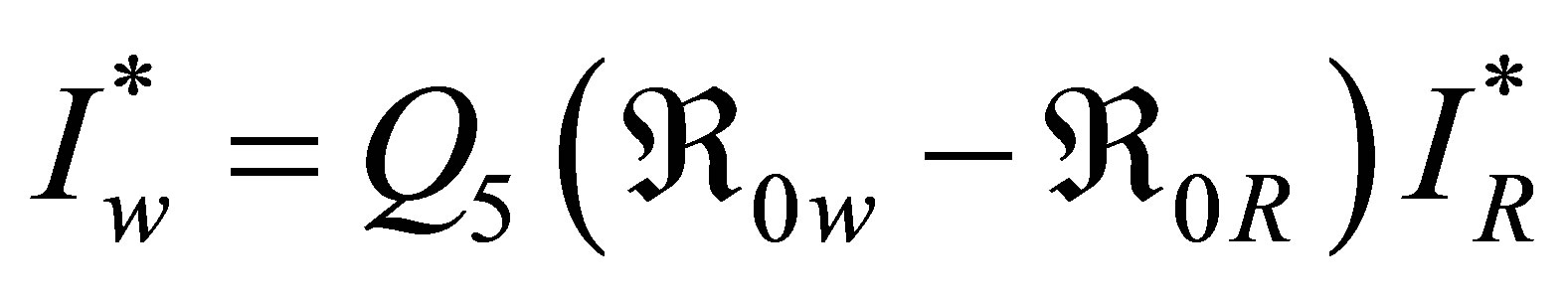
Clearly, 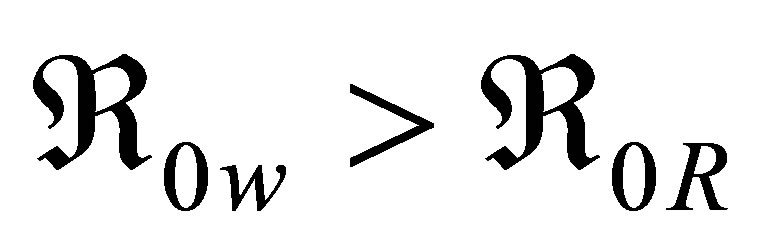 and result confirms the findings in literature which claims that the virulence of resistant strain is weak than the wild strain. The results above and the equation for
and result confirms the findings in literature which claims that the virulence of resistant strain is weak than the wild strain. The results above and the equation for  yield
yield
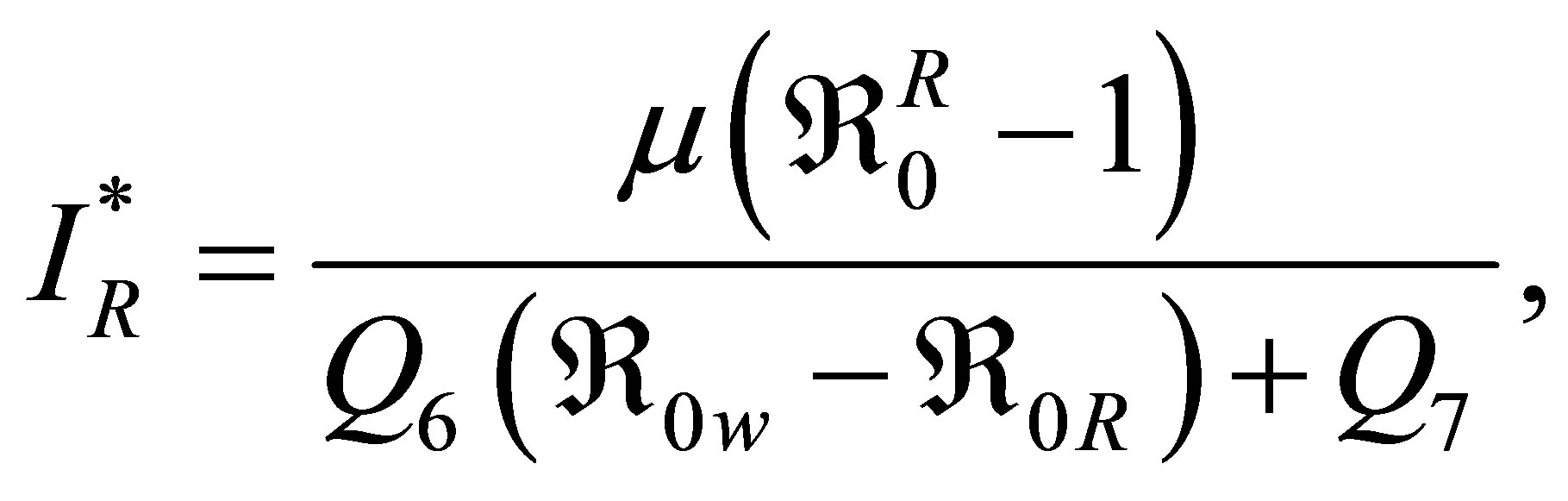
where
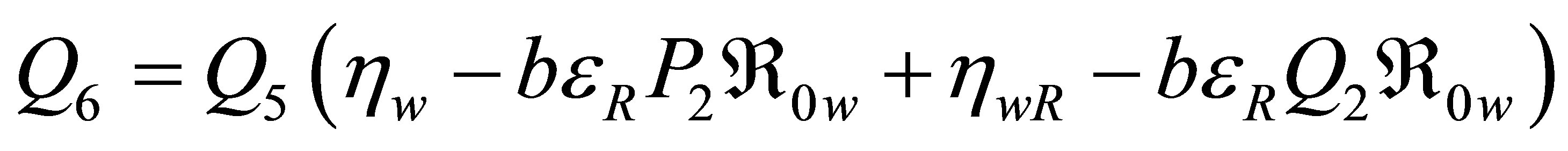
and
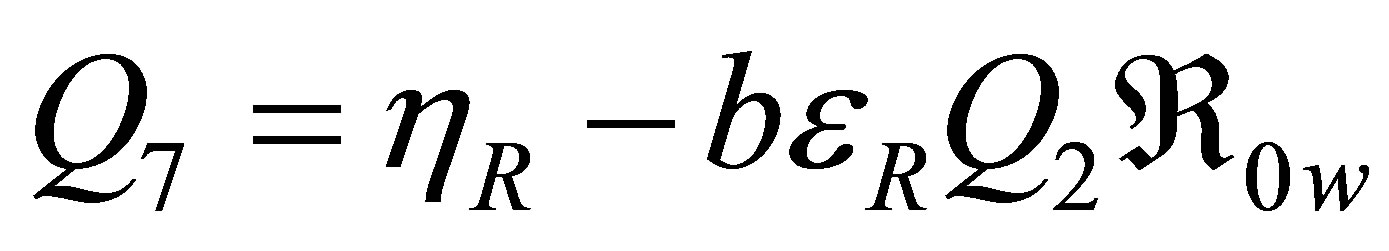
satisfying the conditions
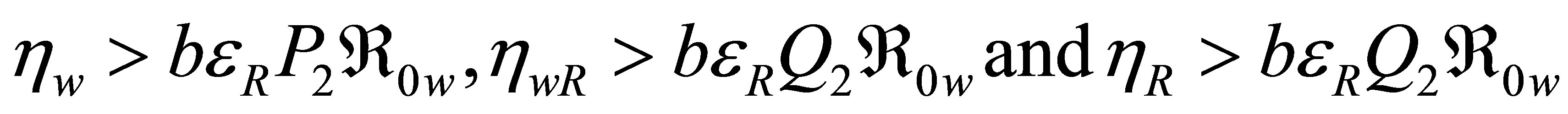
3.2.5. The Model Reproduction Numbers (Thresholds)
Suppose

Then we can express the generation of secondary infections due to horizontal transmission as
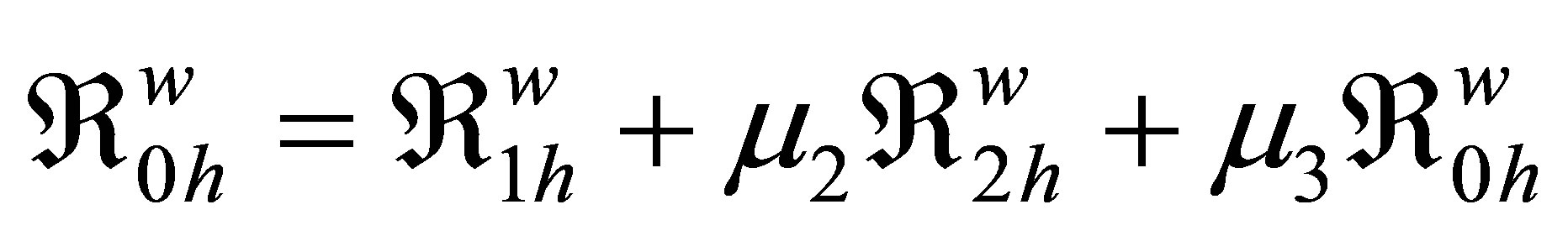
and vertical transmission as

with the net effects of the transmission due to the wild strain given by . The reproduction number of the model is given by
. The reproduction number of the model is given by

with

and 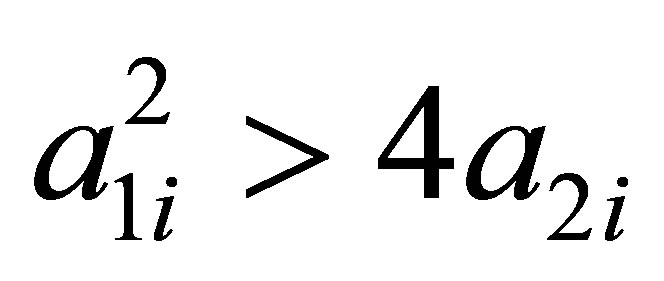 for
for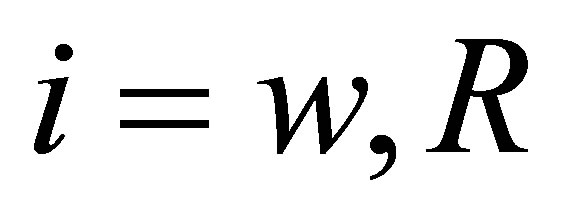 . The parameter
. The parameter 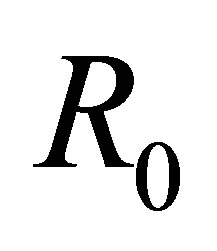 is defined as the average number of secondary infections generated by introducing an infected individual (with either wild or resistant strain) in a wholly susceptible population. The threshold parameters
is defined as the average number of secondary infections generated by introducing an infected individual (with either wild or resistant strain) in a wholly susceptible population. The threshold parameters 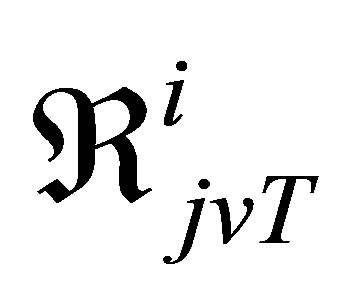 for
for
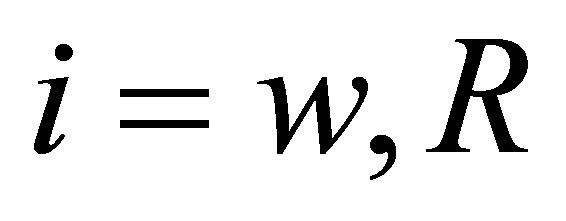 and
and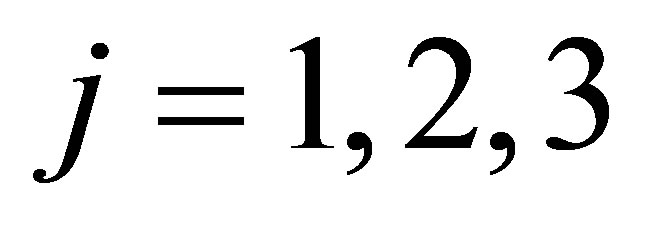 , are the demographic replacement of secondary infections due to vertical transmission by individuals identified and enrolled on antiretroviral therapy (ART) from childhood, while
, are the demographic replacement of secondary infections due to vertical transmission by individuals identified and enrolled on antiretroviral therapy (ART) from childhood, while  for
for 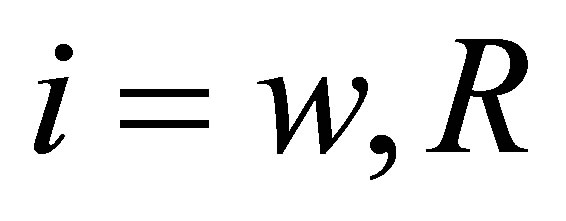 and
and 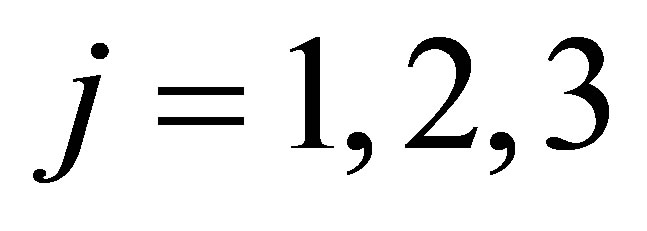 are the demographic replacement of secondary infections due to vertical transmission by offsprings who progress from birth to adulthood without treatment.
are the demographic replacement of secondary infections due to vertical transmission by offsprings who progress from birth to adulthood without treatment.
3.3. Local Stability of Disease-Free Equilibrium Point
Evaluating at the disease-free equilibrium point
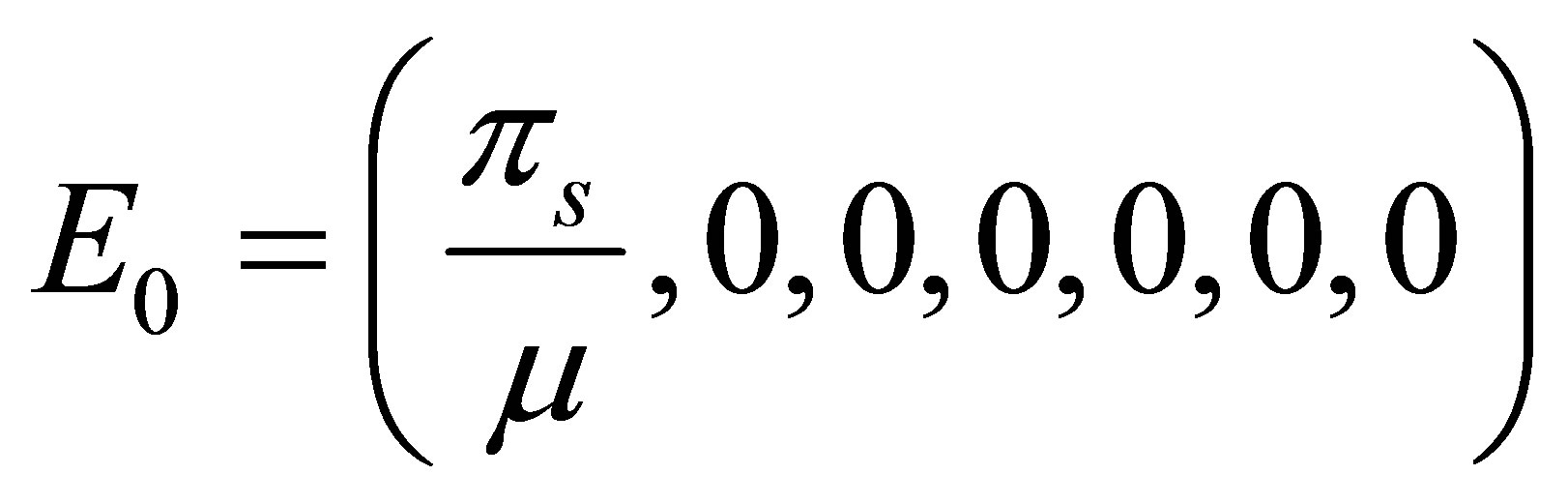 the system has the Jacobian matrix
the system has the Jacobian matrix , given by
, given by

where

We note from matrix  that
that 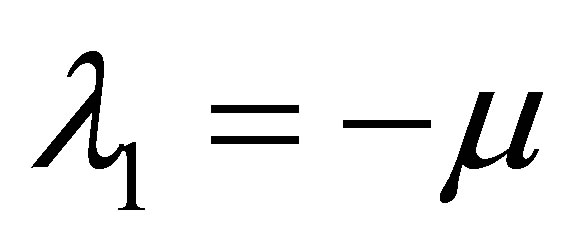 and the other eigenvalues can be found form solving the characteristic polynomials of the block matrices
and the other eigenvalues can be found form solving the characteristic polynomials of the block matrices  and
and . The characteristic polynomial of the block matrix
. The characteristic polynomial of the block matrix  is given by,
is given by,
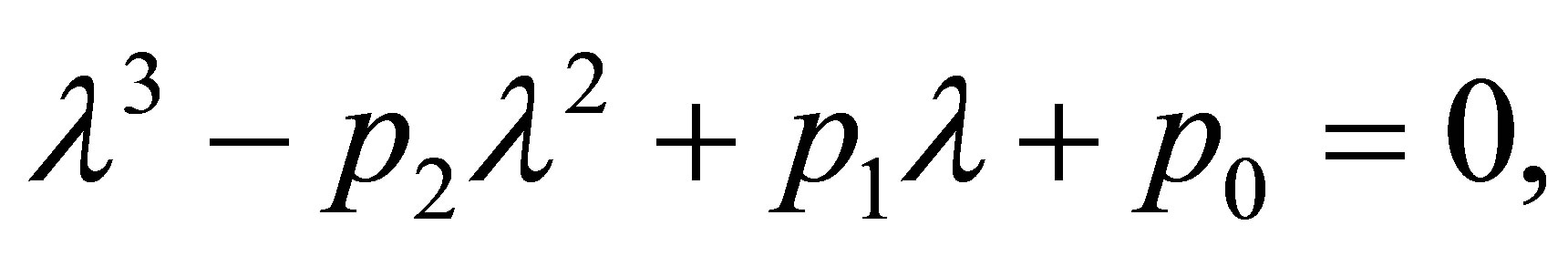
where
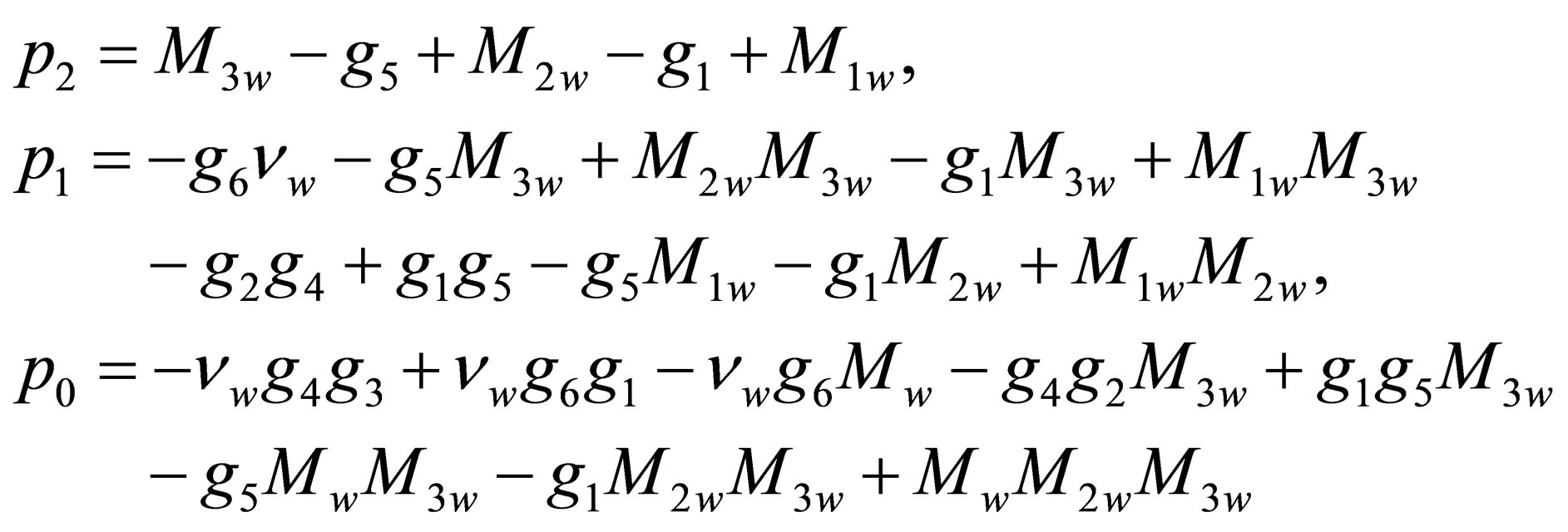
with
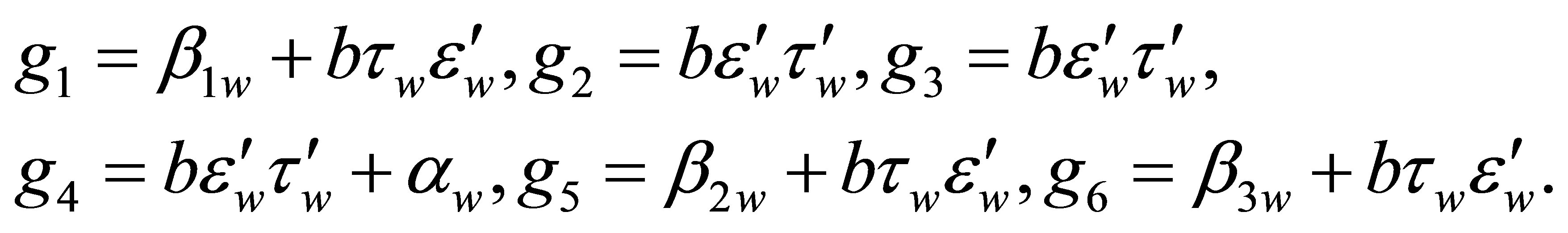
After some manipulations it can be shown that the expression for 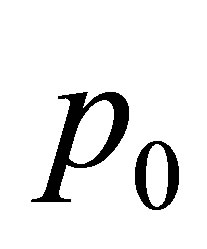 is written as
is written as
 (4)
(4)
where
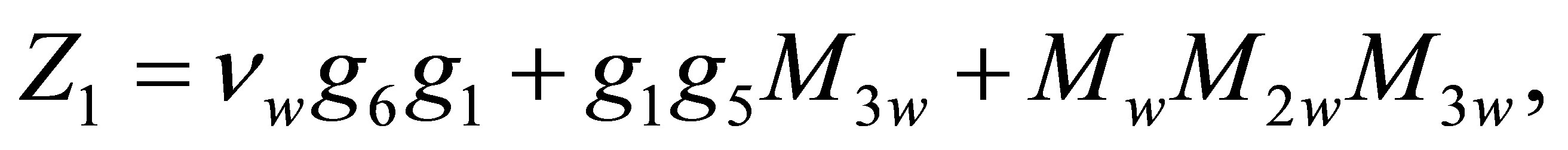
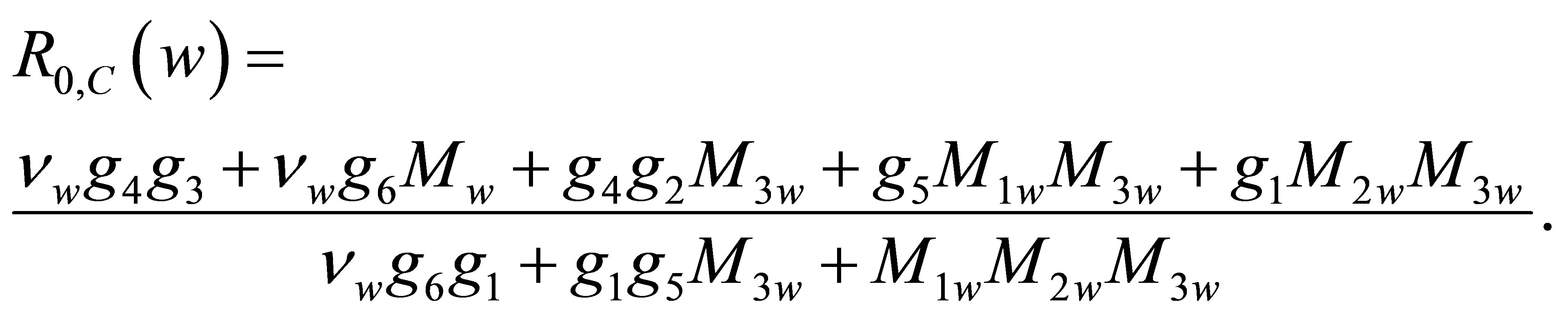 (5)
(5)
The threshold 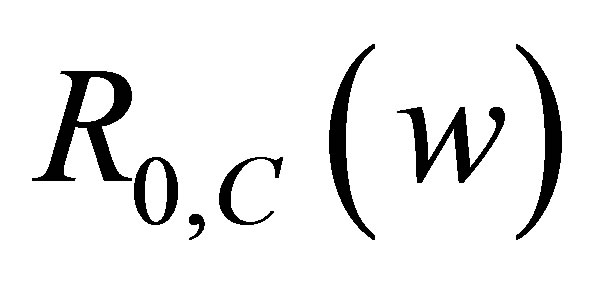 is called the basic reproduction number for wild virus type for the system (2).
is called the basic reproduction number for wild virus type for the system (2).
The characteristic polynomial of block matrix  is given by,
is given by,
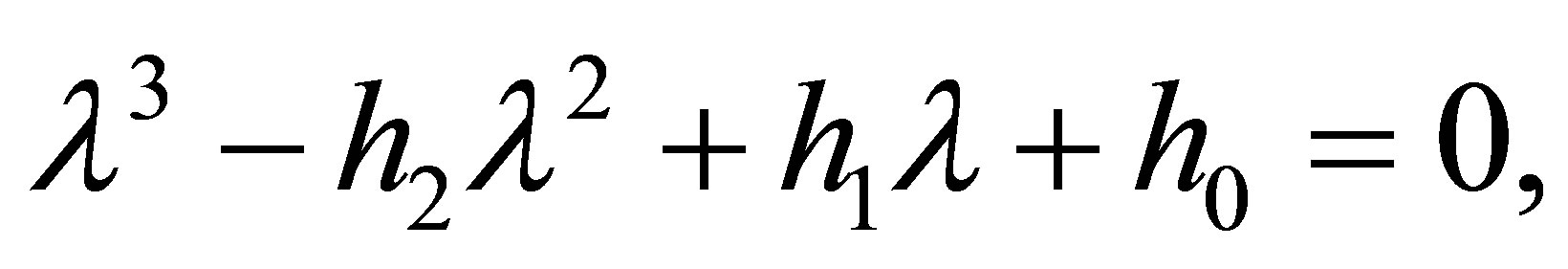
where

The expression for 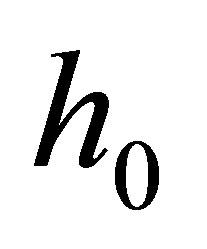 can be written as
can be written as
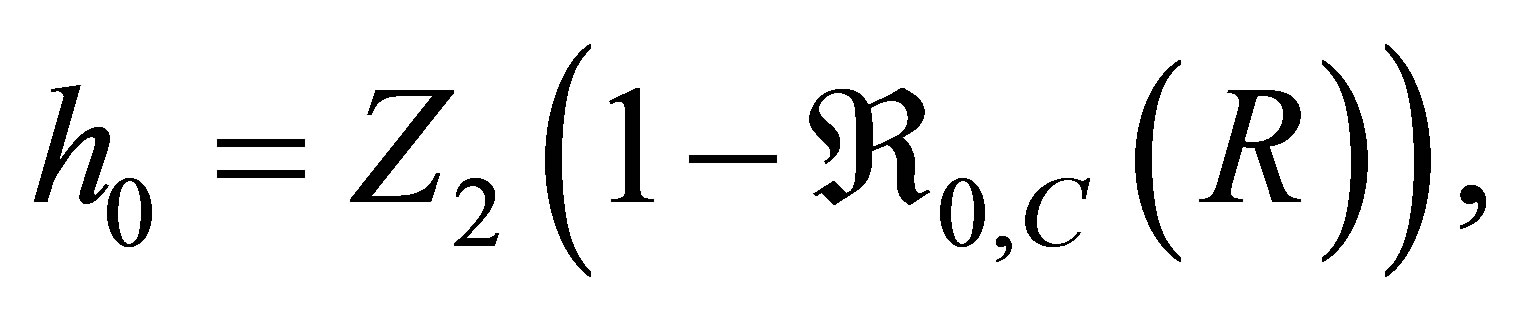 (6)
(6)
where

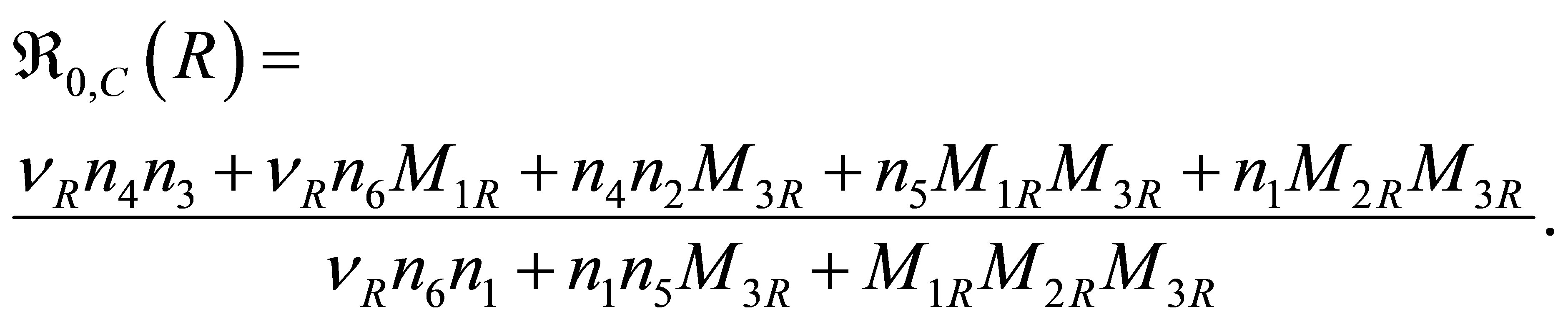 (7)
(7)
The threshold 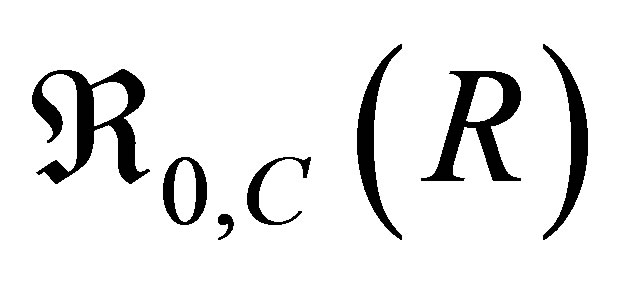 is called the basic reproduction number for drug resistant virus type for the system (2).
is called the basic reproduction number for drug resistant virus type for the system (2).
From Equation (5) and (7), we now have the effective reproduction number of the model (denoted by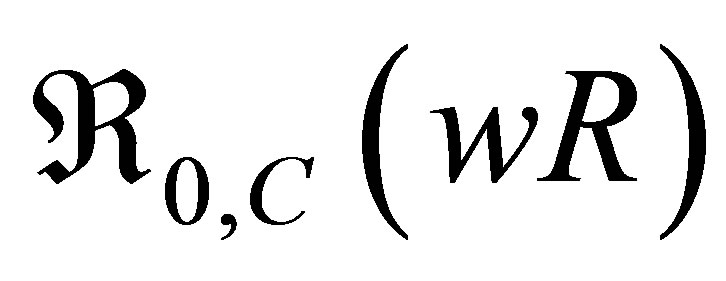 ) given by
) given by
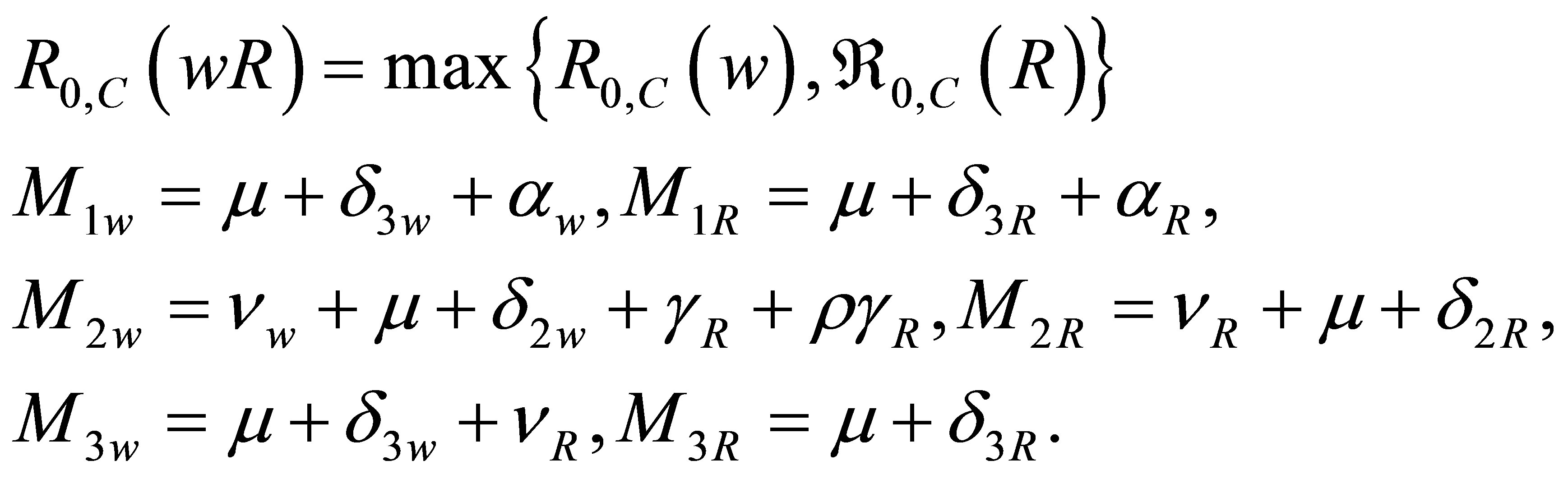
Theorem 1 The disease-free equilibrium point of the vertical transmission model (2) with drug resistance is locally asymptotically stable if 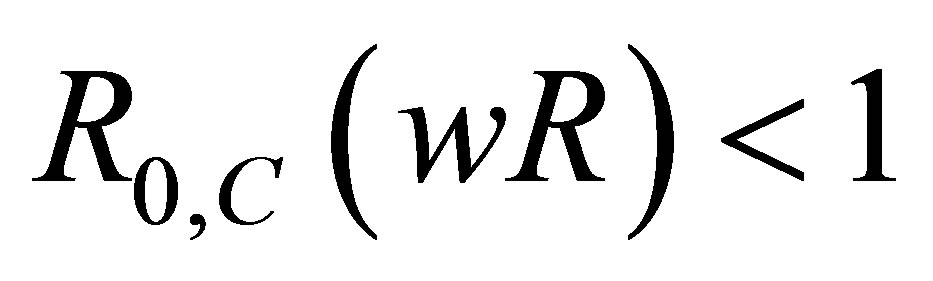 and unstable if
and unstable if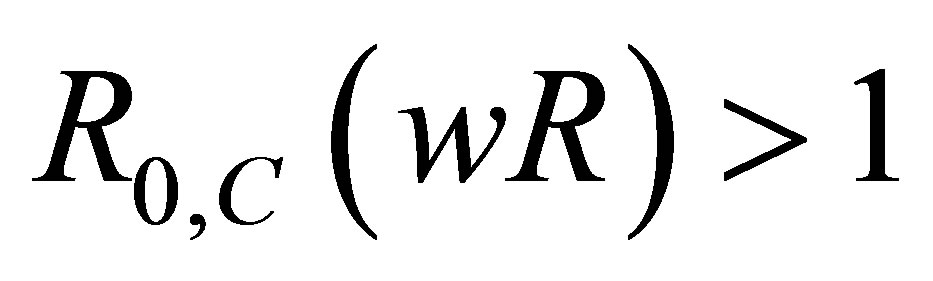 .
.
4. NUMERICAL SIMULATIONS
In order to illustrate some of the analytical results of the study, numerous numerical simulations of the model (2) are carried out using a set of reasonable parameter values given in Table 2 below.

Table 2. Parameter values used in numerical simulation.
However these parameters may (or may not) be biologically feasible.
Figure 2 below shows the variations of the seven classes of HIV/AIDS model with drug resistance.
Form Figure 2 it can be seen is that, infective population is increasing. This leads into the decrease in susceptible class.
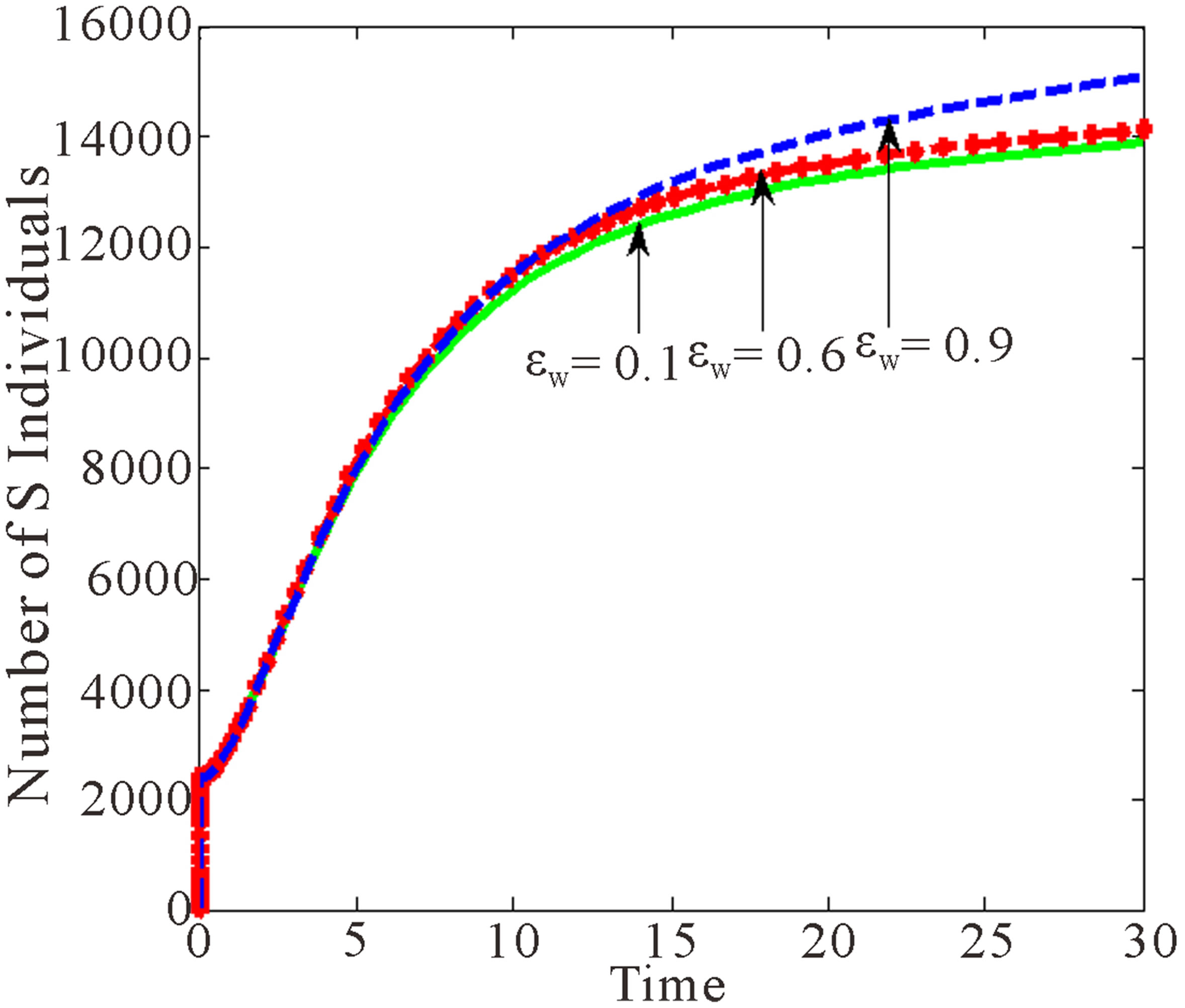
Figure 3 below shows the effects of rate of HIV Free children born with wild sensitive virus.
Figure 3 shows that as  increases, individuals in AIDS and treated classes with drug resistant virus decrease. However, the number of susceptible individuals increases.
increases, individuals in AIDS and treated classes with drug resistant virus decrease. However, the number of susceptible individuals increases.
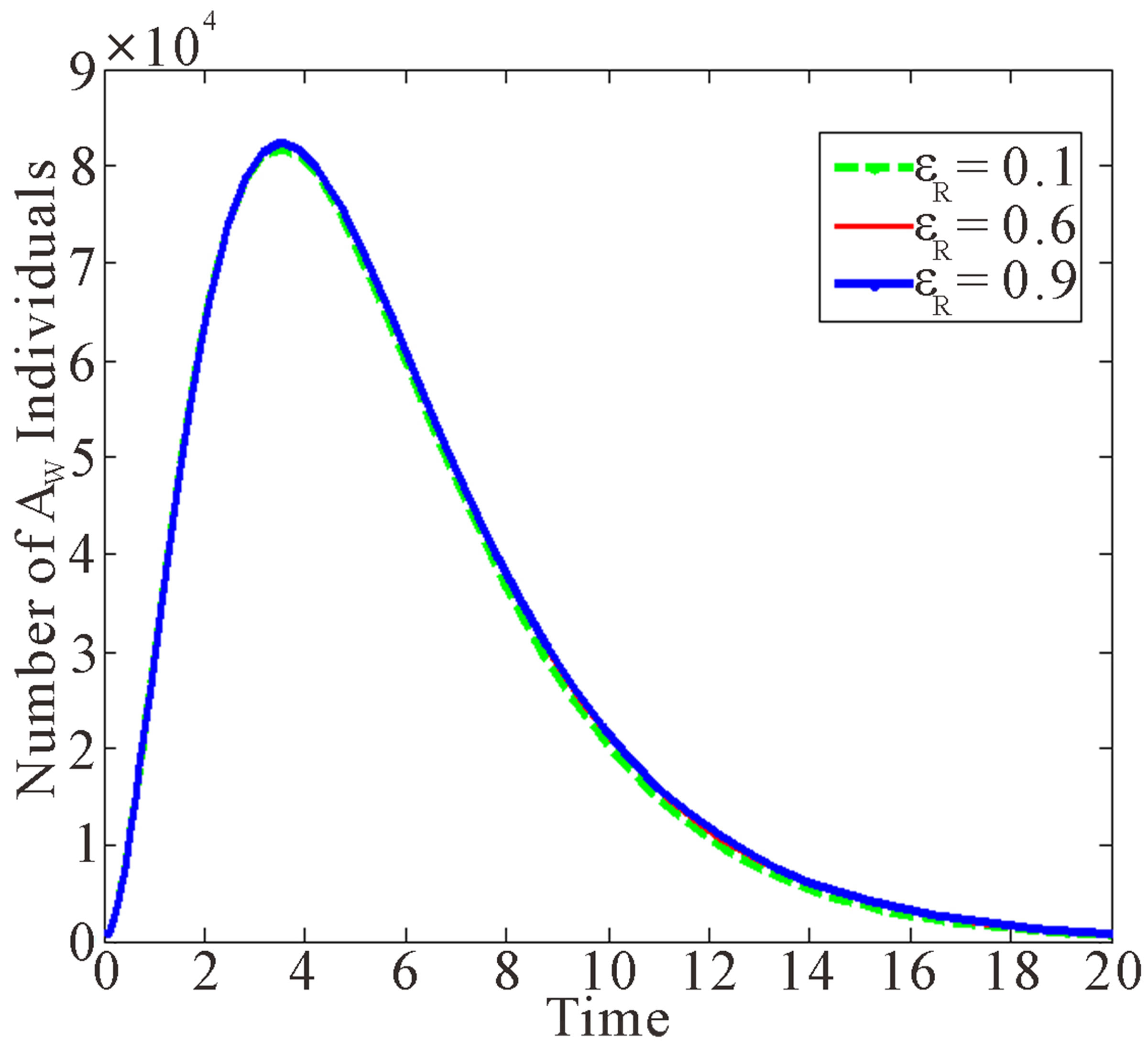
Figure 4 below shows the effects of Rate of HIV Free Children Born with Drug Resistant Virus.
Figure 4 shows that as the proportion of children who are drug resistant born HIV negative increases, the numbers of populations in the drug resistant class and treated drug resistant class decrease.
Figure 5 below depicts the behaviour of the AIDS population with both wild and resistant strains, and treated population with resistant strain as influence by changes in the progression rates of drug resistant individuals to AIDS.
From Figure 5 it is seen that at high progression rates, the three classes reach their peaks much faster than at low values of progression rates, with AIDS class having the highest peak and infective population having the lowest peak.
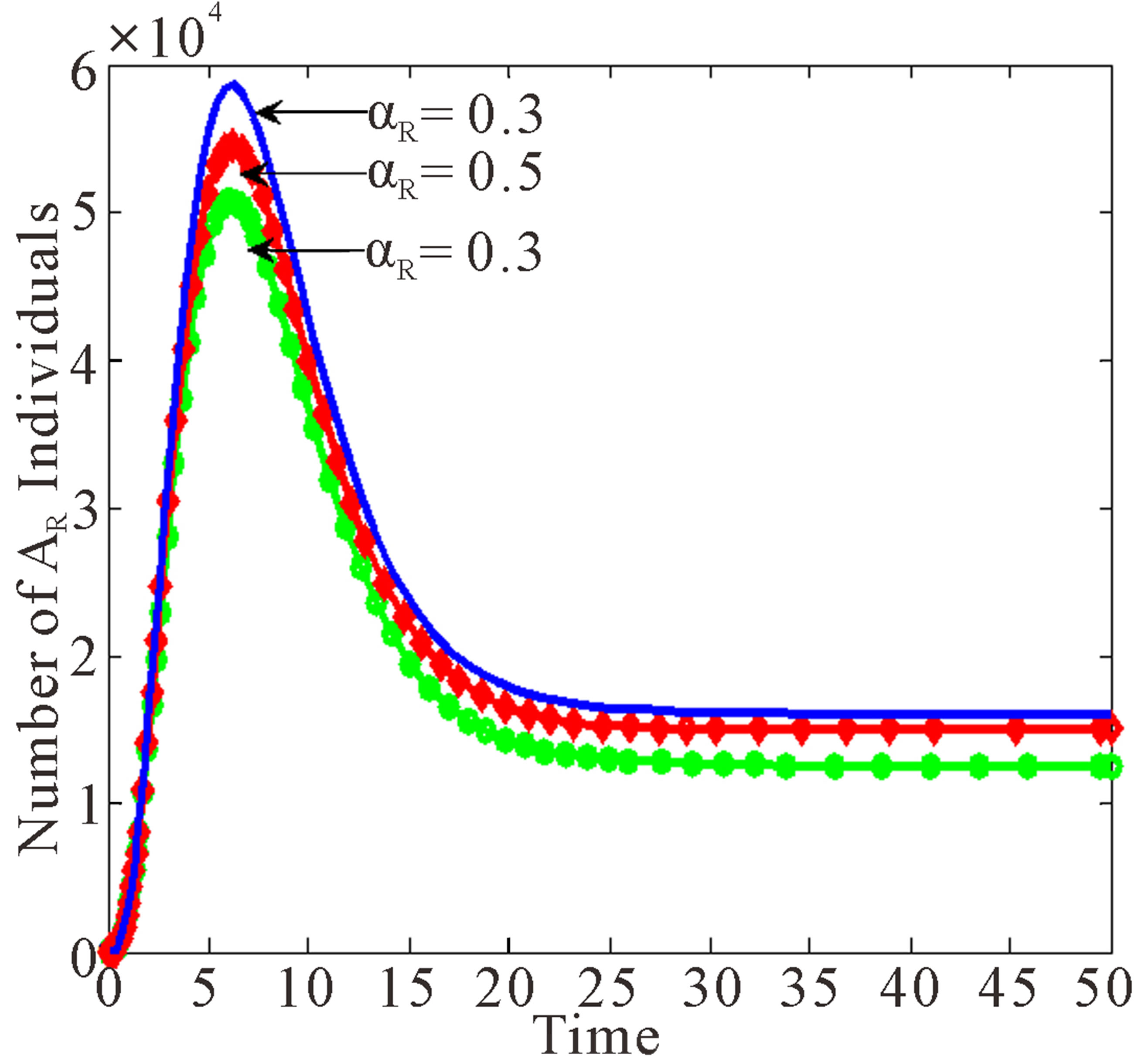
Figure 6 shows the effects of variation of progression rates to 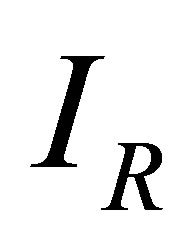 and
and 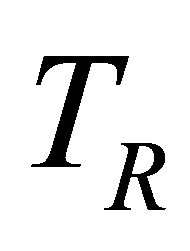 when
when 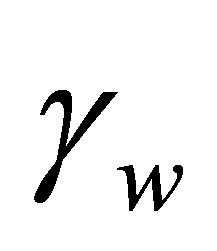 is varied.
is varied.
Figure 6 shows that increasing 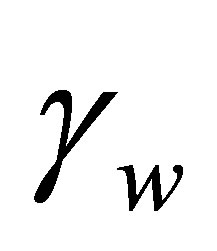 leads to decrease in number of individuals in the treated and infected with wild virus classes. However, individuals in
leads to decrease in number of individuals in the treated and infected with wild virus classes. However, individuals in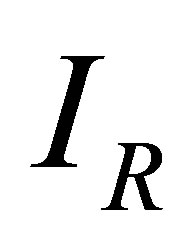 ,
, 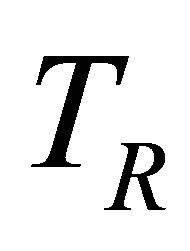 and
and 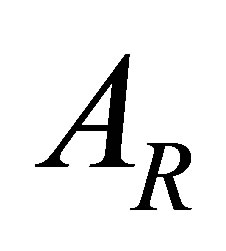 increase as
increase as 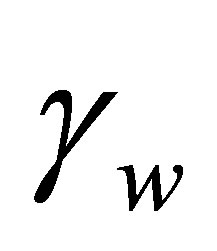 increases.
increases.
Figure 7 below show the effects of treatment rates of
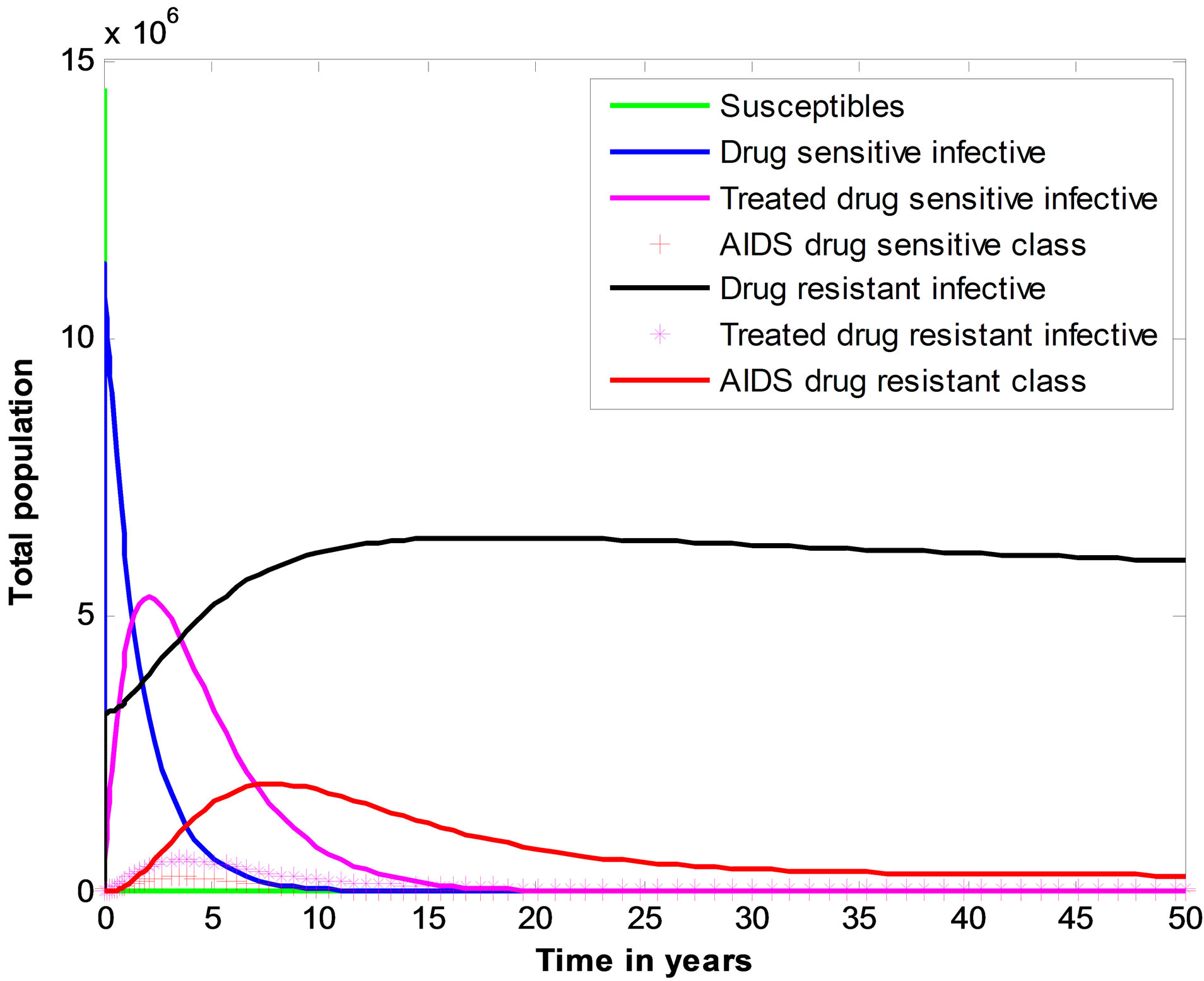
Figure 2. Illustration of the changes in seven state variables of full HIV/AIDS model with drug resistance.
 (a)
(a)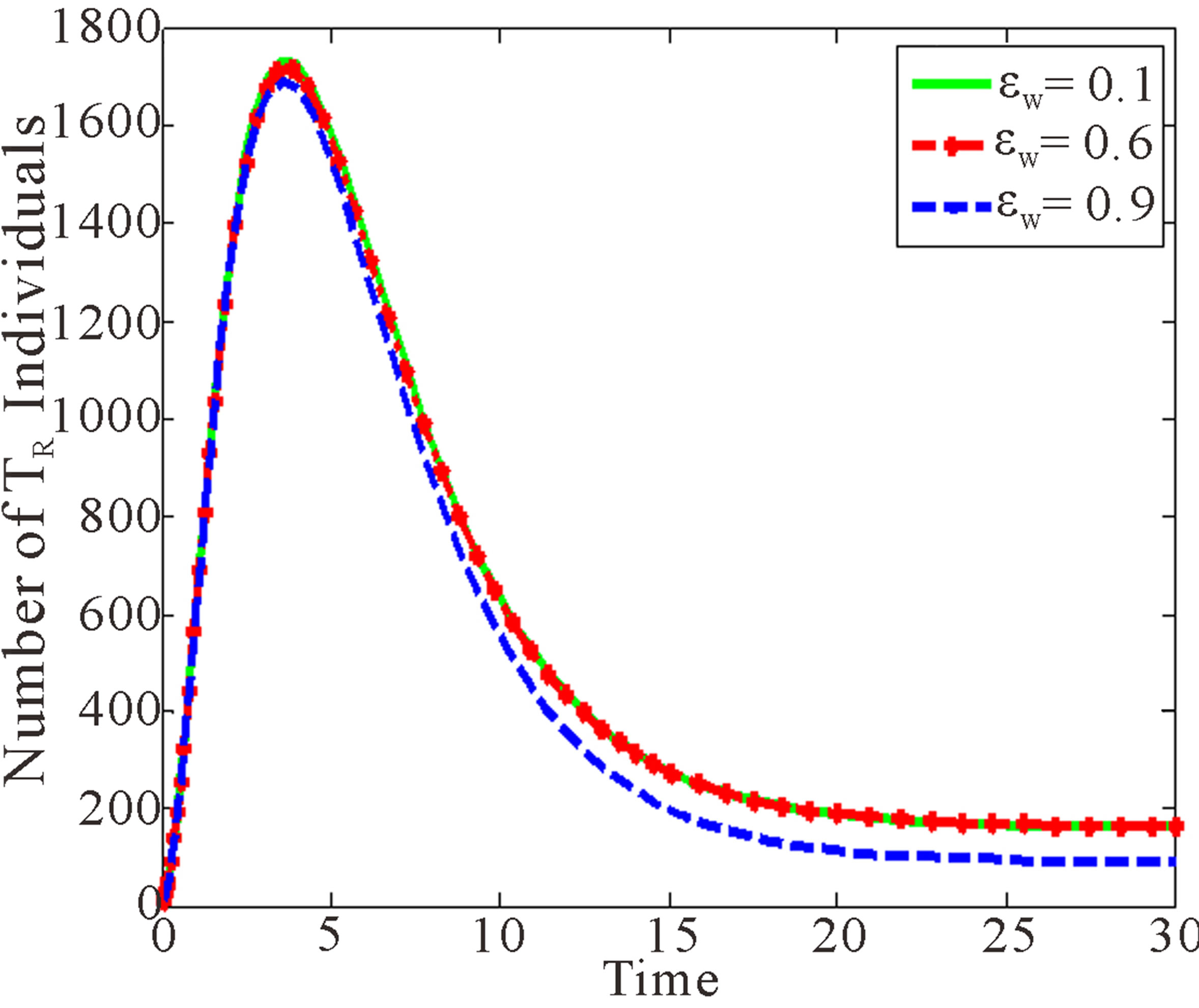 (b)
(b)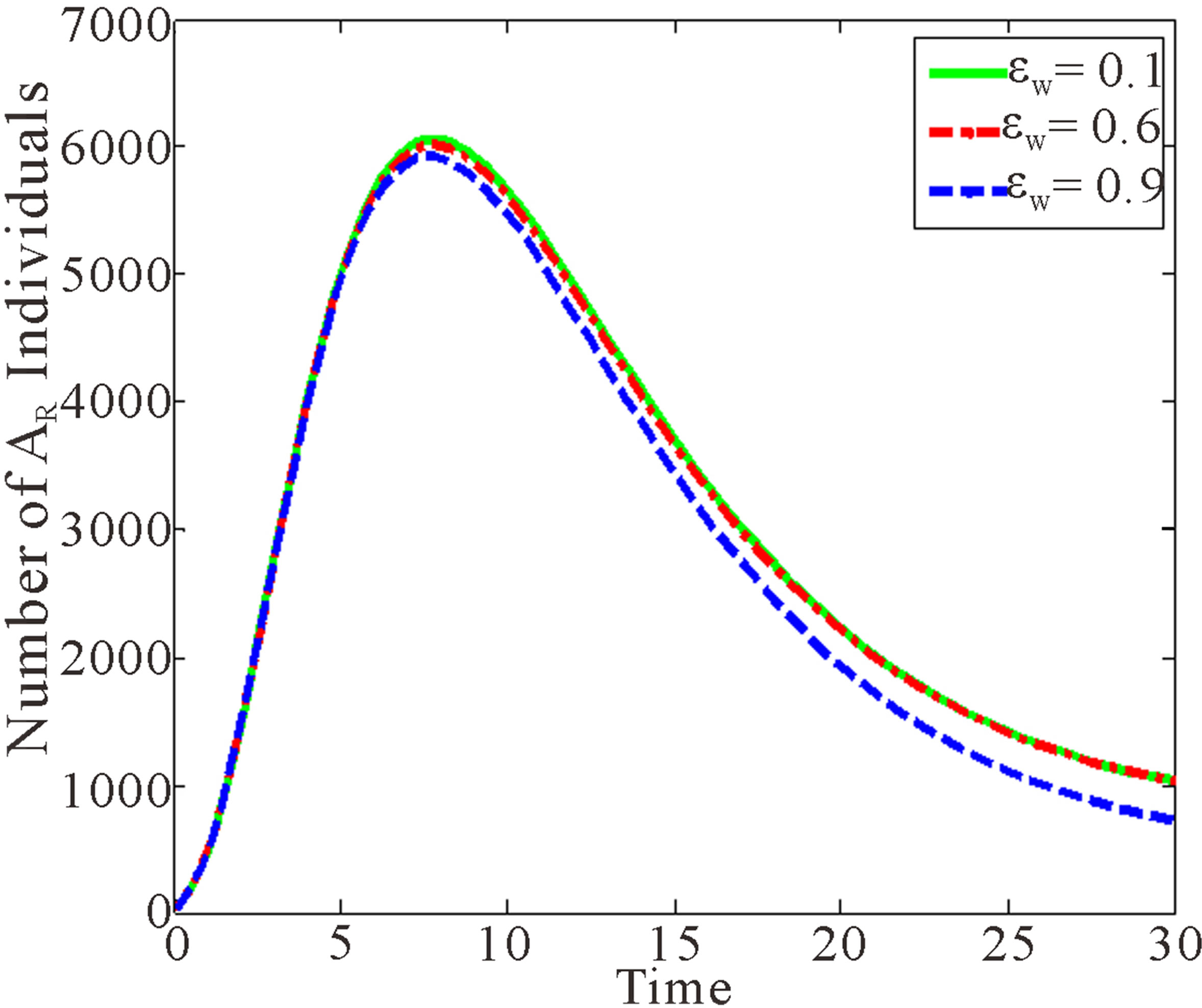 (c)
(c)
Figure 3. Effects of variation of proportion of children born with wild sensitive virus.
 (a)
(a)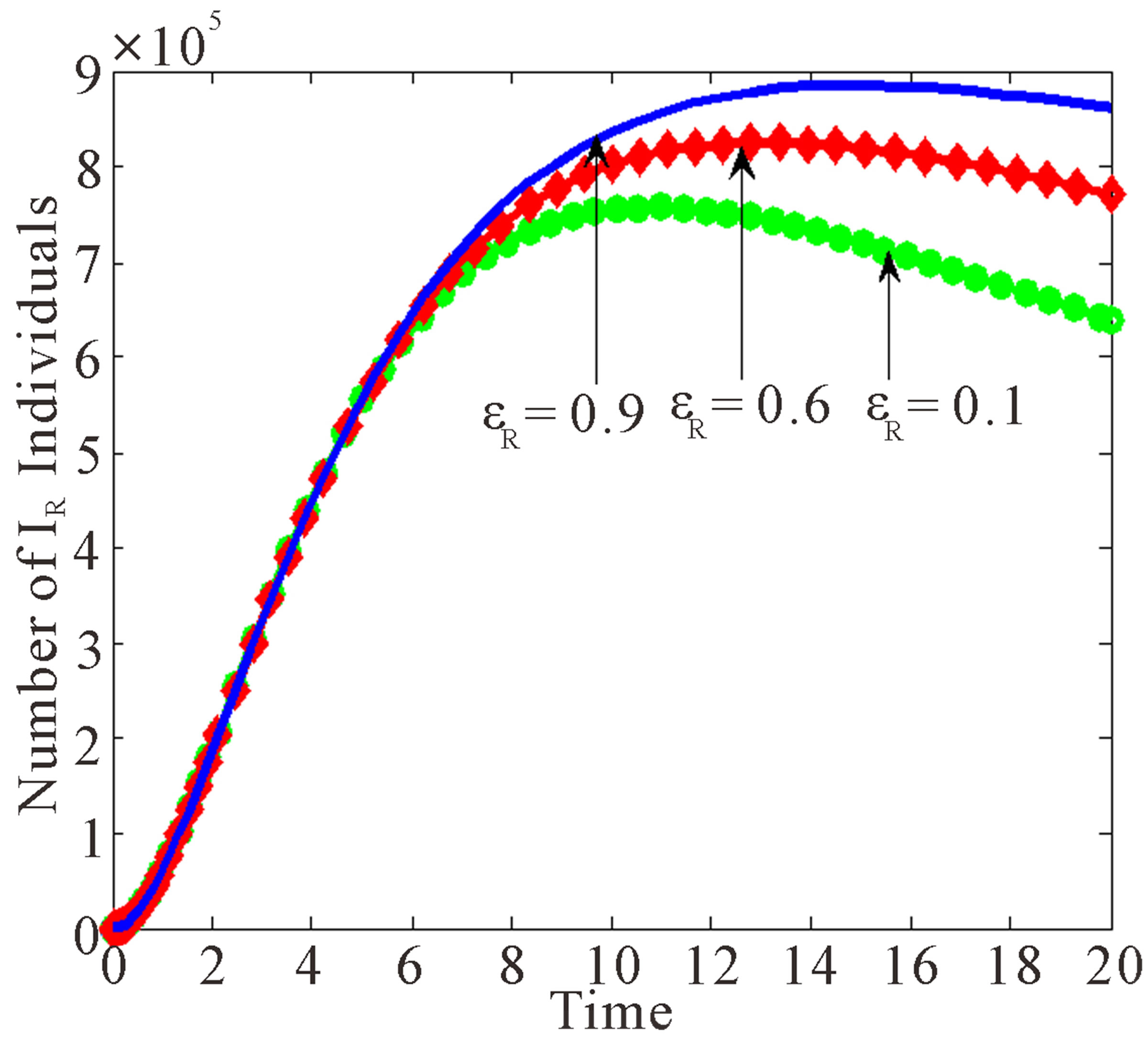 (b)
(b)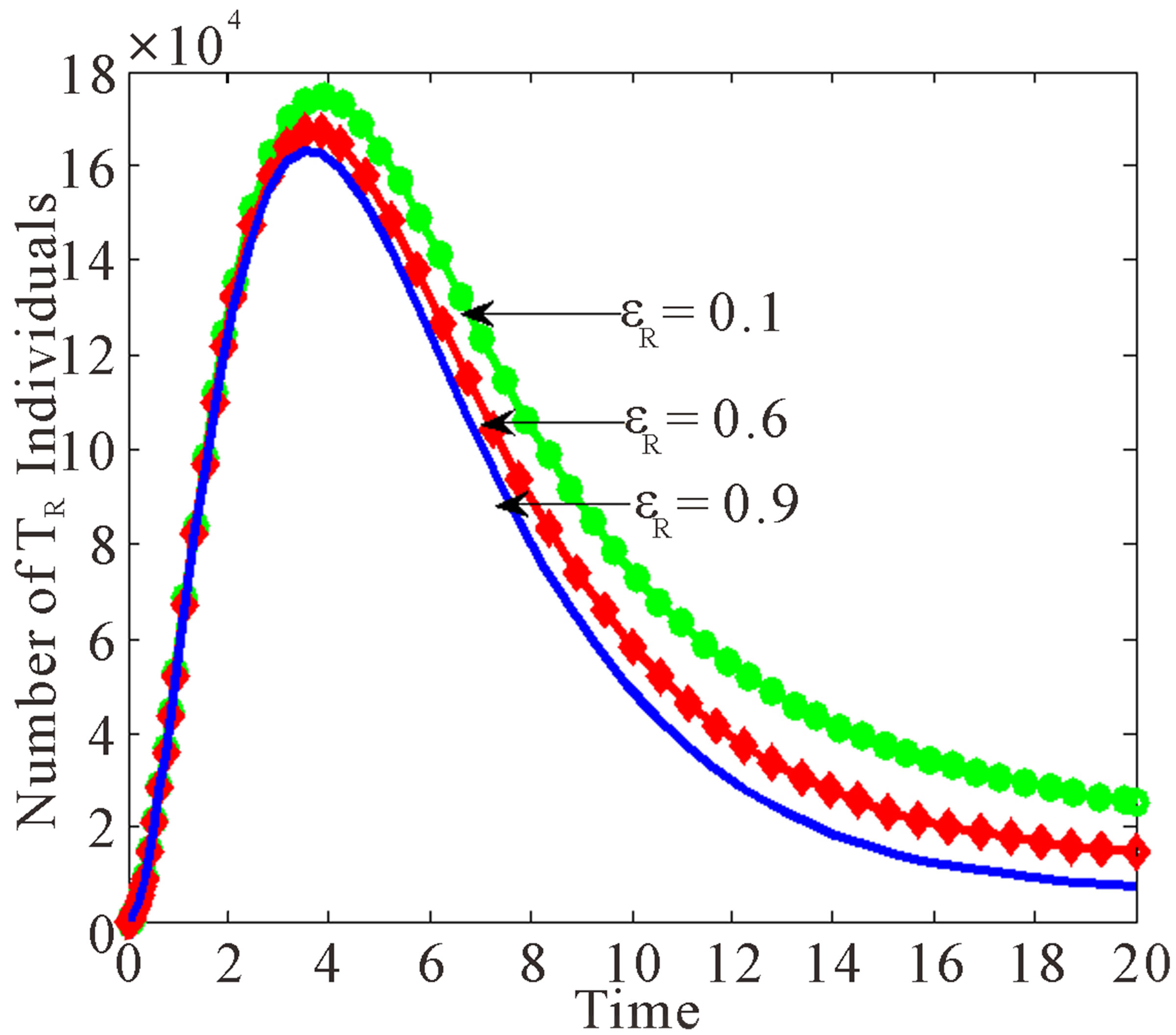 (c)
(c)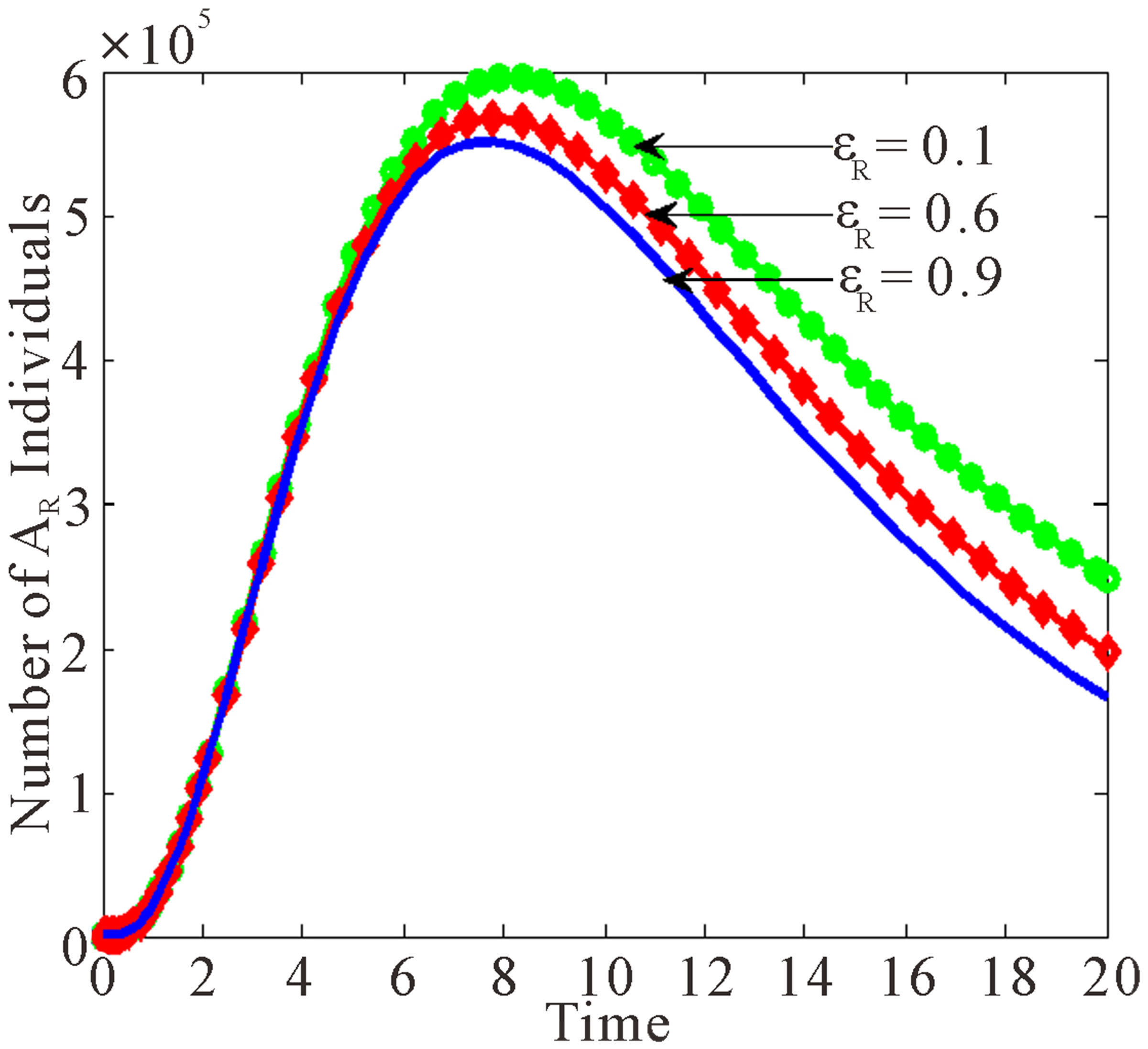 (d)
(d)
Figure 4. Dynamics of drug resistance influenced by vertical transmission with εR being varied.
 (a)
(a)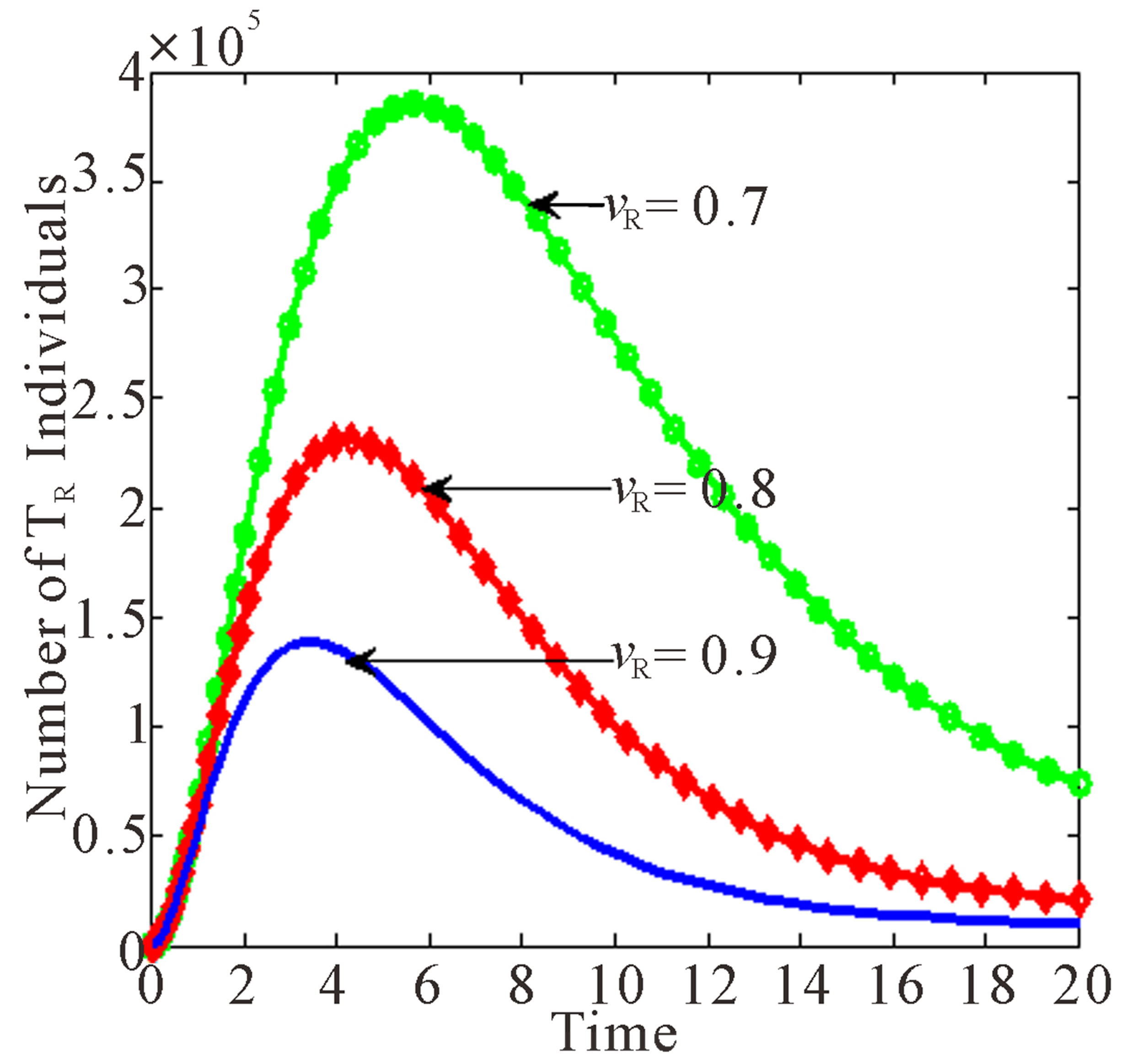 (b)
(b)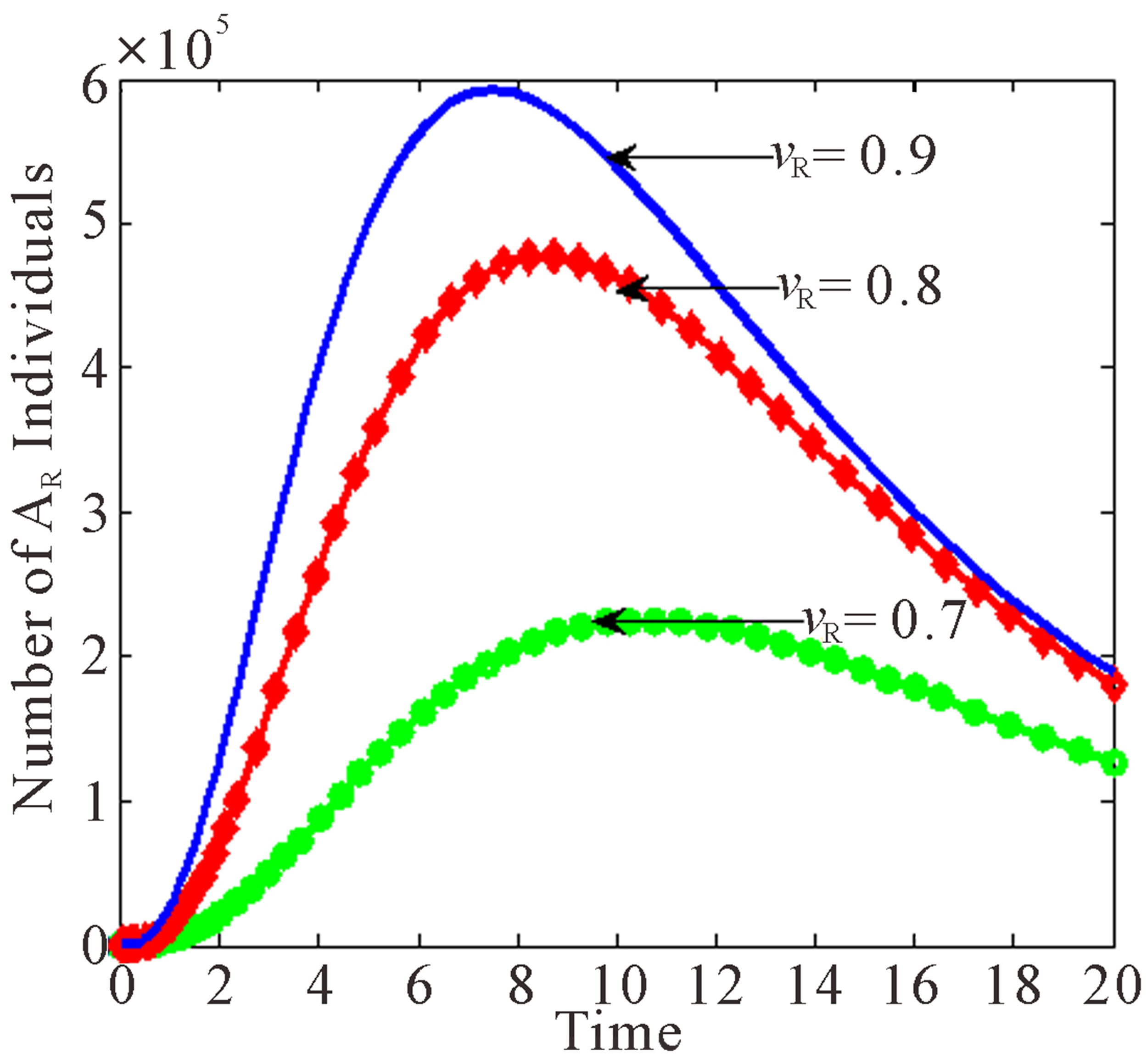 (c)
(c)
Figure 5. Effects of rate of progression to AIDS on vertical transmission.
 (a)
(a)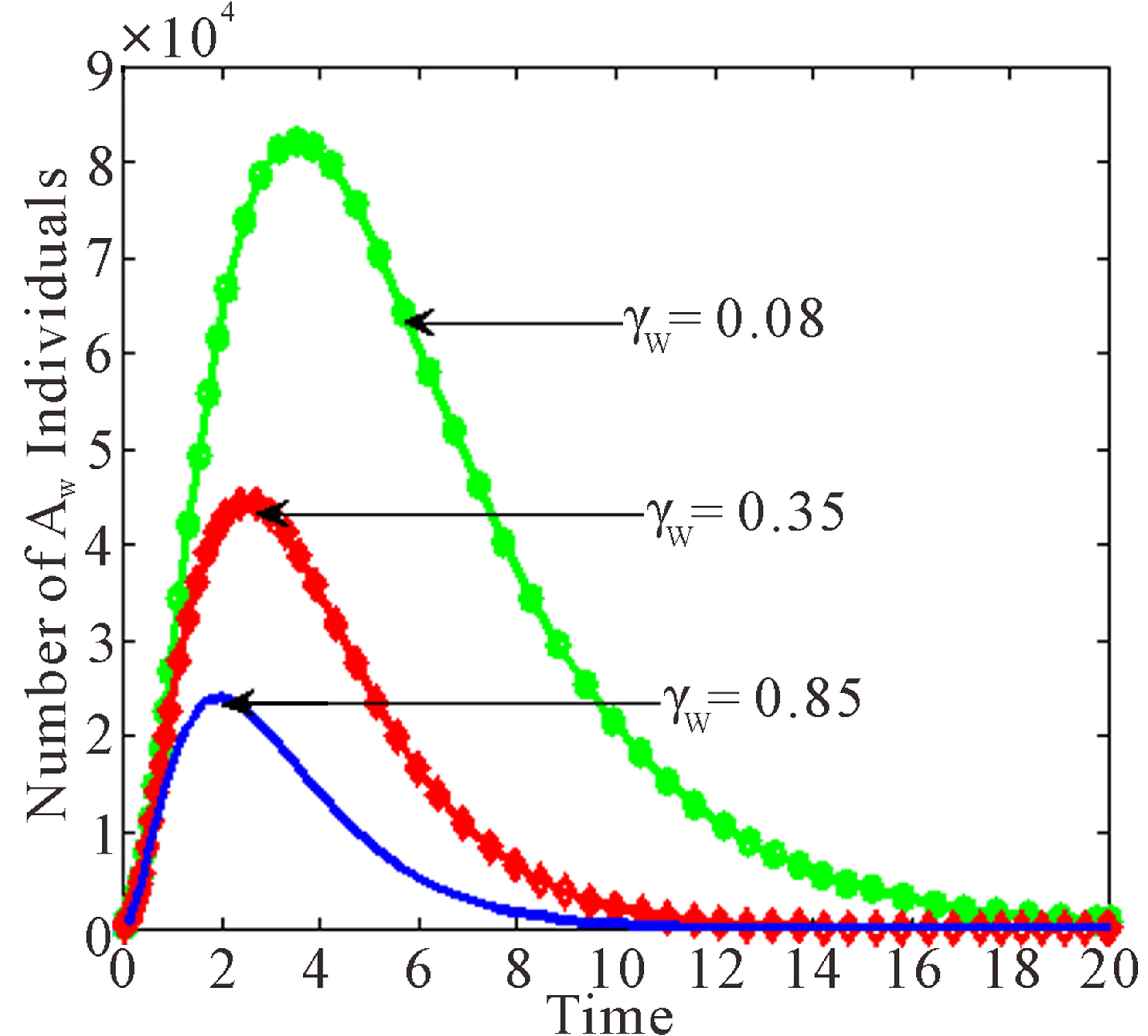 (b)
(b) (c)
(c)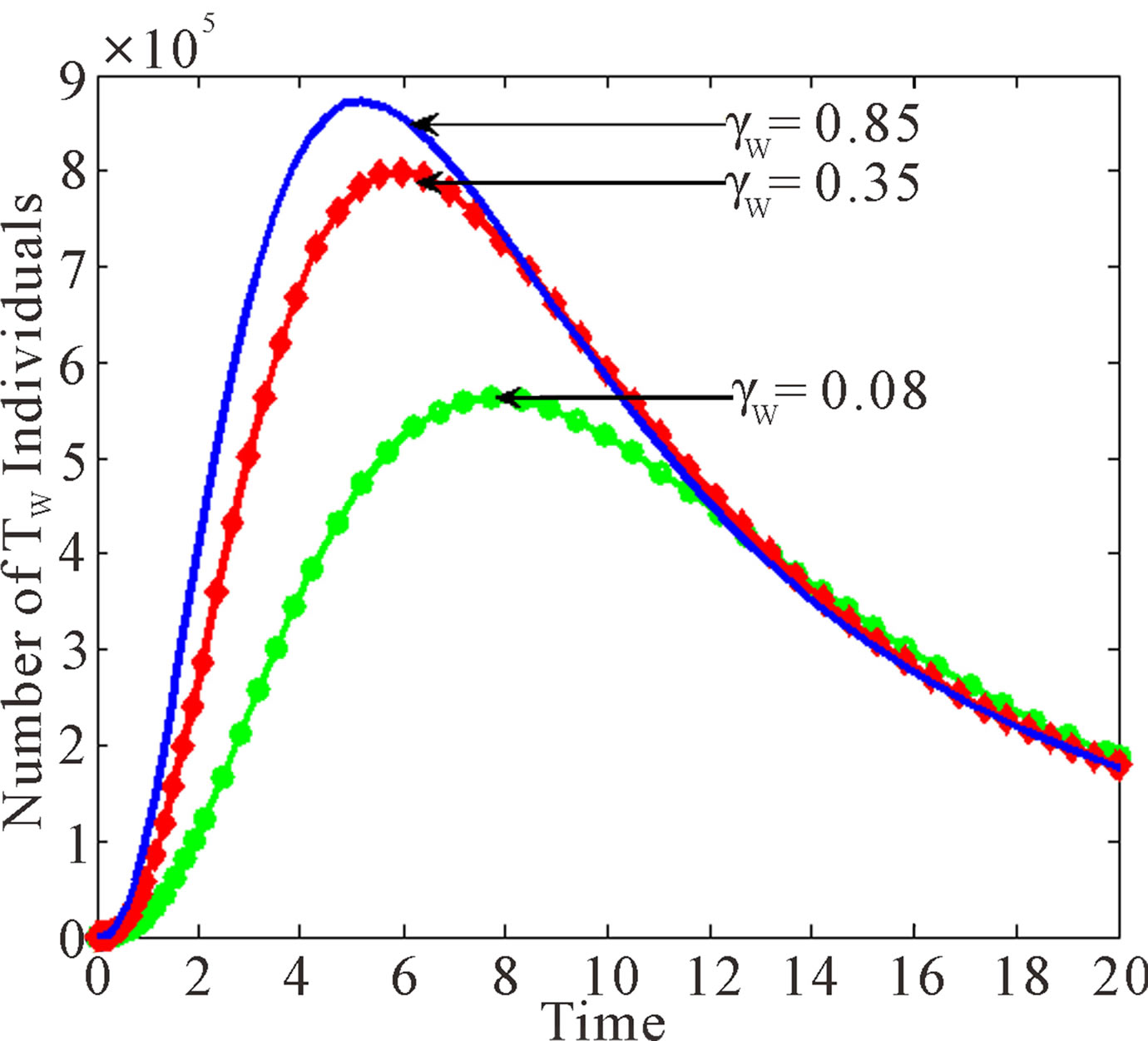 (d)
(d)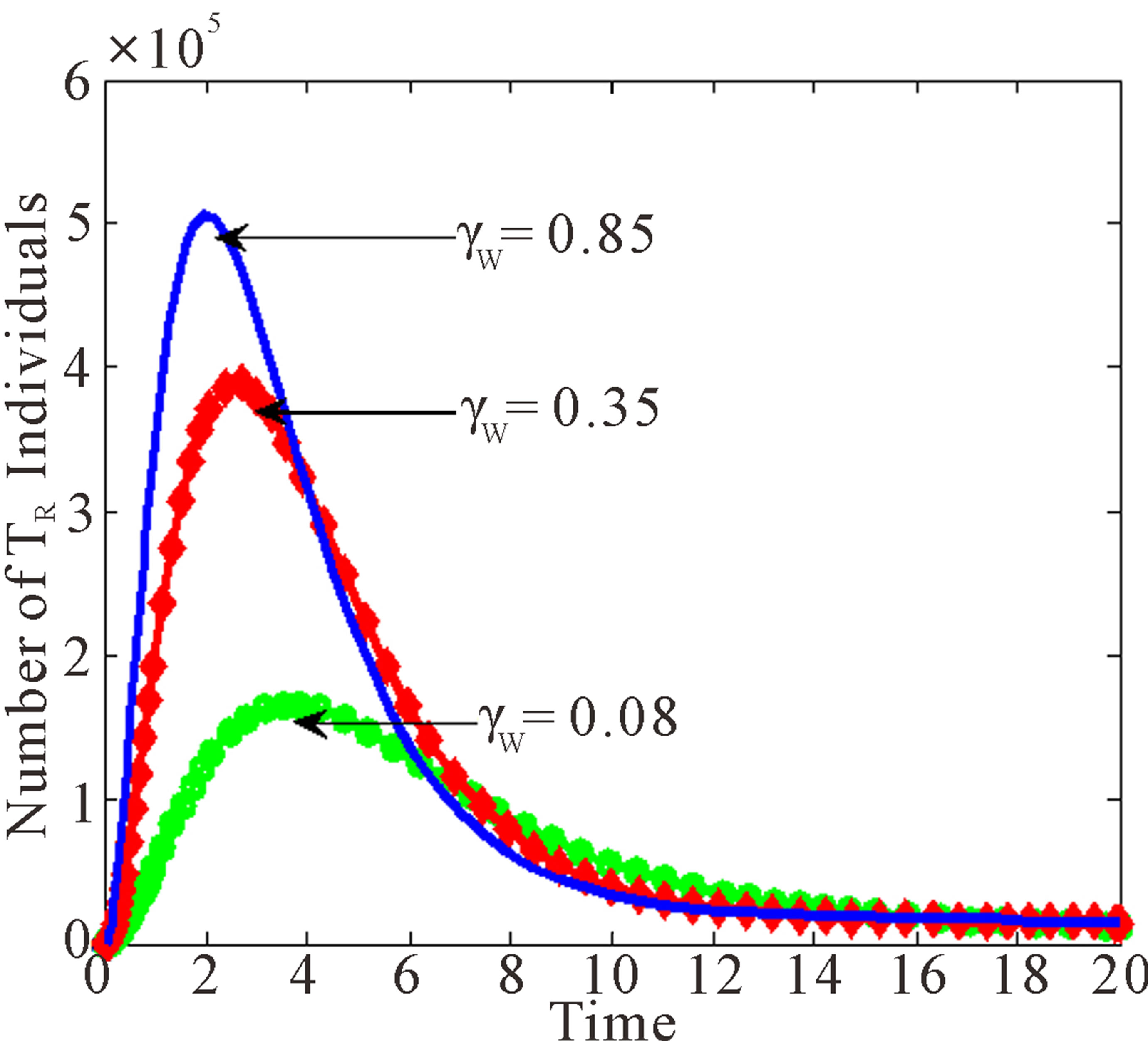 (e)
(e)
Figure 6. Effects of variation of progression rates to  and
and 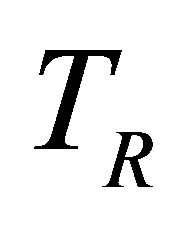 when
when 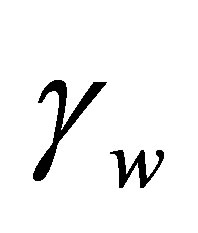 varied.
varied.
 (a)
(a)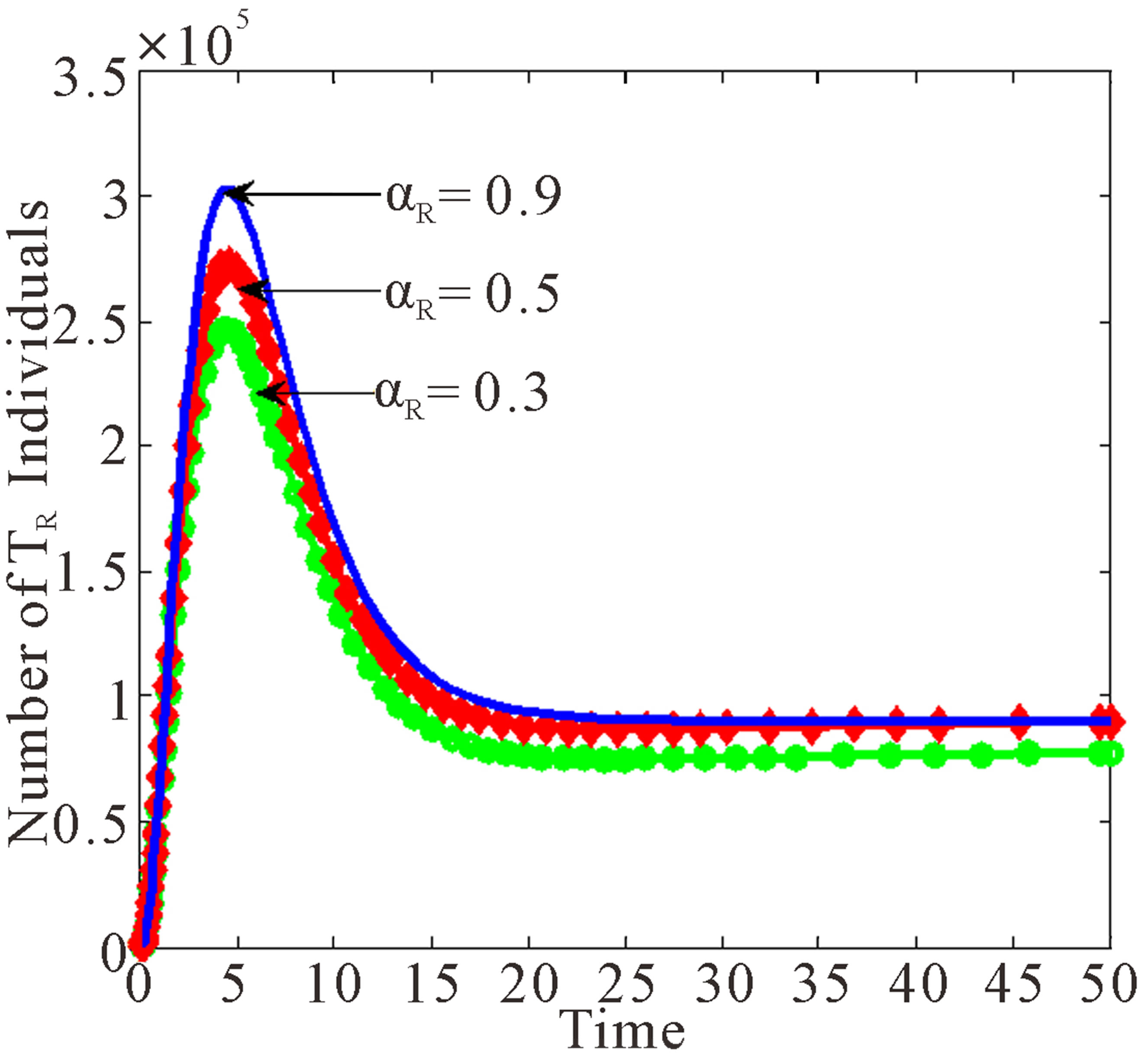 (b)
(b)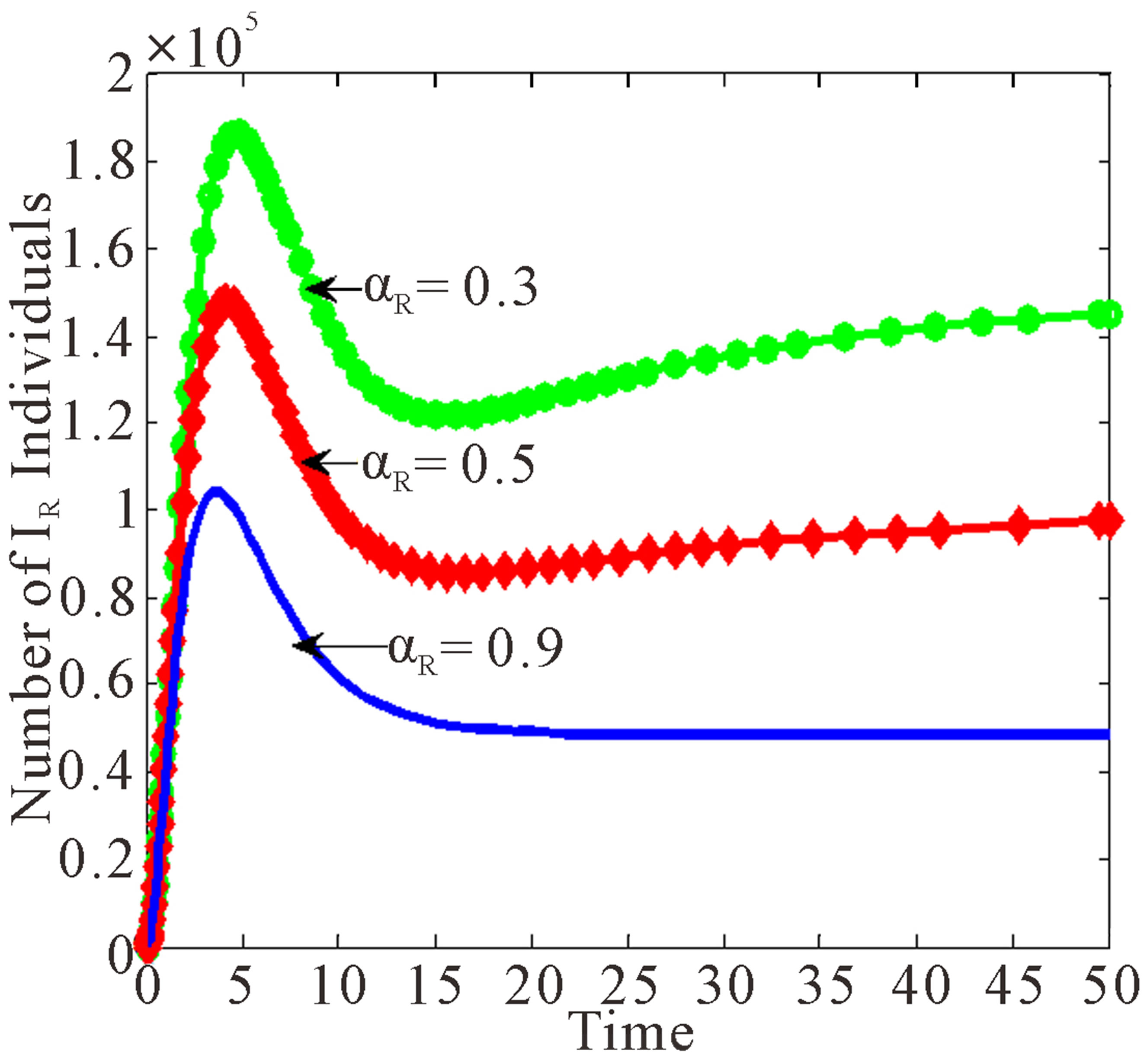 (c)
(c)
Figure 7. Effects of treatment rates of infected individuals with drug resistant virus as 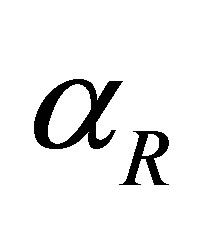 varies.
varies.
infected individuals with drug resistant virus as 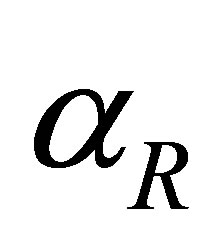 varies.
varies.
As the rate of treatment, 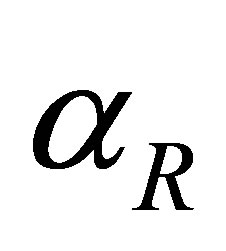 increases, the number of individuals infected with drug resistant virus decreases. From Figure 7(c), as the rate of treatment increases, the number of AIDS patients with drug resistance increase. It is also noted that the peaks for different values of
increases, the number of individuals infected with drug resistant virus decreases. From Figure 7(c), as the rate of treatment increases, the number of AIDS patients with drug resistance increase. It is also noted that the peaks for different values of 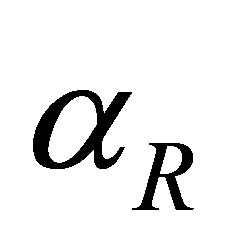 occur at the same time as for
occur at the same time as for ,
, 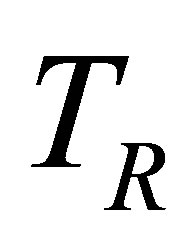 and
and 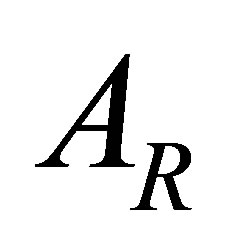 classes.
classes.
5. DISCUSSION AND CONCLUSIONS
In this paper, a non-linear mathematical model to study the transmission of HIV/AIDS in a population of varying size with vertical transmission and drug resistance was proposed and analysed. Both qualitative and numerical analysis of the model was done. The disease-free and endemic equilibrium points were obtained and their stabilities were investigated. A numerical study of the model has been conducted to see the effect of certain key parameters on the spread of the disease. It was established that the disease-free equilibrium is locally asymptotically stable if the basic reproduction number 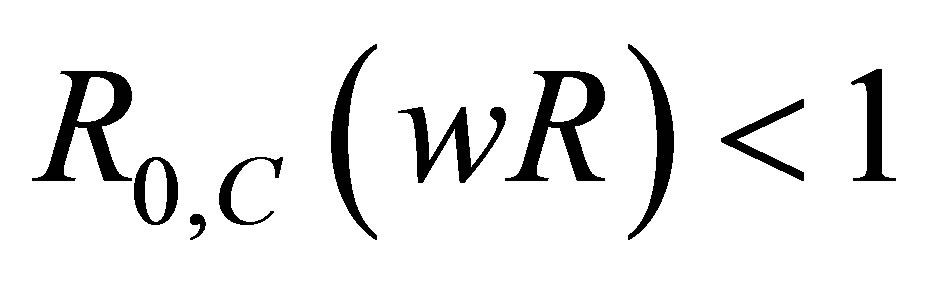 and unstable if
and unstable if 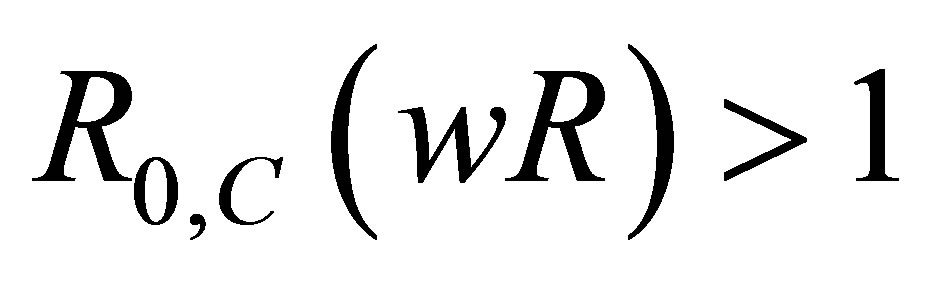 and the infection persists in the population.
and the infection persists in the population.
The results have shown that treatment may increase drug resistance among treated individuals. The results further showed that increase in the rate of children born with HIV with drug resistance leads to increase of the infected individuals with drug resistance and will in long run lead to increase in the AIDS population with drug resistance. It was noted that drug resistant virus is emerging in some of the individuals who are on ARV treatment. This will in the long run cause treatment failure among people who are under ARV treatment. As a result of this, more people will be dying of AIDS related diseases. This clearly shows that drug resistance has an impact on the dynamics of HIV/AIDs transmission.
REFERENCES
- Program for Appropriate Technology in Health (2001) Preventing HIV/AIDS in low-resource settings. Outlook, 19.
- CDC (2011) Basic information about HIV and AIDS. http://www.cdc.gov/hiv/topics/basic/
- Hampanda, K. (2013) Vertical transmission of HIV in sub-Saharan Africa: Applying theoretical frameworks to understand social barriers to PMTCT. ISRN Infectious Diseases, 2013, Article ID: 420361.
- Besser, M. (2010) HIV in pregnancy: Doing more with less: Mothers2Mothers.
- Soderlund, N., Zwi, K., Kinghorn, A. and Grey, G (1999) Prevention of vertical transmission of HIV: Analysis of cost effectiveness of available in South Africa. British Medical Journal, 318, 1650-1656. doi:10.1136/bmj.318.7199.1650
- Prasse, M. (2006) Mother to Child Transmission of HIV. http://the-aids-pandemic.blogspot.com/2006/12/mother-to-child-transmission-of-hiv.html
- Gumbo, F.Z., Duri, K., Kandawasvika, G.Q., Kurewa, N.E., Mapangure, M.P., Munjoma, M.W., Rusakaniko, S., Chirenje, M.Z. and Pedersen, B.S (2010) Risk factors of HIV vertical transmission in a cohort of women under a PMCTCT program at per-urban clinics in the resourcepoor setting. Journal of Prinatology, 30, 717-723. doi:10.1038/jp.2010.31
- Granish, R.M., Gilks, C.F., Dye, C., De Cock, K.M. and Williams, B.G (2009) Universal voluntary HIV testing with immediate antiretroviral therapy as a strategy for elimination of HIV transmission: A mathematical model. Lancent, 373, 48-59. doi:10.1016/S0140-6736(08)61697-9
- WHO (2011) Basic information about HIV and AIDS. http://www.who.int/mediacentre/facsheets/fs360/en/inde.html
- Malunguza, N., Mushayabasa, S., Chiyaka, C. and Mukandavire, Z (2010) Modelling the effects of condom use and antretroviral therapy in controlling HIV/AIDS among heterosexuals, homesexuals and bisexuals. Computational and Mathematical Methods in Medicine, 11, 201- 222. doi:10.1080/17486700903325167
- Mukandavire, Z. and Garira, W (2007) Sex-structurerd HIV/AIDS model to analyse the effects of condom use with application to Zimbabwe. Journal of Mathematical Biology, 54, 669-699. doi:10.1007/s00285-006-0063-5
- Kgosimore, M. and Lungu, E.W (2006) The effects of vertical transmission the spread of HIV/AIDS in the presence of treatment. Mathematical Biosciences and Engineering, 3, 297-312. doi:10.3934/mbe.2006.3.297
- Naresh, R. and Sharma, D (2011) HIV/AIDS model with vertical transmission and time delay. World Journal of Modelling and Simulation, 7, 230-240.
- Velasco-Hernadez, J.X., Gershengorn, H.B. and Blower, S.M (2002) Could widespread use of combination antiretroviral therapy eradicate HIV epidemics? Lancet Infectious Diseases, 2, 487-493. doi:10.1016/S1473-3099(02)00346-8
- Hove-Musekwa S.D. and Nyabadza, F (2009) The dynamics of an HIV/AIDS model with screened disease carriers. Computational and Mathematical Methods in Medicine, 10, 287-305.
NOTES
*Corresponding author.

