Open Journal of Civil Engineering
Vol.3 No.1(2013), Article ID:29476,23 pages DOI:10.4236/ojce.2013.31006
Correlation of Structural Seismic Damage with Fundamental Period of RC Buildings
Laboratory of RC, Department of Civil Engineering, Democritus University of Thrace, Xanthi, Greece
Email: aelefthe@civil.duth.gr
Received March 8, 2012; revised April 20, 2012; accepted May 5, 2012
Keywords: Seismic Damage; Period of Vibration; Fundamental Period; Damage Scale; Observational Damage Database; Athens Earthquake
ABSTRACT
The sufficient estimation of the natural period of vibration constitutes an essential step in earthquake design and assessment and its role in the development of seismic damage is investigated in the current research. The fundamental period is estimated for typical reinforced concrete building types, representative of the building stock of Southern Europe, according to existing relationships. The building typologies also represent groups of 180,945 existing damaged buildings of an observational database created after the Athens (7-9-1999) near field earthquake. The estimated fundamental periods are correlated to several degrees of the recorded damage. Important conclusions are drawn on the parameters (height, structural type, etc.) that influence the seismic response and the development of damage based on the wide database. After conducting a correlation analysis, noticeable is the difference between the seismic demand of the elastic spectrum of the first (1959), the contemporary (2003) Greek Seismic Code and the values of peak ground accelerations of several Athens earthquake records. Moreover, PGAs in most records are often between the lower and the upper bound of the estimated fundamental periods for RC buildings with regular infills (n-normal) and with ground levels without infill panels (p-pilotis) regardless the height. A disparity is noticed when the estimated fundamental period is based on EC8 provisions for the considered as “high” buildings in S. Europe regarding the referring earthquake. The majority of buildings that developed several degree, type and extent of damage are considered of “low” height with estimated fundamental periods close to the PGA values of Athens earthquake ground motions. However, the developed damage was the result of the combination of parameters based on geological, tectonic and morphological characteristics of the affected area. In addition, a damage scale for the measurable recording, beyond the qualitative characterization of seismic damage in Greek post-earthquake surveys, is presented wherein the performance levels are defined according to the physical description of the seismic damage and, as well, in terms of structural and economic damage index.
1. Introduction
The reliable evaluation of a basic dynamic characteristic as the fundamental period is an essential step in estimating the seismic response both in seismic design and assessment. The period of vibration is mainly dependent on mass, stiffness and strength and consequently on all the factors which affect them (dimensions, section properties, irregularities, etc.). The period of vibration is dependent mostly on mass, stiffness and strength and on all the factors which affect the pre-mentioned characteristics such as building material and type, dimensions (in height and plan), morphology and irregularities, section properties, stiffness, cracking, etc. Many simple relationships have been proposed in an effort to determine the fundamental period of structures. These empirical formulas have been produced by fitting curves through regression analysis on the buildings periods of vibration measured from their seismic movements during several earthquakes. However, Goel and Chopra [1,2] noticed that the different soil conditions, seismicity and design and construction practices may affect the measured fundamental periods. Despite the fact that several parameters affect the period of vibration the empirical formulas are given as a function of height as it has been found to play the most important role [3,4].
In the current research the fundamental period of vibration is calculated for several reinforced concrete building types according to existing simple relationships. The typical building typologies are representative of the materials, the seismic codes and the construction techniques of Southern Europe. They also represent groups of existing damaged buildings in several degree, type and extent of a dataset derived from post-earthquake surveys which took place in an extended region of Attica in Greece. The damage database with thousands of recorded buildings created after the occurrence of the Athens (7-9- 1999) near field seismic event in an extended urban region [5-7]. The estimated fundamental period of typical reinforced concrete (RC) structures is correlated with the recorded seismic damage. The advantage of the research is that the empirical vulnerability assessment is the most realistic as it is based on a real experiment in a physical scale 1:1. Important conclusions are drawn on the parameters (height, structural type, etc.) that influence the seismic response and the development of damage based on the wide database. In addition, a damage scale for the measurable recording, beyond the pre-mentioned quailtative characterization of seismic damage in Greek postearthquake surveys, is presented wherein the performance levels are defined according to the physical description of the seismic damage and, as well, in terms of structural and economical damage index. A correlation is fulfilled between the estimated fundamental periods of RC buildings with the different damage states of the proposed scale, FEMA performance levels and the analysis results of the database.
2. Estimation of Period of Vibration for RC Buildings
The reliable and sufficient estimation of the natural period of vibration of a RC building could play an essential role in the understanding of the global demands on the structure under an earthquake. In most design codes the estimation of the fundamental period is related to the building’s height based on simple empirical relationships given the structural typology. These formulas have been derived from empirical data from existing buildings subjected to seismic actions. In the equivalent static method (linear) the prediction of the fundamental period of vibration in a simplified manner allows the calculation of the design base shear force which is then distributed along the height of the building in a linear manner. In the linear dynamic (or modal response spectrum) method an analytical model of the structure is performed (often using structural sections of reduced stiffness) in order to calculate the periods of vibration and a number of significant modes. The forces resulting from each mode are applied to the building using the appropriate modal shape and the seismic actions resulting from these forces are combined according to the provisions [8].
The force-based design produces conservative values of period which consequently leads to conservative estimates of base-shear force. As far as the assessment of building’s response is concerned, the crucial parameter which is correlated to the damage development is the displacement [9] which may also be underestimated due to the conservative period-height estimation [3]. Recently, a deformationbased method was suggested [10] producing displacementperiod capacity curves for determining the non-linear demand at a given limit state using analytical relationships of displacement-height capacity curves and empirical relations of height-elastic period. This evaluated via analytical procedures period, which is larger than the elastic one, deals with the point of yielding and cracked stiffness of the structure and depends on the structural modeling assumptions [11]. It is well known that the stiffness degradation, due to the increase of the degree of damage, when a building is subjected to an earthquake also leads to a period increase.
2.1. RC Resisting Frames (MRF) Buildings
The first empirical formula in seismic design codes was presented in the USA building code ATC3-06 [12] and had the form of Equation (1):
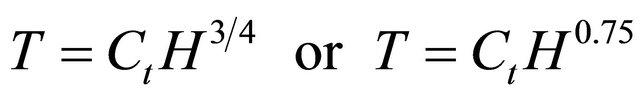 (1)
(1)
where Ct is a regression coefficient calibrated in order to achieve the best fit to experimental data and H represented the height of the building in feet. The form of Equation (1) has theoretically derived from the Rayleigh’s method by assuming that the equivalent static lateral forces are linearly distributed over the height of the building and the base shear force is assumed to be proportional to 1/T2/3. In ATC3-06, the value for the coefficient Ct in Equation (1) was proposed equal to 0.025 as a lower limit for evaluating the period of vibration of RC MRF buildings. In SEAOC-88 [13] it was found that a value of Ct = 0.03 was more appropriate for reinforced concrete buildings and has been adopted in many design codes (UBC-97, SEAOC-96, NEHRP-94, NBCC 2005 and Eurocode 8). Other values (0.035 or 0.04 in feet or 0.085 and 0.097, respectively in metres) for the coefficient Ct have also been recommended [8,14]. ASCE7-05 [15] adopted the period-height formula proposed by Goel and Chopra [1] who found that the best fit lower bound for reinforced concrete frames was given by the following expression:
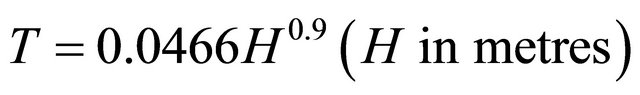 (2)
(2)
In the European EC8 [16] the period-height expression for moment resisting frames adopted the same values by SEAOC ’99:
 (3)
(3)
The last has also been derived using Rayleigh’s method and the height has been transformed from feet in metres (0.03 × 3.2810.75 = 0.073).
2.2. RC Shear Walls (SW) Buildings
The period of vibration of these buildings is usually evaluated with good approximation as the period of an equivalent cantilever. In reinforced concrete shear walls buildings both the lateral load resistance and the lateral stiffness is mainly provided by shear walls. The first period-height relationship for RC Shear Walls (SW) buildings had the form of Equation (4):
 (4)
(4)
where D is the dimension of the building at its base in the direction under consideration. In ATC3-06 [12] Ct was proposed as 0.09 with the dimensions measured in metres. This formula comes from the equation of the frequency of vibration of a cantilever (considering shear deformations only), with the thickness of the wall considered to be more or less constant and thus only the width/length of the building is an input parameter, as demonstrated in Equation (5) [8,17]:
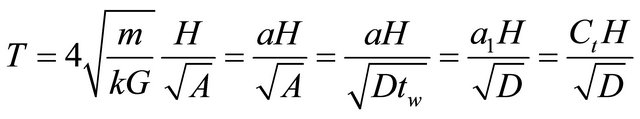 (5)
(5)
where m is the uniformly distributed mass per unit height, G is the shear elastic modulus, k is the shape factor to account for non uniform distribution of shear stresses for the shape of the transverse section (equal to 5/6 for a rectangular section), D is the length of the cantilever, A is the area of the transverse section expressed as the product of the thickness tw and the plan dimension D of the equivalent cantilever parallel to the considered direction. Many seismic codes adopted the pre-demonstrated according to the building type. However, UBC-97 code [18] consisted in the use of empirical equations of the form of Equation (1) for shear wall buildings, where Ct was taken equal to 0.05 with the height measured in metres. Many engineers following Eurocode 8 would probably also use Equation (1) with Ct equal to 0.075 for all RC buildings regardless of the details of the masonry infills. Taking into consideration that many European reinforced concrete buildings are constructed with stiff masonry infill panels which are often not isolated from the RC frame, the period of vibration is probably being overestimated by the designers and hence the forces are subsequently being underestimated.
In SEAOC-96 [19] and UBC-97 [18] the proposed value of Ct regarding the shear walls buildings of Equation (1) is given following the expressions:
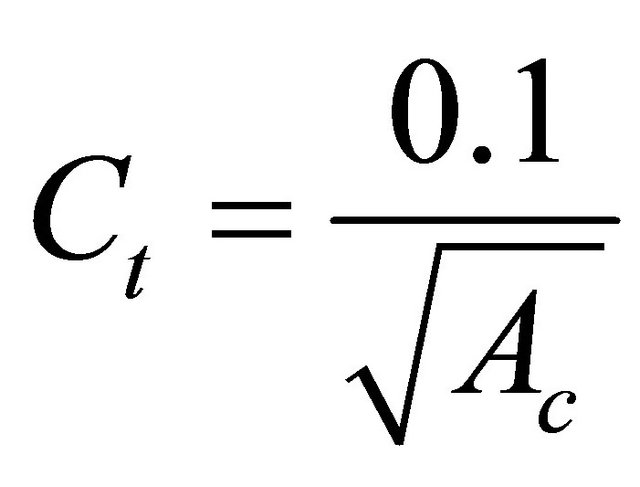 (6)
(6)
and
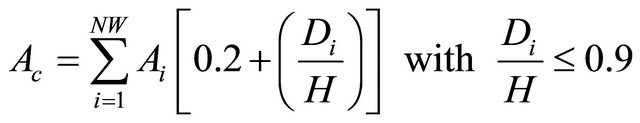 (7)
(7)
where Ac, the combined effective area (in square feet) of the shear walls, Di is the dimension in the direction under consideration (in feet) of the ith shear wall in the first storey of the structure and NW is the number of shear walls.
In ASCE7-05 [15] the relative period-height equation is expressed by Equation (8):
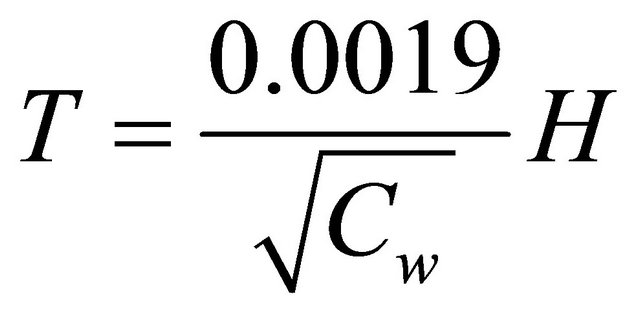 (8)
(8)
with
 (9)
(9)
Finally, in Eurocode 8 [19] the formula has also adopted (as in MRF buildings) the same values by SEAOC ’99 for structures with concrete or masonry shear walls:
 (10)
(10)
where H is the height measured from base in metres.
Simplified expressions are used for the estimation of the fundamental period of typical Greek RC buildings with several heights in order to be afterwards correlated with the spectral accelerations of the 7th of September Parnitha’s seismic event. Both the mean period of Tm (50% reliability) and the characteristic period TR (95% reliability) value have been estimated of the fundamental period of RC buildings with regular infills (uniform stiffness/n-normal) and with ground level without infill panels (p-pilotis) [20]. The following experimental formulas refer to typical buildings in Southern Europe and they are used in the estimation of the above mentioned fundamental periods:
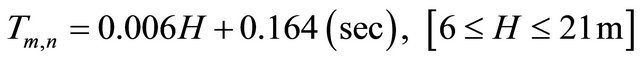 (11)
(11)
 (12)
(12)
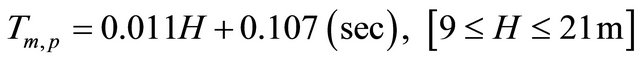 (13)
(13)
 (14)
(14)
Note that the structural types of RC buildings in Southern Europe differ from those in USA due to the fact that the first usually have stiff infill panels (brick masonry) with an influence in building’s total stiffness and hence to its natural period of vibration. Assuming that a two-storey building is considered of type «a» (“low” height), a four-storey of type «b» (“middle” height in Greece) and a seven-storey of type «c» (“high” height in Greece) the fundamental period T1 has been estimated based on the upper expressions: a) Buildings with “low” height with regular infills: Tn,2 = 0.11 - 0.20 sec (Equations (11) and (12)). b) Buildings with “middle” height with regular infills: Tn,4 = 0.15 - 0.24 sec (Equations (11) and (12)). c) Buildings with “middle” height with pilotis: Tp,4 = 0.18 - 0.24 sec (Equations (13) and (14)). d) Buildings with “high” height with regular infills: Tn,7 = 0.20 - 0.29 sec (Equations (11) & (12)). e) Buildings with “high” height with pilotis: Tp,7 = 0.28 - 0.34 sec (Equations (13) and (14)).
According to the EC8 provisions which reflect the design and construction practices of the European building stock the period of vibration has been calculated (Table 1) for: a) Reinforced concrete MRF buildings with “low” height: TMRF,2 = 0.29 sec (Equation (3)). b) Reinforced concrete MRF buildings with “middle” height: TMRF,4 = 0.48 sec (Equation (3)). c) Reinforced concrete MRF buildings with “high” height: TMRF,7 = 0.74 sec (Equation (3)). d) Reinforced concrete SW buildings with “low” height: TSW,2 = 0.19 sec (Equation (10)). e) Reinforced concrete SW buildings with “middle” height: TSW,4 = 0.32 sec (Equation (10)). f) Reinforced concrete SW buildings with “high” height: TSW,7 = 0.49 sec (Equation (10)). Figure 1 presents the stations with the recorded accelerograms in several regions of Athens and the epicentre of the 7th-9-1999 earthquake.
From the notice of the estimated fundamental periods according to the presented formulas for Greek reinforced concrete buildings it comes up the result that the characteristic period TR (95% reliability) value (0.20) of “low” height RC buildings with regular infills (n-normal) [20] is similar to the estimated value (0.19) according to EC8 for seismic design regarding the “low” height RC shear wall buildings T. The respective value (0.11) of the mean period Tm (50% reliability) is lower, whereas the period is greater (0.29) for “low” rise RC MRF of EC8 design provisions. In addition, both the characteristic (0.15 & 0.18) and mean period (0.24) values are almost the same for “middle” height RC buildings with regular infills (n
Table 1. Estimated fundamental periods.

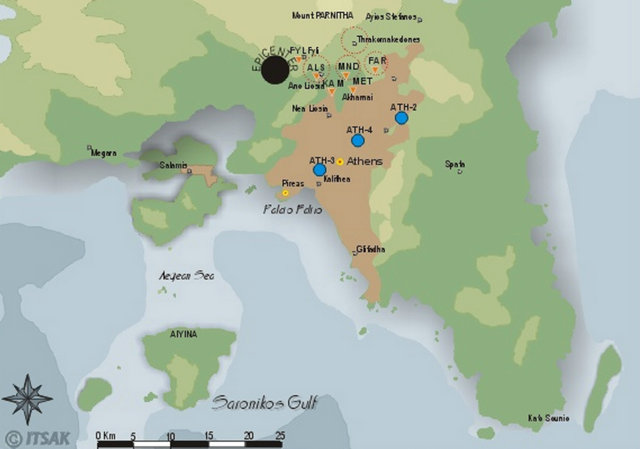
Figure 1. Stations with the recorded accelerograms in Athens and the epicentre of the 7th-9-1999 earthquake.
normal) and with ground levels without infill panels (ppilotis) [20]. As far as the EC8 “middle” rise RC buildings are concerned the period (0.32) is close regarding SW buildings whereas it presents a disparity for MRF. The occasion is also the same regarding “high” rise RC buildings: similar characteristic (0.20 & 0.28) and mean period (0.29 & 0.34) values for RC buildings with regular infills (n-normal) and with ground levels without infill panels (ppilotis) [20], a relatively close period value (0.49) regarding the corresponding EC8 shear wall buildings and a great difference (0.74) regarding the building type of RC moment resisting frames.
The elastic acceleration spectra of artificial seismic ground motions and accelerograms are presented in Figures 2 and 3 [21]. In the same figure are also presented the estimated fundamental periods for “low”, “medium” and “high” buildings along with the elastic spectrum of the first (1959) and the contemporary (2003) Greek Seismic Code. The percentage of damaged buildings in each height level represents the 29.78% (type «a»), 8.58% (type «b») and 1.65% (type «c») of the total number of buildings (164,135) in the studied area, as it has resulted from the damage data analysis (Table 2).
3. Damage Data after the 7-9-1999 Parnitha’s Earthquake
A near field earthquake with moderate to large magnitude, M = 5.9R (according to the Institute of Geodynamics of the National Observatory of Athens) occurred on the 7th of September, 1999 at 14:56 local time (11:56 GMT) with epicentral distance of 18 km from the historical centre of the city of Athens in Greece. The epicenter is located south of the mountain Parnitha, close to the Saronikos Gulf. The meizoseismal area (Figure 4) was considered before this seismic event as of low seismic activity. Although the earthquake magnitude was moderate, the damage was very serious, since the intensity reached IX as it can be observed in existing isoseismal intensity maps of Figure 5 [5-7,22]. Over a hundred of buildings collapsed and thousands sustained considerable damage, causing 143 casualties, about 1000 injuries and thousands of people became homeless. It is the worst natural disaster reported in the modern history of Greece regarding the economic loss. Despite the fact that damage displayed significant differentiation from place to place, the most serious damages were observed at the northern suburbs (e.g. Ano Liosia, Aharnes, Fyli, Menidi, Ilion, Filadelpheia, Kamatero, Zefyri) which was closer to the epicentral area.
The observational database is developed after the first and/or the second round (or level) of inspections, which have been conducted in several regions of Athens, based on instructions provided by the Earthquake Planning and Protection Organization (EPPO) of Greece. The entire initial observational data was collected from different sources (the Post-Earthquake Crisis Management Division
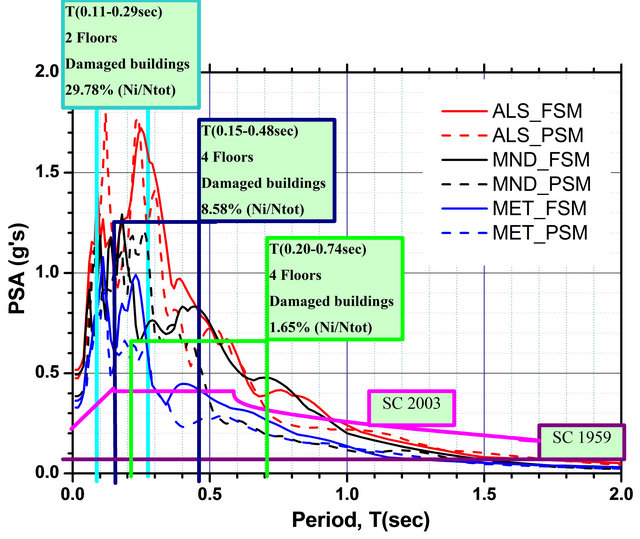
Figure 2. Elastic acceleration spectra of artificial seismic ground motions and the 1st (Greek Seismic Code of 1959) along with the recent design seismic spectrum (Greek Seismic Code of 2003).

Figure 3. Elastic response spectra of the accelerograms ATHS03 & ATH04 and the 1st (Greek Seismic Code of 1959) along with the recent design seismic spectrum (Greek Seismic Code of 2003).
Table 2. Correlation of the estimated fundamental periods with the level of the recorded damage and the number of floors for 164,135 buildings.
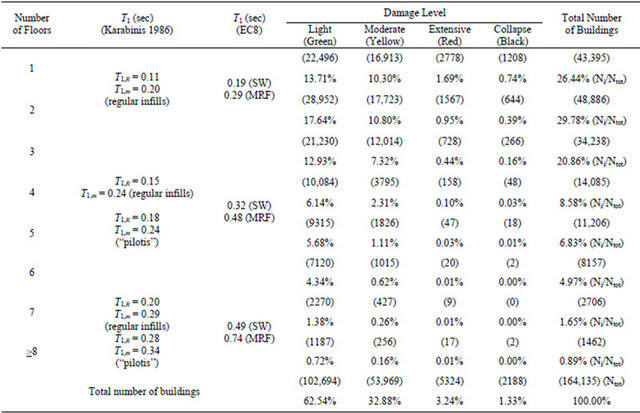
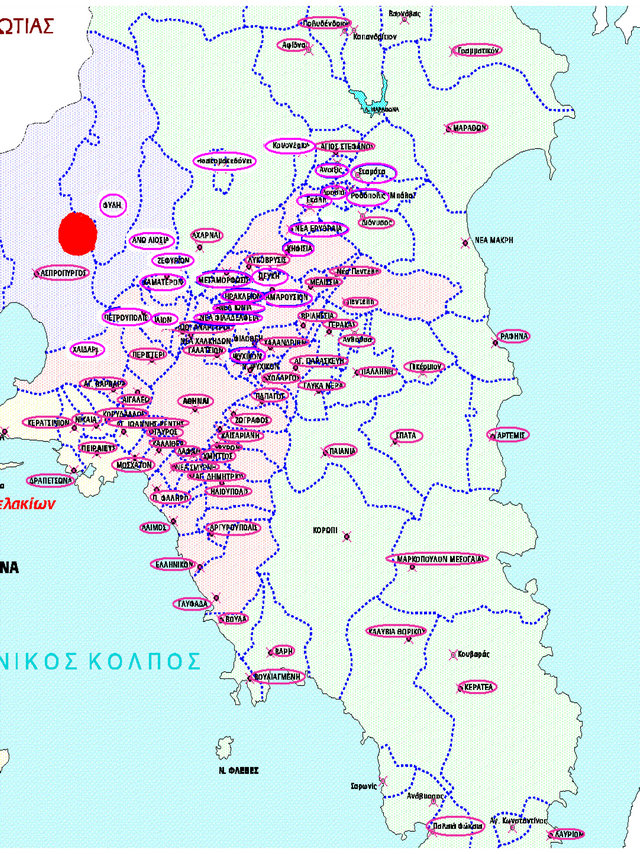
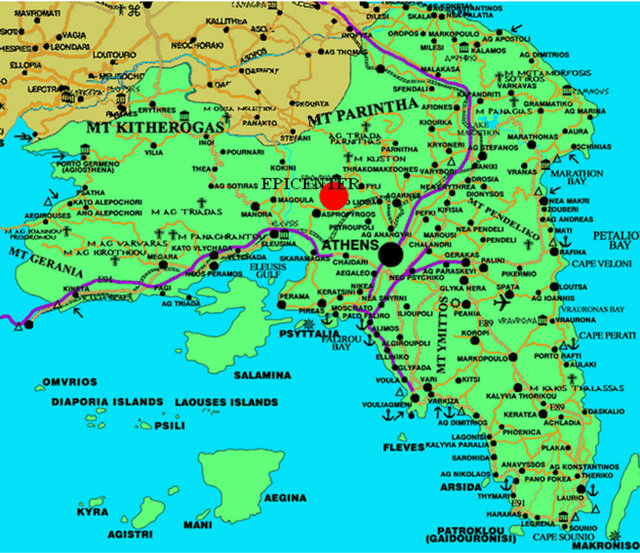
Figure 4. Meizoseimal area of Attica with the regions of the observational damage data.
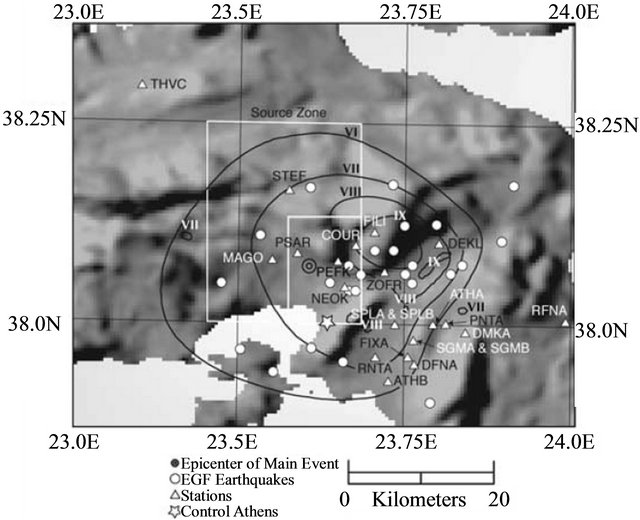
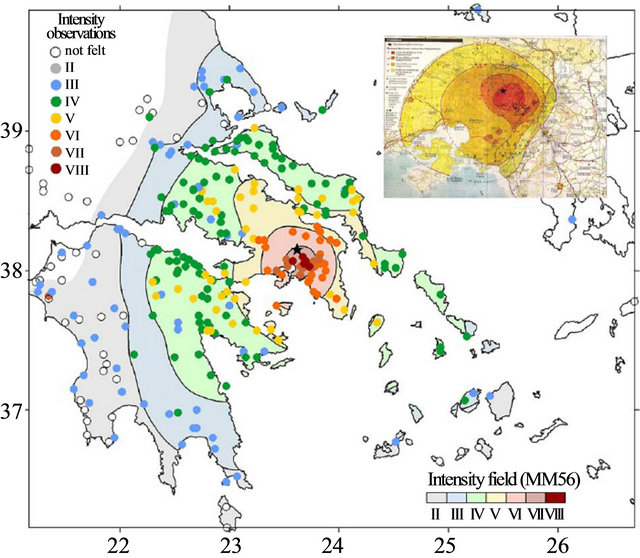
Figure 5. Existing isoseismal intensity maps [23,24].
of Axarnes region (Filadelfeia-Axarnes-Ano Liosia) and of Piraeus region (Piraeus-down town of Athens-PeristeriEleusina) and the National Service for the Rehabilitation of Earthquake Victims) and raised the enormous number of 535,152 reports of post-earthquake surveys. After filtering the collected data (checking one-by-one) and eliminating duplicate reports a unified total database has been created referring to the extended urban region of Attica. This dataset consists of 296,919 unique inspections having avoided the overestimation of the damage level. It is essential to clarify that the number of the above mentioned inscriptions refers to the number of autopsies and does not coincide with the number of buildings. A new process for the unified database has been followed, resulting that the 296,919 inspections are associated with 180,945 damaged buildings. It is noted that many of the 180,945 buildings were not fully described and the corresponding buildings have been disregarded from the process. Information about the total number of buildings per structural type for the regions mentioned in the database is also provided by the National Statistics Agency of Greece (N.S.S.G.) according to the results of the 2000-1 census. Comparing the total number of damaged buildings (180,945) to the total number of buildings in the affected area (753,078) it is concluded that the dataset addresses to 24.03% of the total local population of buildings, which is a wide and reliable statistical sample [5-7, 22].
The vulnerability assessment requires a classification system to characterize the earthquake-exposed building stock and correlate it with the developed damage. This needs the division of buildings into groups with similar seismic behaviour due to a probable earthquake. In the current research, apart from the characteristics that affect the seismic response of a structure, the proposed classification system is also dependent on the information collected from the post earthquake surveys. Unfortunately, the existence or not of ground levels without infill panels (pilotis) or other irregularities, which may influence the development of earthquake damage, is not known. In the statistical database, the structural systems are divided into four groups: 1) Reinforced concrete buildings (RC) with moment resisting frames or dual system (frame + shear walls); 2) Mixed buildings (MIX) with vertical bearing structure constituted by elements of both masonry and reinforced concrete; 3) Masonry buildings (MAS) with vertical elements of masonry and horizontal elements of reinforced concrete, metal or wood; and 4) Other buildings (OTH), which typically include any buildings not belonging to the previous groups. The reinforced concrete structures are further classified based on the different seismic code periods at the time of their design: RC1: without a seismic code or during the period 1959-1985; RC2: during the period 1985-1995; and RC3 after 1995. The mixed structures are further classified into MIX1, MIX2, and MIX3 using identical criteria. The threshold of each period is identified with a change in Greek Seismic Codes. The level of seismic design and detailing for R/C buildings in Greece, could generally be discriminated in four subclasses, as follows: 1) No Seismic Code (before 1959): with very low level or no seismic design and poor quality of detailing; 2) Low Seismic Code (1959-1985: the 1st Seismic Code of 1959 corresponding approximately to pre-1980s codes in Southern Europe) with low level of seismic design; 3) Moderate Seismic Code (1985-1995: the 1st Seismic Code of 1959 with the 1985 Supplement Clauses corresponding approximately to post-1980s codes in Southern Europe): with medium level of seismic design and reasonable seismic detailing; 4) High Seismic Code (after 1995: New Greek Seismic Code of 2003, similar to Eurocode 8): with adequate level of seismic design according to the new generation of seismic codes and ductile seismic detailing of R/C members. Buildings constructed before and after the introduction of the first Seismic Code are often treated similarly in Greece according to the National Technical Chamber of Greece [25]. Even if many buildings have been disregarded from the database due to the lack of information, such as the structural type or the date of construction, the presented here building stock still remains a wide statistical database.
4. Seismic Damage and Fundamental Period
After the time-consuming statistical elaboration and analysis of the database, the correlation for 164,135 buildings of the degree of damage with the number of floors is presented in Table 2 and in Figure 6. The estimated fundamental periods for existing reinforced concrete buildings of several heights (“low”, “medium” and “high”) and structural types (moment resisting frames-MRF, shearwall-SW, with regular infills or no infills on the ground floor-pilotis) are correlated to the different levels of the recorded damage.
The information from the database refers to qualitative characterizations of damage level used in the post-earthquake surveys in Greece, based on instructions provided by EPPO in 1984 and in 1997 in order to define whether its seismic capacity is adequate against future expected seismic forces. The damage level characterized by the inspection crews, as follows: a) Green: building with no or light damage, or building whose earthquake resistance has not been reduced; b) Yellow: building with moderate damage and reduced earthquake resistance; c) Red: building with very heavy damage or partial collapse; and d) Collapse: building that has collapsed or is under demolition. A damage scale for the measurable recording, beyond the pre-mentioned qualitative characterization Correlation for 164,135 buildings of the degree of damage with the number of floors

Figure 6. Correlation of the estimated fundamental periods with the level of the recorded damage and the number of floors for 164,135 buildings.
of seismic damage in Greek post-earthquake surveys, is presented in this research. Furthermore, the qualitative characterization of damage has been correlated to the different damage states of the scale for the calibration of seismic damage referring to the main structural types of RC buildings [26-28].
The correlation for 30149 RC1 buildings of the damage level with the number of floors is presented in Table 3 and in Figure 7. Table 4 and Figure 8 present the correlation of the damage level with the number of floors for 4501 RC2 buildings. The correlation for 1591 RC3 buildings of the damage level with the number of floors is presented in Table 5 and in Figure 9. The estimated fundamental periods for existing RC buildings of several heights are also correlated to the different levels of the recorded damage. The correlation of the damage level buildings with the number of floors for 15654 MIX1 is presented in Table 6 and in Figure 10. Table 7 and Figure 11 present the correlation of the damage level with the number of floors for 538 MIX2 buildings. Finally, the correlation for 87 MIX3 buildings of the damage level with the number of floors is presented in Table 8 and in Figure 12.
5. Seismic Damage Scale
The seismic behavior of the structures during an earthquake represents an experiment in a physical scale (1:1) and constitutes the most objective examination of the sufficiency of seismic codes and construction techniques. However, the reliable estimation of buildings response depends on the used method for the recording of seismic damage. The latter may vary in detail (approximate, analytical, etc.) and extent (numerous buildings, group of buildings or a single structure).
The structural damage can be considered the greatest cause of life and monetary loss in most earthquakes and can be used to assess the performance of buildings. In each database, this is described in terms of either damage state or percentage of loss. Due to the different parameters that influence the recording of damage (building types, seismic design codes, performance levels, etc.), it cannot be easily compared nor is it easy to combine and compare damage data. Comparisons of the recording damage have been presented in the literature [5,26,28-31]. The description of damage of every performance level is often mainly based on ATC-13 [32]. This is also the case for the damage calibration regarding the economic damage index in Greece [25,33] and in several other vulnerability studies [34,35]. Table 9 has been created in order to be able to implement a correlation analysis [36]. It correlates the most important existing damage scales, with the existing method used for the recording
Table 3. Correlation of the estimated fundamental period T1 with the level of the recorded damage for 30,149 buildings of RC1 structural type with low level of seismic design.
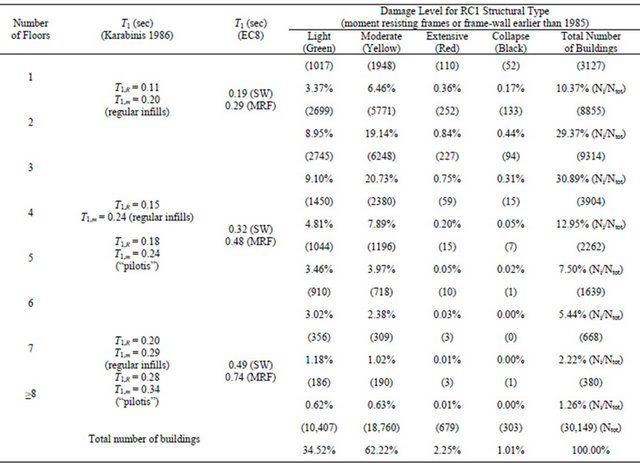
Correlation for 30,149 RC1 buildings of the degree of damage with the number of floors
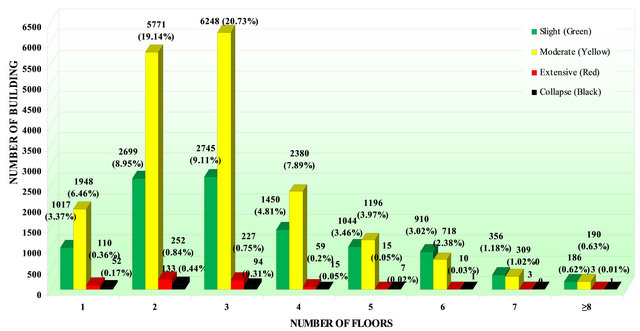
Figure 7. Correlation of the estimated fundamental period T1 with the level of the recorded damage for 30,149 buildings of RC1 structural type with low level of seismic design.
Table 4. Correlation of the estimated fundamental period T1 with the level of the recorded damage for 4501 buildings of RC2 structural type with medium level of seismic design.
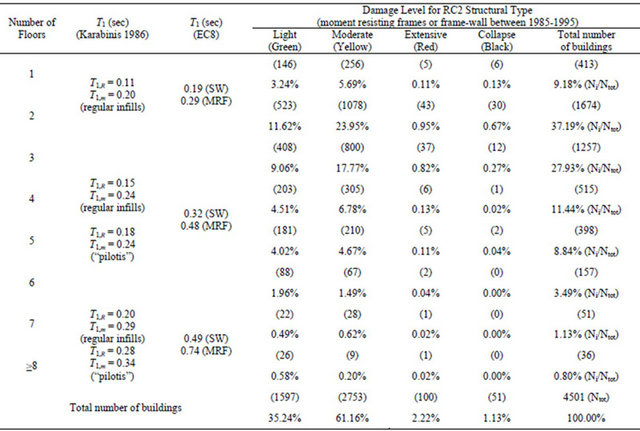
Correlation for 4.501 RC2 buildings of the degree of damage with the number of floors

Figure 8. Correlation of the estimated fundamental period T1 with the level of the recorded damage for 4501 buildings of RC2 structural type with medium level of seismic design.
Table 5. Correlation of the estimated fundamental periods with the level of the recorded damage for 1591 buildings of RC3 structural type with high level of seismic design.
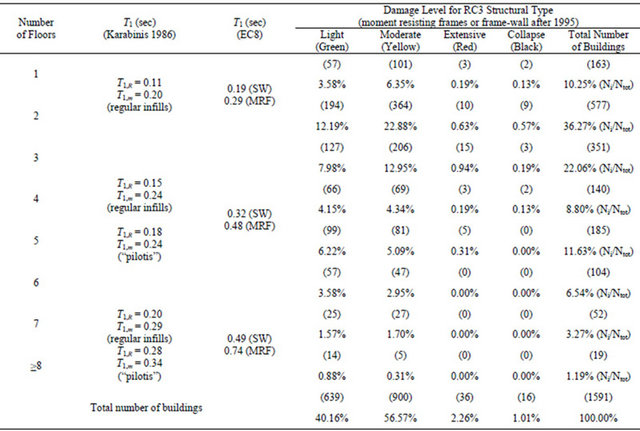
Correlation for 1,591 RC3 buildings of the degree of damage with the number of floors
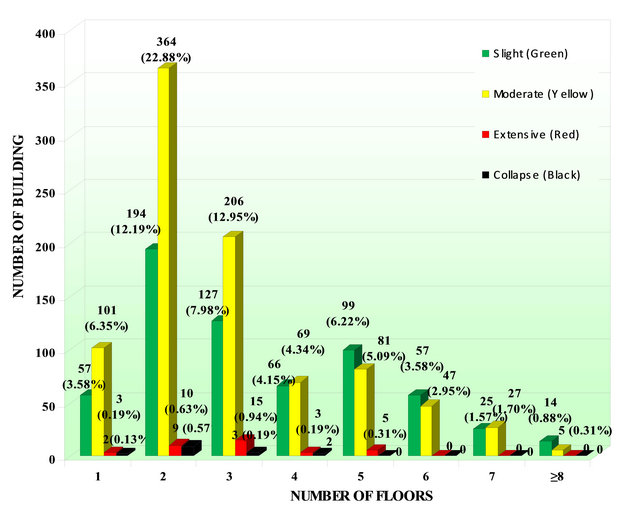
Figure 9. Correlation of the estimated fundamental periods with the level of the recorded damage for 1591 buildings of RC3 structural type with high level of seismic design.
Table 6. Correlation of the level of the recorded damage with the number of floors for 15,654 buildings of MIX1 structural type with low level of seismic design.

Correlation for 164,135 buildings of the degree of damage with the number of floors

Figure 10. Correlation of the level of the recorded damage with the number of floors for 15,654 buildings of MIX1 structural type with low level of seismic design.
Table 7. Correlation of the level of the recorded damage with the number of floors for 538 buildings of MIX2 structural type with medium level of seismic design.

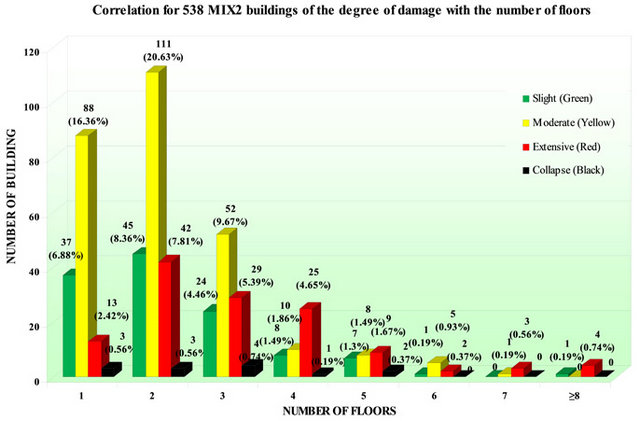
Figure 11. Correlation of the level of the recorded damage with the number of floors for 538 buildings of MIX2 structural type with medium level of seismic design.
Table 8. Correlation of the level of the recorded damage with the number of floors for 87 buildings of MIX3 structural type with high level of seismic design.

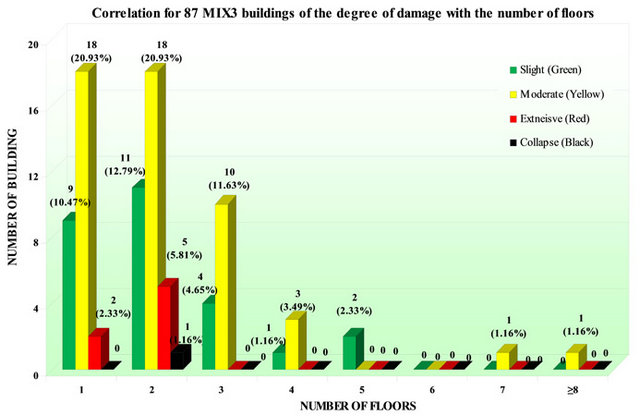
Figure 12. Correlation of the level of the recorded damage with the number of floors for 87 buildings of MIX3 structural type with high level of seismic design.
and classification of damage in Greece and the presented in this research damage scale.
The forms of post-earthquake surveys in Greece commonly use the method of Rapid Visual Screening (R.V.S.), which is based on a macroscopic inspection of the building in order to define whether its seismic capacity is adequate against future expected seismic forces. The characterization of damage by inspection crews in the 7-9- 1999 Athens earthquake was based on instructions provided by EPPO 1997 [37] and to a lesser degree on the EPPO instructions of 1984 [38]. In addition, the vulnerability models proposed by National Technical Chamber of Greece [25,39] were mostly based on a hybrid methodology involving elements from both empirically and analytically calculated structural damage indices which have been correlated to monetary loss [21,33,40].
The observational database is developed after the first or/and the second round (or level) of inspections, which have been conducted in several regions of Athens, based on instructions provided by Earthquake Planning and Protection Organization (EPPO) of Greece. The first round of inspection is a rapid visual screening method conducted by a couple team of engineers in order to define in a short period of time the seismic safety of numerous structures. A second and more detailed level of inspection is followed for those buildings with inadequate estimated seismic performance in order to prioritize them for further more detailed analytical assessment that it would be required to design a rehabilitation scheme. However, the information from the current mentioned database refers only to quailtative characterizations of damage level by the inspection crews as it has been already mentioned: a) Green: building with no or light damage, or building whose earthquake resistance has not been reduced; b) Yellow: building with moderate damage and reduced earthquake resistance; c) Red: building with very heavy damage or partial collapse; and d) Collapse: building that has collapsed or is under demolition. In the collected data, there was no information about the cost of repairs or the description of damage. The need for a measurable calibration of the recorded damage is obvious.
The distribution of buildings (180,427) in the created database according to the pre-described degree of damage is presented in Table 10. Specifically: a) the 2716 structures which were characterised as under demolitioncollapse (black) represent the 1.51% of the total damaged population of buildings; b) the 6423 structures with extensive non-repairable damages (red) to the structural system represent the 3.56%; c) the 56,533 structures with moderate (yellow) repairable damages represent the 31.33% of the total damaged buildings in Attica; and d) most of the structures (114,755) with light (green) repairable damages represent the 63.60%, respectively.
A damage scale is presented for the reinforced concrete (RC) buildings wherein a calibration of seismic damage is presented beyond the qualitative description of the performance levels (Table 11). The use of the new scale does
Table 9. Correspondence between damage states definitions and damage factors ranges (%).
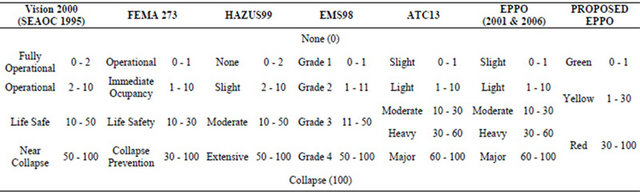
Table 10. Distribution of buildings according to the degree of damage (180,427 buildings).
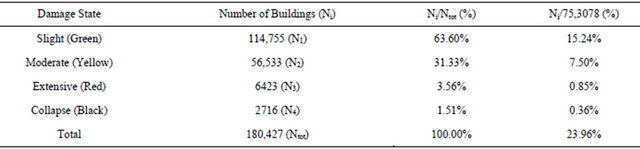
Table 11 The presented damage scale.
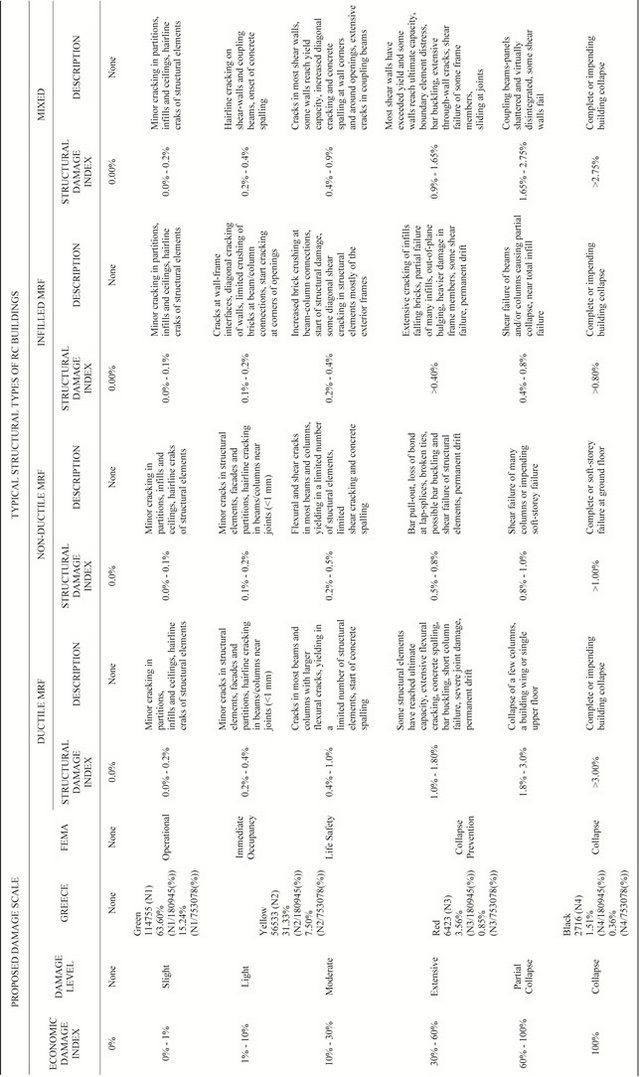
not require specialized knowledge, and is intentionally quite similar to the familiar to many engineers, manner of estimation of post-earthquake damage. The scale is approximate but rational and can be easily and rapidly applied. The novelty of the new scale is that it introduces an empirical measurable damage index, which depends on the severity and the extent of damage, right from the field where in situ inspection is conducted. This characteristic is lacking from the existing scales of measurement. Its inclusion may decrease the need for second round timeconsuming sampling inspections of damaged buildings [26-28].
The proposed scale is subdivided into seven damage levels, each of which is defined in terms of structural and non-structural damage, which would be expected in a future seismic scenario in the four main structural types of RC buildings that are met in Europe: ductile frames, nonductile frames, frames with masonry walls and mixed buildings. Definition of performance levels in descriptive terms is not sufficient for the development of vulnerability curves. In order to consider the different damage rates of lateral-load systems and hence relate the curves to the building type, the scale must be calibrated to a measurable structural response parameter. In the proposed damage scale the performance levels, ranging from “none” damage to “collapse”, are defined according to the physical description of the seismic damage and, as well, in terms of structural and economic damage index. The different drift thresholds, which vary significantly for ductile and nonductile systems, for the associated damage states of each structural type have been adopted by experimental data and theoretical analyses [41,42]. The economic damage index (in monetary loss) expresses the cost of repair as a fraction of the total cost of the building. The calibration of the earthquake damage by presenting both structural and economic damage index in the same scale, allows their direct comparison and correlation. The description of damage in every performance level is based on the main existing damage scales. The proposed calibration for the different levels of seismic damage severity regarding the economic damage index is in accordance with the familiar manner of damage classification in Greece [25]. It must be noted that the proposed methodology regarding the postearthquake surveys and the pre-defined limits of damage severity expressed in monetary losses, is similar to the instructions provided by EPPO and FEMA. Besides, most of the methods for the recording of seismic damage have been adopted by FEMA and ATC. The comparison of the proposed damage scale with FEMA and EPPO is also presented in Table 11. A numerical example is presented in the scale according to the analysis results for the damage distribution of the created database according to the EPPO characterization. The definition of damage levels of the proposed scale and the performance levels of FEMA along with the EPPO results of the database are presented and compared on a typical performance curve for RC frame buildings in Figure 13. In addition, a correlation is fulfilled between the different damage states and the fundamental period regarding building types of RC frames. The numerical values of the drift thresholds in different damage levels for other structural types are given in Table 11. In Figure 13 the damage levels of the proposed scale in terms of structural damage index on the performance curve could be correlated to the damage levels in terms of loss damage index on a qualitative here “primary vulnerability curve”.
6. Summary and Conclusions
In the current research the fundamental period of vibration is calculated for several reinforced concrete building types according to existing simple relationships. The typical building typologies are representative of the materials, the seismic codes and the construction techniques of Southern Europe. They also represent groups of existing damaged buildings in several degree, type and extent of a dataset derived from post-earthquake surveys which took place in an extended region of Attica in Greece. The damage database with thousands of recorded buildings created after the occurrence of the Athens (7-9-1999) near field seismic event in an extended urban region [5,6]. The estimated fundamental period of typical reinforced concrete (RC) structures is correlated with the recorded seismic damage. The advantage of the research is that the empirical vulnerability assessment is the most realistic as it is based on a real experiment in a physical scale 1:1. Important conclusions are drawn on the parameters (height, structural type, etc.) that influence the seismic response and the development of damage based on the wide database. In addition, a damage scale for the measurable recording, beyond the qualitative characterization of seismic damage in Greek post-earthquake surveys, is presented wherein the performance levels are defined according to the physical description of the seismic damage and, as well, in terms of structural and economic damage index. A correlation is fulfilled between the estimated fundamental periods of RC buildings with the different damage states of the proposed scale, FEMA performance levels and the analysis results of the database.
In addition, a correlation analysis is fulfilled between the elastic acceleration spectra of artificial seismic ground motions, accelerograms and the evaluated fundamental periods for the considered in Greece and generally in Southern Europe as “low”, “medium” and “high” height buildings along with the elastic spectrum of the first (1959) and the contemporary (2003) Greek Seismic Code. It is concluded that in the most records the

Figure 13. Correlation of the performance levels of the proposed damage scale with the fundamental period and a “primary vulnerability curve”.
peak ground accelerations of the 7th of September Athens earthquake were between the lower and the upper bound of the estimated fundamental periods based on experimental formulas [20] for all (“low”-“medium”-“high”) RC building types with regular infills (n-normal) and with ground levels without infill panels (p-pilotis). A disparity is noticed for the estimated fundamental period according to EC8 provisions of “high” height buildings regarding the referring earthquake. Noticeable is the difference between seismic demand of the seismic elastic spectrum of the first (1959), the contemporary (2003) Greek Seismic Code and the values of peak ground accelerations of the several Athens earthquake records.
From the analysis results it occurs that the majority of buildings that developed several degree, type and extent of damage belong to “low” height buildings with estimated values close to the peak ground accelerations of the Athens earthquake ground motions. The last conclusion is connected to the fact that these buildings belong to the meizoseismal area of the northern suburbs close to the epicentral area (e.g. Ano Liosia, Aharnes, Fyli, Menidi, Ilion, Filadelpheia, Kamatero, Zefyri) where the most serious damages were observed. In several of these regions the macroseismic intensity reached IX.
The aspect that the causes of the developed damages are owed to a single parameter would be very simplified. In general, damage displayed significant differentiation from place to place, as well as a peculiar geographic distribution. Based on geological, tectonic and morphological characteristics of the affected area and on the elaboration of damage recordings for intensity evaluation, it has been suggested that intensity distribution was the result of the combination of a number of parameters. On the one hand, the parameters are the strike of the seismogenic fault, seismic wave directivity effects and an old NNE ± SSW tectonic structure, and they are also responsible for the maximum intensity arrangement in two perpendicular directions ESE ± WNW and NNE ± SSW. On the other hand, site foundation formations, old tectonic structures buried under recent formations and morphology are the parameters that differentiated intensities within the affected area [43]. Generally, the unlike damage distribution of the 1999 Athens earthquake reflected the destructive combination of two factors: the source directivity and the site effect [44]. Surprisingly heavy damage occurred on the eastern bank of the Kifissos River canyon. A number of these buildings suffered partial or total collapse, while many others were severely damaged. Despite the particular geometry of the slope of about 60 m in height that caused significant motion amplification, topography effects alone cannot explain the disparity in damage distribution which is characterized by a rather uniform structural quality. Soil stratigraphy and material heterogeneity on the topographic aggravation of surface ground motion played important role. Several simulations showed that topographic effects are substantial only within about 50 m from the canyon ridge, materializing primarily because of the presence of relatively soft soil layers near the surface of the profile. The results showed that both topography and local soil conditions significantly affected the spatial variability of seismic motion [45,46].
REFERENCES
- R. K. Goel and A. K. Chopra, “Period Formulas for Moment—Resisting Frame Buildings,” Journal of Structural Engineering, Vol. 123, No. 11, 1997, pp. 1454-1461. doi:10.1061/(ASCE)0733-9445(1997)123:11(1454)
- R. K. Goel and A. K. Chopra, “Period Formulas for Concrete Shear Wall Buildings,” Journal of Structural Engineering, Vol. 124, No. 4, 1998, pp. 426-433. doi:10.1061/(ASCE)0733-9445(1998)124:4(426)
- H. Crowley, “Periods of Vibration for DisplacementBased Assessment of RC Buildings,” MSc Dissertation, ROSE School, Pavia, 2003.
- H. Crowley and R. Pinho, “Period—Height Relationship for Existing European Reinforced Concrete Buildings,” Journal of Earthquake Engineering, Vol. 8, No. 1, 2004, pp. 93-119. doi:10.1080/13632460409350522
- A. K. Eleftheriadou, “Contribution to the Seismic Vulnerability Assessment of Reinforced Concrete Structures (in Greek),” Ph.D. Thesis, Department of Civil Engineering, Democritus University of Thrace, Xanthi, 2009.
- A. K. Eleftheriadou and A. I. Karabinis, “Seismic Vulnerability Assessment of Buildings Based on the Near Field Athens (7-9-1999) Earthquake Damage Data,” International Journal of Earthquakes and Structures, Vol. 3, No. 2, 2012, pp. 117-140.
- A. K. Eleftheriadou and A. I. Karabinis, “Evaluation of Damage Probability Matrices from Observational Seismic Damage Data,” International Journal of Earthquakes and Structures, Vol. 4, No. 3, 2013, in press.
- H. Crowley and R. Pinho, “Revisiting Eurocode 8 Formulae for Periods of Vibration and Their Employment in Linear Seismic Analysis,” Earthquake Engineering & Structural Dynamics, Vol. 39, No. 2, 2010, pp. 223-235.
- M. J. N. Priestley, “Displacement-Based Seismic Assessment of Reinforced Concrete Buildings,” Journal of Earthquake Engineering, Vol. 1 No. 1, 1997, pp. 157-192. doi:10.1080/13632469708962365
- S. Glaister and R. Pinho, “Development of a Simplified Deformation-Based Method for Seismic Vulnerability Assessment,” Journal of Earthquake Engineering, Vol. 7, No. 1, 2003, pp. 107-140.
- G. M. Verderame, I. Iervolino and G. Manfredi, “Elastic Period of Sub-Standard Reinforced Concrete Moment Resisting Frame Buildings,” Bulletin of Earthquake Engineering, Vol. 8, No. 4, 2010, pp. 955-972. doi:10.1007/s10518-010-9176-8
- Applied Technology Council (ATC), “Tentative Provisions for the Development of Seismic Regulations for Buildings,” Report No. ATC3-06, Palo Alto, 1978.
- Structural Engineers Association of California, “Recommended Lateral Force Requirements,” SEAOC, San Francisco, 1988.
- D. Gilles and G. McClure, “Development of a Period Database for Buildings in Montreal Using Ambient Vibrations,” Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, 12-17 October 2008, Paper No. 12-03-0016, 8 p.
- Applied Technology Council (ATC), “Minimum Design Loads for Buildings and Other Structures,” ASCE/SEI 7-05, Structural Engineering Institute of the American Society of Civil Engineers, Reston, 2006.
- CEN, “Eurocode 8: Design of Structures for Earthquake Resistance. Part 1: General Rules, Seismic Actions and Rules for Buildings,” European Standard EN 1998-1:2004, Comité Européen de Normalisation, Brussels, 2004.
- P. Ricci, G. M. Verderame and G. Manfredi, “Analytical Investigation of Elastic Period of Infilled RC MRF Buildings,” Engineering Structures, Vol. 33, No. 2, 2011, pp. 308-319. doi:10.1016/j.engstruct.2010.10.009
- Uniform Building Code (UBC-97), “Structural Engineering Design Provisions,” International Conference of Building Officials, Whittier, 1997, p. 492.
- SEAOC, “Recommended Lateral Force Requirements,” 6th Edition, Seismology Committee, Structural Engineers Association of California, Sacramento, 1996.
- A. I. Karabinis, “Contribution to the Research of Dynamic Characteristics for Reinforced Concrete Structures,” Ph.D. Thesis, Department of Civil Engineering, Democritus University of Thrace, Xanthi, 1986.
- Institute of Engineering Seismology and Earthquake Engineering (ITSAK)—Aristotle University of Thessaloniki (AUTh), “Athens Earthquake: Assessment of Vulnerability in the Disaster Area and Correlation to the Real Distribution of Buildings Damage after the Earthquake,” Research Project, Earthquake Planning and Protection Organization (EPPO), Thessaloniki, 2004.
- A. K. Eleftheriadou and A. I. Karabinis, “Development of Damage Probability Matrices Based on Greek Earthquake Damage Data,” Journal of Earthquake Engineering & Engineering Vibration, Vol. 10, No. 1, 2011, pp. 129-141. doi:10.1007/s11803-011-0052-6
- Z. Schenková, V. Schenk, I. Kalogeras, R. Pichl, P. Kottnauer, C. Papatsimba and G. Panopoulou, “Isoseismal Maps Drawing by the Kriging Method,” Journal of Seismology, Vol. 11, No. 1, 2007, pp. 121-129. doi:10.1007/s10950-006-9023-1
- L. Hutchings, E. Ioannidou, W. Foxall, N. Voulgaris, J. Savy, I. Kalogeras, L. Scognamiglio and G. Stavrakakis, “A Physically Based Strong Ground-Motion Prediction Methodology; Application to PSHA and the 1999 Mw = 6.0 Athens Earthquake,” Geophysical Journal International, Vol. 168, No. 2, 2007, pp. 659-680. doi:10.1111/j.1365-246X.2006.03178.x
- National Technical Chamber of Greece (NTCG), “PreEarthquake Reinforcement of Existing Buildings (in Greek),” National Programme for Earthquake Management of Existing Buildings, Earthquake Planning & Protection Organization, Athens, 2006.
- A. K. Eleftheriadou and A. I. Karabinis, “Damage Probability Matrices Derived from Earthquake Statistical Data,” Proceedings of the 14th World Conference on Earthquake Engineering, Paper No. 07-0201, Beijing, 12-17 October 2008.
- A. K. Eleftheriadou and A. I. Karabinis, “Seismic Vulnerability Assessment with Damage Probability Matrices,” Proceedings of the 3rd Greek Conference on Earthquake Engineering and Technical Seismology, Paper No. 2108, Athens, 2008.
- A. K. Eleftheriadou and A. I. Karabinis, “Seismic Damage Scales in Reinforced Concrete Structures,” Technika Chronika, Scientific Journal of the Technical Chamber of Greece, Vol. 3, No. 1, 2010, pp. 41-60.
- T. Rossetto and A. Elnashai, “Derivation of Vulnerability Functions for European-Type RC Structures Based on Observational Data,” Journal of Engineering Structures, Vol. 25, No. 10, 2003, pp. 1241-1263. doi:10.1016/S0141-0296(03)00060-9
- M. Rota, A. Penna and C. L. Strobbia, “Processing Italian Damage Data to Derive Typological Fragility Curves,” Soil Dynamics and Earthquake Engineering, Vol. 28, No. 10-11, 2008, pp. 933-947.
- P. Sarabandi, D. Pachakis, S. King and A. Kiremidjian, “Development of Empirical Building Performance Functions Data from Past Earthquakes,” Proceedings of ICASP- 9, San Francisco, 6-9 July 2003, pp. 629-635.
- Applied Technology Council (ATC), “Earthquake Damage Evaluation Data for California,” ATC-13 Report, Redwood City, 1985.
- A. J. Kappos, K. Pitilakis, K. Morfidis and N. Hatzinikolaou, “Vulnerability and Risk Study of Volos (Greece) Metropolitan Area,” Proceedings of the 12th ECEE, London, Paper No.74, 9-13 September 2002.
- A. J. Kappos, “Seismic Vulnerability and Risk Assessment of Urban Habitat in Southern European Cities,” Proceedings of the Urban Habitat Constructions under Catastrophic Events Workshop (COST C26), Prague, 30-31 March 2007, pp. 115-129.
- S. Tesfamariam and M. Saatcioglu, “Risk-Based Seismic Evaluation of Reinforced Concrete Buildings,” Earthquake Spectra, Vol. 24, No. 3, 2008, pp. 795-821. doi:10.1193/1.2952767
- A. I. Karabinis and A. K. Eleftheriadou, “Vulnerability Assessment Derived from Earthquake Damage Data,” Proceedings of the ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Rethymno, Paper No.1264, 13- 16 June 2007.
- Earthquake Planning and Protection Organization (EPPO), “Guidelines and Forms for Immediate Post-Earthquake Screening of Reinforced Concrete Buildings (in Greek),” Athens, 1997.
- Ministry of Public Works, Earthquake Planning and Protection Organization, “Post-Earthquake Inspection of Reinforced Concrete Buildings (in Greek),” Athens, 1984.
- National Technical Chamber of Greece (NTCG), “Vulner ability Assessment of Buildings (in Greek),” Final Report, Technical Team No.I.2, National Programme for Earthquake Management of Existing Buildings, Earthquake Planning & Protection Organization, Athens, 2001.
- A. J. Kappos, K. C. Stylianidis and K. Pitilakis, “Development of Seismic Risk Scenarios Based on a Hybrid Method of Vulnerability Assessment,” Journal of Natural Hazards, Vol. 17, No. 2, 1998, pp. 177-192. doi:10.1023/A:1008083021022
- A. Ghobarah, “On Drift Limits Associated with Different Damage Levels,” Proceedings of International Workshop on Performance-Based Seismic Design, Department of Civil Engineering, McMaster University, Bled, 28 June-1 July 2004.
- R. Foltz, “Estimating Seismic Damage and Repair Costs,” MAE Center Project CM-4, The Citadel, Texas A&M, 2004, in press.
- E. Lekkas, “The Athens Earthquake (7 September 1999): Intensity Distribution and Controlling Factors,” Engineering Geology, Vol. 59, No. 3-4, 2001, pp. 297-311. doi:10.1016/S0013-7952(00)00119-8
- R. Roumelioti, A. Kiratzi and N. Theodulidis, “Stochastic Strong Ground—Motion Simulation of the 7 September 1999 Athens (Greece) Earthquake,” Bulletin of the Seismological Society of America, Vol. 94, No. 3, 2004, pp. 1036-1052.
- I. S. Kalogeras and G. N. Stavrakakis, “The Athens, Greece September 7th, 1999 Earthquake: Strong Motion Data Processing (7/9/1999-31/3/2000),” National Observatory of Athens, Geodynamic Institute, Athens, 2001.
- G. Gazetas and Collaborators, “Computational and Experimental Assessment of Strong Motion within the Meizoseismal Area of Parnitha, 7-9-99, Earthquake (in Greek),” Technical Report, Earthquake Planning and Protection Organization, Athens, 2001, pp. 1-207.

