Modern Mechanical Engineering
Vol.4 No.1(2014), Article ID:43268,10 pages DOI:10.4236/mme.2014.41006
Stress Analysis of Bolted Joints Part II. Contact and Slip Analysis of a Four Bolt Joint
Department of Machine and Product Design, Budapest University of Technology and Economics, Budapest, Hungary
Email: varadik@eik.bme.hu
Received November 4, 2013; revised December 23, 2013; accepted January 16, 2014
ABSTRACT
For up-to-date bolted joints, first of all in vehicles, high strength bolts of 10.9 or even 12.9 are used, which are preloaded up to 90% or even 100% of the yield strength. The primary aim of this high degree utilization is the weight reduction. For the analytic dimensioning of bolted joints, the VDI 2230 Richtlinien German standard [1] provides support. However, the analytic model can mostly consider the true structural characteristics only in a limited way. The analytic modeling is especially uncertain in case of multiple bolted joints when the load distribution among the bolts depends reasonably upon the elastic deformation of the participating elements in the joints over the geometry of the bolted joint. The first part of this paper deals with the problems of numerical modeling and stress analysis, respectively specifying the analytic dimensioning procedure by applying elastic or rather elastic-plastic material law. The error magnitude in bolted joint calculation was examined in case of omitting the existing threaded connection(between the bolt and the nut(in order to simplify the model. The second part of the paper deals with the dimensioning of stands and cantilevers’ multi-bolt fixing problems, first of all, with the load distribution among the bolts keeping in view the analysis of the local slipping relations. For demonstrating the above technique, an elaborated numeric procedure is presented for a four-bolted cantilever, having bolted joints pre-tightened to the yield strength.
Keywords:Bolted Joints; Numerical Modeling; Stress Analysis
1. Introduction
In the second part of this paper, the contact and slip behaviors were examined in a cantilever fixed by 4 pieces M20 bolted joints pre-tightened up to the yield strength of the 12.9 bolt material. The design of the studied cantilever is shown in Figure 1.The outer loads are acting on the cantilever of a brake application:
Fleft = 48 kN, (1)
Fright = 1 kN. (2)
The material characteristics used in the analysis are summarized in Table1
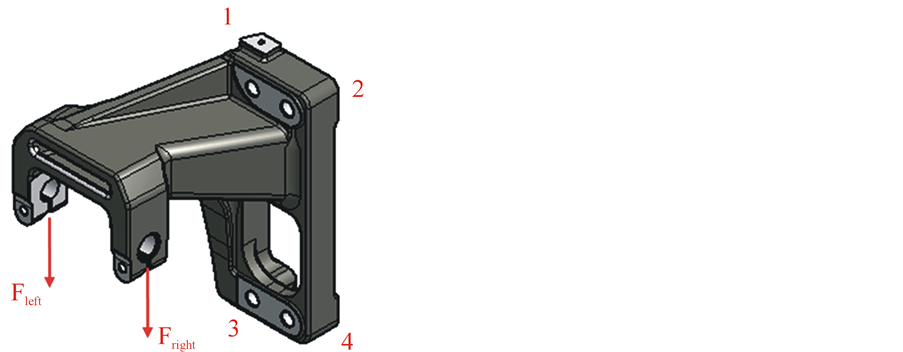
Figure 1. The studied cantilever, having 4 holes specified by numbers and the loadings.
2. The Finite Element Model
The Finite Element Model of the frame, the cantilever
and the bolted joints are shown in Figure 2.
Main characteristics of the FE model:
• Applied type of element: tetra 10;
• Average element size: 7 mm;
• Average element size on the contacting surface: 3 mm;
• Average element size under the bolt head up to 40
Table 1.The material characteristics used during the analysis of the brake cantilever bolted joints.
mm diameter: 3 mm;
• Average element size in the whole bolt: 3 mm;
• Number of elements: 186,041;
• Number of nodes: 291,454;
• Number of the degree of freedom: 872,730.
The applied boundary and loading conditionings are shown in Figure 3. As a boundary condition, the cut plane of the frame structure is fixed. This is noted by green arrows in the figure. The loading is applied through the two holes of the front part. This is noted by magenta color arrows in the figure.
The bolts are cut in the middle of the length and the distance between the two bolt parts is 0.1 mm. This model makes possible to set the bolt pre-tightening along these two surfaces obtained.
Contact conditions were defined between the contacting elements: cantilever and frame structure, under the bolt head and under the nut (Figures 4 and 5), where the principally defined friction coefficient value is μ = 0.12 between the surfaces.
During the evaluation of results the loads get queried in the allocation places and surfaces shown in Figure 5. The reference for the loads is completed with the additional marks denoting the bolt number.
The displacements query and definition agree with the followings:
• Total displacement: on the sectioned (cut) bolt halves (in the query place of Fc1 and Fc2) the sum of the prescribed displacements;
• Compression of the encircled elements: the sum of

Figure 2. FE model of the frame, the cantilever and the bolted joint.

Figure 3. The applied boundary conditions (green) and loading conditions (magenta).
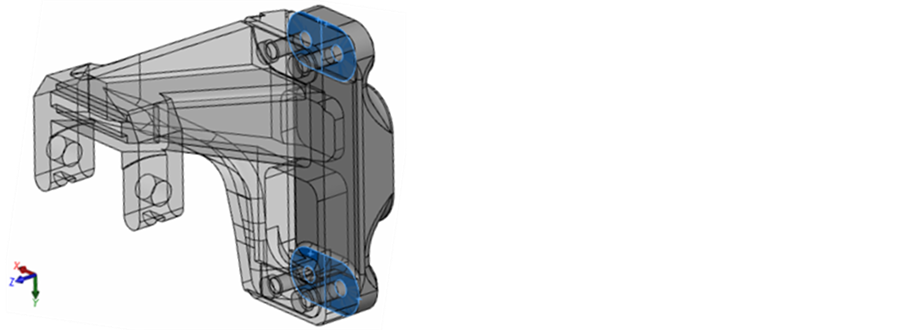
Figure 4. Contact surfaces.
the displacement in the query place of Fa and Fb forces (loads). The displacement of the bolt head and nut planes are identical to the displacements of the plates;
• Elongation of the bolt: the difference of the total displacement and the compression of the encircled elements.
3. The Algorithm to Study the Pre-Tightening and Loosening Behaviour
The elaborated calculation model should equally handle the description of the resulted force and deformation state changes for pre-tightened bolted joint on one hand and the outside loosening force (operation loading) effect on the other hand. Respectively the elaborated algorithm consists of the following steps:
1) The pre-tightening forces act on the opposite sides of the cut bolt—having simplified geometry—sections. (The cut part is 0.1 mm thick. However there will be no defined contacting between the two surfaces in case of bigger elongation then 0.1 mm. They remain hencefor-
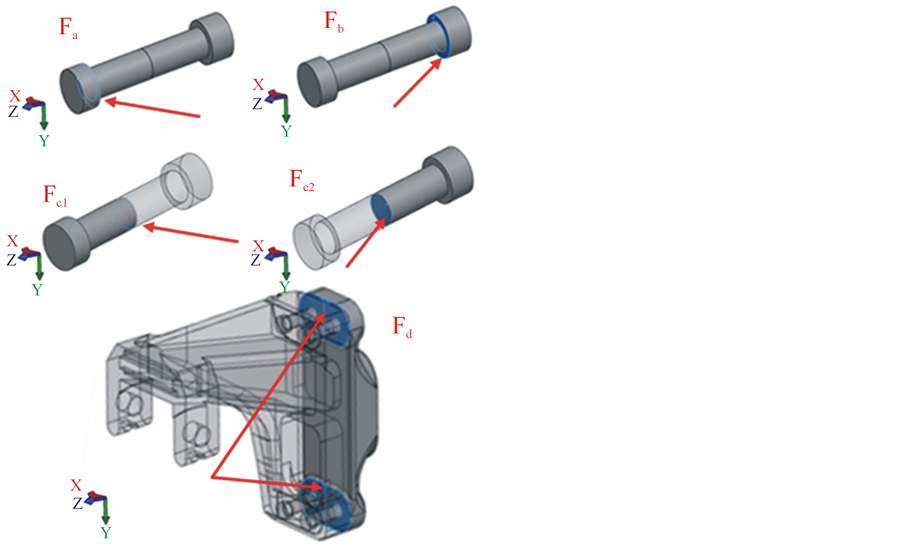
Figure 5. The query places of the forces during the evaluation of the results. Fa—the force between the cantilever and the bolt head; Fb—contact force between the frame structure and the nut; Fc1—the reaction force on the section of the bolt from the cantilever side; Fc2—the reaction force on the section of the bolt from the frame structure side. Fd—force between the contact surfaces of the cantilever and the frame structure, around the bolt locations.
ward separate elements in the model). The cut surfaces displace for the effect of pre-tightening force and these displacements can be queried.
2) The bolted joint pre-tightened by force is not suitable to handle the outside loosening force because in this model the force value remains constant. Therefore the pre-tightening should be achieved by determined displacements (like prescribed displacement-loading), as described in the previous paragraph. These two kinds of pre-tightening are identical both in the behavior of force theorem and deformation.
3) The model applying bolt tightening by prescribed displacement is capable to consider the outer loading forces but it is not capable to follow the whole deformation of the structure. So on the cut surfaces of the boltparts the developed force values are not equal. This is not a correct behavior according to the force equilibrium condition. Therefore such a solution is required which is capable to follow the deformation of the whole structure and hereby to make certain that the forces will have equal values on the “section surfaces” of the cut-bolt parts in deformed state.
The essence of this procedure is: the deformations due to outside loading can be calculated on a glued model, having no bolts (the cantilever and the frame structure is glued along the contacting surfaces, marked in Figure 4).
4) The determined displacement values¾identical in the bolt axis direction¾of the glued model should be superposed on the displacement values according to point b). That is the displacement characterizing the bolt pretightening is added to the displacement values of the whole structure. It is noted that this model works properly only in such a loading range where the contacting surfaces do not start opening due to the outer loosening effect. In case when the contacting surfaces partly separate then the displacement calculated by glued model can be considered only as an approximate value. In such cases to restore the balance of the two forces¾acting on the “cut surfaces”¾needs iteration calculations with which the opened contact range is determined.
Symbolic representation of the applied algorithm is illustrated in Figure 6.
4. Pre-Tightening of the Bolts
The bolts are pre-tightened by the minimum pre-tightening force (FM min) giving the most unfavorable result regarding the slipping aspect (see in Section 7). This pre-tightening force is 145 kN [2]. The pre-tightening force is applied in the section surface of the bolt cut in the middle of the bolt shank (see Figure 5, forces Fc1 and Fc2).
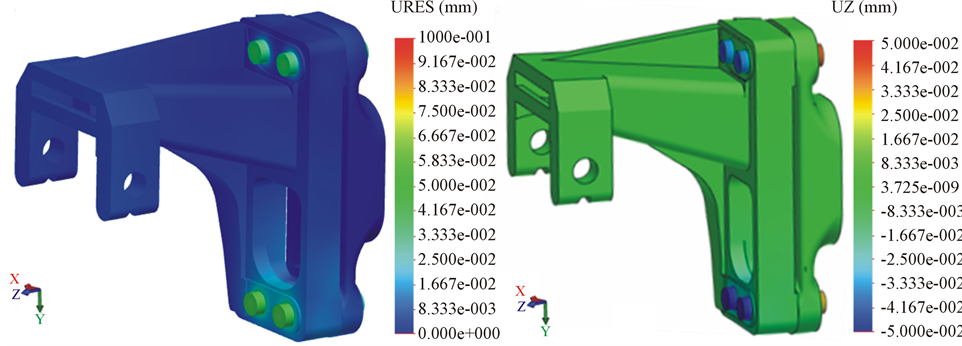
The displacements of the bolts calculated from the pretightening are shown in Figure 7. The resultant displacements are shown in Figure 7(a) and the displacements in z direction are shown in Figure 7(b).
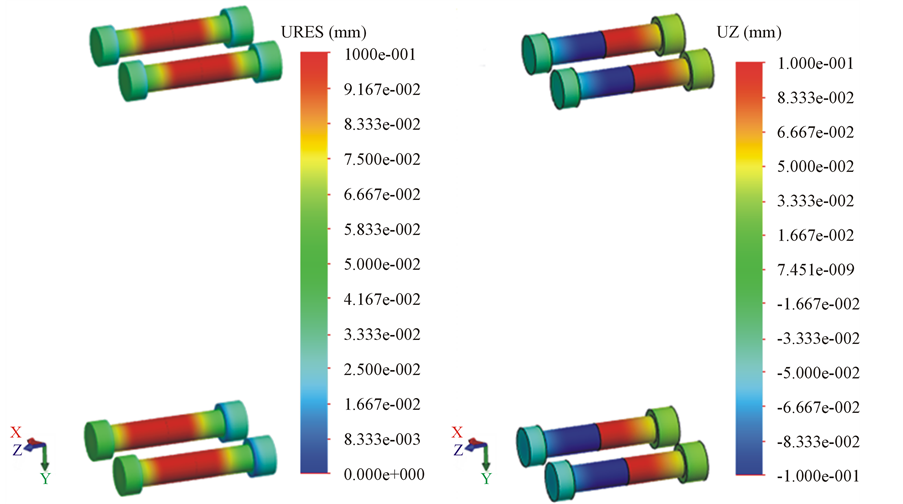
In Figure 8, the bolts are “removed” from the structure and the displacement fields only for the bolts are demonstrated separately.
The formed contact pressure between the cantilever and the frame structure is an important result of the calculations. The contact pressure distribution between the two parts (presented “open” similarly like a book) is shown in Figure 9. It can be seen from the figure that getting away from the holes the contact pressure is reducing. Furthermore it can be observed that the contact pressure is more reasonably uneven on the lower contact surface then on the upper surface. This phenomenon is resulted by the different geometry of the two surfaces.
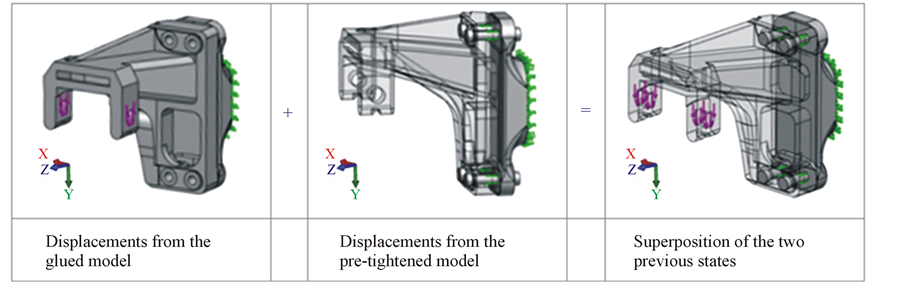
Figure 6. Symbolic representation of the calculation algorithm.
 (a) (b)
(a) (b)
Figure 7. Displacement fields after pre-tightening: (a) Resultant displacement—maximum value of the scale is: 0.1 mm; (b) z direction displacement—maximum value of the scale is ± 0.05 mm.
 (a) (b)
(a) (b)
Figure 8. The displacement fields after the pre-tightening of bolts: (a) Resultant displacement—maximum scale value: 0.1 mm; (b) z direction displacement—maximum scale value: ± 0.1 mm.
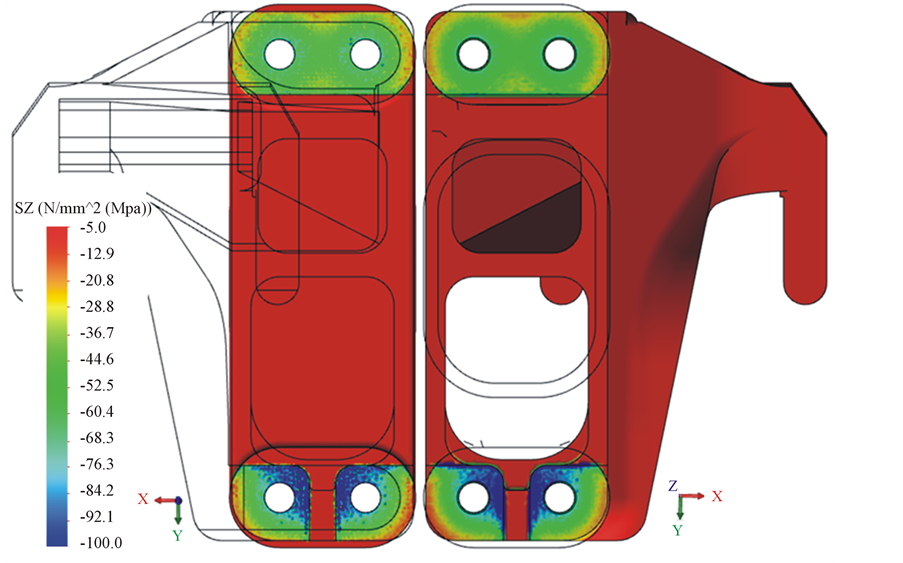
Figure 9. Contact pressure formed on the surfaces of cantilever and the frame structure. The upper and lower limit of scale: −100 - −5 MPa.
Proceeding towards the outer periphery the contact pressure reduces.
The characteristics of pre-tightening by force case calculations are summarized in Table2 The bolt elastic deformation (elongation) (λ1), the compression of the encircled elements (λ2) and also the forces (Fd) on the contact surfaces (see Figure 5) were separately collected for all 4 bolts. The average of total displacements calculated by FE model is 0.321 mm. The analytic value calculated is 0.350 mm. The 9% difference between the two calculations can be reasoned at first: the 0.35 mm value relates to the so called threaded model while the other value belongs to the so called glued bolted model. The other reason of this 9% difference is caused by some differences in the encircled elements geometry of the two models.
Regarding the forces it can be seen that¾as it was expected¾the force values are about equal in all places of query.
5. Bolt Pre-Tightening by Prescribed Displacement
As it was mentioned earlier the bolted joint pre-tightened by force is not capable to handle the outer loadings. Therefore the fixing bolts of the brake supporting cantilever must be pre-tightened by displacement-loading. In the second loading case the displacement-loadings will be the bolt prescribed elongations—applied in the model in the bolt cut section—decided in the previous section. The mechanical characteristics calculated by the displacement-loading will be identical to the mechanical characteristics calculated by force loading. The calculated values by displacement loading are summarized in Table3
6. Cantilever Outer Loading
The forces acting on the cantilever are shown in Figure 1 and the magnitude of the loadings is given in Section 1.
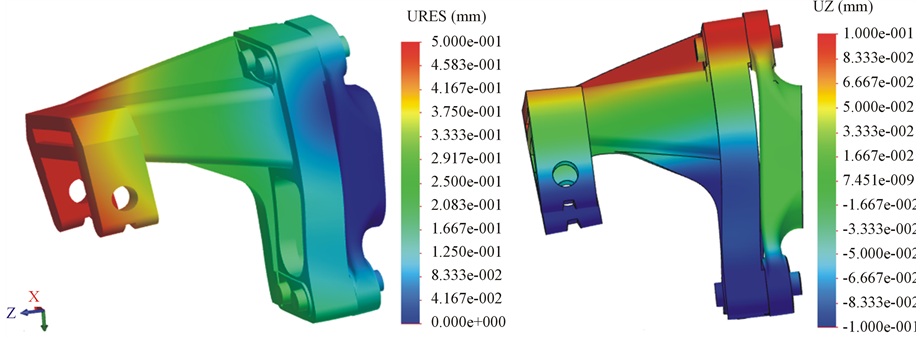
The calculated displacements are shown in Figure 10. The resultant displacements are shown in Figure 10(a)
 (a) (b)
(a) (b)
Figure 10. Displacement fields effected by outer loading: (a) Resultant displacement—maximum value of the scale 0.5 mm; (b) z direction displacement—the maximum/minimum value of scale ± 0.1 mm. Scale of deformation 100:1.
while the displacements along z direction are shown in Figure 10(b).
The contact pressure distribution between the cantilever and the frame structure is shown in Figure 11. The tendency of the contact pressure distribution is similar to Figure 9, but differences can be illustrated by the changes in the bolt forces (see below).
The Figure 12 shows the resultant forces on the surfaces of cantilever and frame structure around each bolt. The number of bolts is shown in the horizontal axis and the normal forces are shown in the vertical axis. The interpretation of Fd force agree with Figure 5 and the number of bolts corresponds to Figure 1. The blue columns indicate the normal contact forces for the pretightened bolts, having displacement loading. The contact forces originated from pre-tightening can be considered equal with good approximation. The light brown columns show the contact forces resulted by the effect of outer loading. It can be seen that the contact forces are reduced under the upper two bolts (location number 1 and 2) while the contact forces are increased under the lower two bolts (location number 3 and 4).
Figure 13 shows the forces developed in the bolt shank. The forces were queried at the cut surfaces. The interpretation of forces Fc1 and Fc2 are according to Figure 5. It is obvious that in all calculations Fc1 = Fc2 equality should exists. The separate querying of forces Fc1, and Fc2 and their comparing are a kind of checking for the accuracy of the model.
The forces Fc1 and Fc2 developed on the cut surface sections of bolts¾pre-tightened by displacement-loadings¾are presented by light and dark blue columns. The red columns show the forces developed in the bolt shanks due to the outer loadings. It is an important result of the calculation that the forces in the bolt shanks practically not changed by the effect of the outer loading. The bolted joint design corresponds to the so called inside loosening case.
The acting outer forces on the cantilever (Figure 1) are in balance with the tangential forces¾acting in the contact plane¾originated from friction. At μ = 0.12 the studied structure is capable to take the following tangential load without overall slipping:
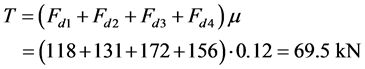 (3)
(3)
If the friction forces provided by the bolt forces are not enough to hinder the slipping of the cantilever then the finite element calculations stop due to numerical instability problems.
7. Examination of the Cantilever Slipping
For the effect of tangential forces¾developed on the
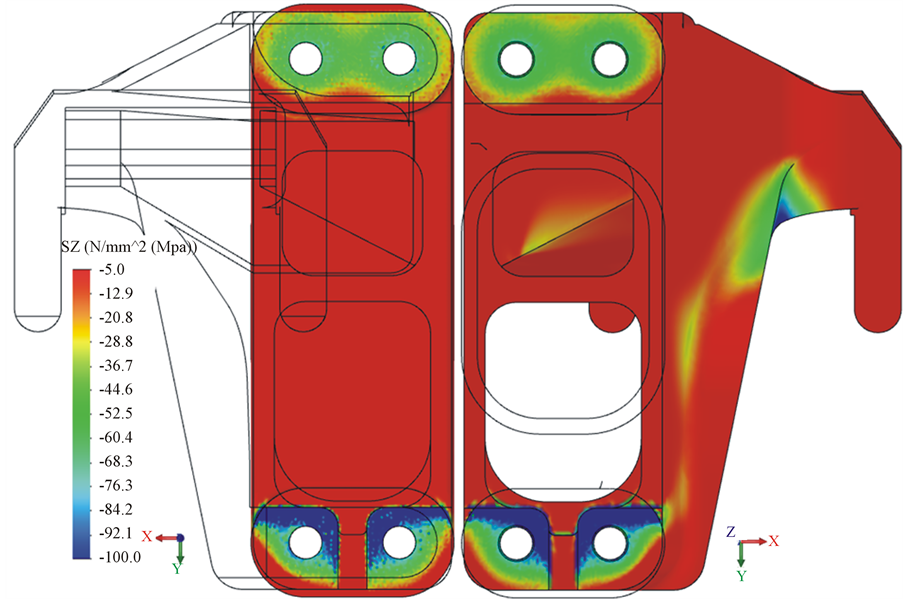
Figure 11. Contact pressure developed on the surfaces of the cantilever and the frame structure. The lower and the upper limits of the scale: −100 - −5 MPa.
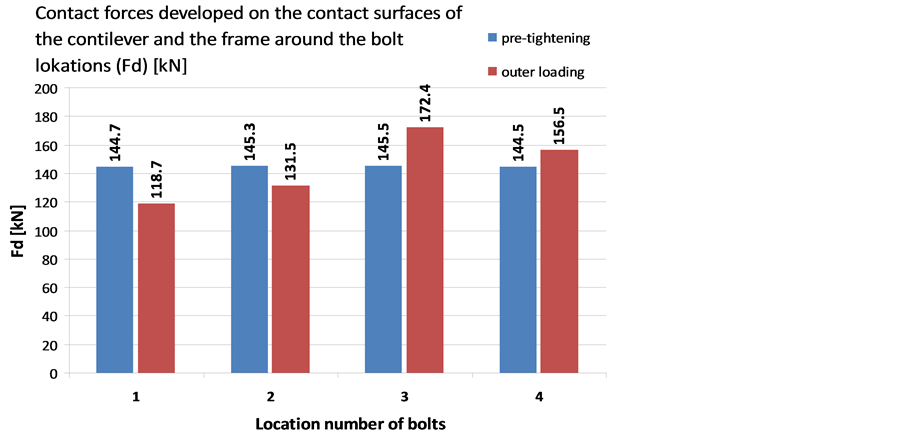
Figure 12. Developed normal contact forces during pre-tightening and also for the effect of outer loading.
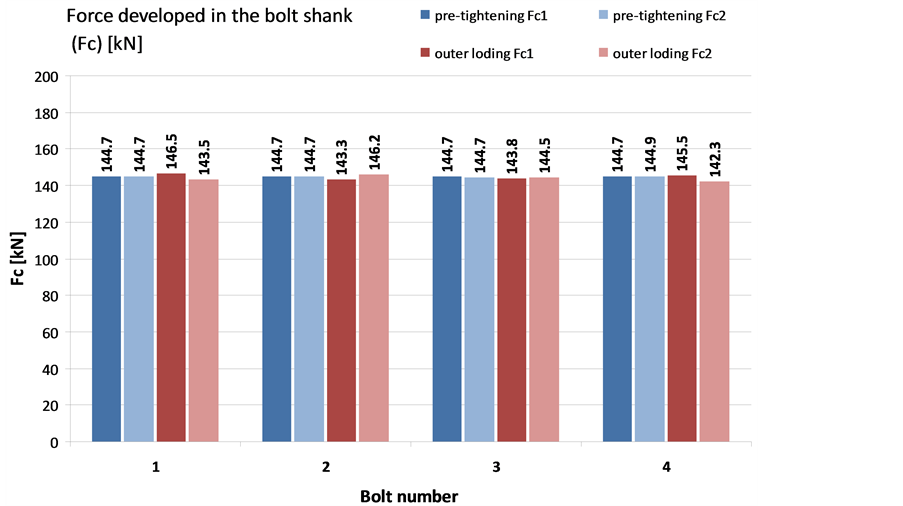
Figure 13. The developed forces in each bolt shank during pre-tightening and for the effect of outer loading.
contact surfaces compressed by bolts¾the contact surfaces are slipping on each other if these forces are exceeding a certain limit. Along the contact surfaces the magnitude of slipping are not equal due to the elastic deformation of the compressed bodies. If sticking or slipping occurs, it depends upon the magnitude of the forces and furthermore of the magnitude of the friction coefficient. For the magnitude of relative tangential displacements of the contacting elements the general requirement is that the displacement value should not exceed 0.1 mm including the elastic deformations as well.
One possible way to examine the slipping phase is “gluing in a spot” between the contacting surfaces (Figure 14). If the developed tangential force in the glued spot is bigger than the force which hinders the slipping then this is the force which hinders the slippage related to the case without gluing.
For slipping studies the force acting on the cantilever has been increased for:
Fleft = 80 kN, (4)
Fright = 2kN. (5)
Assuming μ = 0.12 friction coefficient¾in order to hinder the cantilever displacement¾reasonable magnitude of tangential force is developed (Fx = 15.6 kN and Fy = 44.3 kN) on the glued surface element. The friction coefficient should be increased up to the value of μ = 0.25 in order to have the tangential force on the glued surface smaller then the sticking force, that is the cantilever should not slide over the frame structure.
There is another method for defining the “no-penetration” connection in the surfaces between the bolt shank and the holes. So in case of small friction coefficient—followed by a given magnitude slipping of the cantilever—the hole will get contacted on the bolt shank and the FEM examination will be stable numerically, because of the limited slipping.
Having the model prepared so the calculated values are shown in Figure 15.
It can be seen well in the figure that the brake supporting cantilever has slipped compared to the frame structure and the magnitude of the displacement is bigger then 0.1 mm. Furthermore it can be seen that followed by the slipping (assuming 0.5 mm gap between the hole and the bolt shank) the cantilever get contacted on the surfaces of the bolts (location number 1 and 3) and these bolts suffer shear loading.
In Figure 16, y direction displacement field was presented too and the scale of displacement was limited at ± 0.5 mm. The 0.5 mm corresponds to the gap between the bolt shank and the hole. So it can be seen the cantilever slipping and also the contacting of the bolt shank on the inner hole surface.
With the condition of constant cantilever loading the value of friction coefficient was gradually increased from μ = 0.12 up to μ = 0.23. The calculation was numerically not sable all along a lower friction coefficient range and μ = 0.23 was the first value providing appropriate result. Increasing the friction coefficient further the overall displacement magnitude of cantilever was reduced proportionally. In the surroundings of bolts the displacements of the cantilever in the function of the friction coefficient
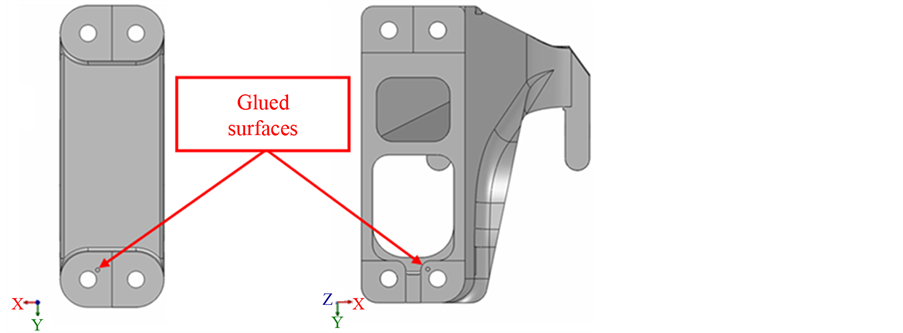
Figure 14. In order to prove the cantilever slipping the cantilever and the frame structure were glued in a spot.
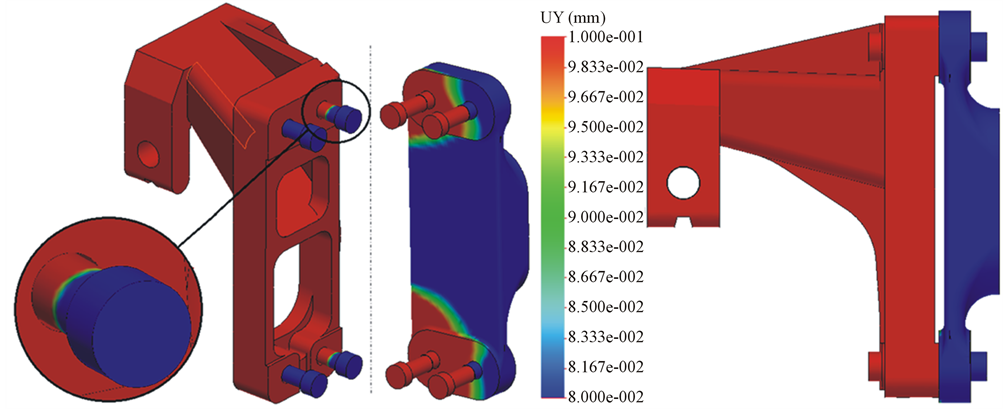
Figure 15. Displacement field in y direction. The lower and upper limit of the scale: 0.08 - 0.1 mm, in order to illustrate the slipping.
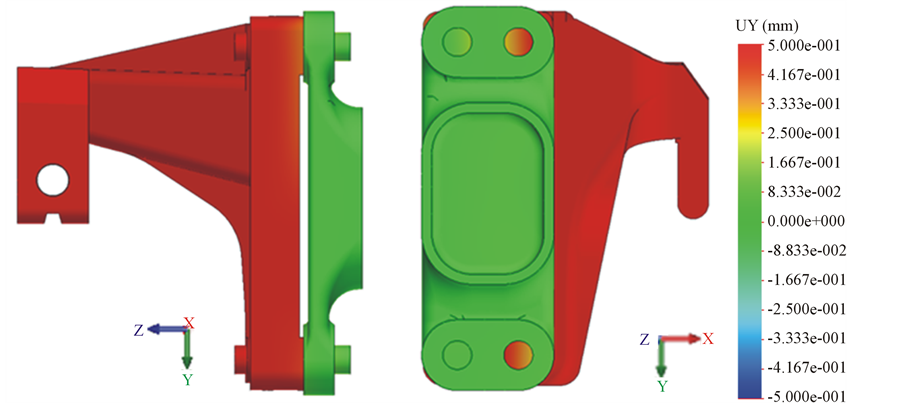
Figure 16. Displacement field in y direction. The upper and lower limit of the scale: ± 0.5 mm.
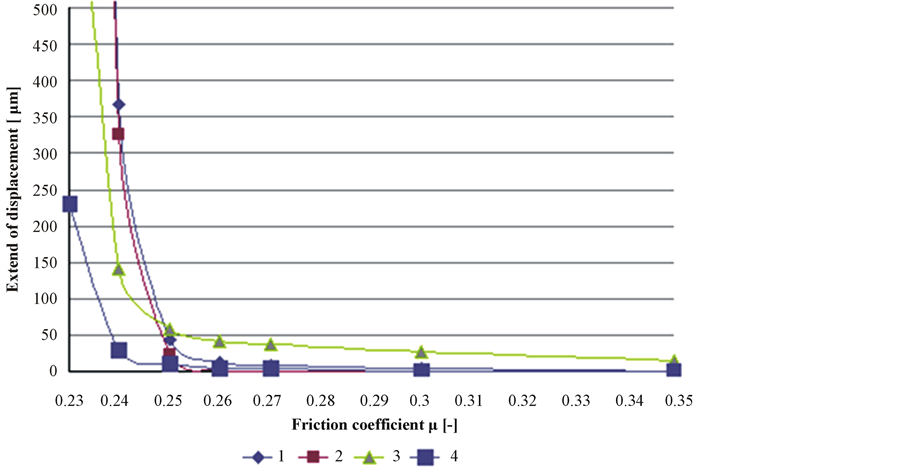
Figure 17. Relative displacement of the brake supporting cantilever¾compared to the frame structure¾in the function of the friction coefficient.
are shown in Figure 17. As it is shown in the figure the friction coefficient should be at least μ = 0.25 for keeping the displacements below the required 0.1 mm value to avoid local slipping.
8. Conclusions
In this paper, a numeric method for multi bolted joint was introduced where all elements participating in the joint were modeled as elastic elements. By applying the introduced method, it is possible to determine more accurately the behavior and loading of all elements participating in the bolted joint.
The elaborated procedure is capable to consider the bolt pre-tightening and the acting outer load on the cantilever by superposing the displacements prescribed for the bolts.
The slipping of the cantilever can be analyzed in the simplest way by changing the friction coefficient, by which it is possible to find the critical condition of slipping.
REFERENCES
- Systematische Berechnung Hochbeanspruchter Schraubenverbindungen Zylindrische Einschrau-Benverbindungen. VDI-Richtlinien, VDI 2230, 2003.
- L. Molnár, K. Váradi and B. Liktor, “Stress Analysis of Bolted Joints. Part I. Numerical Dimensioning Method” Modern Mechanical Engineering.


