Journal of Power and Energy Engineering
Vol.05 No.08(2017), Article ID:78497,12 pages
10.4236/jpee.2017.58006
Simulation Study of Active Noise Control in Wind Turbines Using FxLMS Adaptation Algorithm
Soumya Roy, Pratik Naik
School of Mechanical Engineering, Purdue University, West Lafayette, USA

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: July 14, 2017; Accepted: August 14, 2017; Published: August 17, 2017
ABSTRACT
Utility scale wind turbines produce a significant amount of noise which has been identified as one of the most critical challenges to the widespread use of wind energy. Aerodynamic noise caused primarily by the interaction of the boundary layer and (or) the upstream atmospheric turbulence with the trailing edge of the blade has been identified as the most dominant source of noise in wind turbines. The authors here propose an active noise control system based on the FxLMS algorithm which can achieve suppression of noise from a modern wind turbine. Two types of noise sources have been simulated: monopole and dipole. The results of the active noise control algorithm are validated with simulations in MATLAB. The agreement between the results shows the far impact of active noise control techniques will have in future wind turbines.
Keywords:
Active Noise Control, Monopole, Dipole, FxLMS Algorithm

1. Introduction
Over the past few decades, wind energy has come up to becoming one of the most popular sources of clean energy. Besides being a clean fuel source, it is also cost-effective when compared to the conventional sources of power generation. However, the choice of wind energy has often been criticized owing to the constant noise being generated from wind turbines and farms. Generally, a wind turbine is placed no closer than 300 meters from a home and at this distance, the sound pressure level generated by the turbine is around 43 decibels [1] . Various research studies have shown that constant exposure to noise generated from wind turbines, particularly low frequency noise, may cause sleep disturbances, fatigue and other various physiological effects [2] . Therefore, significant research effort in modern wind turbine technology has been to achieve reduction of wind turbine noise [3] [4] [5] [6] .
Wind turbine noise can be categorized in two ways; first on basis of frequency and the second on basis of the noise source. Based on frequency, wind turbine noise can be either high frequency or low frequency noise. The reduction of high frequency noise can be easily achieved by adopting passive noise control methods such as optimizing the geometry of the airfoil and adding serrations to the trailing edge of the blade. However, controlling low frequency noise is still a major challenge. On basis of the noise source, wind turbine noise can be either mechanical noise or aerodynamic noise. For most utility-scale wind turbines today, controlling aerodynamic noise is the major challenge, since mechanical noise can easily be controlled by using quieter generators & gearboxes or by using gearless power-trains [7] [8] . Aerodynamic noise is of two types: aerodynamic self-noise and inflow-turbulence noise. The aerodynamic self-noise is caused by a moving turbine blade in an undisturbed flow because of the interaction of the boundary layer with the trailing edge of the blade [9] . Self-noise can be caused by several mechanisms (refer Figure 1):
1) Trailing Edge Noise: This is generated when the boundary layer over the suction surface interacts with the trailing edge of the blade.
2) Separation Stall Noise: Separation stall noise happens because of the separation of the boundary layer from the suction surface of the blade. This increases



Figure 1. Different types of aerodynamic noises in a wind turbine. (a) Trailing edge noise; (b) Separation stall noise; (c) Tip-vortex noise; (d) Boundary-layer vortex shedding noise; (e) Trailing edge bluntness noise; (f) Noise due to turbulent inflow.
from the root to the tip, hence a longer blade length, which is desirable for higher power generation, but will also result in a higher stall noise [10] .
3) Tip Vortex Noise: This noise is generated when there is formation of vortices at the side edge of the blade. This also contributes to blade high frequency noise [11] .
4) Boundary Layer Vortex Shedding Noise: This noise takes place because of the interaction of boundary layer vortices with the trailing edge of the blade.
5) Trailing Edge Bluntness Noise: If the trailing edge of the blade is blunt, then it will result in the generation of the bluntness noise.
To characterize the various wind turbine noises, it is important to understand the directivity pattern of the noise types. Directivity patterns define the way power that is generated from a noise source. The inflow-turbulent noise generated by the interaction of turbulent eddies with the blade creates a dipole-like sound source located at the blade leading edge. Trailing edge noise has a directivity pattern of a cardioid, which is an epicycloid having a single cusp. This is the reason why an observer standing on the ground will hear a “swish” like noise because he periodically receives fluctuations in acoustic energy as the blade rotates. In case of downwind turbines, the rotor blade passes through the wake region of the tower and this reason has been attributed to a high level of noise generated from downwind turbines [12] [13] . Most of today’s horizontal axis wind turbines place the rotor upstream of the tower, thus eliminating the wake-rotor interaction. However, the blades still pass through a region of perturbed flow upstream of the tower, creating unsteady lift and hence noise. A summary of other various wind turbine noise mechanisms is as given in Table 1.
This article is aimed at modeling a wind turbine noise source for different directivity patterns and thereafter showing how real-time noise reduction can be achieved for the different acoustic models by employing the FxLMS adaptation algorithm.
2. Active Noise Control
Real time noise reduction is an important aspect of modern-day wind turbines which can be achieved by active noise control. For active control of noise, we generate a noise signal like the sound source we want to suppress and hope that
Table 1. Noise generation mechanisms in wind turbines [13] .
this generated noise destructively interferes with the sound source. Different algorithms have been presented in literature to achieve this. In this paper, our focus is on the implementation of FxLMS algorithm. FxLMS is based on single channel feed forward control loop. To understand how this algorithm works, imagine a noise (refer Figure 2) travelling from a source to the sensor through a fluid medium P(z). The noise is measured by the sensor as yp(k). Now our objective is to generate a noise which can destructively interfere with this noise source. This is achieved by an actuator or a controller C(z) which generate the interfering noise. The least mean square method is used to adjust the weights of the actuators and hence the name FxLMS. Now this generated noise travels from actuator to the sensor through a fluid medium S(z) which is known as the secondary path. Hence to compensate for this, we estimate the secondary path using Sh(Z). Refer Figure 2.
Before implementing this algorithm, we need to first define the domain of our problem. Figure 3 shows the domain of the problem used. In this figure, S1 represents the source that produces the noise. This noise propagates from the source to the sensor S. Using FxLMS algorithm, a control signal is generated by the sensor. Then, this control signal is given to the actuator which generates an attenuating noise. This generated noise interferes destructively at the sensor position resulting in the suppression or active noise control.
3. Acoustic Model of Sound
The following two directivity patterns have been adopted in this paper to model the noise generating source. The surrounding medium has been assumed to be homogeneous in nature for modeling purposes.
3.1. Monopole
An acoustic monopole radiates noise in equal directions. Imagine throwing a
Figure 2. FxLMS adaptation algorithm control loop [14] .
Figure 3. Domain: Source and Sensor position.
stone in a puddle; the ripples generated in the water are similar in nature to the sound radiated by a monopole. If the dimensions of a sound source are smaller than wavelength of the noise being emitted we get monopole sound source.
The far field pressure radiated by a monopole can be given as:
 (1)
(1)
where Q is a constant known as the complex source strength, ρ is density of the medium, c is the sound speed, k is the wave number in a given unit time, r is the distance between source and the position where the pressure is to be measured [14] . For modeling purposes, we have considered r = 1 m and the source emulating a wind turbine to be of a pure sine type, having frequency of 200 Hz and an amplitude a = 0.2 m. The resulting wave number is therefore determined to be , where c = 343 m/s is the speed of sound in air at room temperature (20˚C).
, where c = 343 m/s is the speed of sound in air at room temperature (20˚C).
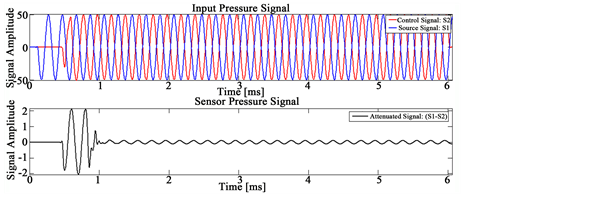
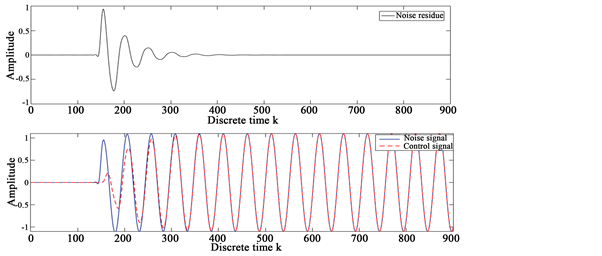
Figure 4 shows monopole sound source which was generated using MATLAB. It can be seen from the figure that as this noise source travels towards sensor, its amplitude decreases. Figure 5 shows the noise signal (blue) measured at the sensor position. The control signal generated using FxLMS algorithm is shown in red. Noise residue is the difference between this noise signal and control signal and our aim is to minimize this noise residue. As it can be seen from the figure, the noise residue almost becomes zero after reaching the steady state. Hence, it can be concluded that FxLMS algorithm produces a good measure of the noise signal.
Figure 4. Monopole noise source.
Figure 5. Output of FxLMS algorithm for monopole.
3.2. Dipole
Two monopoles separated by a very small distance (much smaller than the wavelength) having equal strength but opposite phases constitute a dipole. Dipole is spherically diverging in nature [14] . The far field pressure radiated by a dipole is given by
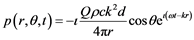 (2)
(2)
The symbols have their meanings as given earlier in Equation (1). The normalized pressure field for a dipole is shown in Figure 6. Similar analysis was carried out for a dipole noise source. Figure 7 shows the identification error which is error generated in the secondary path. This is generated because of error
Figure 6. Dipole noise generation.
Figure 7. Secondary path error for dipole.
estimate of coefficients/weights of sh(z). It decreases and attains a very small value after initial transients.
4. Results and Discussion
4.1. Monopole
Once the monopole sound field has been modelled, the next step is to actuate the controller using the control signal. Figure 8 shows the normalized pressure field for both noise signal and actuating signal. Also, it can be seen from the figure that the control signal is out of phase with the source signal. So, they destructively interfere, attenuating the source signal. Figure 9 shows the measured pressure signal and it can be inferred from the figure that a reasonable attenuation of the control signal can be obtained.
4.2. Dipole
Figure 10 shows the pressure field generated by the actuated noise and the dipole source noise. Figure 11 shows the output of FxLMS algorithm for the dipole sound source.
Figure 8. Destructive interference of noise by the actuating signal for a monopole.
Figure 9. Simulation output of the actuating signal for monopole.
Figure 10. Output of FxLMS algorithm for dipole.
Figure 11. Destructive interference of noise by the actuating signal for a dipole.
The control signal generated by the algorithm in Figure 11 is very similar to the noise signal and this can be inferred from the almost zero residues obtained after initial transients.
4.3. Multiple Sensors
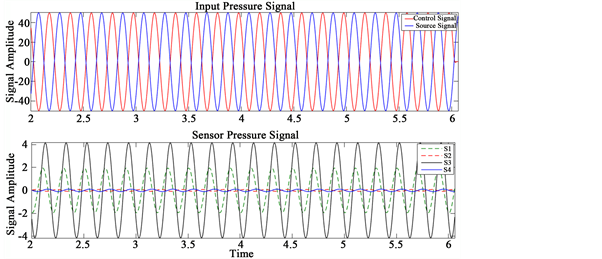
It is evident from the above analysis that reasonable noise suppression can be achieved using FxLMS algorithm at the sensor position. But there is possibility that the noise and control signal may constructively interfere at other locations in the domain resulting in noise increment at these locations. Hence, we need to evaluate the effect of this noise at other locations. To study this, we placed sensors at three more separate locations in the domain. The domain is symmetric in both X and Y directions. Hence, we choose upper quarter of the domain for location of the sensors. Refer Figure 12. The measured pressure signal by the sensor is plotted in Figure 13. It can be clearly seen from this figure that at sensor location S2 and S4 we achieve noise suppression as expected, but at sensor position S1 and S3 there is increase in noise intensity. Hence an efficient algorithm would be to emit the noise only in the forward direction i.e. direction in which we hope to achieve noise suppression.
Figure 12. Domain in case of multiple sensors.
Figure 13. Noise measured at different sensor locations.
5. Conclusion
A brief review of the different types of noises from wind turbines was done to understand the mechanisms and models of wind turbine noise generation. The noise source from a wind turbine was then modeled for two different directivity patterns: first as a monopole and then as a dipole. Active noise control was applied to both cases by implementing the FxLMS adaptation algorithm. Suppression of noise was achieved in both cases and the reaction of the system to the simulated sound was found to be very fast. Only a slight delay was observed because of the complexities of the reference noise. To understand the resulting sound field produced by the system of the noise source and actuator, sensors were placed at various locations and it was observed that equivalent noise reduction was not achieved at all positions in the sound field. This is a major drawback observed in the system so far. Future improvements in the existing FxLMS adaptation algorithm will therefore be required so as to not only achieve noise suppression at all positions in the sound field but also to achieve noise suppression from multiple sound sources, since wind turbines are generally installed together as wind farms.
Cite this paper
Roy, S. and Naik, P. (2017) Simulation Study of Active Noise Control in Wind Turbines Using FxLMS Adaptation Algorithm. Journal of Power and Energy Engineering, 5, 72-83. https://doi.org/10.4236/jpee.2017.58006
References
- 1. Kellner, T. (2014) How Loud Is a Wind Turbine?
http://www.ge.com/reports/post/92442325225/how-loud-is-a-wind-turbine/ - 2. Schust, M. (2004) Effects of Low Frequency Noise up to 100 Hz. Noise and Health, 6, 73.
- 3. Wagner, S., Bareiss, R. and Guidati, G. (1996) Wind Turbine Noise. Springer, New York.
https://doi.org/10.1007/978-3-642-88710-9 - 4. Guidati, G., Ostertag, J. and Wagner, S. (2000) Prediction and Reduction of Wind Turbine Noise—An Overview of Research Activities in Europe. 2000 19th ASME Wind Energy Symposium on Aerospace Sciences Meeting and Exhibit, Reno, NV, 219-229.
https://doi.org/10.2514/6.2000-42 - 5. Howe, M.S. (1978) A Review of the Theory of Trailing Edge Noise. Journal of Sound and Vibration, 61, 437-465.
https://doi.org/10.1016/0022-460X(78)90391-7 - 6. Brooks, T.F., Stuart Pope, D. and Marcolini, M.A. (1989) Airfoil Self-Noise and Prediction. Vol. 1218, National Aeronautics and Space Administration, Office of Management, Scientific and Technical Information Division.
- 7. Ragheb, A. and Ragheb, M. (2010) Wind Turbine Gearbox Technologies. 2010 IEEE 1st International Nuclear & Renewable Energy Conference (INREC), Amman, 21- 24 March 2010, 1-8.
https://doi.org/10.1109/INREC.2010.5462549 - 8. Ayana, P., Izadian, A., Hamzehlouia, S., Girrens, N. and Anwar, S. (2011) Modeling of Gearless Wind Power Transfer. IECON 2011 IEEE 37th Annual Conference on Industrial Electronics Society, Indianapolis, 3176-3179.
- 9. Giorgos, L., Wei, J.Z., Sørensen, J.N., Wen, Z.S. and Hjort, S. (2007) Prediction and Re-duction of Noise from a 2.3 MW Wind Turbine. Journal of Physics: Conference Series, 75, 012083.
https://doi.org/10.1088/1742-6596/75/1/012083 - 10. Arakawa, Chuichi, Fleig, O., Iida, M. and Shimooka, M. (2005) Numerical Approach for Noise Reduction of Wind Turbine Blade Tip with Earth Simulator. Jour- nal of the Earth Simulator, 2, 11-33.
- 11. Doolan, C.J., Moreau, D.J., Brooks, L.A., Hessler Jr., G.F., Schomer, P.D., Tonin, R., Evans, T., et al. (2012) Wind Turbine Noise Mechanisms and Some Concepts for Its Control. Acoustics Australia, 40, 7-13.
- 12. Made, J.E. and Kurtz, D.W. (1970) A Review of Aerodynamic Noise from Propellers, Rotors, and Lift Fans.
- 13. Sun, X., Kuo, S.M. and Meng, G. (2006) Adaptive Algorithm for Active Control of Impul-sive Noise. Journal of Sound and Vibration, 291, 516-522.
https://doi.org/10.1016/j.jsv.2005.06.011 - 14. Russell, D.A., Titlow, J.P. and Bemmen, Y.-J. (1999) Acoustic Monopoles, Dipoles, and Quadrupoles: An Experiment Revisited. American Journal of Physics, 67, 660- 664.
https://doi.org/10.1119/1.19349