Journal of Power and Energy Engineering
Vol.03 No.06(2015), Article ID:57380,10 pages
10.4236/jpee.2015.36006
Power Quality Study of an Isolated Northwest Grid of Saudi Arabia with PV and Storage
Hani Albalawi, Elham Makram
Department of Electrical and Computer Engineering, Clemson University, Clemson, USA
Email: halbala@clemson.edu, makram@clemson.edu
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 May 2015; accepted 22 June 2015; published 25 June 2015
ABSTRACT
One main concern of power quality is harmonics because the distorted waveforms of current and voltage have a huge effect on electrical equipment. Due to the continuous increase of grid connected photovoltaic (PV) and nonlinear loads, as a result of the fast development and growth of power electronics application, power quality becomes more important since it introduces harmonics to the power system. This paper presents a power quality study to the isolated northwest grid of Saudi Arabia in presence of PV system and battery storage. Moreover, the study includes nonlinear loads for more analysis regarding harmonics penetration and the design procedure for passive filters to eliminate the harmonics.
Keywords:
PV, Battery, Nonlinear Load, Harmonics, Passive Filter, Tabuk Grid, Saudi Arabia

1. Introduction
Supplying energy at constant frequency and magnitude of voltage is always the objective for any electrical utility. This can only happen in ideal power system but in practice this condition is hard to achieve. Many studies are required for planning and operation of power system in order to assist system performance, reliability and safety. Power quality is one important aspect of power system. It is the concept for many types of power disturbances such as voltage variation, and transient and harmonic distortion. The most unlikely condition for power quality is the harmonic distortion as it is a steady state condition. With high growth of installing grid connected photovoltaic (PV), power quality becomes more important as the DC-AC inverter can affect the quality of the power delivered to the grid due to the switching mechanism responsible for additional harmonics. Moreover, the widespread nonlinear loads due to power electronics applications result in distorted current and voltage in transmission and distribution networks. A solution for this power quality issue can be achieved by using harmonic filters which are designed to reduce the harmonic penetration to the network [1] .
All appliances that use diode rectifiers to convert AC to DC have a nonlinear characteristic that can lead to introduce harmonics. Examples of nonlinear loads include television, computers, fluorescent lamp and adjustable speed drives (ASD) for air condition and heat pump. Harmonic distortion is unwanted phenomena as it can cause additional line losses and interference in communication system. Therefore, analysis of harmonics and nonlinear loads is vital. A common way to analyze and study harmonics is to represent a load by linear model, then adding nonlinearity by using voltage or current harmonic sources [2] .
This paper presents a complete study of power quality for the isolated northwest grid of Saudi Arabia. A detailed PV model with battery storage is modeled and a combination of nonlinear loads is introduced. Also, the paper includes filter design to reduce harmonics. The outline of this paper is as follows. Section 2 shows PV and battery model. Section 3 explains the filter design. Section 4 describes the nonlinear load modeling. Section 5 provides a brief description of the test system. Section 6 shows the simulation results.
2. PV and Battery Model
2.1. PV Model
Figure 1(a) shows a diagram of a three phase grid connected PV system with battery storage. It consists of a PV array, Inverter and 3 phase reactor which is connected in series with the ac terminal of the inverter. The PV array is connected in parallel to the dc link capacitor and the dc terminal of the inverter. The inverter is controlled by voltage source converter (VSC) modulation strategy based on sinusoidal pulse-width modulation (S-PWM). The main element of the PV array is the solar cell, which has a very small power. In order to increase and have sufficient power to supply a load, single cells are connected in series to form a module. Therefore, PV array is a combination of parallel Np module and series Ns module. By increasing Np PV current increases and the PV voltage rises by increasing Ns. the Capacitor Cf is used to reduce the harmonic produced by the PV system. Figure 1(a) illustrates that, synchronizing the VSC and control to the grid voltage is achieved by a phase-locked loop (PLL). Also, the error between the Vdc reference given by MPPT and the dc-link voltage is passed through PI compensator whose output provides the d-axis reference current . Then, the dq-frame current loop control is fed by
. Then, the dq-frame current loop control is fed by 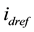 to force d-axis current to track the
to force d-axis current to track the  to control the PV output power, for unity Power factor the q-axis reference current
to control the PV output power, for unity Power factor the q-axis reference current 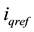 is set to zero [3] .
is set to zero [3] .
Figure 1. (a) Single line diagram of PV system; (b) PV control; (c) Battery control.
2.1.1. Phase Locked Loop
The PLL is used to synchronize VSC’s output voltage with electric-grid angular frequency in order to make dq- frame transformed variables constant and by regulating  to zero the PV system active and reactive power are controlled as follows:
to zero the PV system active and reactive power are controlled as follows:
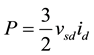 (1)
(1)
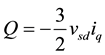 (2)
(2)
From (1) and (2), controlling the active power is archived by regulating 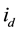 and the reactive power is controlled by regulating
and the reactive power is controlled by regulating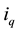 .
.
2.1.2. DC Voltage Control
The control of the dc voltage link is achieved by simply comparing the dc voltage with the reference value. This reference is calculated from MPPT strategy to ensure that the PV works at its maximum output power. The error between these two signals is passed through a PI compensator whose output provide , which will be the input for the current controller as seen in Figure 1(b).
, which will be the input for the current controller as seen in Figure 1(b).  is set to zero to achieve unity power factor.
is set to zero to achieve unity power factor.
2.1.3. Current Controller
The current controller is comparing the dq-reference currents with the actual ones to obtain the modulation signals 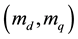 the control scheme is achieved by
the control scheme is achieved by
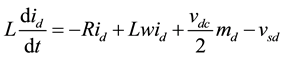 (3)
(3)
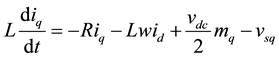 (4)
(4)
The state variables of (3) and (4) are  and
and 







By substituting (5) and (6) into (3) and (4), two control inputs produced which can control 



However, the 

2.2. Battery Model
This paper used the developed battery model in PSCAD [5] . Details of this battery model are described in [6] . It is modeled by a control voltage source with a series resistance. The charging and discharging process is controlled by constant current charging mode. Positive current reference is for charging process while negative reference is for discharging process. When the battery reaches a certain level of state of charge (SOC), the reference current is set to zero to keep the voltage at that level. From Figure 1(c), the DC/DC converter is operating in current control mode; the error signal is passed through a limiter and then compared with a triangular wave carrier to generate the pulse signals for the converter [7] .
3. Filter Design
One way to improve the power quality of power system is to resolve the harmonics issue. This can be done by many approaches described in [8] . One common way for harmonic filtering is to use passive filters, these kinds of filters are designed to provide low impedance path at the tuned frequency to prevent the harmonic current of flowing into the system. In this paper passive filter is used because it is one of the cheapest and economic wayfor harmonic filtering [1] . Harmonic filters are used to reduce the harmonics penetration in power system. A well designed harmonic filter is important to keep the harmonic within acceptable level. One of the most types used of passive filter is the single tuned filter, which is a capacitor designed to eliminate a certain harmonic by adding a reactor so that XC = XL at the tuned frequency (fn) [9] . The tuned frequency for harmonic filter designing usually should be between 2% to 10% below the desired harmonic frequency to avoid parallel resonance and near short circuit at tuned frequency as the filter provides low impedance. However, since the passive filters also provide a reactive compensation, they can also provide a power factor correction to a desired level in parallel to its filtering action.
For a tuned harmonic (hn) with a capacitor

And to eliminate the hn harmonic, the reactor size should be

The reactance resistor can be calculated as follows

where Q is the quality factor and its typical value is between 30 and 100 [10] .
4. Nonlinear Load Model
The increase of nonlinear loads due power electronics applications has introduced more effect on power system quality. Therefore, analysis of nonlinear loads and its affects is important. In power system, one common way to model a nonlinear load is to model it as a load for the fundamental current and as a current source for the harmonics current [11] . Figure 2 shows the configuration of the nonlinear load. In this paper three types of nonlinear loads are used, which are fluorescent lamp, computer and adjustable speed drive (ASD). ASD is used to represent air condition and heat pump. One important parameter is the individual harmonic distortion as it shows the contribution of each harmonic frequency to the distorted waveform. And by knowing the contribution of each harmonic frequency for a specified load, a harmonic current source can be used to inject the magnitude current for each harmonic frequency. Hence, the nonlinear behavior can be modeled by doing so. The contribution of each individual harmonic distortion for the three types of the nonlinear loads is shown in Table 1.
5. Study System
Saudi Arabia grid is divided into four operation areas, West area (WA), East area (EA), South area (SA) and Central Area (CA). Each one has its own control center and operation however they are now under interconnection projects. The WA consists of two parts, the west part and the northwest isolated area which has Tabuk region and its surrounding towns. The grid data was provided from Saudi Electricity Company, Tabuk sector. Line and Peak load data are shown in Table 2. It observed form Figure 3 that, the grid has 12 buses with voltage level of 132 KV, 10 substations are distributed around the city and two substations are connecting two different towns, Timma and Albir. It has two generation stations at bus 1 and 5 with a capacity of 102 MW and 857.2
Figure 2. representation of nonlinear load.
Figure 3. Tabuk Substations.
Table 1. Harmonic Number h (n) VS Individual Harmonic distortion [12] .
MW respectively. Figure 4 provides an over view of the power consumed in the city for a summer and winter day.
6. Simulation Result
The PSCAD software is used to build and simulate the grid with a detailed PV model and Battery storage. A peak loading condition for a summer day, 07/16/2013, with a total load of 720 MW is selected for the simulation. Bus 5 has been selected as a slack bus due to its largest capacity. The PV Farm is connected to bus 6 because it has enough land that can accommodate two PV farms connected in parallel with a total capacity of 40 MW, 20 MW each. The battery is assumed to have a capacity of 50% of the total PV Power. A harmonic current source is used to represent the nonlinear loads; the harmonic injection based on Table 1 is placed at the substation, at
Figure 4. Load Profile for Tabuk. Solid lines is daily load, dashes lines is temprature.
Table 2. Line and Peak load data.
the low voltage side 13.8 KV. At each bus the load is divide into 80% linear load and 20% nonlinear load. The nonlinear loads that used are ASD, to represent air condition and heat pump, fluorescent lamp and a personal computer with percentage of 18%, 1% and 1% respectively. All loads at each bus has the same procedure therefore the highest load at bus 9 is selected to show the result of including the nonlinear loads, Figure 5(a) illustrates the distorted load current after adding the nonlinear loads. Also, Figure 6(a) shows that, the total harmonic distortion (THD) of the total load current is above the limits therefore a single tuned filter has been designed to eliminate the highest harmonic component which is the 5th component as shown in Figure 6(b). Figure 5(b) shows the load current after installing the passive filter. Hence, Figure 7 provides the THD for each bus during the simulation and it observed that as seen in Table 3 the distortion is within the limits based on IEEE standard [13] . The initial irradiation applied for the PV is 1000 W/m2 with initial SOC of 70% for the battery. Figure 8 shows the different stages of PV penetration with battery storage. At 3 second, the charging process starts and stops when the SOC reaches 80% at 16 second. The SOC kept constant until the discharging of the battery begins at 18 second. During the discharge process the irradiation drops by 250 W/m2 at 25 second and 30 second. The THD of the PV current injected to the grid for all penetration stages is within the acceptable limits. It is oscillating around 2.5% as observed from Figure 9; the two high values at the second 16 and 18 are instantaneous due to the switching of the reference current of the battery to keep the SOC at 80% and to start the discharging mode.
One advantage of the Battery model in PSCAD is that, it allows the user to define the characteristic charge and discharge curves. And since the PV farm output power is high and so the dc voltage link,it is hard to find a battery with such voltage level therefore a characteristic charge and discharge curve of lead acid battery has

Figure 5. (a) Load current without filter of bus 9; (b) Load current with filter of bus 9.

Figure 6. (a) THD at bus 9; (b) Harmonic component.
Table 3. Load current THD compared with the standard Limits.






Figure 7. THD for all loads currents with filter. (a) THD of load current at bus 1; (b) THD of load current at bus 2; (c) THD of load current at bus 3; (d) THD of load current at bus 4; (e) THD of load current at bus 5; (f) THD of load current at bus 6; (g) THD of load current at bus 7; (h) THD of load current at bus 8; (i) THD of load current at bus 9; (j) THD of load current at bus 10; (k) THD of load current at bus 11; (l) THD of load current at bus 12.
been scaled up to match the DC link voltage and defined in the battery model. For the control scheme, the reference current for the battery can be obtained based on the DC link voltage and the amount of power to be stored. Since the battery assumed to have 50% of the PV power, the battery reference current is calculated as follows

From Figure 10 it observed that, the battery current follows the reference for both charging and discharging modes, for the discharge process a negative reference is applied. Also, when SOC of the battery reaches 80% the reference current is set to zero to keep the SOC of constant as seen in Figure 11. The battery power is shown in Figure 12.
Figure 8. PV power at PCC.
Figure 9. THD of PV Current at PCC.
Figure 10. Battery current for one farm.
Figure 11. Battery SOC.
Figure 12. Battery Power.
7. Conclusion
This paper presents a power quality study for the northwest grid of Saudi Arabia in presence of PV and battery storage. Different PV power penetrations with battery storage are introduced and the THD of PV current is within the acceptable limit for all penetration stages. Also, nonlinear load has been included for more analysis and it shows that the harmonic impact of introducing such loads has been solved by designing passive filters. It also discusses the passive filter design producer.
References
- Rao, R.N. (2013) Harmonic Analysis of Small Scale Industrial Loads and Harmonic Mitigation Techniques in Industrial Distribution System. International Journal of Engineering Research and Applications, 3, 1511-1540.
- Fauri, M. (1997) Harmonic Modeling of Non-Linear Load by means of Crossed Frequency Admittance Matrix. IEEE Transactions on Power Systems, 12, 1632-1638. http://dx.doi.org/10.1109/59.627869
- Yazdani, A. and Dash, P.P. (2009) A Control Methodology and Characterization of Dynamics for Photovoltaic (PV) System Interfered with a Distribution Network. IEEE Transactions on Power Delivery, 24, 1538-1551. http://dx.doi.org/10.1109/TPWRD.2009.2016632
- Mahmood, F., Yanfretti, L. and Hooshyar, H. (2014) Modeling of a Detailed Photovoltaic Generation System for EMT-Type Simulation. IEEE International Energy Conference, Cavtat, 13-16 May 2014, 916-921. http://dx.doi.org/10.1109/energycon.2014.6850535
- Jiang, S. (2012) Battery Component in PSCAD/EMTDC. Manitoba HVDC Research Centre, Winnipeg.
- Tremblay, O., Dessaint, L.A. and Dekkiche, A.I. (2007) A Generic Battery Model for the Dynamic Simulation of Hybrid Electric Vehicles. IEEE Vehicle Power and Propulsion Conference, Arlington, 9-12 September 2007, 284-289. http://dx.doi.org/10.1109/vppc.2007.4544139
- Clarke, A., Bihani, H., Makram, E. and Corzine, K. (2013) Fault Analysis on an Unbalanced Distribution System in the Presence of Plug-In Hybrid Electric Vehicles. Clemson Power System Conference, March 2013.
- Balaraju, U.P., Kethineni, B., Shewale, R. and Grourishetti, S. (2012) Harmonic Effects and Its Mitigation Techniques for a Nonlinear Load. International Journal of Advanced Technology & Engineering Research, 2, 122-127.
- Badrzadeh, B., Smith, K. and Wilson, R.C. (2011) Designing Passive Harmonic Filters for an Aluminum Smelting Plant. IEEE Transactions on Industry Application, 47, 973-983. http://dx.doi.org/10.1109/TIA.2010.2103544
- Wakileh, G.J. (2001) Power System Harmonics: Fundamental, Analysis and Filter Design. Springer, New York. http://dx.doi.org/10.1007/978-3-662-04343-1
- Gonen, T. (2008) Electrical Power Distributed System Engineering. 2nd Edition, CRC Press, New York.
- Sankaran, C. (2008) Power Quality. CRC Press, New York.
- McGranaghan, M. (1988) Overview of the Guide for Applying Harmonic Limits on Power Systems―IEEE P519A. 8th International Conference on Harmonics and Quality of Power Proceeding, Athens, 14-18 October 1998, 462-469.




















