Open Journal of Social Sciences
Vol.02 No.11(2014), Article ID:51909,10 pages
10.4236/jss.2014.211020
The Factors Affecting Egypt’s Exports: Evidence from the Gravity Model Analysis
Mohamed A. Elshehawy1, Hongfang Shen1, Rania A. Ahmed2
1Research School of Southeast Asian Studies, Xiamen University, Xiamen, China
2Department of Agricultural Economics, Faculty of Agriculture, Tanta University, Tanta, Egypt
Email: shehawy80@yahoo.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 6 October 2014; revised 5 November 2014; accepted 11 November 2014
ABSTRACT
This paper investigates the factors that affect Egypt’s bilateral export flows to its main trading partners. Based on the panel data, the gravity model approach has been used to estimate Egypt’s exports through annual data covering the period 2000 to 2013 for 42 main trading partners. The gravity model in its fixed effects panel data explained 84 percent of the fluctuations in Egypt’s exports. The results show that Egypt’s GDP, importer’s GDP, importer’s population, regional trade agreements (RTA) and the border between Egypt and its trading partner are the main factors affecting Egypt’s exports to its main trading partners. All these factors affect Egypt’s exports positively. Transportation costs (distance variable) are found to have negative but insignificant effect on Egypt’s exports. All these results can help the government and policy makers to undertake appropriate measures to improve the performance of the Egyptian foreign trade sector.
Keywords:
Egyptian Exports, Gravity Model, Panel Data, Fixed Effects Model

1. Introduction
Exports of goods and services represent one of the most important sources of foreign exchange income that ease the pressure on the balance of payments and create employment opportunities [1] . Export trade is crucial to meet the “foreign exchange gap”, to increase the import capacity of the country concerned and to reduce dependence on foreign aid [2] . Exports can increase intra-industry trade, help the country to integrate in the world economy and reduce the impact of external shocks on the domestic economy [3] . Experiences of Asian and Latin American economies provide good examples of the importance of the export sector to economic growth and development, which led economists to stress the vital role of exports as the engine of economic growth [4] .
Egypt is one of the emerging economies in Africa and Middle East region. Egypt’s foreign trade sector constitutes an important part of its economy. The trade openness ratio increased from 39 percent in 2000 to 71.7 percent in 2007 (World Bank). Although this sector has a great importance in the Egyptian economy, it has been suffering from a chronic deficit over the last years. Egypt’s export sector accounts for only slightly more than 10 percent of the overall economy, and this relatively modest contribution cannot by itself end high unemployment or generate enough tax revenue to fix the government’s shattered finances.
Egypt is in the early stages of an export boom, suggesting its economy could begin to recover in the next few months if a minimum level of political stability is restored. Egypt’s total exports has increased from US$ 3.5 billion in 1994 to US$ 28.78 billion in 2013 and exports in gross domestic product (GDP) also increased from 5 to 10.6 percent during the same period, thus reflecting modest importance of exports sector in the economy. However, the Egyptian exports are not widely diversified, but dominated by few products such as chemicals and agricultural products that lead to higher concentration in export products, and in turn to highly concentrated export destinations.
Given this importance and the role foreign trade sector plays in the Egyptian economy, it is important to find out the economic factors influencing Egyptian exports in order to help the government and policy makers to undertake appropriate measures to improve the performance of the foreign trade sector.
Gravity model through the panel data estimation technique is a useful methodological tool in finding out the economic factors that determine trade or export of a country. This model originates from the Newtonian law of gravity through the attraction of two countries’ masses, weakened by distance between them. The gravity model of trade basically states that trade flows between two countries are determined positively by their income and negatively by the distance between them. This model was originally employed by [5] , who introduced three key determinants to explain the size of bilateral trade flows: 1) importers’ demand, 2) exporters’ supply, and 3) the cost associated with the conduct of international trade, with respect to either transport or information. In other words, the model is based mainly on “natural” factors for explaining bilateral trade flows, while economic factors remain constant [6] .
Although few literatures are found with regard to analyzing trade relations and trade policies of Egypt using the gravity model, there is no particular in depth study found out the determinants of Egypt’s total export trade. This study, therefore, is an attempt to fill up this research gap.
To find out the most relevant factors affecting Egypt’s exports in the global market during the period 2000- 2013, the paper used panel data estimation technique and gravity model. The main contribution of this study is that it applies for the first time panel data approach in a gravity model framework to identify the factors influencing Egypt’s total exports.
The rest part of the paper is organized as follows. Section 2 provides an overview of Egypt’s exports and its main trading partner. Section 3 discusses the gravity model methodology and data. Section 4 presents the results of the empirical analysis, and finally conclusion and policy recommendations are briefed at the end.
2. Egypt Exports at a Glance
As Egypt is one of the emerging economies in Africa and Middle East region, it is important to investigate the performance of Egypt’s total exports. During the period 1980-2004, Egypt’s exports increased substantially and made a major contribution to Egypt’s balance of trade account. Total exports in 1980 were around US$ 3 billion and more than doubled in value to US$ 7.7 billion by 2004, growing at an average annual rate of approximately 6 percent. Since then Egyptian exports have increased enormously and reached US$ 27.88 billion in 2013. This represents a 26.33 percent average growth rate between 2004 and 2013 (see Figure 1).
In terms of directions of Egypt’s exports, most have been highly concentrated among a few major trading partners. During 2000-2013, about one-half of total exports went to the top five trading partners, and sixty percent to the top 10 markets (Table 1). The EU-27 remained the top destination for Egyptian exports, though its share fell from 41 percent in 2000 to 29 percent in 2013. India was the second-largest market during this period, with an increasing share from 3 percent in 2000 to 7.7 percent in 2013. The share of Arab countries (Saudi Arabia, Libya, Jordan, United Arab Emirates and Iraq) rose from 7 percent in 2000 to 20 percent in 2013. Egyptian exports to Turkey increased sharply from only US$ 84 million to US$ 1.74 billion over the period 2000-2013 as a result of the Free Trade Agreement that signed between the two countries in 2005.
Figure 1. Egypt’s total exports, 1980-2013 (in billion $).
Table 1. Egypt’s exports by major trading partner, 2000-2013 (in million $).
Source: World Integrated Trade Solution.
3. Gravity Model
Regarding the economic literature, there are a lot of empirical approaches which have used the gravity model to explain the determinants of bilateral trade. Using a gravity model applied to panel data, researcher [7] analyzed export performance in the Middle East and North Africa (MENA). Using gravity model, researcher [8] estimated the magnitude of India’s export potential to the six-member Gulf Cooperation Council (GCC) countries. Researcher [9] attempted to examine Malawi’s trade with her major trading partners using an econometric gravity model. Gravity model approach and panel data estimation techniques have been used by [10] to investigate Australia’s global trade potential taking data of Australia and its 57 trading partners. Using a gravity equation, as in [11] estimated parameters of explanatory variables for “euro zone” countries using panel data, and then these estimated parameters are employed to project trade potentials for Turkey. Researcher [12] identified the major determining factors of Bangladesh trade and investigated whether the gravity model correctly explains Bangladesh’s trade patterns and then estimated the global trade potential of Bangladesh using an augmented gravity model. Researcher [13] examined the trade flow between China and Sub-Saharan Africa with the use of the gravity model. Researcher [14] attempted to estimate Pakistan’s trade potential, using the gravity model of trade. Determinants of Italian agri-food exports in non-EU Mediterranean Partner Countries have been analyzed through the gravity model as in [15] . Using an augmented gravity model as in [16] , estimated using panel data and stochastic frontier methods to investigate the determinants of Brunei Darussalam’s trade and also estimate its trade potential. Regarding analyzing the factors influencing Egypt’s exports in the global market, only few studies have employed the gravity model approach. Researcher [17] employed the gravity model approach to analyze the main factors influencing Egypt’s agricultural exports to its major trading partners. Based on using gravity model as in [18] , investigated the key determinants behind increasing trade flows between Egypt and 50 countries of the Organization of Islamic Cooperation (OIC). Researcher [19] studied the economic effects of trade flows between Egypt and some economic blocs such as AFTA, COMESA and EU.
The gravity model has been used extensively in the international trade literature over the past 50 years [20] . The gravity model can today be considered standard procedure when a country’s directions of trade are analyzed [21] . The model was popular in the 1960s (see, for example, Tinbergen, 1962; Poyhonen, 1963) [22] [23] . After that the interest blanched, despite the model captures directions of trade flows quite well (see, for example, Deardorff, 1998) [24] . Some views said that the gravity model lacks a theoretical foundation but this is less reasonable today. A theoretical underpinnings were provided in 1960s and the 1970s, by Linnemann (1966), Leamer and Stern (1970) and Anderson (1979) [25] -[27] , using different methods but all arriving at similar results. This model originates from the Newtonian physics notion which states that two bodies attract each other proportionally to the product of each body’s mass (in kilograms) divided by the square of the distance between their respective centers of gravity (in meters) [28] . It is supposed that the gravity model relates bilateral trade to the economic mass of the two economic sizes, the distance between them, and other possible influences such as dummy variables. The general form of the gravity equation is as follows:
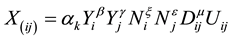 (1)
(1)
where Xij is the exports flow between country i and j, αk is a constant, β, γ, ξ, ε, μ are coefficients, weighted geometric averages, Yi and Yj are gross domestic product (GDP) in country i and j, respectively, Ni and Nj are population in country i and j, and Dij is the distance between the countries’ capitals. The Uij is a lognormal distributed error term with E(lnUij) = 0. Frequently dummy variables are also included in the model to take into account preferential trade factors between i and j.
The linear form of the previous gravity equation can be written as follows:
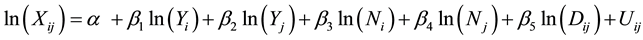 (2)
(2)
4. The Generalized Gravity Model, Sample Size and Data
4.1. The Generalized Gravity Model of Egypt’s Exports
The standard gravity model includes distance and income as independent variables. Most models also include population and different dummy variables [29] . The gravity model is considered suitable for the analysis of export trade in this research, where this model has proven its efficiency as one of the most efficient models in explaining bilateral trade. By modifying and adding some more independent variables to Equation (2), we can investigate and analyze factors affecting Egypt’s exports. The value of flowing exports into country j from Egypt (i) can be expressed as follows:
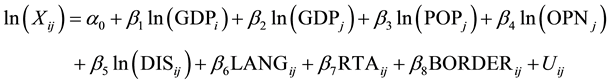 (3)
(3)
where all variables (excluding dummies) are expressed in natural logarithms. The dependent variable  represents the flow of exports into the trading partner j from Egypt. Independent variables include Gross Domestic Product, population, real openness and distance. Dummies are used such as the common language, common free or regional trade agreements and common border (see the summary of independent variables in Table 2). The descriptive statistics of the gravity equation’s variables are presented in Table 3.
represents the flow of exports into the trading partner j from Egypt. Independent variables include Gross Domestic Product, population, real openness and distance. Dummies are used such as the common language, common free or regional trade agreements and common border (see the summary of independent variables in Table 2). The descriptive statistics of the gravity equation’s variables are presented in Table 3.
Each of the independent variables included in Equation (3) has a defined impact on the level of trade flows between Egypt and its trading partners. A high level of income in the exporting country indicates a high level of production, which increases the availability of goods for exports [30] . Therefore the expected sign of β1 will be positive. By the same logic, the expected sign of the coefficient of β2 is also expected to be positive where a high
Table 2. Summary of the independent variables used in the gravity model.
Table 3. Descriptive statistics.
level of income in the importing country leads to higher imports. The coefficient estimate for population of the importer β3, may be positive or negative signed, depending on whether there is more opportunity for trade in a large variety of goods or not. As concern to openness, the more open the country is, the more would be the trade [31] . Therefore the expected sign of β4 will be positive. The expected sign of β5 is expected to be negative, where a long distance between trading partners implies higher costs and lower profit margins for importers [32] . In addition dummies were included for country-pairs sharing the Arabic language and being members of the same free trade areas and sharing common border between them. Accordingly, β6, β7 and β8 are expected to have a positive sign (see the summary of expected signs in Table 2).
4.2. Sample Size and Data
The research covers a total of 42 importing markets. These markets are chosen based on the importance of trading partnership with Egypt and the availability of required data. Eleven markets from EU (Belgium, Cyprus, Germany, Spain, France, United Kingdom, Greece, Italy, Malta, Netherlands and Portugal), fourteen Arab markets (Algeria, Iraq, Jordan, Kuwait, Lebanon, Libya, Morocco, Oman, Qatar, Saudi Arabia, Syria, Tunisia, United Arab Emirates and Yemen), eight markets from non-Asian Arab countries (China, Indonesia, India, Japan, Korea Rep., Malaysia, Pakistan and Singapore) and other nine markets (Brazil, Canada, Switzerland, Kenya, Nigeria, Russian Federation, Turkey, USA and South Africa) are included in our sample for the analysis of Egyptian exports during the period 2000-2013 (14 years). On the whole, the sample markets absorb at least 85% of Egypt’s total exports. The estimation covers 42 countries over the years 2000-2013 with one dependant variable and 8 explanatory variables (a total of observations = 588, N = 42, and T = 14), and all variables are expressed in natural logarithm. The data on Egypt’s total exports to its trading partners (country j) are obtained from the World Integrated Trade Solution (WITS) [33] . The data of GDP and population were obtained from United Nations National Accounts Database [34] and the World Development Indicators (WDI) database of the World Bank [35] . Data on the distance (in miles) between Cairo (the capital of Egypt) and other capital cities of the trading partner are collected from the City Distance Calculator [36] .
4.3. Methodology and Statistics
Many early empirical studies used classical gravity models (cross-section data) to estimate trade effects and trade relationships for a particular time such as models used by [37] [38] . Nowadays, panel data are used widely by many researchers as in [39] -[41] . The panel data technique has been used in this paper. The advantages of panel data method are it can indicate the important relationship between variables over time; monitor trade partners individual effects and avoids biased estimates. To estimate the gravity equation in this paper, the panel data and individual effects included in the regressions.
Panel data contains many models that can be estimated. These models are pooled, fixed effects and random effects. The main problem of the pooled model is that it does not allow for heterogeneity of countries. It does not estimate country specific effects and assumes that all countries are homogenous [42] . Random effects model can be more appropriate when estimating the flows of trade between a randomly sample drawn of trading partners from a large population. Fixed effects model would be a better model when estimating the flows of trade between ex ante predetermined selection of countries [17] [43] . Since this paper deals with the Egyptian export flows to its main importing partners, the fixed effects model will be a more appropriate model than the random effect model. Moreover, Hausman test has been applied to determine which of the models, fixed effects or random effects model is the most appropriate. This test is applied to check whether the null hypothesis that the coefficients of the random effects are the same with the consistent fixed estimator. If the P-value (Prob > chi2) is significant, less than 0.05, then fixed effects model will be used. If P-value is greater than 0.05, then random effects model will be the most efficient model. The fixed effects model has a problem in estimating variables that do not change over time because inherent transformation combs out such variables, and as such the dummy and distance variables need to be dropped. This problem can be solved by estimating these variables in a second step through running a second stage regression with considering the individual effects as the dependent variable whereas the dummy and distance as independent variables. The estimated equation of the second stage regression will be as follows:
 (4)
(4)
where IEij represents the individual effects and the other explanatory variables are as explained before.
4.4. Panel Unit-Root Tests
Before estimating Equation (3), this paper analyzes the univariate characteristics of the data that entails panel unit root tests. Panel unit root test determines a potentially cointegrated relationship between the variables. If all variables have no unit root i.e. are stationary, then the traditional estimation methods can be used to estimate the relationship between the variables. If the variables have unit root test i.e. are non-stationary, a test for cointegration will be performed [44] [45] . There are several different types of panel unit root tests, but in this paper two panel root tests will be investigated which they are Hadri method [46] and Levin, Lin and Chu (LLC) method [47] . These two methods assume that the autoregressive parameters are common across countries. The Hadri method uses the null hypothesis of no unit root, while LLC method uses the null hypothesis of a unit root. The results of these tests are presented in Table 4. The results of the LLC test show that all variables are stationary except Egypt’s exports and importer’s GDP. On the other hand, the results of Hadri test show that all variables are stationary. This paper uses a rejection of unit root by at least one test to conclude that the variables are stationary. Since the variables are stationary according to the Hadri test, it implies that there is no need to cointegration test, and Equation (3) can be estimated using the traditional estimation method.
4.5. Estimation Results
Table 5 contains the estimation results for the pooled, fixed and random effects models. The pooled model does
Table 4. Summary of panel root tests.
Note: */**/***Denote rejection of the null hypothesis at 10%/5%/1% significance level.
Table 5. Estimation results.
Notes: */**/***/Significant at 10%/5%/1% level. The t-statistics are in parentheses.
not allow for heterogeneity of cross sections and cross section specific effects are not estimated. In addition to these problems, the pooled model assumes that all cross sections are homogenous and it assumes a single intercept and same parameters over time and cross countries. The results of pooled panel data model are in the second column of Table 5. The third column in Table 5 contains the results of fixed effects model. Fixed effects model allows the intercept and other parameters to differ across countries, and also it has heterogeneity. To test the data probability, the F-test has been performed. As it is clear from Table 5, the null hypothesis for equality of the individual effects has been rejected by the test. This indicates that the model with individual effects is more efficient than the pooled model.
The results for random effect model are presents in the last column of Table 5. The random effect model assumes that the effects are generated by a specific distribution, so it differ from fixed effect model in this point but it likes fixed effect model in acknowledging heterogeneity of countries. Although acknowledging differences in countries of this model, it does not precede each effect separately. This hinders the loss of freedom degrees which takes place in the fixed effect model.
In order to test the null hypothesis that the regressors and individual effects are not correlated, the Hausman test has been performed. This test can distinguish between fixed and random effects. Failure to reject the null hypothesis implies that the random effect model is efficient than the fixed effect model. The fixed effect model will be more efficient than the random effect model, only if the null hypothesis has been rejected.
Table 5 indicates the results of Hausman test and it is clear that the null hypothesis is rejected, and this implies that country specific effects are correlated with regressors. This means that the fixed effects model is preferred and the interpretation of coefficients in this paper will focus on the fixed effects, because it is the most efficient model. It is clear that the overall performance of the gravity model seems to be good with high R2 values of 84 percent in case of fixed effects model. Almost all estimates of the coefficients are highly significant with expected signs. This indicates that the gravity model is suitable for explaining the flows of Egyptian exports to its major trading partners. As can be seen from Table 5, R2 indicates that approximate 84 percent of the variability in the total exports between Egypt and its trading partners can be explained by the fixed effects model. The value of F-test indicates that the overall significance of the model is highly significant at 1 percent level. The explanatory variables product of GDPs are highly significant at 1 percent level, the explanatory variable importer’s population is weak significant at 10 percent level. The variable of importer’s openness is not significant factor in explaining Egypt’s exports. The results of fixed effects model in Table 5 also indicates that an increase in Egypt’s GDP, importer’s GDP and importer’s population causes Egyptian exports to increase.
The estimated coefficient of Egypt’s GDP is 4.01 which means that, holding constant for other variables, a 1 percent point increases in Egypt’s GDP will result in a roughly 4 percent point increase in Egypt’s total exports. On the other hand, the estimated coefficient of importer’s GDP is 0.84 which means that, holding constant for other variables, a 1 percent point increases in importer’s GDP will result in a roughly 0.84 percent point increase in Egypt’s total exports. Moreover, the estimated coefficient of importer’s population is 0.53 which means that, holding constant for other variables, a 1 percent point increases in importer’s population will result in a roughly 0.53 percent point increase in Egypt’s total exports. Importer’s openness does not show significant coefficient, and thus is not explanatory variables in the flow of Egyptian exports.
The results of second stage regression are presented in Table 6. The results indicate that the distance variable has the expected sign but it is not significant. Egypt exports less products to countries where Arabic is the official language, and this is not consistent with theoretical expectation. It is clear that the regional trading agreements (RTA) variable is highly significant and this implies that the importer country that has RTA with Egypt can affect Egypt’s exports. The variable border has significant and positive effect on the flows of Egyptian exports so if the importer country is close to Egypt, Egypt’s exports will increase.
5. Conclusions
Given the importance and the role foreign trade sector plays in the Egyptian economy, it is important to find out the economic factors influencing Egyptian exports in order to help the government and policy makers to undertake appropriate measures to improve the performance of the foreign trade sector.
The main purpose of this research was to identify and evaluate the main factors that affect Egyptian exports. The analytical procedure includes the gravity model as one of the best theoretical framework to estimate export equations using panel data for the period 2000 to 2013. A sample of 42 was chosen for the empirical analysis.
Regression analysis was performed in three techniques which include the pooled model (common intercept model), the fixed effects model, and the random effects model. In order to choose among methods, the F-test and Hausman test were performed.
Table 6. Second stage regression: Dependent variable is fixed effects.
Note: */**/***/Significant at 10%/5%/1% level.
The F-test rejected the null hypothesis of common intercept. When choosing between fixed and random effects, the Hausman test rejected the null hypothesis. The research demonstrated that the fixed effects model generated the most reliable outcomes and then showed the analysis using this method. The results of the regression indicated that most estimated parameters had the expected signs and were statistically significant.
Egypt’s GDP, GDP of the importing countries, population of the importing countries had a positive influence on Egypt’s exports. The results suggested a positive influence of the increase in Egypt’s GDP, since a greater income stimulated exports. The higher the income, the greater the volume of Egyptian exports which took place. The results also suggested that Egyptian exports was positively influenced by an increase in GDP in the importing countries; the higher the income in importing country, the greater the volume of Egyptian exports. The openness rate of the importing countries did not encourage Egypt’s exports, having a negative influence.
The distance variable between Egypt and the importing countries had its expected sign but it was not significant. The results also indicated that Egypt exports less products to countries where Arabic is the official language, and this is not consistent with theoretical expectation. The regional trading agreements (RTA) variable is highly significant and this implies that the importer country that has RTA with Egypt can affect Egypt’s exports. The common border between Egypt and its neighbors encouraged the exports, where the results indicated the significance and positive effect of this variable on the flows of Egyptian exports.
All these results can help the government and policy makers to undertake appropriate measures to improve the performance of the Egyptian foreign trade sector. However all these results are valuable, more researches and more data on Egypt’s trade will add more and more to the foreign trade sector.
References
- Shihab, R.A., Soufan, T. and Khaliq, S.A. (2014) The Causal Relationship between Exports and Economic Growth in Jordan. International Journal of Business and Social Science, 5, 302-308.
- Rahman, M. (2009) Australia’s Global Trade Potential: Evidence from the Gravity Model Analysis. Working Paper, Oxford Business & Economics Conference, Oxford, 24-26 June 2009, 1-41.
- Stait, F. (2005) Are Exports the Engine of Economic Growth? An Application of Cointegration and Causality Analysis for Egypt, 1977-2003. Working Paper, African Development Bank, No. 76.
- Ijeoma, N.B. (2013) Trade Liberalization in Nigeria: An Examination of Impact and Policy Strategies. International Journal of Scientific & Engineering Research, 4, 1277-1283.
- Linnemann, H. (1966) An Econometric Study of International Trade Flows. Holland Publishing, Amsterdam.
- Papazoglou, C. (2009) Is Greece’s Export Performance Ally Low? Economic Bulletin, No. 32.
- Söderling, L. (2005) Is the Middle East and North Africa Region Achieving Its Trade Potential? IMF Working Paper, No. 05/90.
- Pradhan, S. (2006) India’s Export Potential to the Gulf Cooperation Council (GCC) Countries: A Gravity Model Analysis. Workshop Report, Asia-Pacific Research and Training Network on Trade, WTO/ESCAP.
- Simwaka, K. (2007) Dynamics of Malawi’s Trade Flows: A Gravity Model Approach. Working Paper, Munich Personal RePEc Archive, No. 1122.
- Rahman, M. (2010) Australia’s Global Trade Potential: Evidence from the Gravity Model Analysis. International Journal of Business Research, 10, 242-253.
- Ozdeser, H. and Ertac, D. (2010) Turkey’s Trade Potential with Euro Zone Countries: A Gravity Study. European Journal of Scientific Research, 43, 15-23.
- Rahman, M. and Ara, L. (2010) Bangladesh Trade Potential: A Dynamic Gravity Approach. Journal of International Trade Law and Policy, 9, 130-147. http://dx.doi.org/10.1108/14770021011054296
- Adekunle, B. and Gitau, C. (2011) Illusion or Reality: Understanding the Trade Flow between China and Sub-Saharan Africa. Working Paper, CSAE 25th Anniversary Conference: Economic Development in Africa, Tanzania, 1-27.
- Gul, N. and Yasin, H. (2011) The Trade Potential of Pakistan: An Application of the Gravity Model. The Lahore Journal of Economics, 16, 23-62.
- Crescimanno, M., Galati, A. and Yahiaoui, D. (2013) Determinants of Italian Agri-Food Exports in Non-EU Mediterranean Partner Countries: A Gravity Model Approach. New Medit Journal, 4, 46-54.
- Koh, W. (2013) Brunei Darussalam’s Trade Potential and ASEAN Economic Integration: A Gravity Model Approach. Southeast Asian Journal of Economics, 1, 67-89.
- Hatab, A., Romstad, E. and Huo, X.X. (2010) Determinants of Egyptian Agricultural Exports: A Gravity Model Approach. Modern Economy, 1, 134-143. http://dx.doi.org/10.4236/me.2010.13015
- Abutaleb, A., Taha, E., Hamad, M., Hamdy, M. and Salem, S. (2013) Determinants of Egypt-OIC Countries Trade Flows: System Dynamics Approach. Working Paper, 4th Think Tanks Forum of the OIC Countries, Cairo, 26-27 March 2013, 1-7.
- El-Sayed, M.A. (2012) A Gravity Model Analysis of Egypt’s Trade and Some Economic Blocks. Working Paper, International Conference on Applied Life Sciences, Turkey, 10-12 September 2012, 343-350.
- van Bergeijk, P.A.G., Brakman, S. and Ghosh, S. (2011) The Gravity Model in International Trade. Advances and Applications. Review of International Economics, 19, 979-981. http://dx.doi.org/10.1111/j.1467-9396.2011.01000.x
- Blomqvist, H.C. (2004) Explaining Trade Flows of Singapore. Asian Economic Journal, 18, 25-43. http://dx.doi.org/10.1111/j.1467-8381.2004.00180.x
- Tinbergen, J. (1962) Shaping the World Economy: Suggestions for an International Economic Policy. The Twentieth Century Fund, New York.
- Poyhonen, P. (1963) A Tentative Model for the Volume of Trade between Countries. Weltwirtschaftliches Archive, 90, 93-100.
- Deardorff, V. (1998) Determinants of Bilateral Trade: Does Gravity Work in a Neoclassical World? In: Frankel, J.A., Ed., The Regionalization of the World Economy, University of Chicago for the NBER, Chicago, 7-22.
- Linneman, H. (1966) An Econometric Study of International Trade Flows. Dissertation, Netherlands School of Economics, Amsterdam.
- Leamer, E.E. and Stern, R.M. (1970) Quantitative International Economics. Allyn and Bacon, Boston.
- Anderson, J.E. (1979) A Theoretical Foundation for the Gravity Equation. The American Economic Review, 69, 106- 116.
- Rahman, M. (2010) The Factors Affecting Bangladesh’s Exports: Evidence from the Gravity Model Analysis. Journal of Developing Areas, 44, 229-244. http://dx.doi.org/10.1353/jda.0.0075
- Cortes, M. (2007) Composition of Trade between Australia and Latin America: Gravity Model. Department of Economics, University of Wollongong, Wollongong, Working Paper 07-19.
- Zarzoso, I.M. and Lehmann, F.N. (2003) Augmented Gravity Model: An Empirical Application to Mercosur-European Union Trade Flows. Journal of Applied Economics, 6, 291-316.
- Rahman, M. (2003) A Panel Data Analysis of Bangladesh’s Trade: The Gravity Model Approach. 5th Annual Conference of the European Trade Study Group (ETSG2003), Madrid, 11-13 September 2003, 1-54.
- Abidin, I.Z., Bakar, N. and Sahlan, R. (2013) The Determinants of Exports between Malaysia and the OIC Member Countries: A Gravity Model Approach. Procedia Economics and Finance, 5, 12-19. http://dx.doi.org/10.1016/S2212-5671(13)00004-X
- (2014) World Integrated Trade Solution. https://wits.worldbank.org/
- (2014) United Nations National Accounts Main Aggregates Database. http://unstats.un.org/unsd/snaama/selbasicFast.asp
- (2014) World Development Indicators (WDI) Database of the World Bank. http://databank.worldbank.org/data/home.aspx
- City Distance Calculator. http://www.geobytes.com/citydistance.htm
- Aitken, N.D. (1973) The Effect of the EEC and EFTA on European Trade: A Temporal Cross-Section Analysis. American Economic Review, 63, 881-892.
- Bergstrand, J.H. (1985) The Gravity Equation in International Trade: Some Microeconomic Foundations and Empirical Evidence. The Review of Economics and Statistics, 67, 474-481. http://dx.doi.org/10.2307/1925976
- Matyas, L. (1997) Proper Econometric Specification of the Gravity Model. The World Economy, 20, 363-368. http://dx.doi.org/10.1111/1467-9701.00074
- Grauwe, P. and Skudelny, F. (2000) Inflation and Productivity Differentials in EMU. Working Paper, Center for Economic Studies, No. 0015.
- Glick, R. and Rose, A.K. (2002) Does a Currency Union Affect Trade? The Time Series Evidence. European Economic Review, 46, 1125-1151. http://dx.doi.org/10.1016/S0014-2921(01)00202-1
- Egger, P. and Pfaffermayr, M. (2000) The Proper Econometric Specification of the Gravity Model Equation: A Three Way Model with Bilateral Trade Interaction Effects. Working Paper, Austrian Institute of Economic Research, Vienna.
- Egger, P. (2000) A Note on the Proper Econometric Specification of the Gravity Equation. Economics Letters, 66, 25- 31. http://dx.doi.org/10.1016/S0165-1765(99)00183-4
- Eita, H. (2008) Determinants of Namibian Exports: A Gravity Model. Working Paper, 13th Annual Conference for Econometric Modeling in Africa, University of Pretoria, 9-11 July 2008, 1-23.
- Sichei, M., Erero, J. and Gebreselassie, T. (2005) An Augmented Gravity Model of South Africa’s Exports of Transport Equipments and Machineries. Working Paper, Trade and Uneven Development: Opportunities and Challenges, Glenburn Lodge, 30 November-1 December 2005, 1-26.
- Hadri, K. (2000) Testing for Stationarity in Heterogeneous Panel Data. The Econometrics Journal, 3, 148-161. http://dx.doi.org/10.1111/1368-423X.00043
- Levin, A., Lin, C.F. and Chu, C. (2002) Unit Roots Tests in Panel Data: Asymptotic and Finite Sample Properties. Journal of Econometrics, 108, 1-24. http://dx.doi.org/10.1016/S0304-4076(01)00098-7



