Journal of Applied Mathematics and Physics
Vol.06 No.03(2018), Article ID:83117,22 pages
10.4236/jamp.2018.63046
An Approximate Time-Parallel Method for the Fast and Accurate Computation of Particle Trajectories in a Magnetic Field*
Carl Lederman1, David Bilyeu2
1ERC Inc., Edwards, CA, USA
2Air Force Research Laboratory, Edwards, CA, USA

Copyright © 2018 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: January 26, 2018; Accepted: March 16, 2018; Published: March 19, 2018
ABSTRACT
A temporal multiscale hybridization method is presented that carefully couples coarse scale gyrokinetic models with exact charged particle solution trajectories (that is, with full phase information) in a magnetic field. The approach is based on the careful approximation of a sum, generally employed for time-parallel (TP) computing applications. While the hybridization method presented is highly parallelizable, a computational efficiency gain is seen from considering serial computations only. A complete numerical method is only presented for the aforementioned charged particle application, however, the general approach depicted likely has relevance to a wide swath of challenging multiscale/multiphysics problems. Additionally, the approach has obvious relevance to TP computing applications (such as variable selection on which to perform TP calculations and fine scale sampling strategies).
Keywords:
Hybridization, Time-Parallel, Numerical Methods, Differential Equations

1. Introduction
1.1. Motivation and Objectives
*Distribution A―Approved for public release; distribution unlimited; PA: 16460.
For the modeling of many physical systems, the most detailed and accurate means of simulation may be too computationally expensive, and alternatitve approaches, which provide a less accurate and less detailed solution at a much lower computational cost have been developed. Such model pairs are many, and include fluid equations as an approximation to kinetic equations (such as the Vlasov equation) [1] [2] and complexity reduction techniques for collisional-radiative physics [3] . Construction of approximate solutions, such as these, has been done for eons for some types of problems and includes such approaches as a perturbation analysis of an equilibrium state. More recently, general frameworks for constructing coarse solutions for more challenging types of problems have been developed [4] [5] which are referred to as multiscale methods. The goal of these multiscale methods is to indirectly incorporate information from a fine scale model in a way that produces a good approximation for only the macroscale variables.
Hybridization methods assume that a means of achieving a coarse approximation already exists and aim to use both this coarse approximation and the fine solution, in a more substantial way than multiscale methods, to accurately model both the micro and macro scales. Ideally, the multiscale hybridization should achieve a level of accuracy that is not possible from the coarse model alone at a lower computational cost than what is possible using the fine scale model. Much of the effort in hybridization has been on schemes that switch between coarse and fine propagators in different parts of the space-time domain with a focus on proper interface conditions [2] [6] . However, this needs not be the only way that hybridization is performed, and this manuscript considers a different means of mixing coarse and fine propagators to achieve the goals of accuracy and low computational cost.
In the simplest hybridization case, the coarse and fine propagators act on data that is either the same or trivial to convert. But, for many important cases, there is a nontrival scale difference between the coarse and fine propagators. The hybridization is then referred to as multiscale [7] , and some of the terminology from multiscale methods, which is summarized in Section 1.2, is appropriate even though the desired outcome of applying a multiscale hybridization remains the same as that of a hybridization, i.e. a low cost and accurate simulation.
Time-parallel methods are designed to produce an accurate solution by mixing coarse and fine propagators, but for this type of an approach, it is generally taken as a given that the total computational cost will be higher than simply running the fine scale solution. A “wall clock” speed up is achieved only through parallel computing. The most common type of TP method is the so called Parareal [8] , and variants of Parareal that are designed to work for multiscale problems have been developed [9] [10] [11] .
The method presented here aligns with the goals of a hybridization; there is no parallel computing. But, the reason that TP methods are mentioned in this Section and in more detail in Section 1.4 is that the numerical methods employed to generate the proposed hybridization draw heavily from them. The base equation that is transitioned into a multiscale context is not Parareal, as in [9] [10] [11] [12] , but a related TP equation, and further development is required to improve the “wall clock” speed of the computations as discussed in Section 1.6. Section 1.7 describes the specific physical problem that the proposed hybridization, which we refer to as the hybridization by TP approximation, will be applied to and Section 1.7.4 presents the application details. In Section 3, the accuracy and serial computational cost of the proposed hybridization is compared against the more common temporal hybridization achieved by switching between coarse and fine propagators on the time domain.
1.2. Multiscale Methods Terminology
In general terms, the basic ingredients needed for a multiscale method are 1) the selection of a fine propagator, , which advances fine scale, or microscale, variables u, 2), the selection of a coarse propagator , which advances the coarse, or macroscale, variable U, 3) the selection of a compression operator, Q, to convert data to the macroscale, 4) and the selection of a reconstruction operator, R, which converts data to the microscale [4] . The compression and reconstruction operators satisfy:
(1)
The brackets are often not written for simplicity [4] and this convention is followed with other operators throughout the manuscript as well.
For the current purposes, attention is restricted to differential equations (DEs) of the general form:
(2)
where and . This equation is typically solved sequentially by repeatedly applying a fine propagator :
(3)
for . While the notation of Equation (3) is not standard for serial propagators, the TP equations in Sections 1.4, 1.5, and 1.6 can be written more succinctly in this way. Analogous to Equation (3), on the coarse scale, we have
(4)
It is assumed that the coarse propagator of Equation (4) attempts to model the same general physics as the fine propagator of Equation (3) but with only an approximation of the coarse scale variables. The additional microscale information can be inferred from the macroscale variables and coarse propagator, though it generally cannot be determined with sufficient accuracy. While inaccurate microscale information may not be of interest for multiscale methods, it may be still be accurate enough that it can be corrected using a TP approach [11] . A modified version of U, given by , contains the macroscale information of U along with a poor approximations of the fine scale variable that do not affect the propagation of the macroscale variables. A modified version of the compression and reconstruction operators, and respectively, can be defined in which the reconstruction operator takes the full fine scale variables, u, from the last time it was available as an input:
(5)
It is these modified versions of U, Q, and R that are considered for the remainder of the manuscript. While playing a similar role as the standard general operators employed for multiscale methods, they ensure that microscale information is not lost, and with the inclusion of a TP equation approximation defined through Sections 1.4, 1.5, and 1.6, allow for an accurate modeling of both the macroscale and the microscale.
1.3. Temporal Multiscale Hybridization by Propagator Switching
The degree to which a coarse propagator is appropriate for a given physical simulation can be characterized by considering a coarse propagator suitability function, , where , and and are taken to be equivalent when , and disagree to a larger extent as h increases. A simple type of hybrid solution can then be defined by the multiscale propagator, , which switches between and based on the value of h:
(6)
for . It is implausible in the general case to wait until the physical approximations associated with are exactly met ( ) as the coarse propagator would then likely never be used. A basic consistency criterion for implementing Equation (6) would be to require a set of choices, written succinctly as , to satisfy the following:
(7)
A better criteria for is the set :
(8)
Essentially, the above criterion for this set states that when propagating the coarse variables U, switching to the fine scale and propagating for a negligible amount of time should have a negligible effect on the final solution. Approaches to satisfying this condition, or one like it, have been developed for hybridization schemes [13] .
The simple switching hybrid propagator, , attempts to use the low cost propagator if it will be sufficiently accurate and the higher cost propagator otherwise. Determing the error of relative to directly by evaluating the two types of propagators would negate any computational speed up from this approach, and hence h, which is assumed to be a relatively low cost computation, is used as replacement. In addition to the the sensitivity of on h, another limitation of this type of hybridization is that it relies only on local in time evalutions of the error, i.e. no attempt is made to approximate how an error from the selection of will affect the solution at the end time.
1.4. Time-Parallel Computing Background
TP methods are a means of solving differential equations at a lower “wall clock” time by parallelizing computations in the time domain. They have been applied to surprisingly complicated physics such as plasma turbulence [14] . In this Section, some of the mathematics that underlies TP equations is summarized and two TP equations are highlighted, the standard Parareal equations and an alternative TP equation, that is further modified in Sections 1.5 and 1.6 to derive a temporal multiscale hybridization that serves as an alternative to the simple switching hybridization of Equation (6).
A straightforward characterization of the local in time error of u with respect to a DE of the form in Equation (2), is given by:
(9)
where c and f are similar but not equal. For simplicity, in this section, all equations are written only in terms of the fine variables u. The following Section 1.5 describes the modifications necessary for the multiscale case.
A simple functional, that is always non-negative and 0 when u satisfies Equation (2), is given by:
(10)
where the dot product within the integral is taken over the dimension of u, at every t. The inner product is:
(11)
and the gradient is given explicitly as [15] :
(12)
This gradient can be used to solve a DE in parallel, though the use of other functional gradients produces superior results [16] [17] . One such preferred gradient is derived from an inner product space based on the coarse solution of the differential equation (CDE) at a solution approximation u:
(13)
A formula for the CDE functional gradient is found from comparing the CDE norm and norm.
(14)
A weak form solution of the CDE functional gradient, holding for every , is then given by:
(15)
The finite element method is a natural choice for optimization problems [18] [19] . However, a direct finite element discretization of Equation (15) above would problematic, as it would generate symmetric operators, and this is a hyperbolic problem, in the sense that information should only be propagated forward in time. Finite element methods designed for hyperbolic problems, such as the Discontinuous Galerkin method [18] , may be applicable. But, for the current purposes, a direct strong form solution is found, given by:
(16)
Allowing for the solution to be written in terms of a coarse propagator, (where , where is defined to be a function of the coarse variables U, as in Equation (4)), we have:
(17)
Computation of the CDE gradient can be thought of as a type of propagator itself, as the value is only dependent on computations at previous times, though it is one that need not be computed serially. The functional is locally maximally increased, with respect to the CDE inner product, by advancing the solution u in the direction of the above gradient. Reversing the direction of this propagation and updating u can produce a maximum decrease of the functional . The gradient descent equation, which contains an additional variable , such that should approach the fine solution as is increased, is given by:
(18)
With the propagators taken over discrete steps of size dt, a solution update, , can then be written, for integers , , and , with , , and as:
(19)
The first part of Equation (19), looks at independent, local differences between the current solution u, and the behavior of the fine propagator , and propagates these differences forward in time using the coarse propagator derivative with respect to u. The second part of the equation goes one step further, looking at the differences of the fine propagator derivative and coarse propagator derivative. The second term can significantly add the TP scheme accuracy, [17] , though it adds to the numerical complexity.
Using only the first part of Equation (19) along with the additional approximation that the coarse propagator derivative is computed as:
(20)
leads to the following:
(21)
where the coarse propagator need not be the same as . Convergence can be achieved even when is replaced with a generic operator like a Sobolev Gradient [16] , though a large number of iterations are required. Conversely, replacing with will maximally reduce the solution error but the computing cost will likely be too high in practice.
The standard Parareal equation, denoted , [8] , is the following update in serial after the fine propagator has been applied in parallel on each time interval:
(22)
Both Equations ((21) and (22)) produce similar accuracy in practice, but Equation (22) is more common as it requires fewer applications of the coarse propagator. We refer to [17] for more details. This drawback is not as relevant for the current purposes as the summand will only be sampled and some of the many well established approaches to approximating a sum will be relied upon.
1.5. Time-Parallel Computing with Multiple Scales
Time-Parallel methods that try to incorporate multiscale features generally focus on modifications to Equation (22). A Parareal method that incorporates compression and reconstruction operators into the Parareal equation is presented in [11] . This work explains that a modified reconstruction operator that incorporates fine scale information at a previous time is required for a sensible TP update. In [9] [10] , a very efficient modified Parareal equation is considered for the specific case where the oscillations are linear. And lastly, for the class of problems where the separation of fine and coarse scale variables is unknown, a means of extracting the necessary phase adjustments from both the parallel fine propagators and a sequential propagation alongside the Parareal corrections of Equation (22) is given in [12] .
The serialization of Equation (22) is seen as having an acceptable cost for TP applications due to the lower computational cost of relative to . However, the serialization that is present does not make it immediately clear how to construct an approximation of Equation (22) that does not apply on the entire time domain. In contrast, Equation (21) is simply a sum which can be approximated by a vast and well established number of approaches.
With known modified compression and reconstruction operators, and , respectively, Equation (21) can be altered to account for the fact that propagator only acts on the modified macroscale variables ( ).
(23)
An alternative formulation to Equation (23), which performs the summations with respect to the modified macroscale variables, is given by:
(24)
Equations ((23) and (24)) are only different when and are nonlinear, which is the case for the specific application described in Section 1.7 and many problems of interest. Equation (24) is seen as somewhat preferable, and is the equation implemented for the application given in Sections 1.7 and 2, as the summations are performed in a natural coordinate system for describing the coarse solution, though not the fine. With the modified coarse variables, an approximation that does not run on the entire time domain is constructed more easily and kinetic energy is inherently preserved as discussed in Sections 1.6 and 2.5.
While Equation (24) can offer a considerable improvement in accuracy relative to the simple switching hybridization of Equation (6), on the negative side, the operators and are applied many more times in Equation (24) than Equation (6) which necessitates even more care in their selection. Ideally, the choice for should be in the set:
(25)
(26)
1.6. A Hybridization Approach Derived From Time-Parallel Methodology
The summand of Equation (24) can be written succinctly with the denotation :
(27)
We consider a summand interpolation function I that approximates at an arbitrary . For integers and a mapping from these integers to the time domain, an approximation of Equation (24) is:
(28)
A considerable computational speed up is achieved if I is constructed from functions whose summation is known analytically or can otherwise be easily obtained. A polynomial interpolation function is a standard choice, but is inadequate to describe the complexity of . From Equation (27), it is apparent that the value of is determined from how the propagator differs from the propagator over a single step of size dt and where these evaluations take place. While it is assumed that there is no easy way to characterize the fine propagator, the location where is applied is determined solely by the coarse propagator. Hence, the coarse propagator can inform how the interpolation should be constructed. Section 2 details how this is done along with specific computational strategies including approximation of the sum by an integral and substitution of variables.
A few attempts have been made to bypass performing TP computations over the whole domain, such as the formulation presented in [20] [21] , which incorporates wavelets and only performs TP computation over a beginning portion of the time domain. An approximation of TP terms was also performed in previous work [17] although the time intervals over which this was performed were small enough that simple polynomial interpolation was feasible.
The remaining sections of the manuscript focus on a careful implementation of Equations ((27) and (28)) for the specific application of modeling charged particle trajectories in a magnetic field. The final section of the introduction below, Section 1.7, defines the specific fine propagator , and coarse propagator that will be used. Section 2.1 gives the modified reconstruction operator, and Section 2.2 the modified compression operator . Sections 2.3, 2.4, and 2.5 provide details on how the interpolation and summation of Equation (28) are performed.
Lastly, it is noted that the circumstances under which a stable and accurate solution can be achieved for this general type of approach are a bit more complicated than for standard numerical methods which can be analyzed under the condition that . But from the derivation of Equations ((27) and (28)), it can be seen that reasonable results should be expected if both of the following are true: 1) A pure TP method, with no approximation, can reduce the solution error after one iteration (see [8] [17] for some discussion of TP method convergence) and 2) the approximation of the TP summand can be accurately approximated with the chosen interpolation function. In Section 3.2, some discussion is presented as to how the time parallel approximation differs from an exact TP calculation.
1.7. Particle Trajectories in a Magnetic Field
1.7.1. The Fine Scale Governing ODE
The position and velocity of a charged particle, , in a magnetic field is:
(29)
where, q and m are constants and is the magnetic field. This ODEs will be highly oscillatory, even in the simple case of a constant magnetic field.
1.7.2. The Limitations of Standard Numerical Modeling Techniques
Explicit methods for solving Equation (29) have stability and accuracy limitations that generally restrict the time step size to less than one period of an oscillation [22] . Implicit methods may, in theory, be stable over many periods, but still do not capture the oscillatory nature of the solution with any accuracy. A standard choice for a propagator for Equation (29) is the leapfrog scheme [23] , which, due to its accuracy over only small time scales and full incorporation of the physics, is considered the fine propagator, .
1.7.3. Exponential Propagator
The exponential propagator, , is the exact solution to Equation (29) for the special case when the magnetic field is constant, and the ODE is linear. The scheme can be applied to non-linear magnetic fields by simply recomputing b at each time step. The helical trajectory of this scheme can be described simply by calculating the guiding center:
(30)
and an orthonormal coordinate system defined by the magnetic field:
(31)
In polar coordinates , where the drift direction, is aligned with polar direction, z, ( ), this propagator is then simply:
(32)
One approach to creating a propagator for Cartesian variables , as delineated in [24] , would be through direct expansion and modification of the linear exponential propagator. For the current effort, the coarse propagator is taken to act on only on the coarse scale, or macroscale, variables , and focus is on the careful construction of the compression and reconstruction operators as discussed in Sections 2.1 and 2.2 below. If only the propagation of U is considered, then the propagator is simply the exact solution to the following linear ODE:
(33)
The robustness of the exponential propagator, , is dependent on the degree of non-linearity present in the magnetic field, in contrast to more standard propagators like the leapfrog scheme, , whose stability and accuracy is mostly dependent on the time step size, which will be limited even in the case of a constant magnetic field. Higher fidelity models for when the magnetic field is non-linear, though models that still neglect the fine scale features of the true rapidly oscillating particle trajectories, i.e. gyrokinetic models, can be employed for more accurate propagation of the coarse scale solution.
1.7.4. Gyrokinetic Models
Gyrokinetics generally refers to a means of solving for a charged particle’s trajectory in a magnetic field that neglects the precise modeling of the particle’s rapid orbits, and hence, avoids the time step size limitations of a direct implementation of Equation (29). Rather than modeling the true particle position , only the guiding center, is solved for. As the guiding center does not oscillate in the magnetic field in the way that an actual particle would, the time step size limitations are alleviated. This approach is particularly suitable when the magnetic field is strong and nearly constant, and the gyro radius, , is small. The coarse propagator suitability function, h, is given by [25] :
(34)
A gyrokinetic approximation is suitable for small values of h. A gyrokinetic model in terms of the guiding center, , and the drift velocity , and the phase angle, is given by [25] :
(35)
That Equation (35) only approximates Equation (29) is most apparent from the fact that the b calculations are made non-locally, at rather than at the true particle location x. This is indicative of the need for a sampling of the fine propagation at the true solution location for improved accuracy. It is also noted that additional well established terms can be added to this ODE including time variation in the EM field and additional applied forces [25] .
The propagator that solves the DE of Equation (35) is referred to as the coarse propagator, , and it does not suffer from the fine scale limitations described in Section 1.7.2. A standard high order time stepping scheme (RK4) is implemented for propagating the macroscale variables .
2. Numerical Methods
2.1. Reconstruction Operator
As described in Section 1, the fine scale variables, , are simply the particle position and velocity in three dimensional space, and the coarse scale variables are , that is, the three position coordinates of the guiding center and the drift velocity. In order to facilitate the transition between u and U, auxiliary variables of the coarse scale are defined that are derived from U. Importantly, these auxiliary variables should not affect the propagation of U, as this could potentially introduce fine scale effects and adversely affect the capability for to propagate with large time scales.
For a static magnetic field, the kinetic energy, , is simply:
(36)
where is the radial velocity,
(37)
The phase angle , can be approximated from the radial acceleration implied in Equation (35) (with the assumption that the second derivative in time of is much smaller than , which is consistent with Equation (34)):
(38)
The modified macroscale variables can then be defined as . Though phase information is now included, is very easily off by half a rotation or more and reliable information about the phase can only be achieved by incorporating adjustments from the fine propagation.
The remaining auxiliary variables are given by the polar variables, and can be calculated on the fly only when a reconstruction is needed:
(39)
Computation of these auxiliary variables need not be performed until a reconstruction is needed. When a reconstruction is called for, these polar coordinates need to be paired with a coordinate system (as well as a guiding center, but this is propagated as a part of ). Unlike the case of the linear propagator described in Section 1.7.3, the coordinate system cannot be considered fixed and is written as . While , can be computed on the fly, and rely on , which, after the gyrokinetic propagation, is no longer known. A solution is to remember the coordinate system at its last known time (assumed to be ) and merge it to what is known about the coordinate system at the current time, which is . This is achieved by rotation matrix M, which rotates the other two coordinates based on the rotation of :
(40)
With the guiding center, , the orthonormal coordinate system, , and polar coordinate variables, , established, the conversion to real coordinates is then simply achieved by an inverse polar transform :
(41)
2.2. Compression Operator
If the guiding center only needed to be found a single time, a reasonable choice would be to use Equation (30). However, a guiding center exactly consistent with polar coordinates of Equations (37)-(39) is given by:
(42)
All of the computations are based on magnetic field evaluations at , which is known to the coarse propagator, to allow for a seamless transition between coarse and fine scales. While does need to be solved for, via Newton’s Method, a very good initial guess is given by Equation (30), which can also be differentiated in place of Equation (42).
The compression operator is then simply:
(43)
A simpler compression than the one given by Equations ((43) and (42)) results in error accumulation from just the variable transformations which can degrade the accuracy of the overall time-parallel approximation hybrid approach.
2.3. Time Substitution
The summand of Equation (27) oscillates nonlinearly in time. In order to allow for a simple interpolation of the summand, a substitution is drawn upon from the coarse solution geometry:
(44)
This substitution is inserted directly into the coarse and fine propagators. This makes the non-linear oscillations of the integrand linear, and allows for interpolation of the summand, radially around the guiding center and along its length, by standard techniques. The substitution is derived from the initial coarse propagator and fixed for all computations, allowing for the TP approximation to still compute adjustments related to the phase angle.
2.4. Spline Solution Representation
A coarse solution is used as an initial guess on which the TP approximation improves. In order to allow the TP summand to be easily and accurately evaluated at any , a spline (cubic Hermite) representation of the initial coarse solution is constructed.
(45)
A splines interpolation was chosen for its robustness and ease of implementation [26] . It avoids known problems that can arise from other types of interpolation such as Runge’s phenomenon.
2.5. Approximation of the TP Sum
In order to keep the integration as simple as possible, the TP sum is approximated from 0 to , where H is an even number. Points of TP summand are to be evaluated at the 15 locations given by where and .
(46)
Inceasing the number of points in the temporal domain where D is evaluated should increase the accuracy of subsequent interpolation. The number of points is chosen to be as small as possible while still large enough as to not add significant error to the overall method.
This evaluation is the most computationally intensive part of the algorithm, consisting of 15 compressions, fine propagations, and expansions and 30 coarse propagations. Two propagations of can likely be replaced with a single propagation of the derivative of with respect to , [17] , though this potential computational improvement adds another layer of complexity and remains future work. And, while it is not factored into the results of Section 3, the computation of D is, of course, trivial to parallelize.
The basis , is composed of second order polynomial and sinusoidal components.
(47)
The time parallel approximation is then given by:
(48)
While an analytical sum of is possible, an integral which approximates the sum with sufficient accuracy is less intensive computationally. The overall algorithm for obtaining is summarized in Algorithm 1.
3. Results and Interpretation
3.1. Example Problems
The first simulation is of a charged particle, trapped in a magnetic mirror, given by:
(49)
The other example is of a charge particle near a magnetic dipole (a common type of magnetic field in nature) with fixed magnetic moment vector m,
(50)
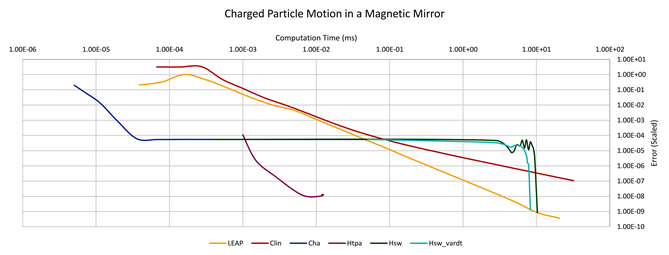
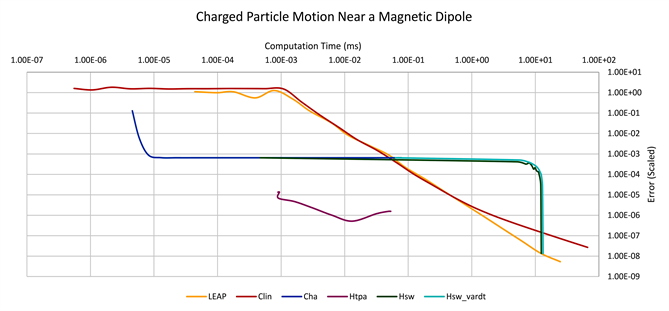
Particle trajectories for these examples are shown in Figure 1. Simulations were performed using 6 different schemes for both examples to assess accuracy and computation time (Figure 2). The simple switching hybrid method is more appropriate when the coarse propagator suitability function, , varies over several orders of magnitude; these conditions were present only for the magnetic mirror. For this example, there is a large area around the center of the magnetic mirror ( near 0) where the magnetic field is nearly constant as can be seen from Equation (49). In this area, should be a good approximation while the fine propagator, will be switched to automatically near the edges of the magnetic mirror where the field is more nonlinear.
For the simple switching hybrid propagator, , the parameter was varied from , where only the fine propagator is run, to , where K is sufficiently large to ensure all coarse propagation, to generate different accuracy/ efficiency tradeoffs. We also considered a slight variant of the simple switching hybrid method that adjusted the time step size to ensure that a coarse propagation was performed over an integer number of rotations ( ). This was done to present the best possible results as some of the error accumulated over one rotation cancels out when a rotation is complete. For the other methods, the time step size was varied. The accuracy was compared against a highly accurate “silver standard” solution and scaled based on the change in the silver standard solution over the course of the simulation. Additionally, Figure 3 presents the error of the coarse gyrokinetic solution in comparison to a highly computationally expensive exact TP and the low computational cost TP approximation.
3.2. Scheme Performance
3.2.1. Coarse Propagator Performance
The coarse gyrokinetic propagator ( , the blue line in Figure 2 and Figure 4)
Figure 1. The trajectory of a charged particle in a magnetic field is shown for a magnetic mirror (top) and for a particle near a magnetic dipole (bottom). Simulations were performed using 6 different schemes for both examples to assess accuracy and computation time.
Figure 2. Computation time was compared against error for a magnetic mirror simulation (top) and magnetic dipole simulation (bottom). The leapfrog scheme (F, orange) and exponential propagator (Lexp, red) achieved high accuracy at a relatively high computational cost. The coarse gyrokinetic propagator (C, blue) with compression and reconstruction operators, achieved moderate accuracy at a low computational cost, but possessed a hard limit on its accuracy regardless of the time step size/computational cost. The simple switching hybrid propagator (Hsw, green) and TP approximation (Htpa, purple) both attempted to bridge the divide between the coarse (C) and fine (F) propagators. The switching hybrid propagator was also run with a variable time step size (Hsw_vardt, cyan) to reduce error, though this had a limited effect. The same simple and direct code for the coarse and fine propagators was shared amongst all schemes. No parallel computing was deployed.
with modified compression and reconstruction operators, which receives and returns microscale variables , achieved moderate accuracy at a low computational cost, but possessed a hard limit on its accuracy regardless of the time step size/computational cost. As discussed in Section 1.7.4, the guiding center model does not resolve the fine scale features of the true rotating particle and does not converge to a solution of Equation (29).
3.2.2. Switching Hybrid Propagator Performance
This magnetic mirror simulation seems, at least at first glance, very suitable to a
Figure 3. The accumulated error in both x (top) and v (bottom) is plotted for the magnetic mirror simulation (left) and dipole simulation (right) over a single time step. (The plots in Figure 1 and data in Figure 2 are performed over longer time intervals.) The error in the gyrokinetic solution is plotted in blue (- ), a highly computationally expensive exact TP update is plotted in red (- ), and the low computational cost TP approximation is marked with purple crosses (´ ).
simple switching hybrid implementation ( , green line in Figure 2 and Figure 4), given by Equation (6), as the coarse propagator suitability function, h, varies over several orders of magnitude. The magnetic field becomes nearly constant at the mirror’s center while being more challenging toward its edges.
The simple switching hybrid propagator produced “oscillations” as seen in Figure 2 and Figure 4 which signify that running more often and less often can result in more error depending on the phase angle change associated with a coarse step size. The simple switching hybrid propagator with a variable time step size ( , the cyan line in Figure 2 and Figure 4) did manage to damp out these “oscillations” by choosing a coarse step size that resulted in an integer number of rotations. Even this result does not produce strictly decreasing error with increased computational cost, on a small scale, for the magnetic mirror example as a result of h not being an exact measure of the difference between and . On a larger scale, the two types of simple switching hybridizations produce similar overall results; the green and cyan curves in Figure 2 and Figure 4 equate to either the coarse or fine solutions at their end points and in between the curves bow strongly to the upper right indicating a long period of increasing computational cost without a substantial reduction in error. This is an undesirable result for a hybridization.
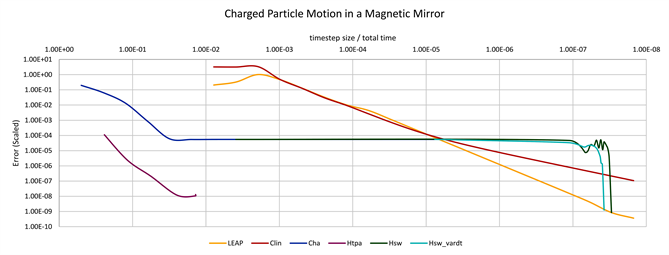
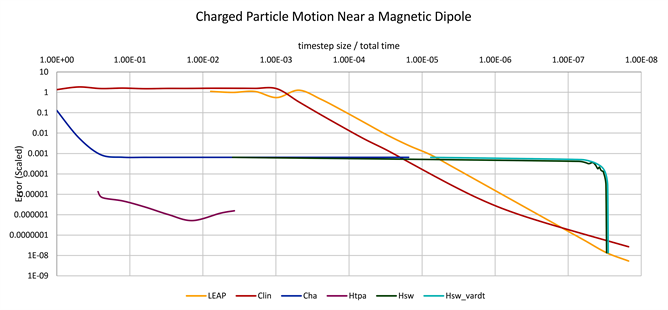
3.2.3. Time-Parallel Sum Approximation Performance
In both examples, the hybridization by TP sum approximation ( , purple
Figure 4. The timestep size is plotted versus error for a magnetic mirror simulation (top) and magnetic dipole simulation (bottom). The timestep axis is flipped to enable a comparison with Figure 2, and for the TP approximation scheme (Htpa,purple) the timestep size refers to the coarse scale on which an entire TP update is performed. The data from this figure is similar to Figure 2 for most of the schemes presented (F,(fine),orange; Lexp,(exponential propagator),red; C,(coarse),blue; Hsw,(simple switching hybrid),green; Hsw_vardt,(simple switching hybrid with a variable time step size),cyan), though it is more clear in this figure that Htpa is being shifted downward (corresponding to error reduction) from the high accuracy coarse propagator (C,blue). The shape of Htpa and C is qualitatively similar when accounting for this shift, though the presence of other, smaller, sources of error in the TP approximation (see Sections 2.5 and 3.2.3) are present.
line in Figure 2 and Figure 4) does seem to be able to achieve a result that is distinct from either the coarse or fine solutions from which it is composed. It offers a solution that is both more accurate than the coarse propagator is capable of achieving at any computational cost while being less computationally costly than the fine for the accuracy achieved (Figure 2). In Figure 4, it can be observed that the TP approximation, for a particular time step size, reduces the error from the high accuracy coarse gyrokinetic propagator on which it is based. The error introduced from the interpolation and integration steps of Section 2.5 should be small in comparison to the error introduced from the coarse and fine propagators. Determining if a significant error is being introduced in this way is simply a matter of comparing to an exact sum, if feasible, or a higher order version of the basis for interpolating the summand, .
4. Conclusions
Overcoming the incongruities present between two computational models of different scales to develop an efficient temporal multiscale hybridization is a challenging problem. But a means to accomplish this was presented, for the specific case of modeling particle trajectories in a magnetic field, by borrowing a key equation from time-parallel computing methods and encompassing it in a suitable multiscale framework. A primary limitation of this approach is the great care that is required when converting between the microscale and macroscale variables to ensure that the error resulting from this conversion is sufficiently small. An additional limitation is that the solution must be stored at a few previous time points, rather than only the current time, though the number of time locations at which the solution must be found is greatly reduced from what is needed in pure TP applications. But the improvement in performance, in terms of both accuracy and computational cost, in comparison to more established multiscale hybridization methods, such as switching back and forth between fine and coarse scale propagators based on the suitability of a coarse model, is substantial. The proposed approach is capable of generating a particle trajectory with accuracy on par with the fine propagator at a computational cost more akin to the pure coarse propagation.
Future work will hopefully extend the general multiscale hybridization approach described here to more challenging areas of study. While the TP sum approximation performs as expected for the charged particle trajectory examples presented, each type of hybridization problem has its own unique challenges, and the generality of this approach remains to be seen. In particular, this approach requires more stringent conditions for the compression and reconstruction operators than typical hybrid approaches, as well as a means of transforming the TP sum to something computationally tractable, akin to the substitution of the time variable presented here. These additional development steps may be justified for other multiscale/multiphysics problems in order to achieve quality results on par with those presented here.
Fund
Air Force Office of Scientific Research Grant Number 17RQCOR463.
Cite this paper
Lederman, C. and Bilyeu, D. (2018) An Approximate Time-Parallel Method for the Fast and Accurate Computation of Particle Trajectories in a Magnetic Field. Journal of Applied Mathematics and Physics, 6, 498-519. https://doi.org/10.4236/jamp.2018.63046
References
- 1. Bardos, C., Golse, F. and Levermore, D. (1991) Fluid Dynamic Limits of the Kinetic Equations. Journal of Statistical Physics, 63, 323-344. https://doi.org/10.1007/BF01026608
- 2. Alaia, A. and Puppo, G. (2012) A Hybrid Method for Hydrodynamic-Kinetic Flow Part II Coupling of Hydrodynamic and Kinetic Models. Journal of Computational Physics, 231, 5217-5242. https://doi.org/10.1016/j.jcp.2012.02.022
- 3. Le, H., Karagozian, A. and Cambier, J.-L. (2013) Complexity Reduction of Collisional-Radiative Kinetics for Atomic Plasma. Physics of Plasmas, 20, Article ID: 123304.
- 4. Engquist, B., Li, X., Ren, W. and Vanden-Eijnden, E. (2007) Heterogeneous Multiscale Methods: A Review. Communications in Computational Physics, 2, 367-450.
- 5. Kevrekidis, I. (2003) Equation-Free, Coarse-Grained Multiscale Computation: Enabling Microscopic Simulators to Perform System-Level Analysis. Communications in Mathematical Sciences, 1, 715-762.
- 6. Tiwari, S. (1998) Coupling of the Boltzmann and Euler Equations with Automatic Domain Decomposition. Journal of Computational Physics, 144, 710-726. https://doi.org/10.1006/jcph.1998.6011
- 7. Degond, P., Dimarco, G. and Mieussens, L. (2010) A Multiscale Kinetic-Fluid Solver with Dynamic Localization of Kinetic Effects. Journal of Computational Physics, 229, 4907-4933. https://doi.org/10.1016/j.jcp.2010.03.009
- 8. Lions, J.-L., Maday, Y. and Turinici, G. (2001) A “Parareal” in Time Discretization of Pde’s. Comptes Rendus del Academie des Sciences Series I Mathematics, 332, 661-668.
- 9. Castella, F., Chartier, P. and Faou, E. (2009) An Averaging Technique for Highly Oscillatory Hamiltonian Problems. SIAM Journal on Numerical Analysis, 47, 2808-2837. https://doi.org/10.1137/080715974
- 10. Haut, T. and Wingate, B. (2014) An Asymptotic Parallel-in-Time Method for Highly Oscillatory Pdes. SIAM Journal on Scientific Computing, 36, A693-A713. https://doi.org/10.1137/130914577
- 11. Legoll, F., Lelievre, T. and Samaey, G. (2013) A Micro-Macro Parareal Algorithm: Application to Singularly Perturbed Ordinary Differential Equations. SIAM Journal on Scientific Computing, 35, A1951-A1986. https://doi.org/10.1137/120872681
- 12. Ariel, G., Kim, S.J. and Tsai, R. (2016) Parareal Multiscale Methods for Highly Oscillatory Dynamical Systems. SIAM Journal on Scientific Computing, 38, A3540-A3564. https://doi.org/10.1137/15M1011044
- 13. Dimarco, G., Mieussens, L. and Rispoli, V. (2014) An Asymptotic Preserving Automatic Domain Decompostion Method for the Vlasov-Poisson-Bgk System with Applications to Plasmas. Journal of Computational Physics, 274, 122-139.
- 14. Samaddar, D., Newman, D. and Sanchez, R. (2010) Parallelization in Time of Numerical Simulations of Fully-Developed Plasma Turbulence using the Parareal Algorithm. Journal of Computational Physics, 229, 6558-6573. https://doi.org/10.1016/j.jcp.2010.05.012
- 15. Fox, C. (1950) An Introduction to the Calculus of Varations. Courier Corporation, North Chelmsford.
- 16. Mujeeb, D., Neuberger, J. and Sial, S. (2008) Recursive form of Sobolev Gradient Method for Odes on Long Intervals. International Journal of Computer Mathematics, 85, 1727-1740. https://doi.org/10.1080/00207160701558465
- 17. Lederman, C., Martin, R. and Cambier, J.-L. (2016) Time-Parallel Solutions to Differential Equations via Functional Optimization. Computational & Applied Mathematics, 37, 27-51.
- 18. Johnson, C. (2012) Numerical Solution of Partial Differential Equations by the Finite Element Method. Courier Corporation, North Chelmsford.
- 19. Lederman, C., Joshi, A., Dinov, I., Van Horn, J.D., Vese, L. and Toga, A. (2016) A Unified Variational Volume Registration Method Based on Automatically Learned Brain Structures. Journal of Mathematical Imaging and Vision, 55, 179-198. https://doi.org/10.1007/s10851-015-0604-x
- 20. Frantziskonis, G., Muralidharan, K., Deymier, S.S., Nukala, P. and Pannala, S. (2009) Time-Parallel Multiscale/Multiphysics Framework. Journal of Computational Physics, 228, 8085-8092. https://doi.org/10.1016/j.jcp.2009.07.035
- 21. Frantziskonis, G. and Deymier, P. (2003) Wavelet-Based Spatial and Temporal Multiscaling: Bridging the Atomistic and Continuum Space and Time Scales. Physical Review B, 68, Article ID: 024105. https://doi.org/10.1103/PhysRevB.68.024105
- 22. Strikwerda, J. (2004) Finite Difference Schemes and Partial Differential Equations. 2nd Edition, SIAM, Philadelphia.
- 23. Tskhakaya, D., Matyash, K., Schneider, R. and Taccogna, F. (2007) The Particle-in-Cell Method. Contributions to Plasma Physics, 47, 563-594. https://doi.org/10.1002/ctpp.200710072
- 24. Cambier, J. and Batishchev, O. (2007) Particle Motion Algorithm for Arbitrary Gyro-Frequencies. Tech. Rep. AFRL-RZ-ED-TP-2007-431.
- 25. Bittencourt, J. (2003) Fundamentals of Plasma Physics. 3rd Edition, Springer, Berlin.
- 26. De Boor, C. (1978) A Practical Guide to Splines. Springer-Verlag, New York, 27. https://doi.org/10.1007/978-1-4612-6333-3
Appendix